מבוא: המעבר ממשתנים רציפים למשתנים קטגוריאליים
עד כה התמקדנו בעיקר בהיסק סטטיסטי עבור משתנים רציפים. כל מה שעשינו היה מבוסס על בדיקת השערות לגבי התוחלת - רווחי סמך לתוחלת או לפרופורציה (שהיא בעצמה תוחלת), ובדיקת השערות על התוחלת. התשתית התיאורטית התבססה בעיקר על משפט הגבול המרכזי וקירובים נורמליים, או על התפלגות $t$ שמאפייניה דומים לנורמלית אך עם זנבות כבדים יותר.
אנחנו עוברים כעת לעולם שונה לחלוטין - עולם המשתנים הקטגוריאליים, שבו נתמודד עם נתונים מסוג “כן/לא”, “זכר/נקבה”, “חולה/לא חולה”, ועוד בחירות מדידות.
סוגי משתנים קטגוריאליים
משתנים דיכוטומיים (בינאריים)
משתנים דיכוטומיים מקבלים רק שני ערכים אפשריים:
- מין: זכר/נקבה
- מצב מחלה: חולה/לא חולה
- עישון: מעשן/לא מעשן
- צד: ימני/שמאלי
- הצלחה/כישלון בטיפול רפואי
משתנים קטגוריאליים רב-ערכיים
משתנים בעלי יותר משתי קטגוריות:
- דרגת שביעות רצון (נפוצה במחקרים פסיכולוגיים): סולם 5-1
- רמת השכלה: יסודי/תיכוני/אוניברסיטאי
- סוג דם: A/B/AB/O
- צבע עיניים: חום/כחול/ירוק
- עיר מגורים
יצירת משתנים קטגוריאליים ממשתנים כמותיים
ניתן להמיר משתנים כמותיים למשתנים קטגוריאליים באמצעות קביעת ספי חתך (binning):
- גיל: 18-0, 35-18, 65-36, מעל 65
- BMI (מדד מסת גוף): תת-משקל, משקל תקין, עודף משקל, השמנה
- לחץ דם: נמוך, תקין, גבוה
ההמרה הזאת נפוצה במחקרים אפידמיולוגיים ובסקרים.
טבלאות שכיחויות (Contingency Tables)
עקרון ההצגה
במקום להציג נתונים בתור רשימה ארוכה של תצפיות בודדות (למשל: “גבר מעשן, אישה לא מעשנת, גבר לא מעשן…”), אנו יכולים להציג את המידע בצורה תמציתית יותר באמצעות טבלת שכיחויות משותפת.
דוגמה: קשר בין השכלה לבין עישון
נניח שאספנו נתונים על 20 משתתפים בנוגע לרמת השכלתם ומצב העישון שלהם:
| השכלה | לא מעשן | מעשן | סה”כ |
|---|---|---|---|
| יסודי | $2$ | $2$ | $4$ |
| תיכוני | $5$ | $3$ | $8$ |
| אוניברסיטה | $6$ | $2$ | $8$ |
| סה”כ | $13$ | $7$ | $20$ |
ניתן להוסיף גם את האחוזים מתוך סך כל הדגימות:
- מעשנים: $\frac{7}{20} = 35\%$
- לא מעשנים: $\frac{13}{20} = 65\%$
- בעלי השכלה יסודית: $\frac{4}{20} = 20\%$
- בעלי השכלה תיכונית: $\frac{8}{20} = 40\%$
- בעלי השכלה אוניברסיטאית: $\frac{8}{20} = 40\%$
כאשר מסתכלים על האחוזים בתוך כל קטגוריית השכלה:
| השכלה | לא מעשן | מעשן | סה”כ |
|---|---|---|---|
| יסודי | $2\ (15\%)$ | $2\ (29\%)$ | $4$ |
| תיכוני | $5\ (39\%)$ | $3\ (43\%)$ | $8$ |
| אוניברסיטה | $6\ (46\%)$ | $2\ (28\%)$ | $8$ |
| סה”כ | $13$ | $7$ | $20$ |
הצגה גרפית של נתונים קטגוריאליים
דרכי הצגה מומלצות
- גרף עמודות מקובץ - מאפשר השוואה ישירה ונוחה בין קטגוריות
- דיאגרמת עוגה - מתאימה להדגשת פרופורציות יחסיות
דרכי הצגה בעייתיות
גרף עמודות מצטבר - אמנם נפוץ, אך מאוד לא מומלץ לצרכי השוואה (לא לצרף לעבודות שלנו). קשה מאוד לקוח במבט להבחין בין הבדלים קטנים כאשר העמודות בנויות זו על זו. למשל, ההבדל בין 5 ל-3 יחידות עלול להיראות זניח כאשר הם מוצגים כחלקים בעמודה מצטברת.
הצורך במבחן חדש: מבחן $\chi^2$ (כִי בָּרִבּוּעַ)
במצגות ובהרצה המרצה כתב ״חי בריבוע״, לדעתי זה יכול לבלבל. מקור השם הוא באות היוונית $\chi$ (chi).
הבעיה עם מבחנים קודמים
כל המבחנים שלמדנו עד כה - מבחני $z$, מבחני $t$, מבחנים מזווגים ולא מזווגים - התמקדו בבדיקת השערות על התוחלת של משתנים רציפים. עבור משתנים קטגוריאליים, המושג “ממוצע” לא רלוונטי במובן הרגיל.
מה נרצה לבדוק?
בטבלת השכיחויות לעיל, נראה שקיים על פניו קשר בין רמת השכלה למצב עישון - בקרב בעלי השכלה אוניברסיטאית יש יותר לא מעשנים יחסית, ואילו בקרב בעלי השכלה יסודית האחוזים דומים יותר. נרצה מדד מספרי לחוזק הקשר ומבחן סטטיסטי שיקבע האם הקשר מובהק סטטיסטית.
מבחן $\chi^2$ של פירסון
דוגמה: קשר בין מין לקוצר ראייה
נדגום 100 גברים ו-100 נשים ונבדוק את שכיחות קוצר הראייה:
| קוצר ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 75 | 25 | 100 |
| נשים | 60 | 40 | 100 |
| סה”כ | 135 | 65 | 200 |
נרצה לדעת: האם התוצאה הזו מובהקת סטטיסטית?
ניסוח השערות
כמו בכל בדיקת השערות שלמדנו, נתחיל בניסוח השערות:
- השערת האפס ($H_0$): אין קשר בין מין לקוצר ראייה (אי-תלות)
- השערה אלטרנטיבית ($H_1$): קיים קשר בין מין לקוצר ראייה (תלות)
השערת האפס היא תמיד השערת ה”כלום” - אין שום דבר, אין קשר, אין תלות. באנגלית קוראים לה “null hypothesis”, כשמילה “null” משמעותה “אפס”, “כלום”.
חישוב ערכים צפויים תחת השערת האפס
תחת השערת האפס, אנחנו מניחים שהערכים בשוליים של הטבלה נתונים (100 גברים, 100 נשים, 135 עם קוצר ראייה, 65 עם ראייה תקינה), ושהקשר בין השורות והעמודות נקבע לפי כלל הכפל להסתברויות בלתי מותנות (independent probabilities).
חישוב אחוזי השוליים
- גברים: $\frac{100}{200} = 50\%$
- נשים: $\frac{100}{200} = 50\%$
- קוצר ראייה: $\frac{135}{200} = 67.5\%$
- ראייה תקינה: $\frac{65}{200} = 32.5\%$
חישוב ערכים צפויים לפי כלל הכפל
תחת הנחת אי-תלות, הסיכוי להיות גם גבר וגם בעל קוצר ראייה הוא מכפלת הסיכויים:
\[P(\text{Male and Myopia}) = P(\text{Male}) \times P(\text{Myopia}) = 0.5 \times 0.675 = 0.3375\]מספר הגברים הצפוי עם קוצר ראייה:
\[E_{11} = 200 \times 0.3375 = 67.5\]באופן דומה עבור יתר התאים:
- גברים עם ראייה תקינה: $E_{12} = 200 \times 0.5 \times 0.325 = 32.5$
- נשים עם קוצר ראייה: $E_{21} = 200 \times 0.5 \times 0.675 = 67.5$
- נשים עם ראייה תקינה: $E_{22} = 200 \times 0.5 \times 0.325 = 32.5$
| קוצר ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 67.5 | 32.5 | 100 |
| נשים | 67.5 | 32.5 | 100 |
| סה”כ | 135 | 65 | 200 |
נוסחה כללית לערך צפוי
\[E_{ij} = \frac{\text{Row } i \text{ total} \times \text{Column } j \text{ total}}{\text{Grand total}}\]התובנה לגבי דרגות החופש
שימו לב: ברגע שחישבנו $E_{11} = 67.5$, והערך של סך השורה קבוע (100), אז $E_{12}$ כבר נקבע אוטומטית: $E_{12} = 100 - 67.5 = 32.5$. באותה צורה, אם אנו יודעים את מספר האנשים עם קוצר ראייה (135), אנו יודעים גם את מספר האנשים עם ראייה תקינה.
מסקנה: ערך אחד בלבד יכול להשלים את כל הטבלה. לכן, לטבלה זו יש דרגת חופש אחת.
הגדרת הסטטיסטי $\chi^2$
הסטטיסטי כי בריבוע מוגדר כ:
\[\boxed{ \chi^2 = \sum_{\text{all cells}} \frac{(\text{Observed} - \text{Expected})^2}{\text{Expected}} = \sum_{i,j} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}}\]כאשר:
- $O_{ij}$ = הערך הנצפה (Observed) בתא $(i,j)$
- $E_{ij}$ = הערך הצפוי (Expected) בתא $(i,j)$
חישוב עבור הדוגמה שלנו
הערכים שנמדדו:
| קוצר ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 75 | 25 | 100 |
| נשים | 60 | 40 | 100 |
| סה”כ | 135 | 65 | 200 |
הערכים הצפויים:
| קוצר ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 67.5 | 32.5 | 100 |
| נשים | 67.5 | 32.5 | 100 |
| סה”כ | 135 | 65 | 200 |
התפלגות $\chi^2$
הגדרה תיאורטית
אם $Z_1, Z_2, \ldots, Z_k$ הם משתנים מקריים נורמליים סטנדרטיים עצמאיים, אז אומרים שהמשתנה המקרי:
\[X = Z_1^2 + Z_2^2 + \cdots + Z_k^2\]מתפלג לפי התפלגות $\chi^2$ עם $k$ דרגות חופש, ומסמנים ב-$\chi^2(k)$.
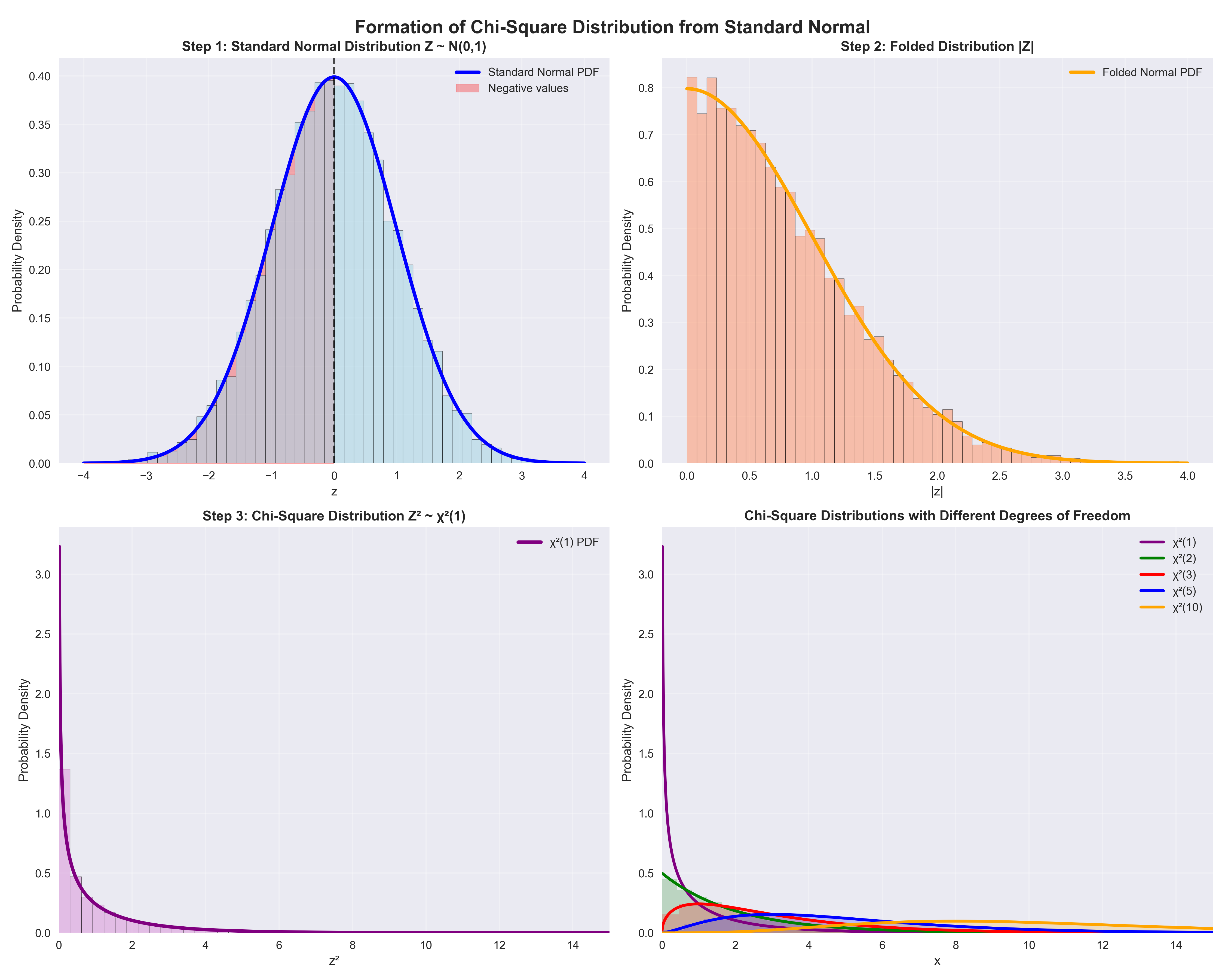
אינטואיציה גיאומטרית
ניתן לחשוב על התפלגות $\chi^2$ כתוצאה של שני שלבים שמפעילים על התפלגות נורמלית:
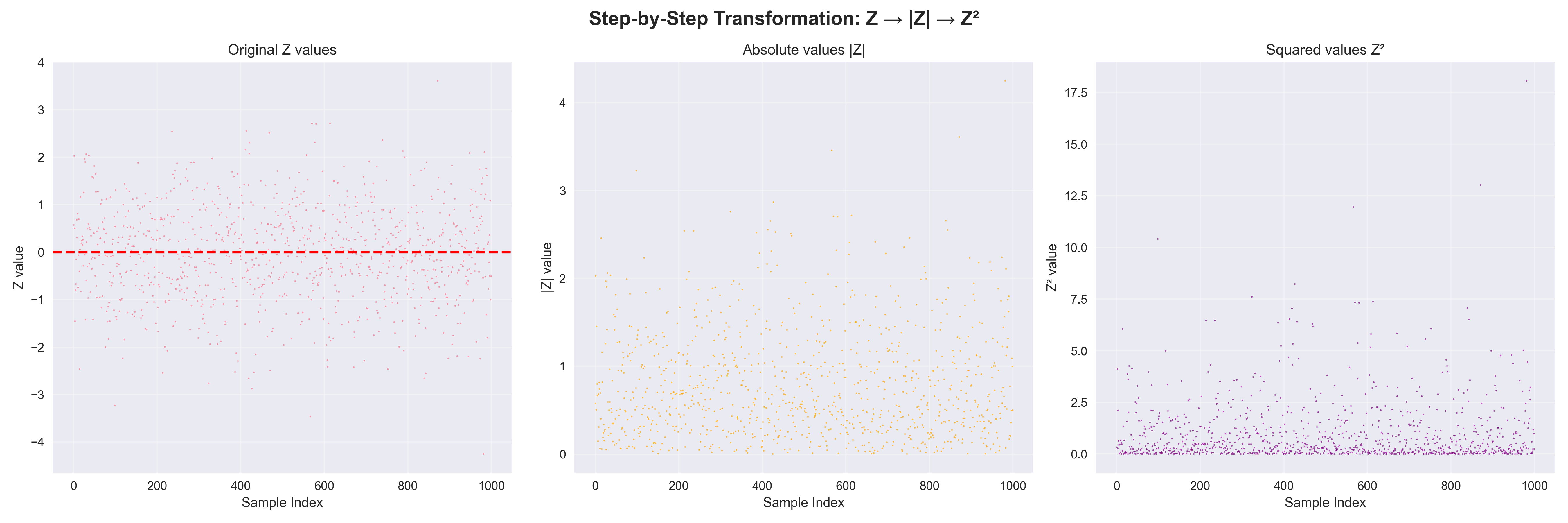
- קיפול: אם יש לנו משתנה נורמלי סטנדרטי (עקומת הפעמון הסימטרית), ואנחנו “מקפלים” אותה סביב הציר האנכי - כל הערכים השליליים מקופלים על החיוביים
- העלאה בריבוע: לאחר מכן מעלים את הערכים בריבוע
התוצאה היא התפלגות חיובית בלבד, עם זנב ארוך וצורה אסימטרית.
 |  |
|---|---|
| דמיון | שלבים |
הקשר להתפלגות נורמלית במקרה $k=1$
במקרה של דרגת חופש אחת, אם $Z \sim \mathcal{N}(0,1)$, אז $Z^2 \sim \chi^2(1)$.
זה מסביר מדוע הערך הקריטי עבור $\alpha = 0.05$ בהתפלגות $\chi^2$ עם דרגת חופש אחת הוא:
\[1.96^2 = 3.84\]שכן אנחנו יודעים ש-$P(\vert Z\vert > 1.96) = 0.05$ עבור משתנה נורמלי סטנדרטי, ולכן $P(Z^2 > 3.84) = 0.05$.
חישוב ה-P-Value
אנו מחפשים את ההסתברות לקבל ערך קיצוני יותר מהערך שראינו. במקרה של התפלגות $\chi^2$, “קיצוני יותר” משמעו “גדול יותר”, מכיוון שהמקרה הכי ״רגיל״ (לא קיצוני) הוא כאשר $\text{Observed} = \text{Expected}$ בכל התאים, ואז $\chi^2 = 0$.
\[\text{P-value} = P(\chi^2(1) > 5.12)\]באמצעות פונקציית הזנב הימני (complement of CDF) של התפלגות $\chi^2$,:
import scipy.stats as stats
print(stats.chi2(df=1).sf(5.12))# Output: 0.0236
קבלת החלטה
מכיוון ש-$0.0236 < 0.05$, אנחנו דוחים את השערת האפס ומסיקים שקיים קשר מובהק סטטיסטית בין מין לבין קוצר ראייה.
הערה חשובה לגבי פרשנות: המבחן הסטטיסטי מזהה קשר, אך לא מוכיח סיבתיות. מכיוון שברור שקוצר ראייה לא יכול לגרום למישהו להיות גבר או אישה, אנו יכולים להסיק שמין הוא גורם הסיכון לקוצר ראייה במקרה זה.
הערה על מבחן פרופורציות
שימו לב שהצורה הטיפוסית של המבחן היא:
- $p_1$: אחוז החשופים שחלו
- $p_2$: אחוז הלא-חשופים שחלו
- השערת האפס: $p_1 = p_2$
- השערת המחקר: $p_1 \neq p_2$
במקרה של טבלה 2×2, מבחן $\chi^2$ ומבחן השוואת פרופורציות נותנים תוצאות שקולות.
הכללה לטבלאות גדולות יותר
דוגמה: קשר בין מדינה לסוג דם
נבחן נתונים של 8,619 אנשים בשלוש מדינות (מיזורי, איווה, פלורידה) לפי ארבעה סוגי דם:
| A | B | AB | O | סה”כ | |
|---|---|---|---|---|---|
| מיזורי | 353 | 269 | 60 | 713 | $\textcolor{blue}{1,395}$ |
| איווה | 1,781 | 1,351 | 289 | 3,301 | 6,722 |
| פלורידה | 122 | 117 | 19 | 244 | 502 |
| סה”כ | $\textcolor{blue}{2,256}$ | 1,737 | 368 | 4,258 | 8,619 |
חישוב ערכים צפויים
הנוסחה הכללית היא:
\[E_{ij} = \frac{\text{Row } i \text{ total} \times \text{Column } j \text{ total}}{\text{Grand total}}\]עבור תא מיזורי-סוג A:
\[E_{11} = \frac{1,395 \times 2,256}{8,619} \approx 365\]עבור תא פלורידה-סוג B:
\[E_{32} = \frac{502 \times 1,737}{8,619} \approx 101\]סך הכל:
| A | B | AB | O | סה”כ | |
|---|---|---|---|---|---|
| מיזורי | 365.1 | 281.1 | 59.6 | 689.2 | 1,395 |
| איווה | 1,759.5 | 1,354.7 | 287.0 | 3,320.8 | 6,722 |
| פלורידה | 131.4 | 101.2 | 21.4 | 248.0 | 502 |
| סה”כ | 2,256 | 1,737 | 368 | 4,258 | 8,619 |
דרגות חופש (degrees of freedom) לטבלה כללית
עבור טבלה בגודל $r \times c$ (r שורות, c עמודות):
\[\text{df} = (r-1) \times (c-1)\]הסבר: אם אנחנו ממלאים $(r-1) \times (c-1)$ ערכים בטבלה, כל השאר נקבע על פי השוליים.
עבור הדוגמה של מדינה וסוג דם, יש לנו 3 מדינות ו-4 סוגי דם:
\[\text{df} = (3-1) \times (4-1) = 2 \times 3 = \boxed{6 \, \, \text{df}}\]חישוב הסטטיסטי והתוצאה
\[\chi^2 = \sum_{i=1}^{3} \sum_{j=1}^{4} \frac{(O_{ij} - E_{ij})^2}{E_{ij}} = 5.65\]נציב בפייתון:
import scipy.stats as stats
print(stats.chi2(df=6).sf(5.65))
# Output: 0.46351568707732305
ניתן להריץ את הקוד בסביבת הפייתון המקוונת של MedInTzfat או בכל סביבת פייתון אחרת עם ספריית scipy מותקנת.
מסקנה: הקשר אינו מובהק סטטיסטית - לא דוחים את השערת האפס. אין קשר מובהק בין מדינה לסוג דם.
מבחן טיב התאמה (Goodness of Fit Test)
עד כה השוונו בין קטגוריות בשתי אוכלוסיות. לפעמים נרצה להשוות מדידות לתחזית תיאורטית ספציפית.
דוגמה: בדיקת הוגנות קובייה
מטילים קובייה 120 פעמים ומקבלים:
| תוצאה | 1 | 2 | 3 | 4 | 5 | 6 | סה”כ |
|---|---|---|---|---|---|---|---|
| שכיחות | 23 | 18 | 21 | 22 | 19 | 17 | 120 |
ניסוח השערות
- $H_0$: הקובייה הוגנת (כל תוצאה בהסתברות $\frac{1}{6}$)
- $H_1$: הקובייה אינה הוגנת
חישוב ערכים צפויים
תחת השערת האפס: $E_i = 120\times\frac{1}{6} = 20$ לכל תוצאה (E היא הערך הצפוי - Expected).
| תוצאה | 1 | 2 | 3 | 4 | 5 | 6 | סה”כ |
|---|---|---|---|---|---|---|---|
| שכיחות | 23 | 18 | 21 | 22 | 19 | 17 | 120 |
| ערכים צפויים | 20 | 20 | 20 | 20 | 20 | 20 | 120 |
חישוב הסטטיסטי
\[\begin{aligned} \chi^2 &= \tfrac{(23-20)^2}{20} + \tfrac{(18-20)^2}{20} + \tfrac{(21-20)^2}{20} + \tfrac{(22-20)^2}{20} + \tfrac{(19-20)^2}{20} + \tfrac{(17-20)^2}{20} \\[5pt] &= \tfrac{9}{20} + \tfrac{4}{20} + \tfrac{1}{20} + \tfrac{4}{20} + \tfrac{1}{20} + \tfrac{9}{20} \\[5pt] &= \tfrac{28}{20} = \boxed{1.4} \end{aligned}\]דרגות חופש
במבחן טיב התאמה:
\[\text{df} = \text{number of catergories} - 1 = 6 - 1 = 5\]P-Value ומסקנה
import scipy.stats as stats
print(stats.chi2(df=5).sf(1.4))# Output: 0.924
הקובייה הוגנת - לא דוחים את השערת האפס.
תנאי תקפות המבחן
תנאים הכרחיים
- עצמאות תצפיות: כל תצפית עצמאית משאר התצפיות
- מדגם אקראי: הנתונים מגיעים ממדגם אקראי מהאוכלוסייה
- גודל מדגם מספק: בכל תא צפויות לפחות 5 תצפיות
הסבר לתנאי הערכים הצפויים
המבחן משתמש מתחת למכסה המנוע בקירוב נורמלי להתפלגות בינומית. עבור כל תא, מספר התצפיות הוא $\text{Binomial}(n,p)$. לקירוב נורמלי אנו זקוקים ל:
- $np \geq 5$ (מספר הצלחות צפוי)
- $n(1-p) \geq 5$ (מספר כישלונות צפוי)
חלופות כאשר התנאים לא מתקיימים
כאשר יש תאים עם פחות מ-5 תצפיות צפויות, ניתן:
- לאחד שורות או עמודות
- להשתמש במבחנים אחרים כמו מבחן פישר המדויק (Fisher’s Exact Test)
דוגמה לאיחוד קטגוריות: במקום שלוש מדינות עם ערכים קטנים (מיין, ורמונט, אלבמה), ניתן לאחד לשתי קטגוריות: “צפון” ו”דרום”.
מקרה מבחן: תיק גילברט
רקע המקרה
כריסטין גילברט הייתה אחות במרכז הרפואי VAMC בנורד-המפטון, מסצ’וסטס, בין השנים 1996-1989. אחיות אחרות שמו לב לספר גבוה של מקרי מוות במשמרותיה של גילברט, אך התעלמו מכך ורק כינו אותה “מלאך המוות” בבדיחות.
בשנת 1996, שלוש אחיות דיווחו על דאגה לגבי עליה במקרי דום לב כתוצאה ממוות, והחלה חקירה בנושא. הן חשדו שגילברט גרמה לדום לב בחולים על ידי הזרקת מנות גדולות של אפינפרין לעירויי התרופות של החולים.
ניסוח הבעיה הסטטיסטית
- $H_0$: אין קשר בין נוכחות גילברט למוות במשמרת (היא חפה מפשע)
- $H_1$: קיים קשר בין נוכחות גילברט למוות במשמרת
אולי נצטרך לקבוע רמת מובהקות הרבה יותר נמוכה מ-0.05, מכיוון שאנחנו לא רוצים להאשים מישהו ברצח עם סיכוי של 5% לטעות. רמת מובהקות של 5% נותנת חמישה אחוז סיכוי לטעות מסוג ראשון - דחיית השערת האפס כשהיא נכונה.
הנתונים
| מישהו מת במשמרת | אף אחד לא מת | סה”כ | |
|---|---|---|---|
| גילברט נוכחת | $\mathbf{40}$ | $217$ | 257 |
| גילברט נעדרת | $34$ | $1,350$ | 1,384 |
| סה”כ | 74 | 1,567 | 1,641 |
ניתן לראות שמשהו חשוד - במשמרות שגילברט נוכחת (257 משמרות) היו 40 מקרי מוות, ואילו במשמרות שהיא נעדרת (1,384 משמרות) היו רק 34 מקרי מוות.
נחשב ערכים צפויים (לפי הנוסחה $E_{ij} = \frac{\text{Row } i \text{ total} \times \text{Column } j \text{ total}}{\text{Grand total}}$):
| מישהו מת במשמרת | אף אחד לא מת | סה”כ | |
|---|---|---|---|
| גילברט נוכחת | 11 $\left(\frac{257 \times 74}{1,641} \approx 11.6\right)$ | 246 $\left(\frac{257 \times 1,567}{1,641} \approx 245.4\right)$ | 257 |
| גילברט נעדרת | 63 $\left(\frac{1,384 \times 74}{1,641} \approx 62.4\right)$ | 1,321 $\left(\frac{1,384 \times 1,567}{1,641} \approx 1,321.6\right)$ | 1,384 |
| סה”כ | 74 | 1,567 | 1,641 |
חישוב הסטטיסטי במקרה של גילברט
\[\begin{aligned} \chi^2 &= \tfrac{(40-11.6)^2}{11.6} + \tfrac{(217-245.4)^2}{245.4} + \tfrac{(34-62.4)^2}{62.4} + \tfrac{(1,350-1,321.6)^2}{1,321.6} \\[5pt] &= \tfrac{(28.4)^2}{11.6} + \tfrac{(-28.4)^2}{245.4} + \tfrac{(-28.4)^2}{62.4} + \tfrac{(28.4)^2}{1,321.6} \\[5pt] &= 69.7 + 3.3 + 12.9 + 0.6 = \boxed{86.5} \end{aligned}\]P-Value והתוצאה
עם דרגת חופש אחת ($\text{df} = (2-1) \times (2-1) = 1$):
\[\text{P-value} = P(\chi^2(1) > 86.5) \approx 10^{-20}\]הערך הזה הוא באופן ליטרלי אפסי. הסיכוי שדבר כזה יקרה במקרה הוא זניח לחלוטין.
ניתן לדחות את השערת האפס גם ברמת מובהקות של 0.000000000000001.
התוצאה המשפטית
יש קשר חזק מאוד בין נוכחותה של גילברט למספר מקרי המוות.
חשוב לזכור: אף על פי שיש קשר חזק, זה לא מוכיח כי גילברט גרמה למקרי המוות! המבחן הסטטיסטי מזהה קשר, לא סיבתיות.
לקחים חשובים
- הסטטיסטיקה יכולה להציל חיים - זיהוי דפוסים חשודים במקרים רפואיים
- מתאם אינו סיבתיות - המבחן מזהה קשר, לא בהכרח קשר סיבתי
- הקשר הביולוגי נדרש - צריך הסבר הגיוני למנגנון הפעולה
- רמת מובהקות במקרים משפטיים - יש לשקול רמות מובהקות נמוכות מאוד כאשר ההשלכות חמורות
הבסיס התיאורטי למבחן $\chi^2$
הקשר לקירוב הנורמלי
האינטואיציה מאחורי הסטטיסטי $\chi^2$ נובעת מכך שבמדגם גדול:
\[\frac{O_{ij} - E_{ij}}{\sqrt{E_{ij}}} \approx \mathcal{N}(0,1)\]כאשר מעלים משתנה נורמלי סטנדרטי בריבוע, מקבלים התפלגות $\chi^2$ עם דרגת חופש אחת. מכיוון שאנו מסכמים על מספר תאים, אנו מקבלים התפלגות $\chi^2$ עם מספר דרגות חופש המתאים.
מדוע מעלים בריבוע?
- הפוך הערכים לחיוביים - מניעת השתקת ערכים חיוביים ושליליים
- הדגשת חריגות גדולות - הריבוע נותן משקל גדול יותר לחריגות חמורות
- התפלגות ידועה - מאפשר לנו לחשב P-values מדויקים
שימושים נוספים למבחן $\chi^2$
יצירת משתנים קטגוריאליים ממשתנים רציפים
אם נרצה להשתמש במבחן $\chi^2$ להשוות משתנים רציפים, אנו יכולים לחלק אותם לקטגוריות:
דוגמה - לחץ דם:
- לחץ דם נמוך: מתחת ל-80 מ”מ כספית
- לחץ דם תקין: 120-80 מ”מ כספית
- לחץ דם גבוה: מעל 120 מ”מ כספית
לאחר מכן ניתן לבחון קשר בין קטגוריות לחץ הדם למשתנה קטגוריאלי אחר.
השוואה למבחנים אחרים
במקום מבחן $\chi^2$, ניתן היה להשתמש במבחן להשוואת פרופורציות. למעשה, במדגם גדול, שני המבחנים נותנים P-values זהים אסימפטוטית. מבחן $\chi^2$ נבחר בגלל פשטותו וכללותו לטבלאות מכל גודל.
מגבלות וזהירויות
מתי המבחן לא מתאים
- תצפיות תלויות - אם התצפיות לא עצמאיות (למשל, מדידות חוזרות על אותם נבדקים)
- מדגם קטן - כאשר התנאי של 5 תצפיות צפויות בכל תא לא מתקיים
- השוואות מרובות - כאשר עורכים בדיקות רבות, יש לתקן את רמת המובהקות
פרשנות תוצאות
- דחיית $H_0$: קיים קשר מובהק סטטיסטית בין המשתנים
- אי-דחיית $H_0$: אין ראיה לקשר (לא אומר שבוודאות אין קשר)
- חוזק הקשר: $\chi^2$ גדול יותר מעיד על קשר חזק יותר, אך עדיין תלוי בגודל המדגם
חיבור לנושאים הבאים: מדדי סיכון
מבחן $\chi^2$ מזהה האם קיים קשר בין שני משתנים קטגוריאליים, אבל הוא לא מכמת את חוזק הקשר או את גודל האפקט. כדי להתגבר על הקושי, משתמשים במחקר הרפואי במדדים נוספים:
- סיכון יחסי (RR - Relative Risk) - יחס בין שכיחות המחלה בקבוצת הסיכון לשכיחות בקבוצת הביקורת
- יחס הסיכויים (Odds Ratio) - מדד המופיע בצורה תדירה במאמרים רפואיים
מדד הסיכון היחסי ומדד יחס הסיכויים מאפשרים גם לכמת את עוצמתם ולהעריך את המשמעות הקלינית שלהם, בנוסף לזיהוי הקשר הסטטיסטי.
סיכום וחזרה
עקרונות מרכזיים
- מבחן $\chi^2$ מתאים לבדיקת קשרים בין משתנים קטגוריאליים
- השערת האפס היא תמיד אי-תלות (אין קשר)
- הסטטיסטי מבוסס על השוואת ערכים נצפים לערכים צפויים תחת השערת האפס
- דרגות החופש = $(r-1) \times (c-1)$ עבור טבלה $r \times c$
- תנאי תקפות: עצמאות, מדגם אקראי, ולפחות 5 תצפיות צפויות בכל תא
נוסחאות מרכזיות
\[\boxed{ \begin{aligned} E_{ij} &= \frac{\text{Row } i \text{ sum} \times \text{Column } j \text{ sum}}{\text{Grand total}} \\[5pt] \chi^2 &= \sum_{i,j} \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \\[5pt] \text{P-value} &= P(\chi^2(\text{df}) > \chi^2_{\text{observed}}) \end{aligned} }\]הכנה לנושא הבא
בשיעור הבא נלמד כיצד לכמת את חוזק הקשר שזוהה במבחן $\chi^2$ באמצעות מדדי סיכון. מדדי סיכון הם קריטיים לרופאים ומופיעים כמעט בכל מאמר אפידמיולוגי או מחקר קליני. קשה מאוד לפרש ספרות רפואית מודרנית באופן נכון בלי להבין אותם.
תודה למרצה.
תרגול
שאלה 1: מנדל והאפונים
מנדל והאפונים: ביצע במאה ה-19 ניסויי גנטיקה על אפונים. בגנטיקה מנדליאנית הכי פשוטה יש 2 גנים\אללים אחד רצסיבי והשני דומיננטי ראו ציור
בניסוי אחד מדדו את התכונות של 400 צאצאי אפון עם תכונה דומיננטית של צמח גבוה ויפה ואחרת רסציבית של צמח מסולסל ונמוך. להלן תוצאות הניסוי.נסחו השערת 0 + השערה אלטרנטיבית ודחו או קבלו אותה ברמת מובהקות נדרשת של 95%.
תוצאות הניסוי:
נמוך מסולסל גבוה ויפה 100 300 Expected 95 305 Observed
- $H_0$: הגנטיקה של מנדל עובדת, כלומר התפלגות התכונות היא 3:1 (75% גבוה ויפה, 25% נמוך מסולסל)
- $H_1$: הגנטיקה של מנדל לא עובדת, כלומר התפלגות התכונות שונה מ-3:1
נזכר בהגדרה:
\[\chi^2 = \sum_{i=1}^{k} \frac{(O_i - E_i)^2}{E_i}\]יש כאן דרגת חופש אחת (שורה אחת פחות מהמספר הכולל של קטגוריות, כלומר 2-1=1).
חישוב ערכים צפויים - המקרה הזה דומה יותר לגרסה של מבחן טיב התאמה, כי יש לנו התפלגות צפויה של 3:1 (תחזית תאורטית).
\[\chi^2 = \frac{(305-300)^2}{300} + \frac{(95-100)^2}{100} = \frac{25}{300} + \frac{25}{100} = 0.0833 + 0.25 = 0.3333\]עכשיו נחשב את ה-P-value:
import scipy.stats as stats
p_value = stats.chi2.sf(0.3333, df=1)
print(p_value) # Output: 0.563722359266274
ה-P-value הוא 0.563, שהוא הרבה יותר גבוה מ-0.05, ולכן לא דוחים את השערת האפס. כלומר, התוצאות תואמות את התחזית של מנדל.
שאלה 2: לידות
בזמן ניתוח קיסרי, עלול להיווצר תת-לחץ דם בעקבות מנח הגוף, ולכן נהוג לתת תרופה שמטרתה להעלות את לחץ הדם, ששמה הוא פנילפרין.
אחת מתופעות הלוואי של פנילפרין היא רפלקס-בריקרדיה (דופק נמוך).
כידוע, קיימת תרופה נוספת בשוק בשם נוראפינפרין, שיש לה פחות תופעות לוואי.
החוקרים ערכו מחקר בו רצו להשוות בין שתי התרופות הנ”ל בעת ניתוח קיסרי, בניסוי דאבל-בליינד רנדומלי (=גם הרופאים וגם המטופלות לא ידעו איזו תרופה ניתנת, ההקצאה לסוג התרופה רנדומלית). נתחו את הנתונים שנאספו בטבלה למטה וסגננו אמירה מדויקת ככל הניתן על ההבדל בין התרופות
| Bradycardia | Phenylephrine | Norepinephrine | Total | |
|---|---|---|---|---|
| Yes | Observed | 21 | 6 | 27 |
| Expected | 13.5 | 13.5 | ||
| No | Observed | 35 | 50 | 85 |
| Expected | 42.5 | 42.5 | ||
| Total | 56 | 56 | 112 |
ננסח השארת אפס:
- $H_0$: אין הבדל בין התרופות פנילפרין לנוראפינפרין בהקשר לרפלקס ברדיקרדיה (כלומר, ההסתברויות זהות)
- $H_1$: יש הבדל בין התרופות פנילפרין לנוראפינפרין בהקשר לרפלקס ברדיקרדיה (כלומר, ההסתברויות שונות)
יש דרגת חופש אחת. היה מספיר למלא $21 (13.5)$ ו-$6 (13.5)$ כדי לקבל את הערכים הצפויים, אבל.
נחשב את הסטטיסטי $\chi^2$:
\[\begin{aligned} \chi^2 &= \frac{(21-13.5)^2}{13.5} + \frac{(6-13.5)^2}{13.5} + \frac{(35-42.5)^2}{42.5} + \frac{(50-42.5)^2}{42.5} \\[5pt] &= \frac{(7.5)^2}{13.5} + \frac{(-7.5)^2}{13.5} + \frac{(-7.5)^2}{42.5} + \frac{(7.5)^2}{42.5} \\[5pt] &= \frac{56.25}{13.5} + \frac{56.25}{42.5} + \frac{56.25}{42.5} + \frac{56.25}{13.5} \\[5pt] &= 4.17 + 1.32 + 1.32 + 4.17 = \boxed{10.98} \end{aligned}\]עכשיו נחשב את ה-P-value:
import scipy.stats as stats
p_value = stats.chi2.sf(10.98, df=1)
print(p_value) # Output: 0.000921
ה-P-value הוא 0.000921, שהוא הרבה יותר נמוך מ- 0.05 (המובהקות הנדרשת), ולכן דוחים את השערת האפס. כלומר, יש הבדל מובהק סטטיסטית בין התרופות פנילפרין לנוראפינפרין בהקשר לרפלקס ברדיקרדיה.
נמשיך בבדיקה של מבחן חד צדדי.
נשתמש בפרופורציה.
\[\bar{P} = \frac{6}{27} = 0.222\] \[P_0 = 0.5\] \[n = 27\] \[Z = \frac{\bar{P} - P_0}{\sqrt{\frac{P_0(1-P_0)}{n}}} = \frac{0.222 - 0.5}{\sqrt{\frac{0.5(1-0.5)}{27}}} = \frac{-0.278}{0.192} \approx -2.88\]נחשב את ה-P-value:
import scipy.stats as stats
p_value = stats.norm.cdf(-2.88)
print(p_value) # Output: 0.002
תוצאות המדגם מראות כי ה-P-value הוא 0.002, שהוא נמוך מ-0.05, ולכן דוחים את השערת האפס גם במבחן פרופורציות חד צדדי. כלומר, יש הבדל מובהק סטטיסטית בין התרופות פנילפרין לנוראפינפרין בהקשר לרפלקס ברדיקרדיה.
שאלה 3: נשים וגברים בסכרת
כדי לבדוק האם אחוז הנשים שחולות בסוכרת זהה לאחוז הגברים שחולים בסוכרת, חוקר דגם מדגם מקרי של 150 נשים ושל 100 גברים ומצא ש- 40 מהנשים ו- 30 מהגברים חולים בסוכרת. עזרו למתרגל למלא את הטבלה וקבעו בעזרתה האם ישנו קשר בין מגדר לבין מחלת הסוכרת (ברמת מובהקות של 95%)?
נכפיל את הסיכוי לחלות בסוכרת במדגם הנשים והגברים:
| סוכרת | כן | לא | סה”כ |
|---|---|---|---|
| נשים | 40 | 110 | 150 |
| גברים | 30 | 70 | 100 |
השערת האפס היא שאין הבדל בין אחוז הנשים והגברים החולים בסוכרת, כלומר:
- $H_0$: אחוז הנשים שחולות בסוכרת שווה לאחוז הגברים שחולים בסוכרת
- $H_1$: אחוז הנשים שחולות בסוכרת שונה מאחוז הגברים שחולים בסוכרת
הסיכוי לחלות בסוכרת במדגם הוא:
\[\bar{P} = \frac{40 + 30}{150 + 100} = \frac{70}{250} = 0.28\]נחשב את הערכים הצפויים:
| סוכרת | כן | לא | סה”כ |
|---|---|---|---|
| נשים | \(\frac{150 \times 70}{250} = 42\) | \(\frac{150 \times 180}{250} = 108\) | 150 |
| גברים | \(\frac{100 \times 70}{250} = 28\) | \(\frac{100 \times 180}{250} = 72\) | 100 |
| סה”כ | 70 | 180 | 250 |
נחשב את הסטטיסטי $\chi^2$:
\[\begin{aligned} \chi^2 &= \frac{(40-42)^2}{42} + \frac{(110-108)^2}{108} + \frac{(30-28)^2}{28} + \frac{(70-72)^2}{72} \\[5pt] &= \frac{(-2)^2}{42} + \frac{(2)^2}{108} + \frac{(2)^2}{28} + \frac{(-2)^2}{72} \\[5pt] &= \frac{4}{42} + \frac{4}{108} + \frac{4}{28} + \frac{4}{72} \\[5pt] &= 0.0952 + 0.0370 + 0.1429 + 0.0556 \\[5pt] &= 0.3307 \end{aligned}\]עכשיו נחשב את ה-P-value:
import scipy.stats as stats
p_value = stats.chi2.sf(0.3307, df=1)
print(p_value) # Output: 0.565
מכאן שה-P-value הוא 0.565, שהוא הרבה יותר גבוה מ-0.05, ולכן לא דוחים את השערת האפס. כלומר, אין הבדל מובהק סטטיסטית בין אחוז הנשים והגברים החולים בסוכרת.
דור פסקל