משוואת מיכאליס-מנטן - הגזירה המלאה
נזכיר שהנוסחה לראקציה אנזימטית פשוטה היא:
\[\ce{E + S <=>[k_1][k_{-1}] ES ->[k_2] E + P}\]הנחות היסוד
בפיתוח משוואת מיכאליס-מנטן, אנחנו מבססים את הניתוח על מספר הנחות יסוד קריטיות:
הנחה ראשונה: הזנחת הריאקציה ההפוכה
\[k_2 \gg k_{-2}\]כלומר, קצב יצירת התוצר גדול בהרבה מקצב הריאקציה ההפוכה (מתוצר לקומפלקס $\ce{ES}$). ההנחה הזאת מוצדקת כשאנחנו מודדים את מהירות הריאקציה ההתחלתית - כשריכוז התוצר הוא כמעט אפסי.
הנחה שנייה: עודף סובסטרט
\[\left[ \text{S} \right] \gg \left[ \text{E} \right]_{total}\]ריכוז הסובסטרט תמיד בעודף גדול מאוד ביחס לריכוז האנזים הכולל. משמעות ההנחה הזאת היא שהסובסטרט הוא לא הגורם המגביל בריאקציה.
הנחה שלישית: המצב העמיד (Steady State)
\[\frac{d\left[ \text{ES} \right]}{dt} = 0\]ריכוז הקומפלקס $\ce{ES}$ נשאר קבוע לאורך המדידה. זאת הנחת המצב העמיד - היא שונה משיווי משקל, כי היא מתייחסת לרכיב בודד במערכת ולא למערכת כולה.
גזירת המשוואה
במצב העמיד, קצב היצירה של $\ce{ES}$ שווה לקצב הפירוק שלו:
יצירת $\ce{ES}$:
\[\text{Formation rate} = k_1\left[ \text{E} \right]\left[ \text{S} \right]\]במבחן של הטכניון ראיתי את הביטוי הבא לקצב יצירת הקומפלקס $\ce{ES}$:
\[\text{Formation rate} = k_1\left( \left[ \text{E} \right]_{total} - \left[ \text{ES} \right] \right)\left[ \text{S} \right]\]להבנתי, היא מתקבלת מכך שניתן לבטא את ריכוז האנזים החופשי כ-$\left[ \text{E} \right] = \left[ \text{E} \right]_{total} - \left[ \text{ES} \right]$ (כי האנזים יכול להיות רק חופשי או בקומפלקס).
פירוק $\ce{ES}$:
\[\text{Breakdown rate} = [k_{-1} + k_2](ES)\]במצב העמיד קצב היצירה שווה לקצב הפירוק (ראו את ההנחה השלישית לעיל), מכאן:
\[k_1\left[ \text{E} \right]\left[ \text{S} \right] = [k_{-1} + k_2](ES)\]נגדיר את קבוע מיכאליס-מנטן:
\[K_{\text{m}} = \frac{k_{-1} + k_2}{k_1}\]זהו יחס בין קבועי הקצב של פירוק $\ce{ES}$ (לשני הכיוונים) לקבוע הקצב של יצירת $\ce{ES}$.
מכאן:
\[K_{\text{m}} = \frac{[\text{E}][\text{S}]}{[\text{ES}]}\]כאשר ריכוז האנזים הכולל:
\[[\text{E}]_{total} = [\text{E}] + [\text{ES}]\]נציב ונקבל:
\[[\text{ES}] = \frac{[\text{E}]_{total} \cdot [\text{S}]}{K_{\text{m}} + [\text{S}]}\]המהירות ההתחלתית:
\[V_0 = k_2\left[ \text{ES} \right] = \frac{k_2[\text{E}]_{total} \cdot [\text{S}]}{K_{\text{m}} + [\text{S}]}\]כאשר כל האנזים רווי בסובסטרט:
\[V_{\text{max}} = k_2\left[ \text{E} \right]_{total}\]לכן משוואת מיכאליס-מנטן:
\[\boxed{V_0 = \frac{V_{\text{max}} \cdot [\text{S}]}{K_{\text{m}} + [\text{S}]}}\]המשמעות של KM
ההגדרה המתמטית: כאשר $[\text{S}] = K_{\text{m}}$:
\[V_0 = \frac{V_{\text{max}} \cdot K_{\text{m}}}{K_{\text{m}} + K_{\text{m}}} = \frac{V_{\text{max}}}{2}\]לכן: $K_{\text{m}}$ הוא ריכוז הסובסטרט שבו מהירות הריאקציה היא מחצית המהירות המקסימלית.
מקרה פרטי - אפיניות: כאשר $k_2 \ll k_{-1}$ (השלב הקובע-קצב הוא יצירת התוצר):
\[K_{\text{m}} \approx \frac{k_{-1}}{k_1} = K_d\]במקרה זה בלבד, $K_{\text{m}}$ משקף את האפיניות בין האנזים לסובסטרט.
פרמטרים קינטיים חשובים
מספר התחלופה (Turnover Number)
\[K_{\text{cat}} = \frac{V_{\text{max}}}{\left[ \text{E} \right]_{total}}\]מספר מולקולות הסובסטרט שאנזים בודד הופך לתוצר ביחידת זמן (בתנאי רוויה).
דוגמאות:
- קרבוניק אנהידרז: $K_{\text{cat}} = 600,000 \, \mathrm{s}^{-1}$
- ליזוזים: $K_{\text{cat}} = 0.5 \, \mathrm{s}^{-1}$
השפעת תנאים סביבתיים
pH: כל אנזים פועל באופן אופטימלי ב-pH מסוים:
- פפסין (קיבה): pH אופטימלי = 2
- גלוקוז-6-פוספטאז (רקמות): pH אופטימלי = 6-7
טמפרטורה: השפעה דרמטית על קצב הריאקציה - אנזים שחותך חלבון ב-3 שעות ב-4°C יבצע את אותה ריאקציה ב-10 דקות ב-25°C.
גרף ליינוויבר-בורק
כדי לקבוע במדויק את $V_{\text{max}}$ ו-$K_{\text{m}}$ (שלעיתים קשה להגיע אליהם ניסויית), משתמשים בלינאריזציה:
\[\boxed{\frac{1}{V_0} = \frac{K_{\text{m}}}{V_{\text{max}}} \cdot \frac{1}{\left[ \text{S} \right]} + \frac{1}{V_{\text{max}}}}\]זאת משוואת קו ישר מהצורה $y = ax + b$ כאשר:
- ציר Y: $1/V_0$
- ציר X: $1/\left[ \text{S} \right]$
- שיפוע: $K_{\text{m}}/V_{\text{max}}$
- חיתוך עם ציר Y: $1/V_{\text{max}}$
- חיתוך עם ציר X: $-1/K_{\text{m}}$
איזוזימים - משמעות פיזיולוגית
הגדרה
איזוזימים הם אנזימים שונים שמקטלזים את אותה ריאקציה אך נבדלים ב:
- רצף חומצות אמינו
- ערכי $K_{\text{m}}$
- ערכי $V_{\text{max}}$
דוגמה: מטבוליזם של אלכוהול
אצטאלדהיד דהידרוגנז (ALDH):
- איזוזים מיטוכונדריאלי: $K_{\text{m}}$ נמוך - פועל ביעילות בריכוזי אצטאלדהיד נמוכים
- איזוזים ציטופלזמטי: $K_{\text{m}}$ גבוה - נכנס לפעולה רק בריכוזים גבוהים
מוטציה ב-ALDH המיטוכונדריאלי גורמת לתסמונת רגישות לאלכוהול (הסמקה, בחילה, טכיקרדיה).
דוגמה: הקסוקינאז מול גלוקוקינאז
שניהם מזרחנים גלוקוז ל-גלוקוז-6-פוספט:
הקסוקינאז (רוב הרקמות):
- $K_{\text{m}} = 0.1 \, \text{mM}$
- פועל ביעילות בריכוזי גלוקוז נמוכים
- מבטיח אספקת גלוקוז לתאים
גלוקוקינאז (כבד):
- $K_{\text{m}} = 10 \, \text{mM}$ (גבוה פי 100!)
- פועל רק בריכוזי גלוקוז גבוהים
- מאחסן עודפי גלוקוז כגליקוגן
המשמעות: הכבד “לוקח” גלוקוז רק אחרי שהרקמות החיוניות קיבלו את צרכיהן.
עיכוב אנזימים
עיכוב בלתי הפיך
מעכבים הנקשרים קובלנטית לאנזים ומוציאים אותו מכלל פעולה לצמיתות.
דוגמאות:
DIPF (גז עצבים):
- נקשר קובלנטית לסרין באתר הפעיל של אצטילכולין אסטראז
- משבש העברה עצבית בסינפסות
פניצילין:
- נקשר קובלנטית ל-Glycopeptide Transpeptidase
- מונע יצירת קשרי צילוב בדופן התא החיידקי
- גורם למות החיידק
עיכוב הפיך
קיימים מספר סוגים של עיכוב הפיך, כאשר שני הסוגים העיקריים הם עיכוב תחרותי ועיכוב אל-תחרותי (Uncompetitive).
עיכוב תחרותי (Competitive)
המעכב מתחרה עם הסובסטרט על האתר הפעיל.
מאפיינים קינטיים:
- $V_{\text{max}}$ לא משתנה (ניתן להתגבר על העיכוב בריכוזי סובסטרט גבוהים)
- $K_{\text{m}}^{apparent} = K_{\text{m}} \cdot \alpha$ כאשר $\alpha = 1 + \frac{[I]}{K_i}$
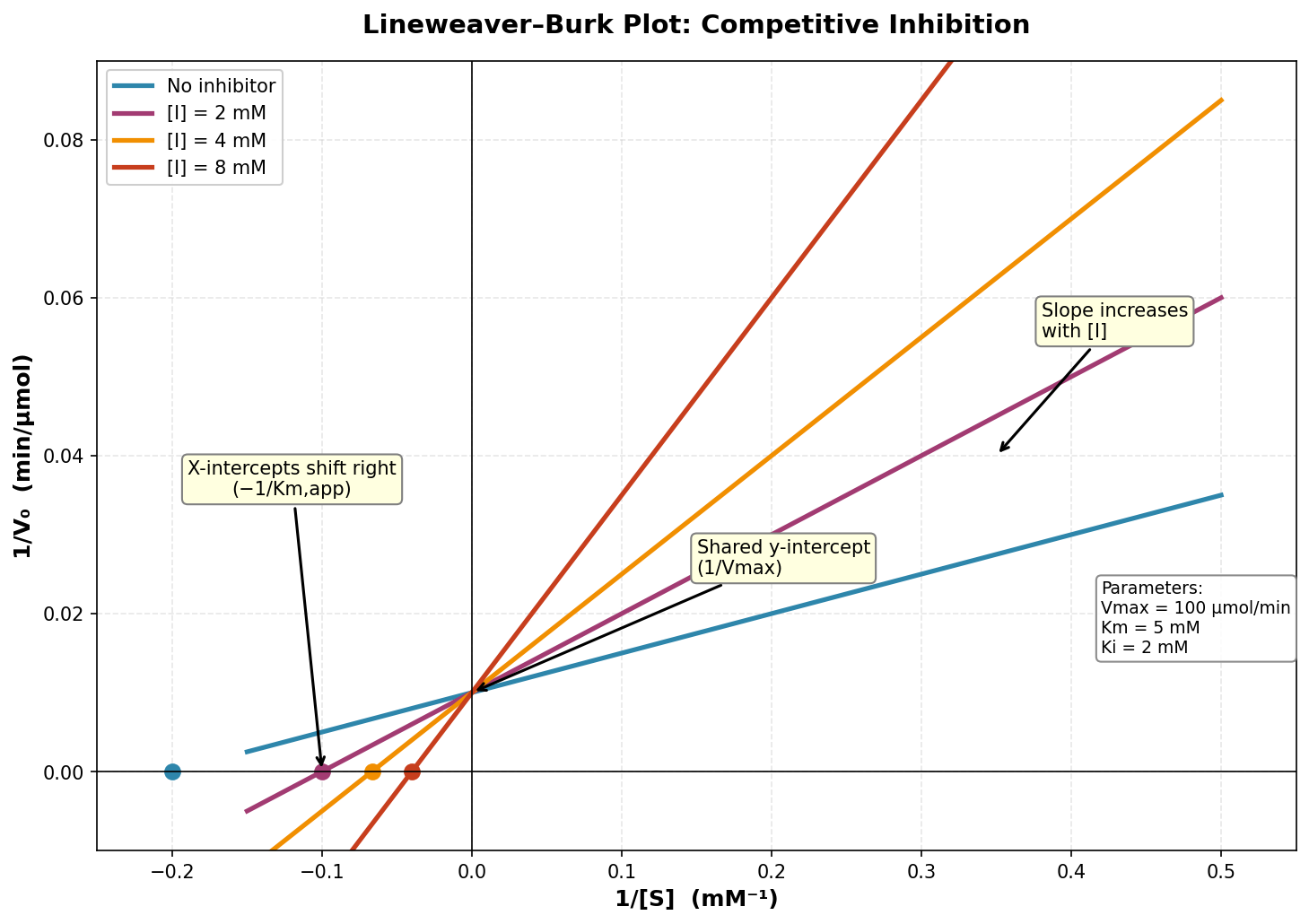
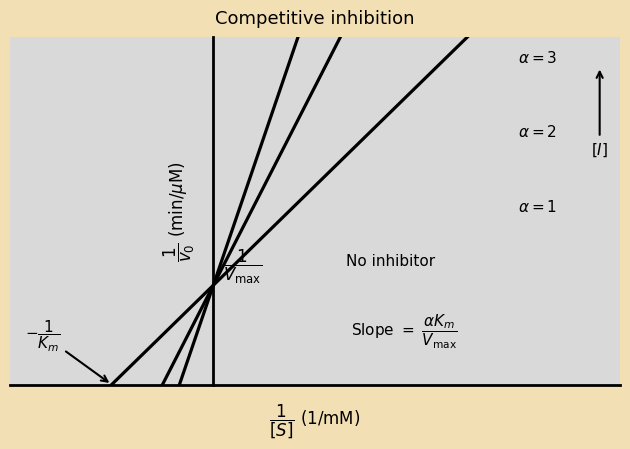
בגרף ליינוויבר-בורק:
- כל הקווים נחתכים על ציר Y (אותו $1/V_{\text{max}}$)
- שיפוע עולה עם ריכוז המעכב - משקף את העלייה ב-$K_{\text{m}}$ שהמשמעות שלה היא לכאורה ירידה באפיניות בין האנזים לסובסטרט. בפועל, המעכב תופס את האתר הפעיל ומונע מהסובסטרט להיקשר, ולכן נדרש ריכוז סובסטרט גבוה יותר כדי להגיע לאותה מהירות (כזכור, $K_{\text{m}}$ הוא הריכוז שבו המהירות היא חצי מ-$V_{\text{max}}$).
דוגמה: מתוטרקסט - מעכב של דיהידרופולאט רדוקטאז, משמש בכימותרפיה.
עיכוב אל-תחרותי (Uncompetitive)
המעכב נקשר רק לקומפלקס ES, לא לאנזים החופשי.
מאפיינים קינטיים:
- גם $V_{\text{max}}$ וגם $K_{\text{m}}$ יורדים באותו יחס
- היחס $V_{\text{max}}/K_{\text{m}}$ נשאר קבוע
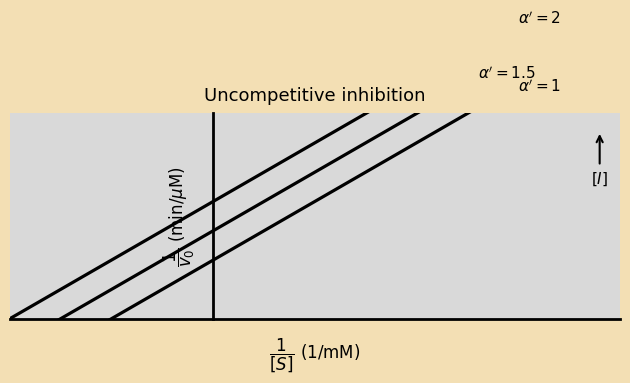
בגרף ליינוויבר-בורק:
- קווים מקבילים (אותו שיפוע)
- חיתוך שונה עם שני הצירים
הקווים בנוכחות מעכב אל-תחרותי תמיד יופיעו בגרף ליינוויבר-בורק מעל הקו של האנזים ללא המעכב, כתוצאה מהירידה גם ב-$V_{\text{max}}$ וגם ב-$K_{\text{m}}$ (נקודות החיתוך זזות שמאלה על ציר X וגבוהות יותר על ציר Y).
בגרף רגיל ($V_0$ מול $[\text{S}]$), הקווים בנוכחות מעכב אל-תחרותי יופיעו מתחת לקו של האנזים ללא המעכב, כי המהירות בכל ריכוז סובסטרט תהיה נמוכה יותר. האפיניות דווקא עולה (כי $K_{\text{m}}$ יורד) אבל המהירות בכל ריכוז סובסטרט נמוכה יותר בגלל הירידה ב-$V_{\text{max}}$.
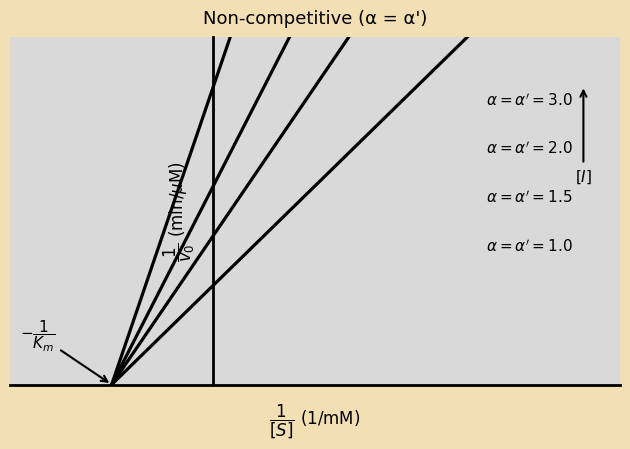
עיכוב לא תחרותי (Non-competitive)
לא הרחבנו על זה בשיעור למיטב זכרוני אבל כן הופיע בתרגול.
מדובר במקרה פרטי של Mixed Inhibition (מעכב שיכול להיקשר גם לאנזים החופשי E וגם לקומפלקס ES), שבו הנטייה של המעכב להיקשר לאנזים החופשי שווה לנטייה שלו להיקשר לקומפלקס ES. במצב כזה:
- $V_{\text{max}}$ יורד
- $K_{\text{m}}$ נשאר קבוע
המשוואה הכללית לעיכוב
עבור עיכוב תחרותי:
\[V_0 = \frac{V_{\text{max}} \cdot \left[ \text{S} \right]}{\alpha K_{\text{m}} + \left[ \text{S} \right]}\]כאשר $\alpha$ הוא מקדם העיכוב התלוי בריכוז המעכב ובקבוע העיכוב $K_i$.
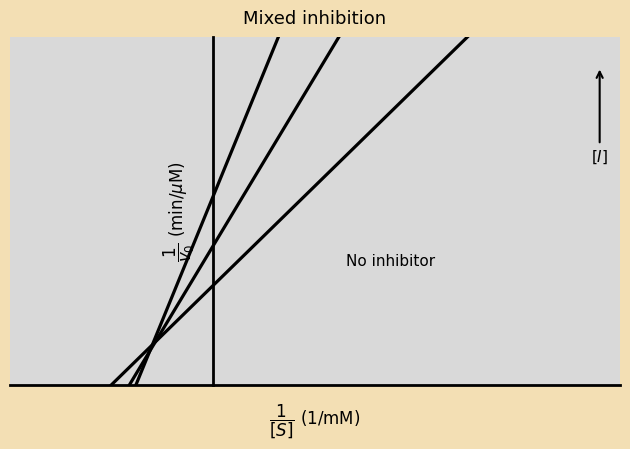
כאשר בעיכוב מסוג Mixed הנטייה של המעכב להיקשר ל־E גבוהה מזו של הקישור ל־ES (כלומר $\alpha > \alpha’$),
- ערך $K_{\text{m}}$ עולה (ירידה באפיניות),
- השיפוע עולה (כי $\alpha K_m$ גדל),
- החיתוך עם ציר X זז ימינה (כלומר ערך $-1/K_m$ מתקרב לאפס).
חישוב דוגמה
נתון: ריאקציה אנזימטית שמתנהגת לפי מיכאליס מנטן עם הנתונים הבאים:
$\left[ \text{S} \right] \, (\mathrm{M})$ $V \, (\mathrm{M/s})$ $1\times10^{-4}$ $1\times10^{-4}$ $4\times10^{-3}$ $6\times10^{-4}$ $2\times10^{-3}$ $6\times10^{-4}$ מה יהיו $K_{\text{m}}$ ו-$V$ אם ריכוז הסובסטרט יהיה $5\times 10^{-4} \, \mathrm{M}$?
אפשר ללמוד מהטבלה על המהירות המקסימלית (הוספת ריכוז לא מעלה את המהירות מעבר לה):
\[V_{\text{max}} = 6\times10^{-4} \, (\mathrm{M/s})\]$K_{\text{m}}$ הוא הריכוז שבו המהירות היא בדיוק חצי. נציב במשוואה כדי למצוא אותו:
\[\frac{6\times10^{-4}}{2} = \frac{ 6\times10^{-4} \times 5\times 10^{-4}}{K_{\text{m}} + 5\times 10^{-4}}\] \[K_{\text{m}} + 5\times 10^{-4} = 10 \times 10^{-4}\] \[\boxed{K_{\text{m}} = 5\times 10^{-4}}\]כעת נציב שוב בנוסחה כדי למצוא את המהירות בנתוים ששאלו עליהם:
\[V = \frac{ 6\times10^{-4} \times 5\times 10^{-4}}{ 5\times 10^{-4} + 5\times 10^{-4}} = \boxed{3\times10^{-4}}\]עקרונית היה ניתן להגיע למהירות גם בדרך אחרת - בריכוז של $k_{\text{m}}$ המהירות היא חצי מהמהירות המקסימלית.
סיכום
קינטיקה אנזימטית מספקת כלים כמותיים להבנת פעילות אנזימים ולפיתוח תרופות. משוואת מיכאליס-מנטן ונגזרותיה מאפשרות:
- אפיון כמותי של אנזימים ($K_{\text{m}}$, $V_{\text{max}}$, $K_{\text{cat}}$)
- הבנת מנגנוני עיכוב
- תכנון רציונלי של תרופות
- הבנת המשמעות הפיזיולוגית של איזוזימים
העקרונות הללו הם הבסיס להבנת רגולציה מטבולית ולפיתוח טיפולים תרופתיים רבים.
שאלות ממוצאות לתרגול
שאלה 1: המשמעות של Km
מהי המשמעות המתמטית של $K_m$ במשוואת מיכאליס-מנטן, ומתי הוא משקף את האפיניות בין האנזים לסובסטרט?
- $K_m$ הוא תמיד שווה לקבוע הדיסוציאציה ($K_d$) ומשקף את האפיניות בכל מקרה.
- $K_m$ הוא ריכוז הסובסטרט שבו המהירות מקסימלית, ומשקף אפיניות רק כש-$k_2 \gg k_{-1}$.
- $K_m$ הוא ריכוז הסובסטרט שבו המהירות היא מחצית המהירות המקסימלית, ומשקף אפיניות רק כש-$k_2 \ll k_{-1}$.
- $K_m$ הוא ריכוז האנזים שבו המהירות היא מחצית המהירות המקסימלית.
פתרון
התשובה הנכונה היא (3).
ההגדרה המתמטית של $K_m$:
כאשר $[\text{S}] = K_m$:
\[V_0 = \frac{V_{max} \cdot K_m}{K_m + K_m} = \frac{V_{max}}{2}\]לכן: $K_m$ הוא ריכוז הסובסטרט שבו מהירות הריאקציה היא מחצית המהירות המקסימלית.
מתי $K_m$ משקף אפיניות?
\[K_m = \frac{k_{-1} + k_2}{k_1}\]רק כאשר $k_2 \ll k_{-1}$ (השלב הקובע קצב הוא יצירת התוצר):
\[K_m \approx \frac{k_{-1}}{k_1} = K_d\]במקרה זה בלבד, $K_m$ משקף את האפיניות בין האנזים לסובסטרט.
חשוב לזכור:
- $K_m$ נמוך = האנזים מגיע לחצי מהירות מקסימלית בריכוזי סובסטרט נמוכים
- $K_m$ גבוה = צריך ריכוז סובסטרט גבוה כדי להגיע לחצי מהירות מקסימלית
שאלה 2: איזוזימים - הקסוקינאז מול גלוקוקינאז
הקסוקינאז וגלוקוקינאז שניהם מזרחנים גלוקוז לגלוקוז-6-פוספט. ל-הקסוקינאז $K_m = 0.1 \text{ mM}$ ולגלוקוקינאז $K_m = 10 \text{ mM}$. מה המשמעות הפיזיולוגית של ההבדל?
- גלוקוקינאז יעיל יותר ולכן נמצא ברקמות החיוניות.
- הכבד (עם גלוקוקינאז) “לוקח” גלוקוז רק אחרי שהרקמות החיוניות קיבלו את צרכיהן.
- הקסוקינאז פועל רק בריכוזי גלוקוז גבוהים.
- אין משמעות פיזיולוגית - זו רק וריאציה גנטית.
פתרון
התשובה הנכונה היא (2).
השוואה בין האיזוזימים:
| פרמטר | הקסוקינאז | גלוקוקינאז |
|---|---|---|
| מיקום | רוב הרקמות | כבד |
| $K_m$ | $0.1 \, \mathrm{mM}$ (נמוך) | $10 \, \mathrm{mM}$ (גבוה פי 100!) |
| מתי פועל | בריכוזי גלוקוז נמוכים | רק בריכוזי גלוקוז גבוהים |
| תפקיד | מבטיח אספקת גלוקוז לתאים | מאחסן עודפי גלוקוז כגליקוגן |
המשמעות הפיזיולוגית:
- כשרמת הגלוקוז בדם נמוכה ← הקסוקינאז ברקמות פועל ביעילות
- גלוקוקינאז בכבד לא פעיל (צריך ריכוז גבוה בהרבה)
- רק כשיש עודף גלוקוז בדם ← גלוקוקינאז נכנס לפעולה ומאחסן בכבד
התוצאה: הכבד “מחכה בתור” - לוקח גלוקוז רק אחרי שהרקמות החיוניות (מוח, שרירים) קיבלו את צרכיהן.
שאלה 3: גרף ליינוויבר-בורק ועיכוב תחרותי
בניסוי מעבדה נמדדה פעילות אנזימטית עם ובלי מעכב. בגרף ליינוויבר-בורק, כל הקווים נחתכים באותה נקודה על ציר Y. מה סוג העיכוב?
- עיכוב אל-תחרותי (Uncompetitive) - המעכב נקשר רק לקומפלקס ES.
- עיכוב תחרותי (Competitive) - המעכב מתחרה עם הסובסטרט על האתר הפעיל.
- עיכוב בלתי הפיך - המעכב נקשר קובלנטית לאנזים.
- עיכוב מעורב - המעכב נקשר גם לאנזים וגם לקומפלקס ES.
פתרון
התשובה הנכונה היא (2) - עיכוב תחרותי.
עיכוב תחרותי (Competitive Inhibition):
המעכב מתחרה עם הסובסטרט על האתר הפעיל.
מאפיינים קינטיים:
- $V_{max}$ לא משתנה (ניתן להתגבר על העיכוב בריכוזי סובסטרט גבוהים)
- $K_m^{apparent}$ עולה (צריך יותר סובסטרט כדי להגיע לחצי מהירות)
בגרף ליינוויבר-בורק:
- כל הקווים נחתכים על ציר Y (אותו $1/V_{max}$)
- שיפוע עולה עם ריכוז המעכב
- חיתוך עם ציר X משתנה ($-1/K_m$ הופך לפחות שלילי)
לעומת עיכוב אל-תחרותי:
- קווים מקבילים (אותו שיפוע)
- גם $V_{max}$ וגם $K_m$ יורדים
דוגמה קלינית: מתוטרקסט - מעכב תחרותי של דיהידרופולאט רדוקטאז, משמש בכימותרפיה.
שאלה 4: עיכוב בלתי הפיך
פניצילין הוא אנטיביוטיקה שפועלת כמעכב בלתי הפיך. מה מנגנון הפעולה שלו?
- מתחרה עם הסובסטרט על האתר הפעיל של אנזימי החיידק.
- נקשר קובלנטית ל-Glycopeptide Transpeptidase ומונע יצירת קשרי צילוב בדופן התא החיידקי.
- נקשר לקומפלקס ES בלבד ומונע שחרור התוצר.
- משנה את ה-pH באתר הפעיל של האנזים.
פתרון
התשובה הנכונה היא (2).
עיכוב בלתי הפיך:
מעכבים הנקשרים קובלנטית לאנזים ומוציאים אותו מכלל פעולה לצמיתות.
מנגנון הפעולה של פניצילין:
- נקשר קובלנטית ל-Glycopeptide Transpeptidase
- מונע יצירת קשרי צילוב (Cross-links) בדופן התא החיידקי
- דופן התא נחלשת ← החיידק מת
דוגמה נוספת - DIPF (גז עצבים):
- נקשר קובלנטית לסרין באתר הפעיל של אצטילכולין אסטראז
- משבש העברה עצבית בסינפסות
- גורם לשיתוק ומוות
ההבדל מעיכוב הפיך:
- עיכוב הפיך: המעכב יכול להתנתק מהאנזים
- עיכוב בלתי הפיך: קשר קובלנטי = האנזים “מת” לצמיתות
שאלה 5: הנחות מיכאליס-מנטן
איזו מההנחות הבאות היא הנחת “המצב העמיד” (Steady State) בגזירת משוואת מיכאליס-מנטן?
- ריכוז הסובסטרט שווה לריכוז האנזים.
- ריכוז הקומפלקס ES נשאר קבוע לאורך המדידה: $\frac{d[ES]}{dt} = 0$
- הריאקציה נמצאת בשיווי משקל תרמודינמי מלא.
- קצב יצירת התוצר שווה לאפס.
פתרון
התשובה הנכונה היא (2).
שלוש הנחות היסוד של מיכאליס-מנטן:
| הנחה | משמעות |
|---|---|
| 1. הזנחת הריאקציה ההפוכה | $k_2 \gg k_{-2}$ - מודדים מהירות התחלתית כשאין עדיין תוצר |
| 2. עודף סובסטרט | $[S] \gg [E]_{total}$ - הסובסטרט לא הגורם המגביל |
| 3. המצב העמיד | $\frac{d[ES]}{dt} = 0$ - ריכוז הקומפלקס ES קבוע |
מה זה המצב העמיד?
- קצב יצירת ES = קצב פירוק ES
- ריכוז ES קבוע (לא משתנה עם הזמן)
- זה לא שיווי משקל - הריאקציה ממשיכה להתקדם!
ההבדל משיווי משקל:
- שיווי משקל = כל המערכת לא משתנה
- מצב עמיד = רכיב בודד (ES) קבוע, אבל הריאקציה ממשיכה
מהנחת המצב העמיד נגזרת המשוואה:
\[k_1[E][S] = (k_{-1} + k_2)[ES]\]ומכאן מגיעים למשוואת מיכאליס-מנטן.