1. מבוא: ארבעת הכוחות היסודיים בטבע
בטבע קיימים ארבעה כוחות יסודיים:
-
כוח הכבידה - מחזיק את הכוכבים ואת הגלקסיות במסלולם. זה הכוח שבונה את היקום שלנו בממדים גדולים - שמש וירח בגלקסיות, צבירי גלקסיות והיקום כולו.
-
הכוח האלקטרומגנטי - זה הכוח שנלמד לעומק בקורס. הכוח האלקטרומגנטי אחראי לכל הכימיה שבעולם ובלעדיו אין בעולם גיוון.
-
הכוח הגרעיני החזק והכוח הגרעיני החלש - כוחות חשובים ביותר שבלעדיהם אין לכוח האלקטרומגנטי על מה לפעול.
התורה האלקטרומגנטית עברה שתי פאזות משמעותיות במהלך ההיסטוריה. הפאזה הראשונה הייתה סוף המאה ה-19, תחילת המאה ה-20, כאשר מספר אנשים אינטליגנטים פיתחו את התורה האלקטרומגנטית הקלאסית. התורה האלקטרומגנטית הקלאסית נותנת תיאור יפה לגבי אינטראקציות אלקטרומגנטיות בין גופים שנמצאים במעבדה ומעגלים חשמליים.
יש רמות שונות של תיאורים אלגנטיים בתורה. ככל שהרמה גבוהה יותר, התיאור אלגנטי יותר, יפה יותר ומעורר השראה. הבעיה היא רמת המתמטיקה הנדרשת, שבמקרה שלנו לא מספיקה בלשון המעטה (דור - יש לי תואר במדעי המחשב שגם לא מספיק, ככל הנראה). לכן נלמד בעיקר דברים פחות אלגנטיים, למרבה הצער.
2. המטען החשמלי - אבן הראשה של התורה האלקטרומגנטית
קיימת תכונה בסיסית ביותר שמכונה מטען חשמלי. זאת תכונה של הטבע, שמנקודת מבטנו כרפואנים שלעולם לא יהיו מהנדסים, צריכה להיות “God given” - אבן היסוד הבסיסית ביותר.
המטען החשמלי דומה ל״מטען הכבידתי״ שהזכרנו על פניו בשיעורי מכניקה. מטען כבידתי הוא משהו שמרגיש כוח כבידה - אם יש למשהו מטען כבידתי, הוא יודע אם יש כבידה בסביבה או אין כבידה בסביבה. באופן דומה, קיים מטען שחש כוח מסוג חדש שנקרא כוח חשמלי.
2.1 תיאור המטען החשמלי
המטען החשמלי ניתן לתיאור בשני אופנים:
-
מטען נקודתי או מטען של גוף סופי:
- $q$ (קטן) - מטען של גוף נקודתי (כמו אלקטרון)
- $Q$ (גדול) - מטען כולל של גוף שאינו נקודתי (כמו כדור טעון)
-
צפיפות מטען רציפה:
כשנעסוק בריכוז גדול של מטענים (למשל $10^{30}$ אלקטרונים), מרחוק זה ייראה כמו “נוזל של אלקטרונים”. במקרה כזה נתאר את המטען באמצעות צפיפות:
\[\rho(\vec{r}, t)\]זה שדה סקלרי - פונקציה של המקום ושל הזמן, שנותנת את צפיפות המטען בכל נקודה ונקודה.
2.2 יחידות ודוגמאות
יחידות: ביחידות $\mathrm{MKS}$, המטען נמדד בקולון $(\mathrm{Coulomb})$.
דוגמאות למטענים:
-
מטען כדור הארץ: $Q_{\text{Earth}} = 0$ בדיוק, תודה לאל. זה מזל גדול - אם כדור הארץ והירח היו טעונים במטענים חשמליים, לא היו חיים. הכוח החשמלי חזק בעשרות סדרי גודל מכוח הכבידה (כ-40 סדרי גודל!). האינטראקציות היו חזקות עד כדי התפרקות כדור הארץ במקרה אחר.
-
מטען האלקטרון: $q_e = -1.6 \times 10^{-19} \, \mathrm{C}$ (מטען שלילי)
-
מטען הפרוטון: $q_p = +1.6 \times 10^{-19} \, \mathrm{C}$ (מטען חיובי)
להבדיל ממטענים כבידתיים שהם תמיד חיוביים, מטענים אלקטרומגנטיים מגיעים בשני סימנים - חיוביים ושליליים.
מטען האלקטרון הוא עשירית של מיליארדית של מיליארדית של קולון - מטען קטן מאוד. קולון הוא מטען גדול מאוד - צריך $10^{19}$ אלקטרונים כדי לקבל מטען של קולון אחד.
מטענים במעבדה הם בדרך כלל מסדר גודל של:
- $10^{-6} \, \mathrm{C}$ (מיקרו-קולון)
- $10^{-9} \, \mathrm{C}$ (ננו-קולון)

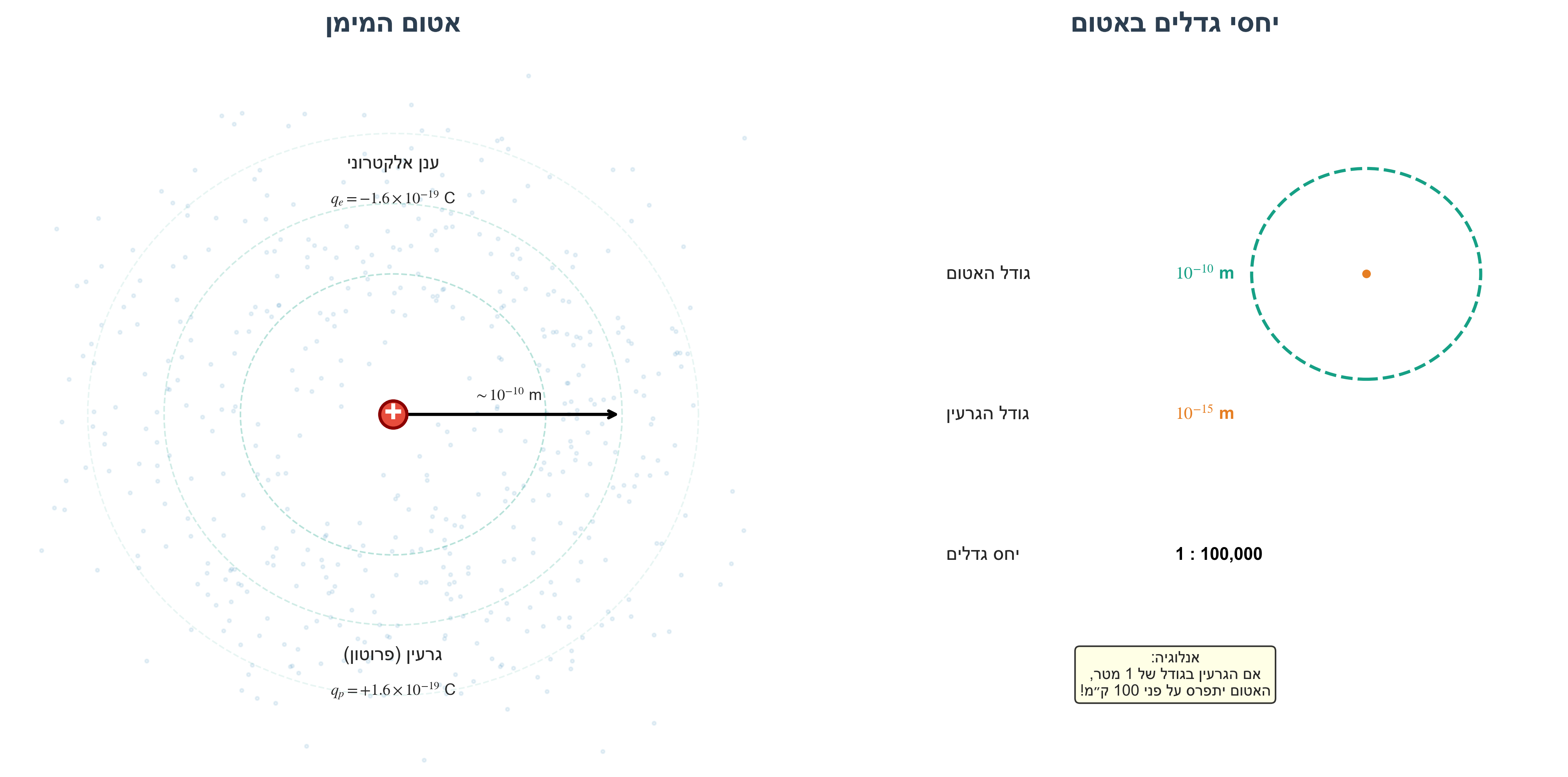
2.3 אטום המימן - דוגמה לניטרליות
באטום מימן יש גרעין עם פרוטון טעון חיובית ($+1.6 \times 10^{-19} \, \mathrm{C}$) וענן אלקטרוני טעון שלילית ($-1.6 \times 10^{-19} \, \mathrm{C}$). בסך הכל האטום ניטרלי.
יחסי הגדלים באטום:
- קוטר אטום המימן: כ-$10^{-10}$ מטר (1 אנגסטרם)
- גודל הגרעין (פרוטון): כ-$10^{-15}$ מטר
הגרעין קטן בחמישה סדרי גודל מהאטום. אם נגדיל את הפרוטון למטר אחד, הענן האלקטרוני יתפרס למרחק של כ-100 קילומטר - מהאזור הזה עד בירות בצפון, עכו במערב, רבת עמון או ירושלים בדרום (לא מעט).
הנפח של הפרוטון קטן ב-15 סדרי גודל מנפח האטום (כי נפח הולך כמו רדיוס בשלישית). כמעט כל המסה של האטום מרוכזת בגרעין (רק 1/2000 מהמסה בענן האלקטרוני). לכן האטום הוא ברובו ריק מוחלט.
דוגמה מעודדת: אם מסלקים מאדם את כל הנפח המיותר (הנפח האלקטרוני) ומשאירים רק את החומר בצפיפות גרעינית, האדם מצטמצם לגודל של בקטריה - כ-50 מיקרון. כל השאר הוא שדה אלקטרוני כמעט חסר מסה.
בטבע קיימים כוכבי נייטרונים - כוכבים שקרסו מהם כל האלקטרונים. כוכב עם מסה של השמש (333,000 מסות כדור הארץ) מרוכז בכדור בקוטר של כ-20 קילומטר - כגודל תל אביב.
כולנו בסך הכל ריקים, עם מעט מאוד חומר אמיתי בתוכנו.
2.4 חישוב מטען כולל מצפיפות
כשנתונה צפיפות מטען רציפה $\rho(\vec{r}, t)$ בנפח $\Omega$, המטען הכולל הוא:
\[Q_\Omega = \int_\Omega \rho(\vec{r}, t) \, d^3r\]כאשר $d^3r = dx \, dy \, dz$ הוא אלמנט הנפח.
3. העיקרון היסודי: מטען חשמלי קורן את השפעתו למרחב
זאת טענה שאין לנו דרך להוכיח אלא באמצעות תצפית.
אחת התופעות שאנחנו שמים אליהן לב היא שגופים טעונים במטען חשמלי קורנים את השפעתם למרחב.
3.1 הגדרת שדה הפוטנציאל החשמלי
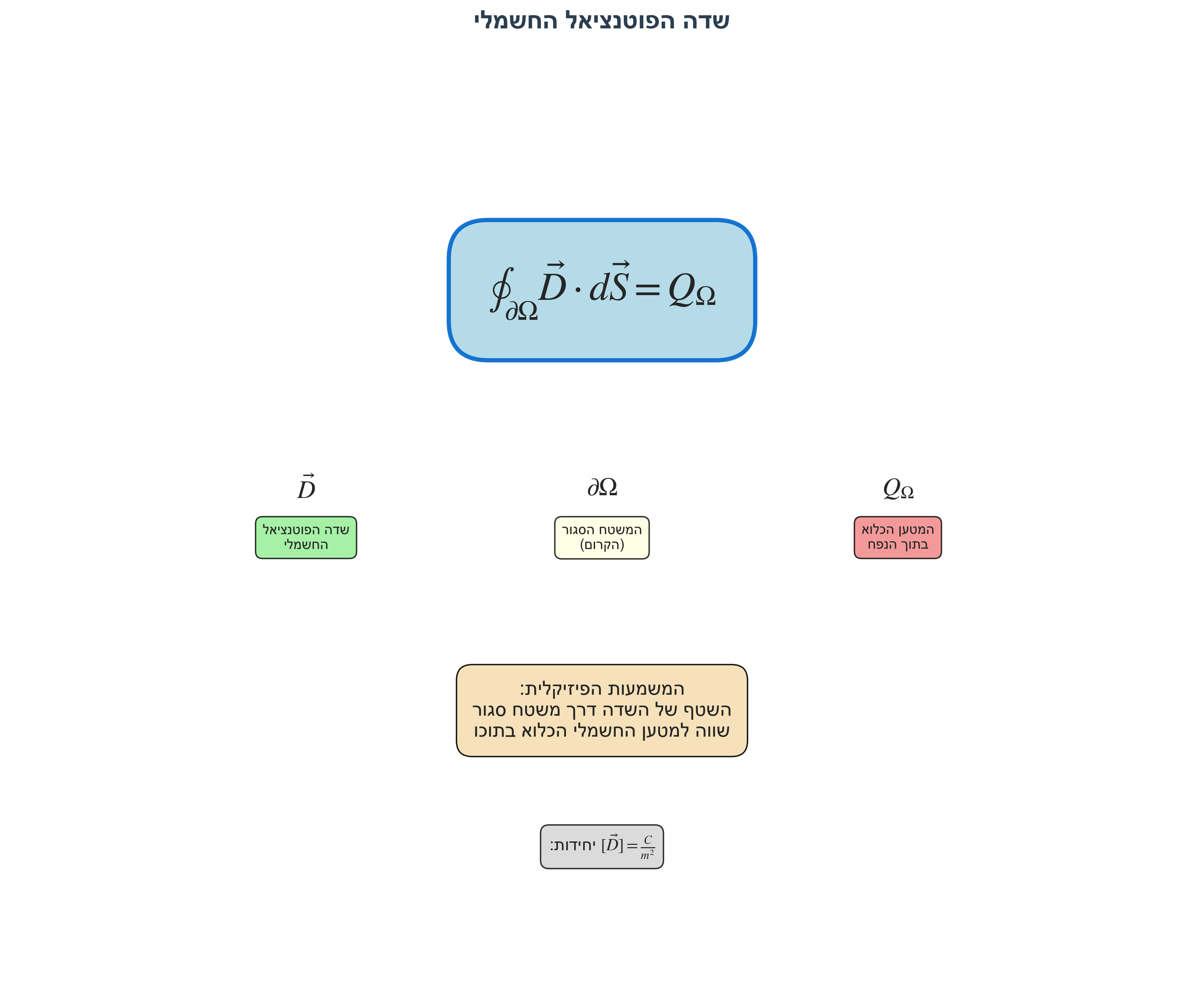
כדי לתת ביטוי מתמטי לרעיון ש״מטען קורן השפעה למרחב״ (שטרם ברור לכותב שורות אלו, לשם ההגינות), נגדיר שדה וקטורי $\vec{D}$ שמאפיין את המטען החשמלי או שמושרה על ידי המטען החשמלי.
ההגדרה המתמטית:
קיים שדה וקטורי המושרה על ידי המטען החשמלי כך ש:
\[\Phi = \oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = Q_\Omega\]כאשר:
- $\Phi$ - השטף (flux) של השדה דרך המשטח
- $\partial\Omega$ - הקרום (המשטח הסגור) שתוחם את הנפח $\Omega$
- $Q_\Omega$ - המטען הכולל הכלוא בתוך הנפח
במילים לא פשוטות: השטף שיוצא מהקרום שתוחם את $\Omega$ שווה למטען החשמלי שכלוא בתוך $\Omega$.
3.2 חישוב השטף
השטף דרך אלמנט שטח אינפיניטסימלי:
\[d\Phi = \vec{D} \cdot d\vec{S} = \vec{D} \cdot \hat{n} \, dS\]כאשר $d\vec{S} = \hat{n} \, dS$ - וקטור ששטחו $dS$ וכיוונו בכיוון הנורמל $\hat{n}$.
השטף הכולל דרך משטח סגור:
\[\Phi = \oint_{\partial\Omega} \vec{D} \cdot d\vec{S}\]3.3 שם השדה ויחידותיו
לשדה $\vec{D}$ קוראים:
- שדה הפוטנציאל החשמלי (Electric Displacement Field)
- או מסיבות היסטוריות: שדה ההעתק
יחידות: כדי שיהיה שוויון יחידות בין שני האגפים:
\[[\vec{D}] = \frac{\text{C}}{\text{m}^2}\]4. חוק גאוס ומשוואת מקסוול הראשונה
4.1 הצורה האינטגרלית - חוק גאוס
\[\boxed{\oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = Q_\Omega}\]כאשר המטען הכולל ניתן על ידי:
\[Q_\Omega = \int_\Omega \rho(\vec{r}, t) \, d^3r\]לכן:
\[\oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = \int_\Omega \rho(\vec{r}, t) \, d^3r\]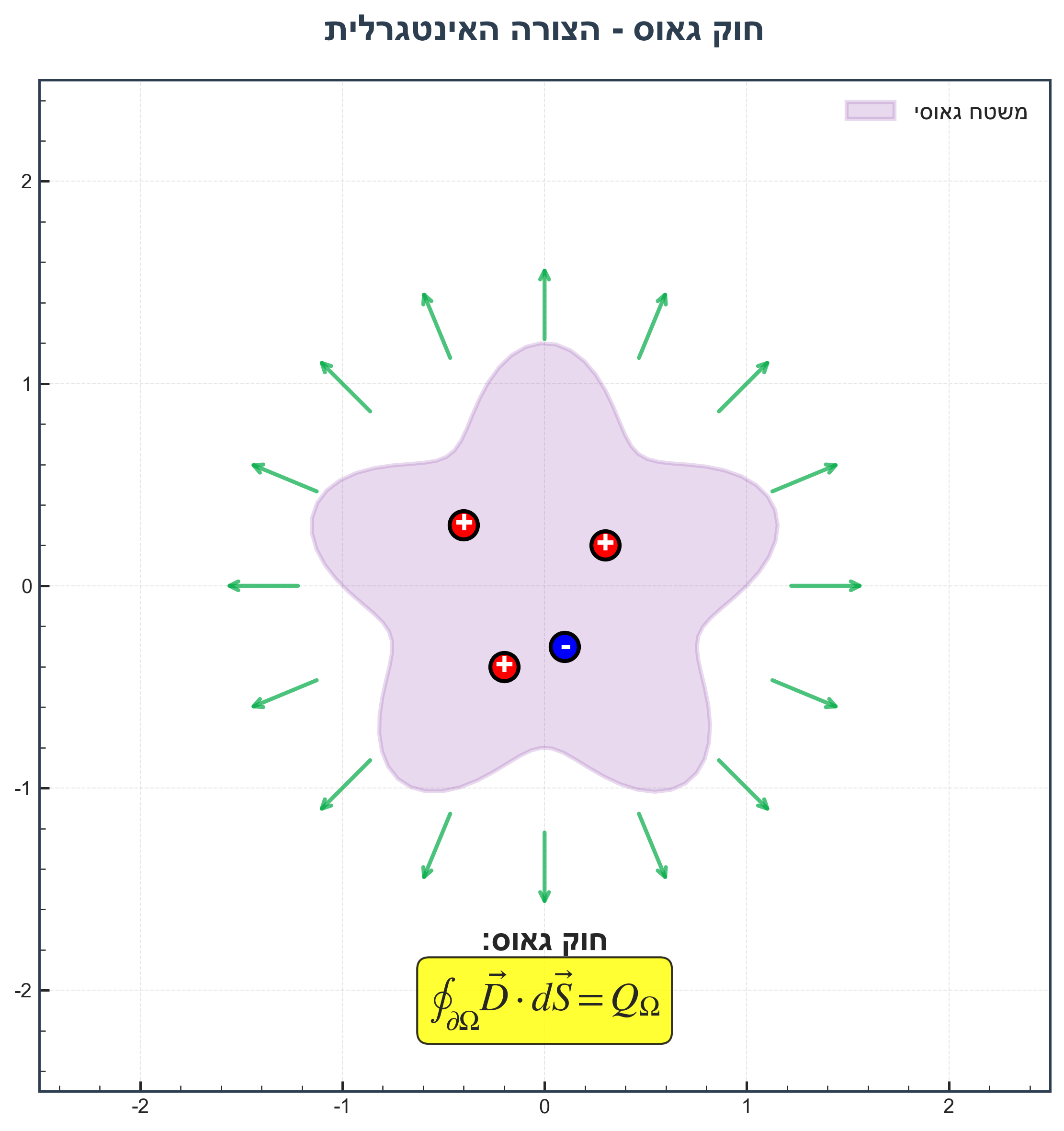
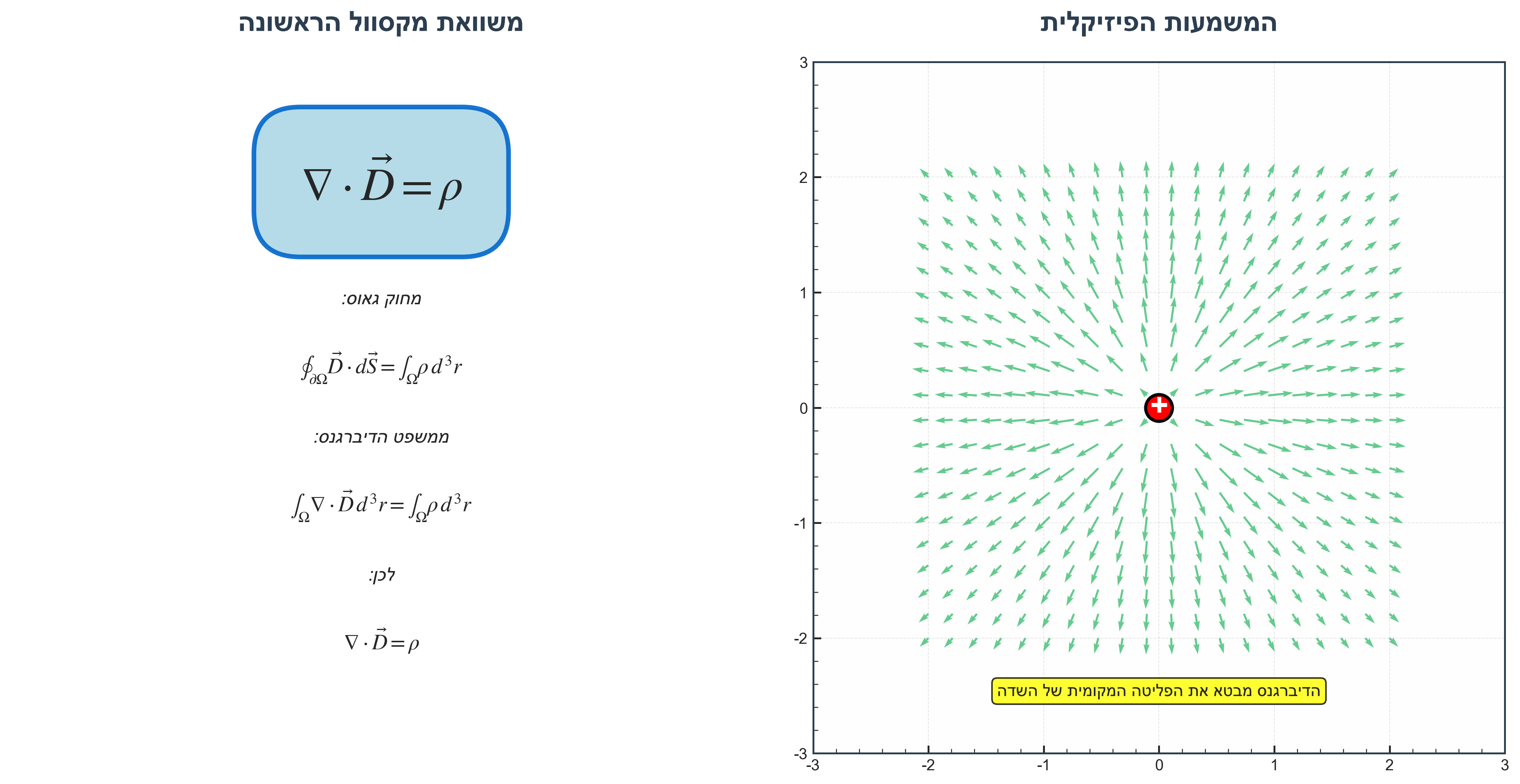
4.2 הצורה הדיפרנציאלית - משוואת מקסוול הראשונה
באמצעות משפט הדיברגנס:
\[\oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = \int_\Omega \nabla \cdot \vec{D} \, d^3r\]משילוב עם חוק גאוס:
\[\int_\Omega \nabla \cdot \vec{D} \, d^3r = \int_\Omega \rho \, d^3r\]מכיוון ששני האינטגרלים המרחביים שווים לכל נפח $\Omega$, האינטגרנדים שווים:
\[\boxed{\nabla \cdot \vec{D} = \rho}\]זאת משוואת מקסוול הראשונה - אחת מארבע משוואות מקסוול שמתארות את כל התורה האלקטרומגנטית.
המשמעות הפיזיקלית: הדיברגנס של $\vec{D}$ (הפליטה המקומית של השדה) מבטא את צפיפות המטען החשמלי המקומית.
הבדל בין הצורות:
- חוק גאוס - חוק גלובלי (אינטגרל על משטח סופי)
- משוואת מקסוול - חוק לוקלי (נכון בכל נקודה ונקודה)
חשוב להדגיש: פיזיקאים בסוף המאה ה-19 עשו אינספור ניסויים במעבדה כדי להגיע למשוואות האלו. אנחנו הגענו אליהן בלי שום ניסוי, רק משיקולים פילוסופיים נטו - מההנחה שמטען קורן השפעה למרחב (ומכך שבכלל קיים דבר כזה ״מטען״).
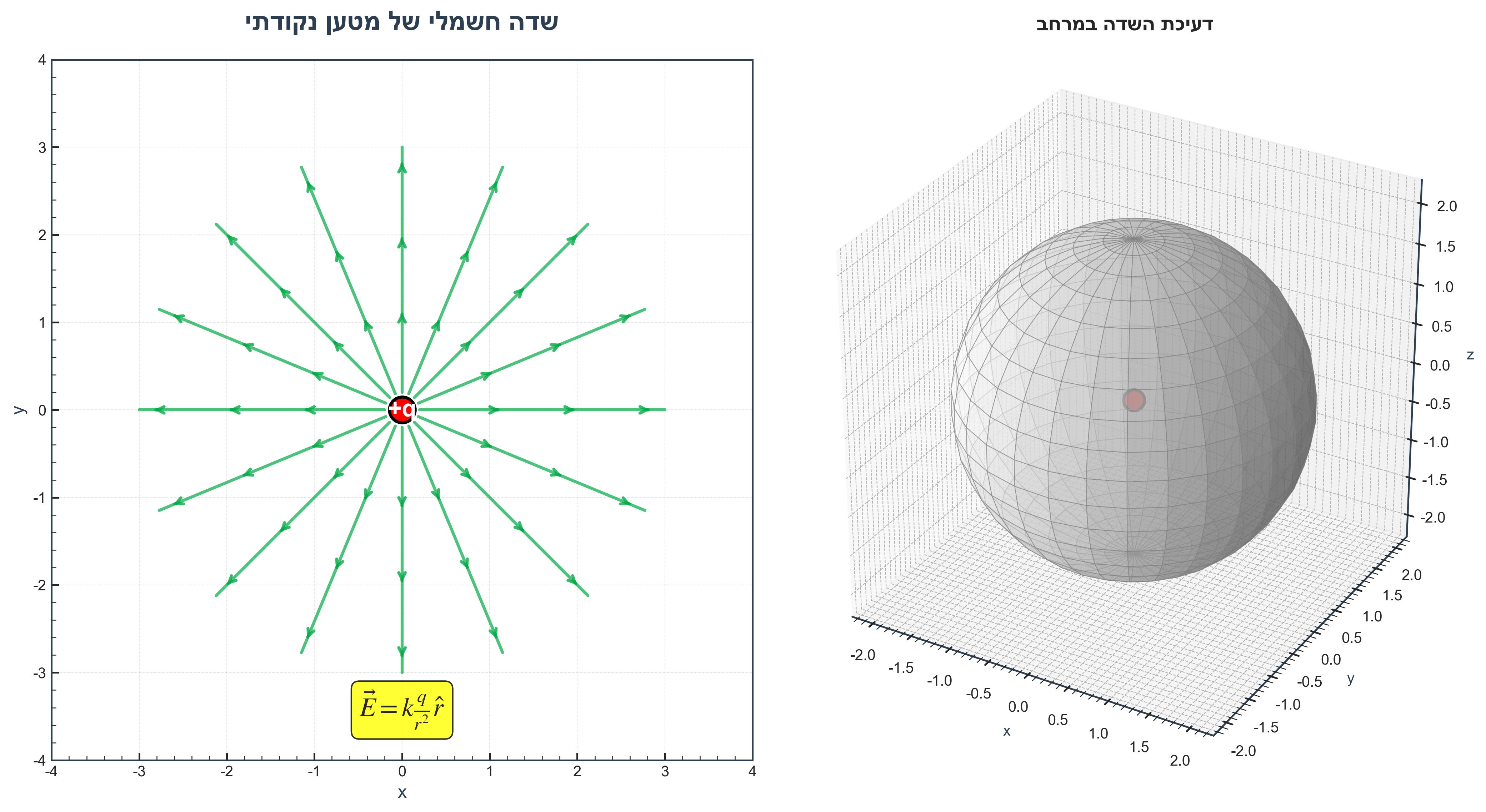
5. יישום חוק גאוס - מטען נקודתי
5.1 הבעיה והסימטריה
נחשב את השדה $\vec{D}$ שמושרה ממטען נקודתי $q$ (למשל אלקטרון).
נבנה בדמיון כדור סביב המטען - הכדור קיים רק בראש, לא במציאות. המטען ממוקם במרכז הכדור. לנפח הכדור נקרא $\Omega$, ולקרום (הקליפה) שתוחם אותו נקרא $\partial\Omega$.
זאת בעיה עם סימטריה רדיאלית קלאסית - לא משנה איפה אנחנו על הקליפה, הקונפיגורציה תמיד תיראה אותו הדבר. אין העדפה של נקודה מסוימת על הקליפה. המרחק מהמטען הוא תמיד אותו מרחק, וכיוון ההשפעה תמיד בכיוון הנורמל (הרדיאלי).
5.2 החישוב
מסימטריה:
- השדה $\vec{D}$ חייב להיות בכיוון רדיאלי: $\vec{D} = D_r(r) \hat{r}$
- הגודל $D_r$ יכול להיות פונקציה רק של המרחק $r$, לא של הזוויות
לכן:
\[\vec{D} \cdot \hat{n} = D_r(r)\]כיוון ש-$D_r$ קבוע על פני כל הקליפה:
\[\oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = D_r(r) \oint_{\partial\Omega} dS = D_r(r) \cdot 4\pi r^2\]מחוק גאוס:
\[4\pi r^2 D_r(r) = q\]לכן:
\[D_r(r) = \frac{q}{4\pi r^2}\]או בצורה וקטורית:
\[\boxed{\vec{D} = \frac{q}{4\pi r^2} \hat{r}}\]השדה דועך כמו $1/r^2$ והוא מכוון רדיאלית.
6. הגדרת שדה העוצמה החשמלית
נגדיר שדה חדש $\vec{E}$ דרך הקשר:
\[\vec{E} = \frac{\vec{D}}{\epsilon}\]כאשר $\epsilon$ הוא קבוע שמאפיין את התווך שבו מונח המטען.
עבור ריק (ואקום): $\epsilon = \epsilon_0$ (הפרמיטיביות של הריק)
עבור מטען נקודתי בריק:
\[\vec{E} = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} \hat{r}\]נגדיר:
\[k = \frac{1}{4\pi\epsilon_0} = 9 \times 10^9 \text{ (some units)}\]אז:
\[\boxed{\vec{E} = k \frac{q}{r^2} \hat{r}}\]ההקבלה לכבידה:
- שדה כבידה: $\vec{g} = G \frac{M}{r^2} \hat{r}$
- שדה חשמלי: $\vec{E} = k \frac{q}{r^2} \hat{r}$
7. קונפיגורציות סימטריות נוספות
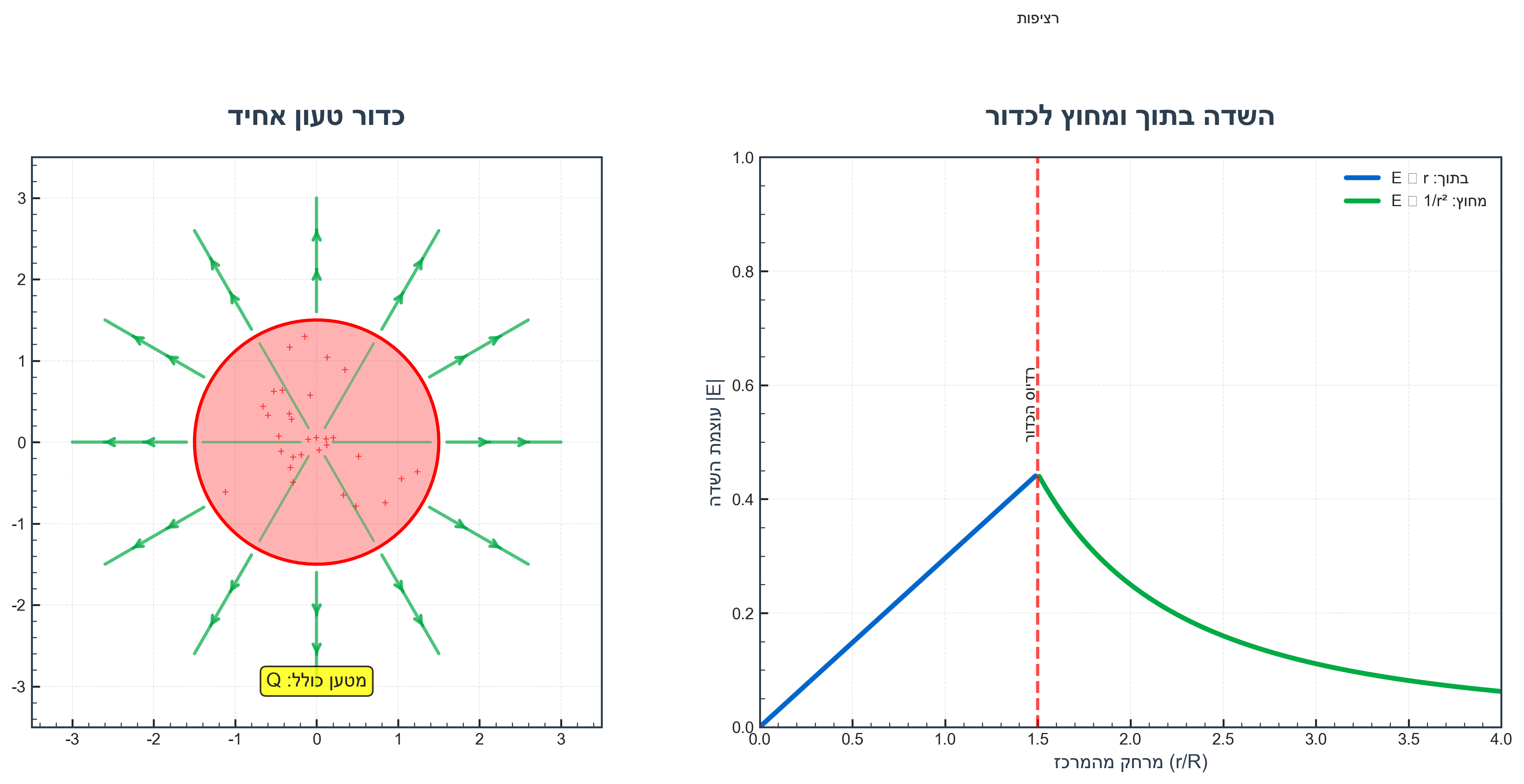
7.1 כדור מלא טעון
כדור ברדיוס $R$ עם מטען כולל $Q$ מפוזר בתוכו.
מאותם שיקולי סימטריה כדורית, עבור $r > R$:
\[\vec{E} = k \frac{Q}{r^2} \hat{r}\]מסקנה חשובה: מבחינת השדה מחוץ לכדור, אין הבדל אם המטען נקודתי או מפוזר בכדור - הסימטריה הכדורית נשמרת.
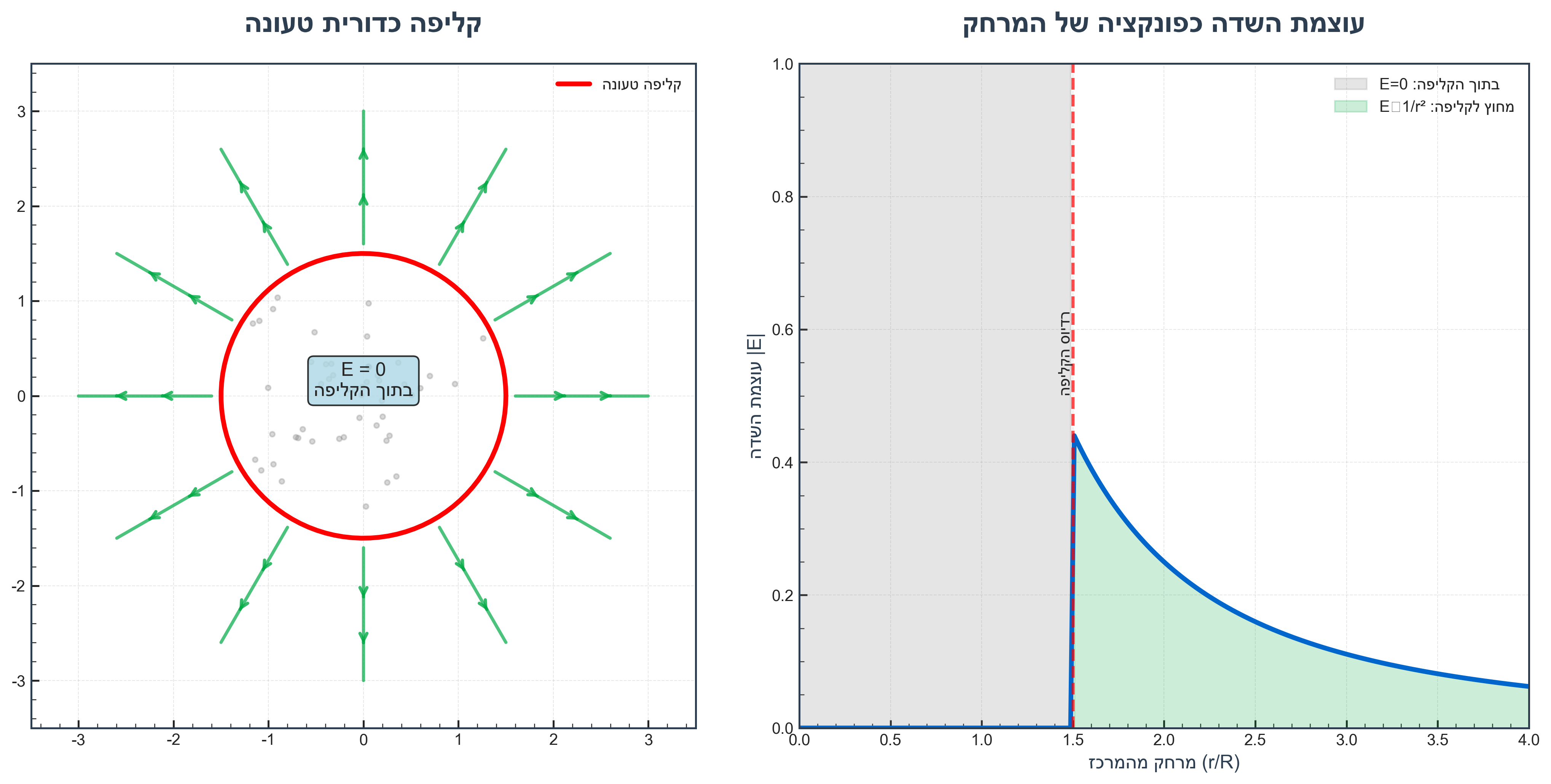
7.2 קליפה כדורית טעונה
קליפה כדורית דקה עם מטען $Q$ על הקליפה.
מחוץ לקליפה ($r > R$):
מאותם שיקולי סימטריה:
\[\vec{E} = k \frac{Q}{r^2} \hat{r}\]בתוך הקליפה ($r < R$):
נבנה משטח גאוסי כדורי בתוך הקליפה. מסימטריה, השדה (אם קיים) חייב להיות רדיאלי.
אבל המטען התחום על ידי המשטח הגאוסי הפנימי הוא: $Q_{\text{inside}} = 0$
לכן מחוק גאוס:
\[4\pi r^2 E_r = 0 \Rightarrow E_r = 0\]מסקנה: בתוך קליפה כדורית טעונה השדה החשמלי הוא אפס!
8. מטענים חיוביים ושליליים
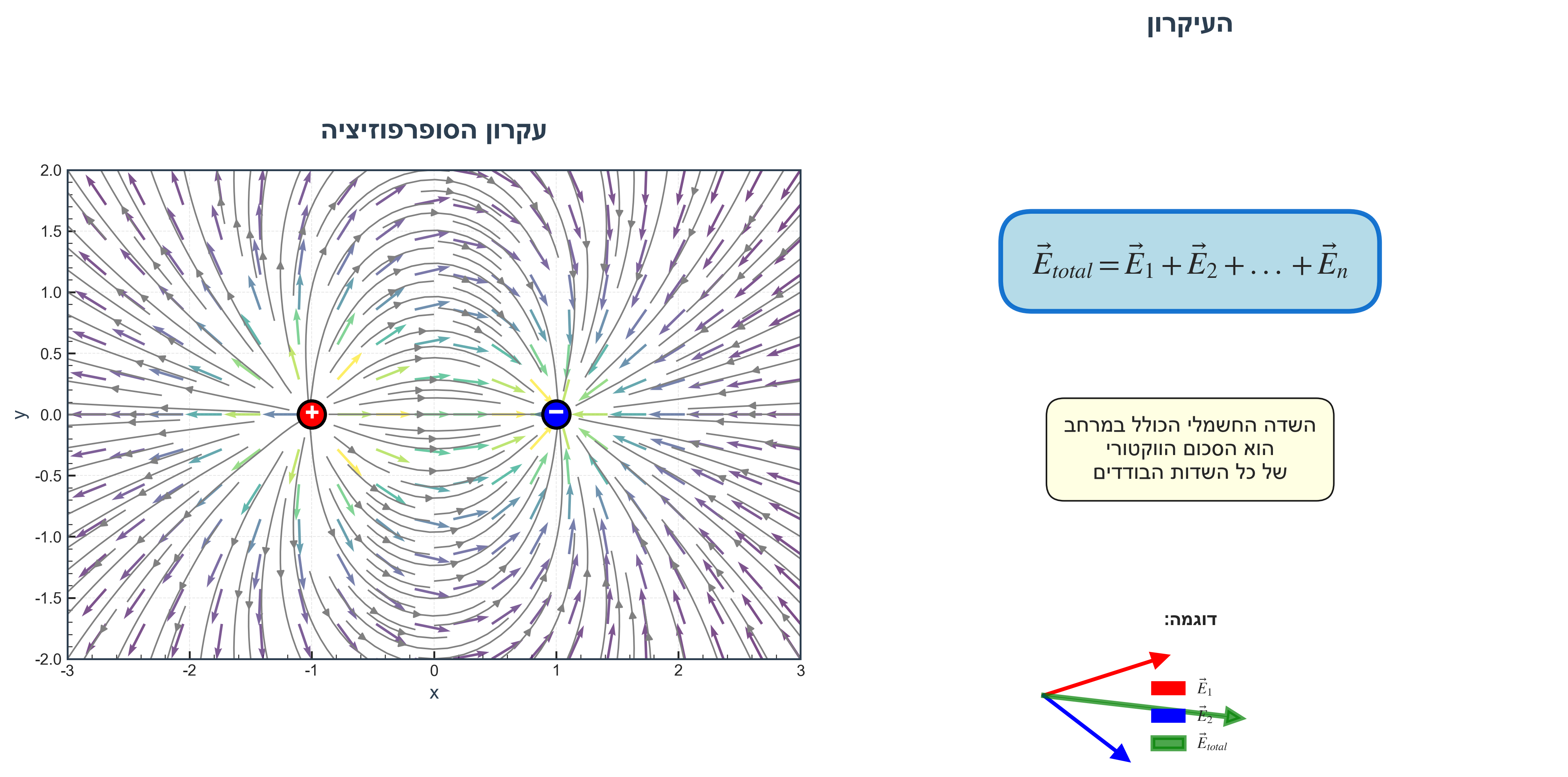
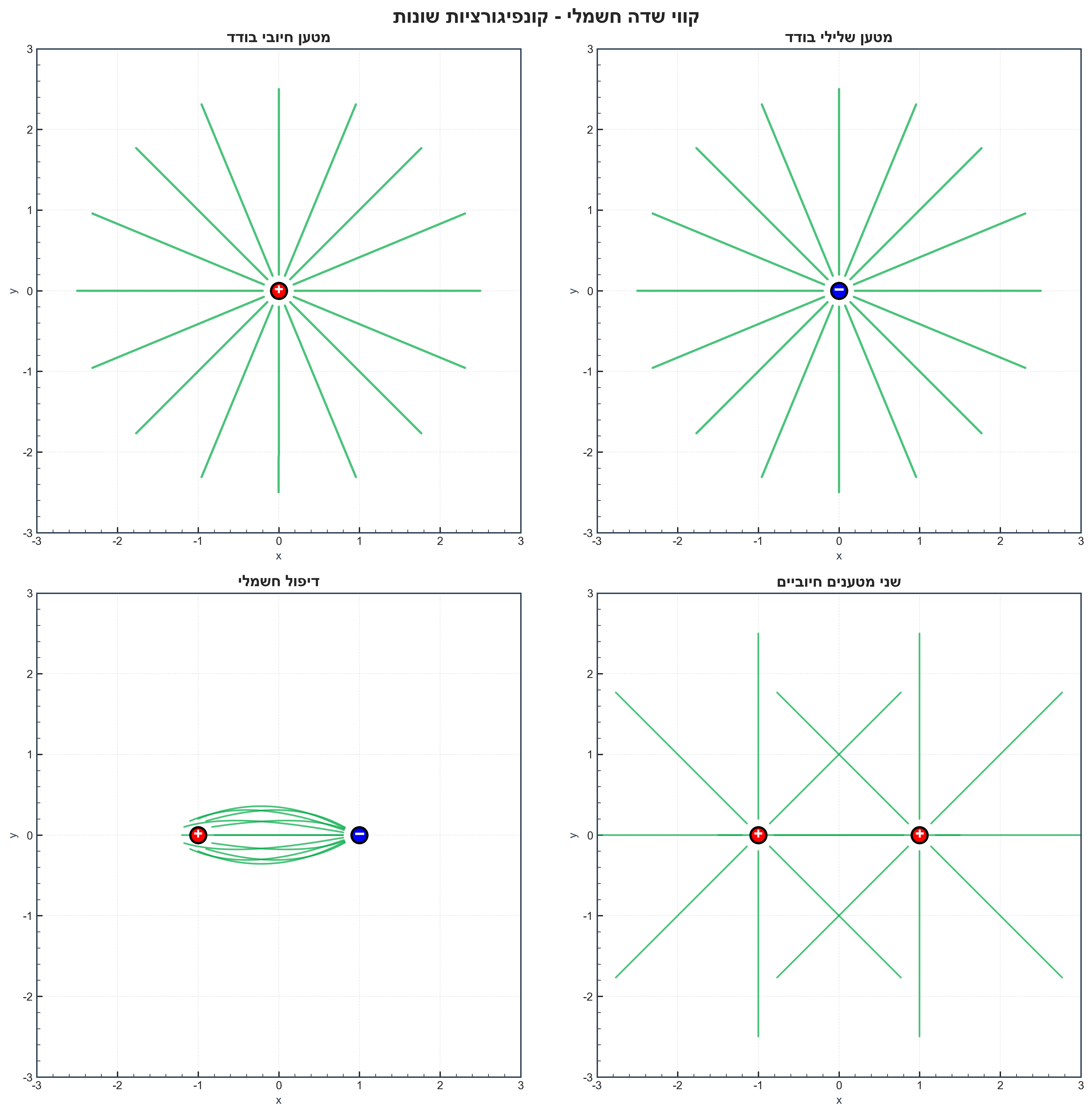
- מטען חיובי - מקור: קורן את השפעתו החוצה מהמרחב. קווי השדה יוצאים ממנו.
- מטען שלילי - בולען: קורן את השפעתו מהמרחב פנימה. קווי השדה נכנסים אליו.
כאשר יש במרחב שני מטענים או יותר, השדה הכולל הוא הסכום הוקטורי של השדות הבודדים - עקרון הסופרפוזיציה.
9. הערות על הפיתוח
חוק גאוס, שהיה צריך לבנות אותו במשך עשרות שנים עד שהבינו שהוא מתאר את התופעות החשמליות במציאות, התגלה כאן כהגדרה של שדה ההשפעה החשמלית. משוואת מקסוול הראשונה התגלתה כביטוי הלוקלי של אותה הגדרה.
שיהיה בהצלחה!
 דור פסקל
דור פסקל