הצעת פתרון למבחן לדוגמה

להלן הצעת פתרון לשאלות מהמבחן לדוגמה. תשומת הלב ש GPT ושות׳ לא מצליחים, אולי בגלל האפשרות לכמה תשובות נכונות. הקובץ מתעדכן בחלקים, לפי קצב הפתרון. מוזמנים להתעדכן.

כמו תמיד - אין לנו יכולת לדעת מה צפוי במבחן האמיתי, האם התשובות שהצענו נכונות, ומה המשמעות של הספרה 42. אם יש לכם אינפורמציה מסייעת, תיקונים או ערך אחר שאתם רוצים לתרום - מוזמנים לפנות.

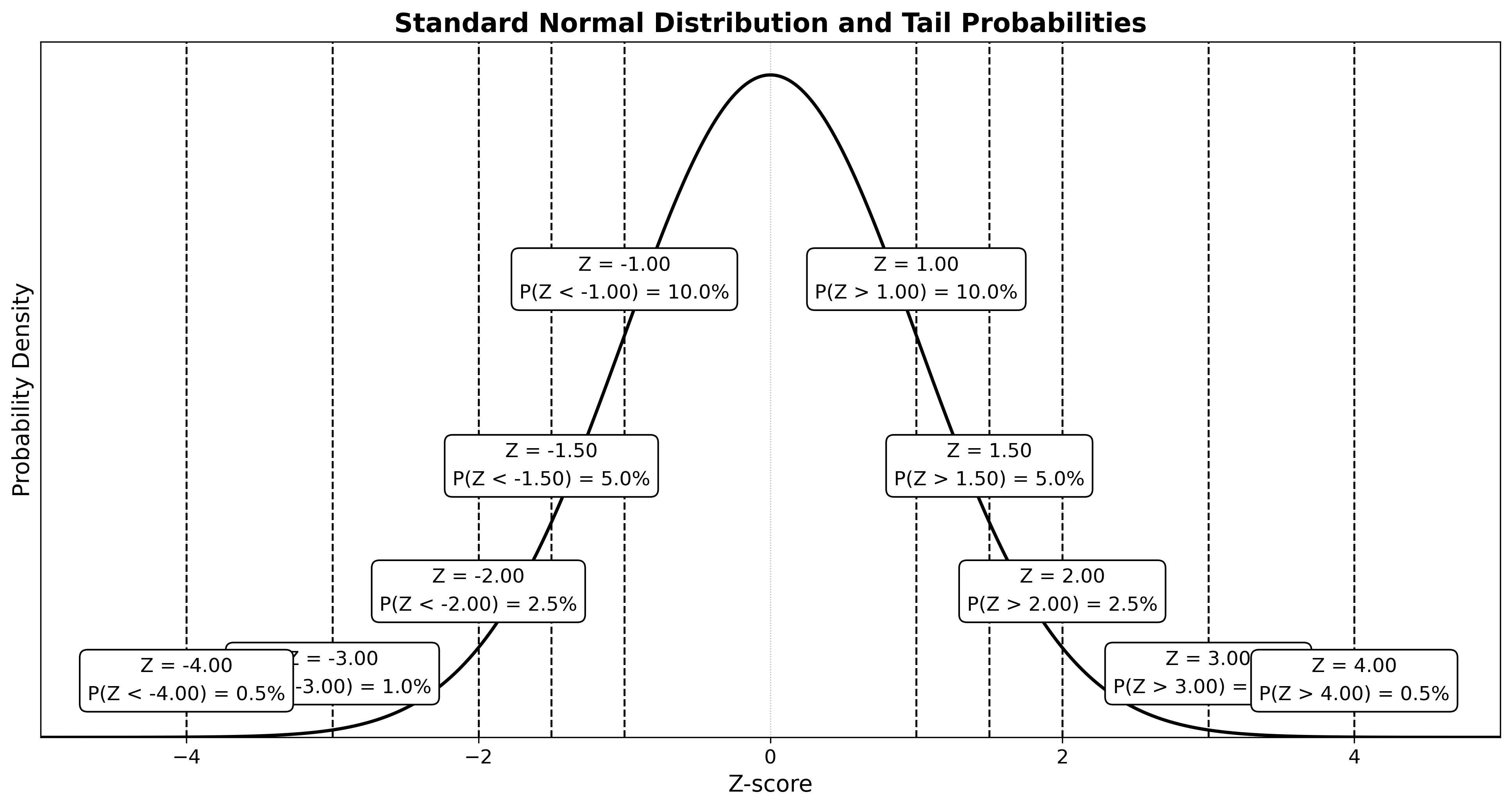
שאלה 1

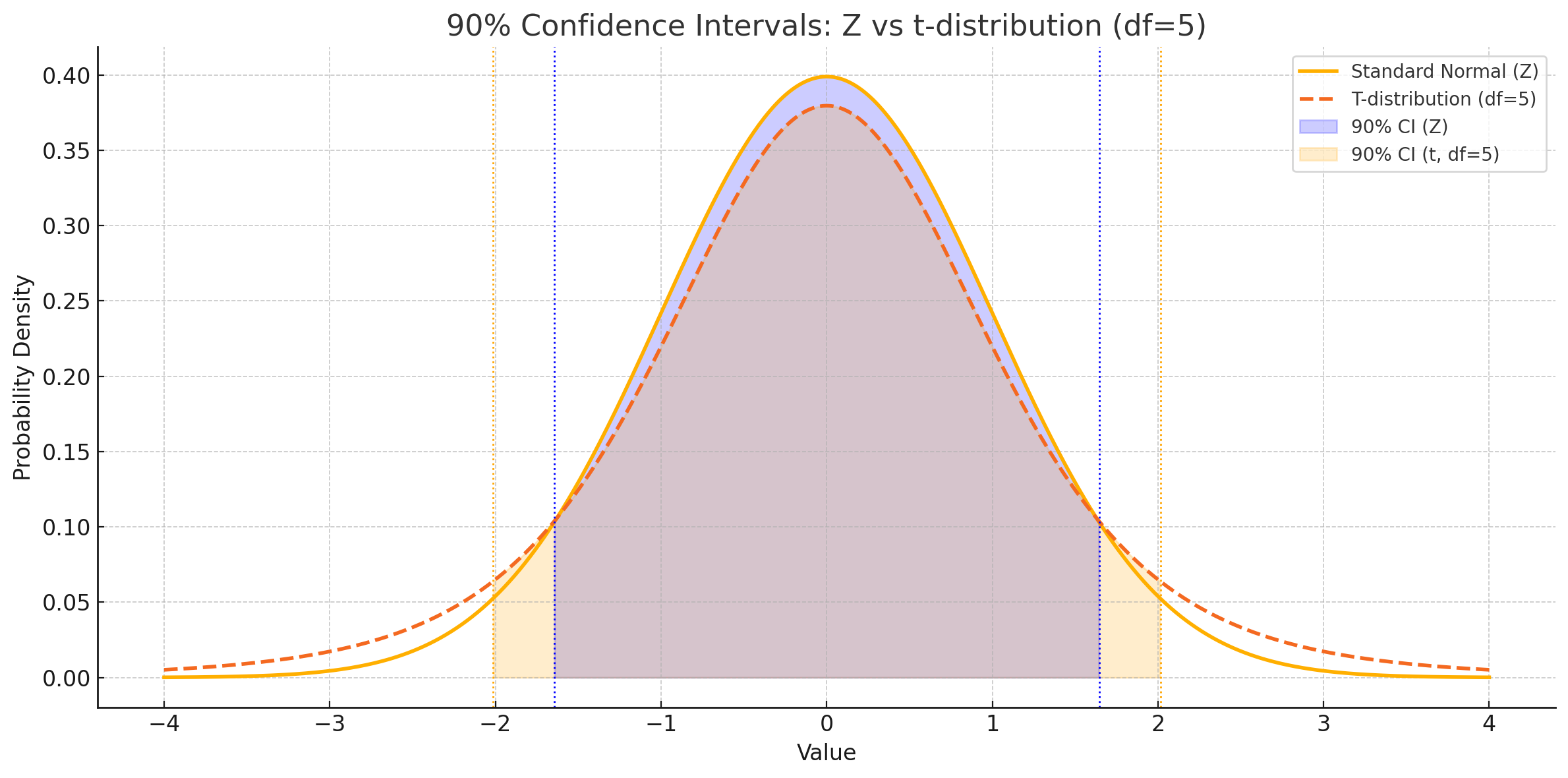
חוקרת בנתה רווח סמך ברמת סמך של 90% עבור התוחלת כאשר השונות ידועה והתפלגות נורמלית.

• א. לא נכון - הנוסחה לרמת הסמך היא:

  \[\bar{x} \pm z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\]

  לכן, אם נגדיל את $n$, רמת הסמך תקטן - לא תגדל.

• ב. לא נכון - אם התוחלת מכילס אפס - זה לא נכון. התוחלת היא לא טווח אלא ערך.

• ג. נכון - החוקרת הייתה יכול לבנות סמך גם בלי לדעת את השונות, באמצעות שימוש בהתפלגות t.

• ד. נכון - אם החוקרת לא הייתה יודעת את השונות רווח הסמך היה מתרחב, לא מצטמצם.

  הסבר: כאשר השונות ידועה, אנחנו משתמשים בהתפלגות נורמלית, שהיא מדויקת יותר. כאשר השונות לא ידועה, אנחנו משתמשים בהתפלגות t, שהיא רחבה יותר ולכן רווח הסמך יהיה רחב יותר.

  

שאלה 2: בדיקת TB

בדיקה מזהה ב 0.9 הסתברות. מזהה בריאים כחולים ב 0.05. השכיחות באוכלוסיה היא 0.01.

מה ההסתברות שמישהו חולה אם אובחן כחולה?

אפשר להשתמש בקירוב מגניב שיאיר לימד בשיעור 7:

נניח לנוחות שיש אוכלוסייה גדולה של 100,000 איש.

אז מתוכם $1,000$ יהיה חולה (השכיחות באוכלוסייה).

הFP יהיו 0.05 מתוך 99,999 הבריאים, כלומר. נעגל לנוחות ל־$5,000$.

סך הכל נקבל :

התוצאה האמיתית מעט קטנה יותר (כי חילקנ במספר קטן יותר כשעיגלנו למטה).

התשובה המתאימה היא ב:

הבהרה: אם היינו רוצים לחשב במדויק היינו צריכים גם להכפיל את החולים ב־$0.9$ ו־$0, כלומר:

שאלה 3

מודל רגרסיה:

\[\text{vaccine uptake} = \alpha + \beta_1 \times \text{health} + \beta_2 \times \text{gender} + \beta_3 \times \text{education}\]

הפרמטרים הם:

• α: קבוע
• β₁: השפעת הבריאות (health)
• β₂: השפעת המגדר (gender)
• β₃: השפעת ההשכלה (education)

לרופא גבר (gender=0), בריא לחלוטין (health=4), עם 18 שנות לימוד:

\[\text{vaccine uptake} = α + 4β₁ + 0×β₂ + 18β₃ = α + 4β₁ + 18β₃\]

אני לא בטוח אגב, נראה שאפשר לפרש בכמה אופנים את השאלה.

שאלה 4

מבחן $\chi^2$ על טבלת שכיחויות בגודל 3x3, נותן סטטיסטי $\chi^2 = 7.5$.

מה ה-p-value של המבחן?

1. chi2(df=4).sf(7.5)
2. chi2(df=1).sf(7.5)
3. 2*chi2(df=1).sf(7.5)
4. 2*chi2(df=4).sf(7.5)
5. chi2(df=8).sf(7.5)
6. 2*chi2(df=9).sf(7.5)

ה־p-value של מבחן $\chi^2$ תלוי בדרגות החופש. במקרה של טבלת שכיחויות 3x3, דרגות החופש הן:

לכן, ה־p-value הוא:

import scipy.stats as stats
p_value = stats.chi2.sf(7.5, df=4)
print(p_value)

נבדוק האם יש תשובות נסופות נכונות:

• תשובה 1: chi2(df=4).sf(7.5) - נכון, כי דרגות החופש הן 4.
• תשובה 2: chi2(df=1).sf(7.5) - לא נכון, דרגות החופש לא מתאימות.
• תשובה 3: 2*chi2(df=1).sf(7.5) - לא נכון, דרגות החופש לא מתאימות.
• תשובה 4: 2*chi2(df=4).sf(7.5) - לא נכון, הכפלנו ב־2 שלא לצורך.
• תשובה 5: chi2(df=8).sf(7.5) - לא נכון, דרגות החופש לא מתאימות.
• תשובה 6: 2*chi2(df=9).sf(7.5) - לא נכון, דרגות החופש לא מתאימות.

שאלה 5

חוקרים רוצים לבדוק השערה כי תוחלת עלות חדרי המלון בצפת גבוהה מהתוחלת הארצית. נתון שהתוחלת הארצית היא 280 ש״ח ללילה. הם אספו מידע על 16 בתי מלון והריצו בפייתון מבחן t כלהלן:

CopyRun

scipy.stats.ttest_1samp(x=280, popmean=0,alternative='two-sided')

התקבל הפלט:

CopyRun

TtestResult(statistic=np.float64(1.94), pvalue=np.float64(0.071), df=np.int64(15))

מהו ה־p-value של המבחן?

תהשובה היא ו׳ - לא ניתן לדעת, החוקרים טעו בשימוש בפייתון:

scipy.stats.ttest_1samp(x=280, popmean=0, alternative='two-sided')

אין לפונקציה ttest_1samp פרמטר x - היא מקבלת מדגם, לא תוחלת. החוקרים העבירו את התוחלת הארצית במקום מדגם.

הם לא העבירו את המדגם אלא את התוחלת הארצית, ולכן הפלט לא יהיה תקין. הדרך הנכונה לבדוק את ההשערה היא:

import scipy
sample_data = [290, 300, 310, 270, 280, 290, 295, 285, 275, 300, 310, 320, 280, 290, 295, 305] # example data
print(scipy.stats.ttest_1samp(a=sample_data, popmean=280, alternative='greater'))

הפלט אגב הוא:

TtestResult(statistic=3.909090909090909, pvalue=0.0006975605805789302, df=15)

זה אומר שה־p-value הוא בערך 0.0007, כלומר הרבה יותר קטן מ־0.05. לכן ההשערה שהעלות גבוהה מהתוחלת הארצית סבירה.

שאלה 6

בחירת 3 חולים מתוך 8 מתנדבים:

תשובה: ה

שאלה 7

תשובות: ו

שאלה 8

רגרסיה: גיל ~ אורך טלומרים

• R² = 0.810 (מודל מסביר 81% מהשונות)
• המודל מובהק (p < 0.001)

תשובות נכונות: א, ג

שאלות 11-9

הנתונים הבאים מתייחסים לשאלות 9–11. בחוג לרפואה 30 תלמידים. בסמסטר מסוים מסיימים שני קורסים.

ידוע כי ההסתברות שכל אחד מהתלמידים יעבור את הקורס הראשון היא 0.75 ואילו ההסתברות לעבור את הקורס השני היא 0.85.

הציונים של תלמידים הם בלתי תלויים, וכך גם הציון של כל תלמיד בשני הקורסים (ניתן להשתמש במחשבונים אך אפשר לפתור את השאלה בלעדיו).

שאלה 9

מה ההסתברות שלפחות 29 תלמידים יעברו את הקורס הראשון?

ההסתברות שלפחות 29 יעברו היא ההסתברות שבדיוק 29 או 30 תלמידים יעברו את הקורס הראשון:

התשובה הכי קרובה היא ד׳, אבל אני לא בטוח אם לא צריך לבחור שכל התשובות לא נכונות.

הערה: דרך פשוטה יותר היא לחשב את המשלים - ההסתברות שרק 1 או 0 תלמידים ייכשלו:

\[P(X \geq 29) = 1 - P(X < 29) = 1 - P(X = 0) - P(X = 1)\]

שאלה 10

…

שאלה 11

נסמן ב-$X$ את מספר התלמידים שעברו את הקורס הראשון וב־$Y$ את מספר התלמידים שעברו את הקורס השני.

חשבו את $Var(X-Y)$.

ההסתברות של תלמיד לעבור את הקורס הראשון היא 0.75, והשנייה 0.85. נחשב את השונות של ההפרש:

כאשר $Cov(X, Y) = 0$ כי הציונים בלתי תלויים.

לכן, נחשב את השונות של כל קורס בנפרד:

שאלות 14-12

הזמן שלוקח לד״ר שקשוקה לבצע ניתוח מתפלג נורמלית עם תוחל 20 וסטיית תקן של 5.

שאלה 12

מה הסיכוי שד״ר שקשושה יסיים ניתוח בזמן של 15 עד 25 דקות?

הערה: אפשר לזהות את התשובות מיידת אם שמים לב שהזמנים שואלים על טווח של 1 סטיית תקן מהתוחלת (20) לכל כיוון. מכאן התשובות הנכונות הן א׳ ו-ג׳:

אפשר גם לנסות לחשב.

נעבור למשתנה מתוקנן:

שאלה 13

מה העשירון התחתון של זמני הניתוח?

אפשר לבחור בתשובה הנכונה מהיגיון - 25 ו-30 נפסלות ישרר כי הן גבוהות מהתוחלת (20). התשובה הנכונה היא ג׳ - 15. 10 דקות נפסל כי הוא הרבה מתחת לתוחלת.

אפשר גם לחשב. לפי הקירוב שנתנו לנו iSF(0.1)=1. כלומר, 10% נמצאים מתחת ל־1 סטיית תקן מהתוחלת. סטיית תקן היא 5 דקות והתוחלת היא 20 דקות, אז התשובה היא 15.

שאלה 14

עלות חדר ניתוח היא 3000 ש״ח לניתוח ועלות הצוות היא 200 ש״ח לדקה. נסמן ב - $X$ את עלות הניתוח. מה השונות של $X$?

עלות חדר הניתוח קבועה אז היא לא תשפיע על השונות.

עלות הצוות מושפעת מזמן הניתוח, וזמן הניתוח מתפלג נורמלית עם תוחלת 20 וסטיית תקן 5.

מה שאומר שסטיית התקן של עלות הצוות היא:

אז השונות של עלות הצוות היא:

(סטיית התקן היא שורש השונות).

שאלות 17-15

שאלה 15

בניסוי עם 50 משתתפים חוקרים מצאו רווח סמך של 90% לתוחלת. רווח הסמך הוא (10,16).

מה יהיה רווח סמך של 98%?

התשובה ההגיונית היחידה היא ג - (7,19).

הרווח הגדול יותר יותר רחב, והשינוי נפרש באופן שווה לשני הצדדים.

אפשר להגיע מדרכים נוספות. למשל מהנוסחה לאורך של רוחב של רווח סמך:

מהקירובים בתחילת המבחן מה שמתאים ל-90% זה 1.5, ומזה שמתאים ל-98% זה 3. מכאן שהרוחב החדש יהיה 12.

שאלה 16

מה יהיה p-value שיתקבל מאותם נתונים עבור בדיקת השערת דו צדדית כאשר השערת האפס היא $H_0: \mu_0 = 10$?

ה־p-value עבור השערת אפס דו צדדית הוא:

שאלה 17

חצי מהנדגמים היו ילדים וחצי היו הוריהם. החוקרים מעוניינים לבצע מבחן השערות עבור ההפרש בין התוחלות של ילדים להוריהם. איזה מבחן מתאים?

1. מבחן t למדגם יחיד - לא מתאים כי יש לנו שני מדגמים (ילדים והורים).
2. מבחן t למדגמים מזווגים - מתאים אם מתייחסית לילדים וההורים כקבוצות תלויות (לדעתי זאת התשובה).
3. מבחן t לשני מדגמים בלתי תלויים - לדעתי לא מתאים כאן.
4. לא ניתן לדעת - לא נכון, אפשר לדעת. אבל כן יוצאים מנקודת הנחה כלשהי. שתי הקבוצות קטנות מ-30 וכו׳ גם לא בטוח ששונות ההפרשים וכו׳.

שאלה 18

מה רוחב רווח סמך 95% של יחס צולב של הנתונים הבאים:

	פיתחו תוצאה	לא פיתחו תוצאה
חשופים	5	50
לא חשופים	50	100

מתוך הנוסחאות בתרגול:

השונות של הלוגריתם של יחס הצולב (odds ratio) היא:

\[Var(log(OR)) = \frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}\]

ה-SE של הלוגריתם של יחס הצולב הוא השורש של השונות:

\[SE = \sqrt{Var(log(OR))} = \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}\]

רווח סמך ב-95%:

\[\log(OR) \pm 1.96 \cdot \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}\]

סטטיסטי נורמלי סטנדרטי:

\[\text{P-value} = P(Z < Z_0) \implies Z_0 = \frac{\log(OR)}{\sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}}\]

רווח הסמך ל-OR ב-95%:

\[e^{\left(\log(OR) \pm 1.96 \cdot \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}\right)}\]

הערה: ייתכן שהמתרגל טעה בחישוב בשאלה הזאת (הוא חילק ב 250 במקום ב- 2,500). בכל מקרה, נראה שאפשר לפתור בלי לחשב בכלל את CI.

רוחב רווח סמך של הלוגריתם של OR נתון על ידי הנוסחה:

צריך 90%, אז הערך הקריטי הרלוונטי הוא $Z_{\alpha/2}=Z_{0.025}$.

לפי הקירובים שניתן להשתמש בהם, $Z_{0.025} = 2$.

סך הכל נקבל:

אפשר להגיע לזה גם בדרך הארוכה:

רווח סמך ב־95% של הלוגריתם של יחס הצולב הוא:

לכן:

אפשר להמשך לחשב ולהגיע לרווח של 2, אבל זה לא הכרחי.

הערה נוספת - שימו לב להבדל בין הלוגריתם הטבעי ללוגריתם בבסיס 10 במחשבון.

שאלה 19

עבור משתנה מקרי נורמאלי $X \sim \mathcal{N}(\mu, \sigma^2)$, מגדירים את המשתנה $W=\frac{X - \mu}{2\sigma}$.

מה ההסתברות $P(W>w)$?

1. $P(Z>2w)$
2. norm().sf(2*w)
3. $P(X > \mu + 2\sigma w)$

תיתכן יותר מתשובה אחת נכונה (וגם שום תשובה נכונה).

נשים לב ש־$W$ הוא משתנה מקרי נורמלי עם תוחלת 0 וסטיית תקן 0.5:

1. נכון: $P(Z > 2w)$ - כי $W$ הוא משתנה מקרי נורמלי עם תוחלת 0 וסטיית תקן 0.5, ולכן $Z = \frac{W}{0.5}$.
2. נכון: norm().sf(2*w) - כי norm().sf מתאר את ההסתברות של משתנה מקרי נורמלי להיות גדול מ־$2w$.
3. נכון: $P(X > \mu + 2\sigma w)$ - כי $W$ הוא משתנה מקרי נורמלי עם תוחלת 0 וסטיית תקן 0.5, ולכן $X = \mu + 2\sigma W$.?

שאלות 21-20

מנהל המחלקה בונה לו״ז לרביעי ל 12 ניתוחים. חצי דחופים וחצי לא. יש 3 חדרי ניתוח ושלושה צוותים. הצוות בכל חדר יכול לבצע שלושה ניתוחים ביום.

מה הסיכוי שאולו צוות יבצע גם ניתוח מעקפים וגם תיקון בקע?

…

שאלות מהתרגול

שאלה 3: הסתברות בבחירת תלמידים

בכיתה 30 תלמידים מתוכם 12 תלמידים ו-18 תלמידות. יש לבחור למשלחת 4 תלמידים מהכיתה. התלמידים נבחרים באקראי:

1. מה ההסתברות שהמשלחת תורכב רק מבנות?
2. מה ההסתברות שבמשלחת תהיה רק בת אחת?
3. מה ההסתברות שבמשלחת תהיה לפחות בת אחת?

נתון: אורך חיי סוללה מתפלג מעריכית עם תוחלת של 8 שעות.

1. מה ההסתברות שסוללה תחזיק מעמד פחות מ-9 שעות?
2. מה הסיכוי שהיא תחזיק יותר מ-9 שעות?
3. מה סטיית התקן של אורך חיי הסוללה?
4. אם הסוללה החזיקה מעמד כבר שעתיים, מה הסיכויים שתחזיק מעמד מעל 7 שעות?

בהתפלגות מעריכית:

• אם התוחלת היא $\mu = 8$, אז הפרמטר $\lambda = \frac{1}{\mu} = \frac{1}{8}$
• פונקציית הצפיפות: $f(x) = \lambda e^{-\lambda x} = \frac{1}{8}e^{-\frac{x}{8}}$ עבור $x \geq 0$

• פונקציית ההתפלגות המצטברת:

  \[P(X \leq x) = F(x) = 1 - e^{-\lambda x} = 1 - e^{-\frac{x}{8}}\]

א. ההסתברות שסוללה תחזיק מעמד פחות מ-9 שעות:

ב. הסיכויים שהיא תחזיק יותר מ-9 שעות:

ג. סטיית התקן של אורך חיי הסוללה:

בהתפלגות מעריכית, סטיית התקן שווה לתוחלת:

ד. אם הסוללה החזיקה מעמד כבר שעתיים, מה הסיכויים שתחזיק מעמד מעל 7 שעות:

זו תכונת חוסר הזיכרון של ההתפלגות המעריכית:

סיכום התשובות:

• א. 0.6754 או 67.54%
• ב. 0.3246 או 32.46%
• ג. 8 שעות
• ד. 0.5353 או 53.53%