עבודה ואנרגיה במכניקה - כוחות משמרים וחוקי שימור: סיכום שיעור ותרגול 10
הקדמה: חזרה על מושג הגרדיאנט מהשיעור הקודם
בשיעור הקודם התחלנו ללמוד על מושג הגרדיאנט, מושג חשוב שישמש אותנו בלימודי אנרגיה. נחזור על עיקרי הדברים.
נגזרות חלקיות
כהקדמה להגדרת הגרדיאנט, יש להגדיר תחילה את מושג הנגזרת החלקית. עבור פונקציה של מספר משתנים - במקרה זה, פונקציה של שלושה משתנים המייצגת נקודה במרחב - ניתן לסמן אותה כפונקציה של וקטור המקום $\mathbf{r}$.
בפונקציה מרובת משתנים, הנגזרת החלקית של $F$ מוגדרת לפי כל אחד מהמשתנים - כלומר, הנגזרת של $F$ ביחס למשתנה מסוים כאשר שאר המשתנים נשארים קבועים.
לדוגמה, $\frac{\partial F}{\partial x}$ היא הנגזרת של $F$ לפי המשתנה $x$, והיא מוגדרת באופן הבא:
\[\frac{\partial F}{\partial x} = \lim_{\Delta x \to 0} \frac{F(x + \Delta x, y, z) - F(x, y, z)}{\Delta x}\]כאשר $y$ ו-$z$ נשארים קבועים.
באופן אנלוגי מוגדרות הנגזרות החלקיות לפי $y$ ולפי $z$, כאשר בכל מקרה שני המשתנים האחרים נשארים קבועים.
לפיכך, לפונקציה של שלושה משתנים קיימות שלוש נגזרות חלקיות: $\frac{\partial F}{\partial x}$, $\frac{\partial F}{\partial y}$ ו-$\frac{\partial F}{\partial z}$. כל נגזרת מתארת את השינוי האינפיניטסימלי של $F$ בעת תזוזה אינפיניטסימלית לאורך הציר המתאים.
אופרטור הגרדיאנט
הגרדיאנט הוא אופרטור וקטורי המוגדר כך:
\[\nabla = \hat{\mathbf{x}} \frac{\partial}{\partial x} + \hat{\mathbf{y}} \frac{\partial}{\partial y} + \hat{\mathbf{z}} \frac{\partial}{\partial z}\]כאשר האופרטור פועל על פונקציה $F$, מתקבל:
\[\nabla F = \hat{\mathbf{x}} \frac{\partial F}{\partial x} + \hat{\mathbf{y}} \frac{\partial F}{\partial y} + \hat{\mathbf{z}} \frac{\partial F}{\partial z}\]חשוב להבחין: בעוד ש-$\nabla$ הוא אופרטור, $\nabla F$ (הגרדיאנט של הפונקציה $F$) הוא וקטור שרכיביו הם הנגזרות החלקיות של $F$:
- רכיב ה-$x$: $\frac{\partial F}{\partial x}$
- רכיב ה-$y$: $\frac{\partial F}{\partial y}$
- רכיב ה-$z$: $\frac{\partial F}{\partial z}$
דוגמה 1: $\nabla \left(\sin\left(xyz\right)\right)$
נתונה הפונקציה:
\[F(x,y,z) = \sin(xyz)\]הגרדיאנט של $F$ מחושב כך:
\[\nabla F = \hat{\mathbf{x}} \frac{\partial F}{\partial x} + \hat{\mathbf{y}} \frac{\partial F}{\partial y} + \hat{\mathbf{z}} \frac{\partial F}{\partial z}\]חישוב כל רכיב:
- רכיב $\hat{\mathbf{x}}$: גזירה לפי $x$ (כאשר $y,z$ קבועים) נותנת $yz \cos(xyz)$
- רכיב $\hat{\mathbf{y}}$: גזירה לפי $y$ (כאשר $x,z$ קבועים) נותנת $xz \cos(xyz)$
- רכיב $\hat{\mathbf{z}}$: גזירה לפי $z$ (כאשר $x,y$ קבועים) נותנת $xy \cos(xyz)$
לכן:
\[\nabla F = yz \cos(xyz) \hat{\mathbf{x}} + xz \cos(xyz) \hat{\mathbf{y}} + xy \cos(xyz) \hat{\mathbf{z}}\]דוגמה 2: $\nabla \left(x e^{yz}\right)$
נתונה הפונקציה:
\[F(x,y,z) = x e^{yz}\]חישוב הגרדיאנט:
- רכיב $\hat{\mathbf{x}}$: $\frac{\partial F}{\partial x} = e^{yz}$
- רכיב $\hat{\mathbf{y}}$: $\frac{\partial F}{\partial y} = xz e^{yz}$
- רכיב $\hat{\mathbf{z}}$: $\frac{\partial F}{\partial z} = xy e^{yz}$
לכן:
\[\nabla F = e^{yz} \hat{\mathbf{x}} + xz e^{yz} \hat{\mathbf{y}} + xy e^{yz} \hat{\mathbf{z}}\]המשמעות הפיזיקלית של הגרדיאנט
הגרדיאנט של פונקציה מצביע בכל נקודה לכיוון השיפוע המקסימלי של הפונקציה באותה נקודה. זהו וקטור התלוי במיקום $(x,y,z)$, כאשר בכל נקודה הוא מצביע לכיוון העלייה התלולה ביותר של הפונקציה.
אינטואיטיבית, אם הפונקציה מתארת משטח גבהים ונניח טיפת מים על המשטח, הטיפה תזרום בכיוון ההפוך לגרדיאנט (כיוון הירידה התלולה ביותר), בעוד הגרדיאנט עצמו מצביע לכיוון העלייה התלולה ביותר.
הדיפרנציאל של פונקציה תלת-ממדית
הגדרה ומוטיבציה
נתבונן בפונקציה סקלרית $\phi(x,y,z)$ - פונקציה המקבלת ערך סקלרי בכל נקודה במרחב התלת-ממדי. דוגמה פיזיקלית לפונקציה כזו היא התפלגות הטמפרטורה בחדר, כאשר לכל נקודה $(x,y,z)$ מותאם ערך טמפרטורה $\phi(x,y,z)$. באופן דומה ניתן לתאר התפלגות לחץ במרחב באמצעות פונקציה סקלרית.
נוסחת הדיפרנציאל
בהכללה לדיפרנציאל של פונקציה חד-ממדית $dF = F’(x)dx$, הדיפרנציאל של פונקציה תלת-ממדית מוגדר כך:
\[d\phi = \frac{\partial \phi}{\partial x} dx + \frac{\partial \phi}{\partial y} dy + \frac{\partial \phi}{\partial z} dz\]ביטוי זה מתאר את השינוי האינפיניטסימלי ב-$\phi$ כתוצאה משינוי אינפיניטסימלי סימולטני בקואורדינטות $x$, $y$ ו-$z$. הוכחה ריגורוזית של נוסחה זו נלמדת בקורסי חשבון דיפרנציאלי ואינטגרלי מתקדמים.
ייצוג וקטורי של הדיפרנציאל
הדיפרנציאל ניתן לביטוי כמכפלה סקלרית של שני וקטורים:
\[d\phi = \begin{pmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{pmatrix} \cdot \begin{pmatrix} dx \\ dy \\ dz \end{pmatrix}\]ניתן לפרק את הביטוי הזה לצורה:
\[d\phi = \left(\frac{\partial \phi}{\partial x} \hat{\mathbf{x}} + \frac{\partial \phi}{\partial y} \hat{\mathbf{y}} + \frac{\partial \phi}{\partial z} \hat{\mathbf{z}}\right) \cdot \left(dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}\right)\]הווקטור הראשון במכפלה הוא הגרדיאנט של $\phi$:
\[\nabla \phi = \frac{\partial \phi}{\partial x} \hat{\mathbf{x}} + \frac{\partial \phi}{\partial y} \hat{\mathbf{y}} + \frac{\partial \phi}{\partial z} \hat{\mathbf{z}}\]הווקטור השני הוא הדיפרנציאל של וקטור המקום $d\mathbf{r}$.
הוכחה ש-$d\mathbf{r} = dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}$
וקטור המקום מוגדר כ:
\[\mathbf{r} = x\hat{\mathbf{x}} + y\hat{\mathbf{y}} + z\hat{\mathbf{z}}\]לפי הגדרת הדיפרנציאל:
\[d\mathbf{r} = \frac{\partial \mathbf{r}}{\partial x} dx + \frac{\partial \mathbf{r}}{\partial y} dy + \frac{\partial \mathbf{r}}{\partial z} dz\]חישוב הנגזרות החלקיות:
- $\frac{\partial \mathbf{r}}{\partial x} = \hat{\mathbf{x}}$ (כאשר $y,z$ קבועים)
- $\frac{\partial \mathbf{r}}{\partial y} = \hat{\mathbf{y}}$ (כאשר $x,z$ קבועים)
- $\frac{\partial \mathbf{r}}{\partial z} = \hat{\mathbf{z}}$ (כאשר $x,y$ קבועים)
לכן:
\[d\mathbf{r} = dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}\]הקשר המרכזי בין גרדיאנט לדיפרנציאל
מהניתוח לעיל מתקבל הקשר החשוב:
\[\boxed{d\phi = \nabla \phi \cdot d\mathbf{r}}\]כלומר, הדיפרנציאל של פונקציה סקלרית $\phi$ הוא מכפלה סקלרית של הגרדיאנט שלה עם הדיפרנציאל של וקטור המקום.
הקשר הזה מהווה כלי יסודי בפיזיקה מתמטית ויישומיו רבים.
עבודה ומשפט עבודה-אנרגיה
הגדרת עבודה
העבודה מוגדרת כמכפלה סקלרית של כוח ותזוזה. עבור תזוזה אינפיניטסימלית:
\[dW = \mathbf{F} \cdot d\mathbf{r}\]ביטוי זה מבטא שרק רכיב הכוח בכיוון התנועה תורם לעבודה (כלומר, כוח שניצב לכיוון התנועה לא מבצע עבודה).
העבודה הכוללת לאורך מסלול מנקודה $\mathbf{r}_1$ לנקודה $\mathbf{r}_2$ היא:
\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F}(\mathbf{r}) \cdot d\mathbf{r}\]כאשר הכוח $\mathbf{F}$ עשוי להיות תלוי במיקום לאורך המסלול.
משפט עבודה-אנרגיה
החוק השני של ניוטון קובע ש-$\mathbf{F} = \frac{d\mathbf{p}}{dt}$. בשילוב עם הקשרים:
- $d\mathbf{r} = \mathbf{v} dt$
- $\mathbf{p} = m\mathbf{v}$
ניתן להראות כי:
\[W = E_{k,\text{final}} - E_{k,\text{initial}}\]כאשר האנרגיה הקינטית מוגדרת:
\[E_k = \frac{1}{2}mv^2 = \frac{p^2}{2m}\]ניסוח מתמטי של המשפט
משפט עבודה-אנרגיה קובע:
\[\begin{aligned} W_{1 \to 2} &= E_k(\mathbf{r}_2) - E_k(\mathbf{r}_1) \\[5pt] &= \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 \\[5pt] &= \frac{p_2^2}{2m} - \frac{p_1^2}{2m} \end{aligned}\]המשפט מבטא את העיקרון הפיזיקלי שהעבודה שמבצע כוח על גוף שווה לשינוי באנרגיה הקינטית שלו.
כוחות משמרים
כוחות משמרים מהווים משפחת כוחות מרכזית ויסודית בפיזיקה. למרות שההגדרה עשויה להיראות אבסטרקטית בתחילה, חשיבותה תתבהר מהתובנות הפיזיקליות הנובעות ממנה.
כוח משמר - הגדרה מתמטית
כוח משמר הוא כוח הניתן לביטוי בצורה:
\[\mathbf{F} = -\nabla \phi\]כאשר $\phi$ היא פונקציה סקלרית של המיקום. הסימן השלילי הוא קונבנציה שנוחה לטיפול המתמטי בהמשך.
בניסוח מקוצר: כוח נקרא משמר אם הוא “נגזר” מפונקציה סקלרית. יש להדגיש שמדובר בגזירה באמצעות אופרטור הגרדיאנט, שכן לא ניתן להפיק וקטור (הכוח) מפונקציה סקלרית באמצעות גזירה רגילה.
חישוב העבודה שמבצע כוח משמר
נחשב את העבודה שמבצע כוח משמר על גוף הנע במסלול כלשהו מנקודה $\mathbf{r}_1$ לנקודה $\mathbf{r}_2$.
מהגדרת העבודה:
\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F} \cdot d\mathbf{r}\]הצבת הביטוי לכוח משמר:
\[W = -\int_{\mathbf{r}_1}^{\mathbf{r}_2} (\nabla \phi) \cdot d\mathbf{r}\]מהקשר שהוכח קודם, $(\nabla \phi) \cdot d\mathbf{r} = d\phi$, לכן:
\[W = -\int_{\mathbf{r}_1}^{\mathbf{r}_2} d\phi\]ביצוע האינטגרל:
\[W = -[\phi]_{\mathbf{r}_1}^{\mathbf{r}_2} = -\phi(\mathbf{r}_2) + \phi(\mathbf{r}_1)\]או בצורה סופית:
\[\boxed{W = \phi(\mathbf{r}_1) - \phi(\mathbf{r}_2)}\]תוצאה מרכזית: העבודה שמבצע כוח משמר תלויה אך ורק בנקודות ההתחלה והסיום, ולא במסלול שעובר ביניהן. זוהי תכונה ייחודית וחשובה של כוחות משמרים.
אנרגיה פוטנציאלית
הגדרה ויחידות
הפונקציה הסקלרית $\phi$ המופיעה בהגדרת הכוח המשמר נקראת אנרגיה פוטנציאלית (לעיתים מסומנת גם ב-$U$). היא מתארת את האנרגיה האצורה במערכת כתוצאה מהכוח המשמר.
מניתוח היחידות:
- עבודה = כוח × מרחק = ניוטון × מטר = ג׳אול
- ממשפט עבודה-אנרגיה: לעבודה יש יחידות של אנרגיה
- לכן ל-$\phi$ יש יחידות של אנרגיה (ג׳אול)
הקשר בין עבודה לאנרגיה פוטנציאלית
מהחישוב לעיל נובע:
\[W_{1 \to 2} = U(\mathbf{r}_1) - U(\mathbf{r}_2) = U_{\text{initial}} - U_{\text{final}}\]כאשר $U \equiv \phi$ מסמנת את האנרגיה הפוטנציאלית.
כלומר, העבודה שמבצע כוח משמר שווה להפרש האנרגיה הפוטנציאלית בין נקודת ההתחלה לנקודת הסיום.
גזירת חוק שימור האנרגיה
מהניתוח הקודם התקבלו שתי משוואות לעבודה:
- ממשפט עבודה-אנרגיה: $W = E_{k,\text{final}} - E_{k,\text{initial}}$
- מהגדרת כוחות משמרים: $W = \phi_{\text{initial}} - \phi_{\text{final}}$
השוואת שתי המשוואות נותנת:
\[E_{k,\text{final}} - E_{k,\text{initial}} = \phi_{\text{initial}} - \phi_{\text{final}}\]סידור מחדש של האיברים:
\[E_{k,\text{initial}} + \phi_{\text{initial}} = E_{k,\text{final}} + \phi_{\text{final}}\]הגדרת האנרגיה המכנית
הגודל $E = E_k + \phi$ מוגדר כאנרגיה מכנית של המערכת.
מהמשוואה לעיל נובע:
\[\boxed{E_{\text{initial}} = E_{\text{final}}}\]זהו חוק שימור האנרגיה המכנית: האנרגיה המכנית הכוללת נשמרת במהלך התנועה תחת כוחות משמרים בלבד.
האנרגיה המכנית מורכבת משני רכיבים:
- אנרגיה קינטית: $E_k = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi(\mathbf{r})$
גודל הנשמר במהלך התנועה נקרא קבוע תנועה או שמורה (invariant). לכן האנרגיה המכנית היא שמורה של מערכת הפועלים בה כוחות משמרים בלבד.
תכונות ייחודיות של כוחות משמרים
אי-תלות במסלול
מהחישוב הקודם עולה תוצאה מרכזית: העבודה של כוח משמר בין שתי נקודות $\mathbf{r}_1$ ו-$\mathbf{r}_2$ היא:
\[W = \phi(\mathbf{r}_1) - \phi(\mathbf{r}_2)\]התוצאה תלויה אך ורק בנקודות הקצה, ללא תלות במסלול המחבר ביניהן. בין אם המסלול ישר, עקום, או מקיף את כל כדור הארץ - העבודה זהה.
זוהי תכונה ייחודית ומגדירה של כוחות משמרים: העבודה אינה תלויה במסלול, אלא רק בנקודות הקצה.
עבודה במסלול סגור
עבור מסלול סגור (המתחיל ומסתיים באותה נקודה $\mathbf{r}$):
\[W = \phi(\mathbf{r}) - \phi(\mathbf{r}) = 0\]לכן, עבור כל כוח משמר:
\[\boxed{\oint \mathbf{F}_{\text{conservative}} \cdot d\mathbf{r} = 0}\]כאשר $\oint$ מסמן אינטגרל על מסלול סגור.
כוחות יסודיים וכוחות משמרים
כל הכוחות היסודיים בטבע הם כוחות משמרים. זוהי תכונה עמוקה של חוקי הטבע. כוחות לא-משמרים (כגון חיכוך) הם תמיד כוחות מקרוסקופיים הנובעים מאינטראקציות מורכבות.
דוגמה: מערכת כדור הארץ-שמש
כוח הכבידה בין השמש לכדור הארץ הוא כוח משמר. כדור הארץ נע במסלול סגור (בקירוב) סביב השמש, ולכן:
- העבודה שמבצע כוח הכבידה במחזור שלם היא אפס
- אין “התעייפות” או הפסד אנרגיה בתנועה זו
- התנועה יכולה להימשך ללא הגבלת זמן
תופעה זו מסבירה כיצד כדור הארץ מקיף את השמש כחמישה מיליארד שנה ללא צורך ב”מקור אנרגיה” חיצוני. העבודה הכוללת במחזור שלם היא אפס, ולכן אין צורך בהשקעת אנרגיה נוספת לשמירת התנועה.
זהו ביטוי ישיר לעקרון שימור האנרגיה ולתכונות המיוחדות של כוחות משמרים.
סיכום עקרונות מקדימים
בחלק הקודם נידונו המושגים הבאים:
- כוח משמר: כוח שהעבודה שהוא מבצע אינה תלויה במסלול התנועה
- עבודה במסלול סגור: עבור כוח משמר, העבודה במסלול סגור היא אפס
- חוק שימור האנרגיה המכנית: סכום האנרגיה הקינטית והאנרגיה הפוטנציאלית נשמר תחת כוחות משמרים
בחלק זה נבחן יישום של עקרונות אלו להתנגשויות בין גופים.
התנגשות אלסטית
התנגשות אלסטית היא התנגשות בה נשמרת האנרגיה המכנית הכוללת של המערכת. במקרה של גופים חופשיים (ללא אנרגיה פוטנציאלית), משמעות הדבר היא שימור האנרגיה הקינטית הכוללת.
תיאור המערכת
נתבונן בשני גופים בעלי מסות $m_1$ ו-$m_2$:
- לפני ההתנגשות: מהירויות $\mathbf{v}_1$ ו-$\mathbf{v}_2$
- אחרי ההתנגשות: מהירויות $\mathbf{u}_1$ ו-$\mathbf{u}_2$
חוקי השימור בהתנגשות אלסטית
בהיעדר כוחות חיצוניים, שני חוקי שימור חלים על המערכת:
1. חוק שימור התנע
\[m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 = m_1 \mathbf{u}_1 + m_2 \mathbf{u}_2\]או בסימון תנע:
\[\mathbf{p}_{1,\text{initial}} + \mathbf{p}_{2,\text{initial}} = \mathbf{p}_{1,\text{final}} + \mathbf{p}_{2,\text{final}}\]2. חוק שימור האנרגיה הקינטית
\[\frac{1}{2}m_1 v_1^2 + \frac{1}{2}m_2 v_2^2 = \frac{1}{2}m_1 u_1^2 + \frac{1}{2}m_2 u_2^2\]פיתוח הקשר בין המהירויות
שלב 1: ארגון מחדש של משוואות השימור
מחוק שימור התנע:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2)\]מחוק שימור האנרגיה (לאחר ביטול הגורם $\frac{1}{2}$):
\[m_1(v_1^2 - u_1^2) = m_2(u_2^2 - v_2^2)\]שלב 2: שימוש בזהות אלגברית
נזכור כי $a^2 - b^2 = (a-b)(a+b)$. בהכללה למכפלות סקלריות:
\[\mathbf{a} \cdot \mathbf{a} - \mathbf{b} \cdot \mathbf{b} = (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b})\]ניתן לוודא זאת על ידי פיתוח הביטוי:
\[(\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} + \mathbf{a} \cdot \mathbf{b} - \mathbf{b} \cdot \mathbf{a} - \mathbf{b} \cdot \mathbf{b}\]כאשר $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$ (תכונת החילופיות של מכפלה סקלרית), האיברים האמצעיים מתבטלים.
לכן משוואת האנרגיה הופכת ל:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) \cdot (\mathbf{v}_1 + \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{u}_2 + \mathbf{v}_2)\]שלב 3: הצבה ופישוט
מחוק שימור התנע:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2)\]הצבה במשוואת האנרגיה:
\[m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{v}_1 + \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{u}_2 + \mathbf{v}_2)\]לאחר צמצום $m_2$ והוצאת גורם משותף:
\[(\mathbf{u}_2 - \mathbf{v}_2) \cdot [(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2)] = 0\]שלב 4: ניתוח התוצאה
חשוב לציין כי אמנם לא ניתן לבצע פעולת חילוק בווקטור (פעולה כזו אינה מוגדרת מתמטית), אך ניתן לנתח מתי מכפלה סקלרית שווה לאפס.
המשוואה
\[(\mathbf{u}_2 - \mathbf{v}_2) \cdot [(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2)] = 0\]מתקיימת באחד משלושה מקרים:
- $\mathbf{u}_2 - \mathbf{v}_2 = \mathbf{0}$ (כלומר $\mathbf{u}_2 = \mathbf{v}_2$)
- $(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2) = \mathbf{0}$
- שני הווקטורים ניצבים זה לזה
המקרה הראשון מתאר מצב בו הגוף השני אינו משנה את מהירותו כלל. זה פתרון בלתי סביר עבור התנגשות כללית, שכן בהתנגשות בין גופים עם מהירויות התחלתיות בלתי תלויות, אין סיבה פיזיקלית מקדימה שהגוף השני ישמור על המהירות המקורית שלו.
המקרה השלישי (ניצבות) דורש תנאי מיוחד על המהירויות שאינו מתקיים באופן כללי.
לכן, עבור התנגשות אמיתית, מתקיים המקרה השני.
התוצאה הסופית
מהמקרה השני נובע:
\[\mathbf{v}_1 + \mathbf{u}_1 = \mathbf{u}_2 + \mathbf{v}_2\]סידור מחדש נותן:
\[\boxed{\mathbf{v}_1 - \mathbf{v}_2 = -(\mathbf{u}_1 - \mathbf{u}_2)}\]פירוש פיזיקלי
משוואה זו מבטאת עיקרון חשוב: בהתנגשות אלסטית, המהירות היחסית בין הגופים משנה כיוון אך שומרת על גודלה.
אם נגדיר:
- $\Delta \mathbf{v} = \mathbf{v}_2 - \mathbf{v}_1$ - המהירות היחסית לפני ההתנגשות
- $\Delta \mathbf{u} = \mathbf{u}_2 - \mathbf{u}_1$ - המהירות היחסית אחרי ההתנגשות
אז:
\[\Delta \mathbf{u} = -(\mathbf{v}_2 - \mathbf{v}_1) = \mathbf{v}_1 - \mathbf{v}_2\]משוואות ההתנגשות האלסטית - סיכום
התנגשות אלסטית בין שני גופים מאופיינת במלואה על ידי שתי משוואות:
-
חוק שימור התנע
\[\boxed{m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 = m_1 \mathbf{u}_1 + m_2 \mathbf{u}_2}\] -
חוק היפוך המהירות היחסית
\[\boxed{\mathbf{v}_1 - \mathbf{v}_2 = \mathbf{u}_2 - \mathbf{u}_1}\]
המשוואה השנייה, שנגזרה משילוב חוקי שימור התנע והאנרגיה, מחליפה למעשה את משוואת שימור האנרגיה. השימוש בה מפשט משמעותית את החישובים בבעיות התנגשות אלסטית, שכן היא מאפשרת עבודה עם משוואות וקטוריות ליניאריות במקום משוואות סקלריות ריבועיות.
שתי המשוואות יחד מספקות מערכת מלאה לפתרון בעיות התנגשות אלסטית, כאשר נתונים הפרמטרים ההתחלתיים של המערכת.
התנגשות פלסטית
התנגשות פלסטית היא התנגשות בה שני הגופים המתנגשים נדבקים זה לזה ונעים לאחר מכן במהירות משותפת. השם נגזר מהאנלוגיה לחומרים פלסטיים כמו פלסטלינה, הנדבקים זה לזה בעת התנגשות.
ניתוח התנגשות פלסטית בין שתי מסות
נתבונן בשתי מסות $m$ ו-$M$:
- לפני ההתנגשות:
- מסה $m$ נעה במהירות $\mathbf{v}$
- מסה $M$ נעה במהירות $\mathbf{V}$
- אחרי ההתנגשות: שתי המסות נעות יחד במהירות משותפת $\mathbf{u}$
יישום חוק שימור התנע:
בהיעדר כוחות חיצוניים, חוק שימור התנע נותן:
\[m \mathbf{v} + M \mathbf{V} = (m + M) \mathbf{u}\]מכאן נובעת המהירות המשותפת:
\[\boxed{\mathbf{u} = \frac{m \mathbf{v} + M \mathbf{V}}{m + M}}\]אי-שימור האנרגיה: בניגוד להתנגשות אלסטית, בהתנגשות פלסטית האנרגיה הקינטית אינה נשמרת.
הסיבה: לאחר ההתנגשות, הפרש המהירויות בין הגופים הוא אפס ($\Delta \mathbf{u} = 0$), בעוד שלפני ההתנגשות $\Delta \mathbf{v} = \mathbf{v} - \mathbf{V} \neq 0$ (בדרך כלל). זה מנוגד לתנאי השימור שנגזר עבור התנגשויות אלסטיות.
חישוב אובדן האנרגיה בהתנגשות פלסטית
האנרגיה הקינטית ה”אובדת” הופכת ל:
- עיוותים פלסטיים: שינויי צורה בלתי הפיכים בגופים
- אנרגיה תרמית: חום הנוצר בעת ההתנגשות
נפתח את הביטוי לאובדן האנרגיה הקינטית. שינוי האנרגיה הקינטית מוגדר כ:
\[\Delta E_k = E_{k,\text{final}} - E_{k,\text{initial}}\]כאשר:
\[E_{k,\text{initial}} = \frac{1}{2}mv^2 + \frac{1}{2}MV^2\] \[E_{k,\text{final}} = \frac{1}{2}(m + M)u^2\]הצבת הביטוי עבור $\mathbf{u}$ וביצוע החישוב האלגברי מובילים לתוצאה:
\[\boxed{\Delta E_k = -\frac{1}{2}\mu(\Delta \mathbf{v})^2}\]כאשר:
- $\Delta \mathbf{v} = \mathbf{v} - \mathbf{V}$ - הפרש המהירויות ההתחלתיות
- $\mu = \frac{mM}{m + M}$ - המסה המצומצמת של המערכת. בניסוח אחר: \(\mu = \frac{1}{\frac{1}{m} + \frac{1}{M}}\)
תכונות התוצאה:
-
סימן שלילי: $\Delta E_k \le 0$, המאשר כי אנרגיה אובדת (או נשמרת במקרה הקיצון) בתהליך
-
תלות בהפרש המהירויות: האנרגיה האובדת פרופורציונית לריבוע הפרש המהירויות ההתחלתיות
-
בדיקת תקינות: כאשר $\mathbf{v} = \mathbf{V}$ (אין מהירות יחסית), $\Delta E_k = 0$ - אין אובדן אנרגיה כיוון שאין התנגשות ממשית
סיכום
התנגשות פלסטית מאופיינת בהידבקות הגופים ותנועה במהירות משותפת. בעוד שהתנע נשמר, האנרגיה הקינטית אינה נשמרת, כאשר האובדן תלוי בהפרש המהירויות ההתחלתיות ובמסה המצומצמת של המערכת.
בחלק הבא נעסוק בשאלה מעשית: בהינתן כוח $\mathbf{F}$, כיצד מוצאים את האנרגיה הפוטנציאלית $\phi$ המקיימת $\mathbf{F} = -\nabla \phi$ (בהנחה שהכוח משמר)?
תהליך זה אינו תמיד טריוויאלי, אך ניתן לביצוע עבור כוחות רבים בעלי חשיבות פיזיקלית.
דוגמה 1: כוח הכבידה בקרבת פני כדור הארץ
בחלק זה נעסוק בשיטה למציאת האנרגיה הפוטנציאלית $\phi$ מתוך הכוח $\mathbf{F}$, בהנחה שמדובר בכוח משמר המקיים $\mathbf{F} = -\nabla \phi$.
הקדמה והבחנה חשובה
נתחיל בניתוח כוח הכבידה בקרבת פני כדור הארץ. יש להדגיש כי הטיפול בכוח הכבידה בקרבת פני כדור הארץ שונה מהותית מהטיפול בכוח הכבידה במרחקים גדולים מכדור הארץ, נושא שיידון בנפרד.
הגדרת הכוח
בקרבת פני כדור הארץ, כאשר ציר ה-$y$ מוגדר כלפי מעלה:
\[\mathbf{F} = -mg\hat{\mathbf{y}}\]כוח הכבידה פועל כלפי מטה, גודלו $mg$, וכיוונו במינוס $\hat{\mathbf{y}}$.
תזכורת: $\hat{\mathbf{y}}$ הוא וקטור יחידה בכיוון ציר ה-$y$ (כלפי מעלה). $g$ הוא סקאלר שמתאים לתאוצת הכבידה (בערך $10 \, \text{m/s}^2$).
מציאת האנרגיה הפוטנציאלית של כוח הכבידה
מהתנאי לכוח משמר:
\[\mathbf{F} = -\nabla \phi = -\frac{\partial \phi}{\partial x}\hat{\mathbf{x}} - \frac{\partial \phi}{\partial y}\hat{\mathbf{y}} - \frac{\partial \phi}{\partial z}\hat{\mathbf{z}}\]השוואה עם הביטוי לכוח הכבידה:
\[-mg\hat{\mathbf{y}} = -\frac{\partial \phi}{\partial x}\hat{\mathbf{x}} - \frac{\partial \phi}{\partial y}\hat{\mathbf{y}} - \frac{\partial \phi}{\partial z}\hat{\mathbf{z}}\]נקודה חשובה: זאת משוואה וקטורית. הזהות חייבת להתקיים לא רק מבחינה אריתמטית אלא גם מבחינה מבנית - אם באגף שמאל יש וקטור בכיוון מסוים, באגף ימין חייב להיות וקטור באותו כיוון.
מכיוון שהכוח הוא בכיוון $\hat{\mathbf{y}}$ בלבד, הרכיבים בכיווני $\hat{\mathbf{x}}$ ו-$\hat{\mathbf{z}}$ חייבים להתאפס:
- $\frac{\partial \phi}{\partial x} = 0$
- $\frac{\partial \phi}{\partial z} = 0$
ולכן נותרת המשוואה:
\[-mg\hat{\mathbf{y}} = -\frac{\partial \phi}{\partial y}\hat{\mathbf{y}}\]ביטול הכיוון הווקטורי משני האגפים:
\[mg = \frac{\partial \phi}{\partial y}\]אינטגרציה נותנת:
\[\phi(y) = mgy + C\]כאשר $C$ הוא קבוע אינטגרציה. מקובל לבחור $C = 0$, ולכן:
\[\boxed{\phi(y) = mgy}\]המשמעות: האנרגיה הפוטנציאלית של גוף בעל מסה $m$ בגובה $y$ מעל מישור הייחוס (למשל, פני הים) היא $mgy$.
יישום: נפילה חופשית ממגדל
נתבונן בגוף הנופל מגובה $h$ (למשל, ממגדל אייפל). נבחר את מישור הקרקע כנקודת הייחוס ($y = 0$).
ניתוח אנרגטי
מצב התחלתי (בגובה $h$):
- אנרגיה קינטית: $E_{k,\text{initial}} = 0$ (התחלה ממנוחה)
- אנרגיה פוטנציאלית: $\phi_{\text{initial}} = mgh$
מצב סופי (רגע לפני הפגיעה בקרקע):
- אנרגיה קינטית: $E_{k,\text{final}} = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi_{\text{final}} = 0$
מחוק שימור האנרגיה:
\[E_{k,\text{initial}} + \phi_{\text{initial}} = E_{k,\text{final}} + \phi_{\text{final}}\]הצבת הערכים:
\[0 + mgh = \frac{1}{2}mv^2 + 0\]פתרון למהירות:
\[v = \sqrt{2gh}\]הערה חשובה: בחירת מישור הייחוס (איפה $y = 0$) היא שרירותית לחלוטין. הגודל הפיזיקלי המשמעותי הוא הפרש האנרגיות הפוטנציאליות, שאינו תלוי בבחירת נקודת הייחוס.
הכללה: התחלה ממהירות שונה מאפס
במקרה כללי יותר, כאשר הגוף מתחיל את תנועתו במהירות $v_{\text{initial}}$:
\[\frac{1}{2}mv_{\text{initial}}^2 + mgh = \frac{1}{2}mv_{\text{final}}^2\]לאחר צמצום המסה:
\[v_{\text{final}}^2 = v_{\text{initial}}^2 + 2gh\]תובנה חשובה: התוצאה אינה תלויה בכיוון המהירות ההתחלתית (כלפי מעלה או מטה), שכן במשוואת האנרגיה מופיע $v^2$ - ריבוע המהירות אינו רגיש לכיוון.
הקשר לקינמטיקה
המשוואה שהתקבלה:
\[v_{\text{final}}^2 = v_{\text{initial}}^2 + 2gh\]זהה למשוואה הקינמטית המוכרת לתנועה בתאוצה קבועה:
\[v^2 = v_0^2 + 2a\Delta x\]כאשר במקרה של נפילה חופשית $a = g$ ו-$\Delta x = h$.
יתרון שיטת האנרגיה: ניתן להגיע לתוצאה ללא צורך בידע מפורט בקינמטיקה. חישובי אנרגיה מפשטים משמעותית בעיות רבות במכניקה.
דוגמה 2: כוח מחזיר (קפיץ)
נתון כוח מחזיר:
\[\mathbf{F} = -k\mathbf{r}\]כאשר $k$ הוא קבוע הקפיץ ו-$\mathbf{r}$ הוא וקטור המיקום.
המטרה: למצוא את האנרגיה הפוטנציאלית $\phi$ המקיימת את התנאי לכוח משמר:
\[\mathbf{F} = -\nabla \phi\]גרדיאנט בקואורדינטות רדיאליות
הערה מקדימה: עבור פונקציה התלויה רק בגודל המרחק $r = \vert \mathbf{r} \vert$, הגרדיאנט בקואורדינטות רדיאליות הוא:
\[\nabla \phi(r) = \frac{d\phi}{dr} \hat{\mathbf{𝒓}}\]כאשר $\hat{\mathbf{𝒓}}$ הוא וקטור היחידה הרדיאלי. נושא זה יידון בהרחבה בשיעור הבא.
מציאת האנרגיה הפוטנציאלית של קפיץ
ננחש את הצורה של האנרגיה הפוטנציאלית:
\[\phi = \frac{1}{2}k\mathbf{r} \cdot \mathbf{r} = \frac{1}{2}kr^2\]אימות התוצאה
נבדוק שאכן $\mathbf{F} = -\nabla \phi$:
שלב 1: חישוב הגרדיאנט
\[-\nabla \phi = -\frac{d\phi}{dr} \hat{\mathbf{𝒓}}\]שלב 2: הצבת הפונקציה
\[-\nabla \phi = -\frac{d}{dr}\left(\frac{1}{2}kr^2\right) \hat{\mathbf{𝒓}}\]שלב 3: ביצוע הגזירה
יש לשים לב כי:
\[\mathbf{r} \cdot \mathbf{r} = |\mathbf{r}|^2 = r^2\]לכן:
\[-\nabla \phi = -\frac{k}{2} \frac{d}{dr}(r^2) \hat{\mathbf{𝒓}}\]על פי כלל הגזירה: $\frac{d}{dr}(r^2) = 2r$
שלב 4: התוצאה הסופית
\[-\nabla \phi = -\frac{k}{2} \cdot 2r \cdot \hat{\mathbf{𝒓}} = -kr\hat{\mathbf{𝒓}} = -k\mathbf{r}\]קיבלנו בדיוק את הכוח הנתון, מה שמאמת את הביטוי לאנרגיה הפוטנציאלית.
המקרה החד-ממדי: קפיץ ליניארי
עבור קפיץ בממד אחד (לאורך ציר $x$), האנרגיה הפוטנציאלית היא:
\[\boxed{\phi(x) = \frac{1}{2}kx^2}\]זהו מקרה פרטי של הנוסחה הכללית $\phi = \frac{1}{2}kr^2$ עבור תנועה חד-ממדית.
הפירוש הפיזיקלי
כאשר מותחים קפיץ, מכניסים לתוכו אנרגיה פוטנציאלית. אנרגיה זו קשורה לכוח המשמר שהקפיץ מפעיל בניסיון לחזור למצב שיווי המשקל.
יישום: תנועת מסה על קפיץ
נתבונן במערכת הבאה:
- קפיץ בעל קבוע $k$
- מסה $m$ מחוברת לקפיץ
- המסה נמתחת למרחק $x$ ומשוחררת ממנוחה
השאלה: מהי מהירות המסה כאשר היא עוברת דרך נקודת שיווי המשקל?
הנחה מפשטת: אורך הקפיץ הרפוי הוא אפס (ניתן להכליל למקרה כללי)
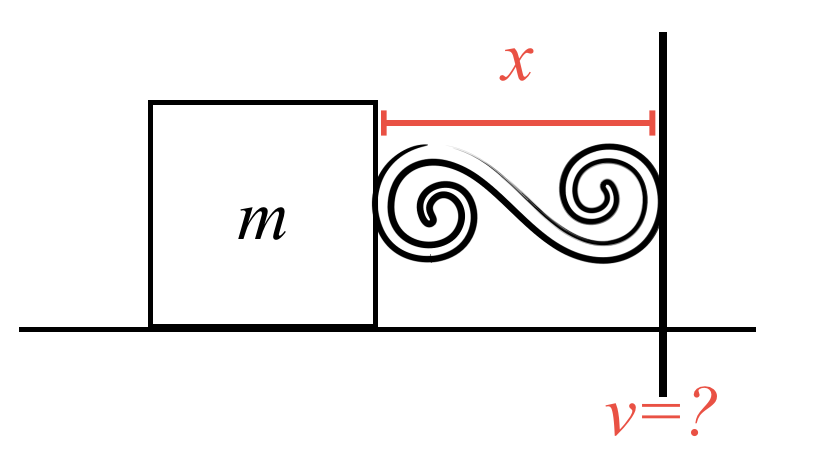
פתרון באמצעות שימור אנרגיה
מצב התחלתי (במרחק $x$ מהמקור):
- אנרגיה קינטית: $E_{k,\text{initial}} = 0$ (התחלה ממנוחה)
- אנרגיה פוטנציאלית: $\phi_{\text{initial}} = \frac{1}{2}kx^2$
מצב סופי (בנקודת שיווי המשקל):
- אנרגיה קינטית: $E_{k,\text{final}} = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi_{\text{final}} = 0$
מחוק שימור האנרגיה המכנית:
\[\underbrace{\frac{1}{2}m \cdot 0^2 + \frac{1}{2}kx^2}_{E_i} = \underbrace{\frac{1}{2}mv^2 + \frac{1}{2}k \cdot 0^2}_{E_f}\]פישוט:
\[\frac{1}{2}kx^2 = \frac{1}{2}mv^2\] \[kx^2 = mv^2\]פתרון למהירות:
\[v^2 = \frac{k}{m}x^2\]קשר לתדירות הזוויתית
נזכור כי $\omega^2 = \frac{k}{m}$ היא התדירות הזוויתית של התנודה, לכן:
\[v = \omega x\]התוצאה הזאת מתאימה לידוע מתורת התנודות ההרמוניות.
סיכום ומבט קדימה
-
כוח האנרגיה: שימוש בשימור אנרגיה מאפשר חישוב מהירויות ללא צורך בפתרון משוואות התנועה המלאות
- תנאי היישום: השיטה יעילה כאשר:
- הכוחות הם משמרים
- ידועה האנרגיה הפוטנציאלית
- האנרגיה המכנית נשמרת
- מגבלות: במקרים של כוחות לא-משמרים (כגון חיכוך) או תהליכים לא-אלסטיים (כגון התנגשויות פלסטיות), חלק מהאנרגיה הופך לחום או לעיוותים, והשיטה דורשת התאמה.
בשיעור הבא נחדד את הנקודה הזאת, נדבר על תהליכים שלא משמרים אנרגיה, ונדבר גם על עוד אנרגיות פוטנציאליות של כוחות, כולל דוגמאות ספציפיות.
תרגול
חזרה - עקרונות יסוד
משפט עבודה-אנרגיה (חזרה)
העבודה הכוללת המבוצעת על גוף שווה לשינוי באנרגיה הקינטית שלו:
\[W_{\text{net}} = \Delta E_k = E_{k,\text{final}} - E_{k,\text{initial}}\]הגדרת עבודה (חזרה)
עבודה מוגדרת כתוצר הכוח בתזוזה:
\[W = \mathbf{F} \cdot \mathbf{d} = Fd\cos\theta\]עבור כוח משתנה:
\[W = \int \mathbf{F} \cdot d\mathbf{r}\]שאלה 1: משפט עבודה-אנרגיה במישור משופע
גוף מחליק במורד מדרון מחוספס עם מקדם חיכוך קינטי $\mu_k$. הגוף משוחרר ממנוחה מגובה $h$ מעל תחתית המדרון.
בהנחה שהגוף התחיל במנוחה, מה השינוי באנרגיה הקינטית שלו במהלך תנועתו?
|\ | \ ↖ fₖ h | \ N↗ 🔹 | \ ↓mg | \ | θ \ ---------
הכוחות הפועלים על הגוף:
- כוח הכבידה: $mg$ (אנכי כלפי מטה)
- כוח נורמלי: $N = mg\cos\theta$
- כוח חיכוך: $f_k = \mu_k N = \mu_k mg\cos\theta$
דרך 1: שימור אנרגיה עם כוחות לא משמרים
\[\begin{aligned} \Delta E_k &= W_{\text{conservative}} + W_{\text{non-conservative}} \\ \Delta E_k &= \Delta E_p -W_{f_k} \\ &= mgh - f_k \cdot \ell \\ &= mgh - (\mu_k mg \cos \theta) \cdot \left(\frac{h}{\sin\theta}\right) \\ &= mgh - \mu_k mg h \frac{\cos\theta}{\sin\theta} \\ \Delta E_k &= \boxed{mgh \left(1 - \mu_k \cot\theta\right)} \end{aligned}\]הבהרה לגבי $h/\sin\theta$:
|\ h | \ ℓ (distance along incline) | \ | \ | θ \ -------השוויון נובע מכך ש:
\[\ell = \frac{h}{\sin\theta}\]
הבהרה נוספת:
לגבי $f_k = \mu_k N = \mu_k mg\cos\theta$:
mg (total gravitational force, pointing straight down) | | ↓ |\ h | \ | \ ← mg cos θ (perpendicular to incline) | \ | θ \ ------- → mg sin θ (parallel to incline, down the slope)השוויון נובע מכך ש:
\[N = mg\cos\theta\]
דרך 2: לפי משפט עבודה-אנרגיה
\[\begin{aligned} \Delta E_k = W_{\text{net}} &= \int_0^{\ell} F_{\text{net}} \, dx \\ &= \int_0^{h/\sin\theta} (mg\sin\theta - \mu_k mg\cos\theta) \, dx \\ &= \left(mg\sin\theta - \mu_k mg\cos\theta \right) \cdot \frac{h}{\sin\theta} \\ &= mgh - \mu_k mgh \cot\theta \\ &= \boxed{mgh(1 - \mu_k \cot\theta)} \end{aligned}\]מסקנה פיזיקלית
- כאשר $\mu_k = 0$ (ללא חיכוך): $\Delta E_k = mgh$ - כל האנרגיה הפוטנציאלית הופכת לקינטית
- כאשר $1 - \mu_k \cot\theta \le 0$:
- $\Delta E_k \le 0$ - הגוף לא יאיץ (או לא יזוז כלל אם החיכוך הסטטי מספיק גדול)
- בכל מקרה אחר: חלק מהאנרגיה הפוטנציאלית “אובד” לחיכוך (הופך לחום)
שאלה 2: כוחות משמרים
כוח הוא משמר אם העבודה שהוא מבצע לאורך כל מסלול סגור שווה לאפס:
\[\oint \mathbf{F} \cdot d\mathbf{r} = 0\]משמעות פיזיקלית: עבודה שמבוצעת על ידי כוח משמר תלויה רק בנקודות ההתחלה והסיום, לא במסלול עצמו.
איזה מהכוחות הבאים אינו משמר?
- $\mathbf{F} = (x,y,0)$
- $\mathbf{F} = (\cos x, 0, 0)$
- $\mathbf{F} = (y,x,0)$
- $\mathbf{F} = (xy,xy,0)$
- $\mathbf{F} = (xy^2,yx^2,0)$
הבהרה: המטרה היא למצוא כוח אחד ומסלול סגור אחד שעבורם:
\[\oint \mathbf{F} \cdot d\mathbf{r} \neq 0\]לשלמות התמונה (ניתן להוכיח באמצעות תנאי הרוטור $\nabla \times \mathbf{F} = \mathbf{0}$):
- $\mathbf{F} = (x,y,0)$ - משמר
- $\mathbf{F} = (\cos x, 0, 0)$ - משמר
- $\mathbf{F} = (y,x,0)$ - משמר
- $\mathbf{F} = (xy,xy,0)$ - לא משמר
- $\mathbf{F} = (xy^2,x^2y,0)$ - משמר (הייתה טעות בניסוח המקורי)
בדיקת שמרנות: $\mathbf{F} = (xy,xy,0)$
נבחר מסלול מלבני במישור $xy$ מ-$(0,0)$ דרך $(1,0)$, $(1,2)$, $(0,2)$ וחזרה ל-$(0,0)$.
(0,2) ←──I₃── (1,2)
↑ ↑
I₄ I₂
↓ ↓
(0,0) ──I₁──→ (1,0)
המסלול כולל ארבע צלעות:
\[\oint \mathbf{F} \cdot d\mathbf{r} = \int_{I_1} + \int_{I_2} + \int_{I_3} + \int_{I_4}\]חישוב אינטגרלים
-
צלע $I_1$: $(0,0) \to (1,0)$ ($y=0, dy=0, d\mathbf{r}=dx\hat{\mathbf{x}}$)
\[\int_0^1 (x \cdot 0, x \cdot 0, 0) \cdot (dx, 0, 0) = \int_0^1 0 \, dx = 0\] -
צלע $I_2$: $(1,0) \to (1,2)$ ($x=1, dx=0, d\mathbf{r}=dy\hat{\mathbf{y}}$)
\[\int_0^2 (1 \cdot y, 1 \cdot y, 0) \cdot (0, dy, 0) = \int_0^2 y \, dy = \left[ \frac{y^2}{2} \right]_0^2 = 2\] -
צלע $I_3$: $(1,2) \to (0,2)$ ($y=2, dy=0, d\mathbf{r}=-dx\hat{\mathbf{x}}$)
\[\int_1^0 (x \cdot 2, x \cdot 2, 0) \cdot (dx, 0, 0) = \int_1^0 2x \, dx = \left[ x^2 \right]_1^0 = 0 - 1 = -1\] -
צלע $I_4$: $(0,2) \to (0,0)$ ($x=0, dx=0, d\mathbf{r}=-dy\hat{\mathbf{y}}$)
\[\int_2^0 (0 \cdot y, 0 \cdot y, 0) \cdot (0, dy, 0) = \int_2^0 0 \, dy = 0\]
סך הכל:
\[\oint \mathbf{F} \cdot d\mathbf{r} = 0 + 2 - 1 + 0 = 1 \neq 0\]ולכן הכוח אינו משמר.
שאלה 3: התפוצצות
עגלה במסה $M$ ובתוכה כדור במסה $m$ נעות ימינה במהירות משותפת $v$ על מסילה ללא חיכוך. ברגע מסוים נפער בור בתחתית העגלה והכדור נפל דרכו למטה.
מהי מהירות העגלה לאחר שהכדור נפל?
before: [m+M]→v after: [M]→U , [m]→u
אם נזניח את האינטראקציה האנכית, על ציר ה-$x$ לא פועלים כוחות חיצוניים על המערכת (עגלה+כדור). לכן התנע האופקי נשמר. כאשר הכדור נופל, אין כוח אופקי שפועל עליו או על העגלה. לכן, המהירות האופקית של כל גוף נשמרת.
מהירות אופקית התחלתית של הכדור: $v_x = v$. מהירות אופקית התחלתית של העגלה: $V_x = v$.
לאחר הנפילה, המהירות האופקית של הכדור היא $u_x = v$. המהירות האופקית של העגלה היא $U_x = v$.
\[\boxed{U = v}\]כלומר, גם העגלה וגם הכדור שומרים על מהירותם האופקית.
שאלה 4: התנגשות אלסטית
כדור שמסתו $m$ נע ימינה בתוך מסגרת מלבנית, במקביל לצלע שאורכה $\ell$, במהירות קבועה $v$.
מסת המסגרת היא $M = \alpha m$ (כאשר $\alpha > 0$).
לאחר זמן מסוים הכדור מתנגש חזיתית ואלסטית במסגרת. התנועה היא במישור אופקי ללא חיכוך.
- חשבו את מהירות הכדור והמסגרת מיד לאחר ההתנגשות.
- מה קורה כאשר $\alpha \to 0, \alpha = 1, \alpha \gg 1$? הסבירו את התוצאות.
- עבור $\alpha > 0$, כמה זמן יעבור בין ההתנגשות הראשונה לשנייה?
M=αm ┌───────────────┐ │ [m]→v │ └───────────────┘ ───ℓ───→ [M=αm]
הקדמה:
- נסמן מהירויות לפני התנגשות: $v_m = v$, $v_M = 0$.
- נסמן מהירויות אחרי התנגשות: $u_m$, $u_M$.
- הבעיה חד-ממדית.
1. חישוב מהירויות לאחר ההתנגשות
מערכת המשוואות להתנגשות אלסטית חד-ממדית:
-
שימור תנע:
\[mv_m + \cancel{Mv_M} = mu_m + Mu_M\] \[\implies \boxed{mv = mu_m + (\alpha m)u_M}\] -
שימור אנרגיה (או היפוך מהירות יחסית):
\[v_m - \cancel{v_M} = u_M - u_m\] \[\implies v = u_M - u_m\]
נפשט את משוואת התנע:
\[v = u_m + \alpha u_M \quad (*)\]ממשוואת המהירות היחסית:
\[u_m = u_M - v \quad (**)\]נציב את \((**)\) ב-\((*)\):
\[v = (u_M - v) + \alpha u_M\] \[2v = u_M(1 + \alpha)\] \[\boxed{u_M = \frac{2v}{1 + \alpha}}\]נציב חזרה ב-$(**)$:
\[\begin{aligned} u_m &= \frac{2v}{1 + \alpha} - v \\[10pt] &= \frac{2v - v(1+\alpha)}{1+\alpha} \\[10pt] &= \frac{v(1-\alpha)}{1+\alpha} \end{aligned}\] \[\boxed{ u_M = \frac{2v}{1 + \alpha}, \quad u_m = v\frac{1 - \alpha}{1 + \alpha}}\]2. מקרים מיוחדים
כאשר $\alpha \to 0$ (מסגרת חסרת מסה):
\[u_M \to 2v, \qquad u_m \to v\]לא פיזיקלי, המסגרת לא יכולה לנוע מהר יותר מהכדור שפגע בה.
כאשר $\alpha = 1$ (מסות שוות):
\[u_M = v, \qquad u_m = 0\]הכדור נעצר ומעביר את כל התנע שלו למסגרת, כמו במטוטלת של ניוטון.
כאשר $\alpha \gg 1$ (מסגרת כבדה מאוד):
\[u_M \to 0, \qquad u_m \to -v\]המסגרת בקושי זזה, והכדור חוזר אחורה באותה מהירות (כמו כדור שקופץ מקיר).
3. זמן בין ההתנגשויות
הכדור צריך לעבור מרחק $\ell$ יחסית לקצה השני של המסגרת. המהירות היחסית לאחר ההתנגשות היא:
\[\begin{aligned} \Delta u &= u_m - u_M \\[10pt] &= v\frac{1 - \alpha}{1 + \alpha} - \frac{2v}{1 + \alpha} \\[10pt] &= \frac{v(1 - \alpha - 2)}{1 + \alpha} \\[10pt] &= \frac{v(-1 - \alpha)}{1 + \alpha} = -v \end{aligned}\]המהירות היחסית היא בגודל $v$ - הכדור מתרחק מהקיר הראשון ומתקרב לקיר השני במהירות יחסית $v$.
\[\boxed{t = \frac{\ell}{|\Delta u|} = \frac{\ell}{v}}\]שאלה 5: התנגשות דו-מימדית
כדור בעל מסה $2m$ מחליק על משטח אופקי חלק במהירות $v_0$ לאורך ציר $x$.
הכדור מתנגש בכדור אחר בעל מסה $m$ שנמצא במנוחה.
לאחר ההתנגשות נע החלקיק שמסתו $m$ במהירות $v_0/2$ בכיוון היוצר זווית בת $\theta = 30^\circ$ עם ציר ה-$x$.
- מה המהירות (גודל וכיוון) של החלקיק שמסתו $2m$ לאחר ההתנגשות?
- האם ההתנגשות אלסטית לחלוטין?
↗ v₀ v₀/2 / → / θ=30° -●------------○-----→ 2m m x
1. מהירות החלקיק בעל המסה $2m$ לאחר ההתנגשות
נשתמש בשימור תנע (לא נתון מידע על סוג ההתנגשות). נסמן את מהירות הגוף $2m$ לאחר ההתנגשות ב-$\mathbf{u}$.
התנע ההתחלתי: לפני ההתנגשות רק הכדור בעל המסה $2m$ נע, ורק על ציר $x$:
\[\mathbf{p}_i = (2m v_0) \hat{\mathbf{x}}\]התנע הסופי: לאחר ההתנגשות שני הכדורים נעים, אחד במהירות $v_0/2$ בזווית של $30^\circ$, והשני במהירות $\mathbf{u}$:
\[\mathbf{p}_f = (2m) \mathbf{u} + m \left(\frac{v_0}{2}\cos\theta \hat{\mathbf{x}} + \frac{v_0}{2}\sin\theta \hat{\mathbf{y}}\right)\]נשווה רכיבים:
ציר $x$: →
\[\begin{aligned} p_{x,i} &= p_{x,f} \\ 2mv_0 &= 2mu_{x} + m\frac{v_{0}}{2} \cos(30^\circ) \\ 2v_0 &= 2u_x + \frac{v_0}{2} \frac{\sqrt{3}}{2} \\ 2u_x &= 2v_0 - \frac{v_0\sqrt{3}}{4} \\ u_{x} &= v_0 \left(1 - \frac{\sqrt{3}}{8}\right) \end{aligned}\]ציר $y$: ↑
\[\begin{aligned} p_{y,i} &= p_{y,f} \\ 0 &= 2mu_{y} + m\frac{v_{0}}{2} \sin(30^\circ) \\ 0 &= 2u_y + \frac{v_0}{2} \frac{1}{2} \\ u_{y} &= -\frac{v_0}{8} \end{aligned}\]גודל $u$:
\[\begin{aligned} u = |\mathbf{u}| &= \sqrt{u_x^2 + u_y^2} \\[10pt] &= v_0 \sqrt{\left(1 - \tfrac{\sqrt{3}}{8}\right)^2 + \left(-\tfrac{1}{8}\right)^2} \\[10pt] &\approx \boxed{0.793 v_0} \end{aligned}\]כיוון $u$:
\[\phi = \arctan\left(\frac{u_y}{u_x}\right) = \arctan\left(\tfrac{-1/8}{1 - \sqrt{3}/8}\right) \approx \boxed{-9.1^\circ}\]2. האם ההתנגשות אלסטית לחלוטין
נבדוק שימור אנרגיה קינטית:
לפני ההתנגשות:
\[E_{k,i} = \frac{1}{2} (2m) v_0^2 = \boxed{mv_0^2}\]אחרי ההתנגשות:
\[\begin{aligned} E_{k,f} &= \frac{1}{2} (2m) u^2 + \frac{1}{2} m \left(\frac{v_0}{2}\right)^2 \\[10pt] &= m (0.793v_0)^2 + \frac{m v_0^2}{8} \\[10pt] &= m v_0^2 (0.793^2 + 1/8) \\[10pt] &= m v_0^2 (0.629 + 0.125) = \boxed{0.754mv_0^2} \end{aligned}\]מכיוון ש-$E_{k,f} < E_{k,i}$, ההתנגשות אינה אלסטית.
הערה: האנרגיה הקינטית של המערכת לאחר ההתנגשות קטנה מהאנרגיה הקינטית לפני ההתנגשות, כפי שצריך להיות בהתנגשות לא-אלסטית.
עקרונות מרכזיים - סיכום
| עקרון | נוסחה | הסבר ותכונות |
|---|---|---|
| משפט עבודה-אנרגיה | \(W_{\text{net}} = \Delta E_k\) | • כולל את כל הכוחות (משמרים ולא משמרים) • חיכוך תמיד מפחית אנרגיה קינטית |
| כוחות משמרים | \(\oint \mathbf{F} \cdot d\mathbf{r} = 0\) | • עבודה תלויה רק בנקודות קצה • מאפשרים הגדרת אנרגיה פוטנציאלית |
| שימור תנע | \(\mathbf{p}_{\text{total}} = \text{constant}\) | • תקף תמיד כשאין כוחות חיצוניים • עובד בכל ממד בנפרד |
| התנגשויות | תלוי בסוג ההתנגשות | • אלסטית: נשמרים תנע ואנרגיה קינטית • אי-אלסטית: נשמר רק תנע • פלסטית (אי-אלסטית מושלמת): הגופים נדבקים יחד |
| שיטות פתרון | - | • חד-מימדי: משוואות אלגבריות פשוטות • דו-מימדי: שימור תנע בכל ציר בנפרד • בדיקת עקביות: תמיד לבדוק שימור אנרגיה |
| טיפים לפתרון בעיות | - | • זהה את כל הכוחות הפועלים • בחר מערכת צירים מתאימה • השתמש בשימורים הרלוונטיים • בדוק עקביות התוצאות • פרש פיזית את התוצאות |