שאלות:
- שאלה מקדימה: פיתוח וקטורי המקום, המהירות והתאוצה בקואורדינטות פולריות
- שאלה 1: השפעת סיבוב כדור הארץ על המשקל
- שאלה 2: חוט מחליק (חבל משתלשל) עם כוחות מעכבים
- שאלה 3: מכונת ארטווד
שאלה מקדימה: פיתוח וקטורי המקום, המהירות והתאוצה בקואורדינטות פולריות
וקטור המקום בקואורדינטות קרטזיות הוא:
\[\vec{r} = x \hat{x} + y \hat{y}\]אם נשתמש בקואורדינטות פולריות $(r,\theta)$, נוכל לכתוב את וקטור המקום כך:
\[\vec{r} = r \cdot \cos \left(\theta\right) \hat{x} + r \cdot \sin \left(\theta\right) \hat{y}\]בכתיבה שמדגישה את התלות בזמן $\theta(t)$:
\[\vec{r}(t) = r(t) \cdot \cos \left(\theta(t)\right) \hat{x} + r(t) \cdot \sin \left(\theta(t)\right) \hat{y}\]מכאן שוקטור היחידה הוא:
\[\boxed{\hat{r}(t) = \cos \left(\theta(t)\right) \hat{x} + \sin \left(\theta(t)\right) \hat{y}}\]הווקטור הזה הוא בכיוון וקטור הרדיוס שמתחיל בראשית ומציע לעבר המיקום המדובר.
וקטור היחידה הפולארי השני הוא $\hat{\theta}$, המכוון בניצב לוקטור $\hat{r}$:
\[\boxed{\hat{\theta}(t) = -\sin \left(\theta(t)\right) \hat{x} + \cos \left(\theta(t)\right) \hat{y}}\]אפשר לוודא על ידי מכפלה סקלרית.
בכתיב מקוצר:
\[\boxed{\hat{r} = \cos \theta \hat{x} + \sin \theta \hat{y}, \quad \hat{\theta} = -\sin \theta \hat{x} + \cos \theta \hat{y}}\]לפי כלל השרשרת:
\[\frac{d\hat{r}}{dt} = \dot{\theta} \hat{\theta} \implies \boxed{\frac{d\hat{r}}{dt} = \dot{\theta} \hat{\theta}}\] \[\frac{d\hat{\theta}}{dt} = -\dot{\theta} \hat{r} \implies \boxed{\frac{d\hat{\theta}}{dt} = -\dot{\theta} \hat{r}}\]חישוב המהירות ורכיביה הפולאריים:
\[\begin{aligned} \vec{r} &= r \cos \theta \hat{x} + r \sin \theta \hat{y} = r \hat{r} \\[10pt] \vec{v} &= \frac{d\vec{r}}{dt} = \dot{r} \hat{r} + r \frac{d\hat{r}}{dt} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta} \end{aligned}\] \[\implies \boxed{\vec{v} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta}}\]חישוב התאוצה ורכיביה הפולאריים:
\[\begin{aligned} \vec{a} &= \frac{d\vec{v}}{dt} = \ddot{r} \hat{r} + \dot{r} \frac{d\hat{r}}{dt} + r \frac{d}{dt}(\dot{\theta} \hat{\theta}) \\[10pt] &= \ddot{r} \hat{r} + \dot{r} \dot{\theta} \hat{\theta} + r \left(\ddot{\theta} \hat{\theta} + \dot{\theta} \frac{d\hat{\theta}}{dt}\right) \\[10pt] &= \ddot{r} \hat{r} + \dot{r} \dot{\theta} \hat{\theta} + r \left(\ddot{\theta} \hat{\theta} - \dot{\theta}^2 \hat{r}\right) \\[10pt] &= \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) \hat{\theta} \end{aligned}\] \[\boxed{\vec{a} = \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) \hat{\theta}}\] \[\boxed{a_r = \ddot{r} - r \dot{\theta}^2, \quad a_\theta = r \ddot{\theta} + 2 \dot{r} \dot{\theta}}\]שאלה 1: השפעת סיבוב כדור הארץ על המשקל
העריכו כיצד משפיעה התנועה הסיבובית של כדור הארץ על הערך שיראה מד המשקל? האם זה קשור למיקום על פני כדור הארץ?
הערה: רדיוס כדור הארץ הוא כ-6300 קילומטר וזמן מחזור סיבובו סביב ציר הסיבוב שלו הוא כ-24 שעות (קצת פחות, למה?)
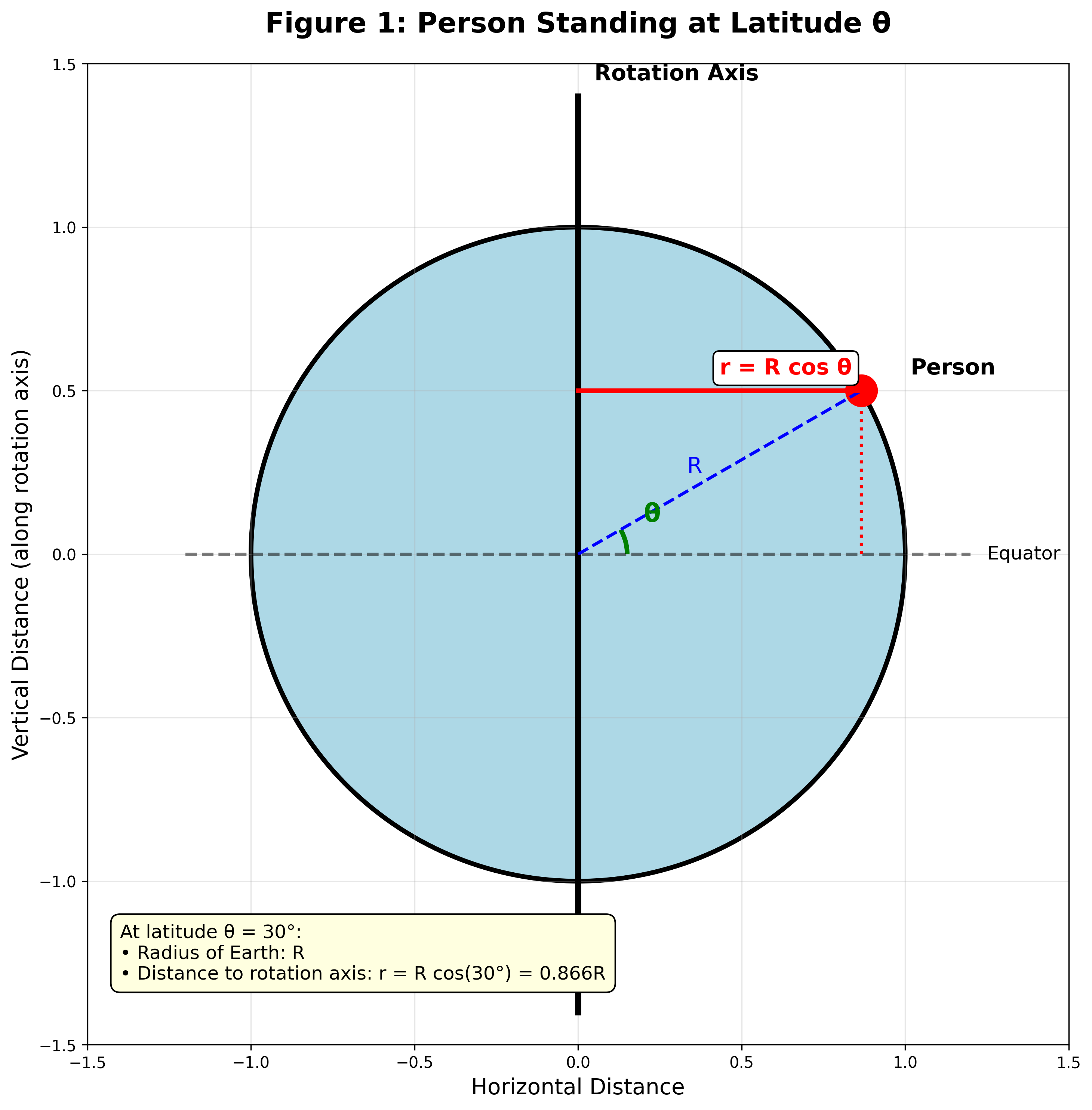
במערכת הייחוס הסובבת עם כדור הארץ, הכוחות הפועלים על אדם העומד על פני כדור הארץ הם:
- כוח הכבידה: $mg$ הפועל לכיוון מרכז כדור הארץ
- כוח הנורמלי מהקרקע: $N$ הפועל מאונך למשטח
- כוח צנטריפוגלי: $m\omega^2 r$ הפועל בכיוון רדיאלי החוצה מציר הסיבוב
עבור אדם הנמצא בקו רוחב $\theta$, רדיוס הסיבוב סביב ציר כדור הארץ הוא:
\[\boxed{r = R_E \cos\theta}\]הכוח הצנטריפוגלי החוצה מציר הסיבוב הוא:
\[F_{cf,\;vertical} = m\omega^{2}R_E\cos^{2}\theta\]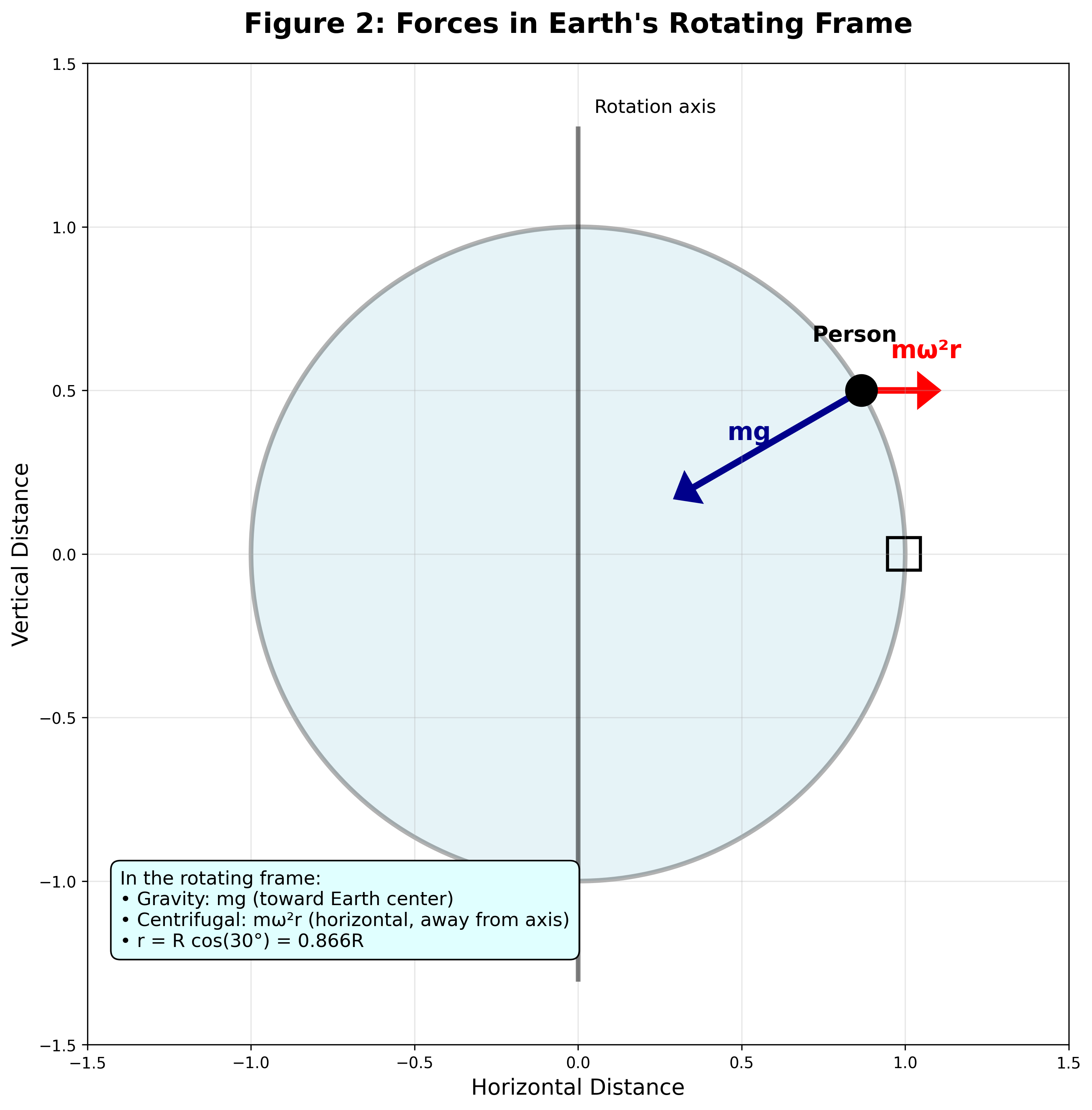
כאשר מפרקים את הכוח הצנטריפוגלי לרכיבים:
- רכיב רדיאלי (ממרכז כדור הארץ לכיוון האדם והחוצה ↗): $m\omega^2 R_E \cos\theta \cdot \cos\theta = m\omega^2 R_E \cos^2\theta$
- רכיב טנגנציאלי (משיק לציר הריאלי ↖): $m\omega^2 R_E \cos\theta \cdot \sin\theta$
מכיוון שהכוח הצנטריפוגלי קטן מאוד ביחס לכוח הכבידה (~0.3%), ניתן לבצע קירוב ולהתייחס רק להשפעה על הרכיב האנכי של התאוצה האפקטיבית. כלומר, להתמקד בציר הרדיאלי ממרכז כדור הארץ (↖). בפתרון שהיה בדפי התרגול התייחסו גם לכוח החיכוך בציר הזה, למרות שלהבנתי מיותר.
הכוחות שפועלים בציר הזה הם $mg$ כלפי מטה ו-$N$ כלפי מעלה - ביחד עם ההיטל של הכוח הצנטריפוגלי, שהוא:
\[\begin{aligned} F_{cf, vertical} &= \cos \left( \theta\right) m\omega^2r \\[10pt] &= m\omega^2 R_E \cos^2\theta \end{aligned}\]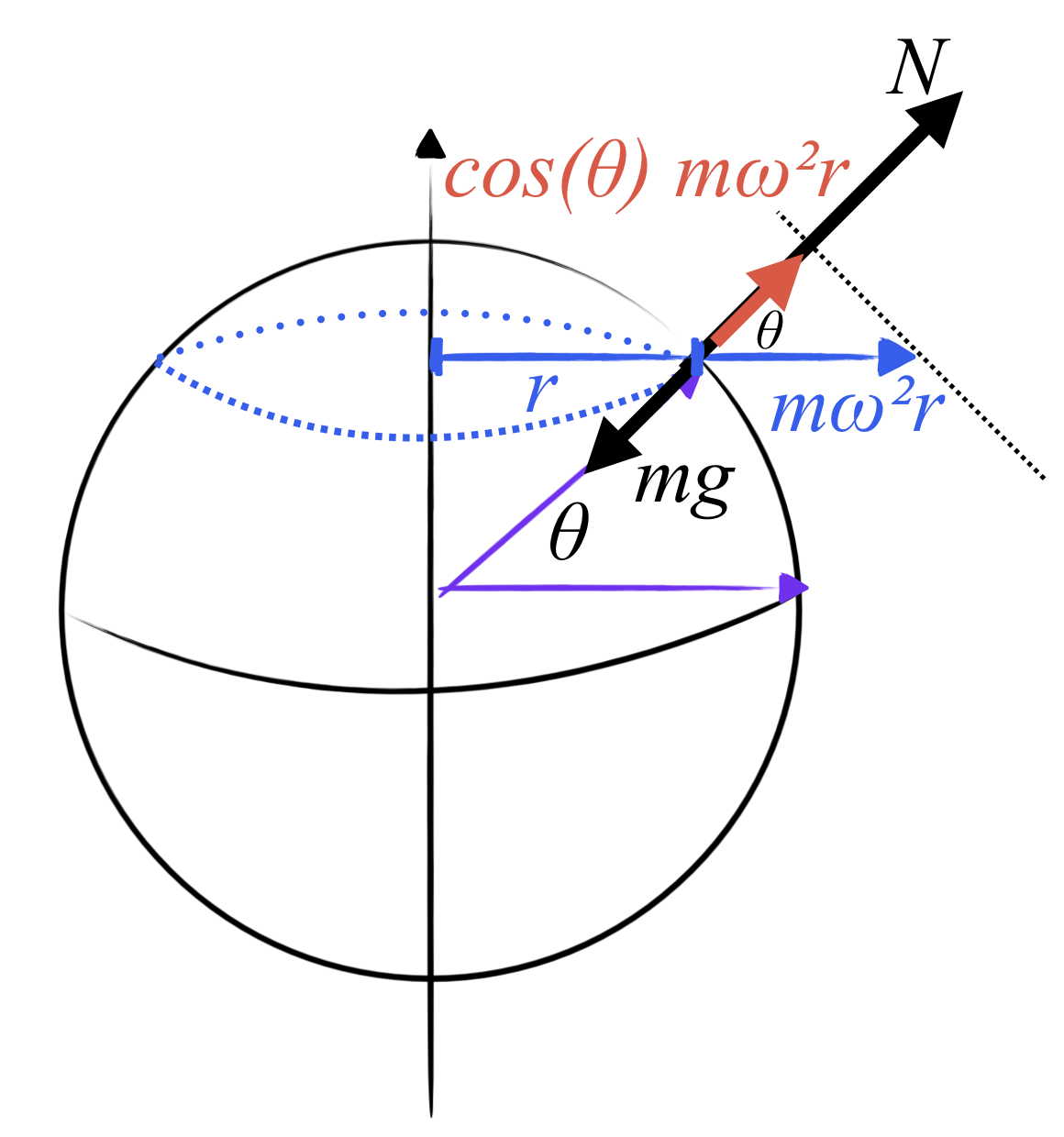
לפי החוק השני של ניוטון במערכת לא אינרציאלית:
\[N + m\omega^2 R_E \cos^2\theta = mg\]מכאן, הירידה במשקל הנמדד ביחס למשקל “האמיתי” היא:
\[\boxed{\Delta W = mg - N = m\omega^2 R_E \cos^2\theta}\]עבור כדור הארץ:
\[\omega = \frac{2\pi}{T} = \frac{2\pi}{24 \mathrm{h} \cdot 3600 \mathrm{s/h}} = \frac{2\pi}{86,400 \mathrm{s}} \approx 7.27 \times 10^{-5} \, \mathrm{rad/s}\] \[R_E \approx 6300 \mathrm{km} = 6.3 \times 10^6 \, \mathrm{m}\]בקו המשווה ($\theta = 0°$):
\[\frac{\Delta W}{W} = \frac{m\omega^2 R_E \cos^2(0°)}{mg} = \frac{\omega^2 R_E}{g} \approx \frac{(7.27 \times 10^{-5})^2 \cdot 6.3 \times 10^6}{10 \mathrm{m/s}^2} \approx 0.0033\]בקוטב ($\theta = 90°$):
\[\frac{\Delta W}{W} = \frac{m\omega^2 R_E \cos^2(90°)}{mg} = 0\]מסקנות:
- ההשפעה מקסימלית בקו המשווה (ירידה של בערך 0.33% במד המשקל)
- ההשפעה מתאפסת בקטבים ($\theta = 90°$)
- בקו רוחב 45° הירידה בכ-0.17%
שאלה 2: חוט מחליק (חבל משתלשל) עם כוחות מעכבים
המערכת הבאה משוחררת ממנוחה כמתואר באיור. צפיפות החבל אחידה ומסתו $M$ ואורך החבל $\ell$. הזווית של המישור המשופע היא $\theta$.
בתוך המים יש כוח גרר כמתואר באיור ($A$ נתון). על המישור המשופע יש כוח חיכוך. כתבו משוואה דיפרנציאלית המתארת את התנועה. בדקו את מקרה הקצה $\theta=\frac{\pi}{2}$ ואין כוח גרר.
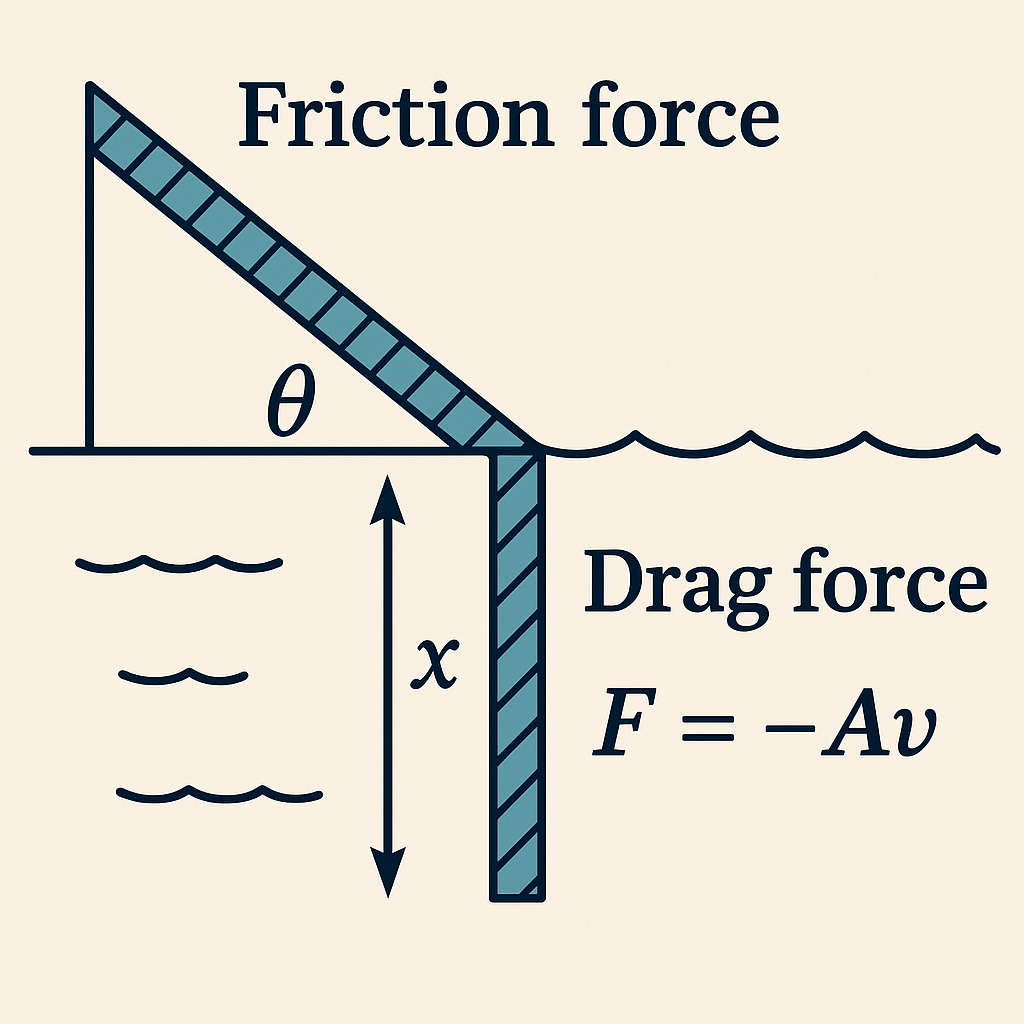
נערוך פירוק כוחות לכל חלק בנפרד, כי כל חלק של החבל חווה כוחות שונים. היחס בין 2 החלקים משתנה.
משקל החוט שבתוך המים:
\[\frac{x}{\ell} \cdot M\]משקל החוט שמעל המים:
\[\left(\frac{\ell - x}{\ell}\right) \cdot M\]משוואת הכוחות על החלק שבתוך המים בכיוון הנפילה היא (↓):
\[\begin{aligned} \underbrace{\frac{x}{\ell} \cdot M}_{\text{mass of fallig part}} a_{\text{falling}} &= \sum F_{\text{falling}} \\[10pt] &= \frac{x}{\ell} \cdot M g - \underbrace{Av}_{\text{drag}} - T \\[10pt] \frac{x}{\ell} M \ddot{x} &= \frac{x}{\ell} M g - A\dot{x} - T \end{aligned}\]נסמן:
\[\boxed{\frac{x}{\ell} M \ddot{x} = \frac{x}{\ell} M g - A\dot{x} - T}\tag{1}\]משוואת הכוחות על החלק שעל ״המגלשה״ בכיוון הנפילה (↘):
\[\underbrace{\left(\frac{\ell - x}{\ell}\right) \cdot M}_{\text{mass of sliding part}} a_{\text{sliding}} = \sum F_{\text{sliding}}\] \[= T - f_k + \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \sin \theta\]נסמן:
\[\boxed{\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - f_k + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta} \tag{2}\]מתוך סכום הכוחות הניצבים לכיוון הגלישה נוכל לקבל משוואה נוספת (↗):
\[0 = \sum F_{\text{normal}} = N - \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta\]מסיקים:
\[\boxed{N = \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta}\]כוח החיכוך הדינמי הוא $f_k = \mu_k N$, כאשר $\mu_k$ הוא מקדם החיכוך הדינמי. נחבר את $N$ שקיבלנו למשוואה זו:
\[\boxed{f_k = \mu_k N = \mu_k \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta}\]נציב את $f_k$ במשוואת הכוחות בכיוון הגלישה (2):
\[\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta \tag{2}\]סך הכל קיבלנו שתי משוואות:
\[\boxed{\frac{x}{\ell} M \ddot{x} = \frac{x}{\ell} M g - A\dot{x} - T}\tag{1}\] \[\boxed{\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta} \tag{2}\]נחבר את שתי המשוואות (1) ו-(2) כדי להיפטר מהכוח $T$:
\[\begin{aligned} \frac{x}{\ell} M \ddot{x} +& \left(\frac{\ell - x}{\ell}\right) M \ddot{x} =\\[10pt] \frac{x}{\ell} M g &- A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta \\[10pt] &+ \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta \end{aligned}\]נפתח את המשוואה:
\[M\ddot{x} \left(\frac{x + \ell - x}{\ell}\right) = \frac{x}{\ell} M g - A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta\]נפשט את המשוואה:
\[M\ddot{x} = \frac{x}{\ell} M g - A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta\]נחלק ב-$M$:
\[\ddot{x} = \frac{x}{\ell} g - \frac{A}{M}\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) g \cdot \sin \theta\] \[\boxed{\ddot{x} = \frac{x}{\ell} g - \frac{A}{M}\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) g \cdot \sin \theta}\]נבדוק מה קורה כאשר $\theta = \frac{\pi}{2}$ וללא כוח גרר עם המים - כלומר, כאשר החוט נופל בנפילה חופשית. נקווה שבמצב כזה יתקיים $M\ddot{x} = Mg$.
במצב זה, נציב $\theta = \frac{\pi}{2}$, כלומר $\cos \theta = 0$ ו-$\sin \theta = 1$. כמו כן, נניח שאין כוח גרר, כלומר $A = 0$. אז המשוואה תהפוך ל:
\[\ddot{x} = \frac{x}{\ell} g - 0 - 0 + \left(\frac{\ell - x}{\ell}\right) g\] \[\ddot{x} = \frac{x}{\ell} g + \left(\frac{\ell - x}{\ell}\right) g\] \[\ddot{x} = \frac{g}{\ell} (x + \ell - x) = \frac{g}{\ell} \ell = g\] \[\boxed{\ddot{x} = g}\]כך שהאצה של החוט היא $g$, כלומר הוא נופל בנפילה חופשית, כפי שציפינו.
שאלה 3: מכונת ארטווד
נתונה המערכת באיור. המסה $M$ יכולה לנוע אנכית. המסה $m$ יכולה לנוע לכל כיוון.
נתון $m = M$.
כתבו מערכת משוואות המתארות את התנועה של מרחק המסה $m$ מציר הסיבוב (הרדיוס) והזווית.
השתמשו בקירוב של זוויות קטנות.
האם יכולות להיות תנודות כאשר הרדיוס קבוע?

חלק א׳: משוואות התנועה
על המסה השמאלית (שמקובעת רק לציר ה-$y$) פועלים כוחות:
- כוח הכבידה $Mg$ כלפי מטה (בחרנו את כיוון $y$ כלפי מטה ומכאן $g$ חיובי)
- מתיחות החוט $T$ כלפי מעלה נגד ציר $y$
לכן, לפי החוק השני של ניוטון:
\[ma_y = \sum F_y = mg - T\]על המסה הימנית (שיכולה לנוע לכל כיוון) נחיל מערכת צירים פולארית.
בציר הרדיאלי (מהחיבור לתקרה - חיובי כלפי המסה מטה):
\[ma_r = \sum F_r = mg \cos \theta - T = m\left(\ddot{r} - r \dot{\theta}^2\right)\]בציר הטנגנציאלי (בניצב לציר הרדיאלי, חיובי בכיוון התנועה):
\[ma_\theta = \sum F_\theta = mg \sin \theta = m\left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right)\]נבחין שמתחקיים :
\[\Delta y = \Delta r\]כי המתיחות בחוט נשמרת. נזכיר ש$r$ הוא המרחק מהמסה הימנית לציר הסיבוב, כלומר אורך החוט. מכאן ש:
\[\boxed{a_y=\ddot{r}}\]קיבלנו שלוש משוואות בקואורדינטות פולריות בשלושה נעלמים: $T$, $r$ ו-$\theta$.
\[\begin{align} m\ddot{r} & = mg-T \tag{1} \\[10pt] m\left(\ddot{r} - r \dot{\theta}^2\right) &= mg \cos \left(\theta\right) = T \tag{2} \\[10pt] m\left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) &= mg \sin \theta \tag{3} \end{align}\]נחלץ את $T$ מהמשוואה (1) ונציב אותו במשוואה (2):
\[T = m\left(g - \ddot{r}\right)\]נציב את $T$ במשוואה (2):
\[\cancel{m}\left(\cancel{\ddot{r}} - r \dot{\theta}^2\right) = mg \cos \theta - \cancel{m}\left(g - \cancel{\ddot{r}}\right)\]נחבר את משוואות (1) ו-(2):
\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= g(\cos \theta - 1) \\[10pt] r\ddot{\theta}^2 + 2\dot{r}\dot{\theta} &= g \sin \theta \end{aligned}}\]זו התשובה הסופית שמתארת את התנועה במשתנים הקינמטיים $r$ ו-$\theta$.
חלק ב׳: קירוב של זוויות קטנות
מטורי טיילור:
\[\begin{cases} \cos \theta -1 \approx - \frac{\theta^2}{2} \\[10pt] \sin \theta \approx \theta \end{cases}\]נציב את הקירובים במשוואות:
\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= -\frac{g\theta^2}{2} \\[10pt] r\ddot{\theta} + 2\dot{r}\dot{\theta} &= g \theta \end{aligned} }\]חלק ג׳: האם יכולות להיות תנודות כאשר הרדיוס קבוע?
השאלה האם תתכן תנועה זוויתית כאשר $r$ קבוע שואלת האם ייתכן כי $\dot{r} = \dot{r} = 0$ וכן $\dot{theta} \neq 0, \, \ddot{\theta} \neq 0$.
המתרגל פיתח את המשוואות הקודמות לביטוי של $\theta$:
\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= -\frac{g\theta^2}{2} \\[10pt] \theta = \pm \sqrt{\frac{2r}{g}} \dot{\theta}^2 \\[10pt] \end{aligned}}\]הוא הציב את הביטוי הזה במשוואה השנייה וקיבל שכאשר $\dot{r} = 0$ ו-$\ddot{\theta} \neq 0$, מתקיים:
\[\boxed{ \begin{aligned} r\ddot{\theta} + 2\underbrace{\dot{r}}_{=0}\dot{\theta} &= g \theta \\[10pt] r\ddot{\theta} &= \pm g \cdot \sqrt{\frac{2r}{g}} \dot{\theta}^2 \end{aligned}}\]למשוואה הזאת יש פתרון, מכאן שייתכנו תנודדות מטוטלת גם כאשר 2 המסות לא עולות ויורדות.
דור פסקל