1. סיכום המשוואות היסודיות
בשיעור הקודם פיתחנו שתי משוואות מרכזיות מתוך הנחת יסוד אחת - שמטען חשמלי קורן את השפעתו למרחב:
1.1 חוק גאוס (הצורה האינטגרלית)
\[\Phi = \oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = Q_\Omega \tag{1}\]במילים: השטף של שדה הפוטנציאל החשמלי $\vec{D}$ דרך הקרום $\partial\Omega$ שווה למטען החשמלי $Q$ שכלוא בתוך הנפח $\Omega$.
זאת ההגדרה של שדה ההשפעה $\vec{D}$ המושרה מהמטען החשמלי.
1.2 משוואת מקסוול הראשונה (הצורה הדיפרנציאלית)
\[\nabla \cdot \vec{D} = \rho \tag{2}\]זאת משוואה לוקלית - נכונה בכל נקודה ונקודה במרחב. הדיברגנס (הפליטה המקומית) של $\vec{D}$ שווה לצפיפות המטען החשמלי $\rho$ באותה נקודה.
כאשר המטען הכולל בנפח נתון על ידי:
\[Q_\Omega = \int_\Omega \rho(\vec{r}, t) \, d^3r\]2. הקשר בין שדה הפוטנציאל לשדה העוצמה החשמלית
הגדרנו את שדה העוצמה החשמלית דרך הקשר:
\[\vec{D} = \epsilon_0 \vec{E}\]כאשר $\epsilon_0$ הוא הפרמיטיביות של הריק, ככל הנראה, אבל בשלב הזה פחות רלוונטי או מובן לנו - לפחות למיטב הבנתי.
עבור מטען נקודתי בריק קיבלנו:
\[\vec{E} = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} \hat{r} = k \frac{q}{r^2} \hat{r}\]כאשר הקבוע האלקטרוסטטי:
\[k = \frac{1}{4\pi\epsilon_0} = 9 \times 10^9 \text{ (some units)}\]הערה פילוסופית: המעבר מ-$\vec{D}$ ל-$\vec{E}$ דרך $\epsilon_0$ אינו טריוויאלי. יש לו משמעות עמוקה שתובהר בהמשך. הקשר הזה דומה במהותו לקשר $E = mc^2$ שמקשר בין אנרגיה למסה.
3. חוק קולון - הכוח בין מטענים
3.1 הכוח על מטען בשדה חשמלי
הכוח האלקטרוסטטי שפועל על מטען $q$ בשדה חשמלי $\vec{E}$ נתון על ידי:
\[\vec{F} = q\vec{E}\]זהו האנלוג החשמלי לחוק $\vec{F} = m\vec{g}$ בכבידה.
3.2 הכוח בין שני מטענים נקודתיים
עבור מטען $q$ שנמצא בשדה של מטען $Q$:
\[\vec{F} = k \frac{qQ}{r^2} \hat{r} = k \frac{qQ}{r^3} \vec{r}\]זהו חוק קולון (Coulomb’s Law).
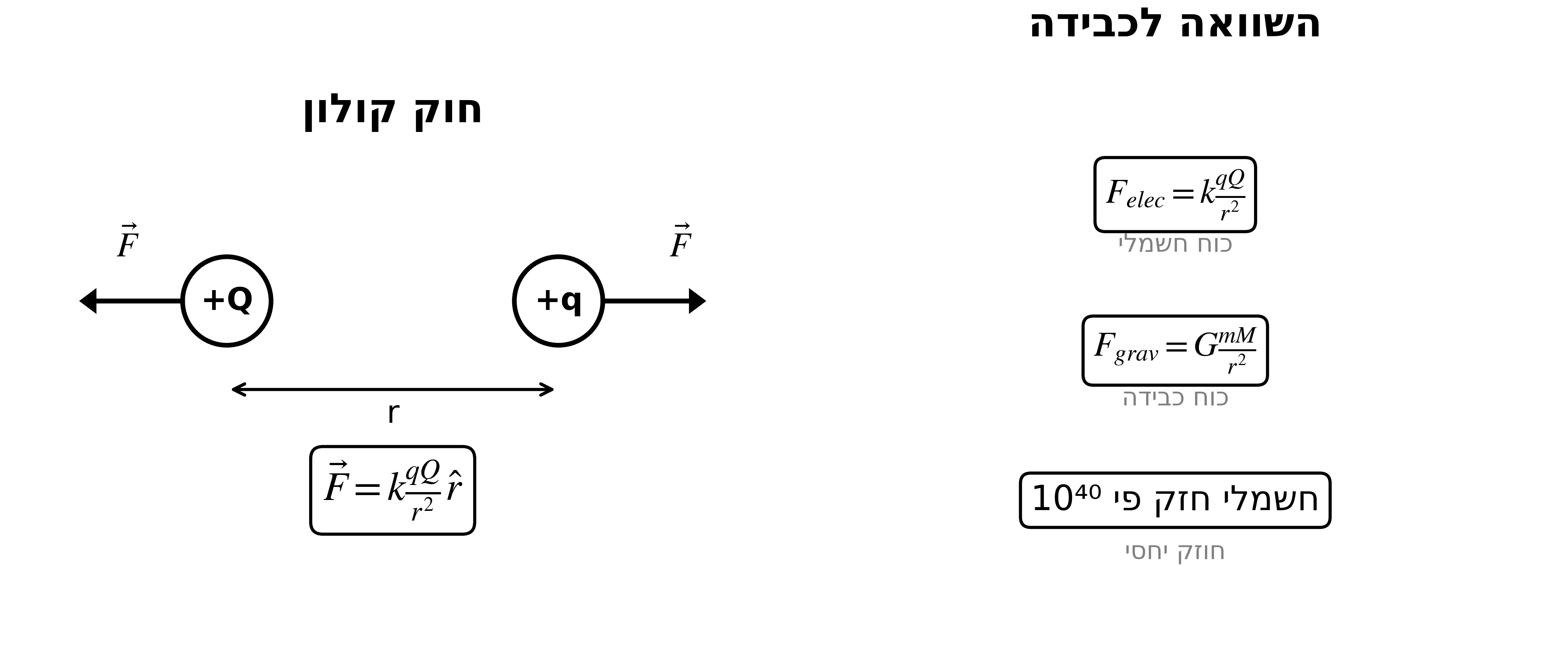
האנלוגיה לכבידה:
- כוח כבידה: $\vec{F} = G \frac{mM}{r^2} \hat{r}$
- כוח חשמלי: $\vec{F} = k \frac{qQ}{r^2} \hat{r}$
שני הכוחות דועכים כ-$1/r^2$, אך הכוח החשמלי חזק בכ-40 סדרי גודל.
4. עקרון הסופרפוזיציה
כשיש מספר מטענים במרחב, הכוח הכולל על מטען כלשהו הוא הסכום הווקטורי של כל הכוחות:
\[\vec{F}_{\text{total}} = q \sum_{i} \vec{E}_i = kq \sum_{i} \frac{Q_i}{r_i^2} \hat{r}_i\]עקרון הסופרפוזיציה נובע מכך שהאלקטרומגנטיות מתוארת באמצעות וקטורים, והוא מהווה הוכחה אמפירית שהתיאור הווקטורי נכון.
4.1 דוגמה: שני מטענים סימטריים
נתונים שני מטענים $Q$ במרחק $a$ מהראשית על ציר ה-$x$ (ב-$x = \pm a$), ומטען $q$ בגובה $b$ על ציר ה-$y$. מה הכוח הכולל על $q$?
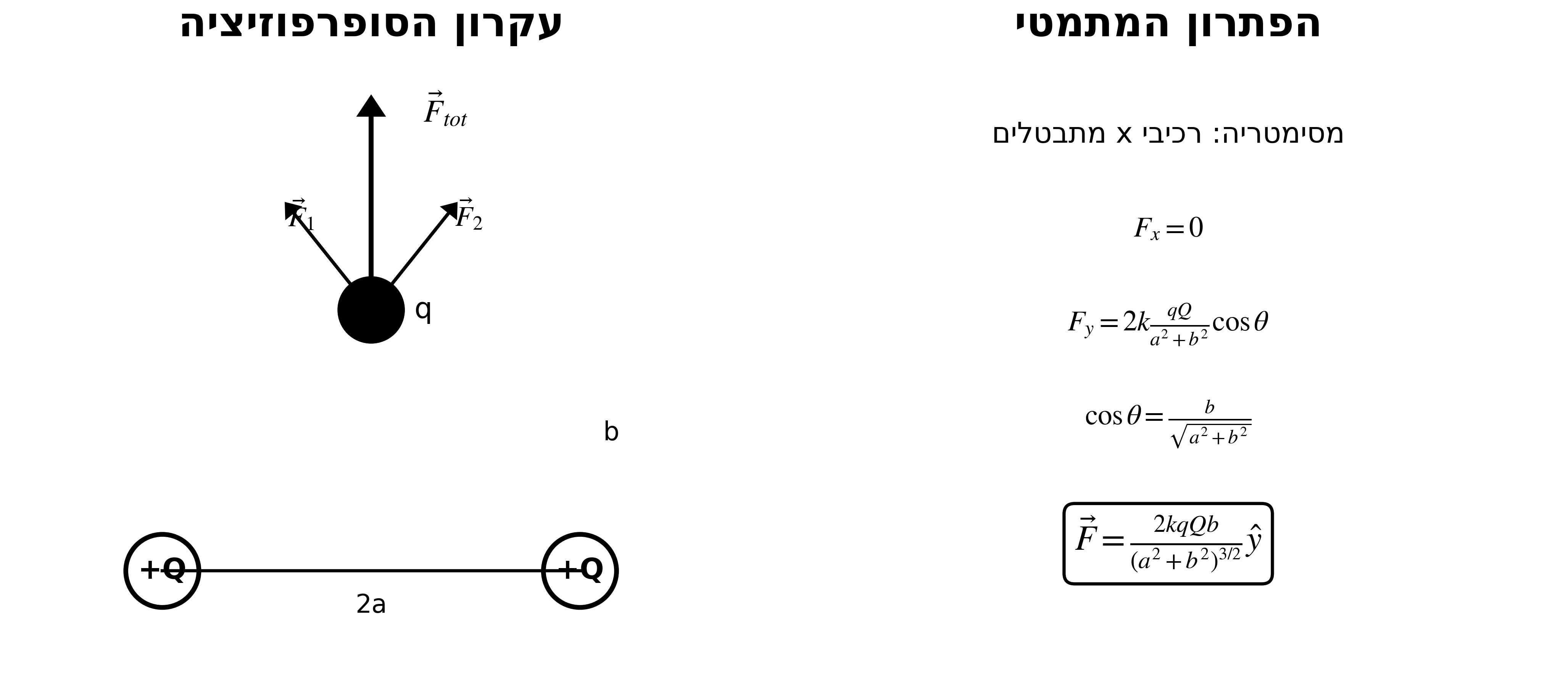
פתרון:
מסימטריה, הרכיבים בכיוון $x$ מתבטלים. הכוח הכולל בכיוון $y$:
\[F_y = 2 \cdot k \frac{qQ}{a^2 + b^2} \cdot \cos\theta = 2k \frac{qQb}{(a^2 + b^2)^{3/2}}\]כאשר $\cos\theta = \frac{b}{\sqrt{a^2 + b^2}}$.
בצורה וקטורית:
\[\vec{F} = \frac{2kqQb}{(a^2 + b^2)^{3/2}} \hat{y}\]5. יישומי חוק גאוס - קונפיגורציות סימטריות
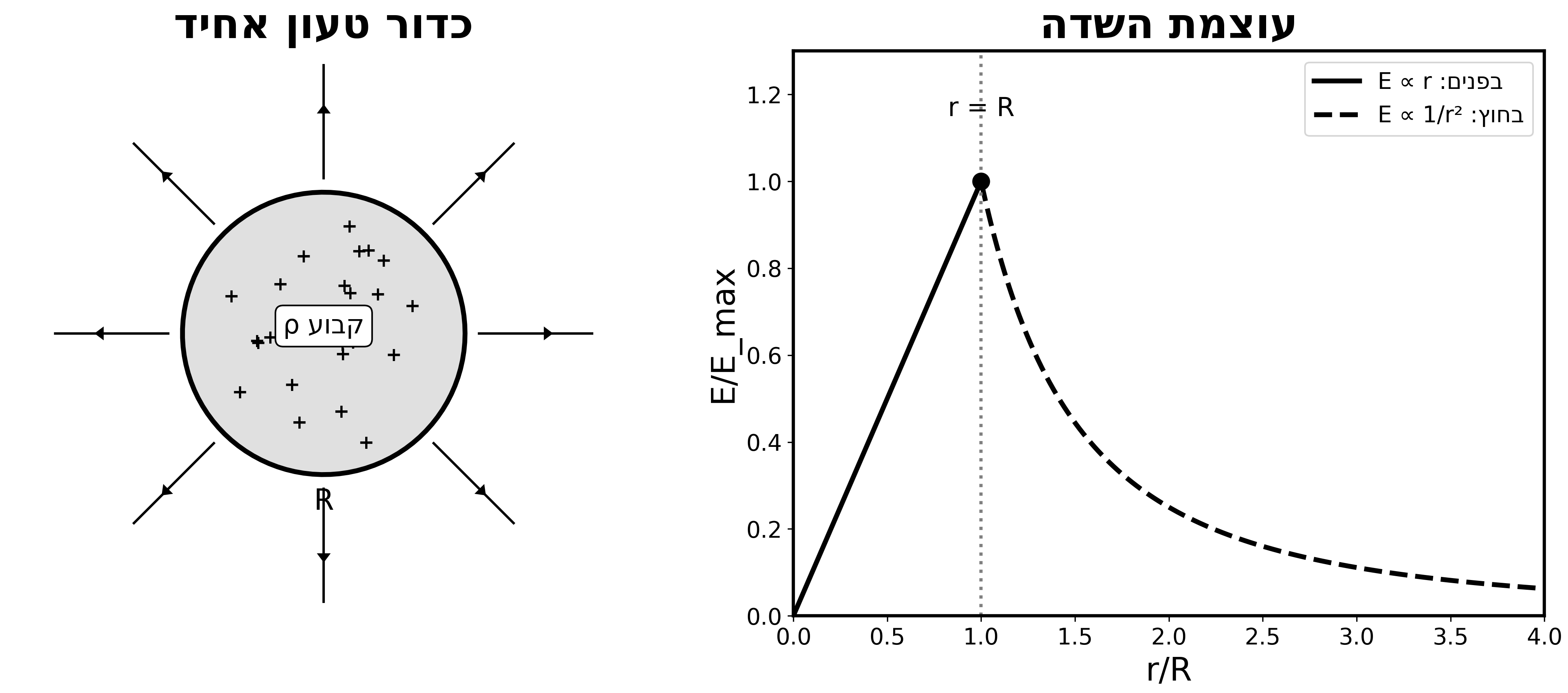
5.1 כדור טעון אחיד
כדור ברדיוס $R$ טעון במטען כולל $Q$ בצפיפות אחידה $\rho$.
מה השדה החשמלי בתוך הכדור ומחוצה לו?
חישוב צפיפות המטען:
\[Q = \rho \cdot \frac{4\pi R^3}{3} \Rightarrow \rho = \frac{3Q}{4\pi R^3}\]השדה בתוך הכדור ($r < R$):
בונים משטח גאוסי כדורי ברדיוס $r < R$. המטען הכלוא:
\[Q(r<R) = \rho \cdot \frac{4\pi r^3}{3} = Q \frac{r^3}{R^3}\]מחוק גאוס:
\[4\pi r^2 D_r = Q \frac{r^3}{R^3}\]לכן:
\[E_{r<R} = \frac{kQ}{R^3} r\]השדה גדל לינארית עם $r$ בתוך הכדור!
השדה מחוץ לכדור ($r > R$):
\[E_{r>R} = \frac{kQ}{r^2}\]כמו מטען נקודתי - הכדור נראה כמטען נקודתי מבחוץ.
גרף השדה:
- בתוך הכדור: $E \propto r$ (עולה לינארית)
- על פני הכדור: $E_{\max} = kQ/R^2$
- מחוץ לכדור: $E \propto 1/r^2$ (דועך)
5.2 משטח אינסופי טעון
משטח אינסופי טעון בצפיפות משטחית אחידה $\sigma$ (קולון למטר רבוע).
מה השדה החשמלי שנוצר על ידי המשטח?
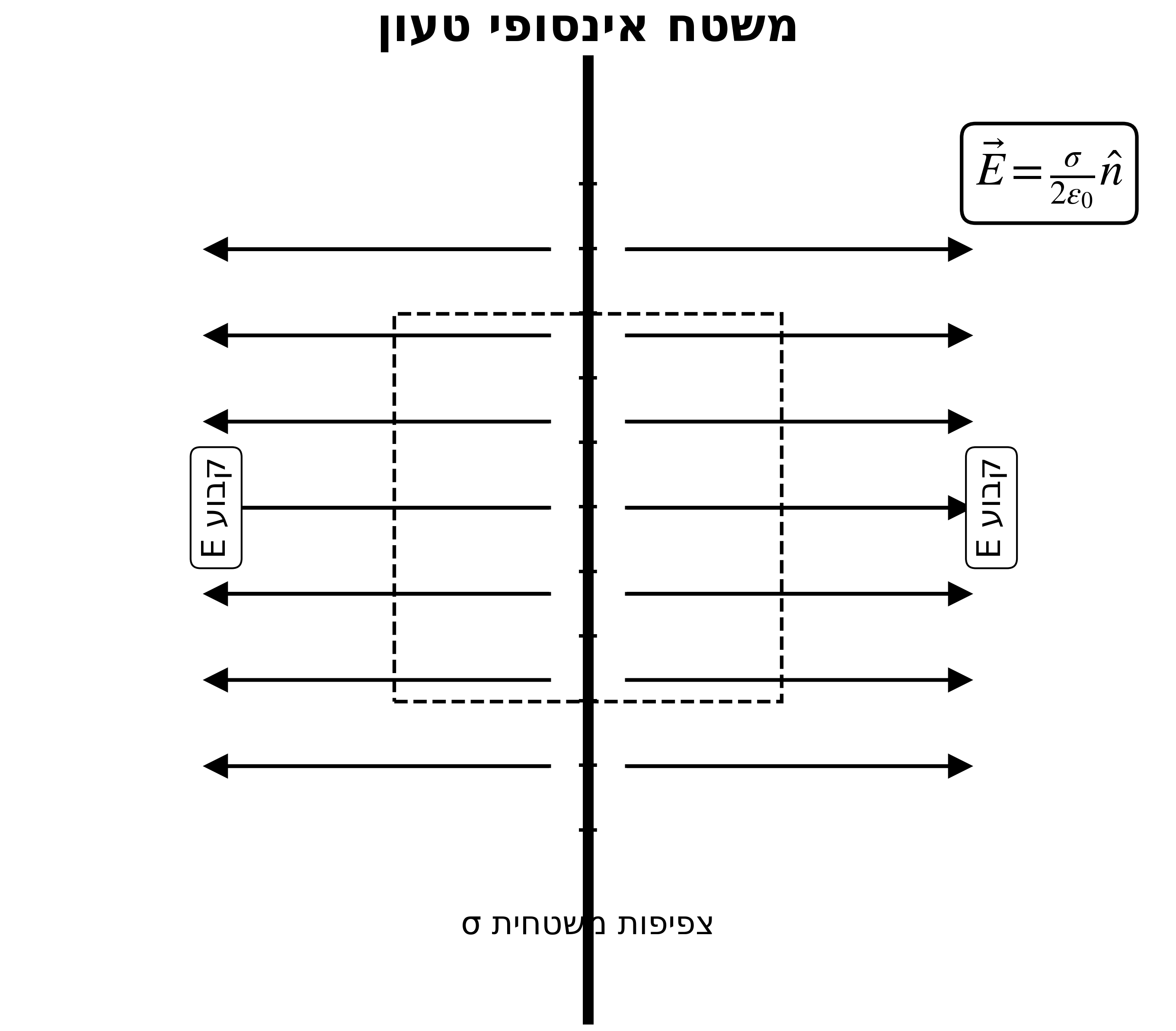
ניתוח סימטריה: מסימטריה, השדה חייב להיות ניצב למשטח. אין רכיב מקביל למשטח כי המשטח אינסופי.
בניית משטח גאוסי: גליל שחותך את המשטח, עם בסיסים מקבילים למשטח.
חישוב:
השטף יוצא רק דרך שני הבסיסים (לא דרך המעטפת):
\[2 \cdot \pi r^2 \cdot D_z = \sigma \cdot \pi r^2\]לכן:
\[D_z = \frac{\sigma}{2}\]ובמונחי שדה חשמלי:
\[E_z = \frac{\sigma}{2\epsilon_0}\]תוצאה מפתיעה: השדה קבוע ואינו תלוי במרחק מהמשטח!
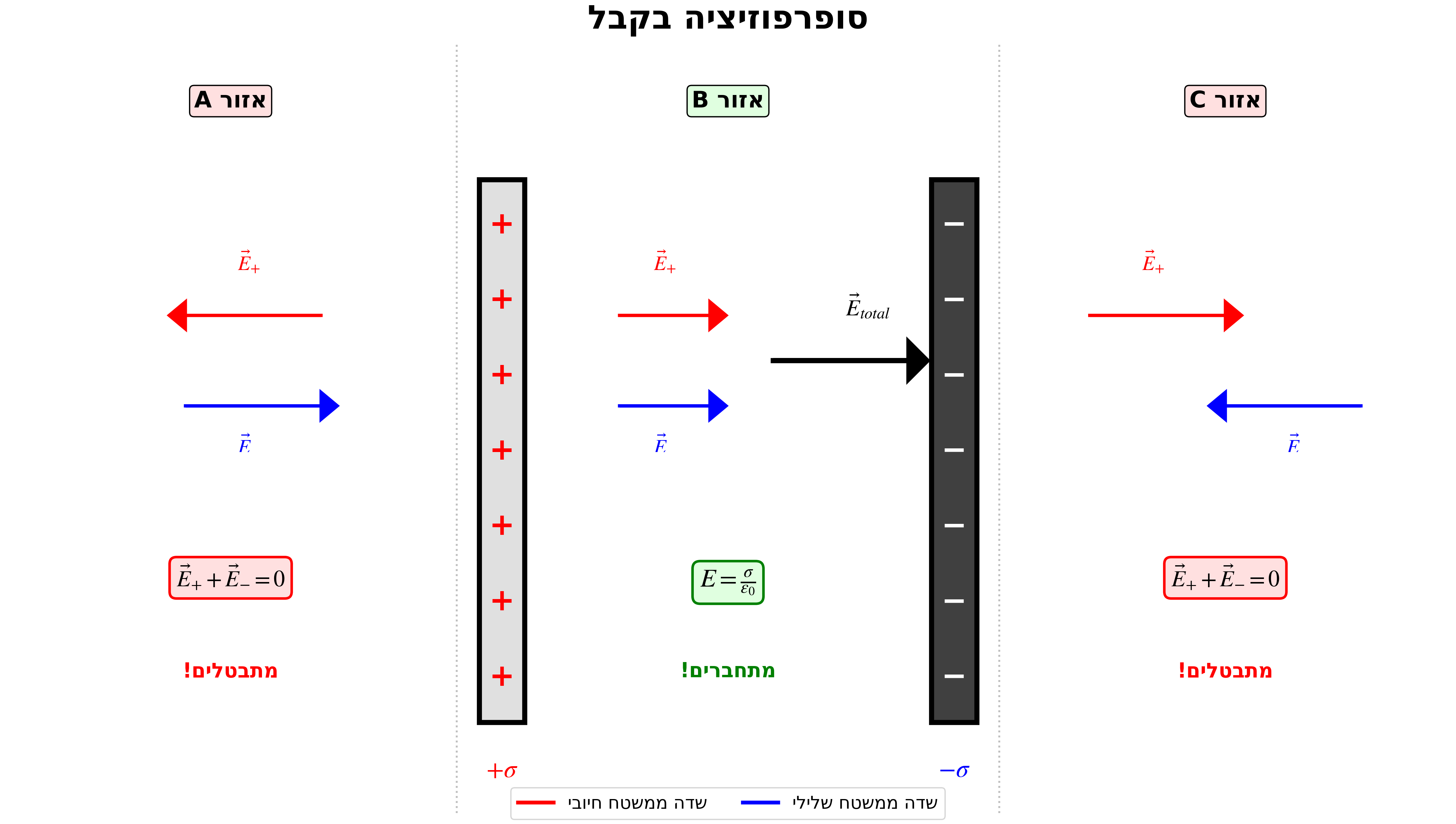
5.3 שני משטחים מקבילים - קַבָּל
שני משטחים אינסופיים מקבילים, האחד טעון ב-$+\sigma$ והשני ב-$-\sigma$.
מה השדה החשמלי בין המשטחים ומחוצה להם?
סופרפוזיציה:
- בין המשטחים: השדות מתחברים, $E = \sigma/\epsilon_0$
- מחוץ למשטחים: השדות מתבטלים, $E = 0$
זוהי הקונפיגורציה הבסיסית של קַבָּל - רכיב אלקטרוני שמגביל שדה חשמלי בתוך נפח מוגדר.
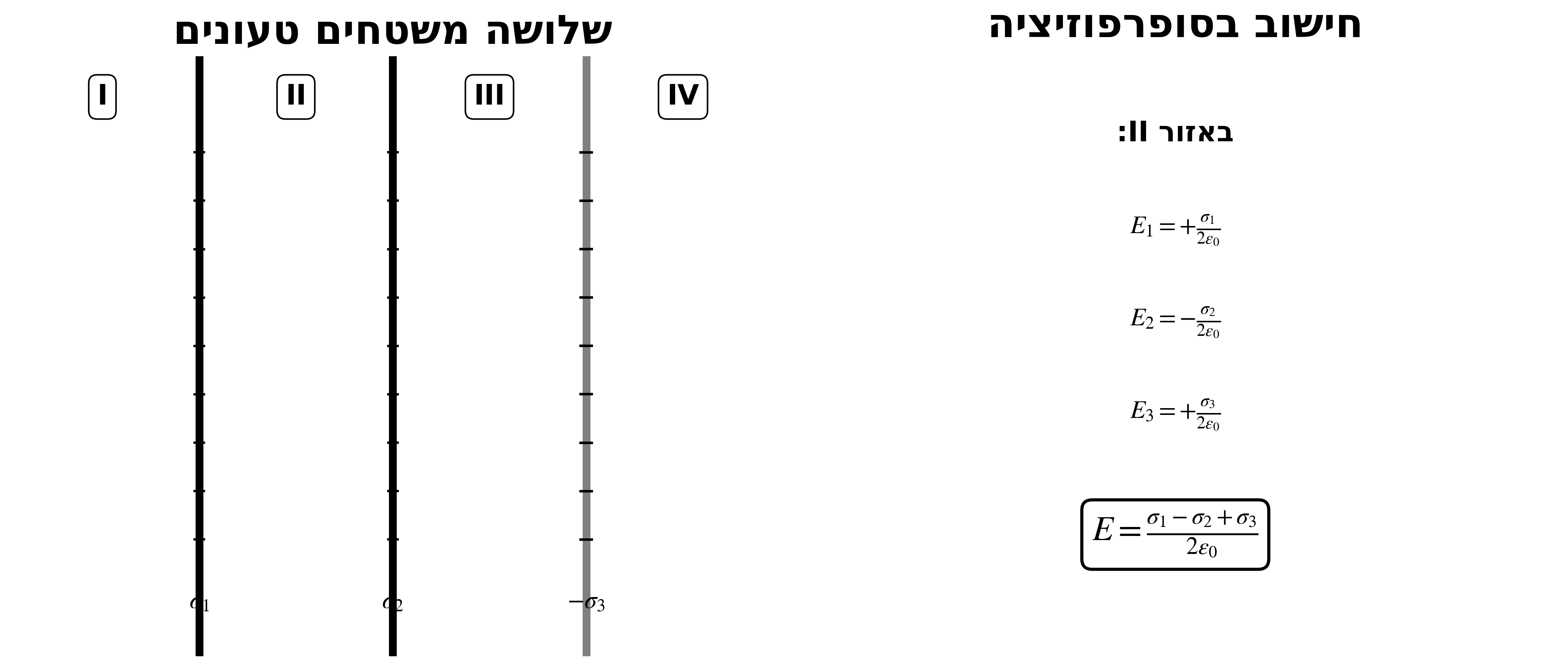
5.4 שלושה משטחים טעונים
עבור שלושה משטחים עם צפיפויות $\sigma_1, \sigma_2, -\sigma_3$, השדה בכל אזור נקבע על ידי סופרפוזיציה.
דוגמה לחישוב באזור 2 (בין המשטח הראשון והשני):
\[\vec{E}_2 = \frac{1}{2\epsilon_0}(\sigma_1 - \sigma_2 + \sigma_3)\hat{z}\]הסימן נקבע לפי כיוון התרומה של כל משטח.
5.5 תַּיִל אינסופי טעון
תַּיִל ישר אינסופי טעון בצפיפות קווית אחידה $\lambda$ (קולון למטר).
מה השדה החשמלי סביב התיל?
ניתוח סימטריה:
- סימטריה גלילית סביב התיל
- אין רכיב בכיוון התיל (מסימטריה: כל נקודה למעלה מבוטלת על ידי נקודה למטה)
משטח גאוסי: גליל ברדיוס $r$ ואורך $L$ סביב התיל.
חישוב:
השטף יוצא רק דרך המעטפת:
\[2\pi r L \cdot D_r = \lambda L\]לכן:
\[D_r = \frac{\lambda}{2\pi r}\]ובמונחי שדה חשמלי:
\[E_r = \frac{2k\lambda}{r}\]השדה דועך כ-$1/r$ (לא כ-$1/r^2$!).

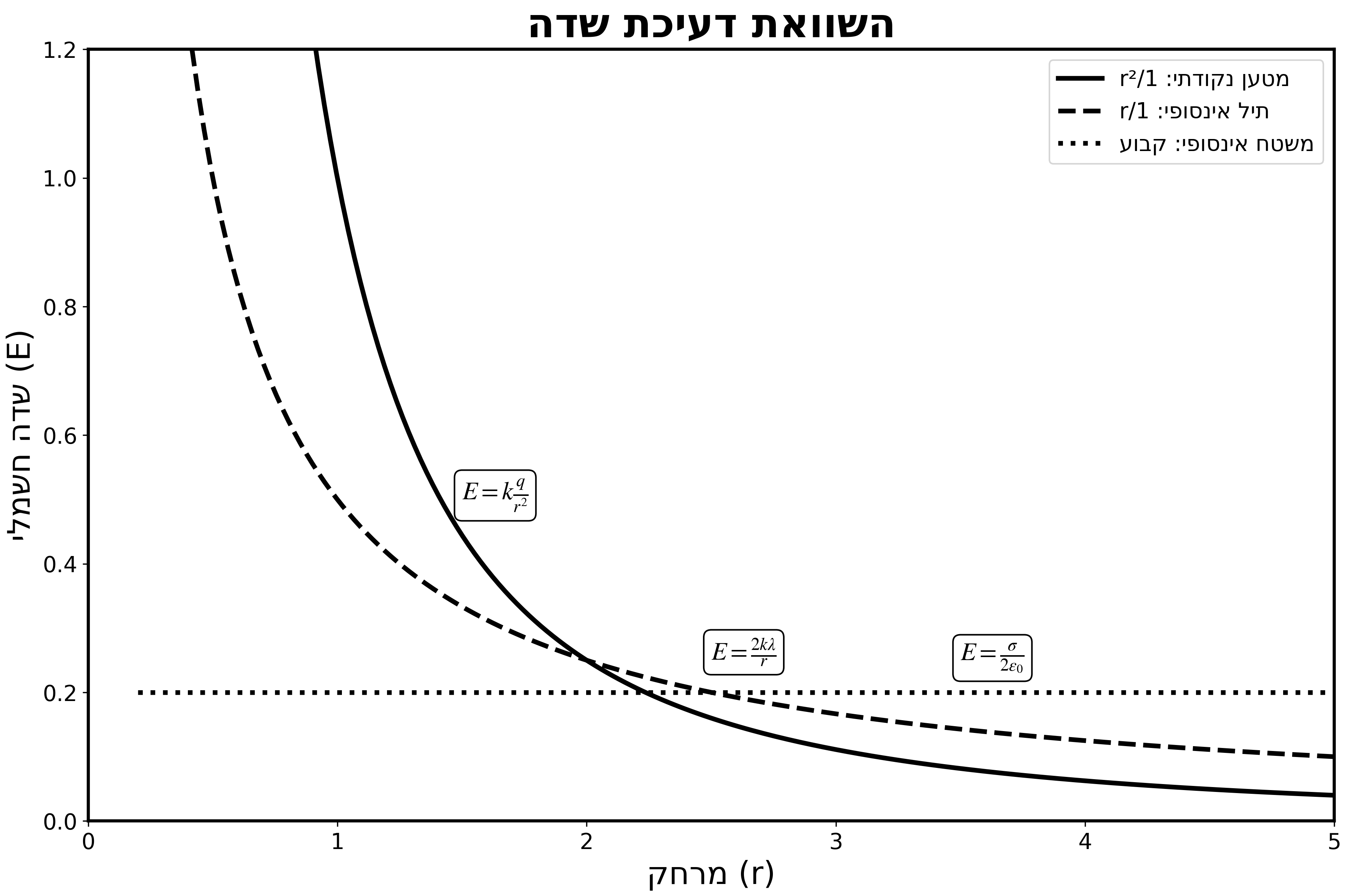
6. סיכום התוצאות החשובות
| קונפיגורציה | השדה החשמלי |
|---|---|
| מטען נקודתי | $\vec{E} = k\frac{q}{r^2}\hat{r}$ |
| כדור טעון (בפנים) | $\vec{E} = k\frac{Q}{R^3}r\hat{r}$ |
| כדור טעון (בחוץ) | $\vec{E} = k\frac{Q}{r^2}\hat{r}$ |
| משטח אינסופי | $\vec{E} = \frac{\sigma}{2\epsilon_0}\hat{n}$ |
| תיל אינסופי | $\vec{E} = \frac{2k\lambda}{r}\hat{r}$ |
7. הערות
-
חשיבות הסימטריה: חוק גאוס שימושי עבור קונפיגורציות סימטריות. ללא סימטריה, החישוב מסובך מאוד.
-
משוואה גלובלית מול לוקלית: חוק גאוס הוא משוואה גלובלית (אינטגרל על נפח), משוואת מקסוול היא לוקלית (נכונה בכל נקודה).
-
עקרון הסופרפוזיציה: מאפשר לחשב שדות מורכבים כסכום של שדות פשוטים.
-
יחידות: חשוב לעקוב אחרי היחידות - קולון, ניוטון, מטר.
עם הכלים שפיתחנו עד כה, לכאורה ניתן לפתור את רוב השאלות על שדות חשמליים סטטיים. בשיעורים הבאים נעסוק בתנועת מטענים ובמוליכים.
 דור פסקל
דור פסקל