פרק א - חומצות אמיניות
מצבי יינון של היסטידין
\[\begin{array}{ccc}& \text{Histidine} & \\[6pt]& \quad\quad\ce{COO-} & \\[-2pt]& \vert \\[-2pt]& \ce{H3N+-C-H} \quad\quad & \\[-2pt]& \vert \\[-2pt]& \quad\textcolor{red}{\ce{CH2}} & \\[-2pt]& \textcolor{red}{\vert} \\[-2pt]& \quad\quad\quad\textcolor{red}{\ce{CH-NH}} & \\[-2pt]& \quad\quad\quad\textcolor{red}{\vert} \quad\quad \textcolor{red}{\diagdown} & \\[-2pt]& \quad\quad \quad\quad\quad\quad\quad\quad\textcolor{red}{\ce{CH3}} & \\[-2pt]& \quad\quad\quad\quad\textcolor{red}{\vert} \quad\quad \textcolor{red}{\diagup\diagup} \\[-2pt]& \quad\quad\textcolor{red}{\ce{HC} - \ce{N}} & \\[-2pt]\end{array}\]4) רשום את ארבעת מצבי היינון בחומצה האמינית היסטידין וציין איזה מצב שולט בערכי ה-$\text{pH}$ הבאים: $1.0$, $3.0$, $5.7$, $7.0$, $11.0$.
נבנה גרף $\text{pH}$:
|--------|--------|
1.7 6.04 9.09
נוסיף את מצבי היינון (ארבעה מצבים):
+2 | +1 | 0 | -1
|--------|--------|
1.7 6.04 9.09
מכאן קל לראות:
- ב-$\text{pH} = 1.0$ המטען הוא $+2$
- ב-$\text{pH} = 3.0$ המטען הוא $+1$
- ב-$\text{pH} = 5.7$ המטען הוא $+1$
- ב-$\text{pH} = 7.0$ המטען הוא $0$
- ב-$\text{pH} = 11.0$ המטען הוא $-1$
פער ב-$pK_a$ בין קבוצות שונות בליזין
5) לקבוצות ה-$\alpha \, \text{-amino}$ יש $pK_a$ גבוה יותר מאשר לקבוצות $\varepsilon \, \text{-amino}$. הסבר את התופעה.
תזכורת:
α β γ δ ε
| | | | |
NH3⁺ — C — CH2—CH2—CH2—CH2— NH3⁺ ← זה ה־ε-amino
|
COOH
ממה שהבנתי השאלה בעצם מתייחסת לכך שהקבוצה האמינית הקרובה יותר לקבוצה הקרבוקסילית (ה-$\alpha$) היא בעלת $pK_a$ גבוה יותר מהקבוצה האמינית הרחוקה יותר (ה-$\varepsilon$), שקיימת למעשה רק בשייר של ליזין.
הסיבה לכך ככל הנראה קשורה לכך שקל יותר להוציא פרוטון מהקבוצה האמינית הרחוקה יותר (ה-$\varepsilon$) מאשר מהקרובה יותר (ה-$\alpha$), בגלל האפקט האלקטרוסטטי של הקרבוקסיל שמושך את האלקטרונים מהקבוצה האמינית הקרובה יותר, מה שמקשה על הוצאת הפרוטון.
מסיסות של חומצות אמיניות
6) חומצה בנזואית ופירידין שניהם בעלי $pK_a = 5$. איזה תרכובת תהיה יותר מסיסה במים לאחר הוספת כמות שווה של $\ce{NaOH}$ או $\ce{HCl}$?
פתרנו את התרגיל בתרגול 1.
בקצרה, דברים עם מטען יותר מסיסים - אנחנו נרצה יונים.
- במקרה של פירידין, הוספת $\ce{HCl}$ תיצור את היון שלה, שיהיה טעון חיובית - יותר מסיס.
- במקרה של חומצה בנזואית, הוספת $\ce{NaOH}$ תיצור את היון שלה, שיהיה טעון שלילית - יותר מסיס.
מציאת אחוז של צורה מסוימת של חומצה אמינית
7) מה ה-$pI$ של החומצה האמינית אלנין? צייר את צורת היינון של אלנין ב-$\text{pH}$ שווה ל-$pI$. האם קיימת בתמיסה ב-$\text{pH}$ שווה ל-$pI$ הצורה המצוירת מטה? אם כן, מה האחוז שלה?
\(\ce{H2N-CH(CH3)-COOH}\) (Uncharged)
\[\begin{array}{ccc}& \text{Alanine (not in zwitterionic form)} & \\[6pt]& \quad\quad\textcolor{red}{\ce{COOH}} & \\[-2pt]& \vert \\[-2pt]& \quad\textcolor{blue}{\ce{H2N}}\ce{-C-H} \quad\quad & \\[-2pt]& \vert \\[-2pt]& \quad{\ce{CH3}} & \\[-2pt]\end{array}\]פתרנו גם כן את התרגיל בתרגול 1.
8) בציור הבא מוצגות עקומות טיטרציה של חומצות אמיניות. זהה לאיזה חומצה אמינית מתאימה כל אחת מעקומות הטיטרציה ונמק.
…
חישוב $pI$ ומטען
10) מה ה-$pI$ של הפפטידים הבאים:
- $\ce{Lys-Gly-Ala-Gly}$
- $\ce{Lys-Gly-Ala-Glu}$
- $\ce{Glu-His-Trp-Ser-Tyr-Gly-Leu-Arg-Pro-Gly}$
מה המטען של הפפטיד האחרון ב-$\text{pH} = 11$?
נתחיל מהראשון. יש לו שלוש קבוצות פרוטונציה:
| קבוצת פרוטונציה | pKa |
|---|---|
| קצה אמיני (Lys) | $8.95$ |
| שייר צד בליזין (Lys) | $10.53$ |
| קצה קרבוקסילי (Gly) | $2.34$ |
Net +2 +1 0 -1
pKa 2.34 8.95 10.53
| | |
|----|----|----|----|----|----|
pH 1 3 5 7 9 11 13
עבור הפפטיד השני, יש לנו את אותם ערכי pKa כמו קודם, אבל יש לנו גם את שייר הצד של חומצה גלוטמית עם pKa = 4.25.
| קבוצת פרוטונציה | pKa |
|---|---|
| קצה אמיני (Lys) | $8.95$ |
| שייר צד בליזין (Lys) | $10.53$ |
| קצה קרבוקסילי (Gly) | $2.34$ |
| שייר צד חומצה גלוטמית (Glu) | $4.25$ |
Net +2 +1 0 -1 -2
pKa 2.34 4.25 8.95 10.53
| | | |
|----|----|----|----|----|----|----|
pH 1 3 5 7 9 11 13
עבור הפפטיד השלישי, יש לנו את ערכי ה-pKa הבאים:
| קבוצת פרוטונציה | pKa |
|---|---|
| קצה קרבוקסילי (Arg) | $2.17$ |
| קצה אמיני (Glu) | $9.47$ |
| (שייר צד חומצה גלוטמית (Glu) | $4.25$ |
| שייר צד היסטידין (His) | $6.04$ |
| שייר צד טירוזין (Tyr) | $10.07$ |
| שייר צד ארגינין (Arg) | $12.48$ |
Net +3 +2 +1 0 -1 -2 -3
pKa 2.17 4.25 6.04 9.47 10.07 12.48
| | | | | |
|------|------|------|------|------|------|------|
pH 1 3 5 7 9 11 13
ב-$\text{pH} = 11$ אפשר לראות שהמטען יהיה $-2$.
ספיגת אספירין במערכת העיכול
11) אספירין הוא חומצה חלשה עם $pK_a = 3.5$. התרופה מוכנסת לדם בכיבה וגם במעי. התרופה עוברת לדם בדיפוזיה. איפה התרופה נספגת לדם יותר?
ה-$\text{pH}$ במעי הוא $6$ ובכיבה $1.5$.
\(\ce{CH3-CO-O-C6H4-COOH}\) (אספירין)
לאספירין יש קבוצה קרבוקסילית עם $pK_a = 3.5$.
בכיבה, ה-$\text{pH}$ הוא $1.5$ שהוא נמוך מה-$pK_a$ של האספירין, ולכן רוב האספירין יהיה במצב הפרוטונטי (לא מיונן):
\(\ce{CH3-CO-O-C6H4-COOH}\) (לא מיונן)
במעי, ה-$\text{pH}$ הוא $6$ שהוא גבוה מה-$pK_a$ של האספירין, ולכן רוב האספירין יהיה במצב הדה-פרוטונטי (מיונן):
\(\ce{CH3-CO-O-C6H4-COO^{-}}\) (מיונן)
תרופות במצב לא מיונן יכולות לעבור דרך הממברנה בקלות רבה יותר מאשר תרופות במצב מיונן, ולכן האספירין ייספג יותר טוב בכיבה.
פרק ב - מבנה חלבונים
יצירת סליל אלפא על ידי פוליליזין ופוליגלוטמית
12) הסבר מדוע פוליליזין יוצר סליל אלפא ב-$\text{pH} = 12$ ואילו ב-$\text{pH} = 7$ הוא בעל מבנה אקראי.
באיזה $\text{pH}$ פוליגלוטמית יוצר סליל?
פתרנו את התרגיל בתרגול 2 (למעשה גם את התרגיל הקודם ותרגילים נוספים). בקצברה, ב-$\text{pH}$ שבו יש מטענים על החלבון תהיה דחייה אלקטרוסטטית בין השיירים הטעונים, מה שמונע יצירת מבנה מסודר כמו סליל אלפא. ב-$\text{pH} = 12$, הליזין יהיה דה-פרוטונטי ולכן לא יהיה טעון, מה שמאפשר יצירת סליל אלפא.
אורך מקסימלי של סליל אלפא וגדיל ביטא
13) חלבון מורכב מ-$584$ חומצות אמיניות. הממד הארוך ביותר בחלבון הוא $13 \, \mathrm{nm}$. מה המספר המקסימלי של חומצות אמיניות שיכיל סליל אלפא בחלבון הזה? אילו החלבון היה מורכב מגדיל ביטא אחד, מה היה האורך המקסימלי של החלבון?
גם את התרגיל הזה פתרנו.
בקצרה, בכל סיבוב של סליל אלפא יש $3.6$ חומצות אמיניות ואורך סיבוב הוא $0.54 \, \mathrm{nm}$. לכן, האורך של חומצה אמינית אחת בסליל אלפא הוא:
\[\frac{0.54 \, \mathrm{nm}}{3.6} = 0.15 \, \mathrm{nm}\]לכן, מספר החומצות האמיניות בסליל אלפא באורך $13 \, \mathrm{nm}$ הוא:
\[\frac{13 \, \mathrm{nm}}{0.15 \, \mathrm{nm}} \approx 87\]זיהוי קבוצות צדדיות בקשר לחלבון טעון שלילי
14) הפפטיד:
\[\ce{Met(1)-Leu(2)-Ser-Leu-Arg-Gln-Ser-Ile-Arg-Phe-Phe-Lys-Pro-Ala-Thr-Arg-Thr-Leu}\]יוצר מבנה $\alpha$-helix ונקשר לחלבון $X$ הטעון במטען שלילי חזק. החומצות האמיניות של הפפטיד הקושרות את החלבון $X$ הן (המספר בסוגריים מסמל את מספר החומצה האמינית בפפטיד כאשר החומצה האמינית בקצה אמינו טרמינלי היא מספר 1):
- $\ce{Lys(12)-Arg(5)-Arg(16)-Arg(9)}$
- $\ce{Met(1)-Lys(12)-Arg(5)-Arg(16)-Arg(9)}$
- $\ce{Ile(8)-Arg(5)-Arg(16)-Arg(9)-Leu(2)}$
- $\ce{Arg(5)-Gln(6)-Ser(7)-Ile(8)-Arg(9)-Phe(10)-Phe(11)}$
- כל התשובות לא נכונות.
חישוב קבוצות צדדיות בקשר לחלבון טעון שלילית
15) הפפטיד הבא:
\[\ce{Met(1)-Lys-Ile-Leu-Arg-Glu-Leu-Arg-Arg-Phe-Phe-Lys-Ser-Lys-Thr-Arg-Leu}\]
יכול להקשר לחלבון טעון שלילית.
החומצות האמיניות המשתתפות בקשר הנכון הן:
- $\ce{Met(1)-Lys(12)-Arg(5)-Arg(16)-Arg(9)-Lys(2)-Lys(14)}$
- $\ce{Met(1)-Lys(12)-Arg(5)-Arg(16)-Arg(9)-Lys(2)}$
- $\ce{Leu(4)-Phe(11)-Leu(7)-Ile(3)-Phe(10)-Leu(17)}$
- $\ce{Phe(11)-Leu(4)-Thr(15)-Arg(8)-Met(1)-Lys(12)-Arg(5)}$
פרק ג - בידוד חלבונים
מסיסות של חלבונים ב-$\text{pH}$ האיזואלקטרי
16) חלבון נמצא ב-$\text{pH}$ האיזואלקטרי שלו. איך הוספת ריכוז מלח נמוך או גבוה משפיעה על המסיסות של חלבון?
ב-$\text{pH}$ האיזואלקטרי של החלבון, המטען נטו שלו הוא אפס, ולכן הוא נוטה להיות פחות מסיס במים. הוספת ריכוז מלח נמוך יכולה להגדיל את המסיסות של החלבון על ידי יצירת שכבת יונים סביב החלבון שמונעת ממנו להצטבר ולהתמוסס. לעומת זאת, הוספת ריכוז מלח גבוה יכולה לגרום ל”התייבשות” של החלבון ולהפחית את המסיסות שלו, תהליך שנקרא “salting out”. לכן, ישנה השפעה דו-כיוונית של ריכוז המלח על מסיסות החלבון ב-$\text{pH}$ האיזואלקטרי שלו.
חישוב יציאת פפטידים על מחליף אניונים
19) נתונה תערובת של $3$ פפטידים על מחליף אניונים:
- $\ce{Gly-Val-Asp}$
- $\ce{Lys-Asp-Gln}$
- $\ce{Asp-Glu-Gln}$
ההפרדה ב-$\text{pH} = 7$. מהו סדר יציאתם מן העמודה (מי לא יקשר, ומי יצא בריכוז מלח גבוה או נמוך)?
תחילה נמצא את ה-$\text{pI}$ של כל פפטיד.
| aa | group | val |
|---|---|---|
| Gly | $\ce{-NH3+}$ | 9.6 |
| Val | ||
| Asp | $\ce{-COOH}$ | 1.88 |
| Asp | $\text{R group}$ | 3.65 |
קיצור דרך - Asp חומצית פשוט אפשר לקחת ממוצע של שני הערכים הנמוכים? בכל מקרה נדרש לבדוק מה המטען ב-$\text{pH}=7$.
נכין אולי גרף ליתר ביטחון:
net +1 0 -1
1.88 3.65 9.6
pKa | | ... |
pH |------|------|------|
1 2 3 4
ב-$\text{pH}=7$: המטען שלילי, מינוס אחת.
נמשיך עם הפפטיד הבא:
| aa | group | val |
|---|---|---|
| Lys | $\ce{-NH3+}$ | 8.95 |
| Lys | $\text{R group}$ | 10.53 |
| Asp | $\text{R group}$ | 3.65 |
| Gln | $\ce{-COOH}$ | 2.17 |
net +2 +1 0 -1
2.17 3.65 8.95
pKa | | ... |
pH |------|------|------| ...
1 2 3 4
ב-$\text{pH}=7$: המטען נייטרלי, אפס.
נמשיך עם הפפטיד האחרון:
| aa | group | val |
|---|---|---|
| Asp | $\ce{-NH3+}$ | 9.6 |
| Asp | $\text{R group}$ | 3.65 |
| Glu | $\text{R group}$ | 4.25 |
| Gln | $\ce{-COOH}$ | 2.17 |
net +1 0 -1 -2
2.17 3.65 4.25 9.6
pKa | | | |
pH |------|------|------|------...------|
1 2 3 4 10
ב-$\text{pH}=7$: המטען שלילי, $(-2)$.
נתון שיש מחליף אניונים, כלומר עמדה טעונה חיובית שקושרת אליה שליליים.
ייקשרו שני הפפטידים שטעונים שלילית.
לפפטיד שטעון במטען שלילי יותר יידרש ריכוז מלח גבוה יותר לשחרור.
1) Lys–Asp–Gln (0) → לא נקשר, נשטף ראשון
2) Gly–Val–Asp (−1) → מלח נמוך
3) Asp–Glu–Gln (−2) → מלח גבוה
הפרדת חלבונים על בסיס $\text{pH}$
20) נתונה תמיסה ובה שני חלבונים:
- מיוגלובין ש-$pI$ שלו הוא $7.0$
- ציטוכרום C ש-$pI$ שלו הוא $10.0$
כיצד תפריד בין החלבונים ובאיזה $\text{pH}$?
נבחר $\text{pH}$ שהוא בין הערכים האלה, למשל 8.5 וכו׳. פתרנו בתרגול.
כיוון נדידה של פפטידים באלקטרופורזה
26) ציין את כיוון הנדידה באלקטרופורזה (ללא נוכחות SDS) לכיוון הקתודה, אנודה או סטטי ב-$\text{pH} = 6.5$ של הפפטידים הבאים:
- $\ce{Lys-Gly-Ala-Gly}$
- $\ce{Glu-Gly-Ala-Glu}$
לאיזה כיוון ינדדו הפפטידים בנוכחות SDS?
פתרנו את השאלה הזאת בתרגול 5.
תחילה נמצא את המטען נטו של הפפטידים.
| aa | group | val |
|---|---|---|
| Lys | $\ce{-NH3+}$ | 8.95 |
| Lys | $\text{R group}$ | 10.53 |
| Gly | ||
| Ala | ||
| Gly | $\ce{-COOH}$ | 2.34 |
net +2 +1 0 -1
2.34 8.95 10.53
pKa | | ... |
pH |------|------|------| ...
1 2 3 4
ב-$\text{pH}=6.5$ המטען חיובי ($+1$), מכאן שהנדידה תהיה לכיוון הקטודה.
אם נוסיף SDS המטען יהיה שלישי והנדידה דווקא תהיה לכיוון האנודה.
נעבוד לפפטיד הבא:
| aa | group | val |
|---|---|---|
| Glu | $\ce{-NH3+}$ | 9.67 |
| Glu | $\text{R group}$ | 3.22 |
| Gly | ||
| Ala | ||
| Glu | $\ce{-COOH}$ | 2.19 |
| Glu | $\text{R group}$ | 3.22 |
מעניין - יש פעמיים שייר מתיינן.
net +1 0 -2 -3
2.19 3.22 9.67
pKa | || |
pH |------|------|------| ...
1 2 3 4
ב-$\text{pH}=6.5$ המטען שלילי ($-2$), מכאן שהנדידה תהיה לכיוון אנודה.
הכיוון עדיין יהיה לאנודה במקרה הזה גם בנוכחות SDS.
כיוון נדידה ללא SDS:
| פפטיד | מטען | כיוון נדידה |
|---|---|---|
| Lys-Gly-Ala-Gly | $+1$ | קתודה (אלקטרודה שלילית) |
| Glu-Gly-Ala-Glu | $-2$ | אנודה (אלקטרודה חיובית) |
כיוון נדידה עם SDS:
SDS (Sodium Dodecyl Sulfate) מצפה את כל החלבונים במטען שלילי אחיד.
לכן, שני הפפטידים ינדדו לכיוון האנודה (+), וההפרדה תהיה לפי גודל בלבד (לא לפי מטען).
הערה כללית: שימו לב לא להתבלבל בין אנודה לקתודה (קורה לי הרבה). אנודה היא האלקטרודה החיובית, וקתודה היא האלקטרודה השלילית.
קביעת משקל מולקולרי של חלבונים - שילוב שיטות
27) המשקל המולקולרי של חלבון $X$ נקבע בג’ל פילטרציה ונמצא שהוא $120,000$ דלטון. כאשר נקבע המשקל המולקולרי של החלבון באולטראצנטריפוגציה אנליטית נמצא שהוא $44,000$ דלטון. כאשר נבדק באלקטרופורזה בנוכחות $\beta \text{-mercaptoethanol}$ ו-SDS הוא נתן חלבון בעל משקל מולקולרי $22,000$ דלטון. הסבר את הממצאים. מכמה שרשראות פוליפפטידיות מורכב החלבון?
נסכם את השיטות בטבלה:
| שיטה | מה בודקת | תוצאה |
|---|---|---|
| ג’ל פילטרציה | תנאים נטיביים (בדרך כלל). מולקולה שלמה ($\text{Native Form}$), תלוי בגודל וצורת הרדיוס ההידרודינמי. | $120,000 \, \mathrm{Da}$ |
| אולטראצנטריפוגציה אנליטית | צורה נטיבית - המולקולה השלמה במצב הטבעי שלה. | $44,000 \, \mathrm{Da}$ |
| $\text{SDS}$ (דנטורציה ונטרול מטען) + $\beta\text{-mercaptoethanol}$ (שבירת קשרי דיסולפיד) | תת-יחידות מופרדות ומקופלות | $22,000 \, \mathrm{Da}$ |
החלבון הוא ככל הנראה דימר במשקל $44,000 \, \mathrm{Da}$.
הפער בין התוצאות בג׳ל לתוצאות לבין התוצאות באולטראצנטריפוגציה נובע כנראה מהצורה של החבלון - השיטה הראשונה מושפעת יותר מהצורה (כדורי גלובולרי או מוערך), ואילו השיטה השנייה מספקת תוצאות מדויקת יותר לשאלת המשקל במנותק מהצורה.
התוצאות בשיטה השלישית מתיישבות עם אלו שבשיטה השנייה. מספר תת היחידות הוא:
\[\frac{44,000}{22,000}=2\]כלומר שהחלבון הוא כאמור דימר.
קביעת מבנה רביעוני של חלבונים המכילים מתכת
28) הברזל מהווה $0.346\%$ ממשקל המוגלובין אנושי. אם נתון שהמשקל המולקולרי של החלבון הוא $64,000$ דלטון, תניח שברזל אחד נקשר לשרשרת פוליפפטידית אחת, מה תוכל להסיק לגבי מספר השרשראות בהמוגלובין אנושי?
המוגלובין מכיל ארבע שרשראות כשבכל אחת מולקולת ברזל (הטרו טטרומר). ננסה להגיע לזה דרך הנתונים. המשקל המולקולרי של ברזל הוא 56, נוכל למצוא את מספר השרשראות.
מסת הברגל במול של המוגלובין:
\[0.00346 \times 64,000 = 221.44\]מספר אטומי הברזל:
\[221.44 / 56 \approx 3.954\]כלומר יש בהמוגלובין ארבעה אטומי ברזל, אחד בכל שרשראת, ולכן סך הכל ארבע שרשראות.
ב) מדען בודד המוגלובין מסרטני ים ומצא כי אחוז הברזל בחלבון הינו $0.345\%$. כשקבע את המשקל המולקולרי של החלבון באלקטרופורזה בנוכחות $\beta\text{-mercaptoethanol}$ ו-SDS מצא כי המשקל המולקולרי של החלבון הוא $32,000$ דלטון. באולטראצנטריפוגציה אנליטית נקבע שהמשקל המולקולרי של החלבון הוא $382,000$ דלטון. הסק לגבי מבנה החלבון.
הפרדה לפי גודל וצפיפות בעזרת צנטריפוגציה
29) באיזה שיטה היית משתמש להפריד תמיסה המכילה מיטוכונדריה, ליזוזומים וחלבון? פרט.
התשובה היא צנטריפוגציה בהפרשי מהירויות (differential centrifugation). בשיטה זו, ניתן להפריד בין הרכיבים השונים בתמיסה על פי צפיפותם וגודלם על ידי סיבוב בתנאים שונים של מהירות וזמן. תחילה יסולקו החלקיקים הגדולים יותר כמו מיטוכונדריה בלחצים נמוכים יותר, ולאחר מכן יוסרו הליזוזומים בלחצים גבוהים יותר, ובסופו של דבר יישאר החלבון בתמיסה.
הפרדה לפי גודל בעזרת ג’ל פילטרציה $\text{(SEC)}$
30) באיזה שיטות היית מפריד מלח $\ce{NaCl}$ וחלבון בעל משקל מולקולרי $64000$ דלטון?
התשובה היא ג׳ל פילטרציה (Size-exclusion chromatography). בשיטה זו, מולקולות גדולות כמו חלבונים אינן נכנסות לנקבוביות של הג’ל ולכן עוברות מהר יותר דרך העמודה, בעוד שמולקולות קטנות כמו מלח $\ce{NaCl}$ נכנסות לנקבוביות ומאחרות את מעברן. כך ניתן להפריד בין החלבון למלח ביעילות.
פרק ד - קינטיקה אנזימטית
מושגים ונקודות מפתח בקינטיקה אנזימטית
- אנרגית אקטיבציה: האנרגיה שיש לספק למערכת כדי להגיע למצב המעבר.
- $K_{\text{m}}$: קבוע מיכאליס מנטן. ריכוז הסובסטרט שבו המהירות הראשונית היא חצי מהמהירות המקסימלית.
- $V_{\text{max}}$: מהירות מקסימלית של ריאקציה אנזימטית כאשר כל אתרי הקישור של האנזים תפוסים בסובסטרט.
- מושגים נוספים: מבנה אנזים. קינטיקה אנזימטית. אנליזת מיכאליס מנטן. שינוי קונפורמציה. עיכוב אנזימטי. $k_{\text{cat}}$. Turnover number. פעילות ספציפית. עיכוב הפיך (עיכוב תחרותי, עיכוב לא תחרותי, עיכוב לא-תחרותי). עיכוב לא הפיך. אנזימים רגולטוריים. אלוסטריות. קואופרטיביות. מסלול אנזימטי. מנגנון ריאקציה של כימוטריפסין.
התנהגות לפי מיכאליס מנטן
31) נמדדו מהירויות יצירת התוצר ($V_0$) של אנזים מסוים בריכוזי סובסטרט שונים. האם אנזים זה מתנהג לפי מיכאליס מנטן (כן או לא)? איזה הסבר יש לתופעה?
[S] mM $V_0$ mmol/min 0 0 1 3 2 5 4 6.5 8 7 12 6.2
לא מתנהג לפי מיכאליס מנטן כי בריכוז גבוה יותר המהירות דווקא יורדת.
עיכוב ע״י סובסטרט.
משוואת Lineweaver-Burk
32) אנזים אחד מקטלז את הריאקציה שבה גלוקוז נהפך לתרכובת $\text{B}$ ומאנוז לתרכובת $C$. בשתי הריאקציות $k_{+2} \gg k_{-1}$. נתונה טבלה של ריכוז הסובסטרט כנגד $V_0$. מה תוכל להסיק לגבי $V_{\text{max}}$, $K_{\text{m}}$, וקבוע הדיסוציאציה של שתי התרכובות עם האנזים?
$\left[ \text{S} \right] \, \mathrm{M}$ $V_0$ mmol/min (glucose) $V_0$ mmol/min (manose) $1 \times 10^{-5}$ 150 82 $2 \times 10^{-5}$ 256 150 $1 \times 10^{-4}$ 600 450 $3 \times 10^{-4}$ 770 670 $5 \times 10^{-4}$ 818 750 אם נתון שבתערובת הריאקציה יש $2 \, \mathrm {mmol}$ אנזים, מה ה-turnover number של האנזים?
כדי לפתור את השאלה צריך להיעזר בגרפים ובליניאריזציה לפי Lineweaver-Burk. נצייר גרף של $1/V_0$ כפונקציה של $1/S$ וממנו נחשב את $K_{\text{m}}$ - נקודת החיתוך עם ציר $x$ היא $-1/K_{\text{m}}$.
הנה למשל גרף ש-GPT ייצר עבור הגלוקוז:
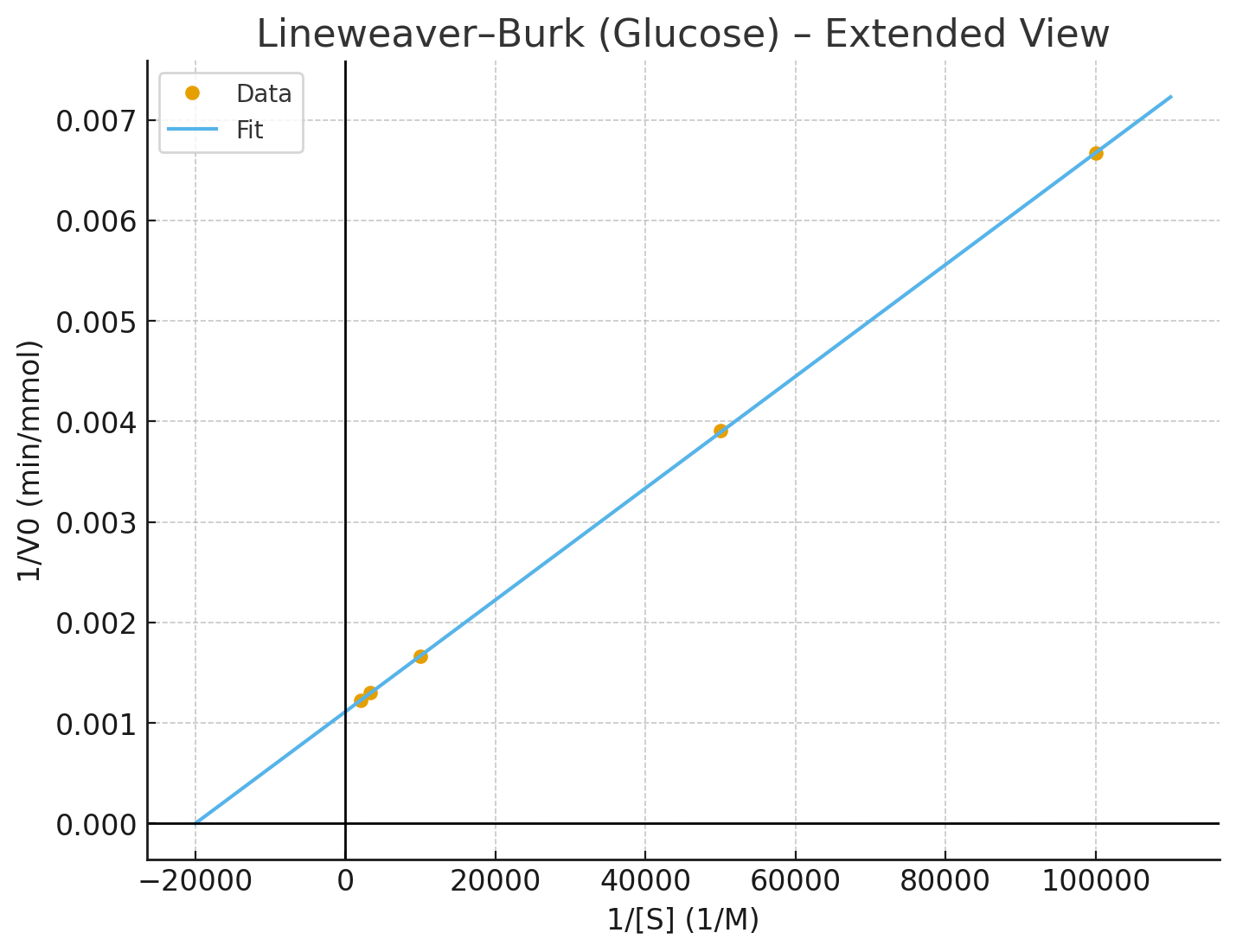
הפתרון המלא זמין בתרגיל 4.
השפעת טמפרטורה על קינטיקה אנזימטית
36) נבדקה פעילות אנזים כפונקציה של הזמן בשתי טמפרטורות שונות. התוצאות מסוכמות בטבלה:
S (mmolar) $V_0\ \text{min}^{-1}$ (30°C) $V_0\ \text{min}^{-1}$ (42°C) 0 0 0 0.01 253 לא נמדד 0.03 378 לא נמדד 1 500 לא נמדד 756 506 4 ה-$K_{\text{m}}$ (במילימולר) של האנזים ב-42°C הוא:
- שווה ל-$K_{\text{m}}$ ב-30 מעלות.
- $0.03$
- $1$
- אין מספיק נתונים להעריך את ה-$K_{\text{m}}$ של האנזים ב-42 מעלות.
אין מספיק נתונים להעריך את ה-$K_{\text{m}}$ של האנזים ב-42 מעלות, כי יש רק נקודה אחת שמדדה את המהירות ההתחלתית ב-42 מעלות.
זיהוי פעילות אנזימטית
37) אצטיל טירוזין אתיל אסטר (ATEE) הודגר עם מיצוי מכנפי נשר במשך שעה (בבאפר ב-$\text{pH} = 8.0$ ב-37°C). בדיקה הוכיחה שכ-$20\%$ מה-ATEE נעלם, והופיע אצטיל טירוזין במקומו. איזה ביקורות נדרשות כדי להוכיח שהיתה ריאקציה הידרוליזה שמקוטלזה על ידי אנזים?
נדגיר את התערובת ללא מיצוי מכנפי נשר בתנאים זהים כדי לוודא שהריאקציה לא מתרחשת ספונטנית. בנוסף, נוכל לחמם את המיצוי כדי להשבית את הפעילות האנזימטית ולבדוק אם הריאקציה עדיין מתרחשת. כמו כן, נוכל להוסיף מעכב אנזימטי ספציפי ולראות אם הוא מפחית את קצב ההידרוליזה.
פעילות ספציפית ו-Turnover number
38) בוצעה סדרת ניסויים בריכוזי סובסטרט שונים ונקבע $V_{\text{max}}$. כיצד תקבע את הפעילות הספציפית של האנזים שנבדק בניסויים אלה? כיצד תקבע את ה-Turnover number?
פעילות ספציפית היא היחס בין מהירות הריאקציה למסת החלבון בניסוי:
\[\text{Specific Activity} = \frac{V_{\text{max}}}{\text{mg protein}}\]ה-Turnover number הוא מספר מולקולות הסובסטרט שהאנזים יכול לעבד ביחידת זמן, כלומר:
\[k_{\text{cat}} = \frac{V_{\text{max}}}{\left[ \text{E} \right]}\]השוואת אנזימים - אפיניות ופעילות
39) $K_{\text{m}}$ של אנזים $\text{A}$ לסובסטרט שלו הוא $5 \times 10^{-3} \, \mathrm{M}$ ואילו של אנזים שני $\text{B}$ הוא $6 \times 10^{-6} \, \mathrm{M}$.
Turnover number של $\text{A}$ הוא $100$ לשניה ואילו של $\text{B}$ הוא $0.5$ לשניה.
לפי נתונים אלו ענה על השאלות הבאות:
- האם הזיקה של אנזים $\text{A}$ לסובסטרט שלו גדולה מהזיקה של אנזים $\text{B}$ לסובסטרט שלו? לפי איזה ערך תקבע זאת?
- לפי המספרים המחזוריים של שני אנזימים אלה, איזה אנזים הוא בעל פעילות גבוהה יותר?
- האם האמור בסעיף ב’ סותר לאמור בסעיף א’?
- הזיקה של $\text{B}$ גדולה יותר זאת לפי $K_{\text{m}}$ נמוך יותר. המשמעות: צריך פחות סובסטרט כדי להגיע לחצי מה-$V_{\text{max}}$
- הערה: זה נכון רק אם $k_{+2} \gg k_{-1}$, כלומר שהשלב הקטליטי הוא השלב קובע הקצב. אחרת, לא ניתן להיעזר ב $K_{\text{m}}$ כמדד לאפיניות.
- אנזים $\text{A}$ בעל פעילות גבוהה יותר לפי הנתון על ה turnover number. המשמעות - אנזים $\text{A}$ מבצע פי 200 יותר מחזורים בשנייה לעומת השני. הערך של $K_{\text{cat}}$מייצג את מספר מולקולות הסובסטרט שהופכות לתוצר ליחידת זמן על ידי אתר פעיל אחד, כשהאנזים רווי לחלוטין בסובסטרט. הוא מחזורים לשנייה. כלומר, האנזים הראשון עובד מהר יותר כשהוא בקומפלקס עם הסובסטרט.
- האמור לא סותר.
הערה: יש פרמטר נוסף שמתייחס ליעילות הקטליטית:
\[\text{Catalytic Efficiency} = \frac{K_{\text{cat}}}{K_{\text{m}}}\]קינטיקה אנזימטית - הסברים לירידה במהירות
40) נמצא שבתנאים מסוימים נוצרת כמות $X$ של תוצר בחמש הדקות הראשונות של ריאקציה אנזימטית. כמות התוצר שנוצרה בעשר דקות ראשונות היא רק פי $1.8$. הצע לפחות שלושה הסברים שונים לתופעה זו. הצע דרכים לבחון כל הסבר.
- עיכוב על ידי התוצר: ייתכן שהתוצר שנוצר מעכב את פעילות האנזים. ניתן לבדוק זאת על ידי הוספת התוצר לריאקציה חדשה ולראות אם המהירות יורדת.
- התייבשות הסובסטרט: ייתכן שהסובסטרט מתכלה מהר מדי. ניתן לבדוק זאת על ידי הוספת סובסטרט נוסף לאחר חמש דקות ולראות אם המהירות עולה שוב.
- שינוי קונפורמציה של האנזים: ייתכן שהאנזים משנה את צורתו לאחר זמן מה ומאבד את פעילותו. ניתן לבדוק זאת על ידי הוספת אנזים טרי לריאקציה לאחר חמש דקות ולראות אם המהירות עולה שוב.
השוואת אנזימים - נתונים קינטיים
41) נמצאה פעילות אנזימטית אותה במיצוי של אוזן ולשון של כבשים, אך התעוררה השאלה האם האנזימים בשני האיברים אכן זהים? נערכה סדרת ניסויים כאשר בתנאים זהים הוספו $0.1$ מ”ל של המיצויים השונים לתערובת ריאקציה בנפח כולל של $1$ מ”ל בריכוזים שונים של סובסטרט:
ריכוז סובסטרט (mM) מיקרו מולים שעוברים ריאקציה בדקה אחת אוזן לשון 1 0.18 0.094 2 0.30 0.15 5 0.5 0.25 10 0.65 0.33 אילו תכונות של האנזים ניתנות לקביעה מהנתונים, ובאיזה מידה ניתן להסיק מהנתונים לגבי הזהות, או חוסר הזהות של האנזימים בשני האיברים?
ניתן לקבוע את ה-$V_{\text{max}}$ וה-$K_{\text{m}}$ של כל אחד מהאנזימים על ידי בניית גרף של מיכאליס מנטן או ליניאריזציה לפי Lineweaver-Burk. אם ה-$K_{\text{m}}$ וה-$V_{\text{max}}$ שונים בין שני המיצויים, ניתן להסיק שהאנזימים אינם זהים. אם הם דומים מאוד, ייתכן שהם זהים או לפחות בעלי תכונות דומות.
לא ניתן לקבוע בוודאות זהות של אנזימים רק על סמך קינטיקה, אך ניתן לקבל רמזים חזקים לגבי דמיון או שונות ביניהם.
חסר לנו את נפח המיצוי שהוסף לכל תערובת ריאקציה, כדי לחשב את ריכוז האנזים בתערובת.
42) נמצאו שני חומרים $\text{A}$ ו-$\text{B}$ המעכבים את הפעילות של אנזים גלוטמט דהידרוגנאז. המהירות ההתחלתית של הריאקציה האנזימטית נקבעה כפונקציה של ריכוז הגלוטמט, בנוכחות אנזים וקואנזים $\ce{NAD}$, ובתנאים שונים:
- ללא מעכב.
- בנוכחות $40$ mM של המעכב $\text{A}$.
- בנוכחות $3$ mM של המעכב $\text{B}$.
התוצאות מובאות להלן. על ידי שימוש בהזילנאה גרפית קבע:
א) האם $\text{A}$ ו-$\text{B}$ מעכבים תחרותיים או לא תחרותיים? ב) מהם ערכי $K_{\text{m}}$ ו-$V_{\text{max}}$? ג) הקבוע $K_i$ עבור $\text{B}$, בידת האפשר. ד) מה ניתן להסיק לגבי צורת האינטראקציה של $\text{A}$ ו-$\text{B}$ עם האנזים?
| ריכוז סובסטרט, גלוטמט (mM) | ללא מעכב | מעכב $\text{A}$ | מעכב $\text{B}$ |
|---|---|---|---|
| 1.5 | 0.072 | 0.082 | 0.2 |
| 2.0 | 0.095 | 0.1 | 0.25 |
| 3.0 | 0.12 | 0.12 | 0.28 |
| 4.0 | 0.16 | 0.13 | 0.33 |
| 8.0 | 0.24 | 0.16 | 0.44 |
| 16.0 | 0.32 | 0.18 | 0.45 |
43) ביד ך מקרה שממנה עליך לבודד אנזים $E$. בטבלה רשומים שלבי הבידוד, נפח הפרקציה שבה התגלתה פעילות האנזים, פעילות ורכוז החלבון בה. השלם את העמודות החסרות:
| Preparation | Volume (ml) | Protein mg/ml | Activity U/ml | Specific Activity U/mg | Yield | Degree of purification |
|---|---|---|---|---|---|---|
| Crude extract | 200 | 2.5 | 100 | |||
| $(NH_4)_2SO_4$ precipitate | 80 | 1.25 | 200 | |||
| Anion exchange chromatography | 20 | 1 | 500 | |||
| Cation exchange | 5 | 1 | 1500 | |||
| Gel filtration | 3 | 0.3 | 2000 | |||
| Crystallization | 1 | 0.5 | 5000 |
44) בריאקציה אנזימטית התקבלו הנתונים הבאים:
Substrate (M) Velocity (nmol·lit⁻¹·min⁻¹) $6.25 \times 10^{-6}$ 15 $7.5 \times 10^{-5}$ 56.25 $1.0 \times 10^{-4}$ 60.0 $1.00 \times 10^{-3}$ 74.9 $1.0 \times 10^{-2}$ 75
- הערך של $V_{\text{max}}$ ו-$K_{\text{m}}$?
- מהו $V$ כאשר $\left[ \text{S} \right] = 2.5 \times 10^{-5}$ וכאשר $\left[ \text{S} \right] = 5 \times 10^{-5}$
- מהו $V$ ב-$\left[ \text{S} \right] = 5.0 \times 10^{-5}$ כאשר ריכוז האנזים מוכפל?
צריך להעיזר בגרף הלינארי. הנה פלט מקלוד:
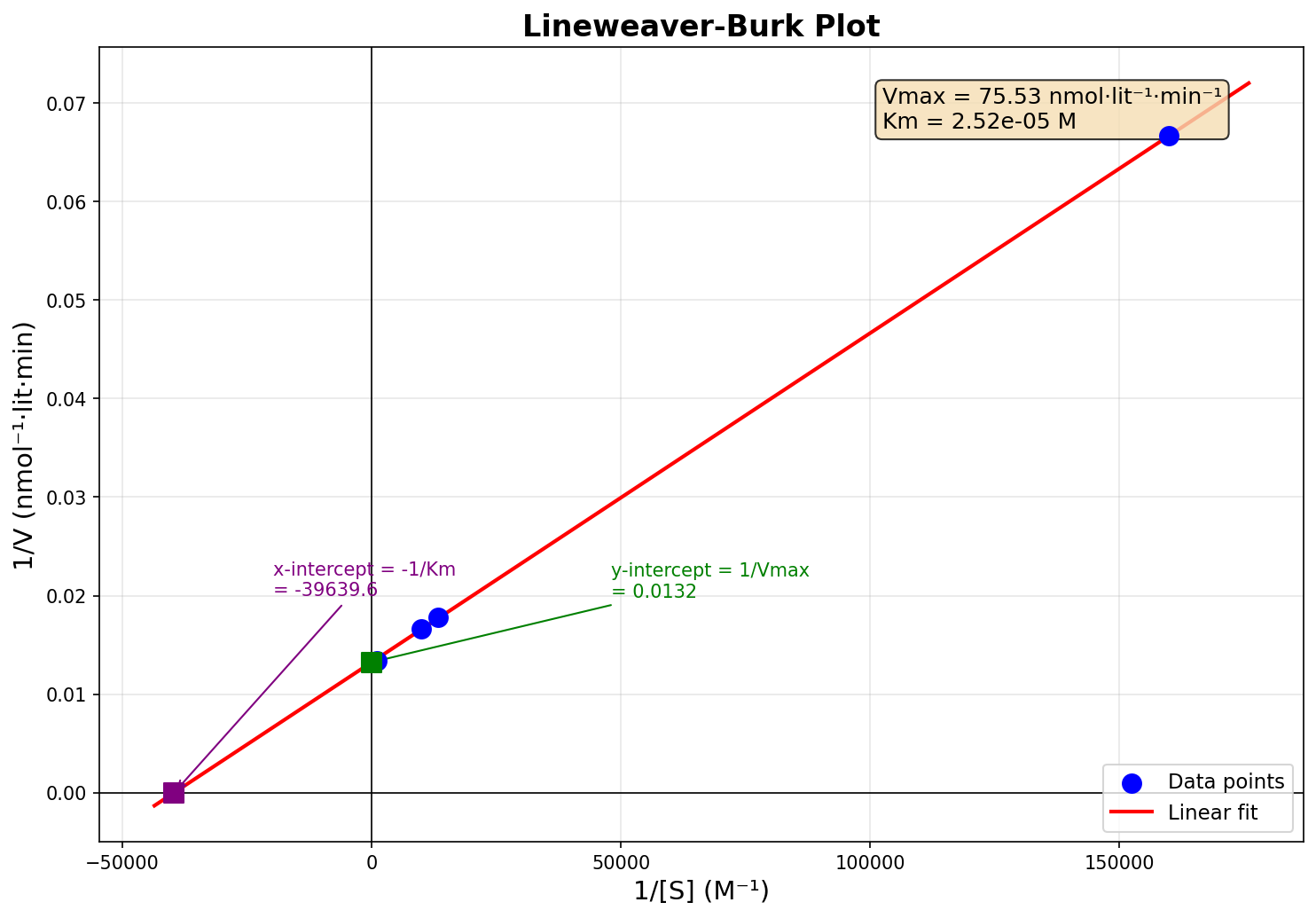
המהירות המקסימלית בגרף היא ההופכי של החיתוך עם ציר $y$.
נניח שהגרף חותך את ציר $y$ בנקודה…
בכל מקרה זה קרוב לשורה האחרונה בטבלה (ניתן לראות שהמהירות לא משתנה הרבה בין השורות האחרונות).
כדי לחשב את $K_{\text{m}}$ נשתמש בנקודת החיתוך עם ציר $x$.
נעבוד בדרך הארוכה - נבנה משוואת קו ישר בעזרת שתי נקודות מהטבלה ונמשיך ישירות מהנתונים. אני לא בטוח שהחישובים להלן נכונים וככל הנראה עדיף להיעזר בגרפים.
נבחר את הנקודות הראשונות:
\[(x_1, y_1) = \left( \frac{1}{6.25 \times 10^{-6}}, \frac{1}{15} \right) = (160000, 0.0667)\] \[(x_2, y_2) = \left( \frac{1}{7.5 \times 10^{-5}}, \frac{1}{56.25} \right) = (13333.33, 0.01778)\]המקדם:
\[m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0.01778 - 0.0667}{13333.33 - 160000} = \frac{-0.04892}{-146666.67} \approx 3.33 \times 10^{-7}\]משוואת הקו הישר:
\[y - y_1 = m(x - x_1)\] \[y - 0.0667 = 3.33 \times 10^{-7} (x - 160000)\] \[y = 3.33 \times 10^{-7} x - 0.0533 + 0.0667\] \[y = 3.33 \times 10^{-7} x + 0.0134\]חיתוך עם ציר $y$:
\[y = 0.0134 \Rightarrow V_{\text{max}} = \frac{1}{0.0134} \approx 74.63\ \text{nmol·lit}^{-1}\text{·min}^{-1}\]חיתוך עם ציר $x$:
\[0 = 3.33 \times 10^{-7} x + 0.0134 \Rightarrow x = -\frac{0.0134}{3.33 \times 10^{-7}} \approx -40240\]מכאן ש:
\[K_{\text{m}} = -\frac{1}{x} = \frac{1}{40240} \approx 2.49 \times 10^{-5}\ \text{M}\]- $V_{\text{max}} \approx 74.63\ \text{nmol·lit}^{-1}\text{·min}^{-1}$, $K_{\text{m}} \approx 2.49 \times 10^{-5}\ \text{M}$
- נשתמש במשוואת מיכאליס-מנטן:
- \[V = \frac{V_{\text{max}} [S]}{K_{\text{m}} + [S]}\]
- כאשר $\left[ \text{S} \right] = 2.5 \times 10^{-5}$:
- \[V = \frac{74.63 \times 2.5 \times 10^{-5}}{2.49 \times 10^{-5} + 2.5 \times 10^{-5}} \approx 37.32\ \text{nmol·lit}^{-1}\text{·min}^{-1}\]
- כאשר $\left[ \text{S} \right] = 5 \times 10^{-5}$:
- \[V = \frac{74.63 \times 5 \times 10^{-5}}{2.49 \times 10^{-5} + 5 \times 10^{-5}} \approx 49.75\ \text{nmol·lit}^{-1}\text{·min}^{-1}\]
- כאשר ריכוז האנזים מוכפל, $V_{\text{max}}$ יוכפל גם כן:
- \[V = \frac{149.26 \times 5 \times 10^{-5}}{2.49 \times 10^{-5} + 5 \times 10^{-5}} \approx 99.5\ \text{nmol·lit}^{-1}\text{·min}^{-1}\]
דור פסקל