שאלה 1
נתונים שני וקטורים:
\[\begin{aligned} \vec{a} &= \hat{x} + \sqrt{2}\,\hat{y} - \sqrt{3}\,\hat{z} \\[10pt] \vec{b} &= \sqrt{3}\,\hat{x} - \sqrt{2}\,\hat{y} + \hat{z} \end{aligned}\]
- מצאו את הזווית בין $\vec{a}$ ל־$\vec{b}$.
- מצאו את וקטור היחידה המצביע בכיוון שהשקול הווקטורי של שני הווקטורים.
מציאת הזווית
הזווית בין הווקטורים נתונה על ידי:
\[\theta = \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}| \vert \vec{b}\vert}\]המכפלה הסקלרית יצאה $-2$. אורך כל אחד מהווקטורים הוא $\sqrt{6}$. לכן:
\[\cos \theta = \frac{-2}{6} = -\frac{1}{3} \rightarrow \theta = 109.47^\circ\](או $2\pi/3$ רדיאן).
דברים שאפשר ליפול בהם:
- לא לשכוח לעשות שורש כשמחשבים את אורך הוקטור בעזרת מכפלה סקלרית שלו עם עצמו.
מציאת וקטור היחידה בכיוון הווקטור השקול
השקול הווקטורי של שני הווקטורים הוא:
\[\vec{c} = \vec{a} + \vec{b} = (1+\sqrt{3})\hat{x} + (\sqrt{2}-\sqrt{2})\hat{y} + (-\sqrt{3}+1)\hat{z}\]כלומר:
\[\vec{c} = (1+\sqrt{3})\hat{x} + 0\hat{y} + (1-\sqrt{3})\hat{z}\]וקטור היחידה בכיוון השקול הוא:
\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{(1+\sqrt{3})\hat{x} + (1-\sqrt{3})\hat{z}}{\sqrt{(1+\sqrt{3})^2 + (1-\sqrt{3})^2}}\]שאלה 2
נתונים שני וקטורים:
\[\begin{aligned} \vec{a} &= (3, -3) \\[10pt] \vec{b} &= (-2, 1) \end{aligned}\]
- קבלו את הסינוס והקוסינוס הזווית של הווקטור $2a - 3b$ ביחס לציר $x$ (אין צורך לחשב את הזווית עצמה).
- נתון הווקטור $\vec{c} = (\pi, e)$. קבלו את כל הווקטורים שבעולם הניצבים לו.
- רשמו את הווקטור $\vec{c}$ בבסיס שנפרס ע״י הווקטורים $\vec{a}$ ו־$\vec{b}$.
מציאת הסינוס והקוסינוס
-
חישוב הווקטור:
\[\begin{aligned} \vec{c} &= 2\vec{a}-3\vec{b} \\[10pt] &= 2(3, -3) - 3(-2, 1) \\[10pt] &= (6, -6) - (-6, 3) = (12, -9) \end{aligned}\] -
לחישוב ה־$\cos$ וה־$\sin$ של הזווית עם ציר ה־$x$:
\[\cos \theta = \frac{x}{c} = \frac{12}{\sqrt{12^2 + (-9)^2}} = \frac{12}{\sqrt{225}} = \frac{12}{15} = \frac{4}{5}\] \[\sin \theta = \frac{y}{c} = \frac{-9}{15} = -\frac{3}{5}\]
המתרגל הסביר:
“אז $\cos$ הזווית שווה ל… נרכיב ה־$x$, זה $\cos$ הזווית, אז נשתמש בזה בהשוואה לאורך. אז זה $x$, בואו נרשום את זה פה, $x$ שווה… תראה לכם, $x$ שווה ל־4, $\cos$ הזווית, אז למה שווה $\cos$ הזווית? $x$ חלקי $r$. $x$ חלקי $r$, $r$ זה האורך.”
חלק שני - מציאת וקטורים ניצבים
וקטור $\vec{d}=(d_x, d_y)$ ניצב ל־$\vec{c}=(\pi, e)$ אם:
\[\vec{c} \cdot \vec{d} = 0\]לכן נדרוש:
\[\pi d_x + e d_y = 0 \rightarrow d_x = -\frac{e}{\pi} d_y\]ולכן כל וקטור מהצורה:
\[\vec{d} = \left( -\frac{e}{\pi} d_y, \, d_y \right)\]יהיה ניצב ל־$\vec{c}$.
חלק שלישי: בסיסים וקטוריים ופריסת וקטורים
נמצא $\alpha$ ו־$\beta$ כך ש:
\[\vec{c} = \alpha \vec{a} + \beta \vec{b}\]נרשום את הווקטורים:
\[\vec{a} = (3, -3) \quad \vec{b} = (-2, 1) \quad \vec{c} = (\pi, e)\]נרשום את המשוואה:
\[\begin{pmatrix} 3 & -2 \\[10pt] -3 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\[10pt] \beta \end{pmatrix} = \begin{pmatrix} \pi \\[10pt] e \end{pmatrix}\]שאלה 3
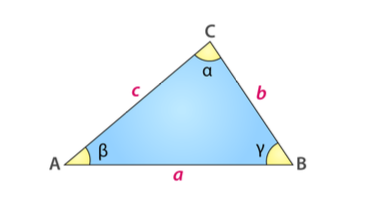
נתון המשולש למעלה. הוכיחו את משפט הקוסנוסים:
\[c^2 = a^2 + b^2 - 2ab \cos \theta\]באמצעות שימוש טריוואלי במכפלה הסקלרית.
הוכחה באמצעות מכפלה סקלרית היא יחסית קצרה: במשולש עם צלעות $a, b, c$ והזווית $\gamma$ ביניהן, ניתן לייצג צלעות $\vec{a}, \vec{b}$ כווקטורים באותו ראש, כך:
\[\vert \vec{a}|=a,\quad \vert \vec{b}|=b,\quad \text{תיווזה } \gamma \text{ ןהיניב}.\]אז הצלע השלישית (אורכה $c$) מתקבלת למשל כ־$\vec{a}-\vec{b}$. לכן
\[\begin{aligned} c^2 &= \vert \vec{a}-\vec{b}|^2 \\[10pt] &= (\vec{a}-\vec{b})\cdot(\vec{a}-\vec{b}) \\[10pt] &= \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b} - 2\,(\vec{a}\cdot\vec{b}) \\[10pt] &= a^2 + b^2 - 2\,ab\,\cos(\gamma) \end{aligned}\]וזהו משפט הקוסינוסים.
שאלה 4 - קואורדינטות כדוריות
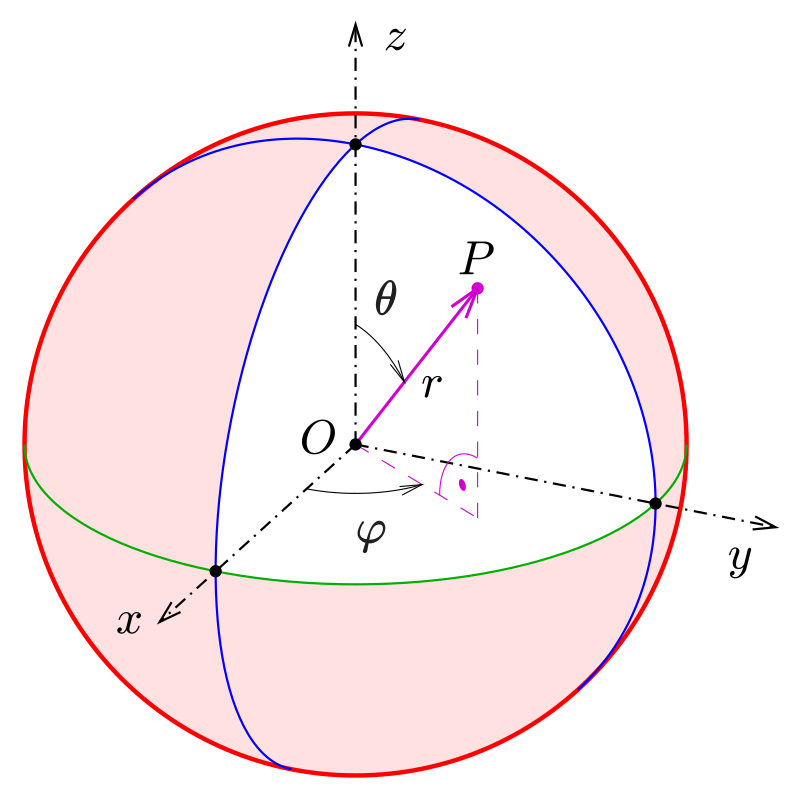
אנו רוצים להראות כי עבור $(r,\theta,\varphi)$ מתקיים:
\[\begin{aligned} x &= r\,\sin(\theta)\cos(\varphi),\\[10pt] y &= r\,\sin(\theta)\sin(\varphi),\\[10pt] z &= r\,\cos(\theta). \end{aligned}\]- (א) זוהי ההגדרה הסטנדרטית של קואורדינטות כדוריות:
- תחילה מקרינים את הנקודה על מישור $xy$ בעזרת $\sin(\theta)$.
- אחר כך מפרקים לרכיבי $\cos(\varphi)$ ו־$\sin(\varphi)$ במישור.
- הרכיב האנכי (ציר $z$) הוא $r\,\cos(\theta)$.
-
(ב) הראו ש־$x^2 + y^2 + z^2 = r^2$:
\[\begin{aligned} x^2 + y^2 + z^2 &= (r\sin\theta\cos\varphi)^2 + (r\sin\theta\sin\varphi)^2 + (r\cos\theta)^2 \\[10pt] &= r^2\sin^2(\theta)\bigl[\cos^2(\varphi) + \sin^2(\varphi)\bigr] + r^2\cos^2(\theta) \\[10pt] &= r^2\bigl[\sin^2(\theta) + \cos^2(\theta)\bigr] \\[10pt] &= r^2. \end{aligned}\]
שאלה 5 - מרחק כתלות בזמן
5. וקטור המקום של גוף מסוים המבצע תנועה קלשתי מתואר באמצעות
\[\vec{r}(t) = \vec{a} \sin(\omega t) + \vec{b} \cos(\omega t)\]באשר $\vec{a}, \vec{b}$ הם וקטורים קבועים (כלומר הם אינם תלויים בזמן).
- קבלו את המרחק של הגוף מהראשית כפונקציה של הזמן.
- קבלו ביטוי עבור וקטור המהירות של הגוף.
- קבלו ביטוי עבור וקטור היחידה תלוי-הזמן המתאר את כיוון תנועתו של הגוף בכל רגע ורגע.
- קבלו את המכפלה $\vec{r}(t) \cdot \vec{v}(t)$.
חלק שלישי: תנועה במישור
6. וקטור המקום של חלקיק כלשהו הנע במישור נתון ע”י
\[\vec{r}(t) = \left( e^{-\alpha t} \cos \omega t \right) \hat{x} + \left( e^{-\alpha t} \sin \omega t \right) \hat{y}\]באשר $\alpha, \omega$ הם פרמטרים כלשהם.
- מהן היחידות של הפרמטרים $\omega, \alpha$?
- הראו שהחלקיק נע בספירלה מעגלית שמתכנסת לעבר המרכז.
- קבלו את וקטור המהירות של החלקיק כתלות בזמן.
- מהו גודל וקטור המהירות של החלקיק כתלות בזמן?
חלק רביעי: המרחק בין שתי נקודות
נדון נושא המרחק בין שתי נקודות:
“מדדו את המרחק בין הצירים. בי, המרחק. אה, עוד דיברנו על המרחק, נכון? איך מוצאים מרחק בין שתי נקודות? נשארי, ספר לדוגמה, נשארי.”
הוסבר שהמרחק בין שני וקטורים $\vec{a}$ ו־$\vec{b}$ הוא:
\[d = \vert \vec{b} - \vec{a}\vert = \sqrt{(b_x - a_x)^2 + (b_y - a_y)^2 + (b_z - a_z)^2}\]חלק חמישי: תנועה במרחב ופונקציות וקטוריות של הזמן
המתרגל הסביר את התיאור של תנועה במרחב באמצעות פונקציות וקטוריות של הזמן:
“אני מצייר שתי נקודות ואז אני מושך קו ישר. פה יש לי סירה אדומה, ופה יש לי סירה צהובה. עם הזמן הסירות זזות, כי הווקטור משתנה.”
דוגמה עם שתי סירות
- סירה ראשונה התחילה בנקודה $(1, 1)$ ונעה בכיוון $(1, 0)$
- סירה שנייה התחילה בנקודה $(2, 2)$ ונעה בכיוון $(1, 1)$
אחרי שנייה אחת:
“רגע לפני זה, אחרי שנייה אחת, איפה הסירה הזאת נמצאת? $(2,1)$ - היא פה. ואיפה זאת? $(3,3)$ - היא פה.”
חישוב המהירות:
“אהלן, מהירות. בואו נמצא את המהירות שלה, ונמצא את המהירות של השנייה. מה המהירות של הראשונה? איך עושים את זה? גוזרים כל רכיב בנפרד. מה קורה כשאני גוזר? מקבלים: $(1,0)$. איזה כיוון זה? $x$. וזה מה שציירתי פה - היא נעה בכיוון $x$. מה הנגזרת של השנייה? $(1,1)$. כלומר, היא זזה אחד ימינה ואחד למעלה כל הזמן.”
חלק שישי: תנועה מעגלית וספירלית
בהמשך התרגול, נדונה תנועה מעגלית ותנועה ספירלית:
“אוקיי, נעבור על תנועה מעגלית וספירלית שמתכנסת. מה זה הגודל הזה? מה זה?”
הוסבר שבתנועה מעגלית קצובה, הזווית משתנה לינארית עם הזמן:
\[\theta(t) = \omega t\]כאשר $\omega$ היא המהירות הזוויתית (ברדיאנים לשנייה):
”$\omega$ זה קצב שינוי הזווית. איך מגדירים את $\omega$?”
וקטור המקום בתנועה מעגלית:
\[\vec{r}(t) = r \cos(\omega t) \hat{x} + r \sin(\omega t) \hat{y}\]לגבי תנועה ספירלית:
“אז זו בעצם תנועה מעגלית עם רדיוס שקטן כל הזמן. הוא יכול להתחיל גדול ואז יקטן, או ההפך, תלוי בזמן.”
תנועה ספירלית אקספוננציאלית:
\[r(t) = r_0 e^{\alpha t}\]- אם $\alpha > 0$ - הרדיוס גדל, תנועה ספירלית החוצה
- אם $\alpha < 0$ - הרדיוס קטן, תנועה ספירלית פנימה
חלק שביעי: מימדים ויחידות פיזיקליות
בסוף התרגול נדונו מימדים ויחידות פיזיקליות:
“יש לנו כמה… יש שלושה ושניים מימדים במכניקה. יש עוד מימד אחד ב… פיזיקה אחת - במכניקה. פיזיקה שתיים - שני מימדים, אז יתווסף עוד מימד.”
בפיזיקה קלאסית קיימים שלושה מימדים בסיסיים:
- זמן
- מסה
- מרחק (אורך)
לגבי יחידות של זווית והקשר למימדים:
“זה גודל זוויתי, מה היחידות שלו? רדיאנים. או… מה לא? רדיאנים. אז מה היחידות של זווית? אין מימדים. אני ארשום את זה כ־1 - חסר מימד.”
מהירות זוויתית $\omega$:
“אז היחידות של $\omega$ הן רדיאנים לשנייה, כלומר: $\left[\omega\right] = \frac{\text{rad}}{\text{sec}}$. זה נכתב עם סוגריים מרובעים סביב הגודל הפיזיקלי.”
חלק שמיני: חישוב וקטור המהירות בתנועה מורכבת
בסיום התרגול, המתרגל הראה כיצד לחשב את וקטור המהירות עבור תנועה מורכבת:
“קיבלת וקטור מיקום של החלקיק כתלות בזמן. מה עושים כדי לקבל את המהירות?”
וקטור מיקום כללי:
\[\vec{r}(t) = r_0 e^{\alpha t} \left( \cos(\omega t) \hat{x} + \sin(\omega t) \hat{y} \right)\]נגזרת של כל רכיב בנפרד:
“נגזור את רכיב ה־$x$ בנפרד, ואז את רכיב ה־$y$. זה קצת ארוך, אבל ככה עושים את זה.”
לגזירת רכיב ה־$x$:
\[\frac{d}{dt} \left( r_0 e^{\alpha t} \cos(\omega t) \right) = r_0 e^{\alpha t} \left( \alpha \cos(\omega t) - \omega \sin(\omega t) \right)\](אותו רעיון לגבי רכיב ה־$y$)
המתרגל הסביר את כלל הנגזרת של מכפלה:
“כשגוזרים $\cos$, מקבלים מינוס סינוס כפול $\omega$.”
לבסוף חושב גודל המהירות:
\[\vert \vec{v}(t)| = \sqrt{v_x^2 + v_y^2}\]דור פסקל“זה מה שנעשה בסוף - מה גודל וקטור המהירות בזמן נתון. כלומר שורש סכום הריבועים של $v_x$ ו־$v_y$.”