ההרצאה ממשיכה את הנושא של הסקה ססטיסטית - הסקת מסקנות על אוכלוסייה בהתבסס על מדגם. החלק הראשון חוזר על חלקים מהשיעור הקודם.
אוכלוסייה היא קבוצת הפרטים שאחננו מעוניינים להסיק עליהם, ומדגם הוא תת-קבוצה של האוכלוסייה שנמדד בפועל.
הכלים שעומדים לרשותנו הם:
- אומדן: שיערוך פרמטר של האוכלוסייה
- בדיקת השערות: האם לאוכלוסייה תכונה מסוימת / השוואה בין תכונות בין אוכלוסיות
הבסיס הרעיוני לבדיקת השערות
בדיקת השערות היא אחד הכלים המרכזיים בסטטיסטיקה הסקית, ומבוססת על עקרון פשוט אך עמוק: אם התוצאה שקיבלנו קיצונית מדי תחת ההנחה הסטנדרטית, כנראה שההנחה הסטנדרטית שגויה.
הרעיון המנחה הוא השוואה מבוקרת - אנחנו מגדירים “עולם רצוי/קיים/סטנדרטי” (השערת האפס) ובודקים אם התוצאות שקיבלנו סבירות בעולם זה. אם התוצאות קיצוניות מדי, אנחנו מסיקים שהעולם הסטנדרטי שבנינו שגוי, ודוחים את השערת האפס לטובת השערה אלטרנטיבית.
השערת האפס היא בדר״כ מהצורה:
\[H_0: \mu = \mu_0\]כלומר, שהתוחלת באוכלוסיה שווה לערך כלשהו המייצג את המצב הרצוי. אבל להבנתי זה לא בהכרך ככה, ואפשר גם לקבוע השערות אפס אחרות, כמו.
הערה נוספת: במצגות ההגדרות לא ברורות, לדעתי. למשל מצויין ביחס להשערת האפס שהיא מייצגת את המצב ״הקיים/הרצוי״ - אבל להבנתי אלה שני דברים שנוים.
תנאים מקדימים למבחן $Z$
תנאים הכרחיים:
- התכונה הנבדקת מתפלגת נורמלית באוכלוסייה, או שמתקיים משפט הגבול המרכזי (מדגם גדול)
- המדגם נלקח באופן אקראי ובלתי תלוי
-
השונות של התכונה באוכלוסייה ידועה מראש
הערה: אנחנו גם יודעים איך לטפל במקרים של שונות לא ידועה - נשתמש במבחן $t$ במקום $Z$, אך נתחיל עם $Z$ כדי להדגיש את העקרונות הבסיסיים.
למרות שהתנאי של שונות ידועה אינו ריאליסטי ברוב המקרים המעשיים, הוא מאפשר לנו להתמקד ברעיונות הבסיסיים של בדיקת השערות בלי סיבוכים טכניים.
הגדרת השערות: השערת האפס והשערה אלטרנטיבית
השערת האפס (H₀)
השערת האפס מייצגת את המצב הסטנדרטי או הדיפולטיבי שבו אנחנו מניחים שאין הבדל או אין אפקט. במונחים מתמטיים:
\[H_0: \mu = \mu_0\]כאשר $\mu$ היא התוחלת של האוכלוסייה הנבדקת ו-$\mu_0$ היא התוחלת הידועה של האוכלוסייה הכללית.
דוגמה: אם אנחנו בודקים את רמת הכולסטרול (LDL) בקרב אנשים בני 100, השערת האפס תהיה שרמת הכולסטרול בקרב בני 100 זהה לרמה באוכלוסייה הכללית.
השערה אלטרנטיבית (H₁)
השערה אלטרנטיבית מציגה את מה שאנחנו חושדים שאולי נכון, או את מה שנוגד את השערת האפס. ישנם שלושה סוגים עיקריים:
השערה אלטרנטיבית חד-צדדית (גדולה מ-):
\[H_1: \mu > \mu_0\]השערה אלטרנטיבית חד-צדדית (קטנה מ-):
\[H_1: \mu < \mu_0\]השערה אלטרנטיבית דו-צדדית:
\[H_1: \mu \neq \mu_0\]ההשערה הדו-צדדית היא “אגנוסטית” - היא אינה מניחה כיוון מסוים להבדל, רק שההבדל קיים.
הסטטיסטי Z והמבנה המתמטי
בניית הסטטיסטי
תחת השערת האפס, הסטטיסטי Z מוגדר כך:
\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]כאשר:
- $\bar{X}$ - ממוצע המדגם שהתקבל בפועל
- $\mu_0$ - התוחלת לפי השערת האפס
- $\sigma$ - סטיית התקן של האוכלוסייה (ידועה)
- $n$ - גודל המדגם
הרעיון המתמטי: אנחנו לוקחים את ההפרש בין מה שקיבלנו לבין מה שציפינו לקבל תחת השערת האפס, ומתקננים אותו בחלוקה בסטיית התקן המתאימה. כך אנחנו מקבלים משתנה מקרי שמתפלג $\mathcal{N}(0,1)$ תחת השערת האפס.
התמיינות בין ערכים היפותטיים לערכים מעשיים
חשוב להבחין בין שני סוגי ערכים:
$\bar{X}$ (X גג גדול) - משתנה מקרי היפותטי תחת השערת האפס, עדיין אין לו ערך מספרי ספציפי
$\bar{x}$ (x גג קטן) - הערך הספציפי של ממוצע המדגם שקיבלנו בפועל, זה מספר קונקרטי שאנחנו “מחזיקים ביד”
חישוב P-value: הלב של בדיקת ההשערות
הגדרה מושגית
P-value הוא הסיכוי לקבל את הערך שקיבלנו, או ערך קיצוני ממנו, בהנחה שהשערת האפס נכונה. זהו המדד המרכזי לקבלת החלטות בבדיקת השערות.
חישוב עבור מבחנים חד-צדדיים
למבחן מהסוג $H_1: \mu > \mu_0$:
אנחנו מחשבים את הסטטיסטי:
\[z_{calc} = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}}\]ואז:
\[\text{P-value} = P(Z \geq z_{calc})\]הרעיון: אנחנו שואלים מה הסיכוי שמשתנה מקרי נורמלי מתוקנן יקבל ערך גדול או שווה לזה שחישבנו.
למבחן מהסוג $H_1: \mu < \mu_0$:
\[\text{P-value} = P(Z \leq z_{calc})\]הצדקה מתמטיקה לחישוב P-value
הנוסחה עובדת מכיוון שאנחנו יכולים לכתוב:
\[P(Z \geq z_{calc}) = P\left(\frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} \geq z_{calc}\right)\]מכיוון ששני הצדדים מתוקננים באותה צורה, אנחנו יכולים לכתוב:
\[= P(\bar{X} \geq \bar{x})\]וזה בדיוק הסיכוי לקבל ממוצע מדגם גדול או שווה לזה שקיבלנו בפועל - הגדרת P-value.
מבחנים דו-צדדיים ועיקרון הסימטריה
עבור מבחן דו-צדדי, אנחנו מעוניינים בסיכוי לקבל ערך קיצוני בכל אחד משני הכיוונים. בשל הסימטריה של ההתפלגות הנורמלית:
\[\text{P-value} = 2 \cdot P(Z \geq |z_{calc}|)\]ההגיון הגרפי: אם הסטטיסטי שלנו נמצא בזנב הימני, אנחנו מחשבים את השטח בזנב הימני ומכפילים ב-2 כדי לכלול גם את השטח המקביל בזנב השמאלי.
קריטריון הדחייה ורמת המובהקות
כלל ההחלטה הבסיסי
אנחנו דוחים את השערת האפס כאשר P-value < α:
כאשר α (אלפא) היא רמת המובהקות שנקבעה מראש, בדרך כלל 0.05 במדעי החיים והרפואה.
המשמעות: אם הסיכוי לקבל את התוצאה שקיבלנו (או קיצונית יותר) תחת השערת האפס קטן מ-5%, אנחנו מחליטים שהשערת האפס כנראה שגויה.
גזירה מתמטית של אזור הדחייה
באמצעות מניפולציות אלגבריות, ניתן להראות שעבור מבחן דו-צדדי ברמת מובהקות של 0.05:
\[\text{reject } H_0 \text{ if } |z_{calc}| > 1.96\]וזה שקול לתנאי:
\[|\bar{x} - \mu_0| > 1.96 \cdot \frac{\sigma}{\sqrt{n}}\]או במילים אחרות:
\[\bar{x} < \mu_0 - 1.96 \cdot \frac{\sigma}{\sqrt{n}} \text{ or } \bar{x} > \mu_0 + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\]הקשר בין רווחי סמך לבדיקת השערות דו-צדדית
הזהות המתמטית
כשאנחנו משווים את תנאי הדחייה במבחן השערות לנוסחת רווח סמך, אפשר לראות ששני הכלים מבוססים על אותו מבנה מתמטי.
רווח הסמך הדו-צדדי של $(1-\alpha) \times 100\%$ עבור $\mu$ הוא:
\[\left[\bar{x} - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}, \bar{x} + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\right]\]ותנאי אי-דחיית השערת האפס $H_0: \mu = \mu_0$ הוא:
\[\left[\mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} < \bar{x} < \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\right]\]התובנה המרכזית: נדחה את $H_0$ ברמת מובהקות $\alpha$ אם ורק אם $\mu_0$ אינו נמצא ברווח הסמך של $(1-\alpha) \times 100\%$.
ההבדל המושגי
למרות הזהות המתמטית, קיים הבדל מושגי חשוב בין שתי הגישות:
| בדיקת השערות | רווח סמך | |
|---|---|---|
| מרכז | $\mu_0$ (הערך לפי השערת האפס) | $\bar{x}$ (הערך שקיבלנו מהמדגם) |
| מטרה | לבדוק האם השערה ספציפית על $\mu$ נכונה | להעריך טווח סביר הפרמטר האמיתי $\mu$ |
| הסתברות | $\bar{x}$ נמצא ב”טווח הקבלה” בהסתברות $(1-\alpha)$ תחת $H_0$ | הפרמטר נמצא ברווח בהסתברות של $(1-\alpha)$ |
יישומים במחקר
הקשר הזה מאפשר לחוקרים להשתמש ברווחי סמך כדרך אלגנטית לבצע בדיקת השערות מרומזת. דוגמאות נפוצות:
במחקר רפואי: כאשר מדווחים על יחס סיכויים (Odds Ratio) של $1.34$ עם רווח סמך $95\%$ של $[1.23, 2.00]$, ניתן להסיק מיידית שהיחס שונה באופן מובהק מ-$1$ (היעדר אפקט), שכן $1$ אינו נכלל ברווח.
בניסויים קליניים: אם תרופה חדשה מאריכה תוחלת חיים ב-$3$ שנים עם רווח סמך $95\%$ של $[2, 4]$ שנים, ההשפעה מובהקת סטטיסטית כי $0$ (היעדר השפעה) אינו ברווח.
בדיקת השערות עבור פרופורציות
המסגרת התיאורטית
כשאנחנו מעוניינים לבדוק השערות לגבי פרופורציה באוכלוסייה, אנחנו משתמשים בתכונות ההתפלגות הבינומית ובקירוב הנורמלי שלה. נסמן ב-$p$ את הפרופורציה האמיתית באוכלוסייה וב-$\bar{p}$ את הפרופורציה במדגם.
תחת השערת האפס $H_0: p = p_0$, כאשר גודל המדגם $n$ גדול מספיק, מתקיים:
\[\bar{p} \sim \mathcal{N}\left(p_0, \frac{p_0(1-p_0)}{n}\right)\]הקירוב הנורמלי תקף כאשר מתקיימים התנאים:
\[np_0 \geq 10\]ו-
\[n(1-p_0) \geq 10\]סטטיסטי המבחן
הסטטיסטי המתוקנן עבור בדיקת השערות על פרופורציה הוא:
\[Z = \frac{\bar{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\]תחת השערת האפס, $Z \sim \mathcal{N}(0,1)$.
דוגמה: יעילות טיפול רפואי
נניח שבמחלקה מסוימת, $20\%$ מהחולים מחלימים ממחלה ללא טיפול.
נניח שמתוך מדגם של $n = 100$ חולים שקיבלו את הטיפול, $25$ החלימו.
רופא מעוניין לבדוק האם טיפול חדש בכימותרפיה מעלה את אחוז ההחלמה.
$p_0 = 0.2$ הוא אחוז ההחלמה ללא טיפול, ורופא רוצה לבדוק אם הטיפול החדש מעלה את האחוז הזה.
ניסוח ההשערות:
השערת האפס:
\[H_0: p = 0.2\]השערת המחקר:
\[H_1: p > 0.2\]איסוף הנתונים: נניח שמתוך מדגם של $n = 100$ חולים שקיבלו את הטיפול, $25$ החלימו, כלומר:
\[\bar{p} = \tfrac{\mathbf{25}}{100} = 0.25\] \[E(\bar{p}) = p_0 = 0.2\] \[Var(\bar{p}) = \frac{p_0(1-p_0)}{n} = \frac{0.2 \times 0.8}{100} = 0.0016 = 0.04^2\]תחת השערת האפס
\[\bar{p} \sim \mathcal{N}(0.2, 0.04^2)\] \[Z = \frac{0.25 - 0.2}{\sqrt{\frac{0.2 \times 0.8}{100}}} = \frac{0.05}{0.04} = 1.25\]חישוב ה-p-value: עבור השערה חד-צדדית:
\[p\text{-value} = P(\bar{p} \geq 0.25) = P(Z \geq 1.25) = 0.11\]אפשר לחשב בפייתון:
from scipy.stats import norm
z_calc = 1.25
p_value = 1 - norm.cdf(z_calc) # = norm.sf(z_calc)
print(f"P-value: {p_value:.4f}")
הפלט:
P-value: 0.1056
מסקנה: ברמת מובהקות של $\alpha = 0.05$, לא נדחה את השערת האפס. אין ראיות מובהקות סטטיסטית לכך שהטיפול החדש מעלה את אחוז ההחלמה.
דוגמה: שינוי בדפוסי טיפול
בעבר, $60\%$ מהמאושפזים עברו ניתוח.
מתוך $n = 400$ מאושפזים, $212$ עברו ניתוח.
מנהל בית חולים מעוניין לבדוק האם ראש מחלקה חדש שינה את אחוז החולים המופנים לניתוח.
ניסוח ההשערות (בדיקה דו-צדדית)
\[H_0: p = 0.6 \quad \quad H_1: p \neq 0.6\]נתוני המדגם
מתוך $n = 400$ מאושפזים, $212$ עברו ניתוח. לכן:
\[\bar{p} = \frac{212}{400} = 0.53\]חישוב סטטיסטי המבחן
\[z = \frac{\bar{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} = \frac{0.53 - 0.6}{\sqrt{\frac{0.6 \cdot 0.4}{400}}} = \frac{-0.07}{0.0245} \approx -2.86\]חישוב ה-p-value
בדיקה דו-צדדית:
\[\text{p-value} = 2 \cdot P(Z > |{-2.86}|) \approx 2 \cdot 0.0021 = 0.0042\]מסקנה
ברמת מובהקות $\alpha = 0.05$, נדחה את $H_0$. יש עדות לכך שאחוז החולים העוברים ניתוח שונה תחת הנהלת ראש המחלקה החדש.
שאלות מהתרגול
בדיקת שיעור תנוכים
מנהל בית החולים זוריה מרגיש שלאחרונה מגיעים אל בית החולים שלו יותר חולי תנוכים מהרגיל (בד”כ מגיעים חולי תנוכים, מרפקים וציפרניים בשיעור שווה)
נסח בדיקת השערות על שיעור חולי התנוכים החדשים בבית החולים זוריה
לבית החולים הגיעו ביממה האחרונה 44 חולי תנוכים, 16 חולי מרפקים ו- 40 חולי ציפרניים.
האם פרופורציית חולי התנוכים גדולה באופן מובהק מבד”כ?
ניסוח ההשערות:
\[H_0: p_0 = 0.33, \quad H_1: p > 0.33\] \[Z = \frac{\bar{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\]n = 44 + 16 + 40 # 100
p_0 = 0.33
bar_p = 44 / n
Z = (bar_p - p_0) / ((p_0 * (1 - p_0) / n) ** 0.5)
print(f"Z: {Z:.4f}")
from scipy.stats import norm
p_value = 1 - norm.cdf(Z)
print(f"P-value: {p_value:.4f}")
הפלט:
Z: 2.3394
P-value: 0.0097
מסקנה: p-value קטן מ-0.05, ולכן נדחה את השערת האפס. יש ראיות מובהקות לכך ששיעור חולי התנוכים בבית החולים זוריה גבוה מהרגיל.
שאלה על מכונה חדשה לבדיקה אוראה
במחלקת הנפרולוגיה של בית החולים המשפחה הסקוטית, הרופאה התורנית מדדה את ריכוז השתנן (אוראה) בדמם של החולים המאושפזים. הרופאה רוצה לבחון את פעולתו של מכשיר הדיאליזה החדש. מצד אחד, המכשיר חדש וצפוי לפעול יותר טוב מהקודם. מצד שני – הצוות הרפואי טרם צבר נסיון בעבודה עימו.
ריכוז האוראה בדמם של המטופלים בדיאליזה עם המכשיר הישן מתפלג נורמלית עם תוחלת 30 מ”ג לדציליטר וסטיית תקן של 10.5 מ”ג לדציליטר. הרופאה התורנית מניחה שסטיית התקן זהה בקרב אוכלוסיות המטופלים במכשיר החדש והישן.
נסחו עבור הרופאה התורנית מבחן השערות מתאים
הרופאה התורנית רושמת את רמות האוראה בדמם של 49 חולים אחרי טיפול במכשיר החדש. ממוצע ריכוז האוראה בדמם הוא 28 מ”ג לדציליטר. מה תסיק הרופאה ברמת מובהקות של 5%.
בשעות הלילה הרופאה סבלה מנדודי שינה. היא החליטה לנסות לגלות עבור אילו ערכים של ממוצע המדגם היא תדחה את השערת האפס. איך היא חישבה ערכים אלו?
לאחר ליל שימורים, הגיע הבוקר. הרופאה התורנית בבוקר החליטה שבדיקת השערות אינה הכלי הסטטיסטי המתאים. היא החליטה לחשב רווח סמך לתוחלת (עם שונות ידועה). שתי הרופאות הסכימו על רמת סמך של 95%. איזה רווח סמך תחשב הרופאה בבוקר?
1. ניסוח השערות
\[H_0: \mu_{old} = \mu_{new} , \quad H_1: \ne \mu_{new}\]נראה שהמבחן כאן דו צדדי.
2. מבחן השערות
בדיקת השערות על התוחלת:
\[\begin{aligned} \text{p-value} &= 2 \cdot P(\bar{X} > |28|) \\ &= 2 \cdot P\left( \frac{\bar{X} - 30}{10.5/\sqrt{49}} > \frac{28 - 30}{10.5/\sqrt{49}} \right) \\ &= 2 \cdot P\left( Z > \frac{-2}{10.5/\sqrt{49}} \right) \\ &= 2 \cdot P\left( Z > -1.3333 \right) \\ &= 2 \cdot (1 - P(Z < -1.3333)) \\ &= 2 \cdot (1 - 0.0918) \\ &= 2 \cdot 0.9082 \\ &= 1.8164 \end{aligned}\]הרופאה התורנית תדחה את השערת האפס אם ה-p-value קטן מ-0.05. במקרה זה, ה-p-value הוא 1.8164, שהוא הרבה יותר גדול מ-0.05, ולכן לא נדחה את השערת האפס.
3. חישוב ערכי דחייה
נדחה את השערת האפס כאשר (כל שורה גוררת את השורה הבאה):
\[2P(Z > |z|) < 0.05\] \[P(Z > |z|) < 0.025\] \[|z| > 1.96\] \[\frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} > 1.96\] \[|\bar{X} - \mu_0| > 1.96 \cdot \frac{\sigma}{\sqrt{n}}\] \[\bar{X} < \mu_0 - 1.96 \cdot \frac{\sigma}{\sqrt{n}} \quad \text{or} \quad \bar{X} > \mu_0 + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\]נשתמש בשורה האחרונה. הערכים שמגדירים את טווח הקבלה (ובהתאם גם את טווח הדחייה) הם:
\[30 - 1.96 \cdot \frac{10.5}{7} = 30 - 1.96 \cdot 1.5 = 27.06\] \[30 + 1.96 \cdot \frac{10.5}{7} = 30 + 1.96 \cdot 1.5 = 32.94\]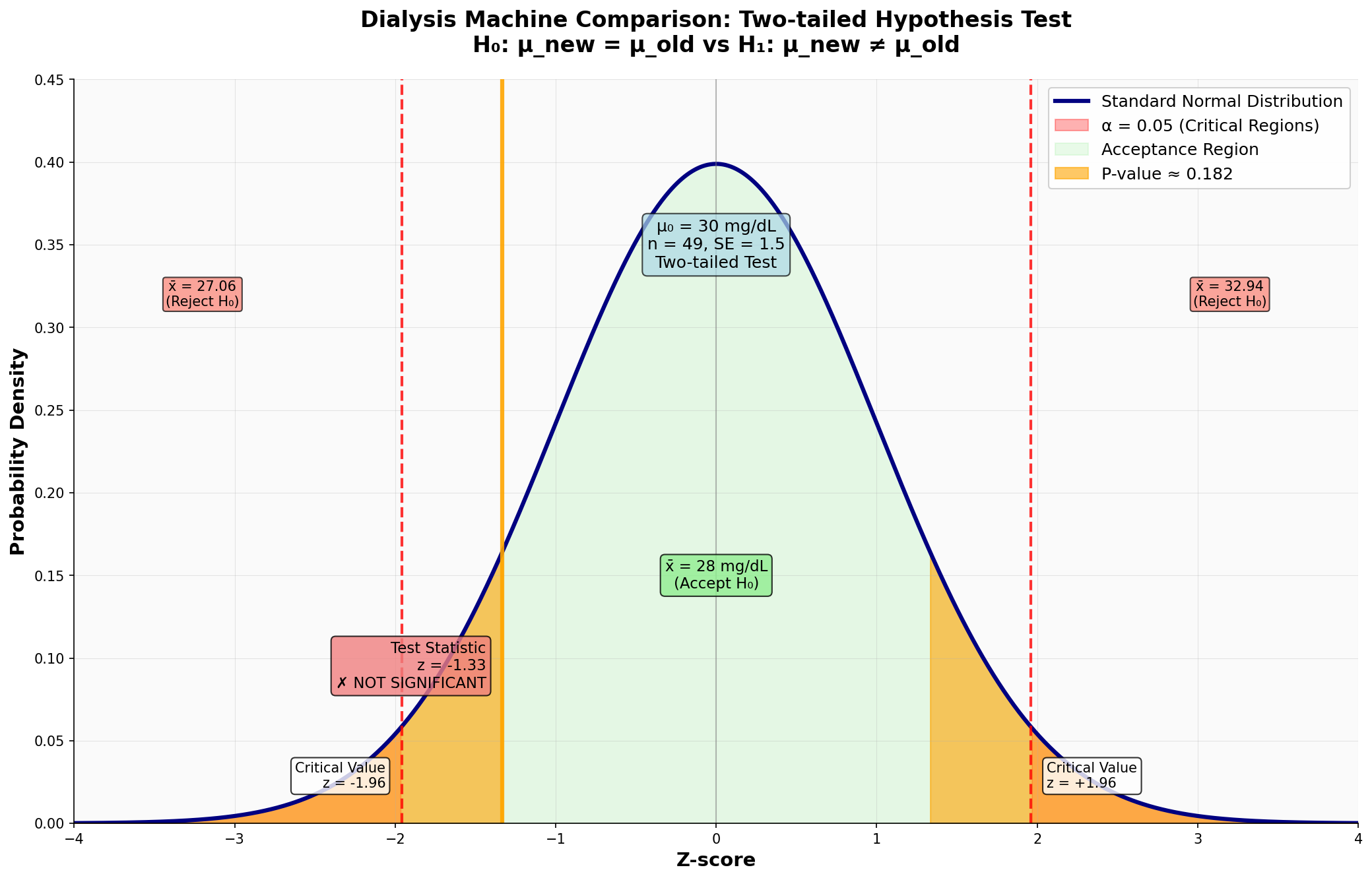
4. רווח סמך לתוחלת
השונות ידועה, אפשר לחשב לפי הנוסחה:
\[\left[\bar{X} - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}, \bar{X} + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\right]\]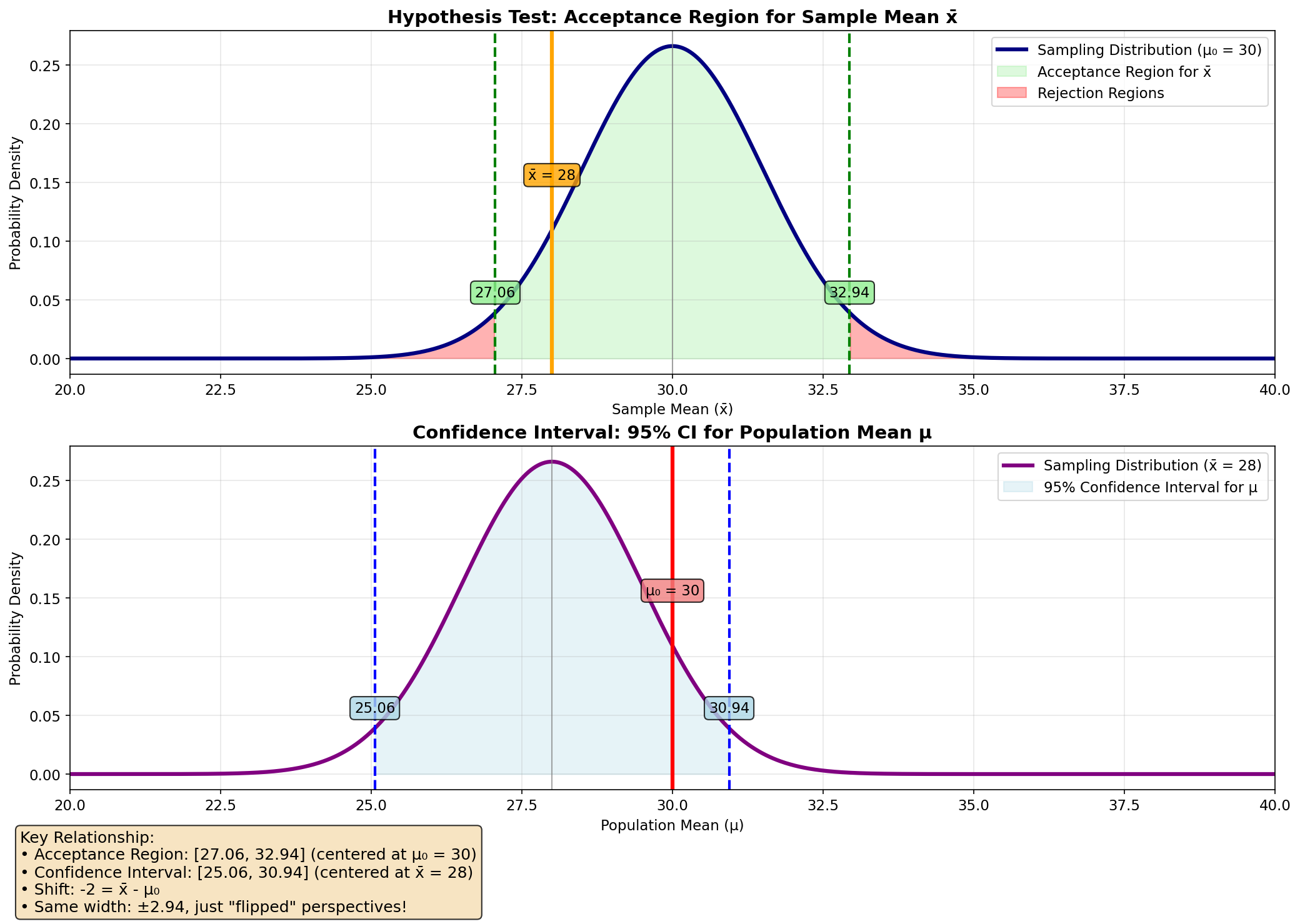
זה כמו מה שחישבנו מקודם, רק צריך להוריד 2:
\[\left[25.06, 30.94\right]\]\[\left[\bar{X} - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}, \bar{X} + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\right] = \left[28 - 1.96 \cdot \frac{10.5}{\sqrt{256}}, 28 + 1.96 \cdot \frac{10.5}{\sqrt{256}}\right]\] \[= \left[28 - 1.96 \cdot \frac{10.5}{16}, 28 + 1.96 \cdot \frac{10.5}{16}\right] = \left[28 - 1.96 \cdot 0.65625, 28 + 1.96 \cdot 0.65625\right]\] \[= \left[28 - 1.2875, 28 + 1.2875\right] = \left[26.7125, 29.2875\right]\]מה יהיה רווח הסמך במקרה שנמדדו 256 חולים?
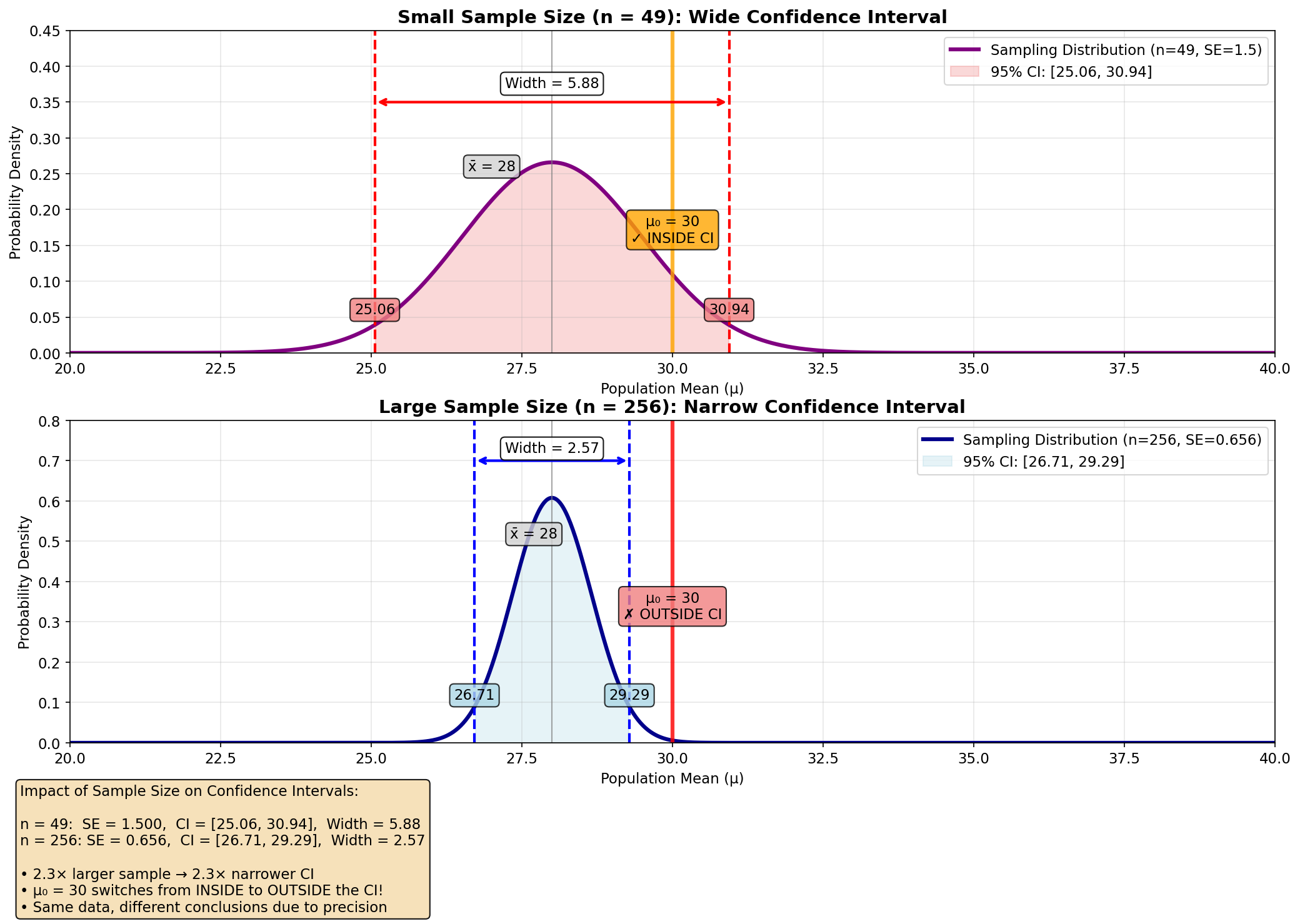
מה היא תסיק לאחר הגדלת המדגם?
היא תסיק שהוא שונה באופן מובהק, כי רווח הסמך התכווץ, והערך 30 לא נמצא ברווח הסמך.
בעיית ההשערות המרובות ו-p-hacking
תופעת ה-p-hacking
אחת הבעיות החמורות במחקר המדעי המודרני היא תופעת ה-p-hacking. תופעה זו מתרחשת כאשר חוקרים מבצעים מניפולציות שונות בנתונים או בניתוח הסטטיסטי כדי להגיע לתוצאות מובהקות סטטיסטית.
ניתוח של התפלגות ערכי $Z$ במחקרים שפורסמו חושף דפוס מדאיג: ריכוז חריג של ערכים סביב $Z = 2$, שמתאים ל-$p\text{-value} \approx 0.05$. זהו סימן לכך שחוקרים רבים “משחקים” עם הנתונים עד להשגת מובהקות סטטיסטית.
המנגנון המתמטי של p-hacking
כאשר חוקר מבצע ניתוחים מרובים על אותם נתונים, ההסתברות למצוא לפחות תוצאה אחת מובהקת עולה באופן משמעותי. אם נבצע $m$ בדיקות בלתי תלויות ברמת מובהקות $\alpha$, ההסתברות לקבל לפחות תוצאה אחת מובהקת בטעות היא:
\[P(\text{At least one false rejection}) = 1 - (1-\alpha)^m\]עבור $m = 20$ בדיקות ו-$\alpha = 0.05$:
\[P(\text{At least one false rejection}) = 1 - 0.95^{20} \approx 0.64\]דוגמה: פול התמנון ובעיית ההשערות המרובות
המקרה של פול התמנון ממחיש היטב את בעיית ההשערות המרובות. פול “חזה” נכונה $12$ מתוך $14$ תוצאות משחקים במונדיאל 2010.
ניתוח סטטיסטי:
תחת השערת האפס שפול מנחש באקראי, מספר הניחושים הנכונים $X \sim \text{Binomial}(14, 0.5)$.
\[p\text{-value} = P(X \geq 12) = \sum_{k=12}^{14} \binom{14}{k} 0.5^{14} = 0.006\]הרחבה: פתרון מפורט עם הבינום של ניוטון (מוקדש לתום)
\[\begin{aligned} P(X \geq 12) &= P(X = 12) + P(X = 13) + P(X = 14) \\ &= \binom{14}{12} 0.5^{14} + \binom{14}{13} 0.5^{14} + \binom{14}{14} 0.5^{14} \\ &= \left( \frac{14!}{12!2!} + \frac{14!}{13!1!} + \frac{14!}{14!0!} \right) 0.5^{14} \\ &= \left( 91 + 14 + 1 \right) = 106 \cdot 0.5^{14} \\ &= 106 \cdot \frac{1}{16384} \\ &= \frac{106}{16384} \approx 0.006 \end{aligned}\]
למרות המובהקות הסטטיסטית, הבעיה היא שפול לא היה החיה היחידה ש”חזתה” תוצאות. כאשר אלפי חיות ברחבי העולם “מנחשות” תוצאות, ההסתברות שלפחות אחת מהן תצליח במקרה היא גבוהה מאוד.
האנלוגיה לניבוי שוק ההון
נניח שאדם שולח למיליון אנשים תחזיות שונות לגבי שוק ההון. לחצי מהם הוא חוזה שמניה מסוימת תעלה, ולחצי השני - שתרד. הוא ממשיך בתהליך זה מספר פעמים. בסופו של דבר, כמה אנשים יקבלו סדרה של תחזיות נכונות ויחשבו שהוא גאון, למרות שהכול היה אקראי לחלוטין.
זוהי בדיוק אותה בעיה: כאשר בוחנים מספר רב של השערות, חלקן ייצאו מובהקות בטעות.
בדיקת השערות עם שונות לא ידועה
כאשר השונות באוכלוסייה לא ידועה, אנחנו צריכים לאמוד אותה מתוך המדגם. במקרה כזה משתמשים בשונות המדגם:
\[s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})^2\]החלוקה ב-$(n-1)$ במקום ב-$n$ נובעת מאיבוד דרגת חופש בחישוב הממוצע, מה שהופך את $S^2$ לאומד חסר הטיה של $\sigma^2$.
שני מקרים עיקריים
1. מדגם גדול (n > 30)
כאשר המדגם גדול מספיק, שונות המדגם נותנת קירוב טוב לשונות האוכלוסייה. במקרה כזה:
\[Z = \frac{\bar{X} - \mu_0}{S/\sqrt{n}} \sim \mathcal{N}(0,1)\]ניתן להשתמש בהתפלגות הנורמלית הסטנדרטית לחישוב p-values.
2. מדגם קטן (n ≤ 30)
כאשר המדגם קטן והאוכלוסייה מתפלגת נורמלית, הסטטיסטי:
\[T = \frac{\bar{X} - \mu_0}{S/\sqrt{n}}\]מתפלג לפי התפלגות t עם $(n-1)$ דרגות חופש:
\[T \sim t_{n-1}\]המבחן הזה נקרא One Sample t-test.
התפלגות t
- דומה להתפלגות הנורמלית הסטנדרטית אך עם זנבות כבדים יותר
- ממורכזת סביב 0
- כאשר דרגות החופש שואפות לאינסוף, התפלגות t שואפת להתפלגות נורמלית סטנדרטית
דוגמה: קצב לב של ספורטאים
נתונים: באוכלוסייה הכללית, קצב הלב הממוצע הוא 70 פעימות לדקה. רוצים לבדוק האם לספורטאים קצב לב נמוך יותר.
מדגם: 15 ספורטאים עם ממוצע קצב לב $\bar{X} = 65$ וסטיית תקן $S = 8$.
השערות:
- $H_0: \mu = 70$
- $H_1: \mu < 70$
חישוב הסטטיסטי:
\[T = \frac{65 - 70}{8/\sqrt{15}} = \frac{-5}{8/3.87} = \frac{-5}{2.07} = -2.42\]p-value: עבור התפלגות t עם 14 דרגות חופש:
\[p\text{-value} = P(T_{14} < -2.42) = 0.015\]מסקנה: ברמת מובהקות 0.05, דוחים את $H_0$. לספורטאים קצב לב נמוך באופן מובהק מהאוכלוסייה הכללית.
הערות חשובות
- במדגם קטן עם שונות לא ידועה, חובה להניח שהאוכלוסייה מתפלגת נורמלית
- ככל שגודל המדגם גדל, ההבדל בין התפלגות t להתפלגות נורמלית קטן
- במבחן תמיד יש לציין את מספר דרגות החופש
בעיית ההשוואות המרובות
כאשר אנו מבצעים בדיקות סטטיסטיות מרובות, ההסתברות למצוא לפחות תוצאה מובהקת אחת במקרה עולה. זוהי בעיית ההשוואות המרובות.
- אם בוחנים 200 השערות ברמת מובהקות α = 0.05, כ-10 תוצאות יהיו מובהקות במקרה בלבד
- זה מוביל לתגליות שקריות ושגיאות מסוג I
- פתרון: שימוש בשיטות תיקון או התמקדות בהשערה אחת מוגדרת מראש
דוגמה: פול התמנון
- בחירת תוצאות המונדיאל על ידי כלבה, דולפין ואריה
- אם בוחנים מספיק השוואות, מישהו יצא מובהק סטטיסטית
- הקשר הלוגי נקרא “בעיית ההשוואות המרובות”
בדיקת השערות עם שונות לא ידועה - מקרה מדגם קטן
כאשר שונות האוכלוסייה לא ידועה וגודל המדגם קטן:
שונות המדגם (אומד חסר התאיה):
\[s^2 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}\]סטטיסטי הבדיקה:
\[t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}}\]התפלגות: $t \sim t_{n-1}$ (התפלגות t עם n-1 דרגות חופש)
דרגות חופש
- מושג: מספר פיסות המידע הבלתי תלויות
- למה n-1? דרגת חופש אחת “נאבדת” בחישוב הממוצע
- הופך את שונות המדגם לאומד חסר התאיה של שונות האוכלוסייה
מאפייני התפלגות t
- דומה להתפלגות נורמלית סטנדרטית אך עם זנבות כבדים יותר
- מתקרבת להתפלגות נורמלית כאשר דרגות החופש ← ∞
- פרמטר: דרגות חופש (df = n-1)
פונקציית צפיפות הסתברות:
\[f(t) = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{t^2}{\nu}\right)^{-\frac{\nu+1}{2}}\]כאשר ν = דרגות חופש
דוגמה: מבחן t למדגם אחד
בעיה: בדיקה האם לספורטאים דופק נמוך יותר מהאוכלוסייה הכללית (μ₀ = 70 פעימות לדקה)
נתונים:
- גודל מדגם: n = 15 ספורטאים
- ממוצע מדגם: $\bar{x} = 65$ פעימות לדקה
- סטיית תקן מדגם: s = 8 פעימות לדקה
השערות:
- $H_0: \mu = 70$
- $H_1: \mu < 70$ (מבחן חד-צדדי)
סטטיסטי הבדיקה: \(t = \frac{65 - 70}{8/\sqrt{15}} = \frac{-5}{2.07} = -2.42\)
תוצאה:
- df = 14
- p-value = 0.015
- מסקנה: דוחים H₀ ברמת α = 0.05 (לספורטאים דופק נמוך יותר באופן מובהק)
השוואה: שונות ידועה מול שונות לא ידועה
| היבט | שונות ידועה | שונות לא ידועה |
|---|---|---|
| סטטיסטי הבדיקה | $Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}}$ | $t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}}$ |
| התפלגות | נורמלית סטנדרטית | התפלגות t |
| דרגות חופש | לא רלוונטי | n-1 |
| הנחות | σ ידוע | σ לא ידוע, נורמליות נדרשת למדגמים קטנים |
בדיקת השערות לשתי אוכלוסיות
הגדרה לשתי אוכלוסיות
פרמטרי אוכלוסייה:
- אוכלוסייה 1: תוחלת μ₁, שונות σ₁²
- אוכלוסייה 2: תוחלת μ₂, שונות σ₂²
סטטיסטיקות מדגם:
- מדגם 1: גודל n₁, ממוצע $\bar{x}_1$
- מדגם 2: גודל n₂, ממוצע $\bar{x}_2$
הנחת אי-תלות
דרישה קריטית: המדגמים חייבים להיות בלתי תלויים
- ללא זיווג (בעל-אישה, אחים)
- ללא מדידות חוזרות על אותם נבדקים
- דגימה אקראית מאוכלוסיות שונות
דגימות תלויות (תצוגה מקדימה)
כאשר המדגמים קשורים:
- מדידות לפני/אחרי על אותם נבדקים
- עיצוב זוגות תואמים
- יתרון: מפחית שונות, מגביר כוח סטטיסטי
- דוגמה: משקל לפני ואחרי דיאטה (90 ק”ג ← 87 ק”ג)
דוגמאות
1. השוואת שכר רופאים לרופאות
- מדגם: 128 רופאות, ממוצע 15,200 ₪
- מדגם: 128 רופאים, ממוצע 14,000 ₪
- שאלה: האם ההבדל מובהק סטטיסטית?
2. תרופה חדשה ללחץ דם
- קבוצה 1: 20 חולים עם תרופה חדשה, ממוצע 130 מ”מ כספית
- קבוצה 2: 20 חולים עם תרופה קיימת, ממוצע 135 מ”מ כספית
- שאלה: האם התרופה החדשה יעילה יותר?
מושגי מפתח
- בדיקות מרובות: זהירות מעלייה בשגיאות מסוג I
- התפלגות t: נעשה בה שימוש כאשר השונות לא ידועה ו-n ≤ 30
- דרגות חופש: n-1 למבחנים למדגם אחד
- אי-תלות: הנחה קריטית להסקה תקפה
- גודל מדגם: משפיע על בחירת סטטיסטי הבדיקה וההתפלגות