שאלה 1: תנועה על מסלול אליפטי
וקטור המקום של חלקיק מסיבי נתון על ידי:
\[\vec{r}(t) = a\cos(\omega t)\hat{x} + b\sin(\omega t)\hat{y}\]
משוואת אליפסה קנונית (זוהי אליפסה אשר מרכזה יושב על ראשית הצירים ושני ציריה מתלכדים עם ציר ה-x וציר ה-y) נתונה על ידי:
\[\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1\]הוכיחו כי החלקיק נע על גבי אליפסה קנונית.
הראו שמתקיים:
\[\vec{r} \cdot \vec{p} = \frac{1}{2}m(b^2 - a^2)\sin(2\omega t)\]כפי שראינו בכיתה, האנרגיה הקינטית של גוף שמסתו $m$ הנע במהירות $v$ היא גודל סקלרי המוגדר דרך:
\[E_k = \frac{p^2}{2m} = \frac{1}{2}mv^2\]קבוע של התנועה הוא קומבינציה (בדרך כלל מכפלה) של משתנים דינמיים שכל אחד מהם תלוי בזמן, אך הקומבינציה בכללותה אינה תלויה בזמן.
קבלו את האנרגיה הקינטית של החלקיק הנע על גבי האליפסה כתלות בזמן. הראו שבמקרה של תנועה מעגלית (a = b), האנרגיה הקינטית היא קבוע של התנועה ומצאו אותו.
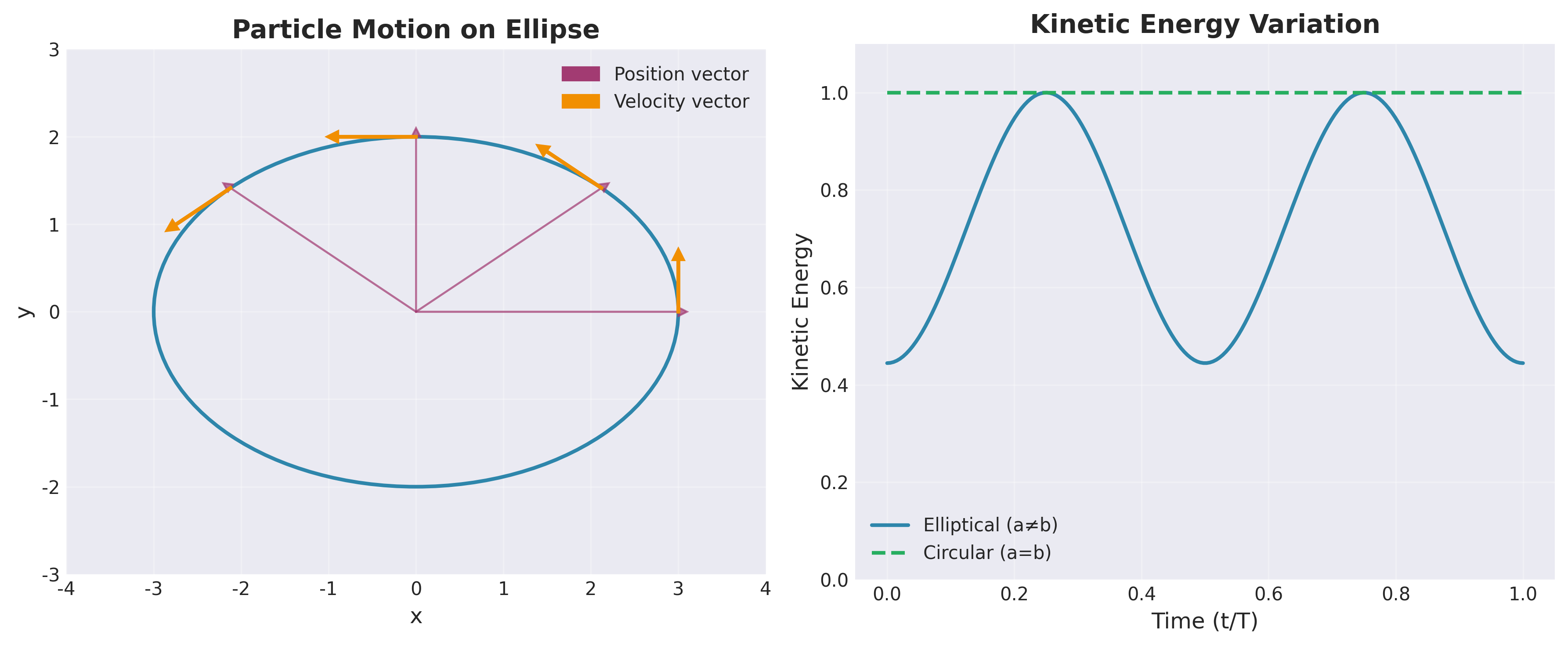
סעיף א - הוכחת תנועה על אליפסה
מוקטור המקום נתון:
\[\vec{r}(t) = a\cos(\omega t)\hat{x} + b\sin(\omega t)\hat{y}\]מכאן נקבל את רכיבי המיקום:
- $x(t) = a\cos(\omega t)$
- $y(t) = b\sin(\omega t)$
כדי להוכיח שהחלקיק נע על אליפסה, נחשב:
\[\frac{x^2}{a^2} = \frac{a^2\cos^2(\omega t)}{a^2} = \cos^2(\omega t)\] \[\frac{y^2}{b^2} = \frac{b^2\sin^2(\omega t)}{b^2} = \sin^2(\omega t)\]לכן:
\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = \cos^2(\omega t) + \sin^2(\omega t) = 1\]קיבלנו את משוואת האליפסה הקנונית, מכאן שהחלקיק אכן נע על מסלול אליפטי.
סעיף ב - מכפלה סקלרית של מיקום ותנע
ראשית, נמצא את וקטור המהירות על ידי גזירת וקטור המקום:
\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -a\omega\sin(\omega t)\hat{x} + b\omega\cos(\omega t)\hat{y}\]וקטור התנע:
\[\vec{p}(t) = m\vec{v}(t) = -ma\omega\sin(\omega t)\hat{x} + mb\omega\cos(\omega t)\hat{y}\]כעת נחשב את המכפלה הסקלרית:
\[\begin{aligned} \vec{r} \cdot \vec{p} &= [a\cos(\omega t)][-ma\omega\sin(\omega t)] + [b\sin(\omega t)][mb\omega\cos(\omega t)] \\ &= -ma^2\omega\cos(\omega t)\sin(\omega t) + mb^2\omega\sin(\omega t)\cos(\omega t) \\ &= m\omega\sin(\omega t)\cos(\omega t)(b^2 - a^2) \end{aligned}\]תזכורת: $\sin(2\alpha) = 2\sin(\alpha)\cos(\alpha)$, לכן $\sin(\alpha)\cos(\alpha) = \frac{1}{2}\sin(2\alpha)$
\[\vec{r} \cdot \vec{p} = \frac{1}{2}m\omega(b^2 - a^2)\sin(2\omega t)\]כפי שנדרשנו.
משמעות פיזיקלית: המכפלה הסקלרית בין מיקום לתנע מתנדנדת בתדירות כפולה (2ω) ומתאפסת כאשר a = b (תנועה מעגלית).
סעיף ג - אנרגיה קינטית וקבועי תנועה
האנרגיה הקינטית מוגדרת כך:
\[\boxed{E_k = \frac{1}{2}m v^2 = \frac{1}{2}m(\vec{v} \cdot \vec{v})}\]נחשב את גודל המהירות בריבוע:
\[v^2 = v_x^2 + v_y^2 = \boxed{a^2\omega^2\sin^2(\omega t) + b^2\omega^2\cos^2(\omega t)}\]נציב בנוסחה לאנרגיה קינטית:
\[E_k(t) = \frac{1}{2}m\omega^2\left[a^2\sin^2(\omega t) + b^2\cos^2(\omega t)\right]\]למקרה של תנועה מעגלית (a = b):
\[E_k = \frac{1}{2}m\omega^2a^2[\sin^2(\omega t) + \cos^2(\omega t)] = \boxed{\frac{1}{2}m\omega^2a^2}\]זה אכן קבוע. מכאן שהאנרגיה הקינטית במקרה של תנועה מעגלית אינה תלויה בזמן.
הסבר: בתנועה מעגלית קצובה, גודל המהירות קבוע (רק הכיוון משתנה), ולכן האנרגיה הקינטית נשארת קבועה. לעומת זאת, בתנועה אליפטית כללית, גודל המהירות משתנה לאורך המסלול - מקסימלי בציר הקצר ומינימלי בציר הארוך.
שאלה 2: מתקף וכוחות
על מסה של חמישה טון הנעה בקו ישר פעל כוח שהאיץ אותה ממהירות של 500 קמ”ש למהירות של 700 קמ”ש במשך שתי דקות. מהו המתקף שהכוח הפעיל על המסה? מהו המתקף שהמסה מפעילה על הכוח?
בתום הזמן הזה המסה התרסקה על הארץ בתהליך שארך עשירית השנייה. מהו הכוח הממוצע שכדור הארץ הפעיל על המסה בזמן זה?
כמה אנרגיה קינטית הרוויחה המסה בתהליך ההאצה?
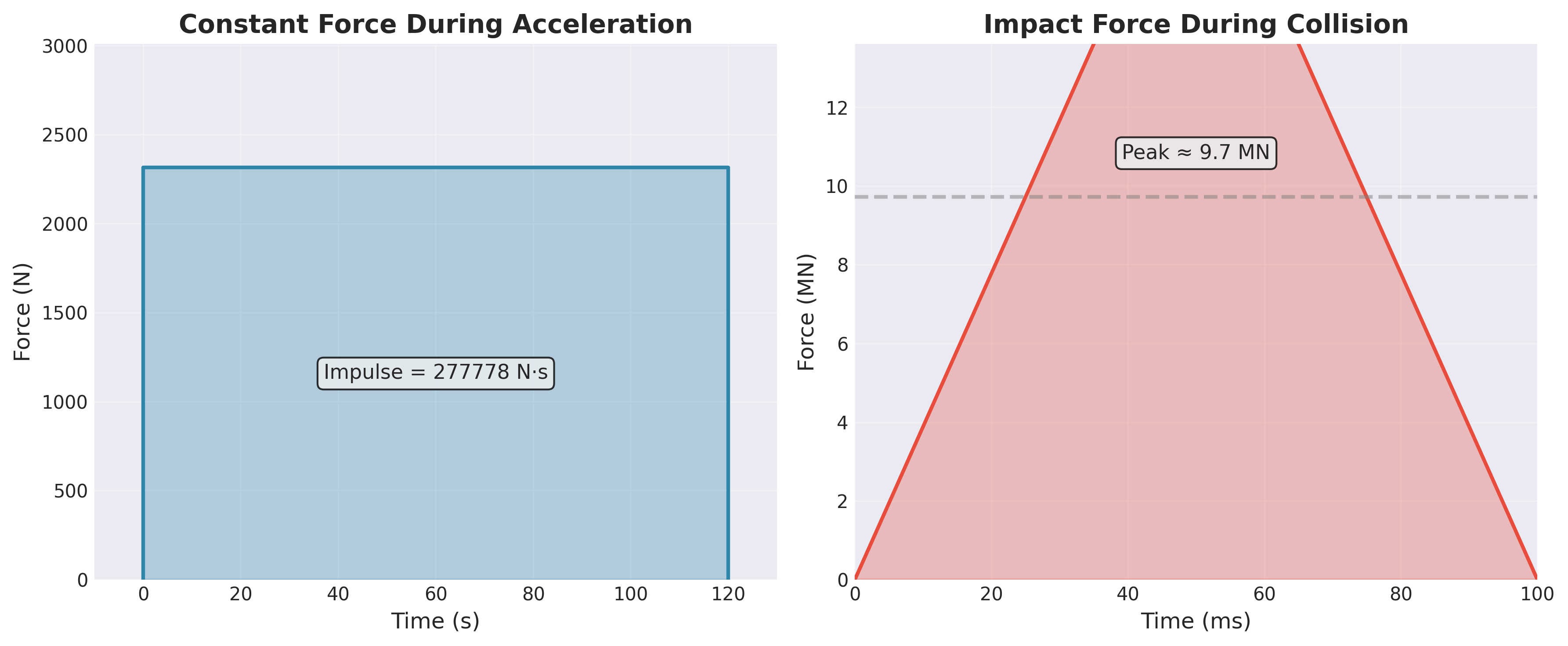
המתקף מוגדר כשינוי בתנע:
\[J = \Delta p = m(v_2 - v_1) \, \mathrm{N \cdot s}\]נמיר את היחידות ליחידות סטנדרטיות:
-
מסה:
\[m = 5000 \, \mathrm{kg}\] -
מהירות התחלתית:
\[v_1 = 500 \, \mathrm{km/h} = \frac{500 \times 1000}{3600} \approx 138.89 \, \mathrm{m/s}\] -
מהירות סופית:
\[v_2 = 700 \,\mathrm{km/h} = \frac{700 \times 1000}{3600} \approx 194.44 \, \mathrm{m/s}\] -
זמן:
\[\Delta t = 2 \mathrm{min} = 2 \times 60 = 120 \, \mathrm{s}\]
נציב את הערכים לחישוב המתקף:
סעיף א - חישוב המתקף
\[\begin{aligned} J &= m(v_2 - v_1) \\[5pt] &= 5000 \times (194.44 - 138.89)\\[5pt] &\approx \boxed{277,750 \, \mathrm{N \cdot s}} \end{aligned}\]ביחס למתקף שהמסה מפעילה על הכוח, נשתמש בחוק השלישי של ניוטון:
לפי החוק השלישי של ניוטון: המתקף שהמסה מפעילה על הכוח שווה בגודלו והפוך בכיוונו:
\[\boxed{J_{\text{mass on force}} = -277,750 \text{ N·s}}\]סעיף ב - כוח ממוצע בהתרסקות
הנוסחה לכוח ממוצע היא:
\[F_{\text{avg}} = \frac{\Delta p}{\Delta t}\]בהתרסקות נתוני המערכת:
-
מהירות התחלתית (המהירות לפני ההתרסקות):
\[v_i = 194.44 \,\mathrm{m/s}\] -
מהירות סופית: (המסה נעצרת)
\[v_f = 0\] -
זמן התרסקות:
\[\Delta t = 0.1 \mathrm{s}\]
שינוי התנע:
\[\Delta p = m(v_f - v_i) = 5000 \times (0 - 194.44) = -972,200 \text{ kg·m/s}\]הכוח הממוצע:
\[F_{\text{avg}} = \frac{\Delta p}{\Delta t} = \frac{-972,200}{0.1} = -9,722,000 \text{ N} = \boxed{-9.72 \text{ MN}}\]הסימן השלילי מציין שהכוח פועל בכיוון ההפוך לתנועה (כוח בלימה).
זה כוח עצום - אל תתרסקו במהירות גבוהה.
סעיף ג - שינוי באנרגיה קינטית
נחשב את ההפרש באנרגיה הקינטית לפני ואחרי ההאצה.
אנרגיה קינטית התחלתית:
\[E_{k1} = \frac{1}{2}mv_1^2 = \frac{1}{2} \times 5000 \times (138.89)^2 = 48,229,167 \text{ J} \approx 48.23 \text{ MJ}\]אנרגיה קינטית סופית:
\[E_{k2} = \frac{1}{2}mv_2^2 = \frac{1}{2} \times 5000 \times (194.44)^2 = 94,618,519 \text{ J} \approx 94.62 \text{ MJ}\]השינוי באנרגיה הקינטית:
\[\begin{aligned} \Delta E_k &= E_{k2} - E_{k1} \\[5pt] &= 94.62 - 48.23 \\[5pt] &= \boxed{46.39 \text{ MJ}} \end{aligned}\]הסבר: האנרגיה שהושקעה בהאצת המסה (46.39 מגה-ג׳אול) הופכת לאנרגיה קינטית. בהתרסקות, כל האנרגיה הזו (94.62 MJ) הופכת לחום, עיוות, וצורות אנרגיה אחרות.
שאלה 3: כוחות מרכזיים
על חלקיק מסיבי פועל כוח מרכזי מהצורה:
\[\vec{F}(r) = f(r)\hat{r}\]
הסבירו מה פירוש כוח מרכזי ומדוע הביטוי למעלה הוא הביטוי הכללי ביותר שאפשר לרשום עבור כוח מרכזי.
הראו שאפשר לרשום את הביטוי עבור כוח מרכזי גם כ:
\[\vec{F}(r) = \frac{f(r)}{r}\vec{r}\]הראו שבשני מימדים אפשר לרשום את הכוח המרכזי גם כך:
\[\begin{aligned} \vec{F}(x,y) = &f(\sqrt{x^2 + y^2})\cos(\tan^{-1}(y/x))\hat{x} \\ & + f(\sqrt{x^2 + y^2})\sin(\tan^{-1}(y/x))\hat{y} \end{aligned}\]
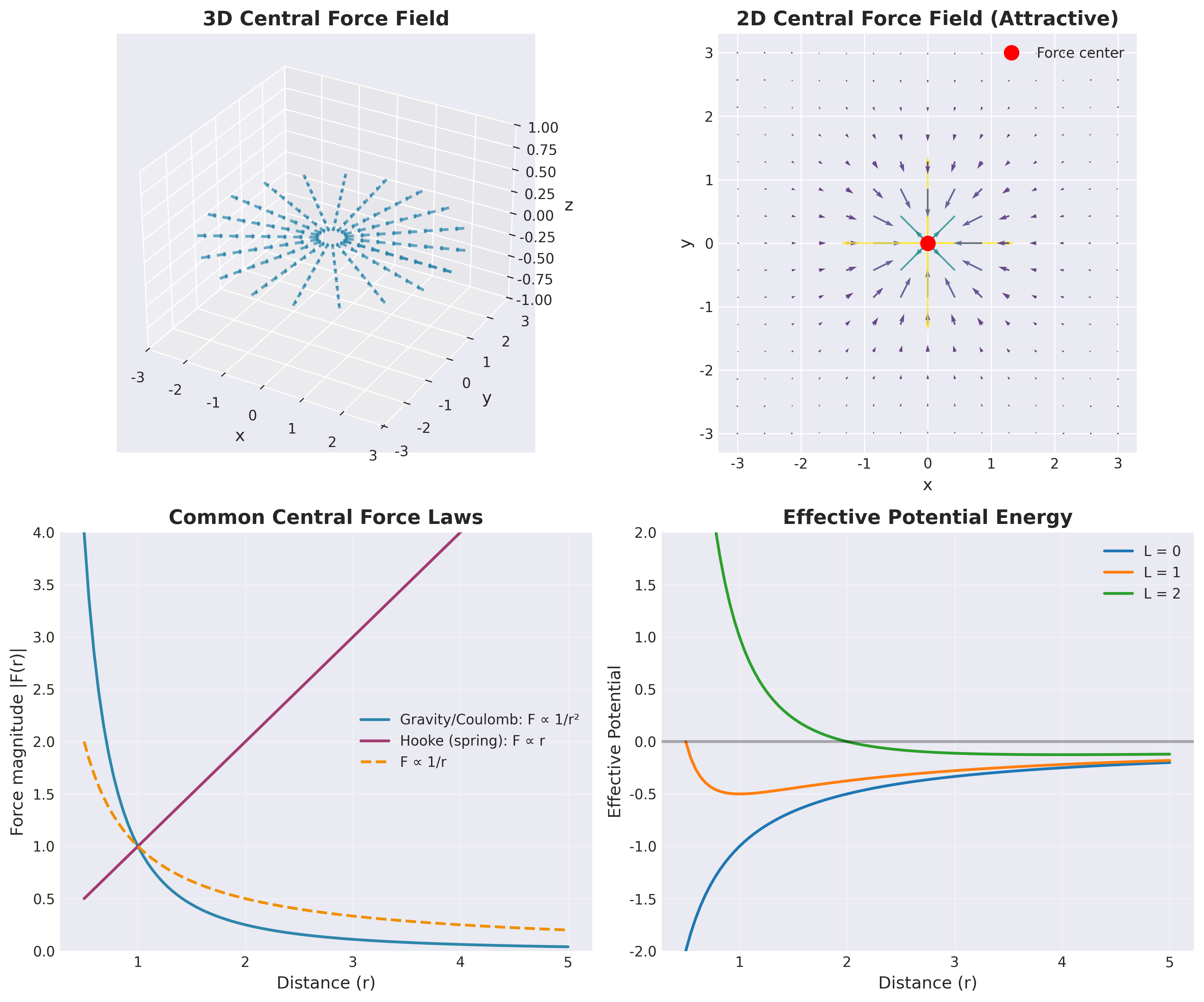
(תודה למודל החדש של Anthropic על הפתרון הבא)
סעיף א - הגדרת כוח מרכזי
כוח מרכזי הוא כוח שמקיים שני תנאים:
- כיוון הכוח: הכוח פועל תמיד לאורך הקו המחבר בין החלקיק למרכז הכוח (בדרך כלל הראשית)
- גודל הכוח: גודל הכוח תלוי רק במרחק מהמרכז, לא בכיוון
הביטוי $\vec{F}(r) = f(r)\hat{r}$ הוא הכללי ביותר כי:
- $\hat{r}$ מבטיח שהכיוון תמיד רדיאלי (מהמרכז החוצה או פנימה)
- $f(r)$ היא פונקציה כללית של המרחק בלבד (יכולה להיות חיובית או שלילית)
- אין תלות בזוויות - רק במרחק
דוגמאות לכוחות מרכזיים:
- כוח הכבידה: $f(r) = -\frac{GMm}{r^2}$
- כוח קולון: $f(r) = \frac{kq_1q_2}{r^2}$
- כוח הוק (קפיץ רדיאלי): $f(r) = -k(r-r_0)$
סעיף ב - ייצוג חלופי
נזכור ש:
\[\hat{r} = \frac{\vec{r}}{r}\]לכן:
\[\vec{F}(r) = f(r)\hat{r} = f(r) \cdot \frac{\vec{r}}{r} = \frac{f(r)}{r}\vec{r}\]זה ייצוג שקול - במקום להשתמש בווקטור היחידה הרדיאלי, משתמשים בווקטור המיקום עצמו ומנרמלים אותו.
סעיף ג - ייצוג בקואורדינטות קרטזיות
בקואורדינטות קרטזיות:
- $r = \sqrt{x^2 + y^2}$
- $\theta = \tan^{-1}(y/x)$
וקטור היחידה הרדיאלי בקואורדינטות קרטזיות:
\[\hat{r} = \cos\theta\hat{x} + \sin\theta\hat{y}\]כאשר:
- $\cos\theta = \cos(\tan^{-1}(y/x)) = \frac{x}{\sqrt{x^2 + y^2}}$
- $\sin\theta = \sin(\tan^{-1}(y/x)) = \frac{y}{\sqrt{x^2 + y^2}}$
לכן:
\[\vec{F}(x,y) = f(r)\hat{r} = f[\sqrt{x^2 + y^2}](\cos(\tan^{-1}(y/x))\hat{x} + \sin(\tan^{-1}(y/x))\hat{y})\]הערה: בפועל, נוח יותר להשתמש בביטוי:
\[\vec{F}(x,y) = f(\sqrt{x^2 + y^2}) \cdot \frac{x\hat{x} + y\hat{y}}{\sqrt{x^2 + y^2}}\]שאלה 4: התנגשות וחוקי שימור
הראו שחוק שימור האנרגיה וחוק שימור התנע הקווי בהתנגשות מצחית של שתי מסות $m_1, m_2$ הנעות על קו ישר מובילים אל הקשר:
\[v_2 - v_1 = -(u_2 - u_1)\]או:
\[\Delta v = -\Delta u\]כאשר $v_1, v_2$ הן מהירויות המסות (בהתאמה) לפני ההתנגשות, ו-$u_1, u_2$ הן מהירויות המסות (בהתאמה) אחרי ההתנגשות.
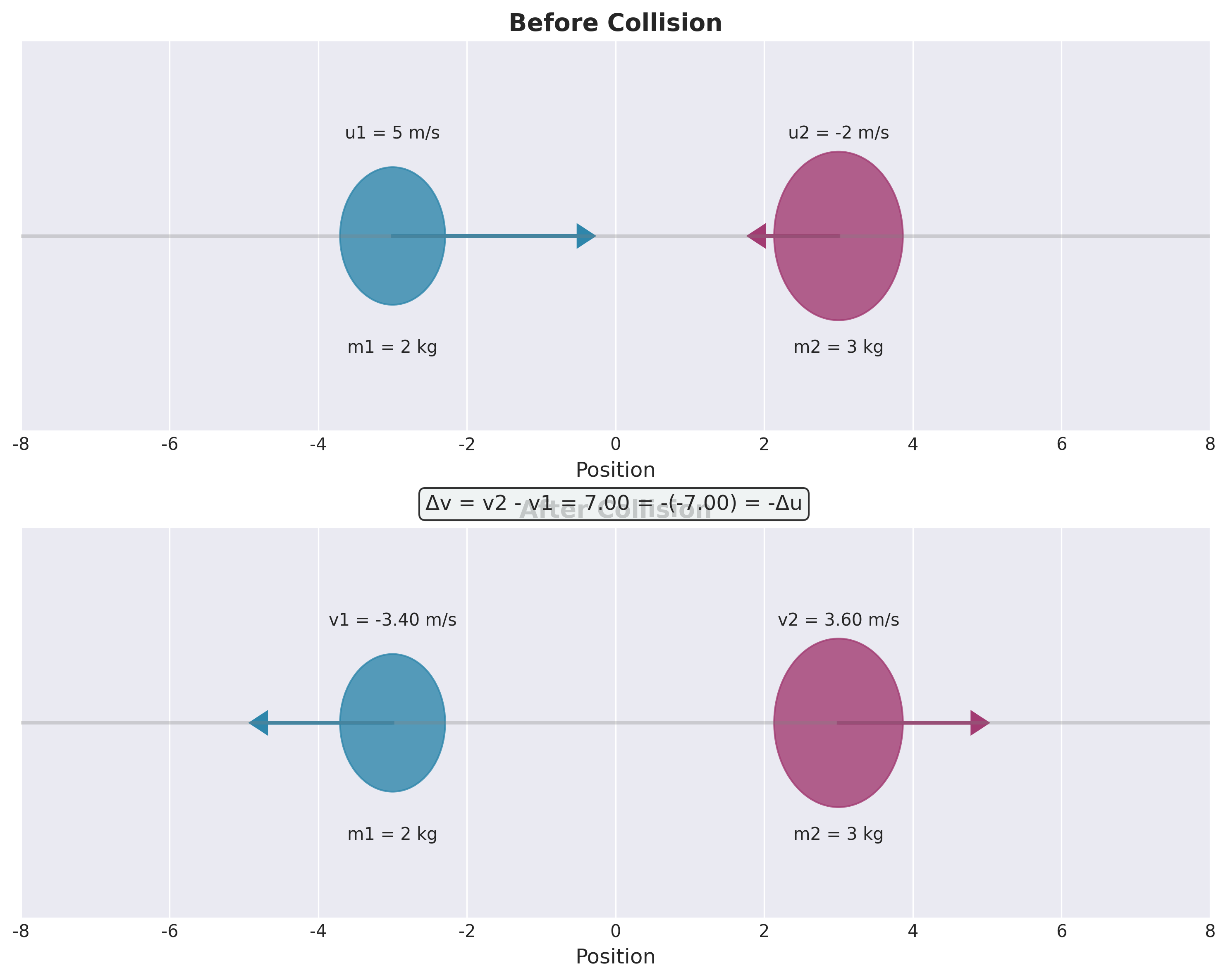
נשתמש בשני חוקי השימור:
1. שימור תנע:
\[m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2\]נסדר מחדש:
\[m_1(u_1 - v_1) = m_2(v_2 - u_2) \quad \tag{1}\]2. שימור אנרגיה (התנגשות אלסטית):
\[\frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2\]נסדר:
\[m_1(u_1^2 - v_1^2) = m_2(v_2^2 - u_2^2)\]נפרק לגורמים:
\[m_1(u_1 - v_1)(u_1 + v_1) = m_2(v_2 - u_2)(v_2 + u_2) \tag{2}\]נחלק משוואה $(2)$ במשוואה $(1)$:
\[\frac{m_1(u_1 - v_1)(u_1 + v_1)}{m_1(u_1 - v_1)} = \frac{m_2(v_2 - u_2)(v_2 + u_2)}{m_2(v_2 - u_2)}\]נקבל:
\[u_1 + v_1 = v_2 + u_2\]נסדר מחדש:
\[v_2 - v_1 = -(u_2 - u_1)\]או:
\[\Delta v = -\Delta u\]המשמעות הפיזיקלית: בהתנגשות אלסטית חד-ממדית, המהירות היחסית בין שני הגופים הופכת את כיוונה אך שומרת על גודלה. נראה שזה תנאי הכרחי לשימור האנרגיה הקינטית בהתנגשות.
שאלה 5: התנגשות פלסטית ומסה מצומצמת
שני גופים שמסתם $m_1, m_2$ נעים זה לעבר זה במהירויות $v_1, v_2$ בהתאמה, ומתנגשים זה בזה בהתנגשות פלסטית. לאחר ההתנגשות הם ממשיכים לנוע יחדיו במהירות $v$.
הראו שהאנרגיה הקינטית שאובדת בתהליך ההתנגשות ניתנת בביטוי:
\[\Delta E_k = \frac{1}{2}\mu(m_1, m_2)(\Delta v)^2\]כאשר $\Delta v = v_1 - v_2$ וכן:
\[\mu(m_1, m_2) = \frac{m_1m_2}{m_1 + m_2}\]היא המסה המצומצמת של שני הגופים.
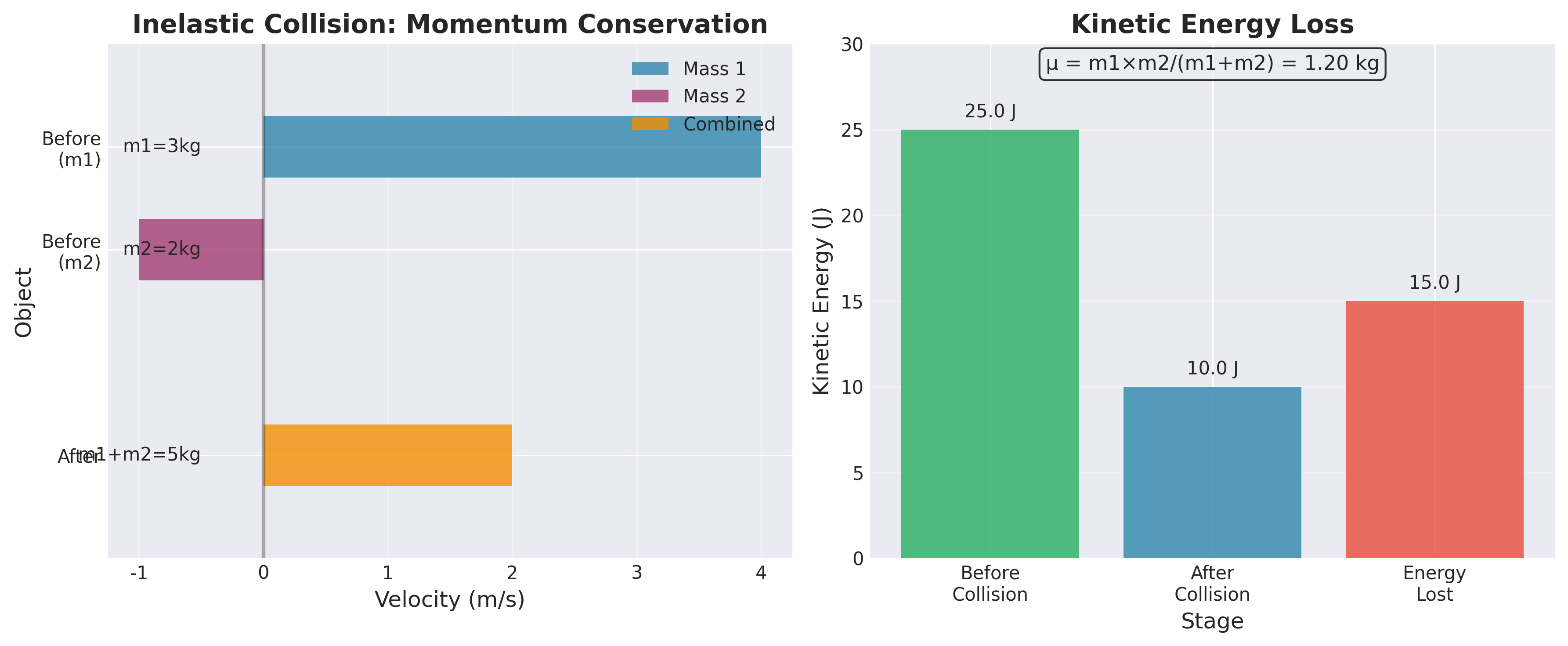
שלב 1: מציאת המהירות הסופית
משימור התנע:
\[m_1v_1 + m_2v_2 = (m_1 + m_2)v\]לכן:
\[v = \frac{m_1v_1 + m_2v_2}{m_1 + m_2}\]שלב 2: חישוב האנרגיה הקינטית ההתחלתית
\[E_{k,i} = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2\]שלב 3: חישוב האנרגיה הקינטית הסופית
\[\begin{aligned} E_{k,f} &= \frac{1}{2}(m_1 + m_2)v^2 \\ &= \frac{1}{2}(m_1 + m_2)\left(\frac{m_1v_1 + m_2v_2}{m_1 + m_2}\right)^2 \\ &= \frac{(m_1v_1 + m_2v_2)^2}{2(m_1 + m_2)} \end{aligned}\]שלב 4: חישוב האובדן באנרגיה
\[\Delta E_k = E_{k,f} - E_{k,i}\]אחרי אלגברה מפורטת (שכוללת פיתוח ריבועים וסידור מחדש) אפשר לכאורה להגיע לביטוי:
\[\Delta E_k = -\frac{1}{2}\frac{m_1m_2}{m_1 + m_2}(v_1 - v_2)^2\]הסימן השלילי מציין אובדן אנרגיה. בערך מוחלט:
\[|\Delta E_k| = \frac{1}{2}\mu(\Delta v)^2\]כאשר $\mu = \frac{m_1m_2}{m_1 + m_2}$ היא המסה המצומצמת.
הסבר פיזיקלי: המסה המצומצמת מייצגת את “המסה האפקטיבית” של מערכת שני הגופים כשבוחנים את התנועה היחסית ביניהם. האנרגיה שאובדת תלויה במהירות היחסית ההתחלתית ובמסה המצומצמת.
שאלה 6: החזרה אלסטית מרצפה
הסבירו לעצמכם: מדוע כדור אלסטי לחלוטין הפוגע ברצפה בזווית $\alpha$ ביחס לאנך לרצפה, חייב לנתר מהרצפה בדיוק באותה זווית ובדיוק באותו גודל של מהירות?
פתרון והסבר
נפרק את המהירות לרכיבים:
- רכיב מאוזן (מקביל לרצפה): $v_x = v\sin\alpha$
- רכיב מאונך (ניצב לרצפה): $v_y = v\cos\alpha$
בהתנגשות אלסטית מושלמת עם רצפה:
- הרכיב המאוזן ($v_x$):
- לא פועל כוח בכיוון המאוזן
- לכן: $v’_x = v_x = v\sin\alpha$
- הרכיב המאונך ($v_y$):
- בהתנגשות אלסטית מושלמת, הרכיב המאונך מתהפך בכיוון
- גודלו נשמר (שימור אנרגיה)
- לכן: $v’_y = -v_y = -v\cos\alpha$ (לכיוון מעלה)
חישוב הזווית והמהירות אחרי ההחזרה:
גודל המהירות:
\[v' = \sqrt{ {v'_x}^2 + {v'_y}^2 } = \sqrt{ (v\sin\alpha)^2 + (v\cos\alpha)^2 } = v\]הזווית ביחס לאנך:
\[\tan \alpha' = \frac{v'_x}{\vert v'_y\vert } = \frac{v\sin \alpha}{v \cos \alpha} = \tan \alpha\]לכן: $\alpha’ = \alpha$
סיכום: בהתנגשות אלסטית מושלמת:
- גודל המהירות נשמר (שימור אנרגיה)
- זווית הפגיעה שווה לזווית ההחזרה (חוק ההחזרה)
מסתבר שזה עיקרון בסיסי באופטיקה גיאומטרית (החזרת אור) ובמכניקה. לא למדתי את הדברים האלה מעולם אבל ככה עולה מגוגל.
שאלה 7: התפוצצות פצצה ושימור תנע
פצצה מתפוצצת בנקודה מסוימת באוויר.
הסבירו מדוע - למרות שפועל כוח חיצוני על הפצצה (כוח הכבידה) - אפשר לומר במידה רבה של אמת שווקטור התנע השקול של כל חלקי הפצצה אחרי ההתפוצצות שווה בקירוב מצוין לווקטור התנע השקול של הפצצה לפני ההתפוצצות?
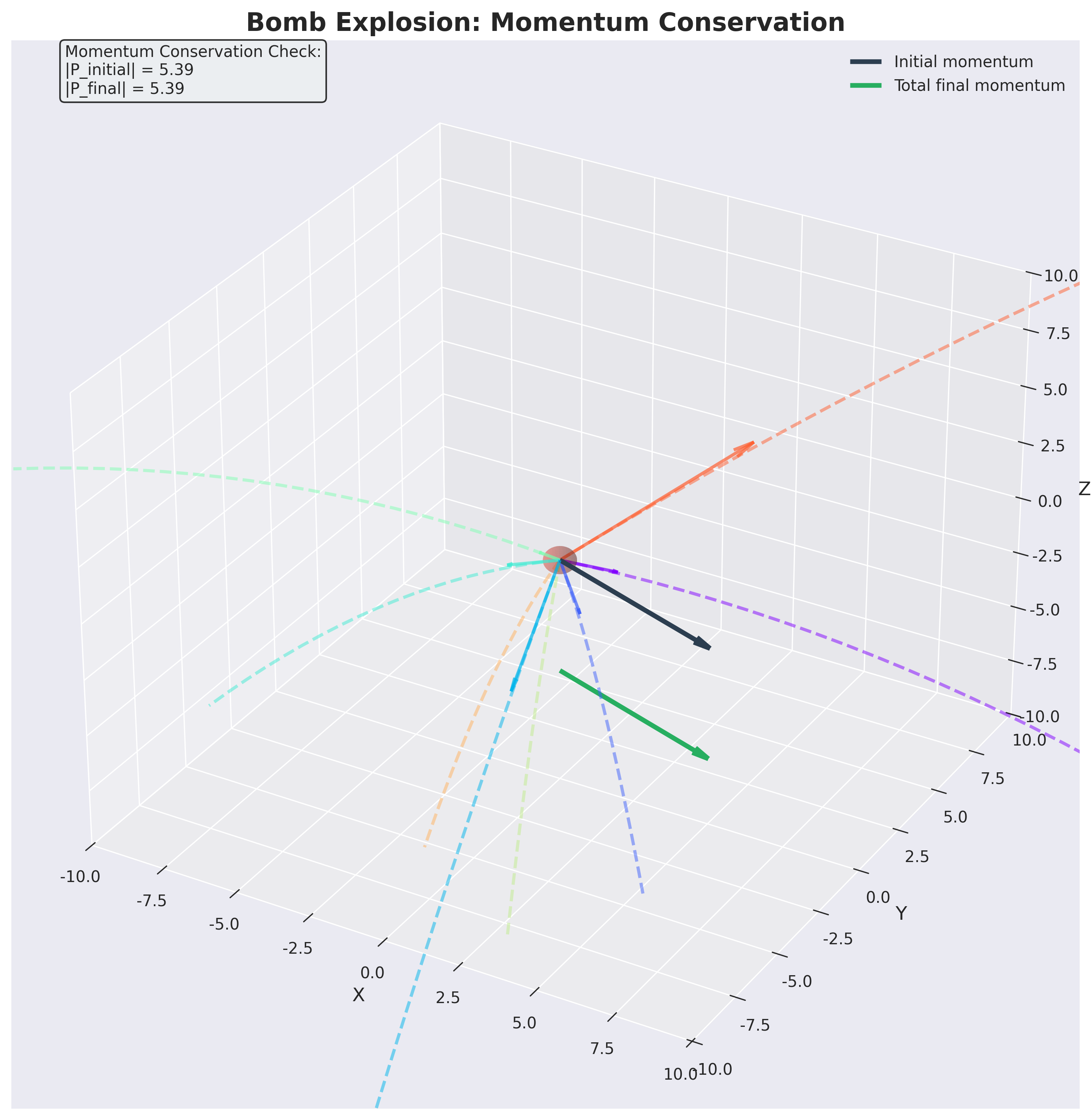
ניתוח הכוחות:
- כוחות פנימיים (הפיצוץ):
- כוחות עצומים בין חלקי הפצצה
- פועלים לזמן קצר מאוד (מילישניות)
- לפי החוק השלישי של ניוטון - מבטלים זה את זה בסכום הכולל
- כוח חיצוני (כבידה):
- $\mathbf{F}_{\text{gravity}} = Mg$ (כאשר M מסת הפצצה)
- פועל באופן רציף
השוואת המתקפים:
המתקף מכוח הכבידה במשך זמן הפיצוץ $\Delta t$:
\[J_{\text{gravity}} = Mg \cdot \Delta t\]כאשר $\Delta t \approx 0.001$ שניות (זמן קצר לפיצוץ), המתקף זניח.
לעומת זאת, השינוי בתנע של חלקקי הפצצה לאחר הפיצוץ הוא עצום:
\[\Delta p_{\text{fragments}} \gg J_{\text{gravity}}\]מסקנה: בזמן הקצר של הפיצוץ, אפשר להזניח את השפעת הכבידה ולהתייחס למערכת כמבודדת. לכן:
\[\vec{P}_{i} \approx \vec{P}_{f}\]הסבר מתמטי מפורט:
נניח שהפצצה בעלת מסה $M$ נעה במהירות $\vec{V}$ לפני הפיצוץ.
התנע לפני הפיצוץ:
\[\vec{P}_{i} = M\vec{V}\]אחרי הפיצוץ, הפצצה מתפרקת ל-n חלקים עם מסות $m_i$ ומהירויות $\vec{v}_i$:
\[\vec{P}_{f} = \sum_{i=1}^{n} m_i\vec{v}_i\]עקרון הקירוב:
-
זמן הפיצוץ:
\[\Delta t \approx 10^{-3} \, \mathrm{s}\] -
שינוי התנע מכבידה:
\[\Delta P_g = Mg\Delta t \approx 10^{-2}M\] -
שינוי תנע מומצע של רסיס:
\[\Delta P_{\text{frag}} \approx m_i \times 1000 \, \mathrm{m/s}\]
היחס:
\[\frac{\Delta P_g}{\Delta P_{\text{frag}}} \approx \frac{10^{-2}M}{m_i \times 1000} \ll 1\]דוגמה מספרית:
- פצצה במסה 100 ק”ג
- זמן פיצוץ: 0.001 שניות
-
מתקף הכבידה:
\[J_g = 100 \times 10 \times 0.001 = 1 \, \mathrm{kg \cdot m/s}\] -
שינוי תנע טיפוסי של רסיס:
\[\Delta P_{\text{frag}} \approx 0.1 \, \mathrm{kg} \times 1000 \, \mathrm{m/s} = 100 \, \mathrm{kg \cdot m/s}\]
היחס: $\frac{1}{1000} = 0.001$ - זניח לחלוטין!
יישומים מעשיים:
- בליסטיקה: חישוב מסלולי רסיסים
- בטיחות: הערכת טווח סיכון
- פירוטכניקה: תכנון זיקוקים (תבנית סימטרית)
סיכום עקרונות מרכזיים מהתרגיל
1. תנועה הרמונית ומסלולים
- שילוב של תנועות הרמוניות בכיוונים מאונכים יוצר מסלולים אליפטיים
- במקרה המיוחד של משרעות שוות - מתקבלת תנועה מעגלית
2. חוקי שימור בהתנגשויות
- התנגשות אלסטית: נשמרים גם תנע וגם אנרגיה קינטית
- התנגשות פלסטית: נשמר רק התנע, אנרגיה “אובדת” (הופכת לחום ולעיוות)
3. כוחות מרכזיים
- כוחות שהכיוון שלהם רדיאלי והגודל שלהם תלוי רק במרחק
- חשובים מאוד בפיזיקה: כבידה, כוחות חשמליים, ועוד
4. מתקף וכוחות
- מתקף = שינוי בתנע = $\int F dt$
- בזמנים קצרים, כוחות גדולים יוצרים מתקפים משמעותיים (הדוגמה בשיעור הייתה לגבי קפיצה ממגדל - מזרן עבה מאריך את זמן ההתרסקות - אם הזמן גדל פי 100, הכוח הממוצע קטן פי 100)
טיפים שספק יעזרו
- המרת יחידות: תמיד וודאו שכל הגדלים באותן יחידות (SI עדיף)
- בדיקת ממדים: וודאו שהתוצאה הסופית ביחידות הנכונות
- בדיקת סבירות: האם התוצאה הגיונית? (למשל, אנרגיה חיובית)
- ציור דיאגרמות: במיוחד בבעיות התנגשות וכוחות
- שימוש בחוקי שימור: לעתים קרובות הדרך הקלה ביותר לפתרון