שיעור 13 פתרון בחינת אמצע לדוגמה

מבנה הבחינה והנחיות כלליות

מועדי הבחינה

• מועד א’: 14 ביולי.
• מועד ב’: 14 באוגוסט.
• מועד ג’: יתקיים במועד נפרד ומיועד בעיקר למשרתי מילואים.
• כללי: ניתן לגשת לשני המועדים (א’ ו-ב’), והציון הגבוה מביניהם הוא הקובע.

פורמט הבחינה

• הבחינה מנוהלת על ידי מדור הבחינות של אוניברסיטת בר-אילן.
• מבנה: 8 שאלות אמריקאיות, יש לענות על 7 שאלות בלבד.
• ניקוד: כל שאלה שווה 15 נקודות.
  • 4 שאלות נכונות = 60 נקודות.
  • 5 שאלות נכונות = 75 נקודות.
  • 6 שאלות נכונות = 90 נקודות.
  • 7 שאלות נכונות = 100 נקודות.
• אופן הבדיקה: התוכנה בודקת את 7 התשובות הראשונות. אם עניתם על 8 שאלות, יש למחוק את השאלה שאינכם רוצים שתיבדק.
• ערבול: סדר השאלות והתשובות (המסיחים) מעורבל, כך שכל סטודנט מקבל טופס ייחודי.
• משך הבחינה: 3 שעות.
• חומר עזר: ניתן להכניס כל חומר עזר כתוב (דפי נוסחאות, סיכומים). לא מומלץ להביא ספרים.
• מחשבון: מותר להשתמש במחשבון מדעי פשוט (לחישוב סינוס, קוסינוס וכו’). אסור להשתמש במחשבונים המסוגלים לפתור משוואות, אינטגרלים או בעיות פיזיקליות מורכבות.
• איסורים: אסור להכניס אמצעי תקשורת מכל סוג.

חומר הלימוד לבחינה

הבחינה כוללת את כל הנושאים שנלמדו במהלך הסמסטר:

1. קינמטיקה: וקטורי מקום, מהירות ותאוצה.
2. דינמיקה: שלושת חוקי ניוטון.
3. מתקף ותנע.
4. עבודה ואנרגיה.

נושאים שלא נכללים בבחינה:

• חישוב אינטגרלים מסלוליים.
• מכניקת זורמים.
• מומנטים ותנע זוויתי.

שיעורי תגבור

• יתקיימו שיעורי תגבור נוספים לפני הבחינה, בתיאום עם הסטודנטים.
• שיעור תגבור יתקיים אם יהיו לפחות שני סטודנטים המעוניינים בכך.
• בשיעורי התגבור המרצה יענה על שאלות ספציפיות של הסטודנטים.

פתרון שאלות לדוגמה

שאלה 1: תנועת מסטיק על גלגל אופניים (ציקלואידה)

הבעיה: מסטיק נדבק לצמיג של גלגל אופניים ברדיוס $a$. הקואורדינטות של המסטיק נתונות על ידי:

\[x(t) = a(\theta(t) - \sin(\theta(t)))\] \[y(t) = a(1 - \cos(\theta(t)))\]

כאשר $\theta(t)$ היא זווית הסיבוב של הגלגל התלויה בזמן.

השאלה: מהו וקטור היחידה המצביע על כיוון המהירות של המסטיק?

פתרון:

1. וקטור המקום: נרשום את וקטור המקום $\vec{r}(t)$ של המסטיק:

   \[\vec{r}(\theta) = a(\theta - \sin\theta)\hat{x} + a(1 - \cos\theta)\hat{y}\]

2. וקטור המהירות: נגזור את וקטור המקום לפי הזמן $t$ כדי למצוא את וקטור המהירות $\vec{v}(t)$, תוך שימוש בכלל השרשרת ($\frac{d}{dt} = \frac{d\theta}{dt} \frac{d}{d\theta} = \dot{\theta} \frac{d}{d\theta}$):

   \[\vec{v}(\theta) = \frac{d\vec{r}}{dt} = \dot{\theta} \frac{d\vec{r}}{d\theta}\] \[\vec{v}(\theta) = a\dot{\theta}(1 - \cos\theta)\hat{x} + a\dot{\theta}(\sin\theta)\hat{y}\]

   נוציא את הגורם המשותף $a\dot{\theta}$:

   \[\vec{v}(\theta) = a\dot{\theta} \left[ (1 - \cos\theta)\hat{x} + \sin\theta\hat{y} \right]\]

3. גודל המהירות: נחשב את הגודל (נורמה) של וקטור המהירות, $\vert \vec{v} \vert$:

   \[\vert \vec{v} \vert = \sqrt{(v_x)^2 + (v_y)^2} = \sqrt{(a\dot{\theta}(1-\cos\theta))^2 + (a\dot{\theta}\sin\theta)^2}\] \[\vert \vec{v} \vert = a\dot{\theta} \sqrt{(1-\cos\theta)^2 + \sin^2\theta}\]

   נפתח את הסוגריים:

   \[\vert \vec{v} \vert = a\dot{\theta} \sqrt{1 - 2\cos\theta + \cos^2\theta + \sin^2\theta}\]

   נשתמש בזהות $\sin^2\theta + \cos^2\theta = 1$:

   \[\vert \vec{v} \vert = a\dot{\theta} \sqrt{1 - 2\cos\theta + 1} = a\dot{\theta} \sqrt{2(1 - \cos\theta)}\]

4. וקטור יחידה: נחשב את וקטור היחידה של המהירות, $\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert}$:

   \[\hat{v} = \frac{a\dot{\theta} \left[ (1 - \cos\theta)\hat{x} + \sin\theta\hat{y} \right]}{a\dot{\theta} \sqrt{2(1 - \cos\theta)}}\]

   הגורם $a\dot{\theta}$ מצטמצם:

   \[\hat{v} = \frac{(1 - \cos\theta)}{\sqrt{2(1 - \cos\theta)}}\hat{x} + \frac{\sin\theta}{\sqrt{2(1 - \cos\theta)}}\hat{y}\]

5. פישוט הביטוי:

   • רכיב x: $\frac{1 - \cos\theta}{\sqrt{1 - \cos\theta}} = \sqrt{1 - \cos\theta}$. לכן הרכיב הוא:

     \[\boxed{\sqrt{\frac{1 - \cos\theta}{2}}\hat{x}}\]

   • רכיב y: נשתמש בזהות

     \[\sin\theta = \sqrt{1-\cos^2\theta} = \sqrt{(1-\cos\theta)(1+\cos\theta)}\]

     מכאן:

     \[\frac{\sin\theta}{\sqrt{1 - \cos\theta}} = \frac{\sqrt{(1-\cos\theta)(1+\cos\theta)}}{\sqrt{1 - \cos\theta}} = \sqrt{1+\cos\theta}\]

     לכן הרכיב הוא $\boxed{\sqrt{\frac{1 + \cos\theta}{2}}\hat{y}}$.

התשובה הסופית:

שאלה 2: כוחות נורמליים על כדור בפינה

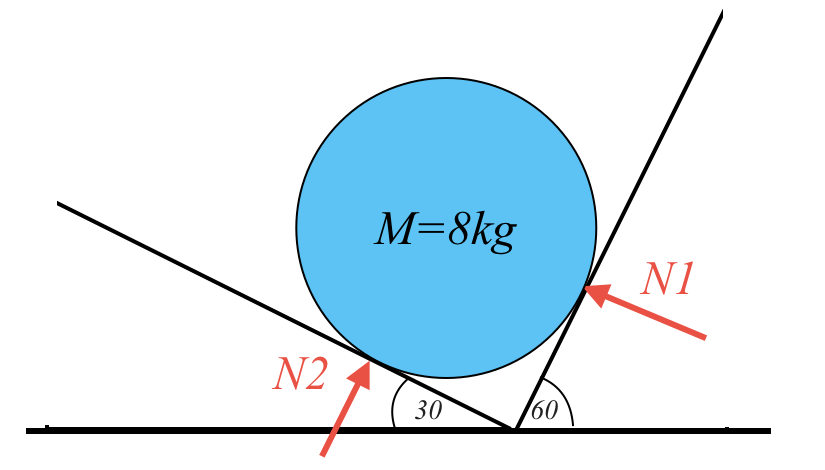
הבעיה: כדור במסה $m$ מונח בתוך פינה ישרה ($90^\circ$). הדופן הימנית נטויה בזווית $60^\circ$ ביחס לאופק, והשמאלית בזווית $30^\circ$. הכדור במנוחה.

• $N_1$: הכוח הנורמלי שהדופן הימנית (זווית $60^\circ$) מפעילה על הכדור.
• $N_2$: הכוח הנורמלי שהדופן השמאלית (זווית $30^\circ$) מפעילה על הכדור.

השאלה: מהו היחס בין $N_1$ ל-$N_2$?

פתרון:

המערכת נמצאת במנוחה, ולכן על פי החוק הראשון של ניוטון, שקול הכוחות הפועלים על הכדור הוא אפס בכל ציר.

ננתח את הכוחות בציר $x$ (אופקי).

• הכוח $N_1$ פועל בזווית $60^\circ$ ביחס לאנך, כלומר $30^\circ$ ביחס לאופק. הרכיב שלו בציר $x$ הוא $N_1 \cos(30^\circ)$ בכיוון ימין.
• הכוח $N_2$ פועל בזווית $30^\circ$ ביחס לאנך, כלומר $60^\circ$ ביחס לאופק. הרכיב שלו בציר $x$ הוא $N_2 \cos(60^\circ)$ בכיוון שמאל.

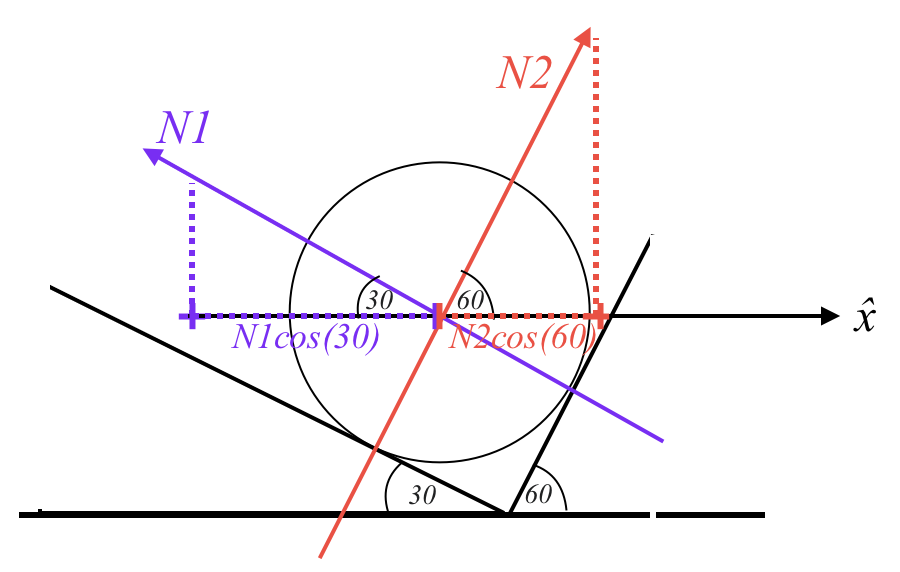
הערה: בשיעור המרצה סימן סינוס, אבל להבנתי ההיטל על ציר $x$ הוא קוסינוס.

שקול הכוחות בציר $x$ הוא אפס:

נציב את ערכי הקוסינוס:

נכפיל ב-2 ונקבל את היחס:

היה אפשר גם לפתור עם סינוסים, אבל אז היה מצטרף למשוואה $mg$ (כוח הכבידה) שצריך היה לבטל.

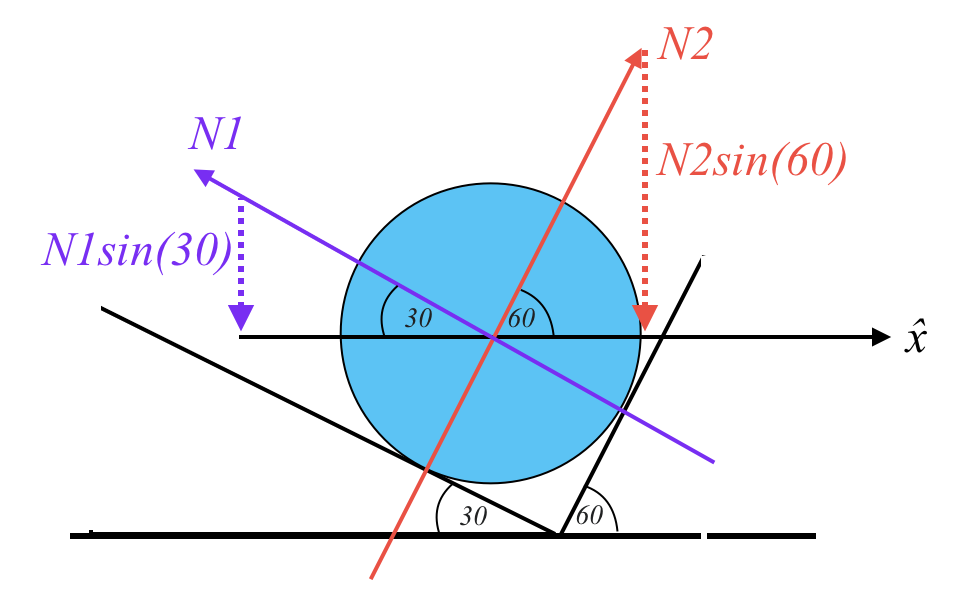
כלומר, היינו מקבלים:

והיינו נתקעים עם:

שאלה 3: התנתקות מסה ממסה אחרת המחוברת לקפיץ

הבעיה: מסה $M$ מונחת על משטח אופקי חלק ומחוברת לקפיץ בעל קבוע $k$. על גבי מסה $M$ מונחת מסה קטנה $m$. מקדם החיכוך הסטטי בין שתי המסות הוא $\mu$. מותחים את הקפיץ במרחק $d$ ממצב שיווי המשקל ומשחררים ממנוחה.

השאלה: מהו הערך המינימלי של $d$ שיגרום למסה $m$ להתנתק (להחליק) מהמסה $M$?

פתרון:

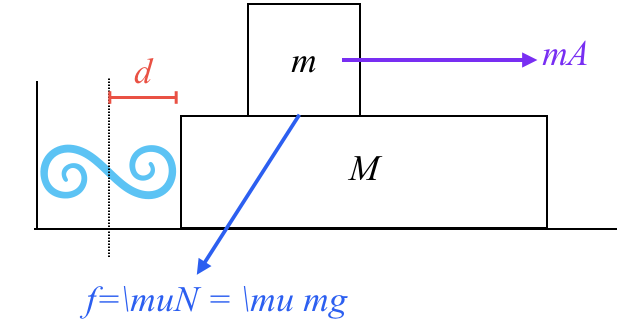
1. התנאי להתנתקות: המסה $m$ תתנתק מהמסה $M$ כאשר התאוצה של המערכת תהיה גדולה מספיק כדי שהכוח המדומה הפועל על $m$ (במערכת הייחוס של $M$) יתגבר על כוח החיכוך הסטטי המקסימלי.
   • כוח החיכוך הסטטי המקסימלי: $f_{s,max} = \mu N \overset{\star}{=} \mu mg$.

     הבהרה לגבי $\star$: $N=mg$ משקול הכוחות ששווה לאפס בציר $y$.

   • הכוח המדומה הפועל על $m$: $F_{inertial} = mA$, כאשר $A$ היא תאוצת המסה $M$.

     עקרונית הכוח המדומה הוא $-mA$, המרצה הציג את זה בעזרת כיוון החץ שצייר.

   • תנאי ההתנתקות:
   \[mA > \mu mg \implies A > \mu g\]

   כלומר, אנחנו צריכים למצוא את $A$ כדי למצוא את $d$.

2. תנועת המערכת: כל עוד המסות נעות יחד, הן מתנהגות כמסה אחת $(M+m)$ המבצעת תנועה הרמונית פשוטה.

   • מיקום המערכת כפונקציה של הזמן (שחרור ממנוחה במרחק $d$):

     \[x(t) = d\cos(\omega t) \tag{1}\]

     לפי הפתרון הכללי כאשר הפאזה ההתחלתית היא אפס, כלומר שחרור ממנוחה.

   • התדירות הזוויתית של התנועה:

     \[\omega = \sqrt{\frac{k}{M+m}} \tag{2}\]

3. תאוצת המערכת:

   אפשר להיעזר גם בנוחסה:

   \[\boxed{A = -\omega^2 d\cos(\omega t)}\]

   נגזור פעמיים את המיקום $(1)$ לקבלת התאוצה:

   \[v(t) = \frac{dx}{dt} = -d\omega\sin(\omega t)\] \[A(t) = \frac{dv}{dt} = -d\omega^2\cos(\omega t)\]

   התאוצה המקסימלית בגודלה מתרחשת ב-$t=0$ (רגע השחרור), כאשר $\cos(\omega t)=1$:

   \[\ddot{x}_{max} = A= -\omega^2 d\]

   היינו יכולים להגיע לביטוי הזה גם מכיוון שבתנועה מעגלית (שהיא מקרה פרטי של תנועה הרמונית פשוטה) התאוצה המקסימלית היא $a_{max} = r\omega^2$, כאשר $r$ הוא הרדיוס של התנועה. כאן $r=d$.

4. מציאת $d$: נציב את התאוצה המקסימלית בתנאי ההתנתקות:

   \[A_{max} > \mu g\] \[d\omega^2 > \mu g\]

   נציב את הביטוי עבור $\omega^2$ מתוך (2):

   \[d \left( \frac{k}{M+m} \right) > \mu g\]

   נבודד את $d$:

   \[\boxed{d > \frac{\mu g (M+m)}{k}}\]

התשובה הסופית: הערך המינימלי של $d$ הוא $\frac{\mu g (M+m)}{k}$.

שאלה 4: כוחות על פשפש בתקליט מסתובב

הבעיה: פשפש נמצא בתוך חריץ ישר על תקליט המסתובב במהירות זוויתית קבועה $\omega$. הפשפש נמצא במרחק קבוע $R$ מהמרכז. הכוחות שפועלים על הפשפש במישור הסיבוב הם:

1. כוח נורמלי ($N$): מהדופן הפנימית של החריץ, מכוון כלפי מרכז הסיבוב.
2. כוח גרר: מתכונתי למהירות, $F_{drag} = -\beta v$, כאשר $\beta$ הוא קבוע.
3. כוח חיכוך ($f_k$): המשטח מפעיל על הפשפש, בכיוון הסיבוב.

השאלה: מהי משוואת התנועה של הפשפש בקואורדינטות פולריות?

פתרון:

1. וקטור שקול הכוחות: נרשום את כל הכוחות שפועלים על הפשפש כווקטורים:
   • כוח נורמלי: $\mathbf{F}_N = -N\mathbf{\hat{r}}$ (מכוון כלפי המרכז, בכיוון רדיאלי שלילי).

     זה הכוח הצנטריפיטלי. הוא הכוח שמשאיר את הפשפש בתנועה מעגלית, כלומר הוא מאזן את התאוצה הרדיאלית.

   • כוח גרר: פועל בניגוד לכיוון המהירות. במקרה הזה המהירות היא משיקית עם רדיוס קבוע, $\vec{v} = R\dot{\theta} \mathbf{\hat{\theta}}=R\omega\mathbf{\hat{\theta}}$. לכן כוח הגרר הוא

     \[\mathbf{F}_{drag} = -\beta (R\omega\mathbf{\hat{\theta}}) = -\beta R\omega \mathbf{\hat{\theta}}\]

   • כוח חיכוך: פועל בכיוון התנועה:

     \[\mathbf{F}_f = f_k \mathbf{\hat{\theta}}= \mu mg \mathbf{\hat{\theta}}\]

   • שקול הכוחות:

     \[\sum \mathbf{F} = -N\mathbf{\hat{r}} + (\mu mg - \beta R\omega)\mathbf{\hat{\theta}}\]

2. וקטור התאוצה בקואורדינטות פולריות:

   \[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\mathbf{\hat{r}} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}}\]

   מכיוון שהפשפש במרחק קבוע $R$ ובמהירות זוויתית קבועה $\omega$:

   \[r=R \implies \boxed{\dot{r}=0, \ddot{r}=0}\] \[\dot{\theta}=\omega \implies \boxed{\ddot{\theta}=0}\]

   נציב ונקבל:

   \[\vec{a} = (\cancel{\ddot{r}} - r\dot{\theta}^2)\mathbf{\hat{r}} + \cancel{(2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}}}\] \[\boxed{\vec{a} = -R\omega^2 \mathbf{\hat{r}}}\]

3. משוואת התנועה (בקואורדינטות פולריות):

   החוק השני של ניוטון: $\sum \mathbf{F} = m\vec{a}$

   \[-N\mathbf{\hat{r}} + (\mu mg - \beta R\dot{\theta})\mathbf{\hat{\theta}} = m(-R\omega^2 \mathbf{\hat{r}})\]
4. השוואת רכיבים:

   • בכיוון הרדיאלי ($\mathbf{\hat{r}}$):

     \[-N = -mR\omega^2 \implies N = mR\omega^2\]

   • בכיוון המשיקי ($\mathbf{\hat{\theta}}$):

     \[\underbrace{mR\ddot{\theta}}_{\overset{\star}{=0}} = \mu mg - \beta R\omega\]

התשובה הסופית: משוואות התנועה המתארות את הכוחות הן:

• בכיוון הרדיאלי: $N = mR\omega^2$
• בכיוון המשיקי: $ \mu mg = \beta R\omega$

סך הכל:

הערה: המרצה לא הרחיב על זה בשיעור אבל להבנתי $\ddot{\theta}$ מתאפס כי נתון שהמהירות הזוויתית קבועה, כלומר $\ddot{\theta} = 0$.