1. חזרה - מטען נקודתי וסופר פוזיציה
1.1 נוסחאות בסיסיות
מטען נקודתי:
\[\vec{E} = \frac{kq}{r^3}\vec{r}\]סופר פוזיציה:
\[\vec{E}(\vec{r}) = \sum_i \vec{E}_i(\vec{r}) = k \sum_i \frac{q_i}{|\vec{r} - \vec{r_i}|^3} (\vec{r} - \vec{r_i})\]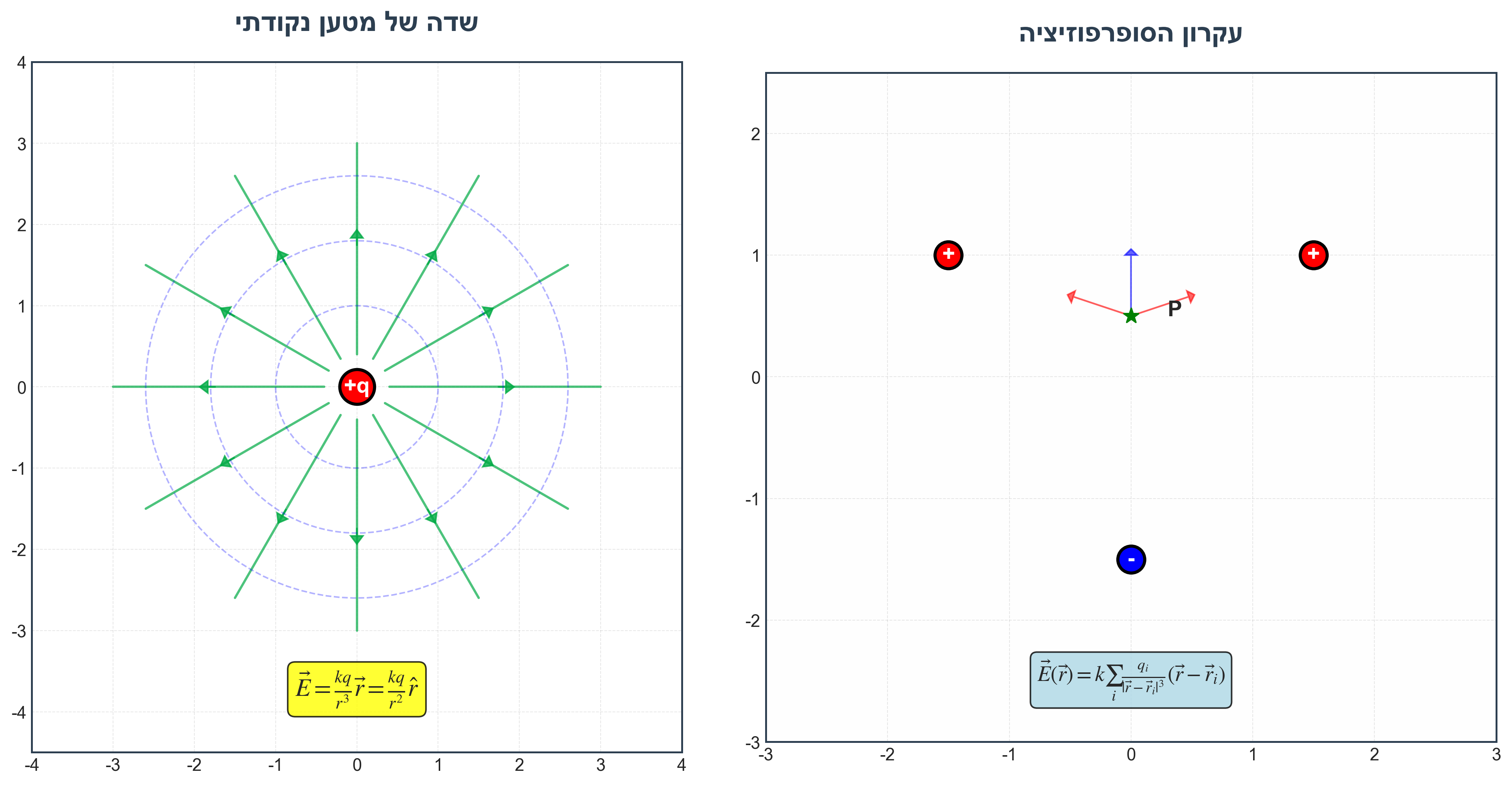
1.2 דוגמה: טבעת עם מטען חסר
נתבונן בטבעת שטעונה בצפיפות מטען $\lambda$ קולון ליחידת אורך.
נוריד נקודה אחת על פני המעגל (נבטל את הסימטריה).
מה יהיה השדה במרכז המעגל?
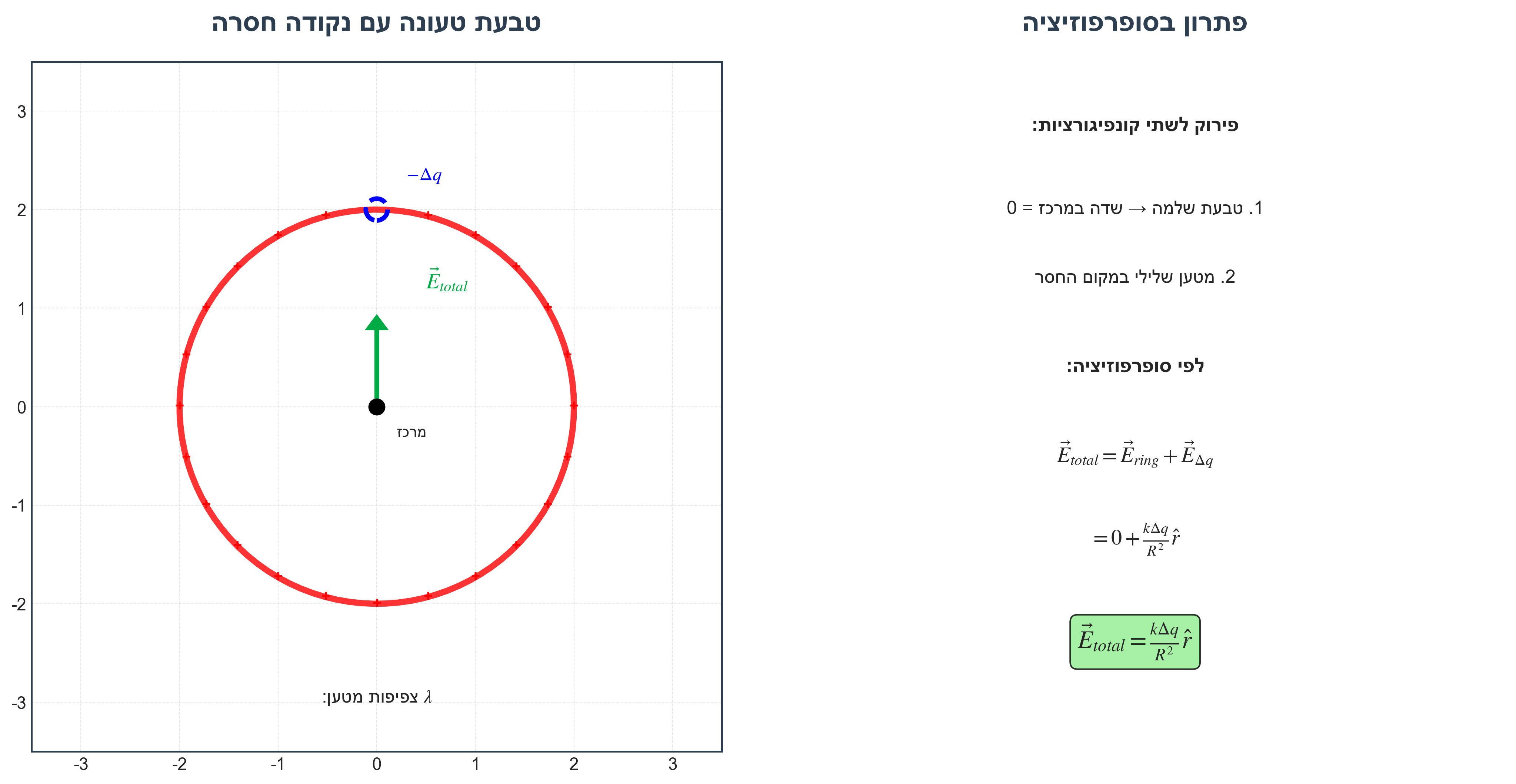
פתרון: סופר פוזיציה של המעגל המלא (שדה אפס במרכז) והמטען השלילי שהורדנו:
\[\vec{E}_{total} = 0 + \frac{k \Delta q}{R^2} \hat{r}\]2. מוליכים לעומת מבודדים
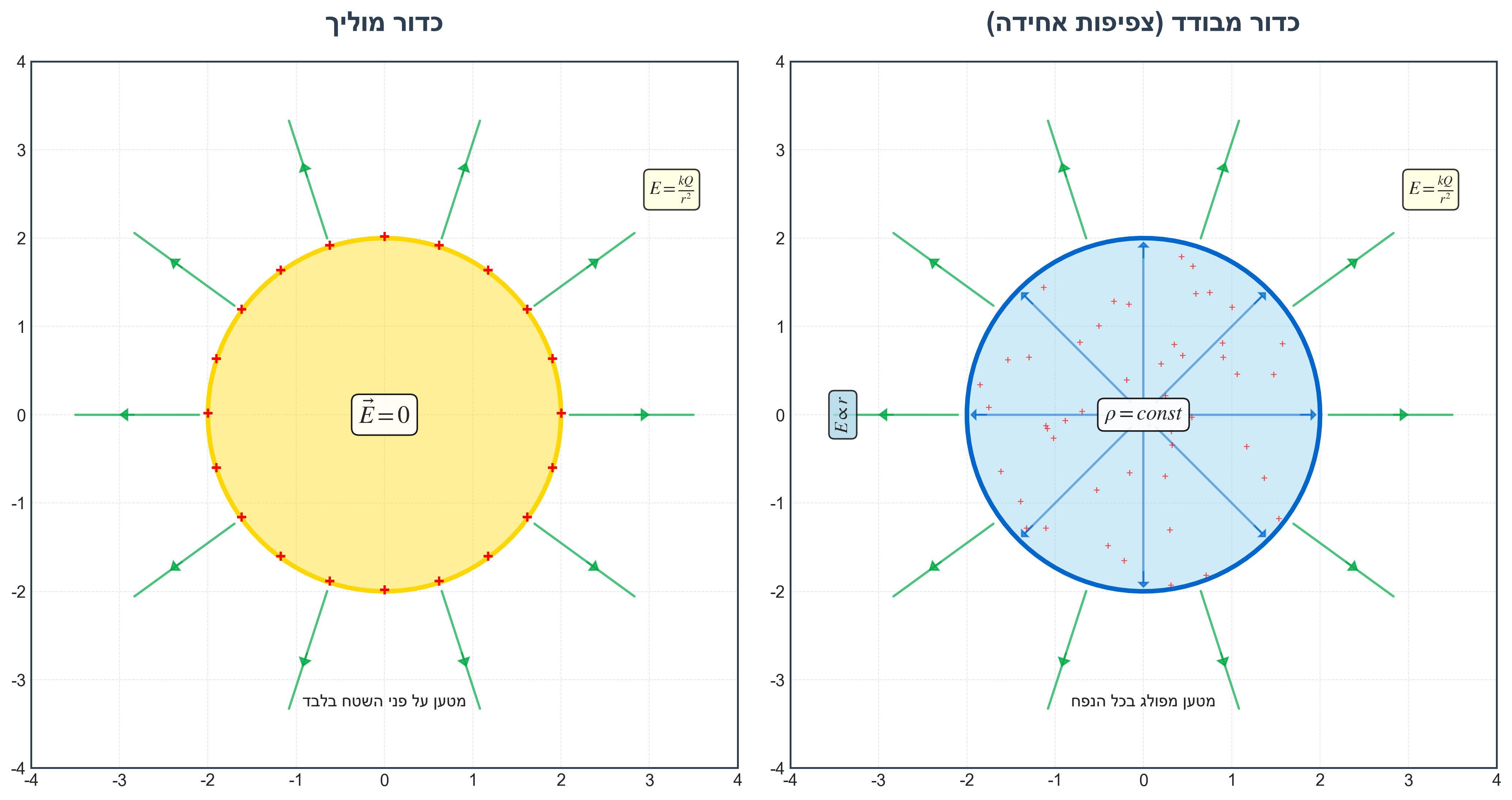
תכונות מוליכים באלקטרוסטטיקה:
- בתוך מוליך בשיווי משקל: $E = 0$
- כל המטען העודף נמצא על פני השטח
- כדור מלא מוליך שקול לקליפה טעונה מבחינה אלקטרומגנטית
3. שדה של כדור טעון בצפיפות אחידה
3.1 הבעיה
כדור מבודד ברדיוס $R$ טעון בצפיפות מטען אחידה $\rho$ (קולון למטר מעוקב).
חשבו את השדה החשמלי בתוך הכדור ומחוצה לו.
3.2 הפתרון
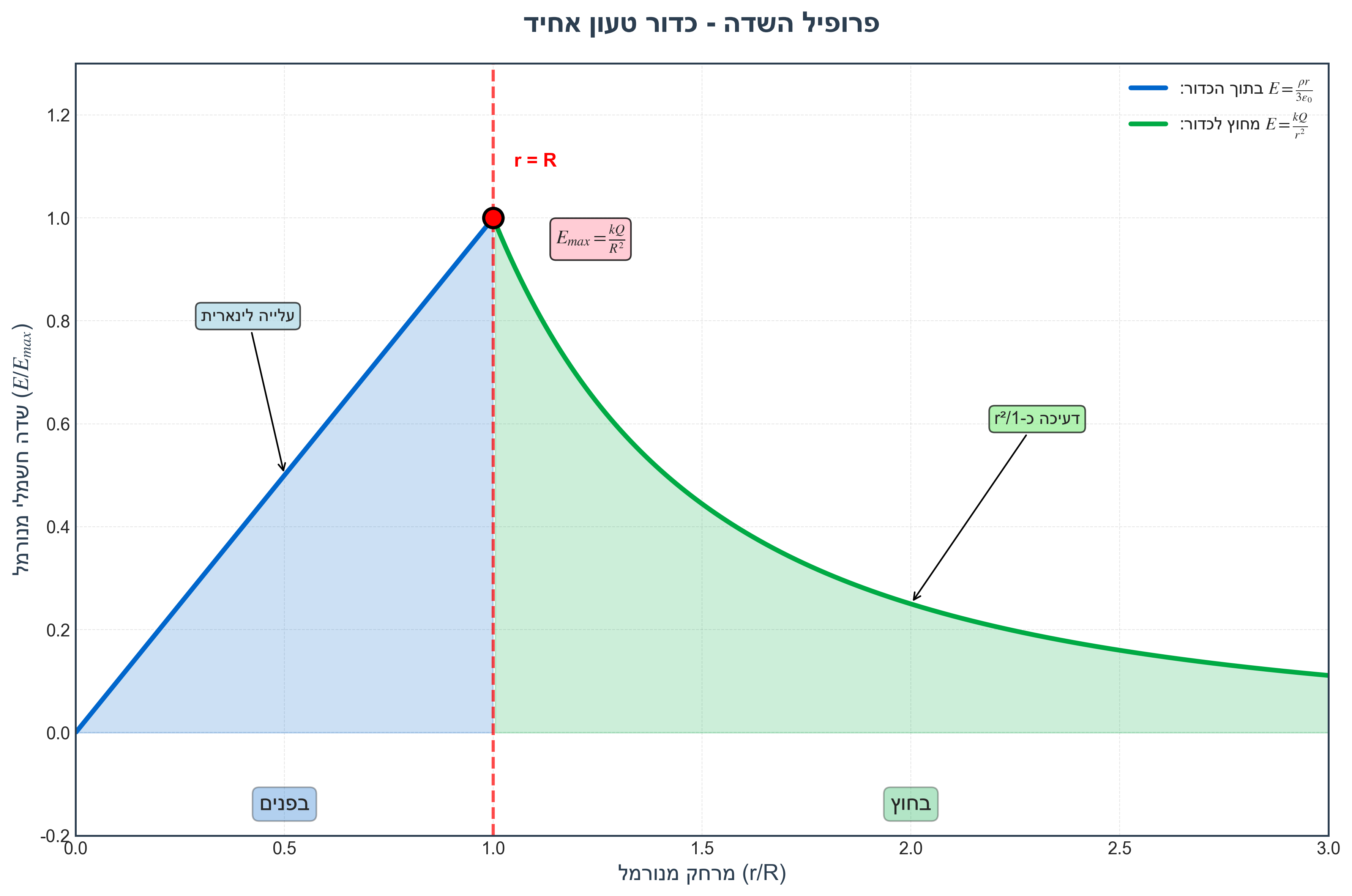
בתוך הכדור ($r < R$):
מבניית משטח גאוסי כדורי ברדיוס $r$:
\[\underbrace{4\pi r^2 E_r}_{\star} = \frac{Q_{inside}}{\epsilon_0} = \frac{\rho \cdot \frac{4\pi r^3}{3}}{\epsilon_0}\]לכן:
\[\boxed{E_r = \frac{\rho r}{3\epsilon_0}}\]השדה גדל לינארית עם הרדיוס!
תזכורת: בשיעור שעבר קיבלנו את אותה התוצאה ברישום אחר:
עבור כדור במילוי אחיד עם צפיפות $\rho$, המטען הכולל הוא:
\[Q = \rho \cdot \frac{4}{3}\pi R^3\]לכן:
\[\rho = \frac{3Q}{4\pi R^3}\]נציב בנוסחה השנייה:
\[E = \frac{\rho r}{3\varepsilon_0} = \frac{3Q}{4\pi R^3} \cdot \frac{r}{3\varepsilon_0} = \frac{Q r}{4\pi\varepsilon_0 R^3} = \frac{kQ}{R^3}r\]
$\star$ Explanation of Gauss’s Law Terms
Looking at your equation:
\[\underbrace{4\pi r^2 E_r}_{\text{?}} = \frac{Q_{inside}}{\epsilon_0} = \frac{\rho \cdot \frac{4\pi r^3}{3}}{\epsilon_0}\]Left Side: $4\pi r^2 E_r$
This is the flux through a spherical Gaussian surface:
\[\oint \vec{E} \cdot d\vec{A} = E_r \cdot A_{sphere} = E_r \cdot 4\pi r^2\]Where:
- $4\pi r^2$ = surface area of a sphere with radius $r$
- $E_r$ = radial component of the electric field (constant on the surface by symmetry)
Important Note for Future Problems!
This equation uses spherical geometry (sphere surface area $4\pi r^2$).
But a coaxial cylinders problem requires cylindrical geometry:
\[\oint \vec{E} \cdot d\vec{A} = E_r \cdot 2\pi r L\]Where $2\pi r L$ is the lateral surface area of a cylinder with radius $r$ and length $L$.
For cylindrical cases with linear charge density $\lambda$:
\[E_r \cdot 2\pi r L = \frac{\lambda L}{\epsilon_0}\] \[E_r = \frac{\lambda}{2\pi \epsilon_0 r}\]
מחוץ לכדור ($r > R$):
\[E_r = \frac{kQ_{total}}{r^2} = \frac{k \cdot \frac{4\pi R^3}{3}\rho}{r^2}\]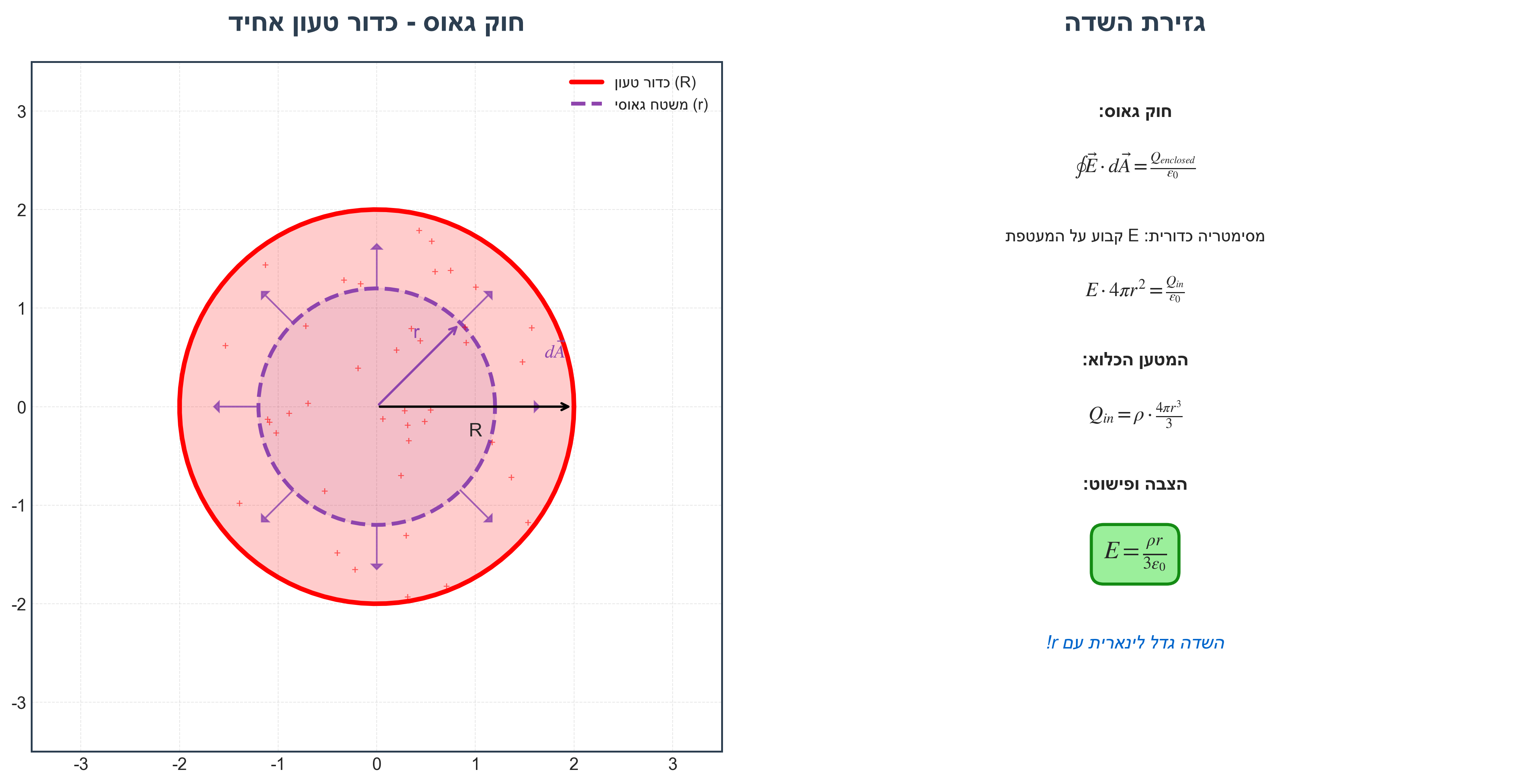
4. כדור עם צפיפות מטען משתנה
4.1 הבעיה
כדור מבודד עם התפלגות מטען:
\[\rho(r) = \frac{\alpha}{r^2} \cosh\left(\frac{\ln 2 \cdot r}{R}\right)\]כאשר $[\alpha] = \text{C/m}$ ו-$R$ רדיוס הכדור.
חשבו את השדה החשמלי בתוך הכדור ומחוצה לו, ואת המטען הכולל.
4.2 חישוב המטען הכלוא
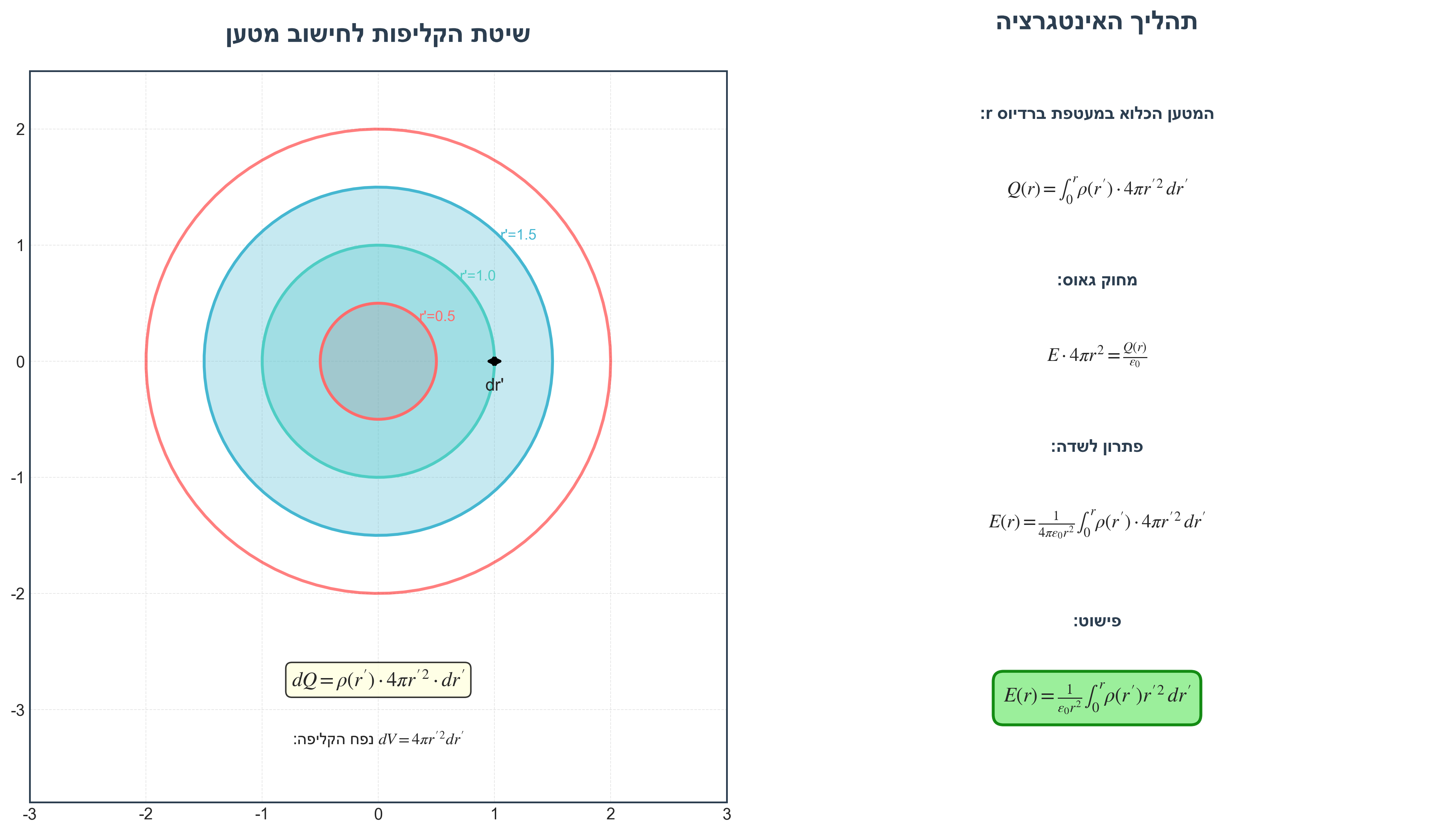
\[Q(r) = \int_0^r 4\pi r'^2 \cdot \frac{\alpha}{r'^2} \cosh\left(\frac{\ln 2 \cdot r'}{R}\right) dr' = 4\pi\alpha \cdot \frac{R}{\ln 2} \sinh\left(\frac{\ln 2 \cdot r}{R}\right)\]4.3 השדה החשמלי
מחוק גאוס:
\[E_r(r) = \frac{\alpha R}{\epsilon_0 \ln 2} \cdot \frac{\sinh\left(\frac{\ln 2 \cdot r}{R}\right)}{r^2}\]4.4 המטען הכולל
ב-$r = R$, עם $\sinh(\ln 2) = \frac{3}{4}$:
\[Q_{total} = \frac{3\pi\alpha R}{\ln 2}\]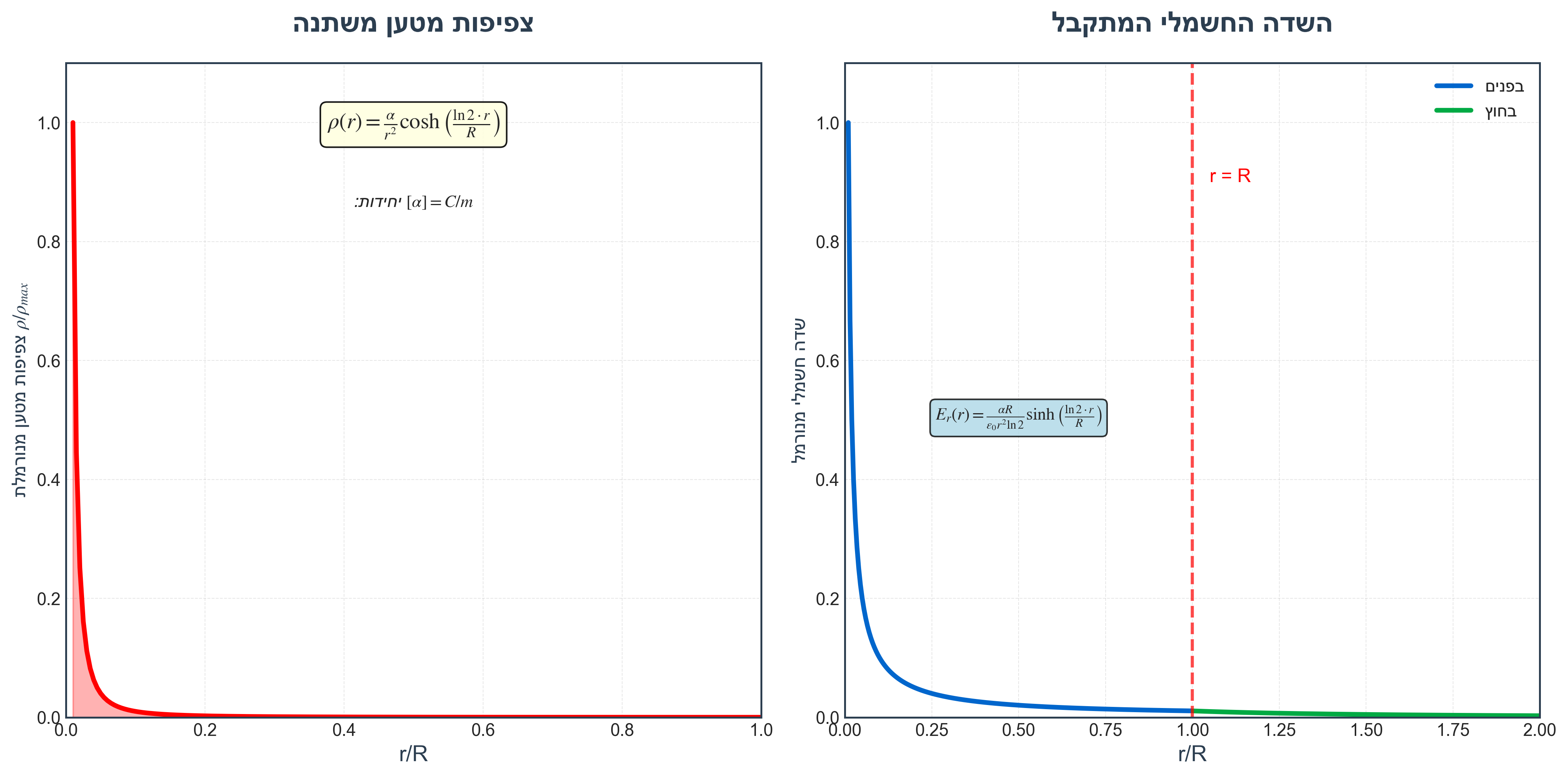
5. התנהגות השדה לפי ממד טופולוגי
5.1 טבלת סיכום
| ממד | דוגמה | התנהגות | נוסחה |
|---|---|---|---|
| 0 (נקודה) | מטען נקודתי | $E \propto r^{-2}$ | $E = kq/r^2$ |
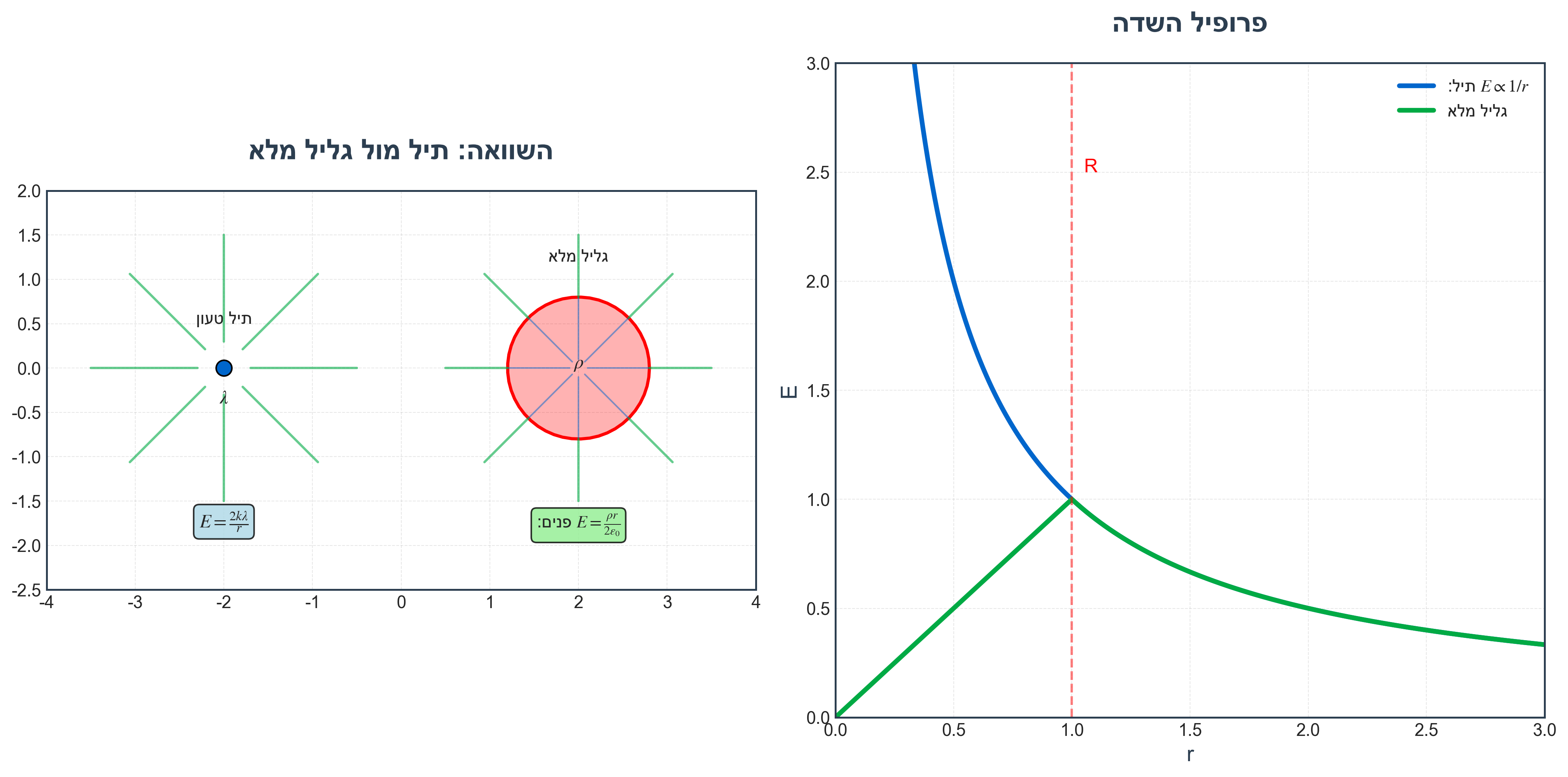
| 1 (קו) | גליל אינסופי | $E \propto r^{-1}$ | $E = 2k\lambda/r$ |
| 2 (משטח) | מישור אינסופי | $E = \text{const}$ | $E = \sigma/2\epsilon_0$ |
| 3 (נפח) | כדור (בפנים) | $E \propto r^1$ | $E = \rho r/3\epsilon_0$ |
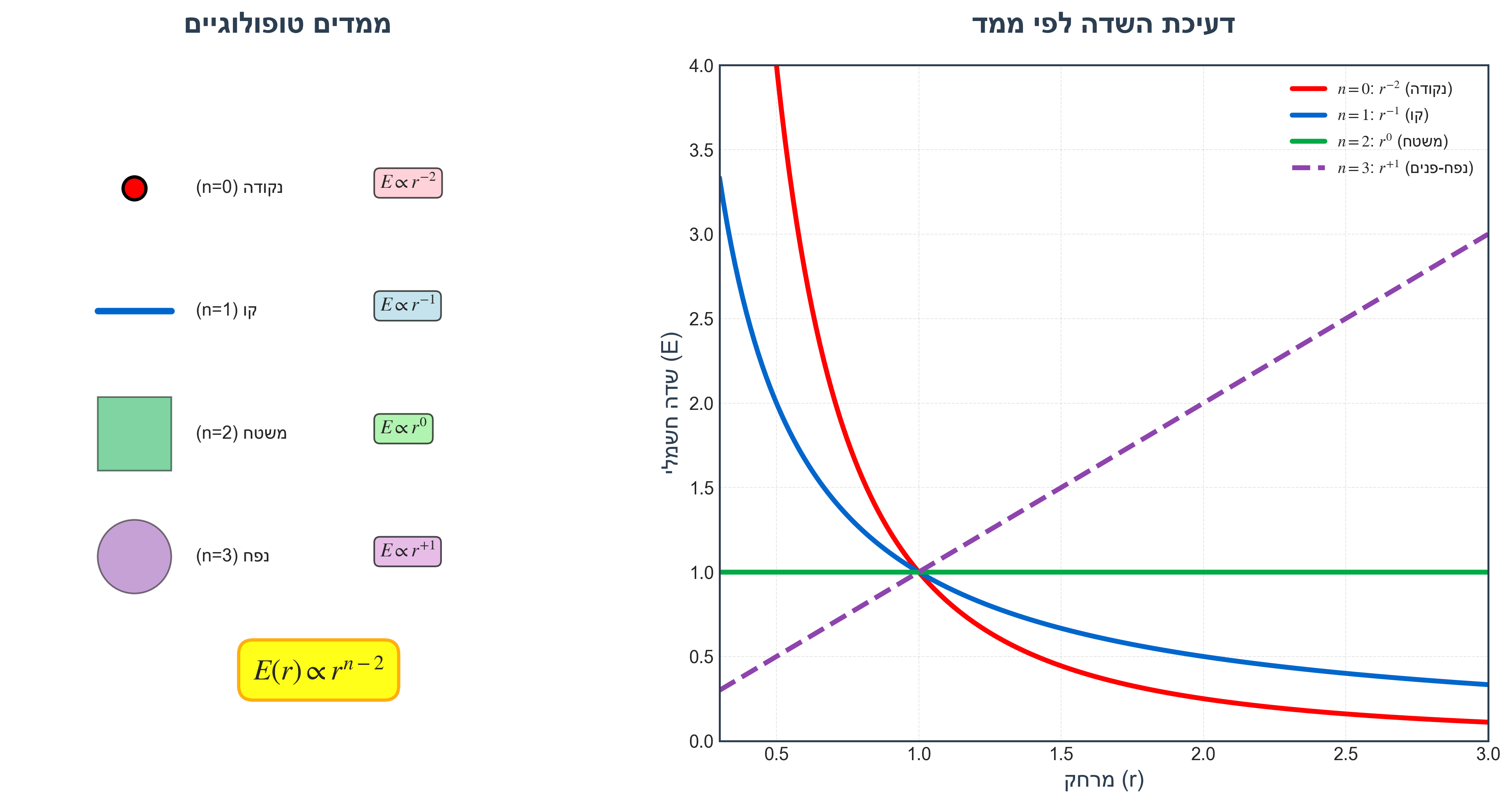
5.2 הכללה מתמטית
עבור מטען בממד טופולוגי $n$:
\[E(r) \propto r^{n-2}\]המשמעות: איזון בין התפשטות השדה במרחב ($r^2$) לבין כמות המטען ($r^n$).
6. סיכום
- חוק גאוס - כלי רב-עוצמה לחישוב שדות בבעיות סימטריות
- צפיפות משתנה - דורשת אינטגרציה לחישוב המטען הכלוא
- ממד טופולוגי - קובע את דעיכת השדה: $E \propto r^{n-2}$
- מוליכים - שדה אפס בפנים, מטען על פני השטח