בעיה 1: תנועה תחת כוח משתנה בזמן
חלקיק נע תחת השפעת כוח הנתון בביטוי:
\[\vec{F}(t) = a \cos(\omega t) \hat{x} + b \sin(\omega t) \hat{y}\]כאשר $a$, $b$, $\omega$ הם פרמטרים.
- מה יחידות הפרמטרים $a$, $b$, $\omega$?
אם בהתחלת התנועה החלקיק נמצא במנוחה בראשית, הראו שוקרטור מהירותו בכל זמן $t$ מאוחר יותר נתון בביטוי:
\[\vec{v}(t) = \frac{a}{m\omega}\sin(\omega t)\hat{x} + \frac{b}{m\omega}(1-\cos(\omega t))\hat{y}\]- מהו וקטור התאוצה של החלקיק ב-$t=0$?
- מהו גודל המהירות של החלקיק בכל זמן $t$?
- מצאו את וקטור המקום של החלקיק בכל זמן $t$.
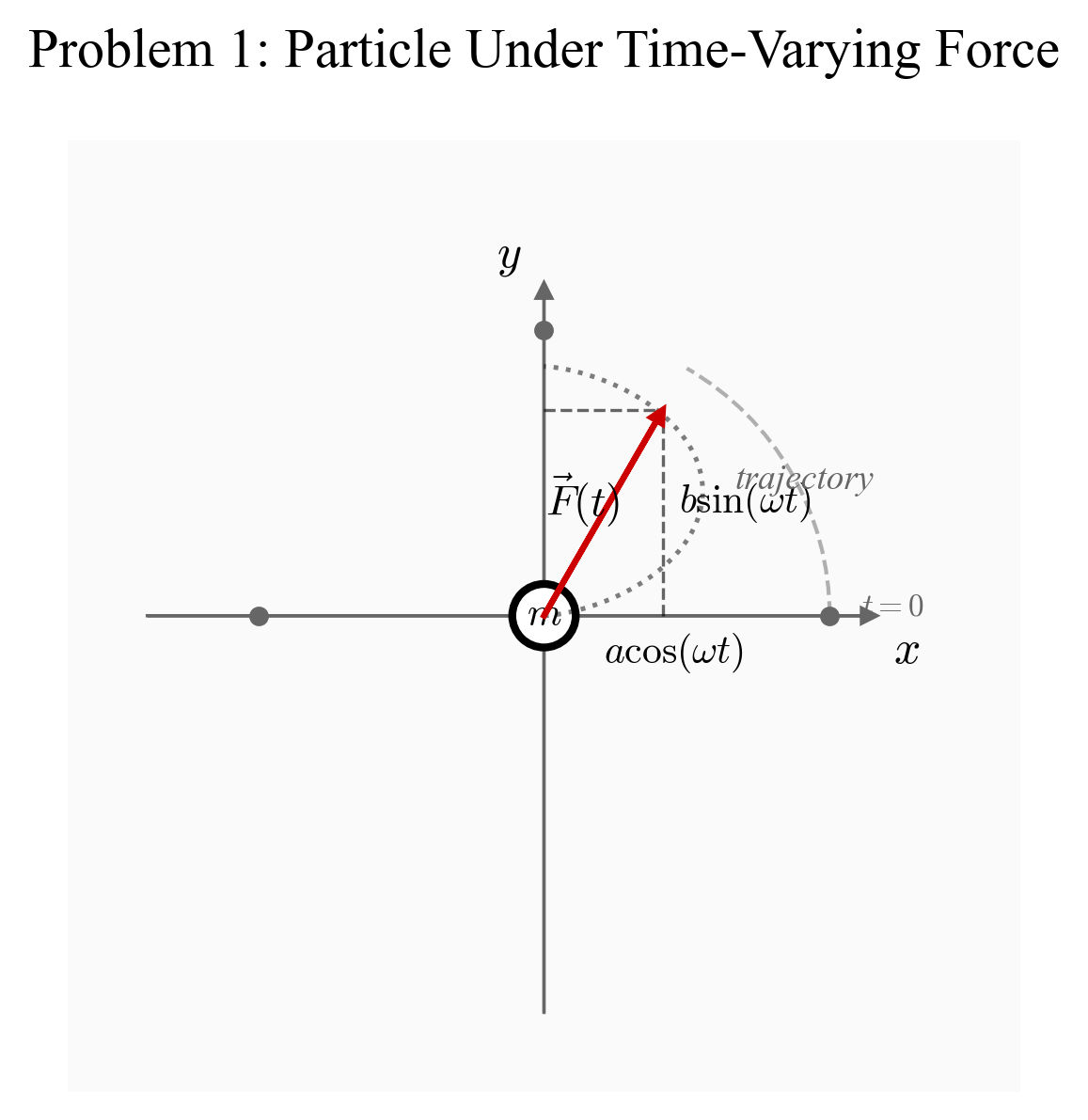
סעיף א: מה יחידות הפרמטרים $a$, $b$, $\omega$?
טיפ: יחידות בפיזיקה נקבעות על פי העקרון שכל איברי משוואה חייבים להיות בעלי אותן יחידות (ממדים).
מכיוון ש-$\vec{F}$ הוא כוח, יחידותיו הן ניוטון [N] או [kg⋅m/s²].
- יחידות של $a$ ו-$b$: מכיוון ש-$\cos(\omega t)$ ו-$\sin(\omega t)$ הם חסרי יחידות (מספרים טהורים), הפרמטרים $a$ ו-$b$ חייבים להיות ביחידות של כוח:
- יחידות של $\omega$: הארגומנט של פונקציות טריגונומטריות חייב להיות חסר יחידות. מכיוון ש-$t$ נמדד בשניות [s], נדרש:
לכן: $\omega = \, [\mathrm{s}^{-1}]$ (רדיאנים לשנייה)
סעיף ב: מציאת וקטור המהירות
החוק השני של ניוטון: $\vec{F} = m\vec{a} = m\frac{d\vec{v}}{dt}$
מכאן:
\[\frac{d\vec{v}}{dt} = \frac{\vec{F}}{m} = \frac{a}{m}\cos(\omega t)\hat{x} + \frac{b}{m}\sin(\omega t)\hat{y}\]כדי למצוא את $\vec{v}(t)$, נבצע אינטגרציה:
\[\vec{v}(t) = \int_{0}^{t} \frac{d\vec{v}}{dt'} dt' = \int_{0}^{t} \left[ \frac{a}{m}\cos(\omega t')\hat{x} + \frac{b}{m}\sin(\omega t')\hat{y} \right] dt'\]חישוב האינטגרל:
-
רכיב x:
\[\int_{0}^{t} \frac{a}{m}\cos(\omega t') \, dt' = \frac{a}{m\omega}\sin(\omega t)\] -
רכיב y:
\[\int_0^t \frac{b}{m}\sin(\omega t') dt' = -\frac{b}{m\omega}\cos(\omega t')\Big|_0^t = \frac{b}{m\omega}(1-\cos(\omega t))\]
תוצאה סופית:
\[\vec{v}(t) = \frac{a}{m\omega}\sin(\omega t)\hat{x} + \frac{b}{m\omega}(1-\cos(\omega t))\hat{y}\](מתקיים כי $\vec{v}(0) = \vec{0}$ כנדרש מתנאי ההתחלה)
סעיף ג: וקטור התאוצה ב-$t=0$
התאוצה היא:
\[\vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{\vec{F}(t)}{m}\]ב-$t=0$:
\[\vec{a}(0) = \frac{\vec{F}(0)}{m} = \frac{a\cos(0)\hat{x} + b\sin(0)\hat{y}}{m} = \frac{a}{m}\hat{x}\]סעיף ד: גודל המהירות
גודל המהירות:
\[\vert \vec{v}(t)| = \sqrt{v_x^2 + v_y^2}\]כאשר:
- $v_x = \frac{a}{m\omega}\sin(\omega t)$
- $v_y = \frac{b}{m\omega}(1-\cos(\omega t))$
לכן:
\[\vert \vec{v}(t)| = \frac{1}{m\omega}\sqrt{a^2\sin^2(\omega t) + b^2(1-\cos(\omega t))^2}\]סעיף ה: וקטור המקום
אינטגרציה של וקטור המהירות:
\[\vec{r}(t) = \int_0^t \vec{v}(t') dt'\]חישוב האינטגרלים:
-
רכיב x:
\[\int_0^t \frac{a}{m\omega}\sin(\omega t') dt' = -\frac{a}{m\omega^2}\cos(\omega t'){\Big|_{0}}^{t} = \frac{a}{m\omega^2}(1-\cos(\omega t))\] -
רכיב y: $\int_0^t \frac{b}{m\omega}(1-\cos(\omega t’)) dt’ = \frac{b}{m\omega}\left[t - \frac{\sin(\omega t)}{\omega}\right]$
תוצאה סופית:
\[\vec{r}(t) = \frac{a}{m\omega^2}(1-\cos(\omega t))\hat{x} + \frac{b}{m\omega}\left(t - \frac{\sin(\omega t)}{\omega}\right)\hat{y}\]בעיה 2: תנועת קליע בתווך עם התנגדות
קליע נע אופקית בתוך תווך, התנגדות התווך לקליע פרופורציונית למהירותו עם קבוע פרופורציה $\gamma$, כלומר $f(v) = \gamma v$. נתון: $\gamma = 10$.
- מה היחידות של $\gamma$?
- קבלו משוואה עבור התנועה האופקית של הקליע בעזרת החוק השני של ניוטון.
- מיצאו ביטוי כלל עבור מהירותו הרגעית.
- מיצאו ביטוי עבור תאוטתו הרגעית.
- הקליע יצא את הלוע במהירות של 200 מטר לשנייה. כמה זמן ייקח לו להאט למהירות של מטר לשנייה בתוך התווך?
- מה הייתה תאוטתו הממוצעת של הקליע בזמן זה?
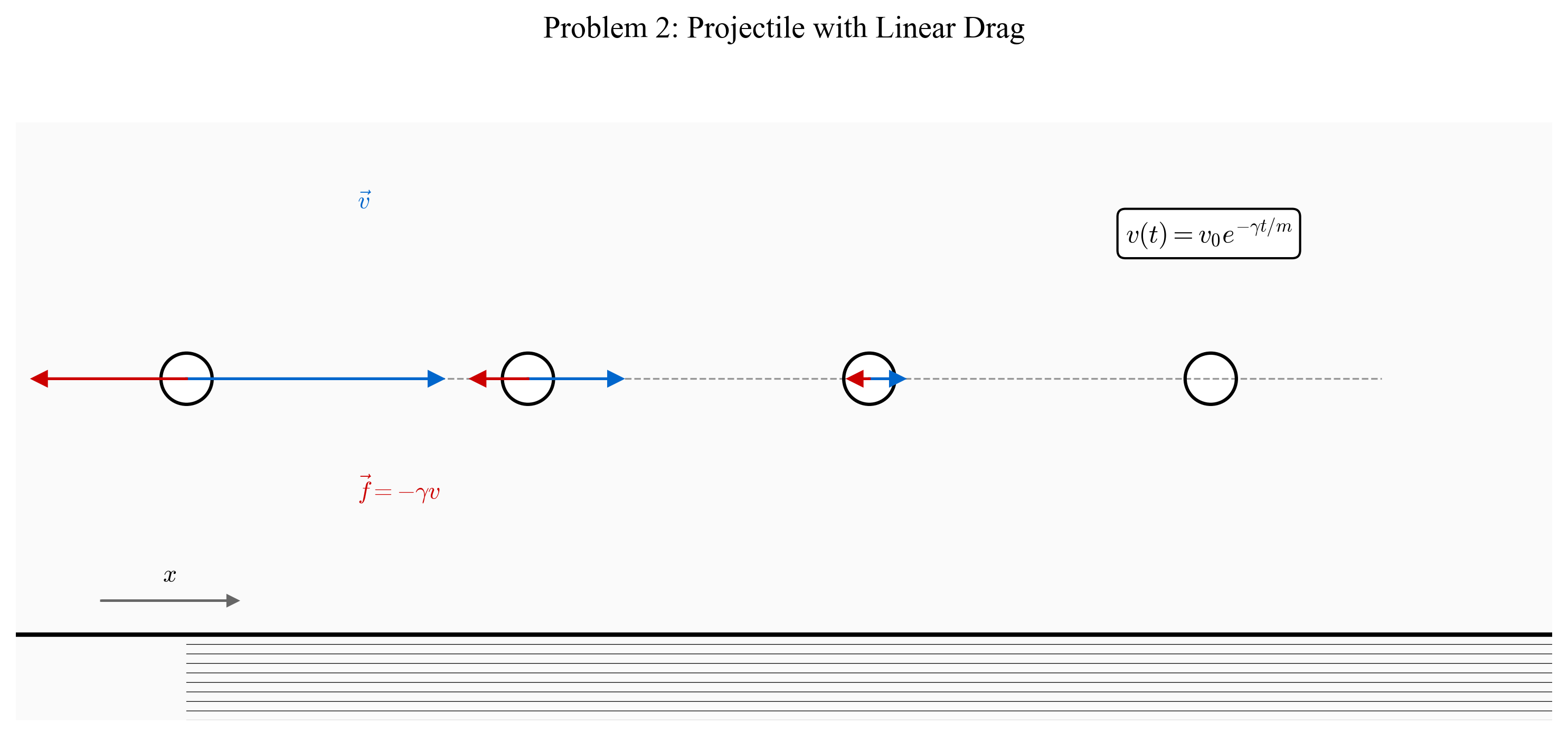
סעיף א: יחידות של $\gamma$
כוח ההתנגדות: $f = \gamma v$
מכיוון ש-$[f] = \mathrm{N}$ ו-$[v] = \mathrm{m/s}$:
\[[\gamma] = \frac{[f]}{[v]} = \frac{\mathrm{N}}{\mathrm{m/s}} = \frac{\mathrm{kg⋅m/s²}}{\mathrm{m/s}} = \, \mathrm{kg/s}\]לכן:
\[\boxed{\gamma = 10 \, \mathrm{kg/s}}\]סעיף ב: משוואת התנועה
החוק השני של ניוטון: הכוח היחיד הוא כוח ההתנגדות (בכיוון הפוך למהירות):
\[F = -\gamma v = ma\]לכן:
\[ma = -\gamma v\]ברישום דיפרנציאלי:
\[\ddot{v} = -\frac{\gamma}{m}v \tag{1}\]סעיף ג: ביטוי למהירות הרגעית
משוואה $(1)$ היא משוואה דיפרנציאלית מסדר ראשון שהפתרון האקספוננציאלי שלה הוא:
\[v(t) = v_0 e^{-\frac{\gamma}{m}t}\]כאשר $v_0$ היא המהירות ההתחלתית.
המשוואה הזאת היא למעשה הפתרון של משוואת התנועה, כאשר $v_0$ הוא המהירות ההתחלתית של הקליע. מגיעים אליה בעזרת הפרדת משתנים:
\[\frac{dv}{v} = -\frac{\gamma}{m} dt\]אינטגרציה נותנת:
\[\begin{aligned} \int \frac{dv}{v} &= -\frac{\gamma}{m} \int dt \\[10pt] \ln|v| &= -\frac{\gamma}{m}t + C_1 \end{aligned}\]נוציא אקספוננט לשני הצדדים:
\[\begin{aligned} v &= e^{-\frac{\gamma}{m}t + C_1} \\[10pt] v &= e^{C_1} e^{-\frac{\gamma}{m}t} \\[10pt] &= v_0 e^{-\frac{\gamma}{m}t} \end{aligned}\]השוויון האחרון מתקבל על ידי קביעת $e^{C_1} = v_0$, כלומר המהירות ההתחלתית.
סעיף ד: תאוטה רגעית
התאוטה היא:
\[a(t) = \frac{dv}{dt} = -\frac{\gamma}{m}v_0 e^{-\frac{\gamma}{m}t} = -\frac{\gamma}{m}v(t)\]סעיף ה: זמן להאטה
נתון: $v_0 = 200 \, \mathrm{m/s}$, ומחפשים זמן שבו $v = 1 \, \mathrm{m/s}$.
מהמשוואה:
\[1 = 200e^{-\frac{10}{m}t}\] \[\frac{1}{200} = e^{-\frac{10}{m}t}\] \[\ln\left(\frac{1}{200}\right) = -\frac{10}{m}t\] \[t = \frac{m}{10}\ln(200) = \frac{m}{10} \times 5.298 \approx 0.53m \mathrm{s}\](התשובה תלויה במסת הקליע $m$ בק”ג)
סעיף ו: תאוטה ממוצעת
שואלים על התאוטה הממוצעת במהלך הזמן בסעיף הקודם, לצורך העניין בין $t=0$ ל-$t=t^*$, כאשר $t^* \approx 0.53m \, \mathrm{s}$.
\[\bar{a} = \frac{\Delta v}{\Delta t} = \frac{1-200}{0.53m} = \frac{-199}{0.53m} \approx -\frac{375.5}{m} \, \mathrm{ m/s²}\]בעיה 3: צניחה חופשית עם התנגדות אוויר
מומחית לצניחה חופשית צונחת בשדה הכבידה של כדור הארץ. תאוצת הכבידה $g \approx 10 \, \mathrm{m/s^2}$, וכוח התנגדות האוויר פרופורציוני לריבוע המהירות: $f = \beta v^2$.
- מהי המהירות הטרמינלית של הצנחנית?
- מיצאו את גודלה $\beta$ אם משקלה של הצנחנית הוא $600 \mathrm{N}$, כלומר $m \approx 60 \, \mathrm{kg}$, ומהירותה הטרמינלית היא $216 \, \mathrm{km/h}$.
- מהו החוק השני של ניוטון במקרה זה?
הראו שהחוק השני של ניוטון במקרה זה מוביל למשוואה דיפרנציאלית:
\[\frac{dv}{dt} = g(1- \alpha^2 v^2)\]מה היחידות של $\alpha = \sqrt{\frac{\beta}{mg}}$?
בהנחה שהצנחנית החלה ממהירות אפס, כלומר $v(0) = 0$, הראו שמהירותה הרגעית של הצנחנית בכל זמן $t$ נתונה בביטוי:
\[v(t) = \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]- מהו הגבול האסימפטוטי של המהירות הרגעית כאשר $t \to \infty$?
- חשבו את המהירויות של הצנחנית ב-$t = 6 \, \mathrm{s}$ ו-$t = 12 \, \mathrm{s}$.
מהו המיקום של הצנחנית בכל זמן $t$? הראו שהמיקום הוא:
\[z(t) = \frac{m}{\beta}\ln\left[\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right]\]- מהו המיקום של הצנחנית ב-$t = 6 \, \mathrm{s}$ ו-$t = 12 \, \mathrm{s}$?
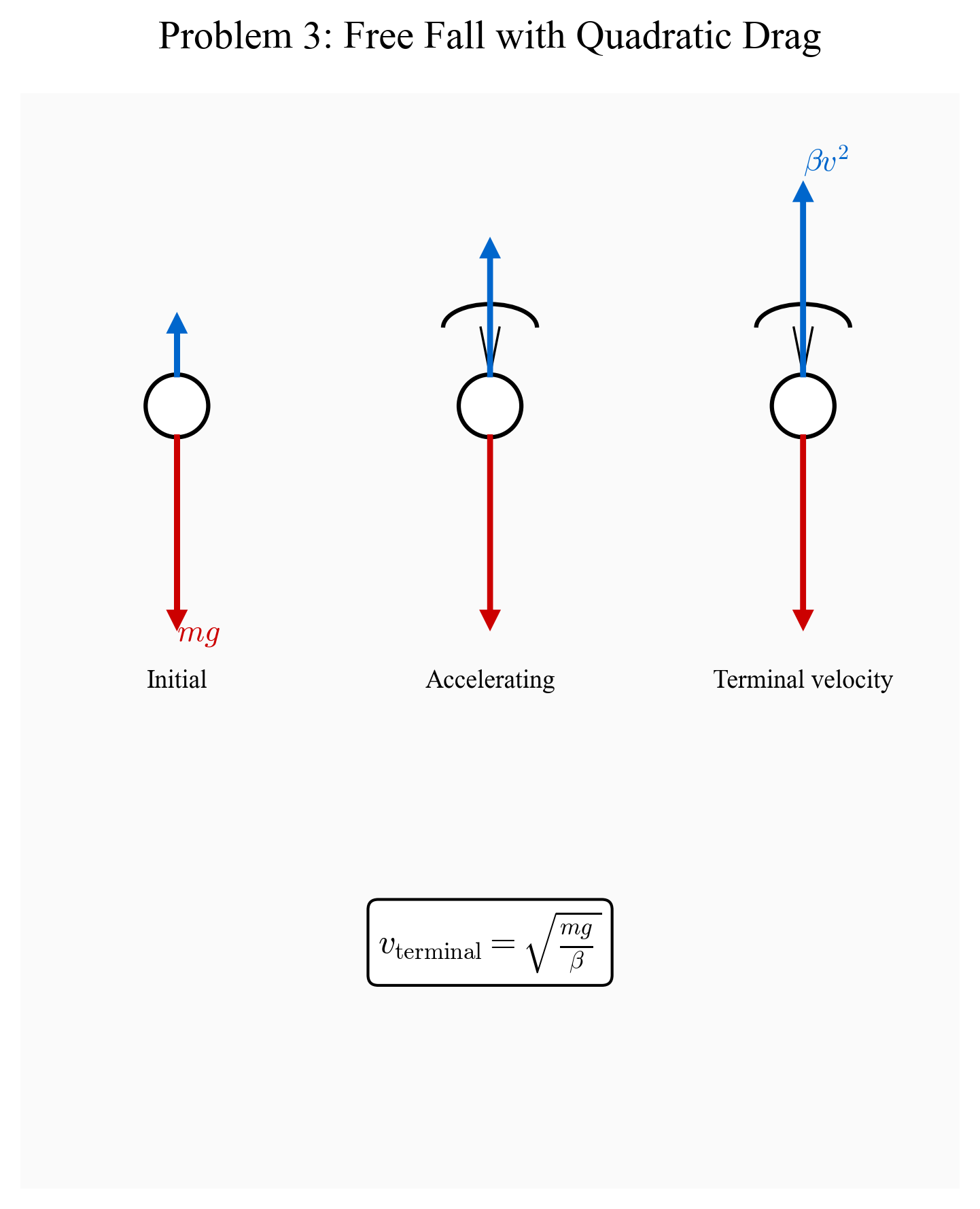
סעיף א: מהירות טרמינלית
הגדרה: מהירות טרמינלית היא המהירות שבה הכוחות מאוזנים והתאוצה מתאפסת.
במצב שיווי משקל:
\[mg = \beta v_{\text{terminal}}^2\]לכן:
\[v_{\text{terminal}} = \sqrt{\frac{mg}{\beta}}\]סעיף ב: מציאת $\beta$
נתון:
- משקל: $W = mg = 600 \, \mathrm{N}$, לכן $m = 60 \, \mathrm{kg}$
- מהירות טרמינלית: $v_{\text{terminal}} = 216 \mathrm{km/h} = 60 \, \mathrm{m/s}$
מהנוסחה:
\[60 = \sqrt{\frac{600}{\beta}}\] \[3600 = \frac{600}{\beta}\] \[\beta = \frac{600}{3600} = \frac{1}{6} \text{ N⋅s²/m²}\]סעיף ג: החוק השני
הכוחות הפועלים:
- כוח כבידה למטה: $mg$
- התנגדות אוויר למעלה: $\beta v^2$
החוק השני (כיוון חיובי כלפי מטה):
\[m\frac{dv}{dt} = mg - \beta v^2\]סעיף ד: משוואה דיפרנציאלית
מהחוק השני:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v^2 = g\left(1 - \frac{\beta v^2}{mg}\right)\]נגדיר $\alpha^2 = \frac{\beta}{mg}$:
\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]יחידות של $\alpha$: $[\alpha^2] = \frac{[\beta]}{[mg]} = \frac{\text{N⋅s²/m²}}{\text{N}} = \text{s²/m²}$
לכן: $[\alpha] = \text{s/m}$
סעיף ה: פתרון המשוואה הדיפרנציאלית
טכניקה: הפרדת משתנים ושימוש באינטגרל של $\frac{1}{1-u^2}$.
לאחר אינטגרציה ושימוש בתנאי התחלה $v(0) = 0$:
\[v(t) = \frac{1}{\alpha}\tanh(\alpha g t)\]כאשר $\alpha = \sqrt{\frac{\beta}{mg}}$, נקבל:
\[v(t) = \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]סעיף ו: גבול אסימפטוטי
\[\lim_{t \to \infty} v(t) = \sqrt{\frac{mg}{\beta}}\lim_{t \to \infty}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right) = \sqrt{\frac{mg}{\beta}} \cdot 1 = v_{\text{terminal}}\](מכיוון ש-$\lim_{x \to \infty}\tanh(x) = 1$)
סעיף ז: חישוב מהירויות
עם הנתונים:
\[m = 60 \, \mathrm{kg}, \qquad \beta = 1/6 \, \mathrm{N⋅s^2/m^2}, \qquad g = 10 \, \mathrm{m/s}^2\]נחשב את $\sqrt{\frac{\beta g}{m}}$:
\[\sqrt{\frac{\beta g}{m}} = \sqrt{\frac{(1/6) \cdot 10}{60}} = \sqrt{\frac{1}{36}} = \frac{1}{6} \text{ s}^{-1}\]- ב-$t = 6$ s: $v(6) = 60\tanh(1) \approx 60 \times 0.762 = 45.7 \, \mathrm{m/s}$
- ב-$t = 12$ s: $v(12) = 60\tanh(2) \approx 60 \times 0.964 = 57.8 \, \mathrm{m/s}$
(המהירויות מתקרבות ל-$60 \, \mathrm{m/s}$, המהירות הטרמינלית)
סעיף ח: מיקום הצונחת
אינטגרציה של המהירות:
\[z(t) = \int_0^t v(t') dt' = \int_0^t \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t'\right) dt'\]תוצאה:
\[z(t) = \frac{m}{\beta}\ln\left[\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right]\]סעיף ט: חישוב מיקומים
- ב-$t = 6$ s: $z(6) = 360\ln[\cosh(1)] \approx 360 \times 0.433 = 156 \, \mathrm{m}$
- ב-$t = 12$ s: $z(12) = 360\ln[\cosh(2)] \approx 360 \times 1.317 = 474 \, \mathrm{m}$
בעיה 4: חבל מחליק מעל מסמר
חבל מסיבי חסר חיכוך באורך $L=1 \, \mathrm{m}$ משתלשל משני צידיו של מסמר חסר חיכוך התקוע אופקית בקיר אנכי. בזמן $t = 0$, החבל ממוקם כך ששליש מאורכו ($L/3$) משתלשל מצידו האחד של המסמר, ושני שליש ($2L/3$) מצידו השני.
כמה זמן ייקח לחבל כולו להחליק מהמסמר?
תנאי ההתחלה:
- בזמן $t = 0$, החבל ממוקם כך ששליש מאורכו ($L/3$) משתלשל מצידו האחד של המסמר (שמאל), ושני שליש ($2L/3$) מצידו השני (ימין). כלומר, $y(t=0) = \frac{2L}{3}$.
- בזמן $t = 0$, החבל לא נע, כלומר מהירותו $v(0) = \dot{y}(0) = 0$.

פתרון בעיית החבל המשתלשל על מסמר
ככל שחולף הזמן, יותר מאסה של החבל עוברת מצד אחד של המסמר לצד השני, מה שמשנה את התאוצה של המערכת.
נקבע ציר $y$ שכיוונו החיובי כלפי מטה. בזמן $t = 0$, הקצה הקצר של החבל (שליש מאורכו) נמצא בצד שמאל של המסמר.
הערה: המתרגל העדיף להשתמש בסימון $z$ במקום $y$. לא קריטי.
בכל רגע נתון, הכוח המניע את החבל הוא ההפרש במשקל בין שני צידי המסמר. ככל שיותר חבל עובר לצד הארוך, הכוח המאיץ את התנועה גדל:
- בצד שמאל של המסמר המסה היא $\frac{L-y}{L}M$, כאשר $y$ הוא אורך החבל המשתלשל מהמסמר בצד שמאל.
- בצד ימין של המסמר המסה היא $\frac{y}{L}M$.
הביטוי לכוח המניע את החבל הוא:
\[\sum F = \frac{y}{L}M \cdot g - \frac{L-y}{L}M \cdot g = M\ddot{y}\] \[\begin{aligned} M\ddot{y} &= \frac{Mg}{L} \times \left[y - (L-y)\right] \\[5pt] &= \frac{Mg}{L} \times \left[y - L + y\right] \\[5pt] &= \frac{Mg}{L} \times \left[2y - L \right] \\[5pt] &= \left(\frac{2y}{L}\right)Mg - Mg \\[5pt] \end{aligned}\]נחלק ב-$M$ ונקבל ונסדר:
\[\boxed{\ddot{y} = \underbrace{\frac{2g}{L}}_{\omega^2} y - g}\]זה ביטוי מהצורה:
\[\ddot{y} = \omega^2 y - g\]כאשר $\omega^2 = \frac{2g}{L}$.
כדי להיעזר בפתרון המוכר (של $\ddot{y} = \omega^2 y$), ניעזר בהזזה: נגדיר מתשנה חדש $z = y - \frac{L}{2}$, כך ש:
\[\ddot{z} = \ddot{y} = \frac{2g}{L}y - g = \frac{2g}{L}\left(z + \frac{L}{2}\right) - g = \frac{2g}{L}z + g - g = \frac{2g}{L}z\]השוויון השמאלי מתקיים מכיוון שהמשתנים שונים בקבוע, ומכאן שהנגזרת השנייה שלהם שקולה.
הפתרון הוא:
\[\boxed{z(t) = A \cosh(\omega t) + B \sinh(\omega t)}\]הערה: שימו לב לפונקציות ההיפרבוליות $\cosh$ ו-$\sinh$, ולא לפונקציות הטריגונומטריות $\cos$ ו-$\sin$, בגלל המקדם של אומגה.
כעת נציב חזרה את $y$:
\[y(t) = z(t) + \frac{L}{2} = A \cosh(\omega t) + B \sinh(\omega t) + \frac{L}{2}\]נציב את תנאי ההתחלה:
- בזמן $t = 0$, $y(0) = \frac{2}{3}L$:
נציב $L = 1 \, \mathrm{m}$:
\[\boxed{A = \frac{2}{3} - \frac{1}{2} = \frac{4}{6} - \frac{3}{6} = \frac{1}{6}}\]- בזמן $t = 0$, $\dot{y}(0) = 0$:
נגזור את הפתרון כדי לקבל את המהירות:
\[\dot{y}(t) = -A \omega \sinh(\omega t) + B \omega \cos(\omega t)\] \[\dot{y}(0) = -A \omega \sinh(0) + B \omega \cos(0) = B \omega\]מכאן נקבל:
\[B = 0\]נציב את $A$ ו-$B$ בחזרה:
\[y(t) = \frac{1}{6} \cosh(\omega t) + \frac{1}{2}\]כעת נציב את $\omega = \sqrt{\frac{2g}{L}}$:
\[y(t) = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right) + \frac{1}{2}\]מציאת הזמן שבו החבל כולו משתלשל
כדי למצוא את הזמן שבו החבל כולו משתלשל, נציב $y(t) = L$:
\[L = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right) + \frac{1}{2}\] \[L - \frac{1}{2} = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right)\]$L=1 \, \mathrm{m}$, ולכן:
\[\frac{1}{2} = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right)\] \[\cosh\left(\sqrt{\frac{2g}{L}} t\right) = 3\] \[\sqrt{\frac{2g}{L}} t = \cosh^{-1}(3)\] \[t = \frac{\cosh^{-1}(3)}{\sqrt{\frac{2g}{L}}}\]נחשב את הערך:
\[t = \frac{\cosh^{-1}(3)}{\sqrt{\frac{2 \cdot 10}{1}}} = \frac{\cosh^{-1}(3)}{\sqrt{20}} \approx \frac{1.7627}{4.472} \approx 0.394 \, \mathrm{s}\]לסיכום, הזמן שייקח לחבל כולו להחליק מהמסמר הוא:
\[\boxed{0.394 \, \mathrm{s}}\]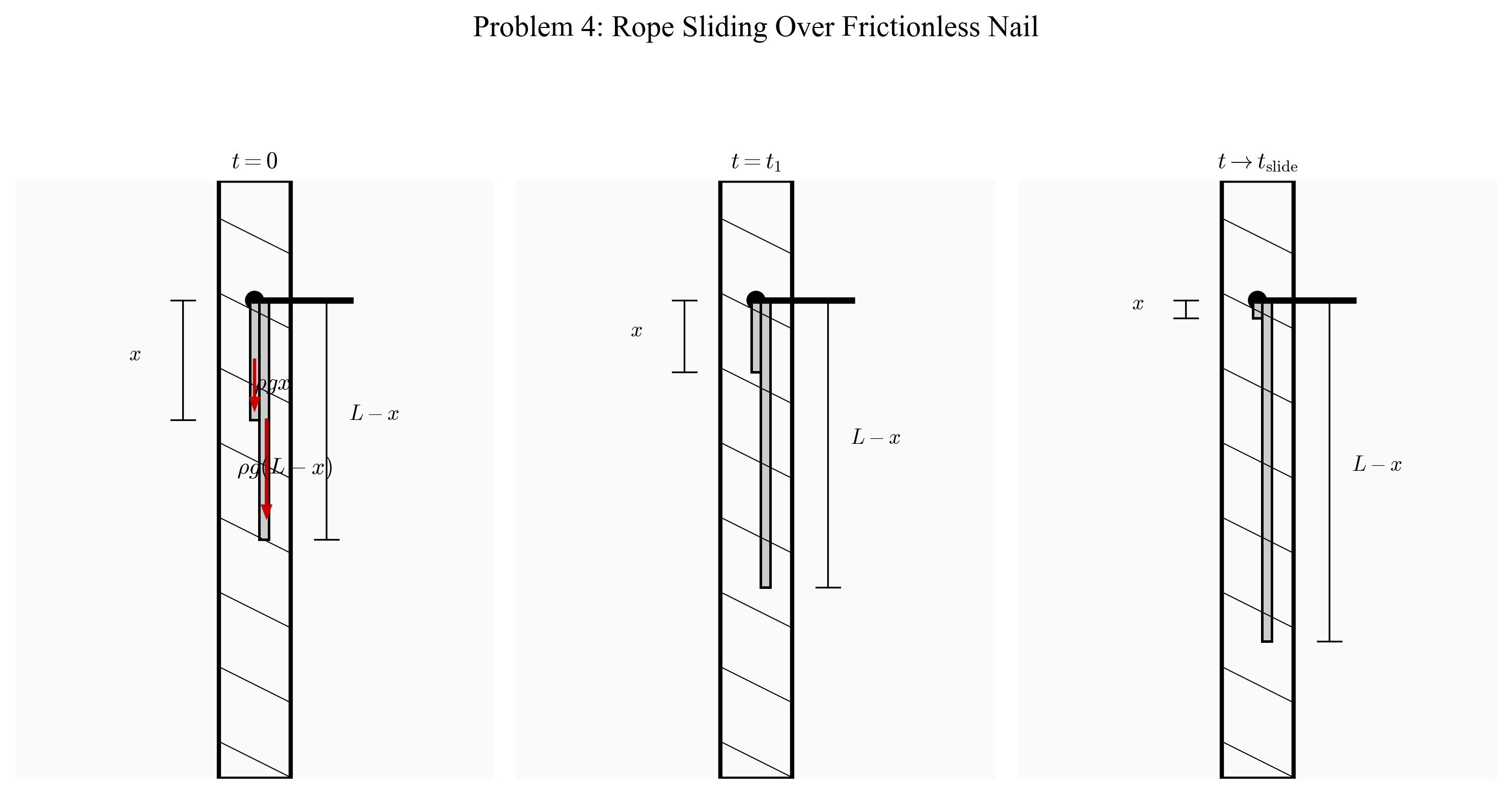
הערה: בתרגול המתרגל פתר את הבעיה בעזרת טור טיילור, אך הפתרון המוצג כאן הוא פתרון מדויק יותר בעזרת משוואות דיפרנציאליות.
בעיה 5: פתרונות של משוואות דיפרנציאליות
סוגי המשוואות הדיפרנציאליות בקורס:
משוואה מסדר ראשון מהצורה $\dot{v} = \alpha v$.
מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למהירות.
הפתרון מהצורה:
\[\boxed{v(t) = A e^{\alpha t}}\]משוואה מסדר ראשון מהצורה $\dot{v} = -\alpha v$.
מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למהירות בכיוון ההפוך.
הפתרון מהצורה:
\[\boxed{v(t) = A e^{-\alpha t}}\]משוואה מסדר שני מהצורה $\ddot{x} = -\omega^2 x$ (תנועה הרמונית).
הפתרון מהצורה:
\[\boxed{x(t) = A\cos(\omega t) + B\sin(\omega t) = C\cos\left(\omega t + \phi\right)}\]משוואה היפרבולית מהצורה $\ddot{x} = \omega^2 x$.
מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למיקום בכיוון ההפוך.
הפתרון מהצורה:
\[\boxed{x(t) = A\cosh(\omega t) + B\sinh(\omega t)}\]
נתון:
\[\alpha = 3 \, \mathrm{Hz}, \qquad \omega = 9 \, \mathrm{Hz}\]הערה: $\omega$ ו-$\alpha$ הם קבועים של תדירות, כלומר שהיחידות שלהם הן $\mathrm{[Hz]}$ או $\mathrm{[1/s]}$.
סעיף א: פתרון משוואות מסדר ראשון
מיצאו את $A$ עבור שני המקרים הראשונים כאשר נתון:
\[x(0) = 1 \, \mathrm{m}. \qquad v(1) = -1 \, \mathrm{m/s}\]עבור $\dot{v} = \alpha v$ (כאשר $\alpha = 3 \mathrm{Hz}$):
\[\begin{aligned} v(t) &= A e^{3t} \\[5pt] v(t=1) &= A e^{3} = -1 \\[5pt] \implies A &= -\frac{1}{e^{3}} \, \mathrm{m} \end{aligned}\]הערה: לא מובן לי מדוע ניתן גם הנתון לגבי $x(0) = 1 \, \mathrm{m}$, מכיוון שמהירות היא נגזרת של מיקום, ולכן תנאי ההתחלה של המהירות מספיק כדי לקבוע את $A$.
לשלמות התמונה אפשר גם לקבל את משוואת המיקום $x(t)$. מהפתרון הכללי של מהירות ומיקום ($v(t) = \dot{x}(t)$):
\[x(t) = \int v(t) dt = \int A e^{3t} dt = \frac{A}{3} e^{3t} + C\]נציב את תנאי ההתחלה $x(0) = 1 \, \mathrm{m}$ ואת $A$ שמצאנו:
\[1 = \frac{-\frac{1}{e^{3}}}{3} e^{0} + C\] \[\boxed{C = 1 + \frac{1}{3e^{3}} \, \mathrm{m}}\]לכן:
\[x(t) = \frac{-\frac{1}{e^{3}}}{3} e^{3t} + 1 + \frac{1}{3e^{3}} = -\frac{1}{3e^{3}} e^{3t} + 1 + \frac{1}{3e^{3}}\]נסדר את התוצאה:
\[\boxed{x(t) = 1 + \frac{1}{3e^{3}} - \frac{1}{3e^{3}} e^{3t}}\]הערה: אפשר להיעזר בווקטור המקום בנקודת ההתחלה בשביל לתא את וקטור המקום הכללי:
\[x(t) = x_0 + \int_0^t v(t') dt' = 1 + \int_0^t A e^{3t'} dt' = 1 + A\left[e^{3t'}\right]_0^t = 1 + A\left(e^{3t} - e^{0}\right) = 1 + A\left(e^{3t} - 1\right)\]נציב את $A$ שמצאנו:
\[x(t) = 1 -\frac{1}{3e^{3}}\left(e^{3t} - 1\right) = 1 - \frac{1}{3e^{3}} e^{3t} + \frac{1}{3e^{3}}\] \[\boxed{x(t) = 1 + \frac{1}{3e^{3}} - \frac{1}{3e^{3}} e^{3t}}\]עבור $\dot{v} = -\alpha v$ (כאשר $\alpha = 3$ Hz):
\[v(t) = A e^{-3t}\]באופן דומה למקודם, נשתמש בתנאי ההתחלה של המהירות:
\[\begin{aligned} v(t=1) &= A e^{-3} = -1 \\[5pt] A &= -e^{3} \, \mathrm{m} \end{aligned}\]לכן:
\[\boxed{A = -e^{3} \, \mathrm{m}}\]סעיף ב: תנועה הרמונית
משוואה:
\[\ddot{x} = -\omega^2 x\]פתרון כללי:
\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]נתון:
\[x(0) = 2 \, \mathrm{m}, \qquad v(\pi/\omega) = 2 \, \mathrm{m/s}\]נדרש: מצאו את $A, \, B, \, C, \, \phi$.
פתרון
מ-$x(0) = 2$:
\[\boxed{A = 2 \, \mathrm{m}}\]המהירות (נגזרת הפתרון):
\[v(t) = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\]מ-$v(\pi/\omega) = 2 \, \mathrm{m/s}$:
\[2 = -2\omega \cdot 0 + B\omega \cdot (-1) = -B\omega\]נציב $\omega = 3 \, \mathrm{Hz}$:
\[\boxed{B = -\frac{2 \, \mathrm{[m/s]}}{\omega \, \mathrm{[1/s]}} = -\frac{2}{3} \, \mathrm{m}}\]ניעזר בנוסחה הנוספת למציאת $C$ ו-$\phi$:
סעיף ג: משוואה היפרבולית
משוואה:
\[\ddot{x} = \omega^2 x\]פתרון כללי:
\[x(t) = A\cosh(\omega t) + B\sinh(\omega t)\]נתון:
\[x(0) = 0 \, \mathrm{m}, \qquad v(1) = \ln 3\, \, \mathrm{m/s}\]מ-$x(0) = 0$:
\[\boxed{A = 0 \, \mathrm{m}}\]המהירות:
\[v(t) = B\omega\cosh(\omega t)\]מ-$v(1) = \ln 3$:
\[\ln 3 = B\omega\cosh(\omega)\] \[B = \frac{\ln 3}{\omega\cosh(\omega)}\]נציב $\omega = 3 \, \mathrm{Hz}$:
\[\boxed{B = \frac{\ln 3}{3\cosh(3)} = \frac{\ln 3}{3\cdot 10.0677} \approx 0.109 \, \mathrm{m}}\]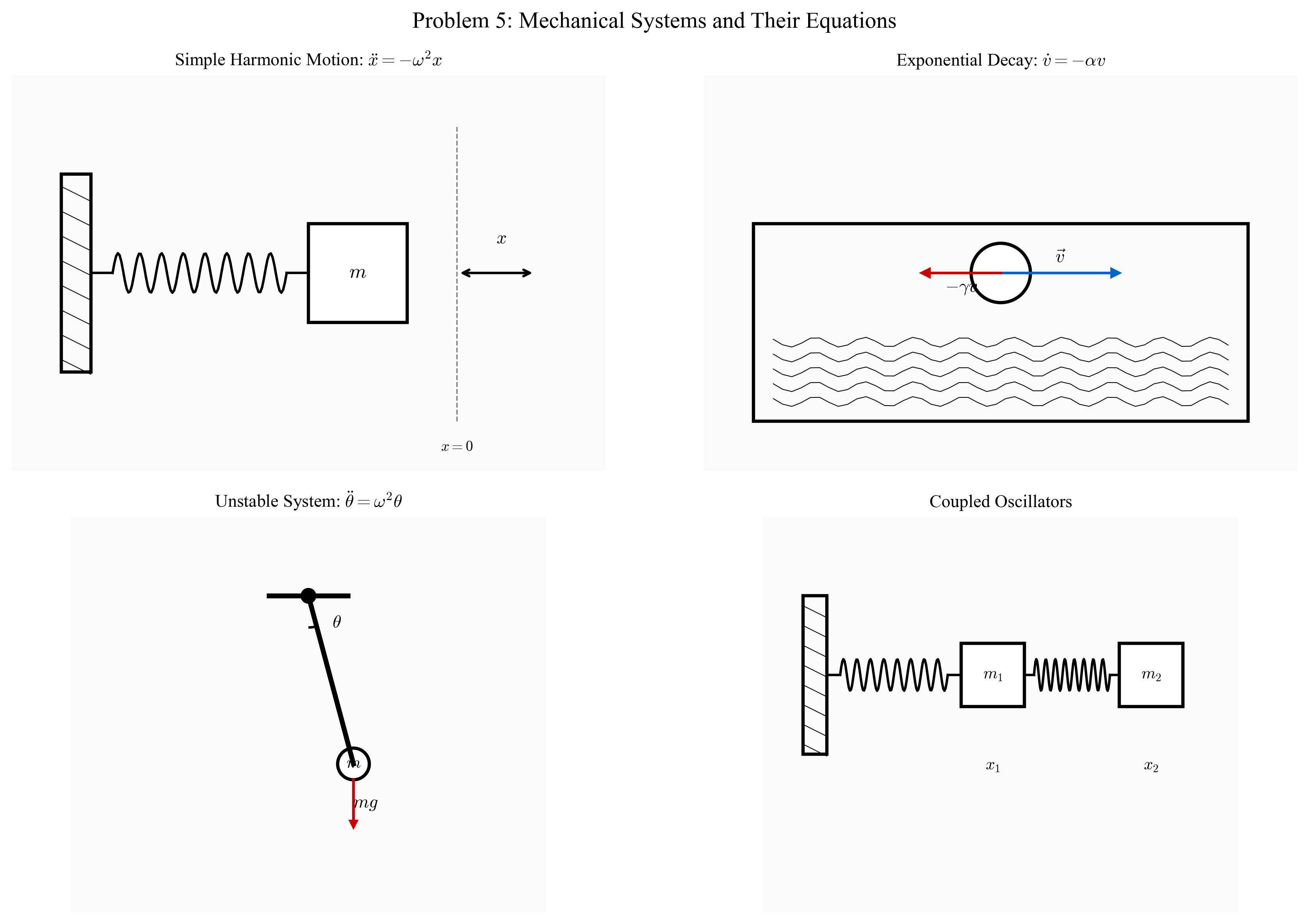 דור פסקל
דור פסקל