חזרה: ארבע משוואות מקסוול
צורה דיפרנציאלית ואינטגרלית
| שם | צורה דיפרנציאלית | צורה אינטגרלית |
|---|---|---|
| חוק גאוס החשמלי | $\vec{\nabla} \cdot \vec{D} = \rho_{free}$ | $\oint_S \vec{D} \cdot d\vec{A} = Q_{free,enc}$ |
| חוק גאוס המגנטי | $\vec{\nabla} \cdot \vec{B} = 0$ | $\oint_S \vec{B} \cdot d\vec{A} = 0$ |
| חוק פאראדיי | $\vec{\nabla} \times \vec{E} = -\dfrac{\partial \vec{B}}{\partial t}$ | $\oint_C \vec{E} \cdot d\vec{l} = -\dfrac{d}{dt}\int_S \vec{B} \cdot d\vec{A}$ |
| חוק אמפר-מקסוול | $\vec{\nabla} \times \vec{H} = \vec{J} + \dfrac{\partial \vec{D}}{\partial t}$ | $\oint_C \vec{H} \cdot d\vec{l} = I_{free,enc} + \dfrac{d}{dt}\int_S \vec{D} \cdot d\vec{A}$ |
קשרי המבנה
| קשר | משמעות |
|---|---|
| $\vec{D} = \epsilon \vec{E}$ | $\epsilon$ = פרמיטיביות (Permittivity) - כמה החומר “מרשה” לשדה חשמלי לעבור דרכו |
| $\vec{B} = \mu \vec{H}$ | $\mu$ = פרמאביליות (Permeability) - כמה החומר “מרשה” לשדה מגנטי לעבור דרכו |
יחידות חשובות
| גודל | יחידות |
|---|---|
| $\epsilon$ (פרמיטיביות) | $\dfrac{\text{F}}{\text{m}}$ (פאראד למטר) |
| $\mu$ (פרמאביליות) | $\dfrac{\text{H}}{\text{m}}$ (הנרי למטר) |
| כא”מ $\mathcal{E}$ | $\text{V}$ (וולט) |
משמעות פיזיקלית
- חוק גאוס החשמלי: מטענים חופשיים הם מקור השפיעה של $\vec{D}$
- חוק גאוס המגנטי: אין מונופולים מגנטיים (קווי $\vec{B}$ תמיד סגורים)
- חוק פאראדיי: שינוי ב-$\vec{B}$ יוצר “מערבולות חשמליות” (שדה $\vec{E}$ עירבולי)
- חוק אמפר-מקסוול: זרמים ושינוי ב-$\vec{D}$ יוצרים “מערבולות מגנטיות” (שדה $\vec{H}$ עירבולי)
שאלה 1: חישוב זרם מחוק אמפר
נתון שדה מגנטי (ביחידות טסלה):
\[\vec{B} = 2y^2 \hat{y}\]פרמאביליות התלויה במיקום:
\[\mu(x) = \mu_0(1 + x)\]חשבו את הזרם החופשי הכולל $I_f$ בכיוון $+\hat{z}$ דרך ריבוע שקודקודיו:
\[A = (0,0), \quad B = (1,0), \quad C = (1,1), \quad D = (0,1)\]המסלול: $A \to B \to C \to D \to A$ (נגד כיוון השעון, לפי כלל יד ימין עבור $+\hat{z}$)
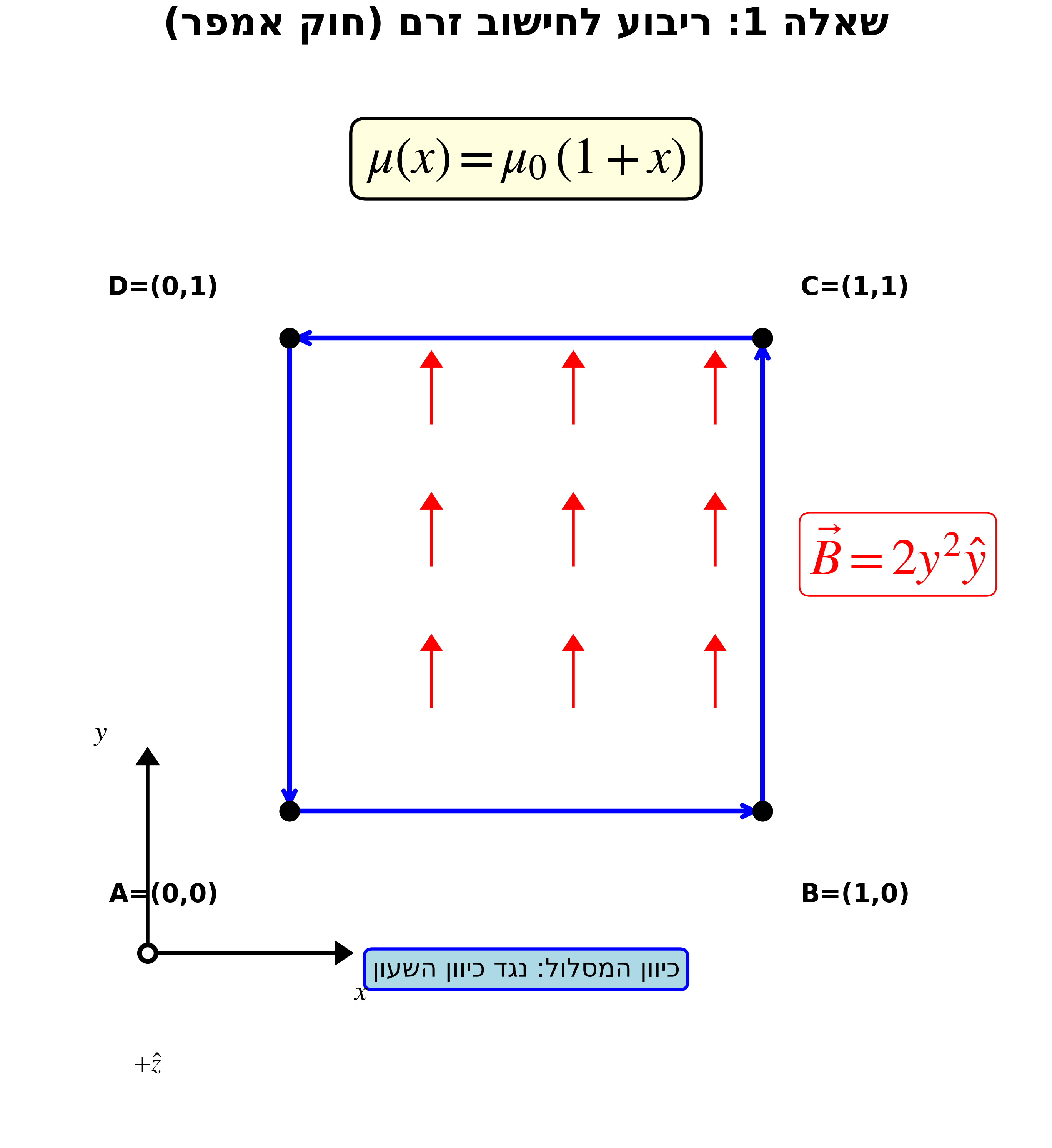
פתרון שאלה 1
שלב 1: חישוב $\vec{H}$ מקשרי המבנה:
\[\vec{B} = \mu \vec{H} \Rightarrow \vec{H} = \frac{\vec{B}}{\mu} = \frac{2y^2}{\mu_0(1+x)} \hat{y}\]שלב 2: שימוש בחוק אמפר (במצב מגנטוסטטי, ללא שינוי ב-$\vec{D}$):
\[I_f = \oint_C \vec{H} \cdot d\vec{l}\]שלב 3: פירוק לארבעה קטעים:
| קטע | מסלול | $d\vec{l}$ | $\vec{H} \cdot d\vec{l}$ |
|---|---|---|---|
| $A \to B$ | $y=0$, $x: 0 \to 1$ | $dx\hat{x}$ | $\dfrac{2(0)^2}{\mu_0(1+x)}\hat{y} \cdot dx\hat{x} = 0$ |
| $B \to C$ | $x=1$, $y: 0 \to 1$ | $dy\hat{y}$ | $\dfrac{2y^2}{\mu_0(1+1)}\hat{y} \cdot dy\hat{y} = \dfrac{2y^2}{2\mu_0}dy$ |
| $C \to D$ | $y=1$, $x: 1 \to 0$ | $-dx\hat{x}$ | $\dfrac{2(1)^2}{\mu_0(1+x)}\hat{y} \cdot (-dx\hat{x}) = 0$ |
| $D \to A$ | $x=0$, $y: 1 \to 0$ | $-dy\hat{y}$ | $\dfrac{2y^2}{\mu_0(1+0)}\hat{y} \cdot (-dy\hat{y}) = -\dfrac{2y^2}{\mu_0}dy$ |
שלב 4: חישוב האינטגרלים:
\[\begin{aligned} I_f &= 0 + \int_0^1 \frac{y^2}{\mu_0}dy + 0 + \int_1^0 \left(-\frac{2y^2}{\mu_0}\right)dy \\[6pt] &= \frac{1}{\mu_0}\left[\frac{y^3}{3}\right]_0^1 + \frac{2}{\mu_0}\left[\frac{y^3}{3}\right]_1^0\\[6pt] &= \frac{1}{\mu_0} \cdot \frac{1}{3} + \frac{2}{\mu_0}\left(0 - \frac{1}{3}\right) = \frac{1}{3\mu_0} - \frac{2}{3\mu_0} \end{aligned}\] \[\boxed{I_f = -\frac{1}{3\mu_0} \text{ [A]}}\]הערה: הסימן השלילי מציין שכיוון הזרם הפוך ל-$+\hat{z}$, כלומר הזרם זורם בכיוון $-\hat{z}$.
שאלה 2: חישוב מטען חופשי מחוק גאוס
נתון שדה חשמלי בקואורדינטות גליליות:
\[\vec{E} = r\hat{z}\]גליל ברדיוס $R$ ואורך $L$, צירו על ציר ה-$z$, ממורכז סביב הראשית.
מקדם דיאלקטרי:
\[\epsilon = \begin{cases} \epsilon_2 & z > 0 \\ \epsilon_0 & z < 0 \end{cases}\]מצאו את המטען החופשי הכולל $Q_{free}$ בתוך הגליל.
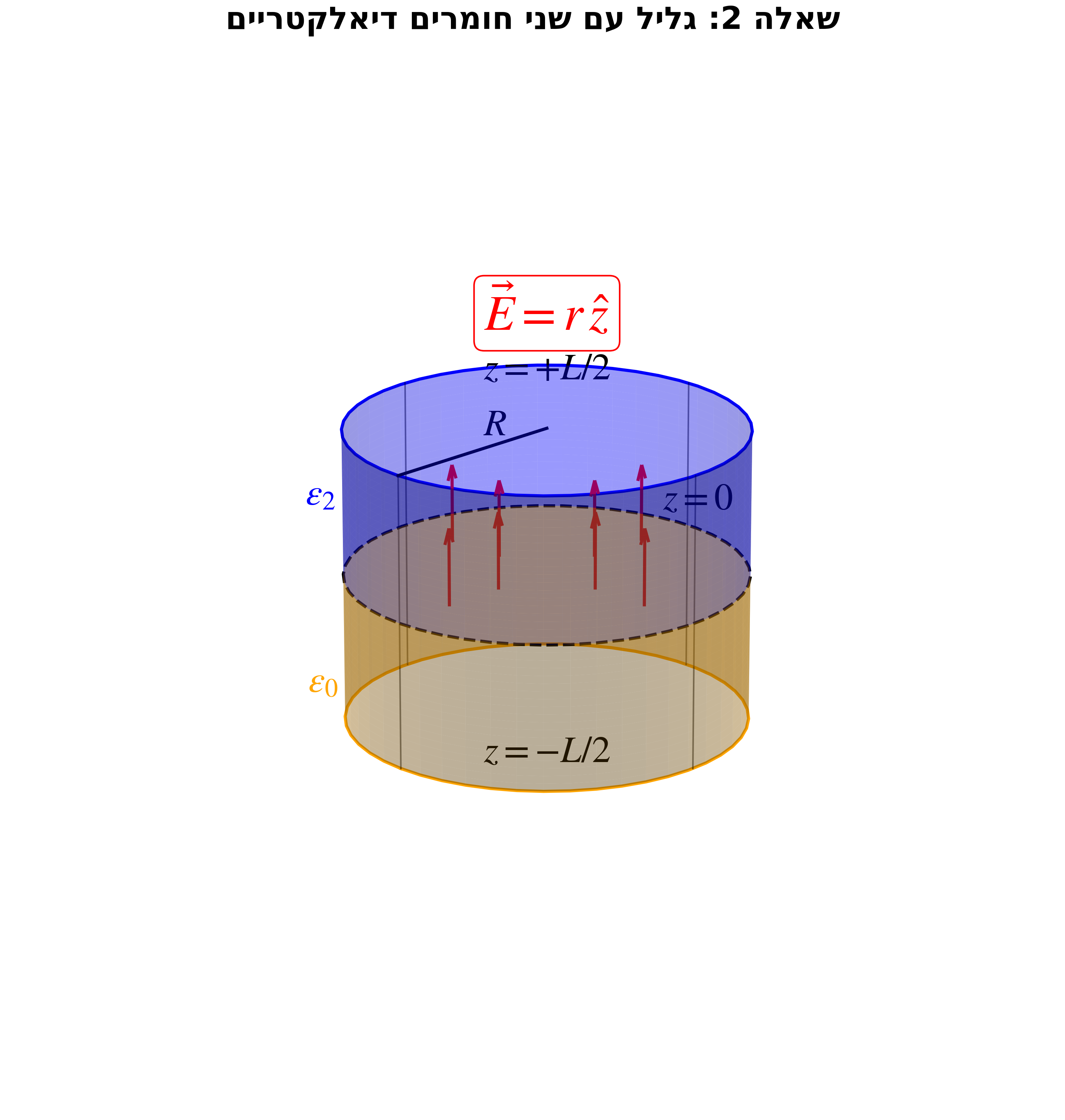
פתרון שאלה 2
שלב 1: חישוב $\vec{D}$:
\[\vec{D} = \epsilon \vec{E} = \epsilon \cdot r\hat{z}\]שלב 2: שימוש בחוק גאוס בצורה אינטגרלית:
\[Q_{free} = \oint_S \vec{D} \cdot d\vec{A}\]שלב 3: פירוק המשטח הסגור:
הגליל מורכב משלושה משטחים:
-
בסיס עליון ($z = +L/2$): עם $\epsilon_2$, ואלמנט שטח:
\[d\vec{A} = +\hat{z} \cdot r \, dr \, d\phi\] -
בסיס תחתון ($z = -L/2$): עם $\epsilon_0$, ואלמנט שטח:
\[d\vec{A} = -\hat{z} \cdot r \, dr \, d\phi\] -
מעטפת צדדית:
\[d\vec{A} = \hat{r} \cdot r \, d\phi \, dz\]← תרומה אפס כי $\vec{D} \perp d\vec{A}$
שלב 4: חישוב האינטגרלים:
בסיס עליון:
\[\Phi_{\text{top}} = \iint \vec{D} \cdot d\vec{A} = \int_0^{2\pi} \int_0^R \epsilon_2 r \cdot (+1) \cdot r \, dr \, d\phi = 2\pi\epsilon_2 \int_0^R r^2 \, dr = 2\pi\epsilon_2 \cdot \frac{R^3}{3}\]בסיס תחתון: מתקבל באופן דומה רק עם סימן אחר וערך שונה של הפרמיטיביות:
\[\Phi_{\text{bottom}} = \iint \vec{D} \cdot d\vec{A} = \int_0^{2\pi} \int_0^R \epsilon_0 r \cdot (-1) \cdot r \, dr \, d\phi = -2\pi\epsilon_0 \cdot \frac{R^3}{3}\]שלב 5: סיכום:
\[Q_{free} = \frac{2\pi R^3}{3}\epsilon_2 - \frac{2\pi R^3}{3}\epsilon_0\] \[\boxed{Q_{free} = \frac{2\pi R^3}{3}(\epsilon_2 - \epsilon_0) \text{ [C]}}\]הערה: התוצאה אינה תלויה ב-$L$ כי השדה $\vec{E}$ אחיד בכיוון $\hat{z}$ ואין תרומה מהמעטפת הצדדית. המטען למעשה “יושב” על המשטח $z=0$ בממשק בין שני החומרים.
שאלה 3: כא”מ מושרה בחצי גליל (חוק פאראדיי)
נתון חצי גליל ברדיוס $R$ ואורך $L$, מונח על מישור ה-$xy$.
שדה מגנטי משתנה בזמן בתוך חצי הגליל:
\[\vec{B} = B_0 \frac{t}{T} \hat{z}\]חומר פרמגנטי עם $\mu = 2\mu_0$.
מצאו את הכא”מ המושרה בלולאה (שפת חצי הגליל).
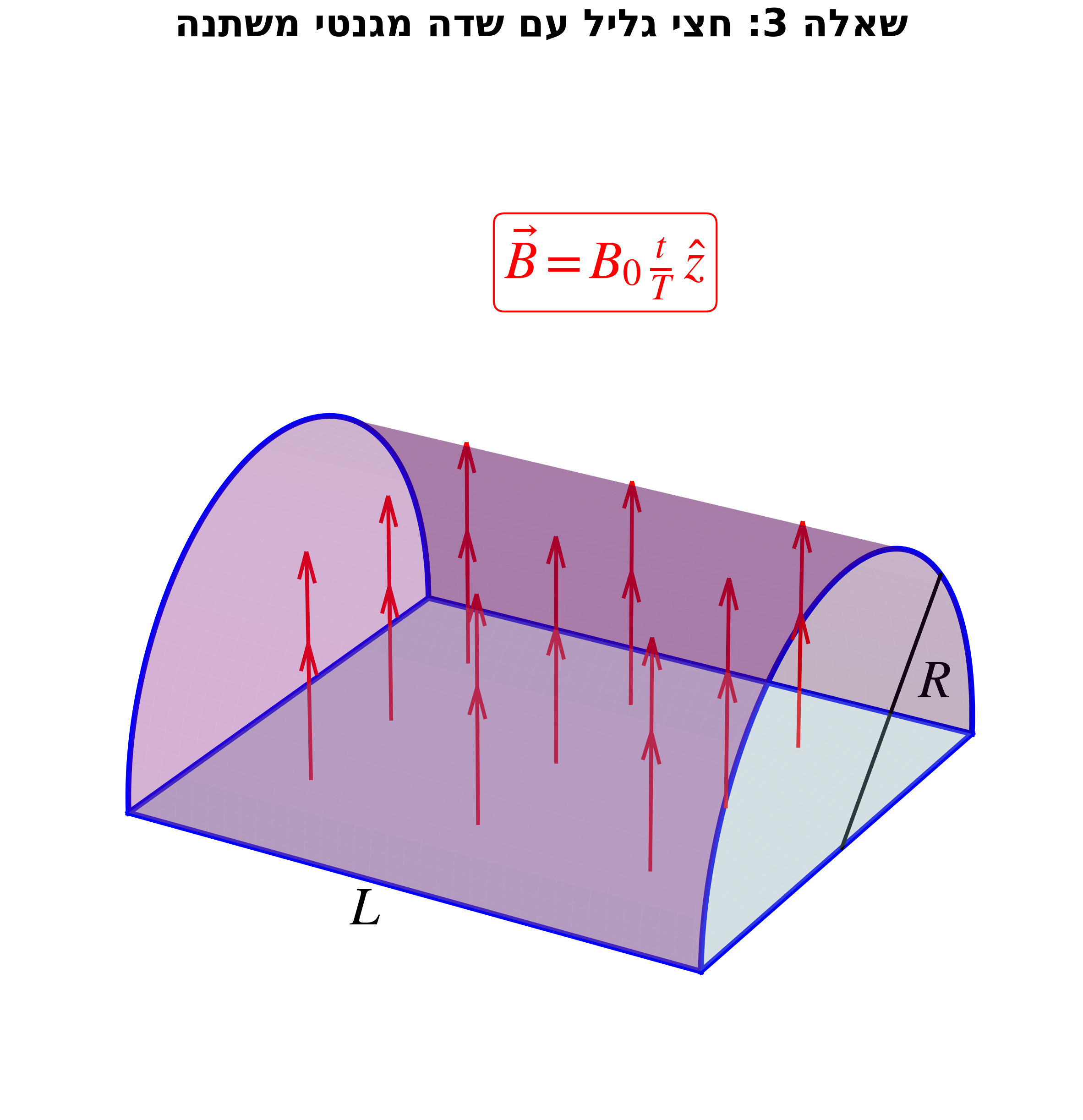
פתרון שאלה 3
הטריק בשאלה הוא לזהות שניתן להסתכל על השטף דרך בסיס חצי הגליל (מלבן), כי שאר המשטחים לא תורמים לשטף (השדה $\vec{B}$ ניצב למעטפת הצדדית - שני חצאי הבסיסים).
\[A = (2R) \times (L) = 2RL\]חישוב השטף המגנטי: (דרך הבסיס של חצי הגליל - מישור ה-$xy$, כיוון $\hat{z}$)
\[\Phi_B = \int_S \vec{B} \cdot d\vec{A} = B(t) \, A = B_0 \frac{t}{T} \cdot 2RL\]חישוב הכא”מ המושרה: (נגזור את השטף לפי הזמן)
\[\mathcal{E} = -\frac{d\Phi_B}{dt} = -\frac{d}{dt}\left(B_0 \frac{t}{T} \cdot 2RL\right) = -B_0 \frac{2RL}{T}\] \[\boxed{\mathcal{E} = -\frac{2B_0 RL}{T} \text{ [V]}}\]הערות:
- הסימן השלילי מציין את כיוון הכא”מ לפי חוק לנץ
- הפרמאביליות $\mu$ לא משפיעה על חישוב הכא”מ כי חוק פאראדיי משתמש ב-$\vec{B}$ ישירות
- כא”מ = כוח אלקטרומוטורי (EMF - Electromotive Force)
שאלה 4: כא”מ וזרם מושרה בקליפה גלילית
נתונה קליפה גלילית מוליכה ברדיוסים $a < b$ ואורך $L$.
שדה מגנטי משתנה בזמן באזור $r < a$:
\[\vec{B} = B(t)\hat{z}, \quad \frac{dB}{dt} = \alpha = \text{const}\]מצאו:
- הכא”מ המושרה בלולאה מעגלית ברדיוס $r$ כאשר $a < r < b$
- כיוון הזרם המושרה בקליפה
- כיוון השדה המגנטי שהזרם המושרה משרה
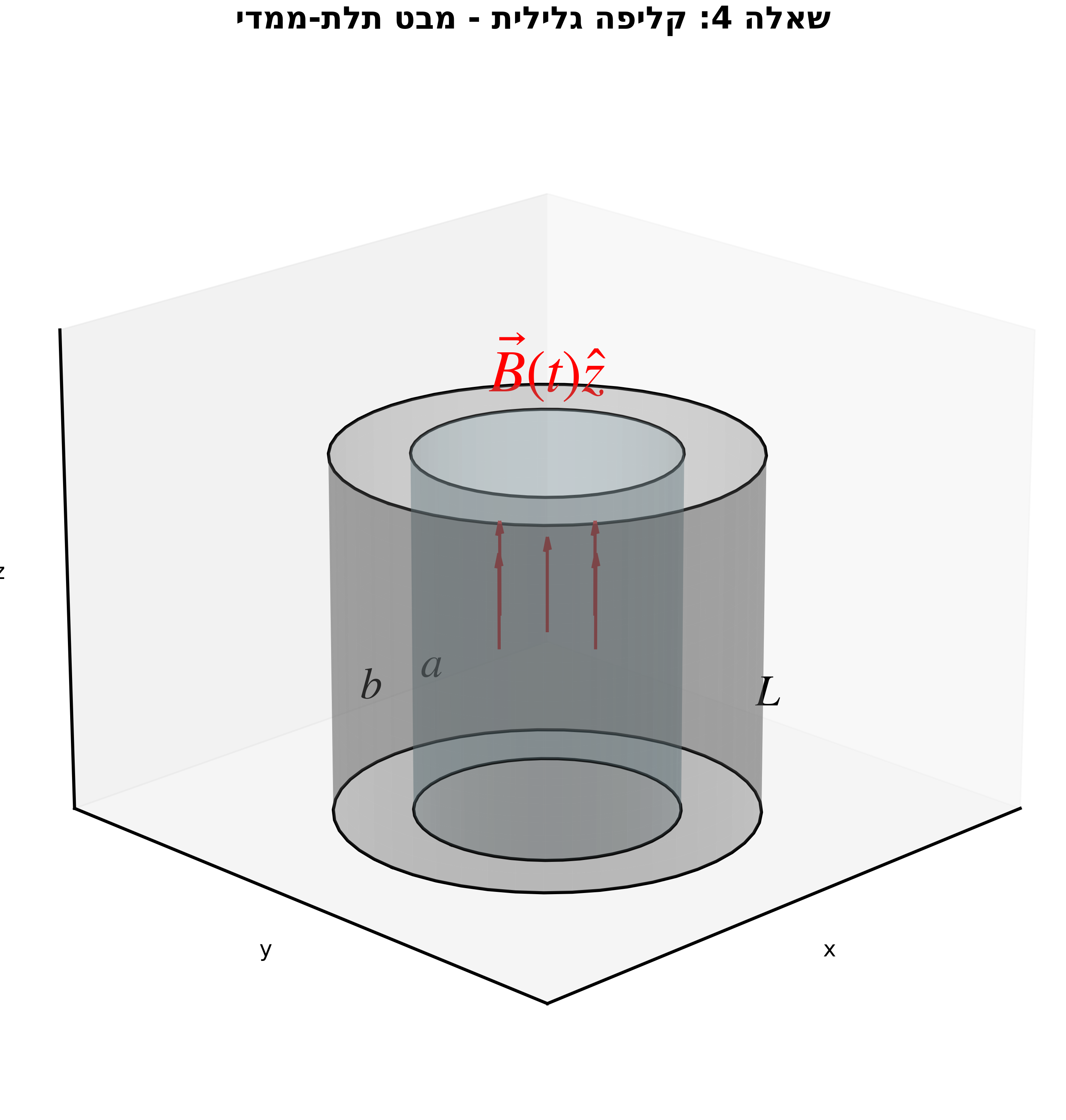
פתרון שאלה 4
חלק 1: חישוב הכא”מ
שימוש בחוק פאראדיי:
\[\mathcal{E} = -\frac{d}{dt} \int_S \vec{B} \cdot d\vec{A}\]חשוב: השדה $\vec{B}$ קיים רק באזור $r < a$, אבל הלולאה ברדיוס $r > a$. לכן, השטף המגנטי דרך הלולאה הוא רק דרך השטח $r < a$:
\[\Phi_B = B(t) \cdot \pi a^2\]גזירה:
\[\frac{d\Phi_B}{dt} = \frac{dB}{dt} \cdot \pi a^2 = \alpha \pi a^2\]הכא”מ:
\[\boxed{\mathcal{E} = -\alpha \pi a^2 \text{ [V]}}\]שימו לב: הכא”מ תלוי ב-$a$ (רדיוס האזור עם השדה) ולא ב-$r$ (רדיוס הלולאה), כל עוד $r > a$.
חלק 2: כיוון הזרם המושרה
שימוש בחוק לנץ:
נתון: $\frac{dB}{dt} = \alpha > 0$ (נניח $\alpha$ חיובי)
המשמעות: השדה המגנטי $\vec{B}$ גדל בכיוון $+\hat{z}$.
לפי חוק לנץ, הזרם המושרה ייצור שדה מגנטי שמתנגד לשינוי, כלומר בכיוון $-\hat{z}$.
לפי כלל יד ימין: כדי ליצור שדה בכיוון $-\hat{z}$, הזרם חייב לזרום בכיוון השעון (כאשר מסתכלים מלמעלה, מכיוון $+\hat{z}$).
\[\boxed{\text{The induced current flows clockwise (Clockwise).}}\]חלק 3: כיוון השדה המגנטי המושרה
השדה המגנטי שהזרם המושרה יוצר הוא בכיוון הפוך לשדה המקורי:
\[\boxed{\vec{B}_{induced} \text{ in direction } -\hat{z}}\]סיכום: מתי להשתמש בכל משוואה
| רוצים למצוא | משוואה לשימוש | הערות |
|---|---|---|
| מטען חופשי $Q_{free}$ | חוק גאוס החשמלי | $\oint \vec{D} \cdot d\vec{A} = Q_{free}$ |
| זרם חופשי $I_{free}$ | חוק אמפר | $\oint \vec{H} \cdot d\vec{l} = I_{free}$ (מגנטוסטטיקה) |
| כא”מ מושרה $\mathcal{E}$ | חוק פאראדיי | $\mathcal{E} = -\dfrac{d\Phi_B}{dt}$ |
| כיוון זרם מושרה | חוק לנץ | הזרם מתנגד לשינוי בשטף |