חלק א’: עבודה ואנרגיה פוטנציאלית חשמלית
עבודה של שדה חשמלי על מטען
העבודה שהשדה החשמלי מבצע על מטען $q$:
\[W = -q \cdot \Delta V = -q(V_B - V_A)\]כאשר:
- $\Delta V$ = הפרש הפוטנציאלים
- $V_A$ = פוטנציאל בנקודה $A$
- $V_B$ = פוטנציאל בנקודה $B$
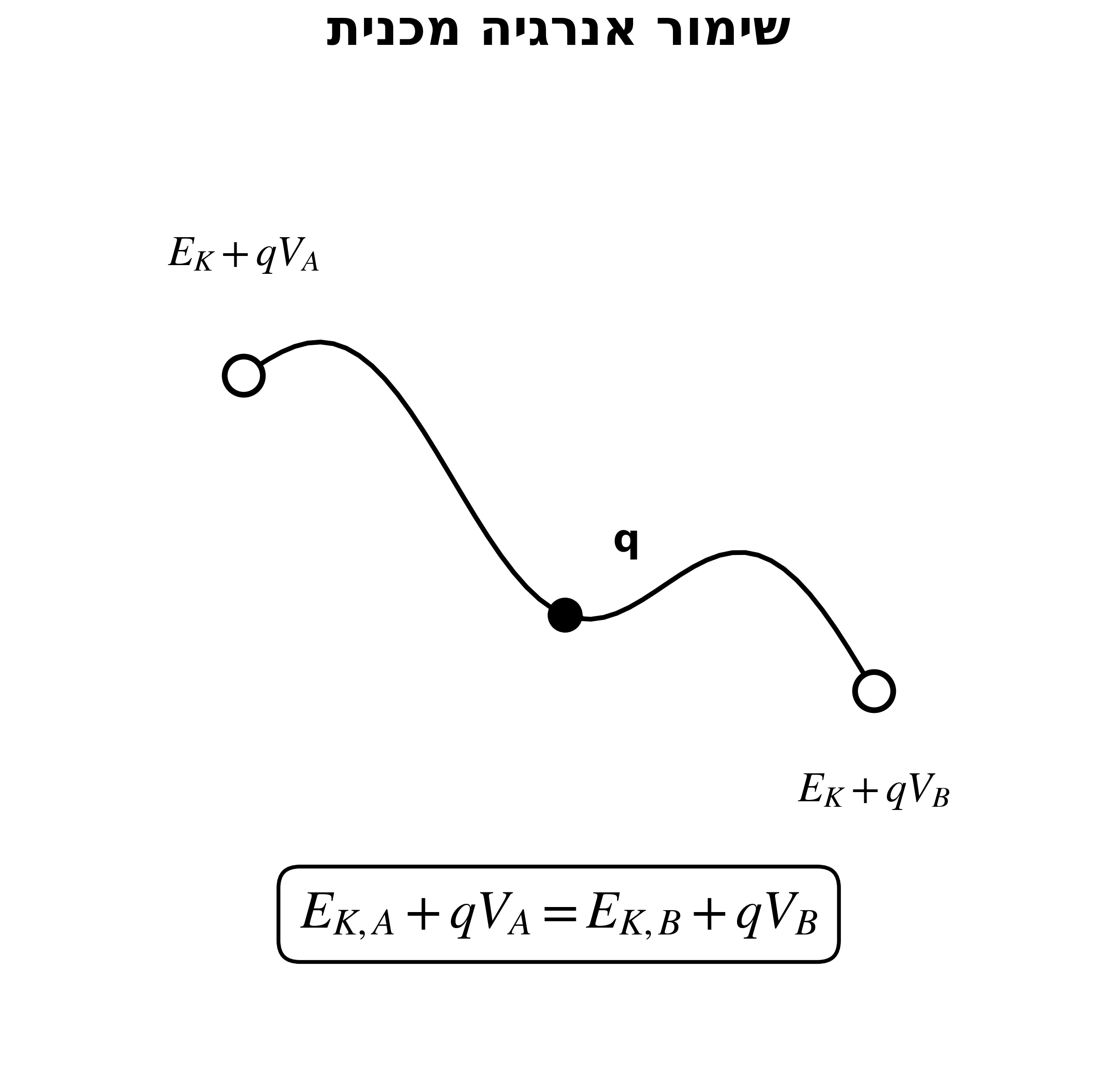
חוק שימור האנרגיה המכנית (האנלוג החשמלי)
המשוואה:
\[E_{K,A} + qV_A = E_{K,B} + qV_B\]משמעות: האנרגיה המכנית בתחילת התהליך שווה לאנרגיה המכנית בסוף התהליך
האנרגיה המכנית הכוללת:
\[E_{mechanical} = E_{kinetic} + E_{potential}\] \[E = \frac{1}{2}mv^2 + qV\]הערה: כשרלוונטי, יש להוסיף גם אנרגיות פוטנציאליות אחרות (כמו כבידה).
למה שימור אנרגיה עדיף על החוק השני של ניוטון?
הבעיה עם החוק השני של ניוטון
כשיש תנועה בשדה חשמלי משתנה:
- הכוח משתנה עם המרחק
- מקבלים משוואה דיפרנציאלית מסובכת
- קשה מאוד לפתור אותה
היתרון של שימור אנרגיה
- לא צריך לפתור משוואות דיפרנציאליות
- מספיק לחשב את הפוטנציאל בשתי נקודות
- הפתרון ישיר ופשוט
דוגמה: מטען נופל בין שני מטענים
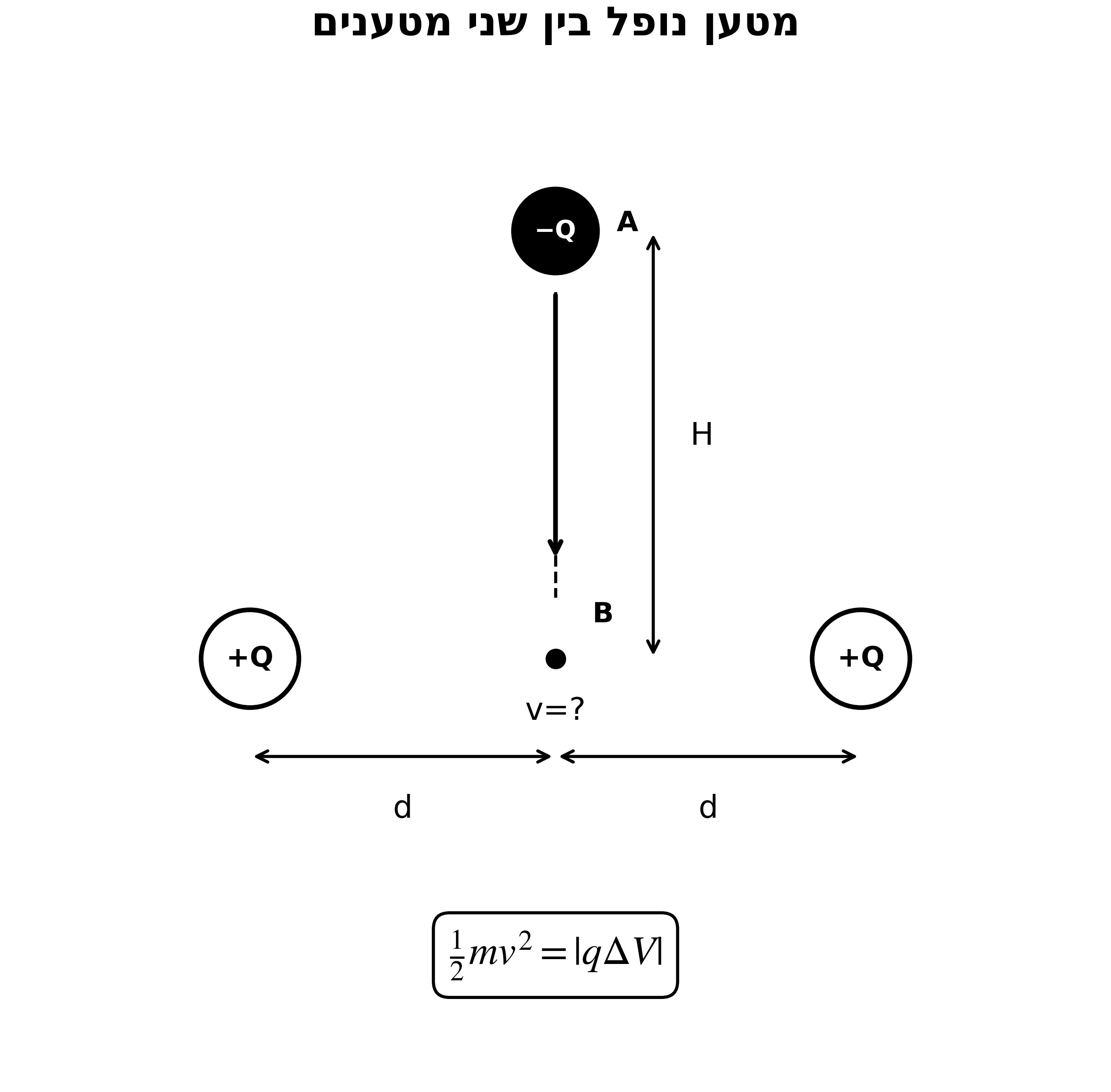
הסיטואציה
-Q (מטען שמשתחרר) ↑ │ H │ ↓ ←───── d ─────→ ←───── d ─────→ • • Q (+) Q (+)
- שני מטענים $+Q$ במרחק $d$ מהראשית (על ציר $x$)
- מטען $-Q$ משתחרר מגובה $H$ (על ציר $y$)
- שאלה: באיזו מהירות יחצה את הראשית?
הפתרון
שלב 1: חישוב הפוטנציאל למעלה (נקודה A)
\[V_A = 2 \cdot \frac{KQ}{\sqrt{d^2 + H^2}}\]הסבר: שני המטענים תורמים באופן שווה (סופרפוזיציה של פוטנציאלים). בפוטנציאל אגב אין כיוון - סכום סקלרי.
שלב 2: חישוב הפוטנציאל בראשית (נקודה B)
\[V_B = 2 \cdot \frac{KQ}{d}\]שימו לב אגב שזה לא אפס, למרות שהשדה אולי מתאפס.
שלב 3: חישוב הפרש הפוטנציאלים
\[\Delta V = V_B - V_A = 2KQ \left( \frac{1}{D} - \frac{1}{\sqrt{D^2 + H^2}} \right)\]שלב 4: שימור אנרגיה
אם המטען משתחרר ממנוחה:
\[\frac{1}{2}mv^2 = |q \cdot \Delta V|\]כי ?
שלב 5: חילוץ המהירות
\[v = \sqrt{\frac{2|q \cdot \Delta V|}{m}}\]נקודות חשובות על פוטנציאל
| תכונה | הסבר |
|---|---|
| סקלרי | פוטנציאל הוא גודל סקלרי, לא וקטור |
| סופרפוזיציה | פוטנציאלים מתחברים אלגברית (לא וקטורית!) |
| יחידות | וולט (V) = ג’אול/קולון - אנרגיה פוטנציאלית ליחידת מטען |
| נוסחה | $V = \frac{KQ}{r}$ למטען נקודתי |
זכרו: $V = \frac{KQ}{r}$ (לא $r^2$!) - זה פוטנציאל, לא שדה!
מתי כבידה רלוונטית?
כבידה זניחה (רוב המקרים)
- אלקטרונים/פרוטונים: מסה קטנה מאוד ($\sim 10^{-31} \, \mathrm{kg}$)
- הכוח החשמלי » כוח הכבידה
- התאוצה החשמלית עצומה
כבידה רלוונטית
- גופים מסיביים (גרמים ומעלה)
- מטענים קטנים יחסית
- יש להוסיף את האנרגיה הפוטנציאלית הכבידתית:
חלק ב’: דוגמה - שתי קליפות כדוריות קונצנטריות
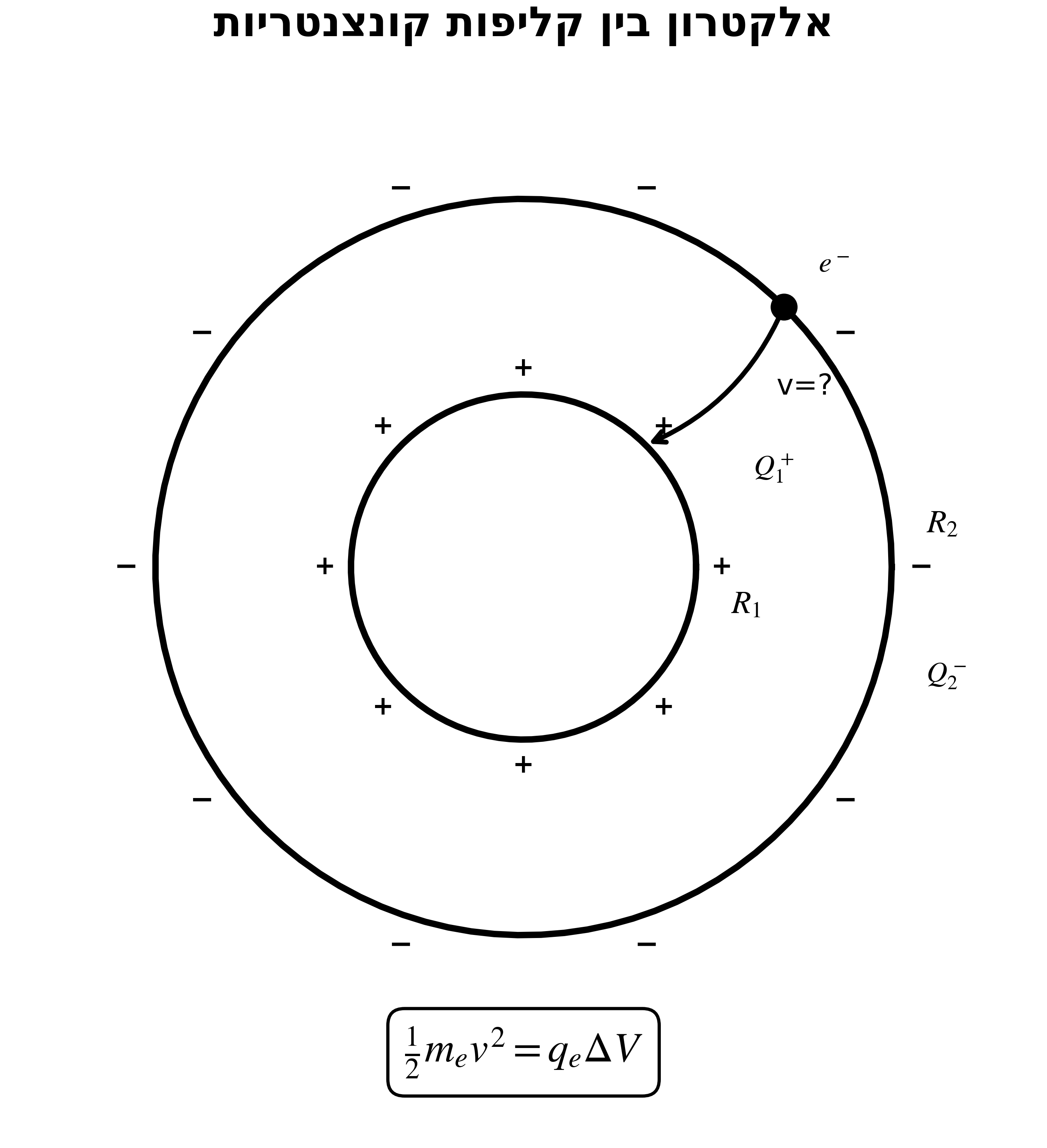
הסיטואציה - שאלה 2
╭──────────────────╮ │ ╭────────╮ │ │ │ │ │ │ │ ● │ │ ← אלקטרון משתחרר מ-R₂ │ │ R₁ │ │ │ │ Q₁(+) │ │ │ ╰────────╯ │ │ R₂ │ │ Q₂(-) │ ╰──────────────────╯
- קליפה פנימית: רדיוס $R_1$, מטען $Q_1$ (חיובי)
- קליפה חיצונית: רדיוס $R_2$, מטען $Q_2$ (שלילי)
- שאלה: באיזו מהירות אלקטרון שמשתחרר מ-$R_2$ יפגע ב-$R_1$?
חישוב הפוטנציאלים
פוטנציאל על הקליפה החיצונית ($V_2$)
סופרפוזיציה של שתי הקליפות:
\[V_2 = \frac{KQ_1}{R_2} + \frac{K(-|Q_2|)}{R_2} = \frac{KQ_1}{R_2} - \frac{K|Q_2|}{R_2}\]פוטנציאל על הקליפה הפנימית ($V_1$)
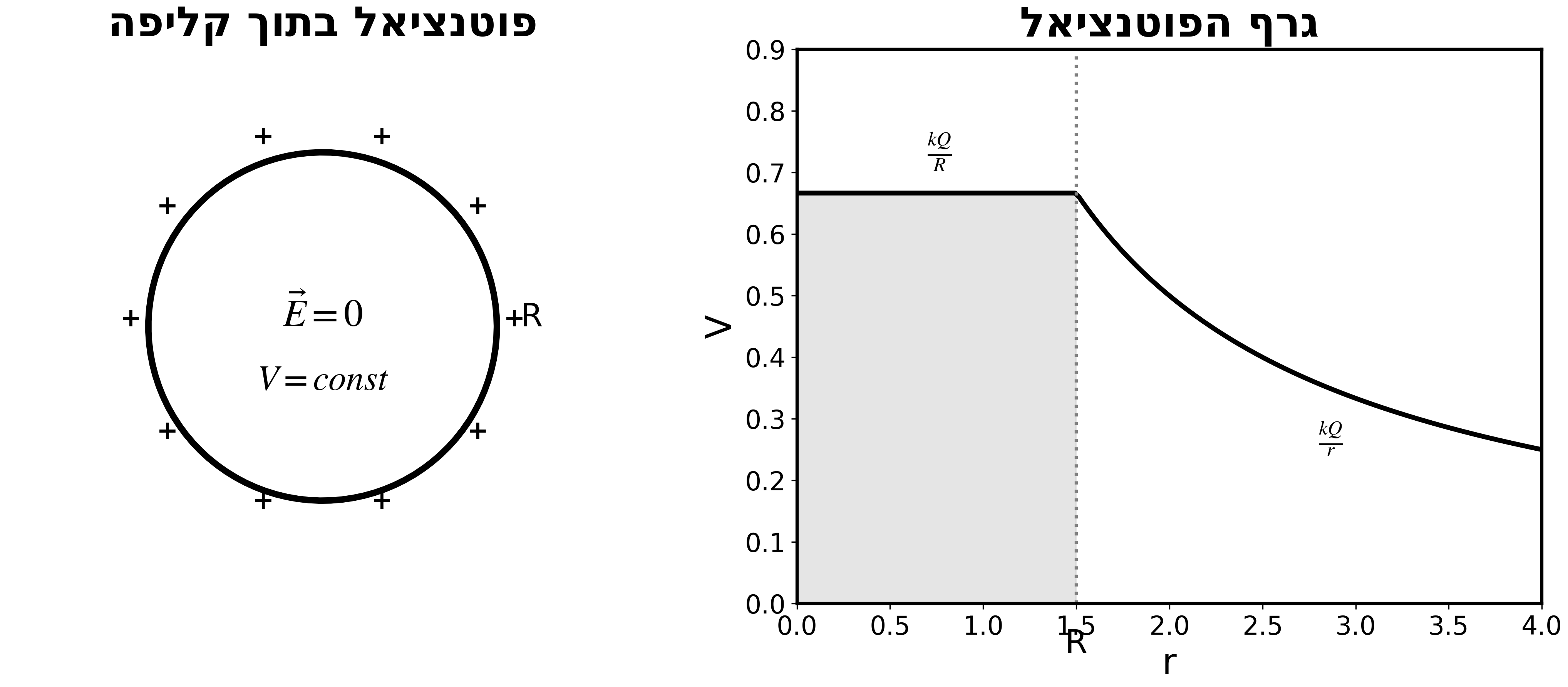
חשוב: הפוטנציאל בתוך קליפה כדורית קבוע!
\[V_1 = \frac{KQ_1}{R_1} + \frac{K(-|Q_2|)}{R_2} = \frac{KQ_1}{R_1} - \frac{K|Q_2|}{R_2}\]למה הפוטנציאל קבוע בתוך קליפה?
- השדה בפנים = 0 (מחוק גאוס)
- אם אין שדה, הפוטנציאל לא משתנה
- הפוטנציאל בפנים = הפוטנציאל על הקליפה
הפרש הפוטנציאלים
\[\Delta V = V_2 - V_1 = KQ_1 \left( \frac{1}{R_2} - \frac{1}{R_1} \right)\]בדיקת סימנים:
- $R_2 > R_1$ מכאן $\frac{1}{R_2} < \frac{1}{R_1}$ ← הסוגריים שליליים
- $Q_1$ חיובי ← $\Delta V$ שלילי
- אבל $Q_e$ (אלקטרון) שלילי ← $Q_e \cdot \Delta V$ חיובי ✓
משוואת שימור האנרגיה
\[Q_e V_2 + \frac{1}{2}m_e v_2^2 = Q_e V_1 + \frac{1}{2}m_e v_1^2\]אם משתחרר ממנוחה ($v_2 = 0$):
\[\frac{1}{2}m_e v_1^2 = Q_e (V_2 - V_1) = Q_e \cdot \Delta V\]התוצאה הסופית
\[v_1^2 = \frac{2Q_e \cdot KQ_1}{m_e} \left( \frac{1}{R_2} - \frac{1}{R_1} \right)\] \[v_1 = \sqrt{\frac{2KQ_1 Q_e}{m_e} \left( \frac{1}{R_2} - \frac{1}{R_1} \right)}\]חלק ג’: שימור מטען חשמלי
הפוסטולט השני של האלקטרומגנטיות
מטען חשמלי אינו נברא יש מאין, ואינו מתעיין אל האין
משמעות: סך המטען הכולל במערכת סגורה נשמר בזמן.
דוגמה: זוג אלקטרון-פוזיטרון
ב-PET scan:
- אלקטרון ($-1.6 \times 10^{-19}$ C) + פוזיטרון ($+1.6 \times 10^{-19} \mathrm{C}$)
- הופכים לאור (פוטונים)
- מטען התחלתי: 0
- מטען סופי: 0
- המטען נשמר! ✓
הגדרות חדשות
צפיפות מטען ($\rho$)
\[\rho = \rho(\vec{r}, t)\]- שדה סקלרי
- יחידות: קולון/מ”ק (C/m³)
- יכול להשתנות במקום ובזמן
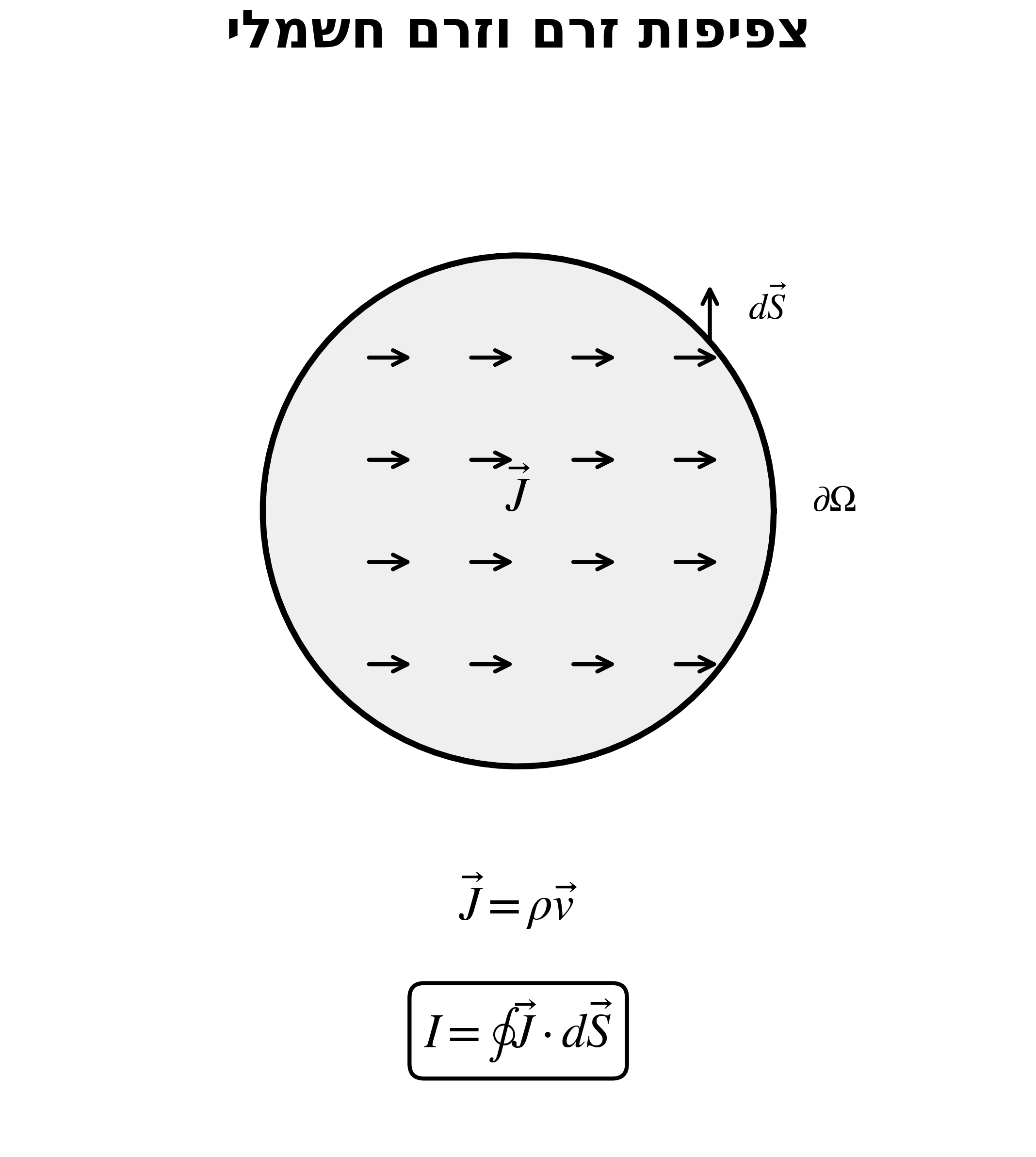
צפיפות זרם ($\vec{J}$)
\[\vec{J} = \rho \cdot \vec{v}\]- שדה וקטורי
- $\vec{v}$ = מהירות מקומית של צפיפות המטען
- יחידות: אמפר/מ”ר (A/m²)
זרם חשמלי (I)
\[I = \oint_{\partial\Omega} \vec{J} \cdot d\vec{S}\]- שטף של צפיפות הזרם דרך משטח
- יחידות: אמפר (A)
משוואת הרציפות (שימור מטען מקומי)
\[\frac{\partial \rho}{\partial t} + \nabla \cdot \vec{J} = 0\]או:
\[\frac{\partial \rho}{\partial t} = -\nabla \cdot \vec{J}\]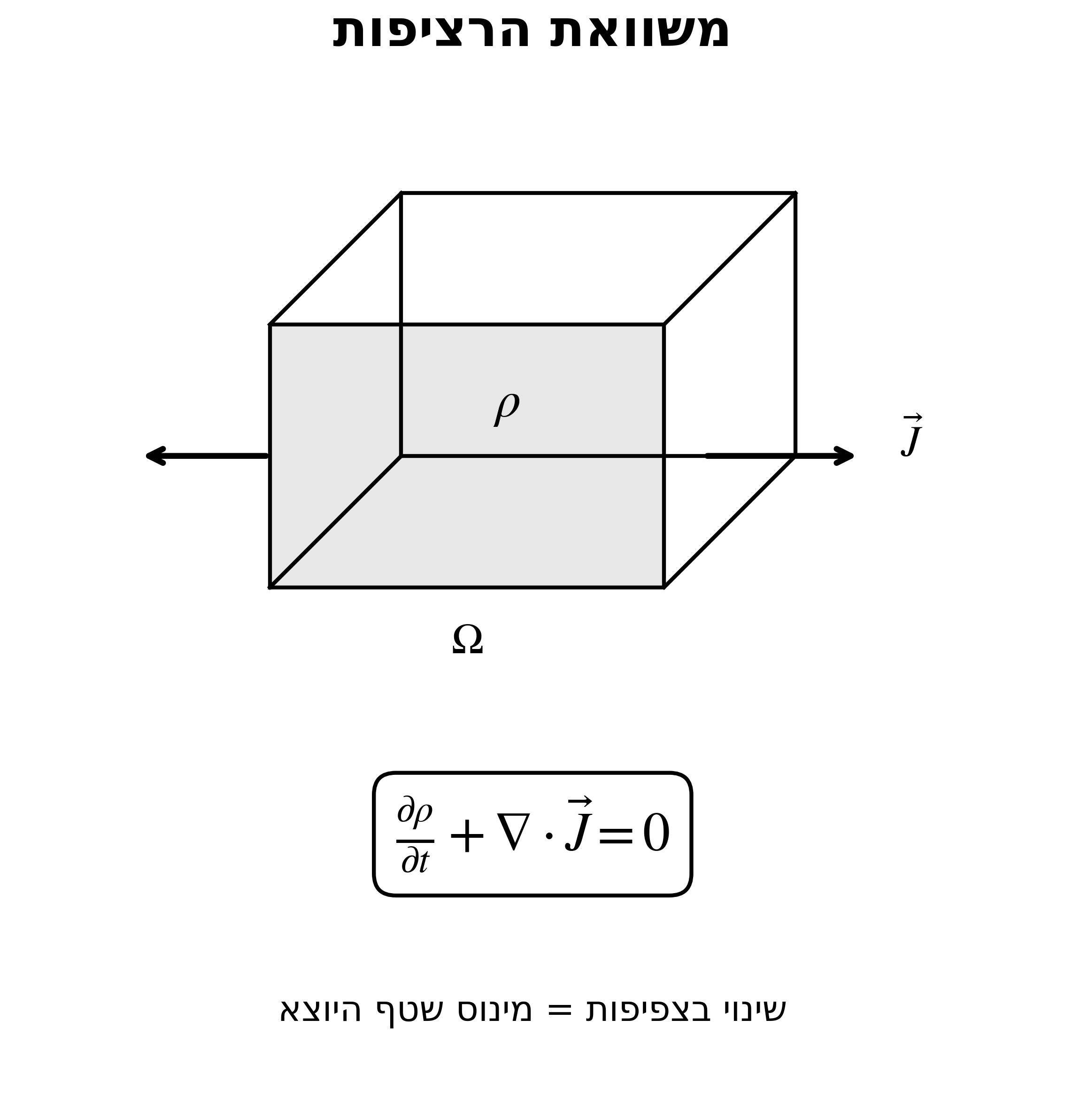
פירוש:
- השינוי בצפיפות המטען = מינוס השפיעה של הזרם
- אם מטען “בורח” מנקודה (שפיעה חיובית) ← צפיפות קטנה (נגזרת שלילית)
שימור מטען גלובלי
אינטגרציה על נפח $\Omega$:
\[\frac{dQ_\Omega}{dt} = -I_{\partial\Omega}\]פירוש: קצב השינוי של המטען בנפח = מינוס הזרם היוצא דרך המעטפת
חלק ד’: משוואות מקסוול
שני הפוסטולטים של האלקטרומגנטיות
| # | פוסטולט |
|---|---|
| 1 | מטען חשמלי קיים וקורן את השפעתו רדיאלית למרחב |
| 2 | כמות המטען החשמלי במערכת נשמרת בזמן |
מתוך שני הפוסטולטים האלה נבנית התורה האלקטרומגנטית כולה!
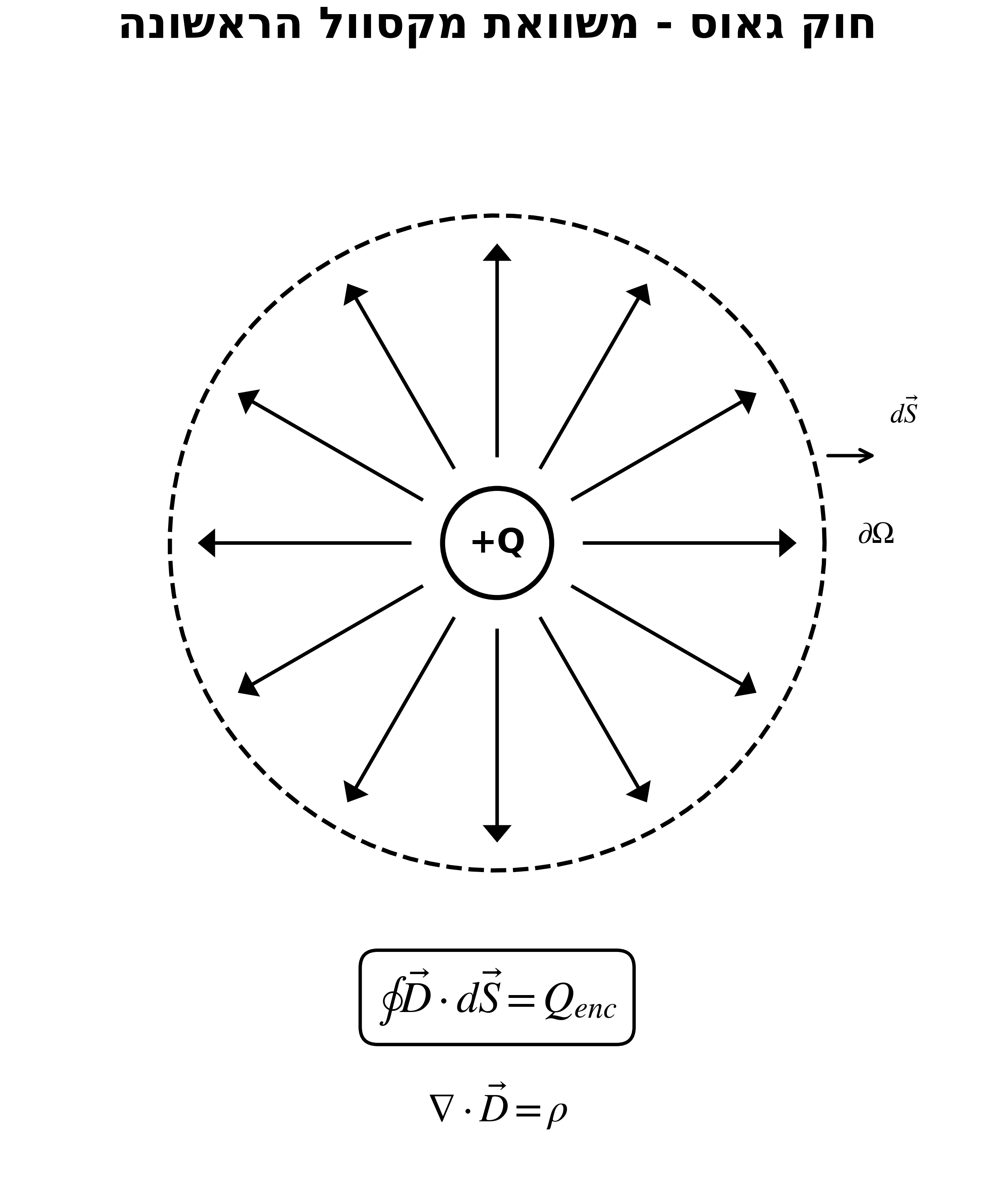
משוואת מקסוול הראשונה (חוק גאוס)
צורה דיפרנציאלית:
\[\nabla \cdot \vec{D} = \rho\]צורה אינטגרלית:
\[\oint_{\partial\Omega} \vec{D} \cdot d\vec{S} = Q_\Omega\]משמעות: השפיעה של שדה ההשפעה = המטען שבפנים
הקשר בין D ל-E:
\[\vec{D} = \epsilon_0 \vec{E}\]כאשר $\epsilon_0$ = מקדם הדיאלקטרי של הריק
גזירת משוואת מקסוול השנייה
שלב 1: גזירת משוואת גאוס לפי הזמן
\[\frac{\partial}{\partial t}(\nabla \cdot \vec{D}) = \frac{\partial \rho}{\partial t}\] \[\nabla \cdot \frac{\partial \vec{D}}{\partial t} = \frac{\partial \rho}{\partial t}\]שלב 2: שימוש במשוואת הרציפות
\[\frac{\partial \rho}{\partial t} = -\nabla \cdot \vec{J}\]שלב 3: הצבה וסידור
\[\nabla \cdot \frac{\partial \vec{D}}{\partial t} = -\nabla \cdot \vec{J}\] \[\nabla \cdot \left( \frac{\partial \vec{D}}{\partial t} + \vec{J} \right) = 0\]שלב 4: הפתרון
אם הדיברגנס של משהו = 0, אז אותו משהו הוא ערבולי (רוטור של שדה אחר):
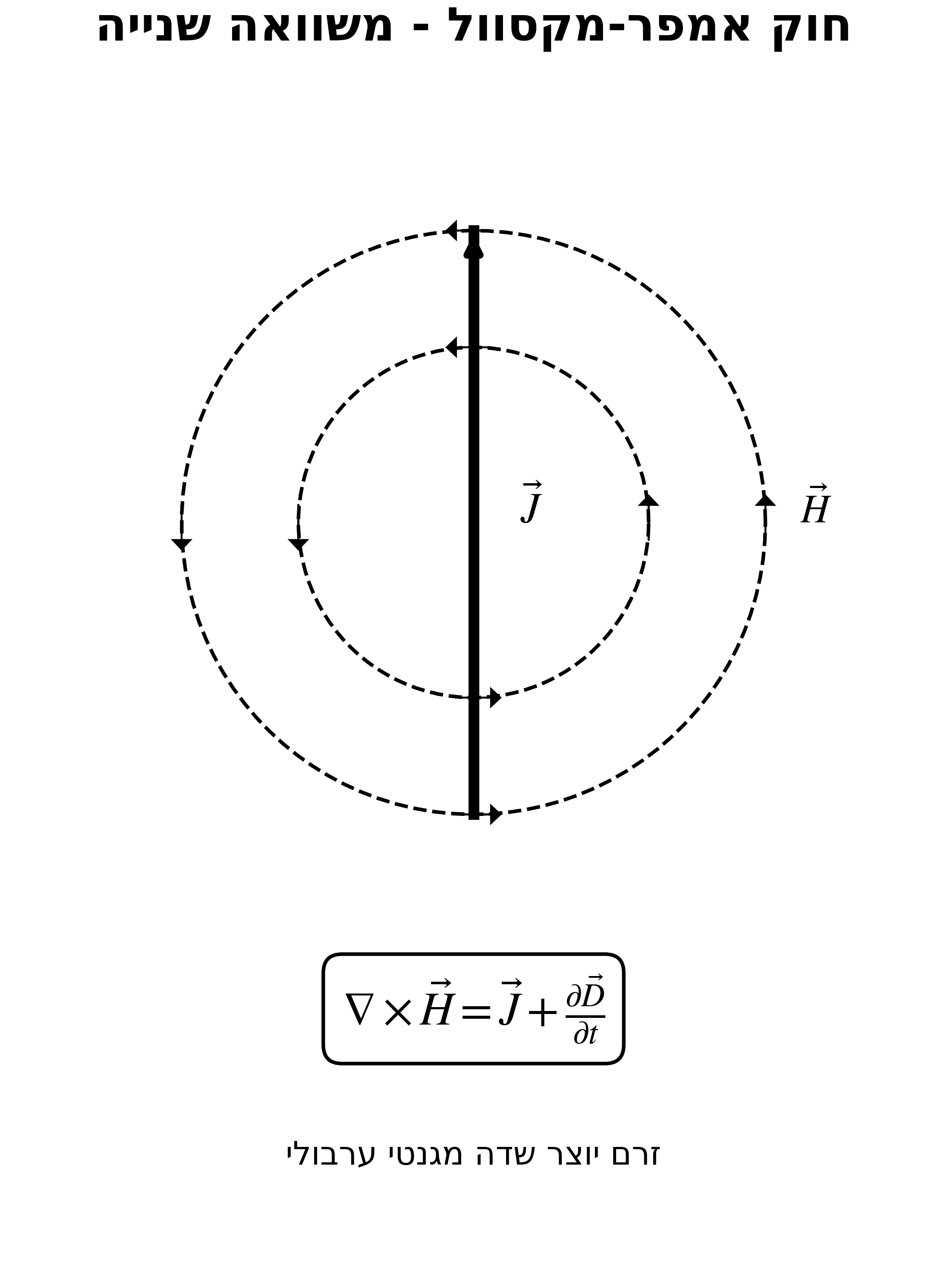
\[\frac{\partial \vec{D}}{\partial t} + \vec{J} = \nabla \times \vec{H}\]משוואת מקסוול השנייה (חוק אמפר-מקסוול)
\[\nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}\]| איבר | שם | משמעות |
|---|---|---|
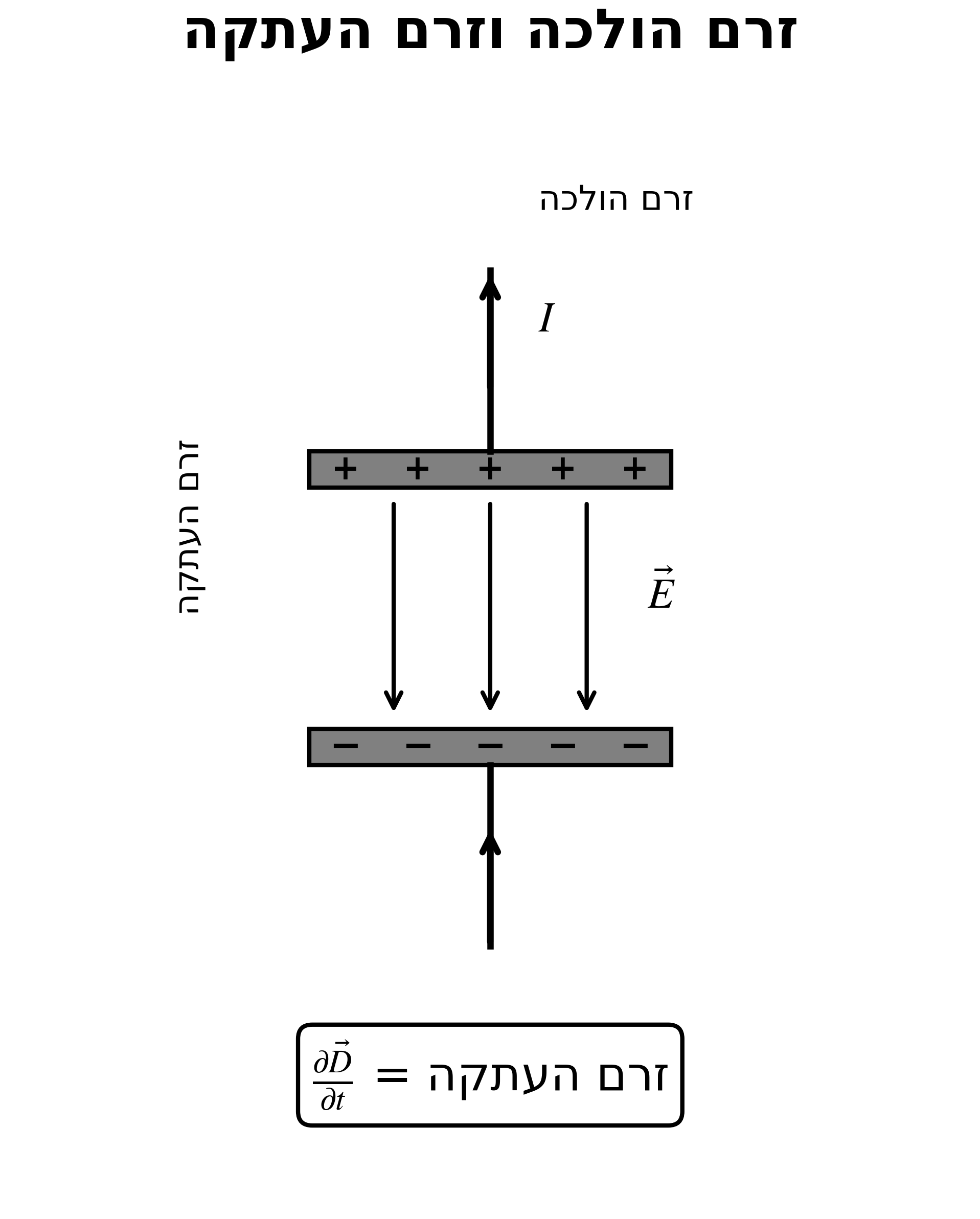
| $\vec{J}$ | צפיפות זרם | זרם הולכה |
| $\frac{\partial \vec{D}}{\partial t}$ | זרם העתקה | שינוי בשדה החשמלי |
| $\vec{H}$ | שדה מגנטי | השדה שנוצר |
המסקנה: בכל מקום שיש זרמים חשמליים, מופיע שדה מגנטי ערבולי!
סיכום - משוואות מקסוול (עד כה)
משוואה ראשונה (חוק גאוס)
\[\nabla \cdot \vec{D} = \rho\]משוואה שנייה (חוק אמפר-מקסוול)
\[\nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}\]משוואת הרציפות (שימור מטען)
\[\frac{\partial \rho}{\partial t} + \nabla \cdot \vec{J} = 0\]נקודות מפתח
אנרגיה פוטנציאלית חשמלית
- $U = qV$
- שימור אנרגיה: $E_{K,i} + qV_i = E_{K,f} + qV_f$
- פוטנציאל הוא סקלרי - מתחבר אלגברית
פוטנציאל של קליפה כדורית
- מחוץ: $V = \frac{KQ}{r}$
- בתוך: $V = \frac{KQ}{R}$ (קבוע!)
שימור מטען
- המטען הכולל נשמר
- משוואת הרציפות מבטאת זאת מקומית
משוואות מקסוול
- נגזרות משני פוסטולטים פשוטים
- מתארות את כל התופעות האלקטרומגנטיות
קבועים חשובים
| קבוע | סימון | ערך |
|---|---|---|
| קבוע קולון | $K$ | $9 \times 10^9 \, \mathrm{N·m²/C²}$ |
| מטען אלקטרון | $q_e$ | $-1.6 \times 10^{-19} \, \mathrm{C}$ |
| מסת אלקטרון | $m_e$ | $9.11 \times 10^{-31} \, \mathrm{kg}$ |
| מטען פרוטון | $q_p$ | $+1.6 \times 10^{-19} \, \mathrm{C}$ |
 דור פסקל
דור פסקל