תוכן עניינים:
- שאלה 1: סופרפוזיציה של כוחות ושריג יונים
- שאלה 2: שיווי-משקל כוחות בין מטענים
- שאלה 3: בעיית השריג החשמלי
- שאלה 4: פוטנציאל חשמלי של חוט אינסופי עם צפיפות משתנה
- שאלה 5: נפילה בשדה מגנטי
- שאלה 6: כא”מ במסגרת מסתובבת בשדה מגנטי משתנה
- שאלה 7: שדה מקווי שווה-פוטנציאל
- שאלה 8: שלושה לוחות אנכיים אינסופיים ומקבילים
שאלה 1: סופרפוזיציה של כוחות ושריג יונים
מהי האנרגיה הפוטנציאלית האלקטרוסטטית האגורה בשריג אשר בנוי משמונה יונים שליליים הממוקמים על קודקודיה של קובייה, אשר אורך צלעה הוא $a$, ועוד יון חיובי בודד היושב במרכזה של הקובייה?
שימו לב:
- מטענו של כל יון שלילי הוא $q_{-} = e$
- מטענו של היון החיובי הוא $q_{+} = e$
הערה: זהו מודל תא יחידה של גביש צזיום כלורידי $\ce{CsCl}$, ראו איור.
$U = 12\frac{Ke^2}{a} + 12\frac{Ke^2}{a\sqrt{2}} - 12\frac{Ke^2}{a\sqrt{3}}$
$U = 12\frac{Ke^2}{a} + 12\frac{Ke^2}{a\sqrt{2}} - 4\frac{Ke^2}{a\sqrt{3}}$
$U = 12\frac{Ke^2}{a} + 12\frac{Ke^2}{a\sqrt{2}} - 8\frac{Ke^2}{a\sqrt{3}}$
$U = 24\frac{Ke^2}{a} + 12\frac{Ke^2}{a\sqrt{2}} - 8\frac{Ke^2}{a\sqrt{3}}$
הבעייה הזאת הופיעה כשאלה 4 בתרגיל 5.
שאלה 2: שיווי-משקל כוחות בין מטענים
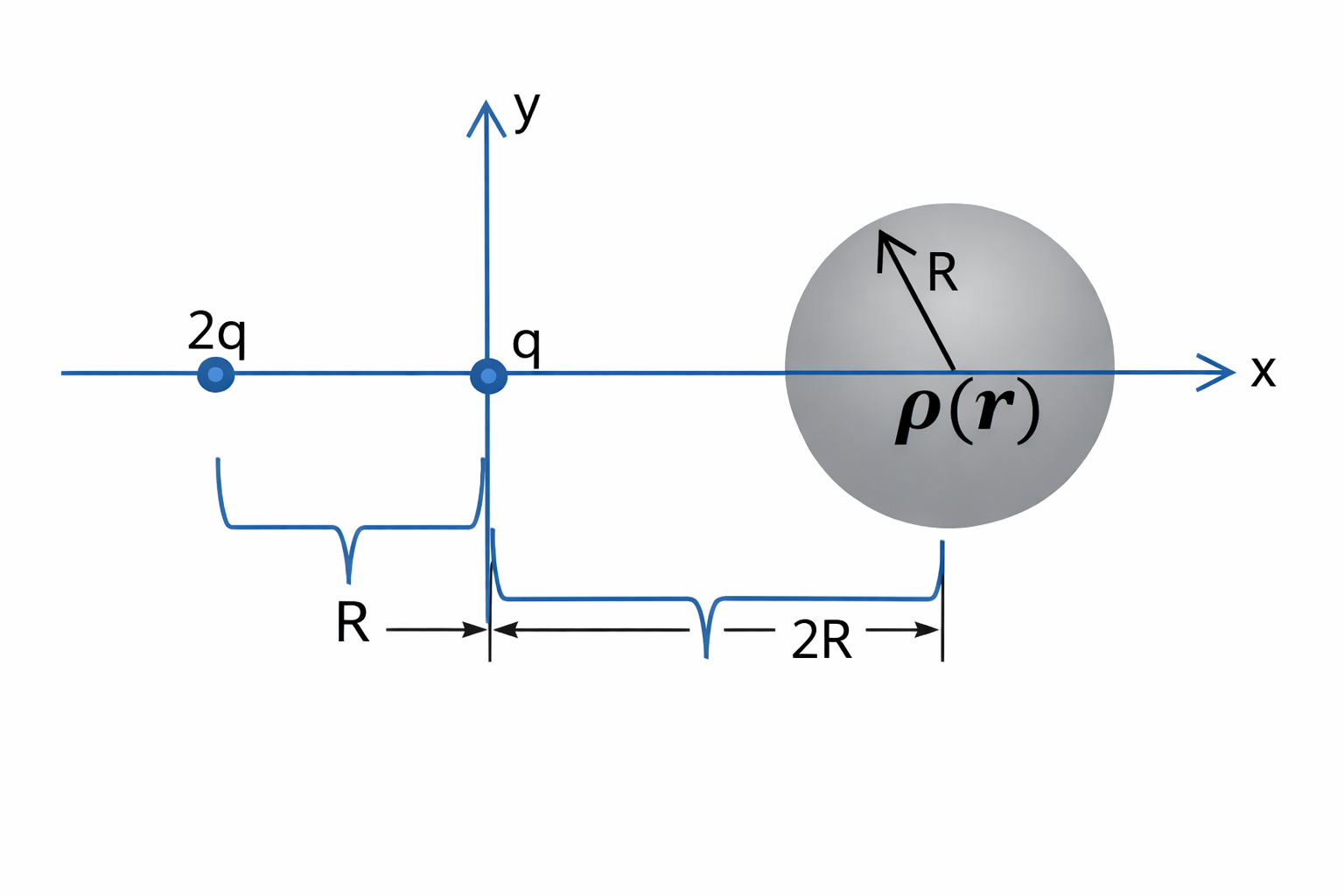
מטען חשמלי נקודתי $q$ נמצא בראשית הצירים כבאיור המצורף מטה. מטען זה אינו מקובע למקומו.
מימינו של מטען זה, ובמרחק $2R$ ממנו, מקובע למקומו כדור העשוי מחומר מבודד, אשר רדיוסו הוא $R$, והוא טעון בצפיפות מטען נפחית התלויה במרחק $r$ ממרכז הכדור באופן הבא:
\[\rho(r) = \left(\frac{\tilde{Q}}{R^5}\right) r^2\]משמאלו של המטען הנקודתי שנמצא בראשית, במרחק $R$ לאורך אותו ציר, מקובע למקומו מטען נקודתי אשר מטענו החשמלי הוא $2q$.
מה צריך להיות גודלו של המטען $\tilde{Q}$ על מנת שהמטען הנמצא בראשית הצירים יישאר במקומו במנוחה?
הערה: נפח קליפה כדורית בעלת עובי אינפיניטסימלי הינו $dV = 4\pi r^2 dr$, ועל כן המטען החשמלי הכלוא בה הוא $dQ = \rho(r)4\pi r^2 dr$
תשובות:
$\tilde{Q} = 10q/\pi$
$\tilde{Q} = -10q/\pi$
$\tilde{Q} = 8q/5\pi$
$\tilde{Q} = -8q/5\pi$
1. חוק קולון:
\[F = \frac{Kq_1 q_2}{r^2}\]2. מטען כולל של הכדור:
\[Q_{total} = \int_0^R \rho(r) \cdot 4\pi r^2 \, dr\]3. כוח מכדור טעון על מטען חיצוני:
כדור עם התפלגות מטען כדורית מתנהג כאילו כל המטען מרוכז במרכזו (משפט הקליפות של גאוס). מרכז הכדור במרחק $2R$ מהראשית.
4. תנאי שיווי משקל:
הכוח מהמטען $2q$ (משמאל, מרחק $R$) שווה לכוח מהכדור (מימין, מרחק $2R$) על המטען $q$ בראשית.
שלבים:
- נחשב $Q_{total}$ מהאינטגרל
- נכתוב את הכוח מ-$2q$ על $q$
- נכתוב את הכוח מהכדור על $q$
- נשווה ונפתור עבור $\tilde{Q}$
חישוב המטען הכולל
\[\begin{aligned} Q_{total} &= \int_0^R \rho(r) \cdot 4\pi r^2 \, dr \\[5pt] &= 4\pi \int_0^R \left(\frac{\tilde{Q}}{R^5}\right) r^2 \cdot r^2 \, dr \\[5pt] &= 4\pi \left(\frac{\tilde{Q}}{R^5}\right) \int_0^R r^4 \, dr \\[5pt] &= 4\pi \frac{\tilde{Q}}{R^5} \left[ \frac{r^5}{5} \right]_0^R \\[5pt] &= 4\pi \frac{\tilde{Q}}{\cancel{R^5}} \frac{\cancel{R^5}}{5} = \boxed{\frac{4 \pi \tilde{Q}}{5}} \\ \end{aligned}\]הכוח מ-$2q$ על $q$
מחוק קולון:
\[F = \frac{K (2q)(q)}{R^2} = \frac{2Kq^2}{R^2} \, \mathrm{N}\]הכוח מהכדור על $q$
באופן דומה:
\[F = \frac{K \cdot Q \cdot q}{4R^2} = \frac{K \cdot \frac{4 \pi \tilde{Q}}{5} \cdot q}{4R^2} = \frac{ \pi K \cdot \tilde{Q} \cdot q}{5R^2} \, \mathrm{N}\]השוואת הכוחות וחילוץ הערך
\[\begin{aligned} \frac{2Kq^2}{R^2} &= \frac{\pi K \cdot \tilde{Q} \cdot q}{5R^2} \\[5pt] 10q^2 &= \pi \tilde{Q} \cdot q \\[5pt] \tilde{Q} &= 10q / \pi \\[5pt] \end{aligned}\]אני חושבת שהיה אפשר להגיע לזה גם משיקולים פיזיקליים - צריך ערך חיובי והערך החיובי השני שבתשובות הוא שבר.
שאלה 3: בעיית השריג החשמלי
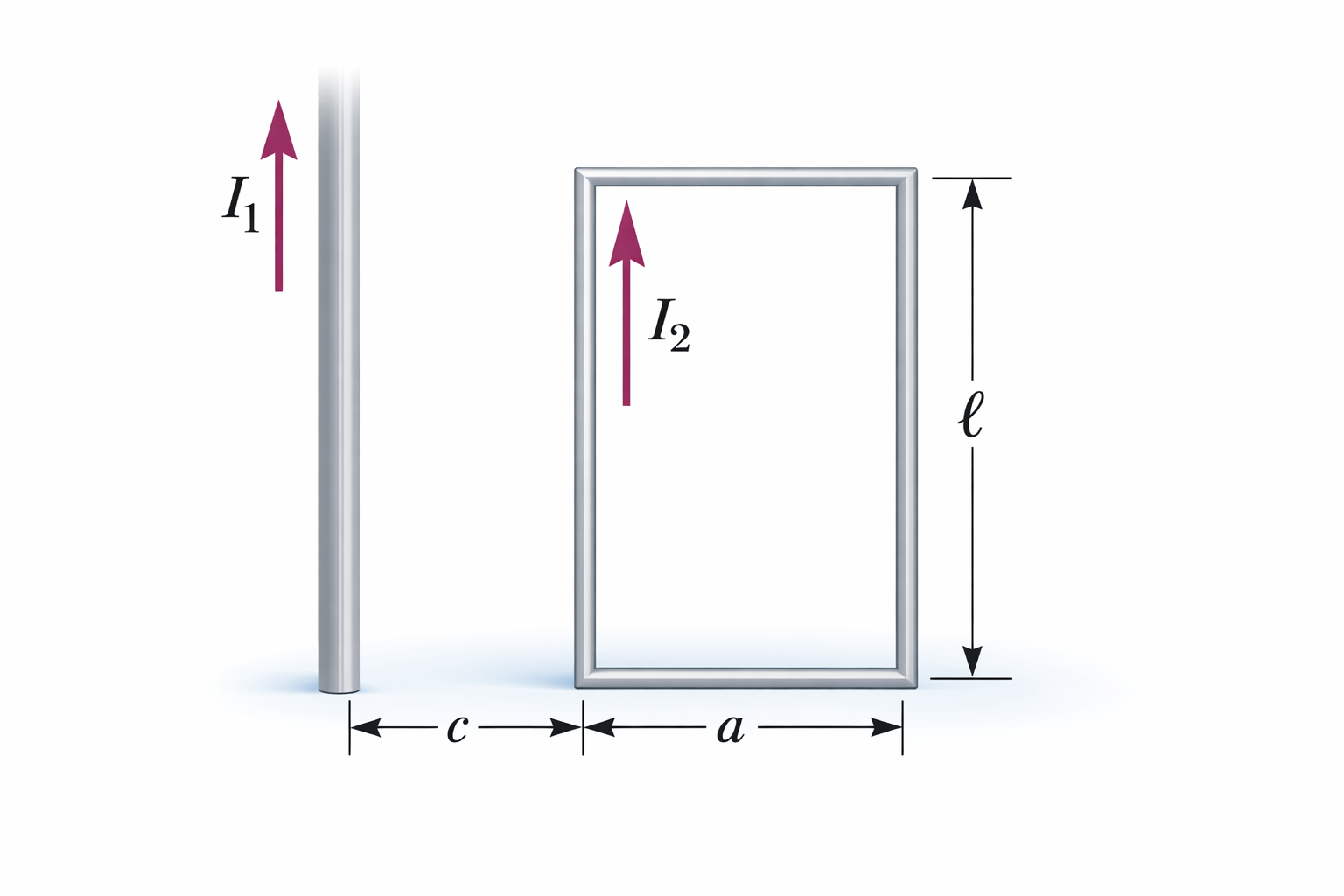
במסגרת המלבנית שבאיור זורם זרם חשמלי $I_2 = 10 \, \mathrm{Ampere}$. מסגרת זו נתונה בהשפעת שדה מגנטי הנוצר על ידי תיל נושא זרם של $I_1 = 5 \, \mathrm{Ampere}$. תיל ישר זה מתלכד עם ציר $y$. קבלו את גודלו וכיוונו של הכוח הפועל על המסגרת.
נתונים:
\[l = 0.45\ \mathrm{m},\quad a = 0.15\ \mathrm{m},\quad c = 0.1\ \mathrm{m},\quad \mu_0 = 4\pi \times 10^{-7}\ \mathrm{N/Ampere^2}\]כיוונים: שמאלה = “−”, ימינה = “+”
$F = -27 \cdot 10^{-6}\ \, \mathrm{N}$
$F = 1.66 \cdot 10^{-7}\ \, \mathrm{N}$
$F = 2.5 \cdot 10^{-5}\ \, \mathrm{N}$
$F = -2.5 \cdot 10^{-6}\ \, \mathrm{N}$
נוסחאות וכללים נדרשים
1. שדה מגנטי מתיל ישר ארוך:
\[B(r) = \frac{\mu_0 I_1}{2\pi r}\]2. כוח על צלע נושאת זרם בשדה מגנטי:
\[F = I_2 l B\](כאשר $\vec{I} \perp \vec{B}$; אם מקבילים ← $F = 0$)
3. כלל חשוב: הצלעות המקבילות לתיל (לאורך $\hat{y}$) חשות שדה $B$ שונה כי הן במרחקים שונים מהתיל. הצלעות המאונכות לתיל מתקזזות (סימטריה).
4. הכוח השקול:
\[F_{net} = I_2 l \left[B(r_{close}) - B(r_{far})\right]\]כאשר $r_{close}$ ו-$r_{far}$ הם המרחקים של שתי הצלעות המקבילות לתיל.
ננסה להציב:
\[B(r_{close}=c)= \frac{\mu_0 I_1}{2\pi c}=\frac{\mu_0 \cdot 5 \, \mathrm{A}}{2\pi \cdot 0.1 \, \mathrm{m}}\] \[B(r_{far}=c+a)= \frac{\mu_0 I_1}{2\pi (c+a)}=\frac{\mu_0 \cdot 5 \, \mathrm{A}}{2\pi \cdot 0.25 \, \mathrm{m}}\] \[\begin{aligned} F_{net} &= I_2 l \left[B(r_{close}) - B(r_{far})\right] \\[5pt] &= 10 \, \mathrm{A} \cdot 0.45 \, \mathrm{m} \left[\frac{\mu_0 \cdot 5 \, \mathrm{A}}{2\pi \cdot 0.1 \, \mathrm{m}} - \frac{\mu_0 \cdot 5 \, \mathrm{A}}{2\pi \cdot 0.25 \, \mathrm{m}}\right] \\[5pt] \end{aligned}\]הערה - זה פשוט:
\[F_{net} = \frac{\mu_0 I_1 I_2 l}{2\pi}\left[\frac{1}{c} - \frac{1}{c+a}\right]\]נמשיך בפתרון עם היחידות וההצבות לשלמות, בדיעבד כנראה עדיף להציב רק בסוף כי איברים יכולים להצמטמצם או להתבטל.
\[\begin{aligned} F_{net} &= \frac{50 \, \mathrm{A}^2 \cdot 0.45 \mu_0}{2\pi} \underbrace{\left[\frac{1}{0.1} - \frac{1}{ 0.25}\right]}_{=10-4=6} \\[5pt] &= \frac{150 \, \mathrm{A}^2 \cdot 0.45 \mu_0}{ \pi} \\[5pt] &= \frac{67.5 \, \cancel{\mathrm{A}^2} \cdot 4\cancel{\pi} \times 10^{-7}\ \mathrm{N/}\cancel{\mathrm{A}^2}}{ \cancel{\pi}} \\[5pt] &= 270 \times 10^{-7}\ \mathrm{N} = \boxed{27 \times 10^{-6}\ \mathrm{N}} \end{aligned}\]לגבי הכיוון, הזרמים באותו כיוון אז יש משיכה כלומר המסגרת נמשכת שמאלה לתייל ולפי ההגדרות התשובה הסופית היא:
\[F = -27 \cdot 10^{-6}\ \, \mathrm{N}\]שאלה 4: פוטנציאל חשמלי של חוט אינסופי עם צפיפות משתנה
לאורך ציר $z$ מונח חוט אינסופי שאינו מוליך ועליו צפיפות מטען חשמלי אורכית שאינה קבועה, והיא נתונה בביטוי:
\[\lambda(z) = \lambda_0 |z| e^{-\frac{|z|}{a}}\]חשבו את הפוטנציאל החשמלי על החוט בנקודה $z = 0$.
הערות:
- אפשר להניח שהפוטנציאל באינסוף הוא אפס.
- הערך המוחלט מבטא את העובדה שצפיפות המטען סימטרית ביחס לראשית. לכן הסכימה ממינוס אינסוף לאינסוף כמוהו כפעמיים הסכימה מאפס לאינסוף.
תשובות:
$V(z=0) = 2K\lambda_0 a$
$V(z=0) = 0_{Volts}$
$V(z=0) = K\lambda_0 a e^{-a}$
$V(z=0) = \infty$
נוסחאות וכללים נדרשים - פוטנציאל ואינטגרלים
1. פוטנציאל חשמלי ממטען נקודתי:
\[V = \frac{Kq}{r}\]2. פוטנציאל מאלמנט מטען אינפיניטסימלי:
אלמנט קטן $dq$ על החוט במיקום $z$ יוצר פוטנציאל בנקודה מסוימת:
\[dV = \frac{K \, dq}{r}\]כאשר $dq = \lambda(z) \, dz$ ו-$r$ הוא המרחק מהאלמנט לנקודה שבה מחשבים.
3. עיקרון הסופרפוזיציה:
סוכמים (אינטגרל) על כל האלמנטים:
\[V = \int_{-\infty}^{\infty} \frac{K \lambda(z)}{r} dz\]4. אינטגרל שימושי:
\[\int_0^{\infty} z \, e^{-z/a} \, dz = a^2\]האנטי-נגזרת של $e^{-z/a}$ היא:
\[\int e^{-z/a} dz = -a \cdot e^{-z/a}\]רמז מפתח: אתה מחשב את הפוטנציאל בנקודה $z = 0$, על החוט עצמו. מה המרחק $r$ מאלמנט במיקום $z$ לנקודה $z = 0$?
פתרון הפוטנציאל
המרחק מאלמנט במיקום $z$ לנקודה הוא פשוט $z$.
מכאן שלכל אלמנט:
\[dV = \frac{K \, dq}{z}\]נציב $dq=\lambda(z) dz$:
\[dV = \frac{K \lambda_0 \cancel{|z|} e^{-|z|/a}}{\cancel{|z|}} dz = K\lambda_0 e^{-|z|/a} dz\]ה-$|z|$ מצטמצם! נעשה אינטגרל ונשתמש בסימטריה:
\[\begin{aligned} V &= \int_{-\infty}^{\infty} K\lambda_0 e^{-|z|/a} dz \\[5pt] &= K\lambda_0 \int_{-\infty}^{\infty} e^{-z/a} dz \\[5pt] \end{aligned}\]אפשר להשתמש בטיפ שבהערות, לכפול בשתיים ולמצמם את גבולות האינטגרל:
\[V = 2K\lambda_0 \left[-a \cdot e^{-z/a}\right]_0^{\infty} = 2K\lambda_0\left(0 - (-a)\right) = \boxed{2K\lambda_0 a}\]תשובה 1 ✓
שאלה 5: נפילה בשדה מגנטי
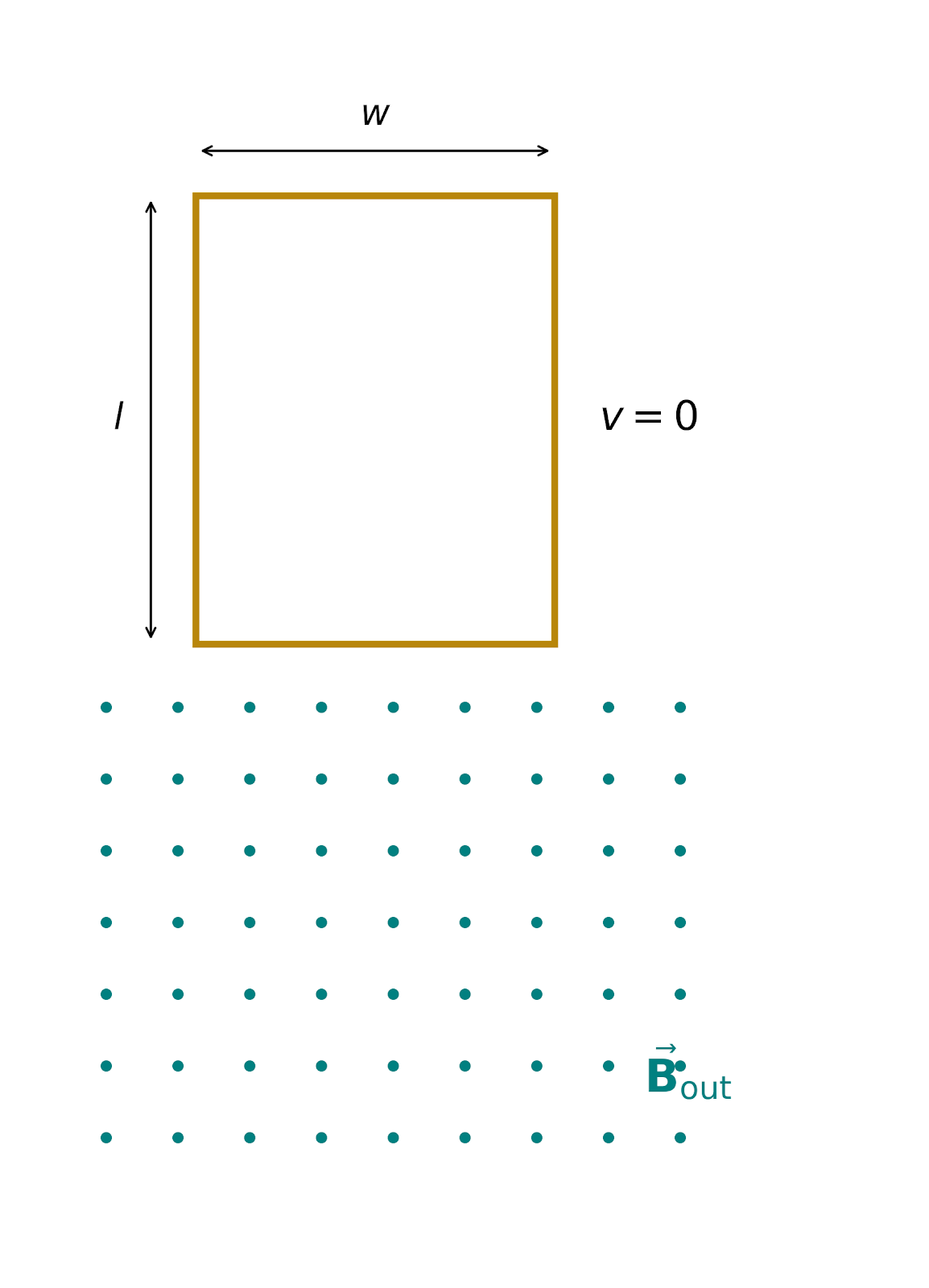
מסגרת מוליכה נופלת בשדה הכבידה של כדור הארץ היישר אל תוך שדה מגנטי כמודגם באיור. השדה המגנטי אחיד וקבוע והוא יוצא מתוך הדף. מסת המסגרת היא $m$ ההתנגדות החשמלית של המסגרת היא $R$, רוחבה ואורכה נתונים על ידי $w, l$ כמודגם באיור.
יהא $x(t)$ אותו “אורך” של המסגרת הנמצא בתוך השדה המגנטי.
המשוואה המתארת את מהירות המסגרת תוך כדי נפילתה אל תוך השדה המגנטי כל עוד $x(t) < l$ היא:
תשובות:
$mg - \left(\frac{w^2 B^2}{R}\right)v = m\dot{v}$
$mg = \left(\frac{w^2 B^2}{R}\right)v$
$\left(-\frac{w^2 B^2}{R}\right)v = \dot{v}$
$v = \frac{w^2 B^2}{R} + gt$
נוסחאות וכללים נדרשים - הכל
1. כא”מ מושרה (חוק פאראדיי):
\[\mathcal{E} = Bwv\](כאשר $w$ הוא רוחב הצלע שחוצה את קווי השדה, ו-$v$ מהירות הנפילה)
2. זרם מושרה (חוק אוהם):
\[i = \frac{\mathcal{E}}{R} = \frac{Bwv}{R}\]3. כוח על מוליך נושא זרם בשדה מגנטי:
\[F_{mag} = Biw = \frac{B^2w^2v}{R}\]כיוון: כלפי מעלה (חוק לנץ - מתנגד לתנועה)
4. חוק ניוטון השני:
\[\sum F = ma = m\dot{v}\]הכוחות: כבידה $mg$ למטה, כוח מגנטי $\frac{B^2w^2v}{R}$ למעלה.
פתרון משוואת המסגרת
מחוק ניוטון - סכום הכוחות שווה $m\dot{v}$:
\[\underbrace{mg}_{\text{gravity downwards}} - \underbrace{\frac{B^2w^2v}{R}}_{\text{magnetic force upward}} = m\dot{v}\]וזו תשובה 1 ✓
שאלה 6: כא”מ במסגרת מסתובבת בשדה מגנטי משתנה
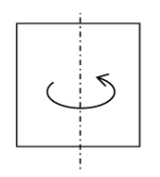
מסגרת ריבועית בעלת צלע $a$ נמצאת בשדה מגנטי אחיד המשתנה בזמן לפי הקשר:
\[\vec{B}(t) = \vec{B}_0 \sin(\omega t)\]בזמן $t = 0_{sec}$ השדה מאונך למשטח המסגרת. ברגע זה ממש היא מתחילה להסתובב במהירות זוויתית קבועה $\omega$ סביב ציר $z$.
מהו הכא”מ שנוצר בתנאים אלה במסגרת?
תשובות:
$\varepsilon(t) = -\omega a^2 B_0 \cos(2\omega t)$
$\varepsilon(t) = -\omega a^2 B_0 \tan(2\omega t)$
$\varepsilon(t) = -\omega a^2 B_0 \sin(\omega t / 2)$
$\varepsilon(t) = 0$
1. שטף מגנטי:
\[\Phi = B \cdot A \cdot \cos\theta\]כאשר $\theta$ הזווית בין $\vec{B}$ לנורמל למשטח.
2. חוק פאראדיי:
\[\mathcal{E} = -\frac{d\Phi}{dt}\]3. נתוני הבעיה:
- $B(t) = B_0\sin(\omega t)$
- $A = a^2$
- המסגרת מסתובבת: $\theta(t) = \omega t$
- ב-$t = 0$: השדה מאונך למשטח ← $\theta = 0$
4. זהות טריגונומטרית שתצטרך:
\[\sin(\alpha)\cos(\alpha) = \frac{1}{2}\sin(2\alpha)\]שלבים:
- נכתוב את $\Phi(t) = B_0\sin(\omega t) \cdot a^2 \cdot \cos(\omega t)$
- נפשט עם הזהות הטריגונומטרית
- נגזור לפי $t$
פתרון - שאלה 6
\[\begin{aligned} \Phi(t) &= B_0\sin(\omega t) \cdot a^2 \cdot \cos(\omega t) \\[5pt] &= \frac{ a^2 \cdot B_0}{2}\sin(2\omega t) \\[5pt] \end{aligned}\]ניעזר בחוק פאראדיי:
\[\begin{aligned} \mathcal{E} = -\frac{d\Phi}{dt} &= -\frac{d\Phi}{dt}\left(\frac{ a^2 \cdot B_0}{2}\sin(2\omega t) \right)\\[5pt] &= -\frac{ a^2 \cdot B_0}{2}\frac{d\Phi}{dt}\left(\sin(2\omega t) \right)\\[5pt] &= -\frac{ a^2 \cdot B_0}{\cancel{2}} \cancel{2} \omega \cos (2\omega t)\\[5pt] \end{aligned}\]סך הכל קיבלנו את תשובה א׳:
\[\boxed{\varepsilon(t) = -\omega a^2 B_0 \cos(2\omega t)}\]שאלה 7: שדה מקווי שווה-פוטנציאל
באיור נראים קווים שווי פוטנציאל, וכמו כן נתון ערך הפוטנציאל (בוולטים) עבור כל קו שווה פוטנציאל. צלע כל משבצת ברקע הוא סנטימטר אחד (בתמונה אצלי בערך רבע?).
א. האם וקטור השדה החשמלי $\vec{E}_A$ שבנקודה $A$ זהה לוקטור השדה החשמלי $\vec{E}_B$ שבנקודה $B$, או שונה ממנו?
ב. חשבו את גודלו של השדה החשמלי $\vec{E}_B$ בנקודה $B$.
שונה, $E = 200_{\mathrm{N/C}}$
זהה, $E = 800_{\mathrm{N/C}}$
שונה, $E = 800_{\mathrm{N/C}}$
זהה, $E = 200_{\mathrm{N/C}}$
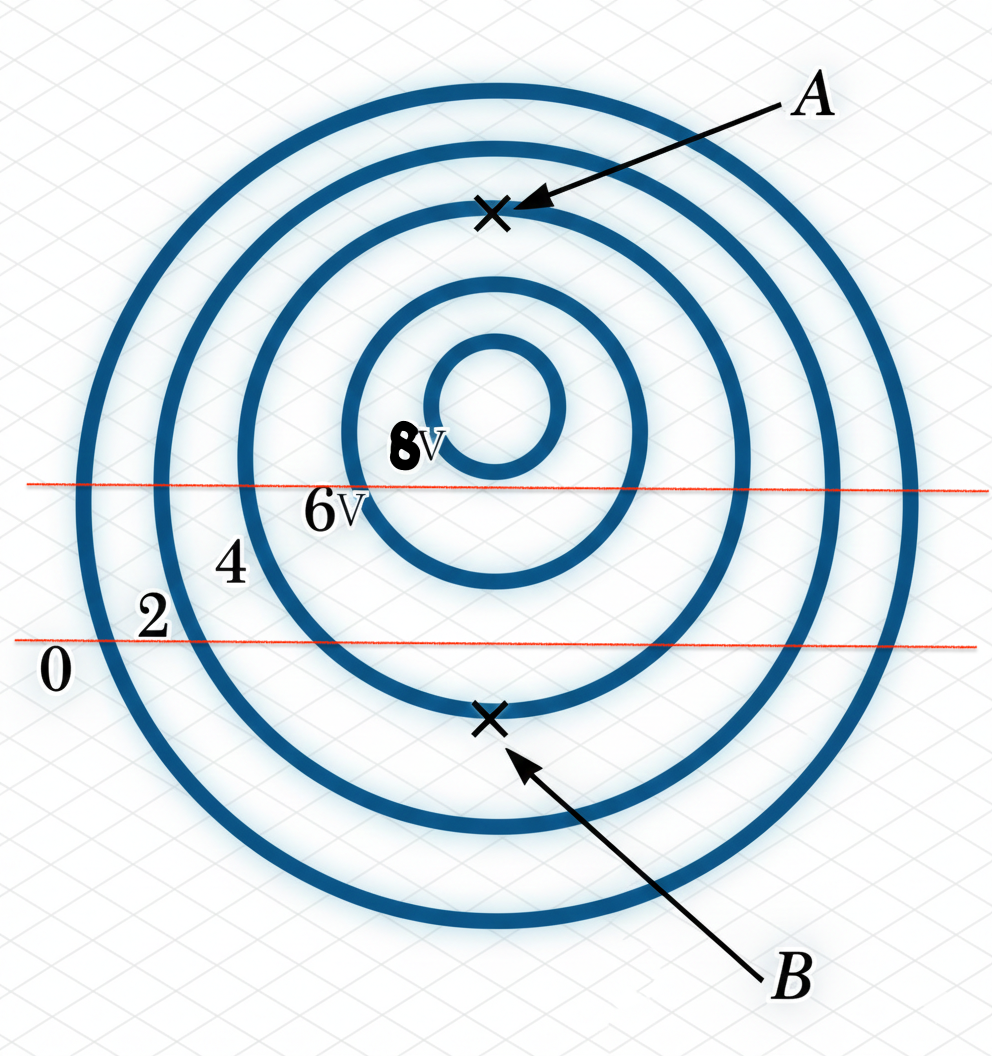
הווקטורים שונים הן בגודל והן בכיוון.
וקטורי השדה החשמלי הם בכיוון המשיק לקווים שווי הפוטנציאל.
מכאן שוקטור השדה החשמלי ב B פונים מטה (במורד הפוטנציאל - מהגבוה לנמוך, החוצה מהמרכז), ובאופן דומה וקטור A פונה מעלה (גם כן במורד הפוטנציאל).
נראה שהקווים באיזור של A גם צפופים יותר, ככה שגם הגודל שלו (ולא רק הכיוון), יהיה שונה מווקטור B.
לגבי החישוב:
\[E_B = \frac{\Delta V}{\Delta d} = \frac{4\text{V} - 2\text{V}}{0.01\text{ m}} = 200 \text{ N/C}\]המספר במכנה הוא אורך של משבצת אחת (באיור שלי לא ברור, אבל מדובר בסנטימטר אחד = 0.01 מטר).
שאלה 8: שלושה לוחות אנכיים אינסופיים ומקבילים
שלושה לוחות אנכיים אינסופיים ומקבילים “מנוקבים” ע”י ציר $x$ האופקי בנקודות:
\[x_1 = a,\quad x_2 = 2a,\quad x_3 = 3a\]הלוח הממוקם בנקודה $x_1$ טעון בצפיפות מטען חשמלית משטחית $\sigma_1$ קולון למטר מרובע.
הלוח הממוקם בנקודה $x_2$ טעון בצפיפות מטען חשמלית משטחית $(-\sigma_2)$ קולון למטר מרובע.
הלוח הממוקם בנקודה $x_3$ טעון בצפיפות מטען חשמלית משטחית $(-\sigma_1)$ קולון למטר מרובע.
$(\sigma_1, \sigma_2 > 0)$
ידוע שהשדה החשמלי מתאפס בין הלוח השני לשלישי, כלומר:
\[\vec{E}(2a < x < 3a) = \vec{0}\]פרוטון משתחרר מהלוח הראשון והוא מואץ בכיוון ציר ה-$x$ החיובי אל עבר הלוח השני. הפרוטון עובר דרך חריך מזערי בלוח זה אל התחום שבין הלוח השני ללוח השלישי. נסמן את מסתו של הפרוטון ב-$m_p$ ואת מטען הפרוטון ב-$q_p$.
מכל האמור לעיל נסיק שריבוע מהירות הפרוטון במעופו בין הלוח השני ללוח השלישי הוא:
תשובות:
$v^2(2a < x < 3a) = \frac{4q_p \sigma_1 a}{m_p \epsilon_0}$
$v^2(2a < x < 3a) = \frac{q_p \sigma_1 (3a)}{2m_p \epsilon_0}$
$v^2(2a < x < 3a) = \frac{q_p \sigma_2 a}{8m_p \epsilon_0}$
$v^2(2a < x < 3a) = \frac{Kq_p (\sigma_2 - \sigma_1)}{m_p a}$
נוסחאות וכללים נדרשים ללוחות
1. שדה חשמלי מלוח אינסופי טעון:
\[E = \frac{|\sigma|}{2\epsilon_0}\]הכיוון: הרחק מהלוח אם $\sigma > 0$, לכיוון הלוח אם $\sigma < 0$.
2. עיקרון הסופרפוזיציה:
השדה הכולל = סכום וקטורי של השדות משלושת הלוחות.
3. משפט עבודה-אנרגיה:
\[\frac{1}{2}m_p v^2 = q_p \cdot E \cdot d\](כאשר הפרוטון מתחיל ממנוחה, $E$ השדה ו-$d$ המרחק)
שלבים:
- השתמש בתנאי $E = 0$ בין לוח 2 ל-3 כדי למצוא את היחס $\sigma_2 = \,?$ בתור $\sigma_1$
- חשב את השדה הכולל בין לוח 1 ל-2
- השתמש בשימור אנרגיה למצוא $v^2$
- בין לוח 2 ל-3 אין שדה ← מהירות קבועה
מה יש לנו?
שלושה לוחות אינסופיים על ציר $x$:
plate 1 plate 2 plate 3
σ₁ -σ₂ -σ₁
| | |
| zone A | zone B |
| (a < x < 2a) | (2a < x < 3a) |
| | |
x = a x = 2a x = 3a
הרעיון הבסיסי
כל לוח אינסופי יוצר שדה חשמלי אחיד לשני הצדדים שלו:
\[E = \frac{|\sigma|}{2\epsilon_0}\]- לוח חיובי ($\sigma_1$): שדה מצביע הרחק מהלוח (ימינה מצד ימין, שמאלה מצד שמאל)
- לוח שלילי ($-\sigma$): שדה מצביע לכיוון הלוח (פנימה משני הצדדים)
שלב 1 — מצא $\sigma_2$ מהתנאי
plate 1 plate 2 plate 3
σ₁ -σ₂ -σ₁
| | zone B |
| ··········→ | |
| | ←·· |
| | ···→ |
x = a x = 2a x = 3a
נתון ש-$E = 0$ באזור B. באזור הזה, כל שלושת הלוחות תורמים שדה. נכתוב את התרומה של כל לוח באזור B (כיוון חיובי = ימינה):
- לוח 1 ($+\sigma_1$, משמאל לאזור): $+\frac{\sigma_1}{2\epsilon_0}$ (ימינה, כי אנחנו מימין ללוח חיובי)
- לוח 2 ($-\sigma_2$, משמאל לאזור): $-\frac{\sigma_2}{2\epsilon_0}$ (שמאלה, כי אנחנו מימין ללוח שלילי — השדה נמשך חזרה אליו)
- לוח 3 ($-\sigma_1$, מימין לאזור): $+\frac{\sigma_1}{2\epsilon_0}$ (אנחנו משמאל ללוח שלילי, אז השדה מצביע ימינה לכיוונו)
סך הכל באזור B (סופרפוזיציה), כשהסימנים ביחס לציר $x$ החיובי (ימינה חיובי ושמאלה שלילי):
\[E_B = \frac{\sigma_1}{2\epsilon_0} - \frac{\sigma_2}{2\epsilon_0} + \frac{\sigma_1}{2\epsilon_0} = 0\]מכאן:
\[\boxed{2\sigma_1 = \sigma_2}\]שלב 2 — שדה באזור A
plate 1 plate 2 plate 3
σ₁ -σ₂ -σ₁
| | |
|·→ zone A | |
| ····→₂| |
| | ············→ |
x = a x = 2a x = 3a
באופן דומה, נחשב את השדה באזור A (בין לוח 1 ללוח 2):
- לוח 1 ($+\sigma_1$, משמאלנו): $+\frac{\sigma_1}{2\epsilon_0}$ (ימינה)
- לוח 2 ($-\sigma_2$, מימיננו): $+\frac{\sigma_2}{2\epsilon_0}$ (ימינה, כי נמשכים לכיוון לוח שלילי)
- לוח 3 ($-\sigma_1$, מימיננו): $+\frac{\sigma_1}{2\epsilon_0}$ (ימינה, כנ”ל)
נציב $\sigma_2 = 2\sigma_1$:
\[E_A = \frac{2\sigma_1 + 2\sigma_1}{2\epsilon_0} = \frac{4\sigma_1}{2\epsilon_0} = \frac{2\sigma_1}{\epsilon_0}\]שלב 3 — מהירות הפרוטון
הפרוטון מתחיל ממנוחה בלוח 1 ומואץ לאורך מרחק $d = a$ (מלוח 1 ללוח 2). משימור אנרגיה:
\[\begin{aligned} \frac{1}{2}m_p v^2 &= q_p E_A \cdot a \\[5pt] &= q_p \cdot \frac{2\sigma_1}{\epsilon_0} \cdot a \\[5pt] \end{aligned}\] \[\boxed{v^2 = \frac{4q_p\sigma_1 a}{m_p\epsilon_0}}\]באזור B אין שדה ← מהירות קבועה ← תשובה 1 ✓
דור פסקל