מבוא
אנחנו מתחילים את החומר שלשמו התכנסנו כאן - הנושא של הסקה סטטיסטית. בפרט, אנחנו נתחיל בנושא של אומדן (Estimation).
״אומדן״ הוא תהליך של אומדן פרמטר, או ניסיון לנחש ערך של פרמטר. ״אומדן ממוצע מדגם״ יהיה הדוגמה שתוביל אותנו - ננסה לנחש ערך של פרמטר תוחלת באוכלוסייה באמצעות התצפיות, למשל, באמצעות ממוצע של המדגם ועוד סטטיסטיים אחרים שלו.
מטרת ההסקה הסטטיסטית
אפשר לחלק את עולם ההסקה הסטטיסטית לשני תתי-תחומים:
אומדן (Estimation)
בתהליך של אומדן אנחנו מעריכים גודל של פרמטר של האוכלוסייה, כמו ערך התוחלת האוכלוסייה ($\mu$).
בדיקת השערות (Hypothesis Testing)
בדיקת השערות היא דרך לשאול שאלה בינארית:
- האם ממוצע אוכלוסייה מסוים גדול מממוצע אוכלוסייה אחר?
- האם תרופה מאריכה חיים באופן מובהק סטטיסטית או לא?
אנחנו נבחן האם לאוכלוסייה מסוימת (למשל אנשים שקיבלו את התרופה), יש תכונה מסוימת (למשל זמן החיים שלהם יותר ארוך מזמן החיים של אוכלוסייה אחרת).
הקשר בין אומדן לבדיקת השערות
בתהליך של אומדן, אנחנו מקבלים טווח של פרמטרים שהגיוניים עבורנו. התהליך של בדיקת השערות מתקשר לתהליך של אומדן במובן של האם המספר שרלוונטי לנו נמצא בתוך הטווח.
דוגמה: האם מי שמגיעים לשיעור גבוהים יותר?
השאלה שלנו: האם הסטודנטים שהגיעו ביום חמישי בבוקר גבוהים יותר מהממוצע?
מה אנחנו עושים:
- מודדים את גובה מי שהגיעו (נגיד 20 סטודנטים)
- מודדים את גובה כל השאר (נגיד 80 סטודנטים)
- מחשבים ממוצע לכל קבוצה
הנקודה החשובה: למרות שמדדנו אנשים אמיתיים, אנחנו חושבים על מי שהגיעו כמדגם אקראי. כלומר - יכלו להגיע סטודנטים אחרים, אז התוצאה שלנו הייתה יכולה להיות שונה.
איך זה עובד: במקום לומר “הממוצע של מי שהגיעו הוא בדיוק 1.80מ׳”, אנחנו אומרים: “הממוצע האמיתי של מי שמגיעים לשיעור הוא בין 1.75מ׳ ל-1.85מ׳”
לאחר מכן נבדוק:
- אם ממוצע כל הסטודנטים הוא 1.78מ׳ ← נופל בטווח ← אין הבדל מובהק
- אם ממוצע כל הסטודנטים הוא 1.65מ׳ ← מחוץ לטווח ← יש הבדל מובהק!
הקשר בין שתי השיטות:
- בדיקת השערות: “האם יש הבדל?” (כן/לא)
- אומדן: “איזה הבדל יש?” (טווח מספרים)
הטווח הוא הגשר - הוא עונה על שתי השאלות בבת אחת.
הגדרות בסיסיות באמידה
אוכלוסייה (Population)
אוכלוסייה היא אוסף הפרטים או היחידות (קוראים להם בשפה הסטטיסטית) שעליהם אנחנו מעוניינים להסיק. למשל:
- סטודנטים לרפואה בישראל
- סטודנטים לרפואה בצפת
- סטודנטים לרפואה שמגיעים לשיעורים
- סטודנטים לרפואה שלא מגיעים לשיעורים
מדגם (Sample)
מדגם זו קבוצה חלקית מתוך האוכלוסייה. אתם מדגם אקראי - סטודנטים שהגיעו לשיעור הם מדגם אקראי, לאו דווקא מייצג.
מאפייני המדגם
בדרך כלל אנחנו נניח שהמדגם שלנו הוא אקראי:
- בוחרים $n$ פרטים בלי החזרה מתוך האוכלוסייה
- לא נוכל לבחור את אותו אדם פעמיים
- בכל אחד משלבי הבחירה, לכל פרט יש סיכוי שווה להיבחר
- בוחרים ללא החזרה באופן טבעי, כי לא נוכל לקבל את אותו נבדק בניסוי פעמיים
ההסתברות להיבחר לא תהיה קבועה לכל אורך המדגם, כי היא ללא החזרה. נתעלם מהבעיה הזאת ונדמיין שיש אוכלוסייה גדולה, שהפרטים באוכלוסייה הם יחסית הומוגניים. זה שנדגום פרט אחד מאוכלוסייה, לא ישנה כל כך את ההתפלגות של האוכלוסייה.
תכונה (Variable/Characteristic)
תכונה היא מאפיין של האוכלוסייה, שנתייחס אליו כמשתנה מקרי בעל התפלגות מסוימת. למשל:
- גובה
- אורך חיים
- כמה זמן הישרדות במחלקה שלכם
- צריכת פחמימות
- רמת אינסולין בדם
פרמטר (Parameter)
פרמטר הוא מספר שמאפיין את ההתפלגות של התכונה באוכלוסייה. להתפלגויות יכולים להיות כמה פרמטרים.
למשל, מעוניינים לאמוד:
- רמות האינסולין בדם בקרב חולי סוכרת
- רמות האינסולין בדם בקרב האוכלוסייה הכללית
- צריכת הפחמימות של חולי סוכרת לעומת צריכת פחמימות של אוכלוסייה כללית
סימונים נפוצים לפרמטרים
- פרמטר כללי: $\theta$ (תטה)
- תוחלת באוכלוסייה: $\mu$ (מיו)
- סטיית תקן: $\sigma$ (סיגמה)
- שונות: $\sigma^2$ (סיגמה בריבוע)
חשוב לזכור: הפרמטר קבוע! בפורמליזם הזה, בעולם שלנו, הפרמטר ידוע וקבוע. אנחנו לא יודעים אותו, אבל הוא קבוע - שום דבר לא משנה אותו. הוא נמצא איפה שהוא מאחורי הלוח. אנחנו לא יודע מה הוא, אבל הוא קבוע, הוא לא משתנה עם התצפיות, הוא לא עושה שום דבר. הוא קיים בעולם שאולי אף פעם לא נדע מה הוא, אבל הוא קבוע.
נתוני המדגם (Sample Data)
מדגם זה הערכים של התכונה עבור $n$ פרטים: $x_1, x_2, \ldots, x_n$.
הערה (דור): לא היה לי ברור ההבדל בין הגדרת המדגם כקבוצה חלקית, לבין ההגדרה שלו כהשמה של הערכים - במצגות שתי ההגדרות הופיעו באותו שם (״מדגם״). הוספתי כאן ״נתוני מדגם״ להבהרת המשמעות, להבנתי.
סטטיסטי (Statistic)
סטטיסטי זו פונקציה של התצפיות. סטטיסטי מסומן בדרך כלל באות $T$ כפונקציה של $x_1, x_2, \ldots, x_n$.
דוגמאות לסטטיסטיים
ממוצע המדגם:
\[\bar{X} = \frac{1}{n}\sum_{i=1}^{n} x_i = \frac{x_1 + x_2 + \cdots + x_n}{n}\]שונות המדגם:
\[s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{X})^2\]למה מחלקים ב-$n-1$? לזה נגיע בהמשך.
ערך מקסימלי במדגם:
\[\max\{x_1, x_2, \ldots, x_n\}\]גם מקדם המתאם יכול להיות סטטיסטי, מקדם הרגרסיה, השיפוע ברגרסיה - כל דבר שניתן להוציא מהמדגם שהוא פונקציה של המדגם.
אומדן ואומד
אנחנו בדרך כלל אומדים את הערך של הפרמטר באמצעות הסטטיסטי, אז הרבה פעמים הסטטיסטי אמור להיות קירוב של אותו פרמטר שמעניין אותנו.
- אומד (Estimate): הערך המספרי של האומדן
- אומדן (Estimator): הסטטיסטי (המשערך או האומדן)
הערך של הסטטיסטי ישתנה בין מדגמים. אם נחזור על הבדיקה לגבי הסטודנטים שהגיעו ביום אחר, הסטטיסטי יהיה שונה גם בגלל שהסטודנטים משתנים וגם בגלל שאולי חלקם לא יגיעו.
התפלגות הדגימה (Sampling Distribution)
התפלגות: הערכים האפשריים וההסתברויות שלהם.
התפלגות הדגימה: ההתפלגות של הסטטיסטי תחת הדגימה.
תכונות של אומדנים: הטיה ושונות
שימושיות של אומד מופיינת על ידי שני גדלים:
הטיה (Bias)
\[\text{Bias}(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta\]הטיה של האומד היא ההפרש בין התוחלת של האומד לפרמטר האמיתי.
המדגם הוא משתנה מקרי, האומד הוא פונקציה של המדגם - גם משתנה מקרי. לאומד יש תוחלת.
אנחנו לא נדע את ההטיה אף פעם (אנחנו לא יודעים את הפרמטר אף פעם), אבל נגדיר את הגודל הזה כדי להבין מה בכלל יכול לקרות.
הטיה בודקת האם ההתפלגות מרוכזת סביב הערך האמיתי של הפרמטר.
שונות (Variance)
\[\text{Var}(\hat{\theta}) = \mathbb{E}[(\hat{\theta} - \mathbb{E}[\hat{\theta}])^2]\]השונות היא מדד לפיזור של ערכי האומד - השונות של אותו סטטיסטי, של אותו מספר תחת ההתפלגות של המשתנה המקרי שרלוונטי לו.
אנלוגיה: זריקת חיצים למטרה
תדמיינו שזורקים חיצים למטרה:
- הטיה נמוכה + שונות נמוכה: כל הנקודות מרוכזות על המטרה (מצב אידיאלי)
- הטיה נמוכה + שונות גבוהה: הנקודות מפוזרות סביב המטרה, אבל בממוצע פוגעות במרכז
- הטיה גבוהה + שונות נמוכה: כל הנקודות מרוכזות, אבל רחוק מהמטרה (סטייה שיטתית)
- הטיה גבוהה + שונות גבוהה: הנקודות מפוזרות ורחוקות מהמטרה
מה האומד הטוב ביותר?
אנחנו רוצים הטיה נמוכה ושונות נמוכה - להיות במצב הראשון.
למה זה חשוב?
הבנת הקונספטים האלה עוזרת לנו להבין מאיפה תכונות מגיעות. למשל:
- בעולם של השונות, נראה שהשערוך של השונות כשאנחנו מחלקים ב-$n-1$ נותן לנו אומד חסר הטיה
- לעומת זאת, אם נחלק את השונות את הסטיות הריבועיות ב-$n$ (כמו שהיינו מצפים לעשות אינטואיטיבית), נקבל אומד מוטה
- לכן נומר: “בואו נדאג שהאומד יהיה חסר הטיה”
אנחנו גם נלמד איך אנחנו יכולים להוריד את השונות של המשערך שלנו.
אומדן התוחלת
הגדרה
תוחלת מסומנת ב-$\mu$ - היא פרמטר לא ידוע.
איך משערכים אותה:
- בוחרים מדגם בגודל $n$
- דוגמים $n$ סטודנטים מאוכלוסיית הסטודנטים
- מסמנים את צריכת הפחמימות שלהם ב-$x_1, x_2, \ldots, x_n$ (לצורך העניין $x_{20}$)
הסטטיסטי הוא ממוצע מדגם:
\[\bar{X} = \frac{1}{n}\sum_{i=1}^{n} X_i\]זאת אומרת, לוקחים את צריכת הפחמימות היומית של כל אחד מהסטודנטים שהגיעו, סוכמים ומחלקים בגודל המדגם.
הסטטיסטי הזה הוא האומד שלנו עבור הפרמטר הלא ידוע $\mu$.
בדיקת איכות האומד
נרצה לבדוק אם האומד הזה טוב לתוחלת של האוכלוסייה. נבדוק תוחלת ושונות.
חישוב התוחלת (בדיקת הטיה)
המדגם הוא משתנה מקרי, הסטטיסטי הוא משתנה מקרי, ממוצע המדגם הוא משתנה מקרי.
\[\mathbb{E}[\bar{X}] = \mathbb{E}\left[\frac{1}{n}\sum_{i=1}^{n} X_i\right]\]בתוחלת הכל עובד כמו שאנחנו רוצים:
- אם כופלים משהו ב-$a$, $a$ פשוט יוצא החוצה
- אם כופלים בקבוע, קבוע יוצא החוצה
נזכור גם שתמיד בתוחלת: תוחלת של סכום היא סכום התוחלות
\[\mathbb{E}[\bar{X}] = \frac{1}{n} \sum_{i=1}^{n} \mathbb{E}[X_i]\]באופן טבעי, נצפה שהתוחלת של צריכת הפחמימות של אדם שנבחר באקראי תהיה תוחלת האוכלוסייה. זה הגיוני.
\[\forall i,\quad \mathbb{E}[X_i] = \mu\]ולכן:
\[\begin{aligned} \mathbb{E}[\bar{X}] &= \frac{1}{n} \sum_{i=1}^{n} \mu \\ &= \frac{1}{n} \cdot n\mu \\ &= \mu \end{aligned}\]כלומר, האומד חסר הטיה!
זה הגיוני ואינטואיטיבי.
הבהרה: ההבדל בין ממוצע לתוחלת
- תוחלת זה פרמטר של האוכלוסייה - הוא נמצא איפשהו, אנחנו לא יודעים אותו
- ממוצע זה הדרך שלנו להתקרב אליו, הדרך שלנו לאמוד את התוחלת
דוגמה: הנסיעה של המרצה לצפת
המרצה גר במרחק של כ-70 קילומטר מצפת.
הפרמטר (לא ידוע): התוחלת האמיתית של מרחק הנסיעה - נניח שהיא 70.534 ק”מ בדיוק. זהו ערך קבוע ולא ידוע שמייצג את הממוצע האמיתי של כל הנסיעות האפשריות (תחת תנאי תנועה שונים, מסלולים חלופיים וכו’).
המדגם: כל נסיעה בפועל היא “דגימה” מההתפלגות. למשל:
- נסיעה ביום שני: 69.8 ק”מ (תנועה קלה)
- נסיעה ביום רביעי: 71.2 ק”מ (עומס תנועה, מסלול חלופי)
- נסיעה ביום שישי: 70.1 ק”מ (מסלול רגיל)
הסטטיסטי (האומד): ממוצע המדגם של הנסיעות שנצפו:
\[\bar{X} = \frac{69.8 + 71.2 + 70.1}{3} = 70.37 \text{ km}\]העיקרון החשוב:
- הפרמטר האמיתי (70.534) קבוע ולא ידוע
- האומד שלנו (70.37) הוא קירוב שמתבסס על המדגם
- אם נדגום נסיעות נוספות, נקבל אומד מעט שונה
- ככל שנגדיל את המדגם, האומד יתקרב לפרמטר האמיתי (בתוחלת)
חישוב השונות של ממוצע המדגם
ממוצע המדגם מוגדר כ:
\[\bar{X} = \frac{1}{n}(X_1 + X_2 + X_3 + \cdots + X_n)\]גזירת הנוסחה לשונות ממוצע המדגם
השונות של ממוצע המדגם $\bar{X}$ מחושבת באמצעות תכונות השונות:
\[\text{Var}(\bar{X}) = \text{Var}\left(\frac{1}{n}\sum_{i=1}^{n} X_i\right)\]שלב 1: הוצאת הקבוע מהשונות
על פי חוקי השונות, כאשר כופלים משתנה מקרי בקבוע $a$, השונות מוכפלת ב-$a^2$:
\[\text{Var}(\bar{X}) = \text{Var}\left(\frac{1}{n}\sum_{i=1}^{n} X_i\right) = \frac{1}{n^2} \text{Var}\left(\sum_{i=1}^{n} X_i\right)\]שלב 2: שונות של סכום משתנים בלתי תלויים
מכיוון שהדגימות $X_1, X_2, \ldots, X_n$ הן בלתי תלויות, שונות הסכום שווה לסכום השונויות:
\[\text{Var}\left(\sum_{i=1}^{n} X_i\right) = \text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n)\]שלב 3: שונות זהה לכל דגימה
כל דגימה $X_i$ מגיעה מאותה אוכלוסייה, ולכן יש לה אותה שונות:
\[\forall i: \quad \text{Var}(X_i) = \sigma^2\]שלב 4: חישוב סופי
\[\begin{aligned} \text{Var}(\bar{X}) &= \frac{1}{n^2}[\text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n)] \\ &= \frac{1}{n^2}[\sigma^2 + \sigma^2 + \cdots + \sigma^2] \\ &= \frac{1}{n^2} \cdot n\sigma^2 \\ &= \boxed{\frac{\sigma^2}{n}} \end{aligned}\]המשמעות המעשית של הנוסחה $\text{Var}(\bar{X}) = \frac{\sigma^2}{n}$
תובנה מרכזית: השונות של ממוצע המדגם קטנה ביחס הפוך לגודל המדגם.
השלכות מעשיות
-
הגדלת המדגם מקטינה אי-וודאות: ככל שנגדיל את $n$, השונות של האומד שלנו תקטן.
-
יחס הקטנה: כדי להקטין את השונות פי $k$, נצטרך להגדיל את המדגם פי $k$.
-
שיקולים כלכליים: הגדלת המדגם דורשת משאבים (זמן, כסף, מאמץ), ולכן יש לשקול את הפשרה בין דיוק לעלות.
מספר הדגימות והשפעתו על סטיית התקן
סטיית התקן של האוכלוסייה: $\sigma$
סטיית התקן של ממוצע המדגם (שגיאת התקן):
\[\text{SE}(\bar{X}) = \sqrt{\text{Var}(\bar{X})} = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}\]תכונה חשובה: יחס השורש
להקטנת סטיית התקן של ממוצע המדגם פי $k$, נדרש להגדיל את המדגם פי $k^2$:
דוגמה: כדי להקטין את שגיאת התקן פי 10, נצטרך להגדיל את המדגם פי 100.
\[\frac{\sigma/\sqrt{n}}{\sigma/\sqrt{100n}} = \frac{\sqrt{100n}}{\sqrt{n}} = \sqrt{100} = 10\]המונח המקצועי: סטיית התקן של ממוצע המדגם נקראת שגיאת תקן (Standard Error) או SE.
משפט הגבול המרכזי (Central Limit Theorem)
משפט הגבול המרכזי: אם לוקחים הרבה השפעות קטנות ומחברים אותן, לא משנה מה ההתפלגות של כל אחת מההשפעות - מקבלים בסוף משהו שנראה נורמלי.
גם אם כל ההשפעות הקטנות נראות כמו הדבר המוזר הזה, אם סוכמים אותן מספיק, מקבלים משהו שהוא בקירוב (ולצרכינו יותר מקירוב) שווה להתפלגות נורמלית.
יישום על ממוצע המדגם
ההתפלגות של המשתנה המקרי $\bar{X}$ היא בעצם התפלגות של:
\[\frac{X_1}{n} + \frac{X_2}{n} + \frac{X_3}{n} + \cdots + \frac{X_n}{n}\]אלה השפעות קטנות - אם $n$ גדול, אז ההשפעה קטנה של כל $X_i$.
ההתפלגות של ממוצע המדגם שואפת להתפלגות נורמלית עם:
- תוחלת: $\mu$ (התוחלת הנכונה)
- שונות: $\frac{\sigma^2}{n}$ (שונות קטנה פי $n$ מהשונות באוכלוסייה)
זה לא משנה איך נראית ההתפלגות הראשונית!
קירוב נורמלי - כמה דגימות נדרשות?
מקובל לקבוע ערך סף של $n \geq 30$. זה שרירותי, אבל אנחנו נשתמש בזה כי זה מקובל בסטטיסטיקה.
אבל נדרשת קצת חשיבה ביקורתית:
- התפלגות הכנסה של עובדי בנק - מאוד לא סימטרית, כי המנכ”ל וההנהלה הבכירה מרוויחים הרבה יותר מהטלרים והמנקים. בשביל לקבל התפלגות נורמלית ממשהו כזה, אני צריך מספר דגימות גדול יותר.
- גבהים בקרב סטודנטים - התפלגות יחסית סימטרית. אתם לא תראו סטודנט שהגובה שלו עשרים מטר, ואתם לא תראו סטודנט שהגובה שלו עשרים סנטימטר. בשביל שהקירוב הנורמלי יהיה תקף, אני צריך פחות דגימות.
שאלות לדוגמה
דוגמה 1: צריכת פרצטמול במחלקה
נניח שצריכת פרצטמול יומית עבור חולה במחלקה היא 200 מיליגרם ליום, סטיית התקן היא 50 מיליגרם.
רוצים לדעת מה תהיה התפלגות ממוצע צריכת הפרצטמול במחלקה של 100 מאושפזים - אולי בשביל לתכנן את מלאי הפרצטמול במחלקה.
מנתוני השאלה:
\[\begin{aligned} \mu &= 200 \text{ mg} \\ \sigma &= 50 \text{ mg} \\ n &= 100 \end{aligned}\]התשובה:
\[\bar{X} \sim \mathcal{N}\left(200, \frac{50^2}{100}\right) = \mathcal{N}(200, 25)\]ממוצע המדגם יתפלג נורמלית עם תוחלת 200 מיליגרם וסטיית תקן של 25 מיליגרם.
דוגמה 2: משקל לידה בבית חולים
משקל לידה בבית חולים מתפלג נורמלית:
- תוחלת: 3,000 גרם
- סטיית תקן: 500 גרם
שאלה א׳: תינוקת בודדת
מה ההסתברות שתינוקת אחת תיוולד במשקל גדול מ-3,150 גרם?
שאלה ב׳: ממוצע 25 תינוקות
מה ההסתברות שמשקל הלידה הממוצע של 25 תינוקות במחלקה יעלה על 3,150 גרם?
עבור תינוקת אחת, ההתפלגות היא ההתפלגות באוכלוסייה:
תקנון:
\[Z = \frac{3150 - 3000}{500} = \frac{150}{500} = 0.3\] \[\begin{aligned} P(X > 3150) &= P(Z > 0.3) \\[10pt] &= 1 - \Phi(0.3) \approx \boxed{0.38} \end{aligned}\]from scipy.stats import norm
p = 1 - norm.cdf(0.3)
print(p) # 0.38208857781104744
כלומר, הסיכוי שתינוקת אחת תיוולד במשקל גדול מ-3,150 גרם הוא כ-38%.
המדגם קטן יחסית ($n=25$), אבל ההתפלגות באוכלוסייה נורמלית, ולכן לממוצע המדגם תהיה גם התפלגות נורמלית.
פרמטרים של ממוצע המדגם:
-
תוחלת:
\[\mu = 3000 \, \mathrm{gr}\] -
סטיית תקן:
\[\sigma = 500 \, \mathrm{gr}\] -
סטיית תקן של ממוצע המדגם (״שגיאת תקן״):
\[\text{SE} = \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{500}{\sqrt{25}} = \frac{500}{5} = 100 \, \mathrm{gr}\]
תקנון:
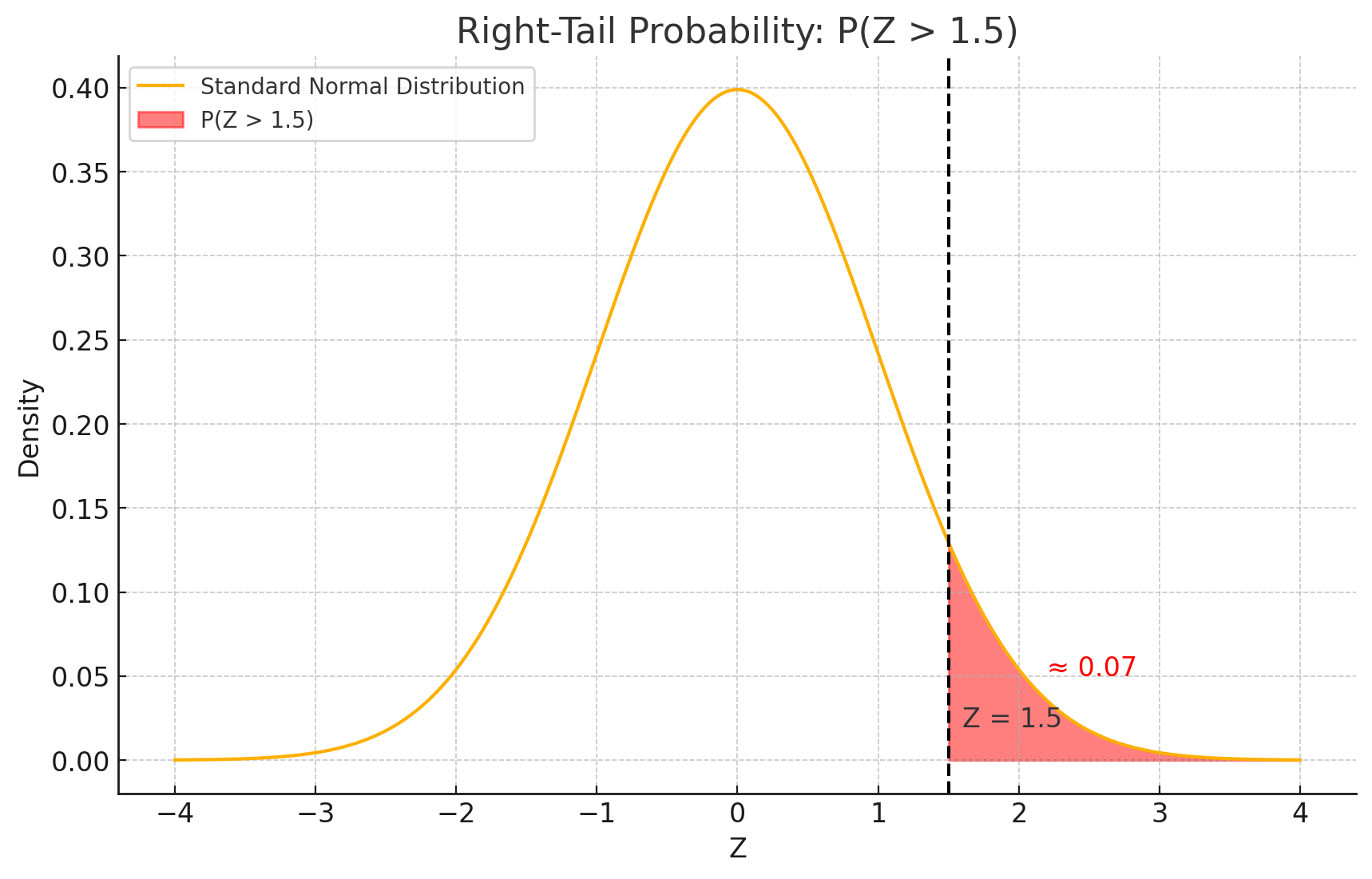
\[Z = \frac{3150 - 3000}{100} = \frac{150}{100} = 1.5\]הצבה בנוסחה להסתברות זנב ימני:
\[P(\bar{X} > 3150) = P(Z > 1.5) \approx \boxed{0.07}\]השוואה: הסיכוי ירד מ-0.38 ל-0.07 - הרבה יותר קטן! זה הכוח של ממוצע המדגם - הממוצע מתמרכז סביב התוחלת באוכלוסייה.
מבוא לרווחי סמך (Cl - Confidence interval)
רווח סמך הוא נושא הסטטיסטיקה הראשון שיש לו ערך מעשי ממש. במאמרים מדעיים רפואיים תמיד נראה רווחי סמך. אף אחד לא יגיד “התרופה הזו נותנת עוד שלוש שנים לחיים”. יגידו: “היא נותנת בממוצע שלוש שנים לחיים, בטווח של רווח סמך $95\%$, עוד שנתיים וחצי עד שלוש וחצי שנים”.
אין כזה ׳ספר מדויק׳ דבר בעולם המדעי או הרפואי. אנחנו לא יודעים. בשביל מספרים לא מדויקים, בשביל להעריך, יש לנו את רווח הסמך.
רווח הסמך הראשון שנלמד הוא רווח סמך לתוחלת.
הערה (דור): השם של רווח סמך באנגלית,
Confidence interval (CI), לדעתי משקף את המשמעות טוב יותר. הייתי מתרגם את המושג בתור ״מרווח ביטחון״, אולי השם ״רווח סמך״ מגיע מ״מרווח״ שניתן ״לסמוך״ עליו.
הגדרת רווח סמך
עבור כל מדגם, יש ערך של האומד, הוא נקרא אומדן נקודתי (Point Estimate) - מספר נקודה על הישר הממשי.
אבל התועלת של הערך הזה מוטלת בספק, כי אנחנו לא יודעים את הערך של הפרמטר האמיתי.
לפיכך, נרצה למצוא תחום ערכים (וזה נורא חשוב) - תחום ערכים בו הפרמטר האמיתי יימצא בהסתברות של $95\%$.
שימו לב: הפרמטר האמיתי לא ידוע, אבל נרצה למצוא תחום, להגדיר פרוצדורה שמכסה את הפרמטר האמיתי הלא ידוע בהסתברות של $95\%$.
אם מאחורי הלוח נמצא הפרמטר האמיתי, ואני זורק את התחום על הלוח, אני רוצה שבכל פעם שאני זורק תחום אחר, הוא יכסה את הפרמטר האמיתי הלא ידוע, הקבוע, בהסתברות של $95\%$.
התחום הזה נקרא רווח סמך, או לפעמים רווח בר סמך, במקרה הזה של $95\%$.
הנחות לחישוב רווח סמך
- רוצים ללמוד את התוחלת של תכונה כלשהי באוכלוסייה - לגיטימי
- המדגם מספיק גדול, כך שמשפט הגבול המרכזי יתקיים - לגיטימי
- השונות $\sigma^2$ של האוכלוסייה ידועה - אנחנו אף פעם כנראה לא נדע את השונות באוכלוסייה, אבל בשביל להבין מה קורה, באופן מתודי ודידקטי, נניח שהשונות $\sigma^2$ ידועה
זה לא יקרה במציאות, אבל בשביל להבין זה יעזור לנו. זה כמו פיגומים לבניין.
הנוסחה לרווח סמך
המטרה
נרצה לבנות רווח סמך (Confidence Interval) עבור התוחלת האמיתית $\mu$ של האוכלוסייה, בהסתמך על מדגם מקרי.
ההגדרה המתמטית
רווח סמך ברמת ביטחון 95% הוא זוג פונקציות של המדגם $(L_1, L_2)$ כך ש:
\[P(L_1 \leq \mu \leq L_2) = 0.95\]כלומר, בהסתברות של 95%, הרווח שנבנה מהמדגם יכיל את הפרמטר האמיתי $\mu$.
הנוסחה לרווח סמך של 95%
\[\text{95\% CI} = \left[ \bar{X} - 1.96 \cdot \text{SE},\; \bar{X} + 1.96 \cdot \text{SE} \right]\]כאשר:
- $\bar{X}$ = ממוצע המדגם
- $\text{SE} = \frac{\sigma}{\sqrt{n}}$ = שגיאת התקן של ממוצע המדגם
- $n$ = גודל המדגם
- $\sigma$ = סטיית התקן של האוכלוסייה
מאיפה מגיע המספר 1.96?
בהתפלגות נורמלית סטנדרטית $N(0,1)$:
- הטווח $[-1.96, 1.96]$ מכיל 95% מהמסה
- נשארים 5% מחוץ לטווח: 2.5% בכל זנב
מתמטית: אם $Z \sim N(0,1)$, אז:
\[P(-1.96 \leq Z \leq 1.96) = 0.95\]גזירת נוסחת רווח הסמך
נוכיח שהפרמטר האמיתי נמצא בין המספרים האלה בהסתברות של 0.95.
שלב 1: התפלגות ממוצע המדגם
על פי משפט הגבול המרכזי, $\bar{X}$ (ממוצע המדגם) הוא משתנה מקרי נורמלי:
\[\bar{X} \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\]שלב 2: תקנון
המשתנה המקרי המתוקנן הוא:
\[Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}}\]$Z$ הוא נורמלי סטנדרטי: $Z \sim N(0,1)$
שלב 3: שימוש בערכים קריטיים
נזכור שהסיכוי למשתנה מקרי נורמלי סטנדרטי:
-
להיות גדול מ-1.96:
\[P(Z > 1.96) = 0.025\] -
להיות קטן מ-(-1.96):
\[P(Z < -1.96) = 0.025\]
זאת אומרת: $P(-1.96 < Z < 1.96) = 0.95$
שלב 4: אלגברה
\[P\left(-1.96 < \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} < 1.96\right) = 0.95\]נכפול בשגיאת התקן:
\[P\left(-1.96 \cdot \frac{\sigma}{\sqrt{n}} < \bar{X} - \mu < 1.96 \cdot \frac{\sigma}{\sqrt{n}}\right) = 0.95\]נעביר את $\bar{X}$ ונכפיל ב-$(-1)$:
\[P\left(\bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}} < \mu < \bar{X} + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\right) = 0.95\]זהו! מכאן מגיעה הנוסחה של רווח סמך.
הראנו שהסיכוי ש-$\mu$ (התוחלת האמיתית) תימצא בטווח:
\[\left[\bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}}, \bar{X} + 1.96 \cdot \frac{\sigma}{\sqrt{n}}\right]\]הוא $95\%$.
סיכום
רווח הסמך הוא $\bar{X} \pm 1.96 \cdot \frac{\sigma}{\sqrt{n}}$, כלומר
\[\boxed{\left[ \bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}},\; \bar{X} + 1.96 \cdot \frac{\sigma}{\sqrt{n}} \right]}\]כלומר, אנו לוקחים את ממוצע המדגם ומוסיפים/מחסירים 1.96 שגיאות תקן (לא “שתיים”, אלא 1.96!).
הערות חשובות
- הנחת יסוד: הנוסחה תקפה כאשר $\bar{X}$ מתפלג נורמלית (בגלל משפט הגבול המרכזי, זה נכון למדגמים גדולים)
- פרשנות נכונה: 95% מרווחי הסמך שנבנה בשיטה זו יכילו את $\mu$ האמיתי
- בפועל: כאשר $\sigma$ לא ידוע, משתמשים בהתפלגות t ובאומד $s$ במקום $\sigma$
דוגמה: יעילות תרופה בהורדת לחץ דם
\[\text{SE} = \frac{\sigma}{\sqrt{n}} = \frac{16}{\sqrt{64}} = \frac{16}{8} = 2\] \[\text{CI} -5 \pm 2 \times 2 = -5 \pm 4\]רוצים לאמוד יעילות של תרופה בהורדת לחץ דם. נתון שסטיית התקן של שינוי לחץ דם היא $16$ מילימטר כספית.
מדגם של $64$ מטופלים - קיבלנו שממוצע הירידה בלחץ דם היה $5$ מילימטר כספית.
אם מישהו תמים, הוא אולי היה אומר: “ממוצע הירידה בלחץ הדם 5 מילימטר כספית, זאת אומרת שהתרופה מועילה, התרופה מורידה את לחץ הדם.” - אנחנו לכאורה לא תמימים. נחשב רווח סמך.
רווח הסמך להורדת לחץ דם הוא: $-9$ עד $-1$ מילימטר כספית.
פירוש התוצאה
האם התרופה מועילה? האם התרופה בכלל מורידה לחץ דם?
התשובה היא: כנראה שכן! למה? כי רווח הסמך לא כולל את האפס. אם הירידה בלחץ דם הייתה אפס (כלומר אין השפעה), זה לא נמצא בטווח הסביר שלנו.
זאת אומרת שיש עדות חזקה לכך שהתרופה אכן מורידה את לחץ הדם.
.png)
השפעת גודל המדגם על רווח הסמך
נניח שגודל המדגם היה 256 מטופלים (פי 4 מטופלים):
\[\text{SE} = \frac{16}{\sqrt{256}} = \frac{16}{16} = 1 \text{ mm Hg}\] \[\text{Confidence interval: } -5 \pm 2 \times 1 = -5 \pm 2\]רווח הסמך החדש: $-7$ עד $-3$ מילימטר כספית.
קיבלנו רווח סמך הרבה יותר צר - זאת אומרת שאנחנו יכולים להעריך, לשערך, לאמוד את התועלת שבתרופה בדיוק הרבה יותר גבוה.
עכשיו אפשר לשאול את אותה השאלה: האם התרופה מורידה לחץ דם? ובהסתברות של $95\%$, רווח הסמך מכיל את הפרמטר האמיתי. ברמת סמך כזו, התרופה כן מורידה לחץ דם, כי אנחנו די משוכנעים שהפרמטר של הורדת לחץ דם הוא שלילי.
תכונות של רווח סמך
מה משפיע על רוחב רווח הסמך?
שונות ממוצע המדגם היא: $\frac{\sigma^2}{n}$
אם יש:
- מדגם גדול או שונות קטנה באוכלוסייה ← ההתפלגות הדגימה צרה ← רווח הסמך שלי יהיה צר ← החיים שלי יהיו טובים
אם:
- המדגם קטן או שונות גדולה באוכלוסייה ← השונות של ממוצע המדגם תהיה יותר גדולה ← רווח הסמך שלי יהיה יותר רחב
איך מקטינים את רווח הסמך?
אני לא יכול לשלוט באוכלוסייה - אני לא יכול להגיד לכולם “תאכלו את אותה כמות של פיתות ביום”, אני לא יכול להכריח את כולם להיות עם אותה רמת אינסולין.
אני כן יכול להגדיל את המדגם. בשביל לצמצם את רווח הסמך:
- $\sigma$ קבוע
- $\sqrt{n}$ יכול לגדול, כתלות במשאבים שלי
- כמה סבלנות, כמה כסף וכמה זמן יש לדגום עוד ועוד אנשים
דוגמה: סקרי חיסון קורונה 2021-2020
דוגמה שמראה בצורה מעשית את ההשפעה של גודל המדגם על רווח הסמך.
בשנת 2021-2020, שלושה גורמים ביצעו סקרים להערכת אחוז האוכלוסייה המחוסנת נגד וירוס הקורונה בארצות הברית:
הסקרים השונים
- דלפי (Carnegie Mellon University) - באמצעות פייסבוק:
- גודל מדגם: 250,000 איש
- השתמשו במידע מפייסבוק, ניחשו עם בן אדם מחוסן או לא
- Census (ממשלת ארצות הברית):
- גודל מדגם: 75,000 איש
- Axios-Ipsos:
- גודל מדגם: 1,000 איש
- זה כלום לעומת 250,000!
התוצאות והשלכותיהן
למזלנו, הכמות העצומה של נשאלים בסקר של פייסבוק ובסקר של Census גרמה לכך שהם היו מאוד בטוחים בתוצאות שלהם.
נסתכל על התוצאות:
-
Axios-Ipsos: היו להם רווחי סמך יחסית גדולים, כי היו להם אלף נדגמים. הם לא היו כל כך בטוחים בתוצאות שלהם.
-
פייסבוק: חישבו את רווח הסמך שלהם לפי הנוסחה עם $\sqrt{n}$. $\sqrt{250,000}$ זה מספר עצום! אז רווח הסמך שלהם כל כך קטן עד שלא רואים אותו בגרף.
-
Census: גם להם יש רווח סמך מאוד קטן, אם כי קצת יותר גדול משל פייסבוק.
השוואה למציאות
מספר המחוסנים בארצות הברית מדווח בפועל על ידי ה-CDC (Center for Disease Control) - הארגון שאחראי על מחלות מדבקות בארצות הברית. מהגרפים אפשר לראות שהסקרים עם המדגמים הגדולים (פייסבוק ו-Census) היו קרובים יותר לנתונים האמיתיים של ה-CDC.
זו דוגמה מעולה לכך שגודל מדגם גדול יותר נותן לנו:
- רווח סמך צר יותר (דיוק גבוה יותר)
- אומדנים טובים יותר של הפרמטר האמיתי
הלקח מדוגמת סקרי קורונה
עידן מעיר שהפינג פונג הראה שלמרות שהסקר של פייסבוק היה עם 250,000 איש, הוא היה פחות מדויק מהסקר של Axios-Ipsos עם 1,000 איש בלבד.
הלקח החשוב: תיזהרו עם ההנחות שלכם!
אנחנו מחלקים פה ב-$\sqrt{n}$ עם הנחה שהדגימות בלתי תלויות. ברור, באופן מובהק, ההנחה הזו לא תופסת במדגם של דלפי-פייסבוק. לא תופסת. ותופסת במדגם הרבה יותר קטן של Axios-Ipsos.
למה זה קרה?
- משתמשי פייסבוק יש להם אולי נטייה לשקר
- האוכלוסייה של הפייסבוקאים שונה מהאוכלוסייה הכללית
- בומרים כמוני למשל לא בטיק טוק או בטוויטר
- הסקר של Axios-Ipsos שתוכנן להיות מדגם מייצג של האוכלוסייה היה הדגם הקרוב ביותר לנתונים האמיתיים של ה-CDC
המסקנה המפתיעה: הסקר של דלפי-פייסבוק, 250 אלף איש, שווה ערך לרמת דיוק של בערך עשרה נדגמים שנדגמו באמת באקראי מהאוכלוסייה.
זה בגלל שהאוכלוסייה של פייסבוק - צרכני הפייסבוק - זה באמת יותר מבוגרים, פחות פוחדים מחיסונים אולי, יותר סאחים מהאוכלוסייה הכללית.
רווחי סמך ברמות ביטחון שונות
הנוסחה הכללית
עבור רמת ביטחון כלשהי, רווח הסמך הוא:
\[\bar{X} \pm C \cdot \frac{\sigma}{\sqrt{n}}\]כאשר $C$ הוא הערך הקריטי שתלוי ברמת הביטחון הרצויה.
איך מוצאים את הערך הקריטי?
עבור רמת ביטחון של 90%
- רוצים ש-90% מהמסה תהיה בתוך הרווח
- נשארים 10% מחוץ לרווח: 5% בכל זנב
- צריך למצוא $C$ כך ש: $P(Z > C) = 0.05$
- התשובה: $C = 1.645$
עבור רמת ביטחון של 95%
- רוצים ש-95% מהמסה תהיה בתוך הרווח
- נשארים 5% מחוץ לרווח: 2.5% בכל זנב
- צריך למצוא $C$ כך ש: $P(Z > C) = 0.025$
- התשובה: $C = 1.96$
עבור רמת ביטחון של 99%
- רוצים ש-99% מהמסה תהיה בתוך הרווח
- נשארים 1% מחוץ לרווח: 0.5% בכל זנב
- צריך למצוא $C$ כך ש: $P(Z > C) = 0.005$
- התשובה: $C = 2.576$
מדוע אין רווח סמך של 100%?
שאלה: האם ניתן לבנות רווח סמך עם ביטחון של 100%?
תשובה: לא!
- כדי לקבל 100% ביטחון, נצטרך $C = \infty$
- הרווח יהיה $(-\infty, \infty)$ - לא אינפורמטיבי
- מסקנה: תמיד יש אי-ודאות בסטטיסטיקה
הטרייד-אוף: ביטחון מול דיוק
| רמת ביטחון | ערך קריטי | רוחב הרווח | יתרונות | חסרונות |
|---|---|---|---|---|
| 90% | 1.645 | צר יותר | מדויק יותר | פחות ביטחון |
| 95% | 1.96 | בינוני | איזון סביר | הסטנדרט המקובל |
| 99% | 2.576 | רחב יותר | ביטחון גבוה | פחות מדויק |
עיקרון: ככל שרוצים יותר ביטחון ← הרווח נהיה רחב יותר ← פחות שימושי
דוגמה: משקל תינוקות
נתונים:
- גודל מדגם: $n = 100$
- ממוצע מדגם: $\bar{X} = 3200 \,\mathrm{gr}$
- סטיית תקן ידועה: $\sigma = 500 \,\mathrm{gr}$
שלב 1: חישוב שגיאת התקן
\[\text{SE} = \frac{\sigma}{\sqrt{n}} = \frac{500}{\sqrt{100}} = 50 \,\mathrm{gr}\]שלב 2: חישוב רווחי סמך
רווח סמך 90%:
\[3200 \pm 1.645 \times 50 = 3200 \pm 82.25 = [3117.75, 3282.25]\]רוחב: 164.5 גרם
רווח סמך 95%:
\[3200 \pm 1.96 \times 50 = 3200 \pm 98 = [3102, 3298]\]רוחב: 196 גרם
רווח סמך 99%:
\[3200 \pm 2.576 \times 50 = 3200 \pm 128.8 = [3071.2, 3328.8]\]רוחב: 257.6 גרם
סימון פורמלי
הגדרת הערך הקריטי
עבור משתנה נורמלי סטנדרטי $Z \sim N(0,1)$:
$Z_\alpha$ = הערך הקריטי המקיים:
\[P(Z > Z_\alpha) = \alpha\]ערכים נפוצים
- $Z_{0.05} = 1.645$ (לרווח סמך 90%)
- $Z_{0.025} = 1.96$ (לרווח סמך 95%)
- $Z_{0.005} = 2.576$ (לרווח סמך 99%)
הנוסחה הכללית
רווח סמך ברמת ביטחון $(1-\alpha) \times 100\%$:
\[\bar{X} \pm Z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\]הסבר: משתמשים ב-$\alpha/2$ כי מחלקים את ה-$\alpha$ בין שני הזנבות
חישוב גודל מדגם נדרש
הבעיה
רוצים רווח סמך של 95% עם רוחב מקסימלי של 100 גרם.
כמה תינוקות צריך לדגום?
הפתרון
רוחב רווח הסמך:
\[\text{width} = 2 \times Z_{0.025} \times \frac{\sigma}{\sqrt{n}} = 2 \times 1.96 \times \frac{500}{\sqrt{n}}\]דרישה: רוחב ≤ 100
\[\frac{1960}{\sqrt{n}} \leq 100\]פתרון:
\[\sqrt{n} \geq 19.6\] \[n \geq 384.16\]מסקנה: נדרשים לפחות 385 תינוקות
נוסחה כללית לגודל מדגם
עבור רווח סמך ברמת ביטחון $(1-\alpha)$ עם רוחב מקסימלי $W$:
\[n \geq \left(\frac{2 \times Z_{\alpha/2} \times \sigma}{W}\right)^2\]סיכום - נקודות מפתח ברווחי סמך
-
הפרמטר $\mu$ הוא קבוע, לא מקרי:
התוחלת האמיתית $\mu$ היא ערך קבוע שאיננו יודעים. היא לא משתנה - אנחנו פשוט לא יודעים מה ערכה.
-
רווח סמך ספציפי - בפנים או בחוץ:
ברגע שחישבנו רווח סמך מסוים (למשל [3102, 3298]), הפרמטר נמצא בתוכו או לא - אין כאן הסתברות.
-
אי-ודאות היא חלק מהשיטה: לעולם לא נדע בוודאות אם רווח סמך ספציפי תפס את הפרמטר. זו המהות של סטטיסטיקה.
-
השיטה נקבעת מראש: מחליטים על השיטה (רמת ביטחון, נוסחה) לפני איסוף הנתונים. אסור “לתפור” את השיטה לתוצאות.
-
משמעות רמת הביטחון: רמת ביטחון של 95% פירושה: אם נחזור על התהליך הרבה פעמים (דגימה ← חישוב רווח), ב-95% מהמקרים הרווח יכיל את $\mu$.
זכרו: הביטחון הוא בשיטה, לא ברווח ספציפי!
דור פסקל