סקירת כוחות ועקרונות יסודיים
הכוחות הנפוצים שאנחנו עובדים איתם פועלים בניגוד לכיוון התנועה. נתחיל בכוח החיכוך בין משטחים - זוהי התנגדות לתנועה בין שני משטחים. כוח זה מוגדר באמצעות מקדם:
- אם שני המשטחים נמצאים במנוחה, זה מקדם סטטי ($\mu_s$) כפול הכוח הנורמלי ביניהם.
- אם שני המשטחים נעים ביחס אחד לשני, אז כוח החיכוך הוא מקדם קינטי ($\mu_k$) כפול הכוח הנורמלי שפועל בין שני המשטחים.
באופן כללי, המקדם הסטטי ($\mu_s$) גדול מהמקדם הקינטי ($\mu_k$).
כוח נוסף שלמדנו ותרגלנו הוא כוח המשיכה של כדור הארץ. קרוב לפני הקרקע, המשקל שלנו (כוח המשיכה של כדור הארץ) הוא המסה שלנו כפול תאוצת המשיכה של כדור הארץ:
\[F_g = m \cdot g\]כיוון הכוח הזה הוא למרכז כדור הארץ, והגודל של תאוצת הכבידה על פני כדור הארץ הוא בקירוב $g = 10 \text{ מטרים לשנייה בריבוע}$.
חשוב לציין שאם לוקחים גוף קל וגוף כבד ומפילים אותם (למשל מהמגדל של פיזה), אז בהיעדר חיכוך משמעותי עם האוויר, שניהם יגיעו לקרקע באותו זמן מכיוון שלשניהם אותה תאוצה. לכולנו יש אותה תאוצה תחת כוח הכבידה.
שלבי עבודה בפתרון בעיות דינמיקה
כשפותרים בעיות דינמיקה, עלינו לעקוב אחר השלבים הבאים:
- הכנת תרשים כוחות לכל גוף
- בחירת מערכת צירים
- רישום משוואות התנועה בהתאם לחוקי ניוטון
- פתרון משוואות קינמטיקה לביצוע המשימה
סקירת שאלות תרגיל
לפני שנעבור לשאלה המרכזית, הפרופסור מזכיר מספר תרגילים חשובים:
- תרגיל 8 מהדף הקודם, שהוא יחסית מורכב
- התרגיל הבא אחריו שעוסק בכוח משתנה ומשוואות דיפרנציאליות
- מהדף החדש (דף חמש), שאלה שלוש שהיא ארוכה ושאלה ארבע שהיא “טריקית”
כמו כן, הפרופסור מציין שהמצגת והתשובות זמינות למעקב.
בעיית הטריז והגליל
הבעיה שאנו פותרים היא כדלקמן:
טריז משולש שמסתו $M$ מונח על רצפה אופקית וצמוד לקיר אנכי. על הטריז מונח גליל שמסתו $m$, המפעיל כוח על הטריז הן כלפי מטה והן כלפי צד. זווית השיפוע של הטריז היא $\alpha = 30^{\circ}$. אין חיכוך בין הטריז לרצפה. כוחות המשיכה שמפעיל כדור הארץ על הטריז והגליל הם $M \cdot g$ ו-$m \cdot g$ בהתאמה.
שאלה א׳: מהם הכוחות הנורמליים הפועלים על המערכת?
נתחיל עם ניתוח הכוחות הפועלים על הטריז:
- כוח המשיכה: $M \cdot g$ (כלפי מטה)
- הכוח הנורמלי מהרצפה: $N_{\text{רצפה}}$ (כלפי מעלה)
- הכוח הנורמלי מהגליל: $N_m$ (בניצב למישור המשופע)
- הכוח הנורמלי מהקיר: $N_{\text{קיר}}$ (בכיוון אופקי שמאלה)
כעת נבחן את הכוחות הפועלים על הגליל:
- כוח המשיכה: $m \cdot g$ (כלפי מטה)
- הכוח הנורמלי מהטריז: $N_m$ (בניצב למישור המשופע בכיוון הפוך)
- הכוח הנורמלי מהקיר: $N_{\text{קיר}}$ (בכיוון אופקי ימינה)
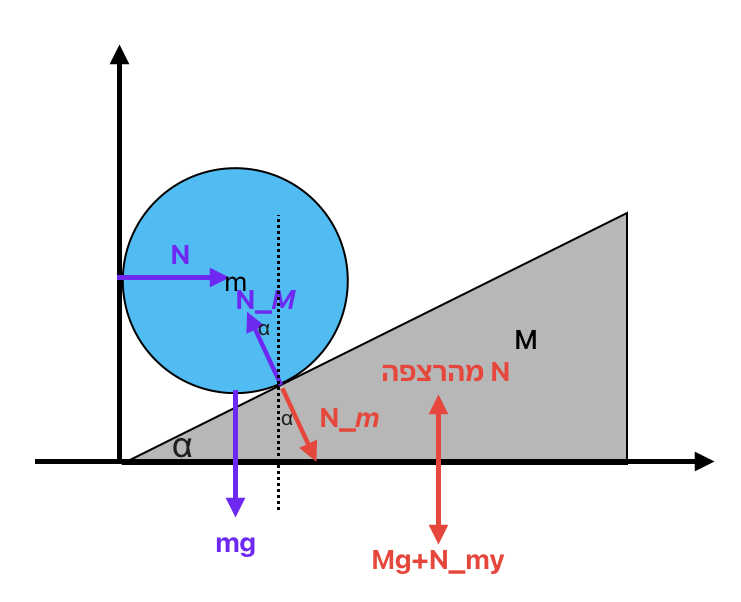
ניתוח הזוויות במערכת
הזוויות במערכת הן כדלקמן:
- זווית הטריז עם הרצפה היא $\alpha = 30^{\circ}$
- הכוח הנורמלי מהרצפה פועל בזווית של $90^{\circ}$ ביחס לרצפה
- הכוח הנורמלי מהקיר פועל בזווית של $90^{\circ}$ ביחס לקיר
- הכוח הנורמלי בין הטריז לגליל פועל בזווית של $90^{\circ} - \alpha = 60^{\circ}$ ביחס לאנך
שאלה ב׳: משוואות התנועה כאשר המערכת לא מקובעת
נבחר מערכת צירים כך ש-$x$ הוא בכיוון אופקי (ימינה חיובי) ו-$y$ הוא בכיוון אנכי (מטה חיובי).
משוואות התנועה עבור הגליל
בכיוון ציר $x$:
\[\sum F_x = m \cdot a_x\] \[N_{\text{קיר}} - N_m \cdot \sin(30^{\circ}) = m \cdot a_x\]מכיוון שהגליל לא יכול לזוז בכיוון $x$ (הוא צמוד לקיר), $a_x = 0$, ולכן: \(N_{\text{קיר}} = N_m \cdot \sin(30^{\circ}) = N_m \cdot \frac{1}{2}\)
בכיוון ציר $y$: \(\sum F_y = m \cdot a_y\) \(M \cdot g - N_m \cdot \cos(30^{\circ}) = m \cdot a_y\) \(a_y = g - \frac{N_m \cdot \cos(30^{\circ})}{m} = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m}\)
משוואות התנועה עבור הטריז:
בכיוון ציר $x$: \(\sum F_x = M \cdot a_x\)
\[N_m \cdot \sin(30^{\circ}) = M \cdot a_x\] \[a_x = \frac{N_m \cdot \sin(30^{\circ})}{M} = \frac{N_m \cdot \frac{1}{2}}{M}\]בכיוון ציר $y$:
\[\sum F_y = M \cdot a_y\] \[M \cdot g + N_m \cdot \sin(30^{\circ}) - N_{\text{רצפה}} = M \cdot a_y\]מכיוון שהטריז לא יכול לזוז בכיוון $y$ (הוא מונח על הרצפה), $a_y = 0$, ולכן: \(N_{\text{רצפה}} = M \cdot g + N_m \cdot \sin(30^{\circ}) = M \cdot g + N_m \cdot \frac{1}{2}\)
בשלב זה, אנו זקוקים לקשר נוסף בין התאוצות כדי למצוא את $N_m$. כשהמערכת אינה מקובעת, הטריז והגליל יתחילו לנוע. הטריז ינוע אופקית (בכיוון ציר $x$) והגליל ינוע אנכית (בכיוון ציר $y$). התנועה המשולבת הזו דורשת ניתוח נוסף כדי למצוא את הקשר בין תאוצות הטריז והגליל ולפתור את המערכת במלואה.
השלמת בעיית הטריז והגליל - מציאת היחס בין התאוצות
בשלב הקודם ניתחנו את הכוחות הפועלים על טריז וגליל, וכעת נמשיך לפתרון המלא.
היחס בין תאוצות הטריז והגליל
כדי להשלים את הפתרון, אנו צריכים למצוא את היחס בין תאוצת הגליל לתאוצת הטריז. בהתאם לגיאומטריה של המערכת:
\[a_y = a_x \cdot \tan(30°)\]כאשר:
- $a_y$ היא תאוצת הגליל בכיוון אנכי (מטה)
- $a_x$ היא תאוצת הטריז בכיוון אופקי (ימינה)
הסבר הקשר: כאשר הטריז נע מרחק $\Delta x$ ימינה, הגליל נע מרחק $\Delta y$ מטה. היחס בין המרחקים האלה הוא $\frac{\Delta y}{\Delta x} = \tan(30°)$. מכאן נובע שגם היחס בין התאוצות הוא אותו יחס.
ידוע ש-$\tan(30°) = \frac{1}{\sqrt{3}}$, ולכן:
\[a_y = a_x \cdot \frac{1}{\sqrt{3}}\]פתרון המערכת
נזכור את המשוואות שפיתחנו קודם:
\[a_x = \frac{N_m \cdot \sin(30°)}{M} = \frac{N_m}{2M}\] \[a_y = g - \frac{N_m \cdot \cos(30°)}{m} = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m}\]כעת נציב את היחס שמצאנו:
\[g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = \frac{N_m}{2M} \cdot \frac{1}{\sqrt{3}}\]נבצע פישוט אלגברי:
\[g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = \frac{N_m}{2M \cdot \sqrt{3}}\] \[g = \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} + \frac{N_m}{2M \cdot \sqrt{3}}\] \[g = N_m \cdot \left( \frac{\sqrt{3}}{2m} + \frac{1}{2M \cdot \sqrt{3}} \right)\] \[N_m = \frac{g}{\frac{\sqrt{3}}{2m} + \frac{1}{2M \cdot \sqrt{3}}}\]לאחר פישוט נוסף:
\[N_m = \frac{2gMm\sqrt{3}}{M\sqrt{3}^2 + m} = \frac{20Mm\sqrt{3}}{3M + m}\]כאשר הצבנו $g = 10 \text{ מ’/שנייה}^2$.
עם ערך זה של $N_m$, אנו יכולים לחשב את התאוצות:
\[a_x = \frac{N_m}{2M} = \frac{10m\sqrt{3}}{3M + m}\] \[a_y = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = 10 - \frac{10M\sqrt{3}^2}{3M + m} = 10 - \frac{30M}{3M + m} = \frac{10(3M+m) - 30M}{3M+m} = \frac{10m}{3M+m}\]סיכום בעיית הטריז והגליל
בתהליך הפתרון ביצענו את השלבים הבאים:
- פירוק כוחות בזהירות - תהליך עדין שבו קל לטעות
- ניתוח הכוחות על כל גוף - לכל אחד מהגופים פעלו שלושה כוחות
- בחירת מערכת צירים מתאימה - בדרך כלל בכיוון התאוצות הצפויות
- משוואות תנועה - ארבע משוואות עם ארבעה נעלמים, אך שתיים מהן מתבטלות מכיוון שאין תאוצה אנכית לטריז ואין תאוצה אופקית לגליל
- מציאת קשר נוסף - היחס הגיאומטרי בין התאוצות התבסס על הגיאומטריה של המערכת
חשוב לציין כי הפתרון תלוי במסות של הגופים - הנורמל בין המשטחים קשור ביחס המסות. ללא ערכים מספריים של המסות, לא ניתן לקבל תשובה מספרית סופית.
בעיה חדשה: כוח התלוי בזמן
נעבור כעת לשאלה האחרונה בדף מספר ארבע:
גוף בעל מסה $M$ ומהירות התחלתית $v_0$ כלשהי בכיוון ציר $x$ מושפע מכוח. מצאו את משוואת המהירות כאשר הכוח תלוי בזמן:
\[F(t) = F_0 \cos(\omega t) \cdot \hat{x}\]כאשר $\omega$ ו-$F_0$ הם קבועים.
פתרון המהירות כתלות בזמן
נזכור שקשר בין מהירות לתאוצה הוא:
\[v(t) = v_0 + \int_0^t a(s) ds\]לפי החוק השני של ניוטון:
\[F(t) = M \cdot a(t)\]מכאן:
\[a(t) = \frac{F(t)}{M} = \frac{F_0 \cos(\omega t)}{M} \cdot \hat{x}\]נציב בביטוי למהירות:
\[v(t) = v_0 + \int_0^t \frac{F_0 \cos(\omega s)}{M} ds\] \[v(t) = v_0 + \frac{F_0}{M} \int_0^t \cos(\omega s) ds\]האינטגרל של $\cos(\omega s)$ הוא $\frac{\sin(\omega s)}{\omega}$, ולכן:
\[v(t) = v_0 + \frac{F_0}{M\omega} \sin(\omega t)\]זהו הפתרון לסעיף א’.
בעיה חדשה: כוח התלוי במהירות (כוח גרר)
בסעיף ב’ נתון שהכוח תלוי במהירות הגוף:
\[F = -\beta v\]זהו כוח גרר (או חיכוך סטוקס) האופייני לתנועה בנוזלים צמיגים. קיים גם כוח גרר מסוג אחר (ברנולי) הפרופורציוני למהירות בריבוע, האופייני למטוסים ולתנועה במהירויות גבוהות.
פתרון כאשר הכוח פרופורציוני למהירות
לפי החוק השני של ניוטון:
\[F = M \cdot a = -\beta v\]נרשום את התאוצה כנגזרת של המהירות:
\[M \cdot \frac{dv}{dt} = -\beta v\]נקבל משוואה דיפרנציאלית:
\[\frac{dv}{dt} = -\frac{\beta}{M} v\]זוהי משוואה דיפרנציאלית מסדר ראשון שניתן לפתור בשיטת הפרדת משתנים:
\[\frac{dv}{v} = -\frac{\beta}{M} dt\]נבצע אינטגרציה:
\[\int \frac{dv}{v} = -\frac{\beta}{M} \int dt\] \[\ln|v| = -\frac{\beta}{M} t + C\]כאשר $C$ הוא קבוע האינטגרציה.
נבצע העלאה ב-$e$:
\[v(t) = e^{-\frac{\beta}{M} t + C} = e^C \cdot e^{-\frac{\beta}{M} t} = A \cdot e^{-\frac{\beta}{M} t}\]כאשר $A = e^C$ הוא דרגת החופש של האינטגרציה.
כדי לקבוע את ערך $A$, נשתמש בתנאי ההתחלה $v(0) = v_0$:
\[v_0 = A \cdot e^0 = A\]ולכן:
\[v(t) = v_0 \cdot e^{-\frac{\beta}{M} t}\]זוהי התוצאה לסעיף ב’.
בעיה חדשה: צניחה חופשית עם התנגדות אוויר
נעבור כעת לבעיה חדשה העוסקת בצניחה חופשית:
צנחנית צונחת ללא פתיחת מצנח בשדה הכבידה של כדור הארץ. אנו מניחים:
- תאוצת הנפילה החופשית היא $g = 10 \text{ מ’/שנייה}^2$
- כוח ההתנגדות של האוויר לתנועתה במהלך צניחתה הוא $F_{התנגדות} = \beta v^2$
חלק א’: מציאת ביטוי למהירות הטרמינלית
המהירות הטרמינלית היא המהירות שבה כוח ההתנגדות של האוויר מאזן את כוח הכבידה, כך שהצנחנית צונחת במהירות קבועה.
נבצע ניתוח כוחות: בכיוון אנכי (חיובי כלפי מטה):
- כוח הכבידה: $F_g = mg$ (כלפי מטה, חיובי)
- כוח התנגדות האוויר: $F_{התנגדות} = -\beta v^2$ (כלפי מעלה, שלילי)
במצב של מהירות טרמינלית ($v_T$), התאוצה מתאפסת:
\(\sum F = ma = 0\) \(Mg - \beta v_T^2 = 0\) \(\beta v_T^2 = mg\) \(v_T = \sqrt{\frac{mg}{\beta}}\)
זהו הביטוי למהירות הטרמינלית של הצנחנית.
ניתוח הכוחות והמהירות הטרמינלית
נתחיל עם ניתוח הכוחות הפועלים על הצנחנית. נבחר ציר $z$ חיובי כלפי מטה (בכיוון התנועה):
- כוח הכבידה: $F_g = mg$ (כלפי מטה, חיובי)
- כוח התנגדות האוויר: $F_{\text{התנגדות}} = -\beta v^2$ (כלפי מעלה, שלילי)
לפי החוק השני של ניוטון: \(\sum F = ma\) \(Mg - \beta v^2 = ma\)
במצב של מהירות טרמינלית ($v_T$), התאוצה מתאפסת ($a = 0$): \(Mg - \beta v_T^2 = 0\) \(\beta v_T^2 = mg\) \(v_T = \sqrt{\frac{mg}{\beta}}\)
חישוב מקדם ההתנגדות $\beta$
נתון כי משקל הצנחנית הוא 600 ניוטון (כ-60 ק”ג), והמהירות הטרמינלית שלה היא 216 קמ״ש.
נמיר את המהירות למטרים לשנייה: \(v_T = \frac{216 \text{ קמ״ש}}{3.6} = 60 \text{ מ'/שנייה}\)
כעת נחשב את $\beta$: \(\beta = \frac{mg}{v_T^2} = \frac{600}{60^2} = \frac{600}{3600} = \frac{1}{6} \text{ ק"ג/מ'}\)
יחידות המידה של $\beta$ הן: \([\beta] = \frac{[F]}{[v]^2} = \frac{\text{ק"ג} \cdot \text{מ'}/\text{שנייה}^2}{\text{מ'}^2/\text{שנייה}^2} = \frac{\text{ק"ג}}{\text{מ'}}\)
משוואה דיפרנציאלית לתנועת הצנחנית
נרשום את החוק השני של ניוטון עבור הצנחנית:
\[Mg - \beta v^2 = ma\]נחלק ב-$m$:
\[g - \frac{\beta}{m}v^2 = a = \frac{dv}{dt}\] \[\frac{dv}{dt} = g \left(1 - \frac{\beta v^2}{mg}\right)\]נגדיר פרמטר $\alpha$ כך ש-$\alpha^2 = \frac{\beta}{mg}$:
\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]יחידות המידה של $\alpha$ הן $\frac{1}{\text{מ’/שנייה}}$ (הופכי של יחידות מהירות).
פתרון המשוואה הדיפרנציאלית
נתון כי הפתרון למשוואה זו, בהנחה שהצנחנית מתחילה ממהירות אפס ($v(0) = 0$), הוא:
\[v(t) = \sqrt{\frac{mg}{\beta}} \tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]נדרשים להוכיח שפתרון זה מקיים:
- את תנאי ההתחלה: $v(0) = 0$
- את המשוואה הדיפרנציאלית: $\frac{dv}{dt} = g(1 - \alpha^2 v^2)$
בדיקת תנאי ההתחלה
נציב $t = 0$:
\[v(0) = \sqrt{\frac{mg}{\beta}} \tanh(0) = 0\]כיוון ש-$\tanh(0) = 0$, התנאי מתקיים.
בדיקת המשוואה הדיפרנציאלית
נחשב את הנגזרת של $v(t)$:
\[\frac{dv}{dt} = \sqrt{\frac{mg}{\beta}} \cdot \frac{d}{dt}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]נזכור כי הנגזרת של $\tanh(x)$ היא $\frac{1}{\cosh^2(x)}$, ונשתמש בכלל שרשרת הנגזרות:
\[\frac{dv}{dt} = \sqrt{\frac{mg}{\beta}} \cdot \frac{1}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)} \cdot \sqrt{\frac{\beta g}{m}}\]נפשט:
\[\frac{dv}{dt} = \frac{mg}{\beta} \cdot \frac{\sqrt{\frac{\beta g}{m}}}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)} = \frac{g}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)}\]נשתמש בזהות טריגונומטרית היפרבולית: $\frac{1}{\cosh^2(x)} = 1 - \tanh^2(x)$:
\[\frac{dv}{dt} = g \left(1 - \tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right)\right)\]נציב את $v(t)$ בחזרה:
\[v^2(t) = \frac{mg}{\beta} \tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right)\]לכן:
\[\tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right) = \frac{\beta}{mg} v^2 = \alpha^2 v^2\]ולבסוף:
\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]מה שמוכיח שהפתרון אכן מקיים את המשוואה הדיפרנציאלית.
התכנסות למהירות הטרמינלית
ניתן להראות כי כאשר $t \to \infty$, המהירות $v(t)$ מתכנסת למהירות הטרמינלית:
\[\lim_{t \to \infty} v(t) = \sqrt{\frac{mg}{\beta}} \lim_{t \to \infty} \tanh\left(\sqrt{\frac{\beta g}{m}}t\right) = \sqrt{\frac{mg}{\beta}}\]זאת כיוון ש-$\lim_{t \to \infty} \tanh(t) = 1$.
מיקום הצנחנית כפונקציה של הזמן
כדי למצוא את מיקום הצנחנית $z(t)$, נבצע אינטגרציה על המהירות:
\[z(t) = \int_0^t v(s) ds = \sqrt{\frac{mg}{\beta}} \int_0^t \tanh\left(\sqrt{\frac{\beta g}{m}}s\right) ds\]האינטגרל של $\tanh(x)$ הוא $\ln(\cosh(x))$, ולכן:
\[z(t) = \sqrt{\frac{mg}{\beta}} \cdot \frac{1}{\sqrt{\frac{\beta g}{m}}} \ln\left(\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right) = \frac{m}{\beta} \ln\left(\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right)\]מכיוון ש-$\ln(\cosh(0)) = 0$, נקבל $z(0) = 0$, כמצופה.
בעיה חדשה: חבל מסיבי על מסמר
נדון כעת בבעיה חדשה: חבל מסיבי, חסר חיכוך, משתלשל משני צידיו של מסמר חסר חיכוך התקוע אופקית בקיר אנכי.
תיאור הבעיה
בזמן $t = 0$, החבל ממוקם כך ששליש מאורכו ($L/3$) משתלשל מצידו האחד של המסמר, ושני שליש ($2L/3$) מצידו השני. השאלה היא: כמה זמן ייקח לחבל כולו להחליק מהמסמר?
גישה לפתרון
כדי לפתור בעיה זו, יש לנתח את התנועה של החבל תוך התחשבות בכך שככל שחולף הזמן, יותר מאסה של החבל עוברת מצד אחד של המסמר לצד השני, מה שמשנה את התאוצה של המערכת.
נקבע ציר $z$ שכיוונו החיובי כלפי מטה. בזמן $t = 0$, הקצה הקצר של החבל (שליש מאורכו) נמצא בצד שמאל של המסמר.
בכל רגע נתון, הכוח המניע את החבל הוא ההפרש במשקל בין שני צידי המסמר. ככל שיותר חבל עובר לצד הארוך, הכוח המאיץ את התנועה גדל.
דור פסקלחזור לשיעור 4
חזרה לעמוד הראשי