הקדמה ועדכונים על הקורס
המרצה התחיל עם כמה עדכונים חשובים:
- המטלה השנייה תהיה מגן - משפרת ציון רק אם זה עוזר
- הגשה עד יום ראשון (29 למונה)
- השיעור מחר יהיה בזום עם עבודה עצמית על דאטה
- מומלץ מאוד לעבוד על הדאטה במהלך השיעור - זה יעזור למטלה המסכמת
מהם ״נתוני הישרדות״?
זמן הישרדות = זמן עד מאורע (Time to Event)
דוגמאות מהעולם הרפואי
- זמן עד מוות
- זמן עד התפרצות מחלה
- זמן עד חזרה של גידול
- זמן עד חזרה לשימוש בסמים
דוגמאות חיוביות
- זמן עד שחרור מבית חולים
- זמן עד כניסה להיריון
- זמן עד הגעת צוות רפואי
דוגמאות נוספות
- זמן עד חזרה לפשע
- זמן עד הפקעת שער של מניה
- זמן עד שחומר רדיואקטיבי מתפרק
נקודה חשובה: זמן הישרדות הוא משתנה מקרי חיובי - לא כמו משתנה נורמלי או T שיכולים לקבל ערכים שליליים.
פונקציית ההישרדות (Survival Function)
הגדרה
\[S(t) = P(T > t)\]כלומר: ההסתברות לשרוד מעבר לזמן $t$.
תכונות
- $S(0) = 1$ - בזמן 0 כולם חיים
- $S(\infty) = 0$ - בסופו של דבר כולם חווים את המאורע
- פונקציה יורדת (לא עולה אף פעם)
דוגמה: מחקר אסתמה
10 חולי אסתמה קיבלו טיפול (למשל ונטולין) ומדדנו זמן עד התקף הבא בימים:
\[\left\{ \begin{array}{l} 11, 7, 17, 28, 25, 2, 13, 14, 6, 15 \end{array} \right\}\]בניית פונקציית ההישרדות
- בזמן 0: כולם שרדו ← $S(0) = 1$
- ביום 2: התקף אחד ← $S(2) = 0.9$ (ירידה של 0.1)
- ביום 6: עוד התקף ← $S(6) = 0.8$
- וכן הלאה…
הגרף נראה כמו “מדרגות יורדות” - כל התקף יוצר ירידה.
חישוב הסתברויות
נמיין את הזמנים בסדר עולה:
\[\left\{ 2, 6, 7, 11, 13, 14, 15, 17, 25, 28 \right\}\]מניחים שהאירוע קורה בסוף כל יום.
בכל $t$, $SF(t)$ הוא מספר השורדים לחלק למספר המשתתפים.
ההסתברות שהתקף יקרה בין זמן $t_1$ ל-$t_2$:
\[P(t_1 < T \leq t_2) = S(t_1) - S(t_2)\]דוגמה: ההסתברות להתקף בין יום 1.5 ליום 2.5:
- $S(1.5) = 1$ (עדיין אף התקף)
- $S(2.5) = 0.9$ (כבר היה התקף אחד)
- ההסתברות = $1 - 0.9 = 0.1$
מדדי מיקום
- חציון: הזמן שבו 50% כבר קיבלו התקף. בדוגמה שלנו: כ-13.5 ימים
- רביעון עליון (Q3): הזמן שבו 75% קיבלו התקף
השוואה בין קבוצות
נניח שיש תרופה חדשה שמעלה את זמן ההישרדות ביום אחד. איך זה נראה?
העקומה החדשה תהיה “מוזזת ימינה” - כל התקף יקרה יום אחד מאוחר יותר.
כלל אצבע: אם עקומה אחת נמצאת “מעל” השנייה לכל אורך הזמן - הטיפול שלה עדיף.
דוגמה ממחקר בריטי (2006-1993)
בדקו קשר בין אורח חיים לתמותה. אנשים עם התנהגות בריאה (פעילות גופנית, הימנעות מאלכוהול וכו’) שרדו באופן משמעותי טוב יותר.
בעיית הצנזורה (Censoring)
מה זה צנזורה?
מצב שבו איבדנו מעקב אחרי משתתף. למשל:
- משתתף שהיה במחקר 16 ימים ואז הפסיק להגיע
- המחקר נגמר והמשתתף עדיין לא חווה את המאורע
הבעיה
- לא יודעים מתי היה לו התקף
- אבל יודעים ששרד לפחות 16 ימים - וזה מידע חשוב!
סוגי צנזורה
- צנזורה ימנית: יודעים שהאירוע קרה אחרי הזמן האחרון שצפינו
- צנזורה שמאלית: יודעים שהאירוע קרה אבל לא יודעים מתי
שיטת קפלן-מאייר (Kaplan-Meier)
הרעיון המרכזי
“עד היום ה-16 אני מחשב כאילו היו 11 משתתפים, אחרי היום ה-16 אני מחשב רק עם 10”
ההנחות
- אירועי פרישה קורים בסוף התקופה
- הנחה בעייתית: זמני פרישה בלתי תלויים בזמני המאורע
- בפועל: מי שמרגיש טוב עלול להפסיק לבוא…
- “כל הנחה שנעשה היא בעייתית”
הנוסחה - הסבר אינטואיטיבי
המרצה הסביר עם דוגמה גרפית:
- אם $T > 6$ אז בהכרח גם $T > 2$
- לכן: $P(T > 6) = P(T > 6 \vert T > 2) \times P(T > 2)$
“זה כל הטריק של קפלן-מאייר!”
טבלת חישוב
| זמן | בסיכון | מתו | P(מוות) | P(שרידה) | P(שרידה מצטברת) |
|---|---|---|---|---|---|
| 0 | 11 | 0 | 0 | 1 | 1.00 |
| 2 | 11 | 1 | 1/11 | 10/11 | 0.91 |
| 6 | 10 | 1 | 1/10 | 9/10 | 0.82 |
| 16* | 4 | 0 | 0 | 1 | 0.36 |
*פרישה - לא משנה את ההסתברות!
בפייתון
# התקנה
pip install kaplanmeier
# שימוש
from kaplanmeier import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(times, events) # events: 1=מוות, 0=צנזורה
מבחן לוג-רנק (Log-Rank Test)
מטרה
לבדוק האם יש הבדל בין שתי עקומות הישרדות
השערות
- $H_0$: אין הבדל (העקומות זהות)
- $H_1$: יש הבדל
חשוב לזכור
“המבחן לא אומר מי יותר טוב - רק שיש הבדל!”
כשעקומות נחתכות
- לפעמים טיפול A טוב בטווח הקצר
- וטיפול B טוב בטווח הארוך
- “ההגדרה של השאלה היא כבר סבוכה”
התפלגויות מיוחדות
משתנה אקספוננציאלי
- “סיכוי זהה למות בכל פרק זמן”
- תכונת חוסר זיכרון
- $S(t) = e^{-\lambda t}$ (דעיכה אקספוננציאלית)
משתנה גיאומטרי
- הגרסה הבדידה
- גם לו יש חוסר זיכרון
שאלות מהכיתה
שאלה של רוזי על החישובים
ש: “בפועל מה שאנחנו עושים זה פשוט לוקחים את ה-T>6?”
ת: המרצה הסביר שמבחינה מתמטית:
- $P(T>6 \cap T>2) = P(T>6)$
- כי אם $T>6$ אז אוטומטית גם $T>2$
- “זה לא משהו שאנחנו מחשבים, אנחנו משתמשים בשוויון הזה”
על ההבדל בין זמנים
ש: “מה עם 3, 4, 5?”
ת: “מבחינת הנתונים, אין הבדל בין 3 ל-4. לא קרה שום דבר בזמן 3, לא קרה שום דבר בזמן 4. מה שמעניין אותי זה האירועים שבהם יש צניחה בעקומת ההישרדות.”
טיפים מהמרצה
-
למטלה: “מי שמצייר עקומת הישרדות באמצעות טכניקות מתקדמות - מבחינתי זה בונוס”
-
לגבי עבודה בקבוצות: “גם חמישה זה יותר מדי… אתם בטח יודעים יותר טוב ממני שכנראה חלקכם פשוט רשמו את השם על המטלה”
-
הגשות: “תגישו קצת לפני הזמן, לא ברגע האחרון… אל תביאו אותי למצב שאני מתעצבן על דברים כאלה”
-
בונוס: מי שיכתוב למייל הפרטי של המרצה איזו התפלגות נותנת פונקציית הישרדות שיורדת בקו ישר - יקבל 3 נקודות בונוס!
נקודות שחשוב לזכור
-
רזולוציה נמוכה בסוף: “הרבה פעמים בעקומות הישרדות בסוף יש לנו בלגן”
-
הנחות בעייתיות: “ההנחה שפרישה בלתי תלויה - היא לא נכונה. הנחות הן אף פעם לא נכונות”
-
המטרה: “דרך לסכם את הנתונים בצורה גרפית ומתמטית, ולאפשר השוואה”
סיכום
ניתוח הישרדות הוא כלי “מאוד רלוונטי לכם בתור רופאים” שמופיע “המון המון במאמרים רפואיים”.
העקרונות המרכזיים:
- הבנת פונקציית ההישרדות
- התמודדות עם צנזורה דרך קפלן-מאייר
- השוואת טיפולים עם מבחן לוג-רנק
- זהירות בפרשנות כשעקומות נחתכות
שאלה מהתרגול - השוואת הישרדות חולים עם ובלי טיפול
במרכז רפואי בישראל, נערך מחקר לבדיקת היעילות של טיפול חדשני (טיפול A) במחלת כליות כרונית, לעומת הטיפול הסטנדרטי (טיפול B) עשרה חולים השתתפו במחקר.
עבור כל חולה, נרשמו מספר הימים מתחילת הטיפול ועד לאירוע (מוות) או צנזור (יציאה מהמחקר או סיום תקופת המעקב).
- בנו עקומות קפלן-מאייר עבור כל אחת מקבוצות הטיפול.
- העריכו את שיעור ההישרדות לאחר
200ימים בכל אחת מהקבוצות.- האם נראה שיש הבדל משמעותי בהישרדות בין שתי קבוצות הטיפול?
| חולה | קבוצת טיפול | ימים עד לאירוע/צנזור | אירוע (1) / צנזור (0) |
|---|---|---|---|
| 1 | A | 120 | 1 |
| 2 | A | 180 | 0 |
| 3 | A | 210 | 1 |
| 4 | A | 250 | 0 |
| 5 | A | 300 | 1 |
| 6 | B | 100 | 1 |
| 7 | B | 150 | 0 |
| 8 | B | 200 | 1 |
| 9 | B | 220 | 1 |
| 10 | B | 280 | 0 |
נבנה טבלה כדי לייצר את העקומה:
לקבוצה A:
| ימים עד לאירוע (t) | מספר חולים בסיכון | מספר מקרי מוות באירוע | הסתברות לא לחלות בזמן t | הסתברות מצטברת ללא אירוע |
|---|---|---|---|---|
| 120 | 5 | 1 | $1-\frac{1}{5}=0.8$ | $0.83 |
| 180 | 4 | 0 | $1$ | $0.8\times 1 =0.8$ |
| 210 | 3 | 1 | $1-\frac{1}{3}=0.67$ | $0.8\times 0.67 =0.53$ |
| 250 | 2 | 0 | $1$ | $0.53\times 1 =0.53$ |
| 300 | 1 | 1 | $0$ | $0.53\times 0 =0$ |
לקבוצה B:
| ימים עד לאירוע (t) | מספר חולים בסיכון | מספר מקרי מוות באירוע | הסתברות לא לחלות בזמן t | הסתברות מצטברת ללא אירוע |
|---|---|---|---|---|
| 100 | 5 | 1 | $1-\frac{1}{5}=0.8$ | $0.83 |
| 150 | 4 | 0 | $1$ | $0.8\times 1 =0.8$ |
| 200 | 3 | 1 | $1-\frac{1}{3}=0.67$ | $0.8\times 0.67 =0.53$ |
| 220 | 2 | 1 | $1-\frac{1}{2}=0.5$ | $0.53\times 0.5 =0.265$ |
| 280 | 1 | 0 | $1$ | $0.265\times 1 =0.265$ |
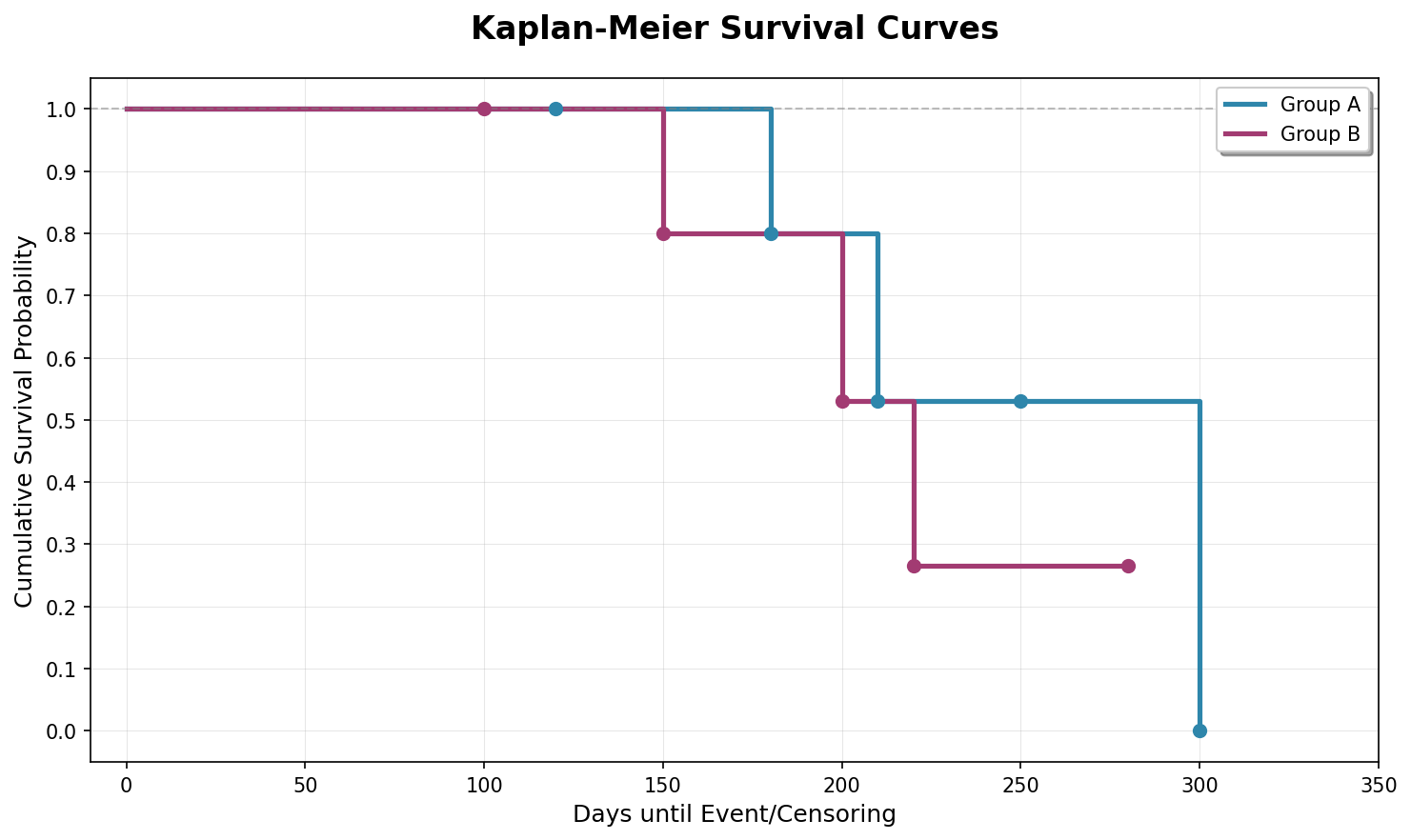
עקומות קפלן-מאייר
אבנה בעזרת ‘matplotlib’, עקרונית אפשר גם להתקין את הספרייה של קפלן-מאייר:
import matplotlib.pyplot as plt
import numpy as np
# Original data
days_A = [120, 180, 210, 250, 300]
survival_A = [1.0, 0.8, 0.53, 0.53, 0.0]
days_B = [100, 150, 200, 220, 280]
survival_B = [1.0, 0.8, 0.53, 0.265, 0.265]
# Add starting point at (0, 1.0) for both curves
days_A_complete = [0] + days_A
survival_A_complete = [1.0] + survival_A
days_B_complete = [0] + days_B
survival_B_complete = [1.0] + survival_B
# Create the plot with improved styling
plt.figure(figsize=(10, 6))
# Plot survival curves with improved styling
plt.step(days_A_complete, survival_A_complete, where='post',
label='Group A', color='#2E86AB', linewidth=2.5)
plt.step(days_B_complete, survival_B_complete, where='post',
label='Group B', color='#A23B72', linewidth=2.5)
# Add markers at event times for better visibility
plt.scatter(days_A, survival_A, color='#2E86AB', s=40, zorder=5)
plt.scatter(days_B, survival_B, color='#A23B72', s=40, zorder=5)
# Improved plot formatting
plt.title('Kaplan-Meier Survival Curves', fontsize=16, fontweight='bold', pad=20)
plt.xlabel('Days until Event/Censoring', fontsize=12)
plt.ylabel('Cumulative Survival Probability', fontsize=12)
# Set axis limits - start y-axis slightly above 0 and go slightly above 1
plt.xlim(-10, 350)
plt.ylim(-0.05, 1.05) # This allows us to see S(0)=1 clearly
# Improved ticks
plt.xticks(np.arange(0, 351, 50))
plt.yticks(np.arange(0, 1.1, 0.1))
# Add horizontal line at y=1 for reference
plt.axhline(y=1, color='gray', linestyle='--', alpha=0.5, linewidth=1)
# Improved legend
plt.legend(loc='upper right', frameon=True, fancybox=True, shadow=True)
# Better grid
plt.grid(True, alpha=0.3, linestyle='-', linewidth=0.5)
# Tight layout for better spacing
plt.tight_layout()
plt.show()
 דור פסקל
דור פסקל