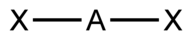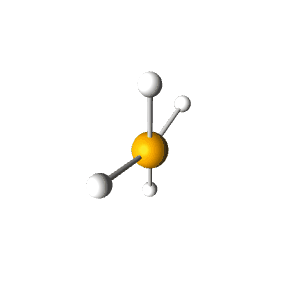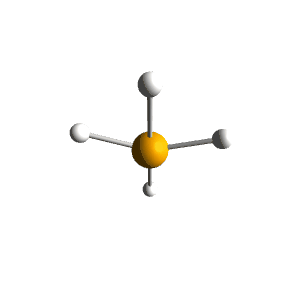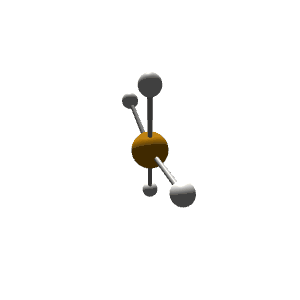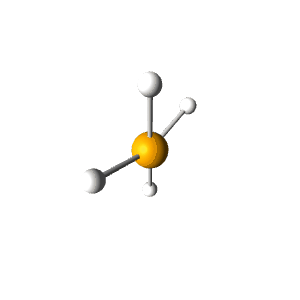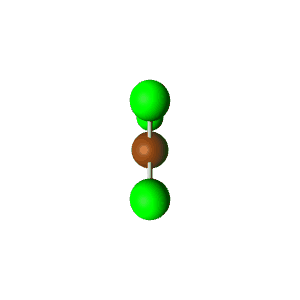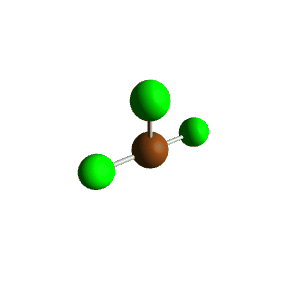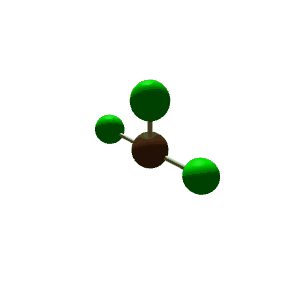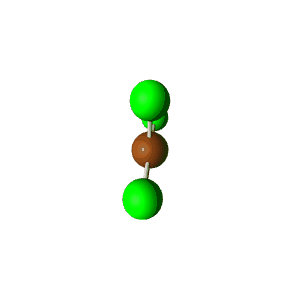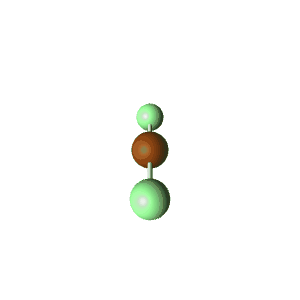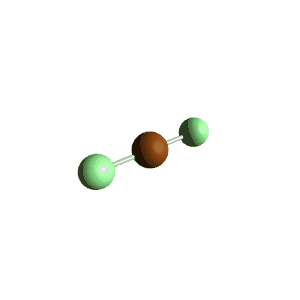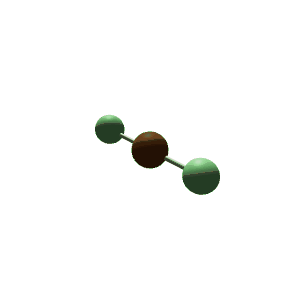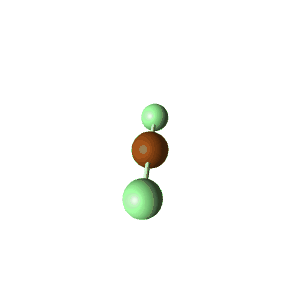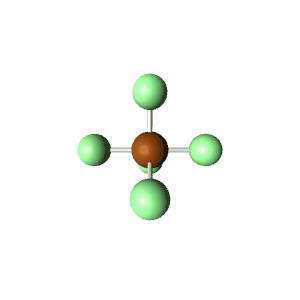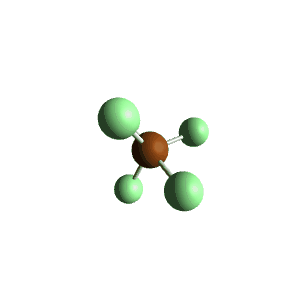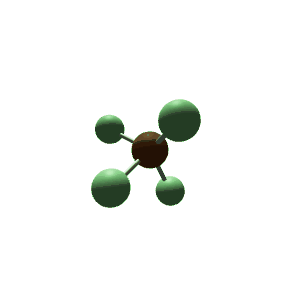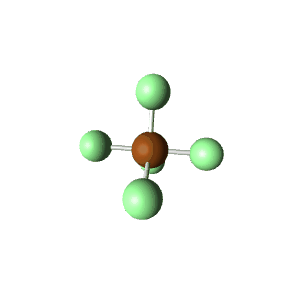פתח בקובץ PDF

\[\begin{aligned} \text{A} &= \text{Central Atom} \\ \text{X} &= \text{an atom bonded to A} \\ \text{E} &= \text{a lone pair on A} \end{aligned}\]
Total Domains Geometric Formula Picture Bonded Atoms Lone Pairs Molecular Shape Electronic Geometry Example Hybridization Bond Angle
1 $\text{AX}$ $\text{A}\mathrel{\huge{-}}\text{X}$ 1 0 Linear Linear $\text{H}_2$ $s$ 180°
2 $\text{AX}_2$ 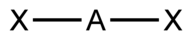alt text 2 0 Linear Linear 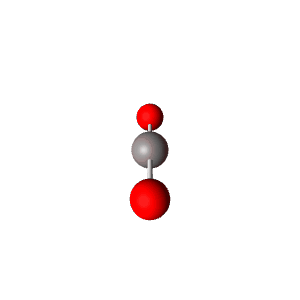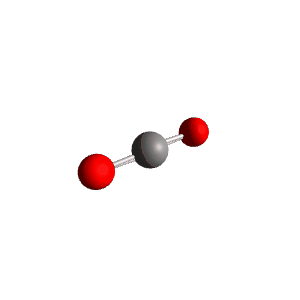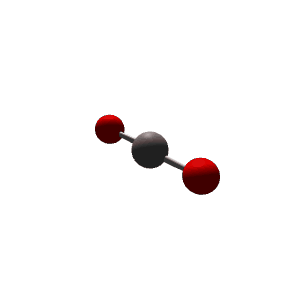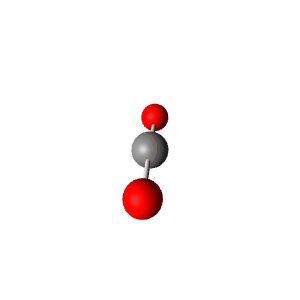$\text{CO}_2$ $sp$ 180°
2 $\text{AXE}$ $\mathrel{\huge{:}}\text{A}\mathrel{\huge{-}}\text{X}$ 1 1 Linear Linear 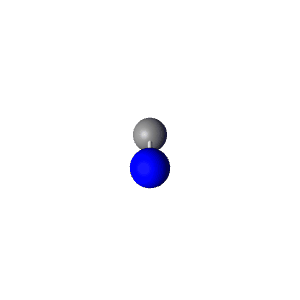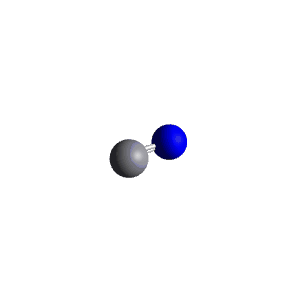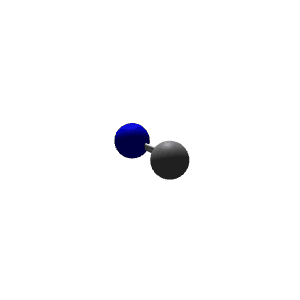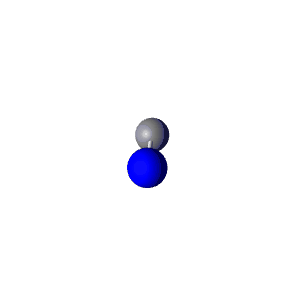$\text{CN}^-$ $sp$ 180°
3 $\text{AX}_3$ 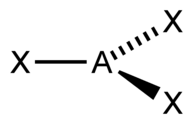alt text 3 0 Trigonal Planar Trigonal Planar 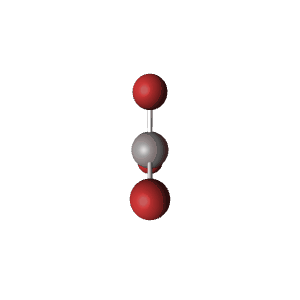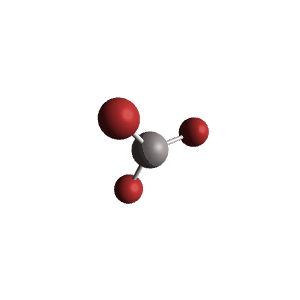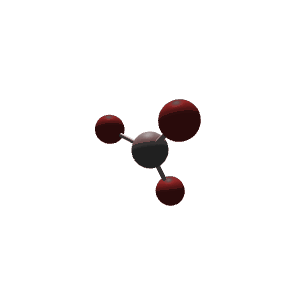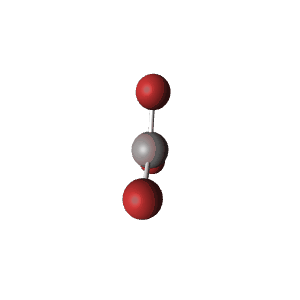$\text{AlBr}_3$ $sp^2$ 120°
3 $\text{AX}_2\text{E}$ 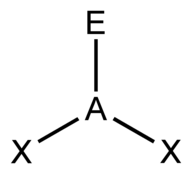alt text 2 1 Bent Trigonal Planar 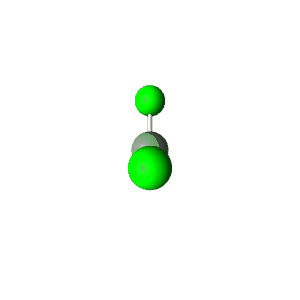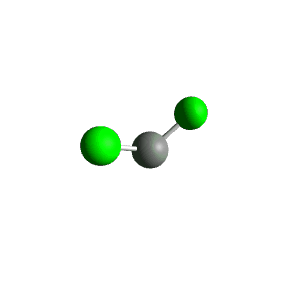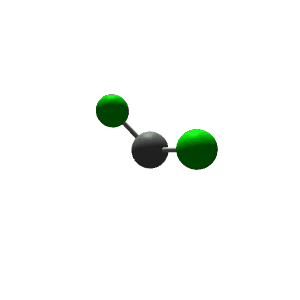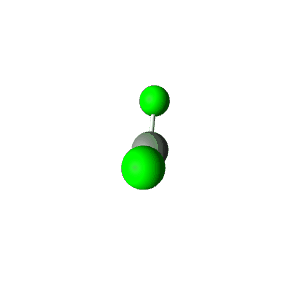$\text{SnCl}_2$ $sp^2$ 120°
3 $\text{AXE}_2$ $\mathrel{\huge{:}}\overset{\mathrel{\huge\cdot\cdot}}{\text{A}}\mathrel{\huge{-}}\text{X}$ 1 2 Linear Trigonal Planar O2 $sp^2$ 120°
4 $\text{AX}_4$ 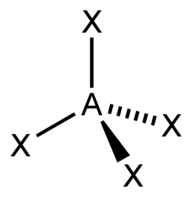alt text 4 0 Tetrahedral Tetrahedral 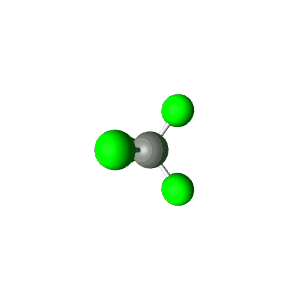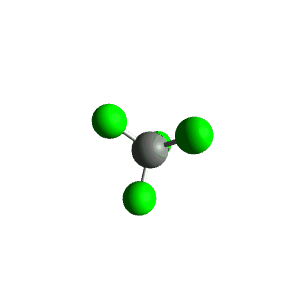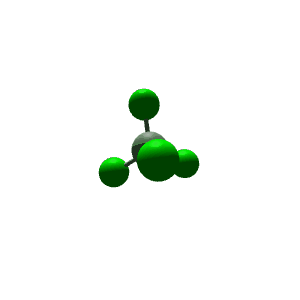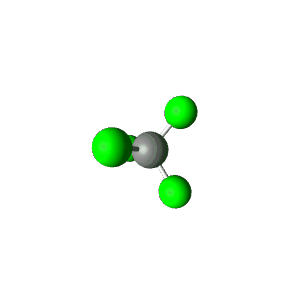$\text{SiCl}_4$ $sp^3$ 109.5°
4 $\text{AX}_3\text{E}$ 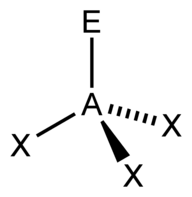alt text 3 1 Trigonal Pyramidal Tetrahedral $\text{PH}_3$ $sp^3$ 109.5°
4 $\text{AX}_2\text{E}_2$ 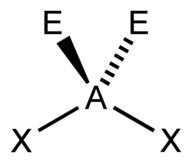alt text 2 2 Bent Tetrahedral 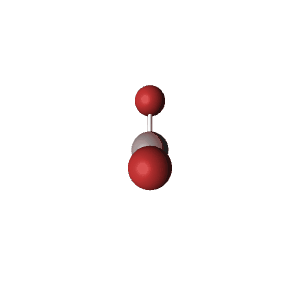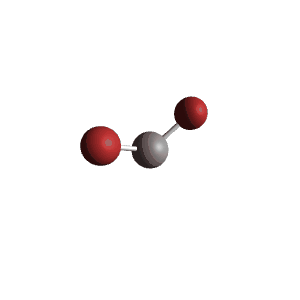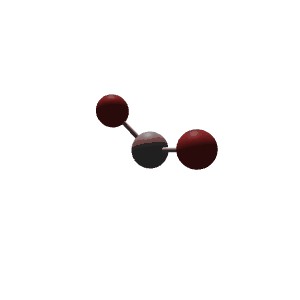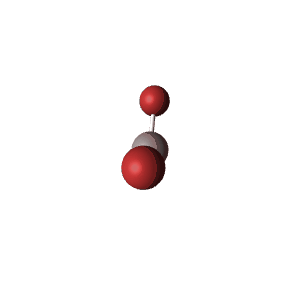$\text{SeBr}_2$ $sp^3$ 109.5°
4 $\text{AXE}_3$ $\mathrel{\huge{:}} \overset{\mathrel{\huge{\cdot\cdot}}}{\underset{\mathrel{\huge{\cdot\cdot}}}{\text{A}}} \mathrel{\huge{-}} \text{X}$ 1 3 Linear Tetrahedral Cl2 $sp^3$ 109.5°
5 $\text{AX}_5$ 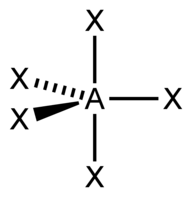alt text 5 0 Trigonal Bipyramidal Trigonal Bipyramidal 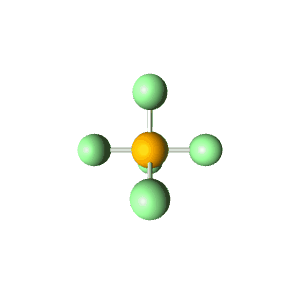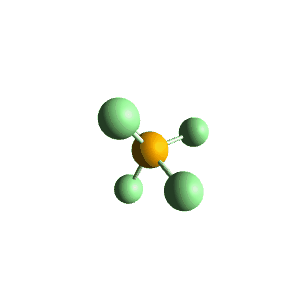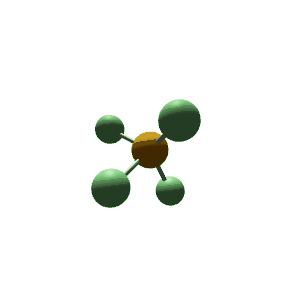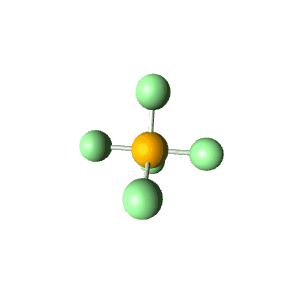$\text{AsF}_5$ $sp^3d$ 90°, 120°
5 $\text{AX}_4\text{E}$ 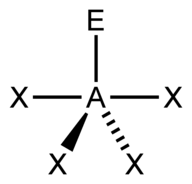alt text 4 1 Seesaw Trigonal Bipyramidal 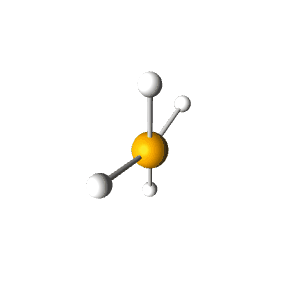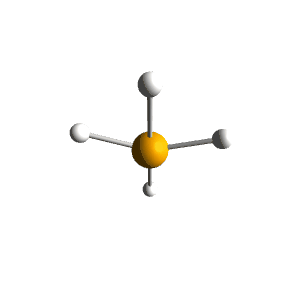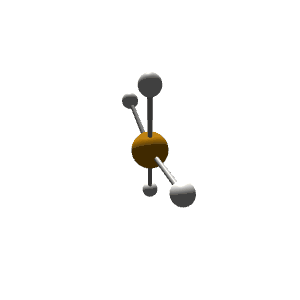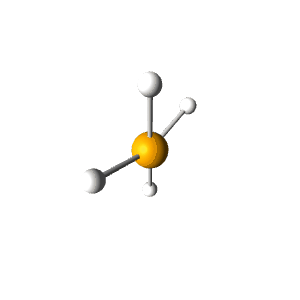$\text{SeH}_4$ $sp^3d$ 90°, 120°
5 $\text{AX}_3\text{E}_2$ 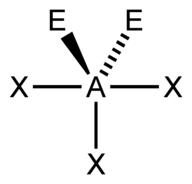alt text 3 2 T-Shaped Trigonal Bipyramidal 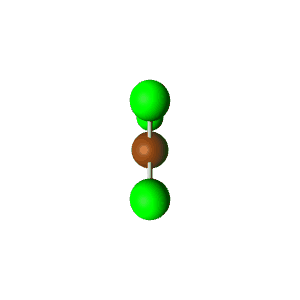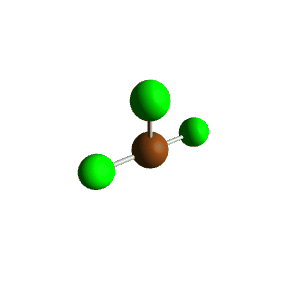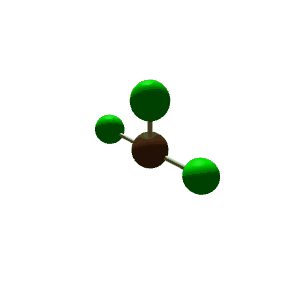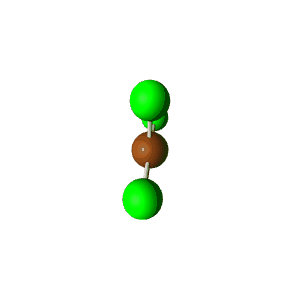$\text{ICl}_3$ $sp^3d$ 90°, 120°
5 $\text{AX}_2\text{E}_3$ 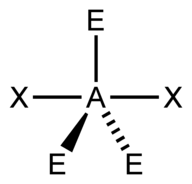alt text 2 3 Linear Trigonal Bipyramidal 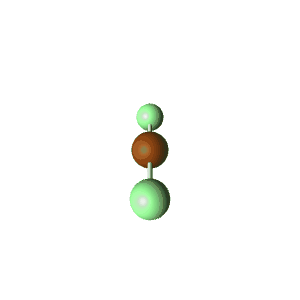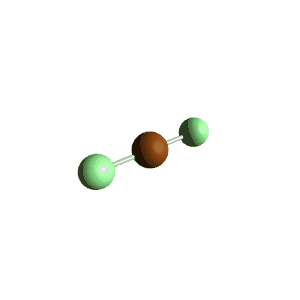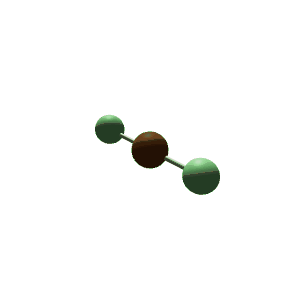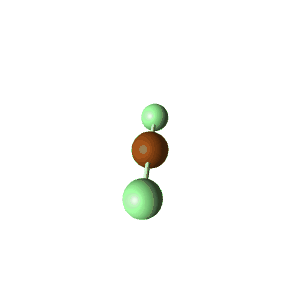$\text{BrF}_2^-$ $sp^3d$ 90°, 120°
6 $\text{AX}_6$ 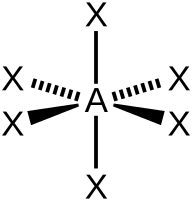alt text 6 0 Octahedral Octahedral 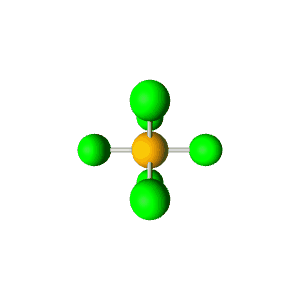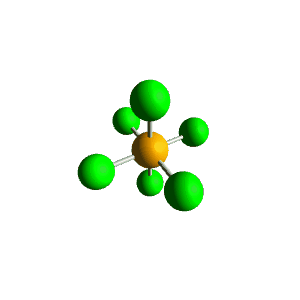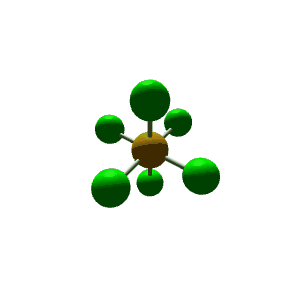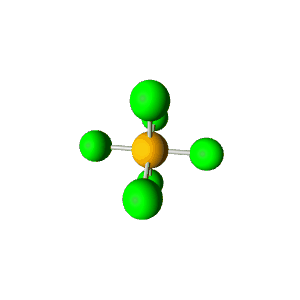$\text{SeCl}_6$ $sp^3d^2$ 90°
6 $\text{AX}_5\text{E}$ 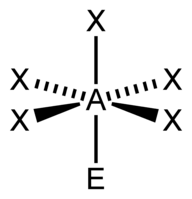alt text 5 1 Square Pyramidal Octahedral 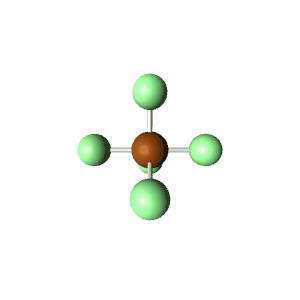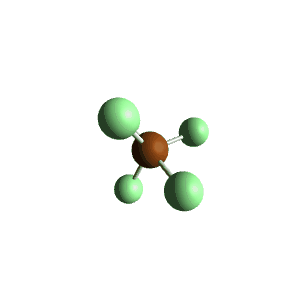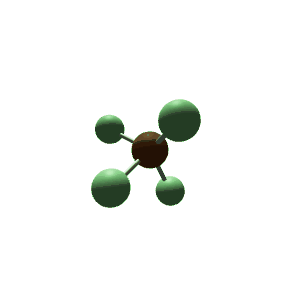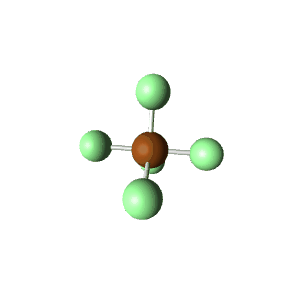$\text{IF}_5$ $sp^3d^2$ 90°
6 $\text{AX}_4\text{E}_2$ 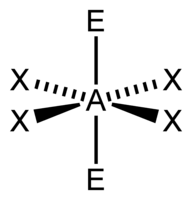alt text 4 2 Square Planar Octahedral 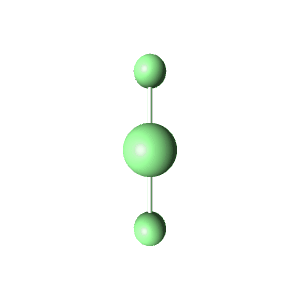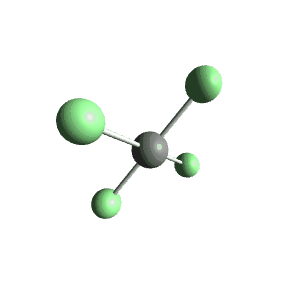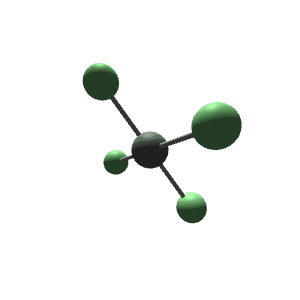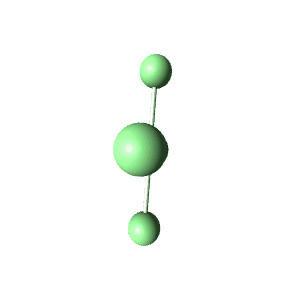$\text{XeF}_4$ $sp^3d^2$ 90°