חלק 1: סיכום השיעור הקודם - וקטורים ותנועה
וקטור התאוצה ומשמעותו
בשיעור שעבר נראה כי וקטור התאוצה, שהוא הנגזרת לפי הזמן של וקטור המהירות, מבטא את קצב שינוי המהירות. כשם שהמהירות היא קצב שינוי המקום, כך וקטור התאוצה הוא קצב שינוי קצב שינוי המקום.
כאשר נאמר שגוף נע בתאוצה של $X$ מטר לשנייה בריבוע, הכוונה היא שהגוף משנה את מהירותו בכל שנייה ב-$X$ מטר לשנייה. למשל, גוף הנופל בתאוצה של $10$ מטר לשנייה בריבוע (תאוצת הנפילה החופשית בקרבת פני כדור הארץ), פירוש הדבר שבכל שנייה גדלה מהירותו ב-$10$ מטר לשנייה.
לדוגמה, גוף הנופל מגג מגדל גבוה:
- ברגע $t = 0$ מהירותו היא $0$ מטר לשנייה
- ברגע $t = 1$ שנייה מהירותו היא $10$ מטר לשנייה
- ברגע $t = 2$ שניות מהירותו היא $20$ מטר לשנייה
- ברגע $t = 3$ שניות מהירותו היא $30$ מטר לשנייה
זוהי המשמעות של תאוצת נפילה חופשית של $10$ מטר לשנייה בריבוע.
אופי וקטורי של מהירות ותאוצה
חשוב להזכיר שוקטור המקום הוא וקטור ולא סקלר. המשמעות היא שקצב שינוי וקטור המקום לפי הזמן, וקטור המהירות, הוא בעל גודל וכיוון. כך גם לגבי וקטור התאוצה - יש לו גודל וכיוון.
בתנועה מעגלית קצובה, וקטור המקום תלוי בזמן, משום שהגוף נמצא בכל רגע ורגע בנקודה אחרת על פני המעגל. וקטור המהירות משיק למסלול המעגלי וגם הוא תלוי בזמן. העובדה שגודל המהירות הוא קבוע אינה אומרת שוקטור המהירות הוא קבוע - הוא משתנה בכיוונו ללא הרף.
לכן, כאשר נגזור את וקטור המהירות לפי הזמן בתנועה מעגלית, לא נקבל אפס. כפי שנראה, בתנועה מעגלית, וקטור התאוצה שונה מאפס והוא מכוון לעבר מרכז המעגל.
סיכום מתמטי
\[\mathbf{r}(t) = \text{position vector}\] \[\mathbf{v}(t) = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}} = \text{velocity vector}\] \[\mathbf{a}(t) = \frac{d\mathbf{v}}{dt} = \ddot{\mathbf{r}} = \text{acceleration vector}\]בתנועה מעגלית קצובה מתקיים:
\[\mathbf{a}(t) = -\omega^2 \mathbf{r}(t)\]משמעות הקשר הזה היא שהתאוצה מכוונת לעבר מרכז המעגל (הסימן השלילי). $\mathbf{r}$ יוצא ממרכז המעגל החוצה, ולכן $-\mathbf{r}$ מכוון לעבר מרכז המעגל. $\omega^2$ הוא המהירות הזוויתית בריבוע, שהוא גודל סקלרי חיובי.
עוד נראה כי מתקיים:
\[\mathbf{v} \cdot \mathbf{r} = 0\]כלומר, המהירות תמיד ניצבת לוקטור המקום.
קשר בין תאוצה, מהירות ומיקום באמצעות אינטגרלים
אם נתון $\mathbf{a}(t)$, ניתן לקבל את $\mathbf{v}(t)$ באמצעות אינטגרציה:
\[\mathbf{v}(t) = \int \mathbf{a}(t) dt + \mathbf{v}_0\]כאשר $\mathbf{v}_0$ הוא וקטור קבוע (לדוגמה, המהירות בזמן $t=0$).
באופן דומה:
\[\mathbf{r}(t) = \int \mathbf{v}(t) dt + \mathbf{r}_0\]כאשר $\mathbf{r}_0$ הוא המיקום בזמן $t=0$.
במקרה של תנועה בתאוצה קבועה, האינטגרציות פשוטות (אינטגרל על קבוע).
חלק 2: מבוא לפיזיקה ניוטונית
המעבר מקינמטיקה לפיזיקה
מה שנעשה עד כה הוא למעשה קינמטיקה - אין בזה פיזיקה, אלא רק מתמטיקה. זהו חשבון אינפיניטסימלי שבו משווים פונקציות וקטוריות. כל מה שנעשה היו הגדרות של מושגים:
- הגדרת וקטור המקום בצורה אינטואיטיבית
- הגדרת קצב שינוי המקום, אשר נקרא מהירות
- הגדרת קצב שינוי המהירות, אשר נקרא תאוצה
מהי פיזיקה?
כאשר עוסקים בפיזיקה, נשאלת השאלה: מהי החוקיות שלפיה מתנהלת המציאות? לאיזו חוקיות מצייתת המציאות הפיזיקלית שסובבת אותנו?
אם לא הייתה שום חוקיות, המציאות הייתה קאוטית לחלוטין, ושום דבר מסודר לא היה יכול להתקיים בה. המציאות היא מסודרת ביותר. כל גוף הוא דוגמה חיה לעולם מסודר - אוסף אדיר של גופיפים מסודרים מאוד, וכל גופיף כזה מכיל מבנה פנימי מסודר מאוד. ניתן לרדת לרמה של גרעיני אטומים, וגם שם מתקיימת חוקיות וסדר.
חשיבות הסדר והמידול המתמטי
בפיזיקה, המטרה היא להתחקות אחרי הסדר הזה. אם עושים זאת בצורה מדויקת, מתקבל לא רק תיאור של המציאות, אלא גם תיאור של האופן שבו היא מתפתחת בזמן. הכרת החוקיות מאפשרת לראות איך מצב מתפתח למצב אחר.
אם ניתנת מערכת פיזיקלית וחוקיותה ידועה, ניתן לבנות למערכת מודל מתמטי שמבטא את החוקיות הזו, והמודל המתמטי הזה יאפשר לדעת את מצב המערכת בכל זמן עתידי. הישג זה הושג לראשונה בתקופתו של ניוטון עם שלושת החוקים שלו.
מרגע שפוענחה החוקיות ונוסחה בשפה מתמטית מדויקת, ניתן להשתמש בשפה המתמטית הזו כדי לגזור אמיתות על המציאות, לגזור תובנות עליה, ויותר מכך - לגזור ניבויים (פרדיקציות) לגביה.
חלק 3: מושגי יסוד בפיזיקה ניוטונית
לתיאור מדויק של חוקי ניוטון, נגדיר כמה מושגי יסוד:
מערכת ייחוס
מערכת ייחוס היא מושג בסיסי ביותר בפיזיקה. בשלב ראשון, מערכת ייחוס היא מערכת צירים עם ראשית שנבחרת באופן שרירותי.
לדוגמה, ניתן לבחור את הכיתה כמערכת ייחוס - למקם את הראשית במקום כלשהו, ולפרוס ממנה שלוש קואורדינטות במרחב התלת-מימדי. כל נקודה בכיתה ובעולם ניתנת לתיאור במערכת הייחוס הזו.
ניתן גם לחשוב על מערכת ייחוס אחרת - למשל, מערכת שצמודה למכונית הנוסעת ברחוב. הראשית יכולה להיות, למשל, מרכז המכונית, וממנו יוצאים שלושה צירים.
חשוב לציין: המציאות כשלעצמה אינה תלויה בבחירת מערכת הייחוס. תיאור של תופעות במערכת הייחוס של הכיתה צריך להיות ניתן לתרגום, באמצעות חוקי טרנספורמציה, למערכת הייחוס שצמודה לנהג.
אינטראקציה
אינטראקציה היא השפעה שמתרחשת בין שני גופים כלשהם הממוקמים במרחב. הם לא חייבים לגעת זה בזה, הם יכולים להיות רחוקים זה מזה, אך החשוב הוא שבאינטראקציה מתקיימת פעולת גומלין - כל גוף משפיע על משנהו.
יש הרבה סוגים של אינטראקציות. בכימיה מוכרות אינטראקציות כימיות, שהן פעולות גומלין בין אטומים ומולקולות. האינטראקציה במקרה של הכימיה מתבצעת באמצעות כוחות חשמליים.
ארבע האינטראקציות היסודיות בטבע
בטבע יש ארבע אינטראקציות אלמנטריות המוכרות כיום:
- אינטראקציה כבידתית - קשורה בכוח המשיכה בין מסות.
- אינטראקציה אלקטרומגנטית - קשורה בכל התהליכים הכימיים, יצירת אור וכל התופעות החשמליות.
- אינטראקציה גרעינית חלשה - מתרחשת בליבות של כוכבים, משנה את זהותם של חלקיקים אלמנטריים ואחראית לקרינה רדיואקטיבית.
- אינטראקציה גרעינית חזקה - מקורה בגרעיני אטומים, ומתבצעת בין חלקיקים הנקראים קוורקים.
כוחות אפקטיביים
בעולם המכניקה, העיסוק הוא פחות באינטראקציות היסודיות (למעט אולי האינטראקציה הכבידתית) ויותר בכוחות אפקטיביים.
דוגמה לכוח אפקטיבי: כאשר גוף עומד על הרצפה, הרצפה מפעילה עליו כוח כלפי מעלה. כוח זה נקרא הכוח הנורמלי. כל שני גופים שבאים במגע חווים כוח שאחד מפעיל על השני, והכוח הזה ניצב למישור המגע בין שני הגופים.
הערות סיום
בהמשך נדון ב:
- מערכת מנוחה
- מסה
- טרנספורמציית גלילאו
- שלושת חוקי ניוטון
- סוגי כוחות מעולם המעבדה
אינטראקציות אלקטרומגנטיות
כל כוח בסיסי בטבע או כוח אפקטיבי מקורו למעשה באינטראקציה אלקטרומגנטית. פחות או יותר, מבלי להיכנס לדקויות, רוב הכוחות הנחווים ביומיום הם תוצאה של אינטראקציה אלקטרומגנטית.
מבנה האטום והריק
האטומים הם בבסיסם ריק כמעט מושלם. קוטר האטום גדול פי 100,000 מקוטר גרעין האטום. מכיוון שנפח של כדור תלוי ברדיוס בשלישית, נפח האטום גדול ב-15 סדרי גודל מנפח הגרעין:
- רדיוס האטום גדול בחמישה סדרי גודל (פי 100,000) מגרעין האטום.
- נפח האטום גדול ב-15 סדרי גודל: $(10^5)^3 = 10^{15}$.
- $10^{15}$ זה מיליון מיליארדים.
לסבר את האוזן, אם נבחן את הנפח האמיתי של החומר שנמצא בגוף אנושי:
- נניח שמסת הגוף היא $100\ \mathrm{kg}$ והוא מורכב בעיקר ממים.
- $100\ \mathrm{kg}$ מים הם $0.1\ \mathrm{m}^3$ (עשירית קוב).
- הנפח האמיתי של החומר (ללא הריק) הוא 15 סדרי גודל קטן יותר.
-
כלומר:
\[\frac{0.1\ \mathrm{m}^3}{10^{15}} = 10^{-16}\ \mathrm{m}^3\] - $10^{-16}\ \mathrm{m}^3 = 100 \times 10^{-18}\ \mathrm{m}^3 = 100\ \mathrm{\mu m}^3$
כל אדם, מבחינת החומר הממשי שבו, הוא בגודל של בקטריה גדולה - רק שזו “בקטריה” שמסתה 70-100 ק”ג.
מדוע גופים תופסים נפח?
מה הופך אותנו לגוף בסדר גודל של מטר? מדוע כאשר דוחפים קיר, היד אינה חודרת לתוכו, אם הקיר והיד הם כמעט לגמרי חלל ריק?
הסיבה היא שהאטומים עטופים בשדות אלקטרומגנטיים. גם בקיר וגם ביד יש שדות אלקטרומגנטיים שמונעים מהיד לחדור לתוך הקיר - יש התנגדות של אינטראקציה אלקטרומגנטית שמונעת זאת.
אם האינטראקציה הזאת לא הייתה קיימת, ניתן היה לדחוף את היד לתוך הקיר בלי כל קושי, וגם ליפול לעבר מרכז כדור הארץ. אלו האינטראקציות האלקטרומגנטיות שמונעות מחומר להיכנס בחומר.
כוח נורמלי
מנקודת המבט של המעבדה, אנו רואים לא יותר מאשר כוח נורמלי. הוא מסומן באות $N$ מהמילה “נורמלי”.
הכוח הנורמלי תמיד:
- נובע ממגע בין גופים.
- ניצב למשטח המגע ביניהם.
חשוב להבין שכאשר מדובר על כוח נורמלי, מקורו בכוח האלקטרומגנטי, אבל מתייחסים אליו באופן אפקטיבי כאל כוח ששני גופים מפעילים זה על זה כשהם נוגעים זה בזה.
עוד כוח שנובע מהאינטראקציה האלקטרומגנטית הוא כוח החיכוך, שגם הוא סוג של כוח מגע, ועליו נדבר בהמשך.
אינטראקציות יסודיות נוספות
האינטראקציות הגרעיניות החלשות והחזקות פחות רלוונטיות לקורס זה, למרות שבעקיפין נעשה בהן שימוש ברפואה (למשל, בשימוש בקרינה רדיואקטיבית לאבחונים).
רוב האינטראקציות שנדון בהן מקורן באינטראקציות אלקטרומגנטיות, ואולי גם נדבר קצת על אינטראקציות כבידתיות (הקשורות בעובדה שגופים נושאים מסות).
מסת התמדה
לכל חלקיק אלמנטרי יש תכונה יסודית המגדירה אותו, והתכונה הזאת נקראת התמדה.
מסת התמדה היא:
- ההתנגדות של הגוף לשינוי במצבו תחת פעולת כוח.
- מידת ה”התמדה” ב”אישיות” של הגוף.
- מידת האינרציה, ההתנגדות לשינוי במצב התנועה.
חוקי ניוטון
כעת יוצגו שלושת חוקי ניוטון, המשמשים בסיס לכל המכניקה הניוטונית ששלטה בכיפה המדעית במשך כ-250 שנה, ובאמצעותם ניתן להסביר תופעות רבות.
מושג התנע (Momentum)
נגדיר גודל וקטורי דינמי שנקרא תנע (באנגלית: “מומנטום”):
\[\mathbf{p} = m\mathbf{v}\]כאשר:
- $\mathbf{p}$ הוא התנע
- $m$ היא המסה של הגוף או של מערכת הגופים
- $\mathbf{v}$ הוא וקטור המהירות של הגוף
המסה נמדדת ביחידות של קילוגרם, והיא מבטאת את מידת ההתמדה של הגוף:
- מסה של אדם היא כ-80 קילוגרם (זו לא משקלו, זו מסתו).
- מידת ההתמדה של זבוב היא כחצי גרם.
- מידת ההתמדה של נושאת מטוסים היא כ-200 מיליון קילוגרם.
יש הבדל גדול בין מסה למשקל:
- משקל זה כוח.
- מסה זה מידת התמדה.
ניסיון לעצור נושאת מטוסים ביד בזמן שהיא שטה באוקיינוס יהיה קשה מאוד - יש לה המון התמדה. לעומת זאת, עצירת אדם או זבוב קלה יותר בהתאם למסתם הקטנה יותר.
התנע מבטא במידה רבה את המדד הווקטורי לתנועתיות הקווית של הגוף - גם את כמות התנועתיות וגם את כיוונה.
שימו לב שהתנע תלוי במערכת ייחוס. אם גוף נמצא בתנועה במהירות מסוימת, יש לו תנע ששונה מאפס. אם הוא נמצא במנוחה, התנע שלו שווה לאפס. אבל זה תלוי במערכת הייחוס שבה הוא נמדד. התנע אינו גודל אבסולוטי, אלא גודל שבכל מערכת ייחוס מקבל ערך אחר.
החוק הראשון של ניוטון
החוק הראשון של ניוטון קובע:
בהיעדר השפעות חיצוניות (או בהיעדר אינטראקציות), התנע נשמר בזמן:
\[\mathbf{p} = \text{constant}\]
בהקשר מסוים, חוק זה נקרא “חוק שימור התנע”.
המשמעות היא שאם גוף נמצא בתנועה בכיוון מסוים ובמהירות מסוימת, ולא פועלים עליו כוחות חיצוניים, הגוף ימשיך לנוע באותה מהירות ובאותו כיוון לנצח (כל עוד לא פועלים עליו כוחות חיצוניים).
החוק הראשון נקרא גם “חוק ההתמדה”.
זה מנוגד לחלוטין לאינטואיציה של אריסטו, שסבר שאם הוא מקנה מהירות לגוף מסוים, הגוף יקבל תנופה, אבל לאט לאט התנופה תדעך והוא יעצור. לפי ניוטון, בהיעדר השפעות חיצוניות, הגוף ימשיך לנוע עם התנופה שהוקנתה לו מלכתחילה עד אין קץ.
בהמשך נשתמש בחוק זה במקרה שהמערכת במנוחה (כולל מהירות קבועה). כלומר, כאשר הכוח השקול הפועל על הגוף הוא אפס, נקבל:
\[\sum \mathbf{F} = 0\]כי $\sum \mathbf{F} = 0 \implies \frac{d\mathbf{p}}{dt} = 0 \implies \mathbf{p} = \text{constant}$. החוק הראשון הוא בעצם מקרה פרטי של החוק השני, כאשר הכוח השקול הוא אפס.
החוק השני של ניוטון
נגדיר כוח כהשפעה חיצונית ונסמן אותו ב-$\mathbf{F}$.
כוח הוא וקטור, כי השפעה חיצונית יכולה להיות בעלת גודל וכיוון מסוימים. גוף יכול לדחוף גוף אחר בכיוון מסוים ובכוח מסוים, או בכיוון אחר ובכוח אחר.
יכולות להיות השפעות חיצוניות רבות. נסמן כוחות בודדים ב-$\mathbf{F}_i$ כאשר $i$ הוא אינדקס ($\mathbf{F}_1$, $\mathbf{F}_2$, $\mathbf{F}_3$, וכו’).
שקול הכוחות יסומן ב-$\mathbf{F}$ ויהיה:
\[\mathbf{F} = \mathbf{F}_1 + \mathbf{F}_2 + ... + \mathbf{F}_n\]החוק השני של ניוטון קובע:
שקול הכוחות שווה לקצב השינוי של התנע:
\[\mathbf{F} = \frac{d\mathbf{p}}{dt}\]
שימו לב לעובדה המעניינת הבאה: כאשר שקול הכוחות שווה לאפס, קצב השינוי בתנע שווה לאפס, ואינטגרציה לפי הזמן נותנת $\mathbf{p} = \text{constant}$, וכך חוזרים אל החוק הראשון של ניוטון.
כאשר $\mathbf{F} = 0$, אז $\frac{d\mathbf{p}}{dt} = 0$, ומכאן $\mathbf{p}$ אינו תלוי בזמן.
בהקשר זה, החוק הראשון הוא חוק שימור התנע. כלומר, כאשר מבינים שבמערכת שקול הכוחות מתאפס, ידוע שהתנע נשמר בזמן.
הקשר בין כוח ותאוצה
נזכור ש-$\mathbf{p} = m\mathbf{v}$, ולכן:
\[\mathbf{F} = \frac{d\mathbf{p}}{dt} = \frac{d(m\mathbf{v})}{dt} = \frac{dm}{dt}\mathbf{v} + m\frac{d\mathbf{v}}{dt} = \frac{dm}{dt}\mathbf{v} + m\mathbf{a}\]כאשר $\frac{d\mathbf{v}}{dt} = \mathbf{a}$ (התאוצה).
ברוב המקרים נטפל בבעיות שבהן המסה היא גודל קבוע, ולכן כאשר המסה אינה משתנה בזמן:
\[\mathbf{F} = m\mathbf{a}\]
זוהי הצורה המוכרת יותר של החוק השני של ניוטון.
אולם, יש סיטואציות שבהן המסה כן משתנה בזמן. לדוגמה, כאשר משגרים טיל או רקטה ושורפים דלק, מסת הרקטה משתנה בזמן. טילים גדולים כמו אלה של SpaceX שורפים דלק בקצב של מאות קילוגרמים בשנייה, ואז לאיבר $\frac{dm}{dt}\mathbf{v}$ יש משמעות.
משוואת תנועה דיפרנציאלית
הקשר $\mathbf{F} = m\mathbf{a}$ נראה תמים, אבל זוהי משוואת מפתח.
מכיוון ש-$\mathbf{a} = \frac{d^2\mathbf{r}}{dt^2}$, הכוח החיצוני יכול להיות תלוי במקום של הגוף או במהירות הגוף:
\[\mathbf{F}(\mathbf{r}, \dot{\mathbf{r}}) = m\ddot{\mathbf{r}}\]זוהי משוואה דיפרנציאלית עבור $\mathbf{r}(t)$ - וקטור המקום כפונקציה של הזמן - שמכילה את הנגזרות של $\mathbf{r}(t)$: את $\dot{\mathbf{r}}$ (המהירות) ואת $\ddot{\mathbf{r}}$ (התאוצה).
למשוואה שמכילה את הפונקציה ונגזרותיה קוראים משוואה דיפרנציאלית, והפתרון של המשוואה הדיפרנציאלית נותן לנו את הנעלם שהוא הפונקציה הווקטורית $\mathbf{r}(t)$.
לפעמים קורה שהכוח תלוי רק במהירות:
\[\mathbf{F}(\dot{\mathbf{r}}) = m\ddot{\mathbf{r}}\]ואז זו תהיה משוואה דיפרנציאלית ביחס לווקטור המהירות.
החוק השני של ניוטון - משמעות עמוקה
זוהי משוואה שמכילה לא את $\mathbf{r}$ עם $\dot{\mathbf{r}}$ ו-$\ddot{\mathbf{r}}$, אלא רק את $\dot{\mathbf{v}}$ ו-$\mathbf{v}$.
החוק השני של ניוטון הוא משוואת המפתח. הפתרון שלו, ברגע שמתארים את המציאות באמצעותו, שקול הכוחות שווה למסה כפול תאוצה, הוא חוק טבע. זה לא רשום בעולם המתמטיקה - זו תוצאה של הבנת המציאות, הבנת החוקיות במציאות.
לקיחת ההבנה של החוקיות במציאות, יישומה על מערכת פיזיקלית מסוימת, מניבה משוואה דיפרנציאלית עבור וקטור המקום של הגוף, ופתרון המשוואה נותן את וקטור המקום של הגוף כפונקציה של הזמן בכל זמן $t$, ובפרט בזמן $t$ עתידי.
הנגזרות תמיד הן לפי הזמן. בהמשך נדבר על מושגים שגם דורשים אינטגרציה לפי מקום, אך נניח לזה לעת עתה.
מקור החוק השני
מאין מגיע חוק זה? ניוטון הגיע לחוק זה בצורה אמפירית. הוא בחן מערכות של גופים, בדק את קצב שינוי התנע שלהם, וגילה שהוא פרופורציונלי לשקול הכוחות.
אפשר לומר במידה רבה שהשינוי בתנע מגדיר את שקול הכוחות שפועל על הגוף, אבל זו התחכמות פילוסופית. ניוטון הגיע לכך באופן אמפירי - המשוואות האלו הגיעו מתוך תובנות אמפיריות.
כיום, ההבנה היא לא רק “איך” אלא גם “למה”. המשוואה הזאת היא משוואה שממזערת פונקציה מסוימת (הנקראת “פעולה”) המתארת את המציאות, ושצריכה לקבל מינימום כדי שהמציאות תתפתח כפי שהיא מתפתחת. זהו פורמליזם מורכב, עמוק ומעניין, אך לא ניכנס אליו כעת.
בכל מקרה, זהו פורמליזם קלאסי. תורת היחסות, שמחליפה את המכניקה הניוטונית, נותנת פרספקטיבה אחרת לגמרי על המציאות.
החוק השלישי של ניוטון
החוק השלישי של ניוטון קובע שאם שני גופים באים במגע, כל אחד מפעיל על הגוף השני כוח ששווה בגודלו והפוך בכיוונו לכוח שהגוף השני מפעיל עליו.
במילים אחרות, באינטראקציה:
\[\mathbf{F}_{1\rightarrow2} = -\mathbf{F}_{2\rightarrow1}\]
אם גוף 1 מפעיל על גוף 2 כוח $\mathbf{F}$ בכיוון מסוים, הרי שגוף 2 יפעיל על גוף 1 את אותו כוח רק בכיוון ההפוך. כוחות אלה נקראים “כוחות פעולה ותגובה”.
אלו הם שלושת החוקים של ניוטון, ואיתם אפשר לעשות נפלאות. להלן כמה דוגמאות.
יישום חוקי ניוטון
אם חל תנאי ההתמדה (החוק הראשון) בציר מסוים, אז בציר הזה יש משוואה אלגברית שמסכמת את הכוחות לאפס.
אם חל החוק השני, אז יכולה להיות אחת משתי אפשרויות: מתקבלת או משוואה אלגברית עבור התאוצה, או משוואה דיפרנציאלית עבור המהירות או המקום.
הקשר בין כיוון הכוח וכיוון התנועה
נקודה חשובה לפני שניגש לדוגמאות ספציפיות: כפי שדובר בשיעור שעבר, המהירות קובעת את כיוון תנועת הגוף. וקטור המהירות תמיד משיק למסלול תנועתו של הגוף.
מהחוק השני של ניוטון, $\mathbf{F} = m\mathbf{a}$, רואים מיד שהכוח הוא בכיוון התאוצה והתאוצה היא בכיוון הכוח. כלומר, וקטור התאוצה הוא בכיוון וקטור שקול הכוחות.
זה מעניין ולא אינטואיטיבי. בהחלט ייתכן שהתאוצה תהיה ניצבת למהירות.
לדוגמה, אם נזרוק חפץ בכיוון אופקי, כוח המשיכה של כדור הארץ מושך אותו למטה, אבל המהירות ההתחלתית שניתנה לו גורמת לו להמשיך בכיוון אופקי. בכיוון הניצב לרדיוס כדור הארץ לא פועלים כוחות, אז אם הוענקה לו מהירות $v_0$ בכיוון אופקי, הוא ימשיך לנוע באותה מהירות כל הזמן בכיוון האופקי. אבל פועל עליו כוח בכיוון אנכי שמאיץ אותו כלפי מטה.
כלומר, הוא יואץ כלפי מטה, התאוצה תהיה בכיוון מטה, מהירות קבועה תהיה בכיוון אופקי (כי החוק הראשון חל בכיוון זה), ותתקבל כתוצאה מכך תנועה פרבולית כלפי מטה.
התאוצה אינה בכיוון המהירות; התאוצה היא כלפי מטה. למרות שהמהירות משיקה לפרבולה, התאוצה תהיה כלפי מטה.
זו נקודה חשובה: התאוצה תמיד בכיוון שקול הכוחות, ושקול הכוחות תמיד בכיוון התאוצה. המהירות תמיד משיקה למסלול התנועה. לא חייב להיות קשר בין המהירות לבין שקול הכוחות, למעט בתנועה בממד אחד. בממד אחד, המהירות, התאוצה ושקול הכוחות עשויים להיות באותו כיוון או בכיוון מנוגד.
דוגמה 1: מסה תלויה משני חוטים
הנה דוגמה טריוויאלית: תקרה, חוט, זווית $\alpha$ וזווית $\beta$, ומסה התלויה מהתקרה באמצעות שני חוטים. בסיטואציה הזאת, המערכת נמצאת במנוחה. המסה נמצאת במנוחה.
אם היא נמצאת במנוחה, החוק הראשון של ניוטון רלוונטי לגביה. כלומר, חל על המסה תנאי ההתמדה.
ראשית, נאתר את כל הכוחות שפועלים על המסה. בבדיקה פיזיקלית על מסה מסוימת, מה שמסביב אינו מעניין; מה שמעניין הוא המסה הספציפית הזאת.
יש כאן שני חוטים. יש להגדיר את הכוח שהחוט מפעיל על המסה. כוח זה נקרא המתיחות בחוט. מקור המתיחות בחוט הוא אינטראקציה אלקטרומגנטית - כוח המשיכה בין האטומים שבונים את החוט.
במעבדה, מסתכלים על זה באופן אפקטיבי כמתיחות בחוט. המתיחויות אינן ידועות והבעיה אינה סימטרית, ולכן נסמן אותן ב-$T_1$ ו-$T_2$. האות $T$ היא מהמילה tension (מתיחות).
בקירוב לבעיה הספציפית הזאת, החוטים חסרי מסה. אם הייתה להם מסה, היה צורך לקחת אותה בחשבון.
המסה לא הייתה חשה שום מתיחות בחוט אם כדור הארץ לא היה מושך אותה כלפי מטה. לכוח המשיכה שבו כדור הארץ מושך כלפי מטה נקרא $W$, מהמילה Weight (משקל). משקל אינו מסה. משקל מבטא את כוח המשיכה.
ניתוח הכוחות במערכת
כעת נפעיל את החוק הראשון על הגוף הזה. החוק הראשון נותן משוואה וקטורית:
\[\mathbf{T}_1 + \mathbf{T}_2 + \mathbf{W} = 0\]זאת המשוואה הווקטורית שמתארת את הבעיה. החוק הראשון אומר ששקול הכוחות שווה לאפס.
כעת נפרק את המשוואה לרכיביה. כלומר, נחפש שני צירים נוחים, עדיף שאחד הצירים לפחות יתלכד עם אחד הכוחות, ונבנה את שיווי המשקל בכל אחד מהצירים.
אם נבחר את ציר $x$ בכיוון אופקי וציר $y$ בכיוון אנכי, בציר $x$ מתקיים:
\[T_2 \cos\beta - T_1 \cos\alpha = 0\]ובציר $y$:
\[T_2 \sin\beta + T_1 \sin\alpha - W = 0\]ניתן לרשום זאת כך:
\[T_1 \cos\alpha = T_2 \cos\beta\]כלומר שני הכוחות בציר $x$ מאזנים זה את זה, ומתקיים:
\[T_1 \sin\alpha + T_2 \sin\beta = W\]הזוויות $\alpha$ ו-$\beta$ נתונות, $T_1$ ו-$T_2$ אינם ידועים (המתיחות לא ידועה), ו-$W$ (המשקל) בדרך כלל נתון. קיבלנו שתי משוואות בשני נעלמים: הגודל של $T_1$ והגודל של $T_2$, ומתוכן ניתן לחלץ את $T_1$ ו-$T_2$ במונחים של $\alpha$, $\beta$ ו-$W$.
מקרה מיוחד: זוויות זהות
נבחן את המקרה המעניין שבו הזוויות זהות, כלומר המסה תלויה כך שבשני הצדדים יש את אותה זווית $\alpha$.
מתנאי שיווי המשקל בציר $x$ מתקיים:
\[T_1 \cos\alpha = T_2 \cos\alpha\]או $T_1 = T_2 = T$. מהמשוואה השנייה בציר $y$ מקבלים:
\[T \sin\alpha + T \sin\alpha = W\]כלומר, $2T \sin\alpha = W$. מכאן:
\[T = \frac{W}{2\sin\alpha}\]המתיחות בחוט הולכת כמו אחד חלקי סינוס הזווית.
שימו לב, כאשר $\alpha = \frac{\pi}{2}$ (זווית ישרה), $\sin\alpha = 1$, ואז $T = \frac{W}{2}$. כלומר, כל חוט נושא מחצית מהמשקל, וזה הגיוני.
אבל מה קורה כאשר $\alpha \to 0$ (החוטים אופקיים)? אז $\sin\alpha \to 0$ ו-$T \to \infty$. לא יכול להתקיים מצב שבו המסה נמצאת במרכז ושני חוטים אופקיים תומכים בה. הסיבה היא שבציר ה-$y$ אין מה שיאזן את המשקל $W$. אין רכיב אנכי בציר $y$ מהמתיחות בחוטים, ולכן נדרש כוח אינסופי כדי להחזיק את החוטים במצב מאוזן.
דוגמה 2: גוף על מישור משופע
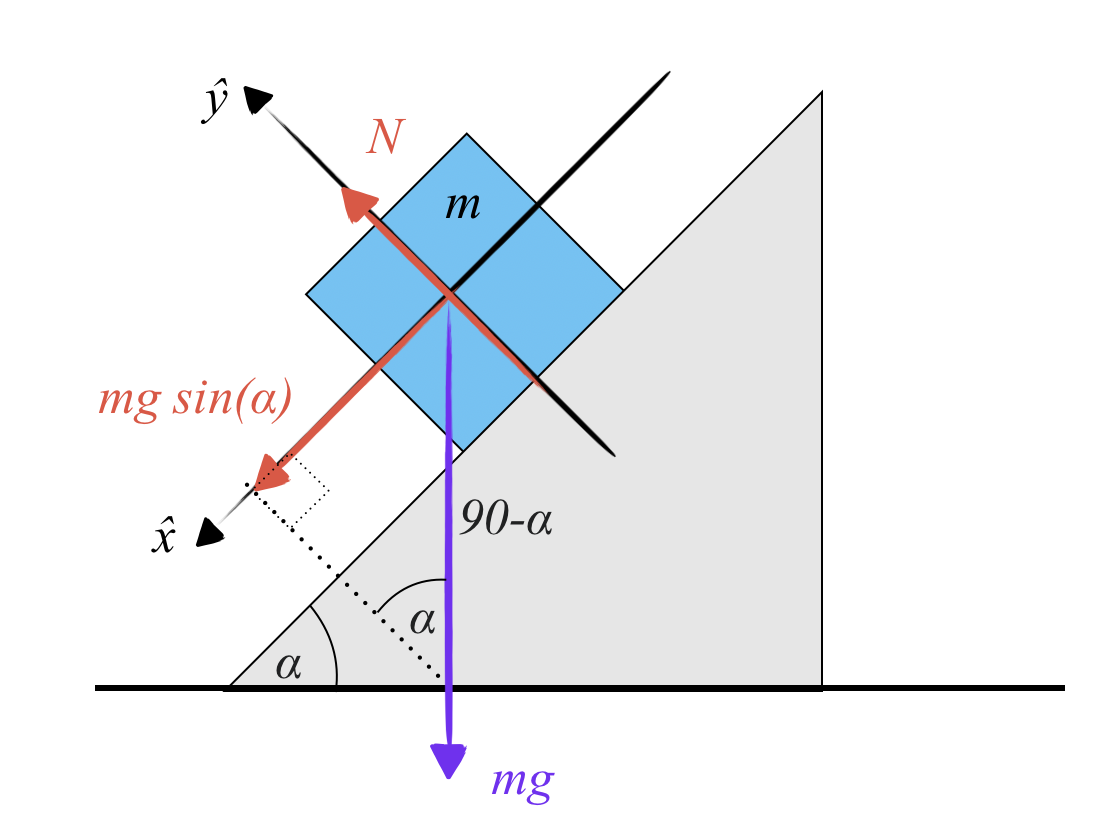
כעת נתבונן בגוף על מישור משופע בזווית $\alpha$. פועל עליו כוח משיכה $W$ כלפי מטה, וגם כוח נורמלי $N$ שהמשטח מפעיל על הגוף.
כפי שדובר, שני גופים במגע מפעילים זה על זה כוחות נורמליים הניצבים למשטח המגע ביניהם.
אלו הם הכוחות שפועלים על הגוף. אם זו זווית $\alpha$, ניתן לפרק את כוח המשיכה $W$ לשני רכיבים: רכיב מקביל למישור שגודלו $W \sin\alpha$, ורכיב ניצב למישור שגודלו $W \cos\alpha$.
על הציר הניצב למישור, המסה אינה נעה - היא לא קופצת מהמישור ולא חודרת אותו. כלומר בציר זה מתקיים חוק ההתמדה, ולכן:
\[N = W \cos\alpha\]תנאי ההתמדה בכיוון הניצב למישור מתקבל מהפעלת החוק הראשון של ניוטון.
בעוד שבציר המקביל למישור, פועל רק כוח אחד - רכיב המשקל $W \sin\alpha$ - ואין מה שיאזן אותו. ולכן מתקיים החוק השני של ניוטון:
\[ma = W \sin\alpha\]אז יש שתי משוואות שמתארות שתי תנועות. בכיוון מקביל למישור יש תאוצה:
\[ma = W \sin\alpha\]ובכיוון ניצב למישור יש תנאי התמדה (אין תנועה):
\[N = W \cos\alpha\]בשיעור הבא יוצגו דוגמאות מורכבות ועמוקות יותר, עם יותר פיזיקה ומתמטיקה.
 דור פסקל
דור פסקל