חזרה על מושגי יסוד
שטף חשמלי
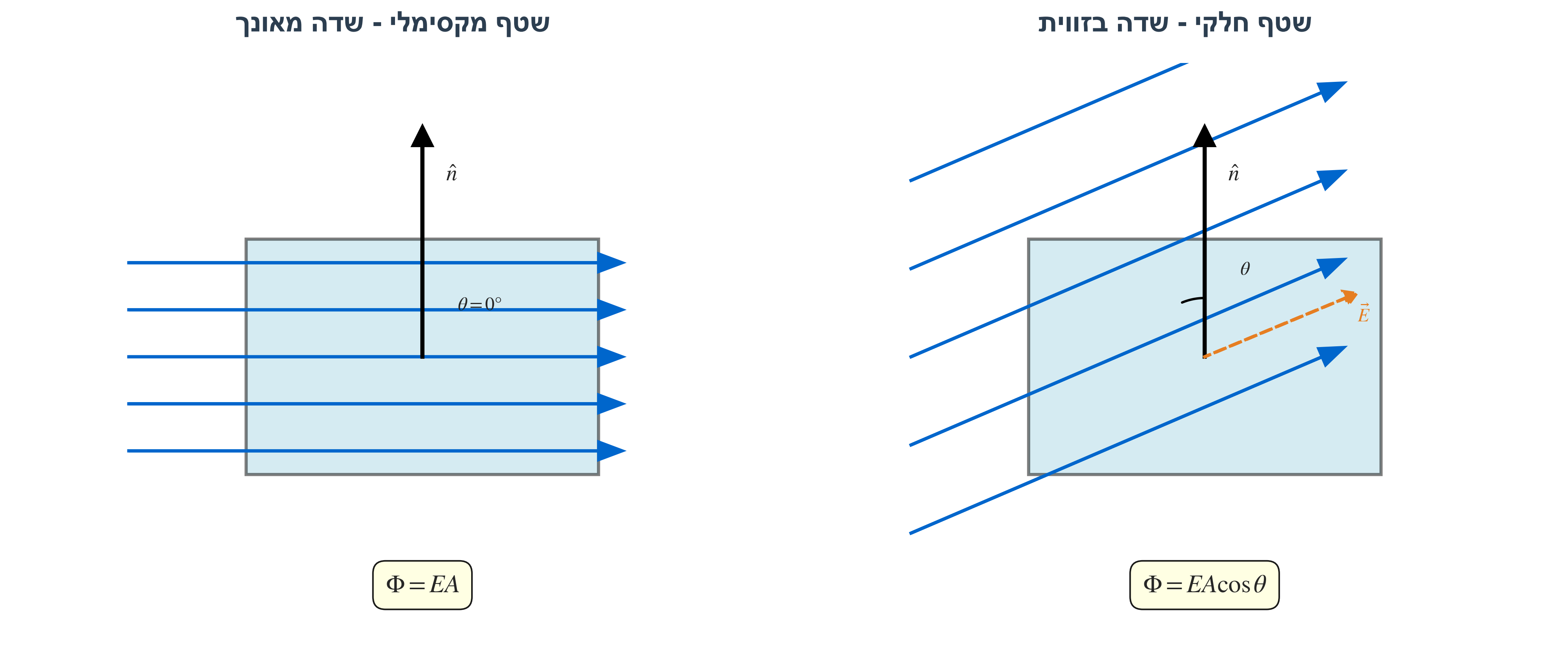
שטף מתאר כמה שדה חשמלי עובר דרך משטח.
כאשר יש שדה חשמלי $\vec{E}$ ומשטח, מפרקים את השדה ל:
- רכיב מאונך למשטח - תורם לשטף
- רכיב משיק למשטח - לא תורם לשטף
רק הרכיב המאונך יוצא מהמשטח ותורם לשטף.
שדה חשמלי - מקור והשפעה
מי מייצר שדה?
מטען חשמלי $Q$ מייצר סביבו שדה חשמלי.
מי מרגיש שדה?
מטען אחר $q$ שנמצא בשדה מרגיש כוח:
\[\vec{F} = q\vec{E}\]- מטען חיובי ← כוח בכיוון השדה
- מטען שלילי ← כוח נגד כיוון השדה
שדה של מטען נקודתי
\[\vec{E} = \frac{kq_1}{r^2}\hat{r}\]- $k \approx 9 \times 10^9 \, \text{N·m}^2/\text{C}^2$ - קבוע קולון
- השדה דועך כמו $\frac{1}{r^2}$
- מטען חיובי ← שדה יוצא (מעיין)
- מטען שלילי ← שדה נכנס (בולען)
צפיפויות מטען
צפיפות קווית $\lambda$
\[\lambda = \frac{dq}{dl} \quad \text{[C/m]}\]מטען ליחידת אורך.
צפיפות משטחית $\sigma$
\[\sigma = \frac{dq}{dA} \quad \text{[C/m²]}\]מטען ליחידת שטח.
צפיפות נפחית $\rho$
\[\rho = \frac{dq}{dV} \quad \text{[C/m³]}\]מטען ליחידת נפח.
עקרון הסופרפוזיציה
כאשר יש רצף של מטענים:
- לוקחים אלמנט מטען קטן $dq$
- מחשבים את השדה שהוא מייצר: $d\vec{E} = \frac{k \cdot dq}{r^2}\hat{r}$
- סוכמים (אינטגרל) על כל המטענים
תרגיל 1: שני מטענים שליליים
נתונים שני מטענים נקודתיים זהים $-q$ כל אחד, נמצאים במרחק $2d$ זה מזה על ציר $x$ (אחד ב-$+d$ ואחד ב-$-d$).
- האם קיימת נקודה במרחב שבה השדה מתאפס?
- מהו השדה ב- $\vec{r}=b\hat{y}$?
- מהו הכוח על הפרוטון בנקודה הזו?

סעיף א’: נקודה שבה השדה מתאפס
שאלה: האם קיימת נקודה במרחב שבה השדה מתאפס?
פתרון:
שני המטענים שליליים ← השדה נכנס לכל אחד מהם.
בנקודה בדיוק באמצע (בראשית):
- השדה מ-$-q$ הימני מכוון שמאלה
- השדה מ-$-q$ השמאלי מכוון ימינה
- המרחקים שווים ← הגדלים שווים ← השדות מתבטלים
בכל נקודה אחרת השדה לא מתאפס.
סעיף ב’: השדה על ציר Y
שאלה: מהו השדה בנקודה $(0, b)$ על ציר $y$?
פתרון:
בנקודה על ציר $y$, כל מטען מייצר שדה לכיוונו (כי הם שליליים).
ניתוח סימטריה:
- רכיבי $X$ מתבטלים (סימטריה)
- רכיבי $Y$ מתחברים (שניהם כלפי מטה)
כאשר:
\[r = \sqrt{d^2 + b^2}, \quad \cos\theta = \frac{b}{r}\] \[\boxed{E_y = -\frac{2kqb}{(d^2 + b^2)^{3/2}}}\](הסימן השלילי מציין כיוון $-\hat{y}$)
סעיף ג’: כוח על פרוטון
שאלה: מהו הכוח על פרוטון בנקודה $(0, Y)$?
פתרון:
\[\vec{F} = q\vec{E} = e \cdot \vec{E}\]הפרוטון חיובי, לכן הכוח בכיוון השדה (כלפי מטה).
סעיף ד’: תנועת הפרוטון
שאלה: איזו תנועה תהיה לפרוטון?
פתרון:
הכוח פועל כלפי מטה (לכיוון $-Y$). הפרוטון יואץ כלפי מטה.
הערה: התנועה אינה הרמונית פשוטה כי הכוח אינו פרופורציונלי להעתק באופן לינארי.
תרגיל 2: שדה חשמלי של טבעת טעונה
נתונה טבעת ברדיוס $R$ טעונה במטען $Q$ בצפיפות אחידה $\lambda$.
- מהו השדה במרכז הטבעת?
- מהו השדה בנקודה על ציר הטבעת במרחק $Z$ מהמרכז?
- מה קורה לשדה כאשר $Z \gg R$?
- מה קורה לשדה כאשר $Z \ll R$?

סעיף א’: השדה במרכז הטבעת
פתרון:
מסימטריה: בכל כיוון שמסתכלים מהמרכז, רואים את אותה תמונה.
לכל אלמנט מטען יש אלמנט מנוגד בצד השני שמבטל את השדה שלו.
\[\boxed{\vec{E}(0) = 0}\]סעיף ב’: השדה על הציר (בגובה $Z$)
פתרון:
ניתוח סימטריה:
- רכיבי $X$ ו-$Y$ מתבטלים
- השדה השקול בכיוון $Z$ בלבד
חישוב:
אלמנט מטען $dq$ תורם:
\[dE = \frac{k \cdot dq}{r^2}\]כאשר $r = \sqrt{R^2 + Z^2}$.
הרכיב בכיוון $Z$:
\[dE_z = dE \cos\theta = \frac{k \cdot dq}{r^2} \cdot \frac{Z}{r} = \frac{kZ \cdot dq}{(R^2 + Z^2)^{3/2}}\]סכימה על כל הטבעת:
\[E_z = \int dE_z = \frac{kZ}{(R^2 + Z^2)^{3/2}} \int dq = \frac{kQZ}{(R^2 + Z^2)^{3/2}}\] \[\boxed{\vec{E}(Z) = \frac{kQZ}{(R^2 + Z^2)^{3/2}}\hat{z}}\]טריק: במקום לעבור לזוויות ולעשות אינטגרל מ-$0$ עד $2\pi$, ניתן להוציא את כל הקבועים מהאינטגרל ולהישאר עם $\int dQ = Q$.
חוק גאוס
הניסוח
\[\Phi = \oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]משמעות: השטף של השדה החשמלי דרך מעטפת סגורה שווה למטען הכלוא בתוכה חלקי $\epsilon_0$.
מתי משתמשים?
חוק גאוס שימושי כאשר יש סימטריה:
- סימטריה כדורית
- סימטריה גלילית
- סימטריה מישורית
עקרונות
- מטען בתוך המעטפת ← תורם לשטף
- מטען מחוץ למעטפת ← השטף שנכנס = השטף שיוצא ← תרומה כוללת אפס
- בוחרים מעטפת גאוס שמתאימה לסימטריה
תרגיל 3: שני גלילים קונצנטריים
נתונים:
שני גלילים אינסופיים קונצנטריים (בעלי ציר משותף):
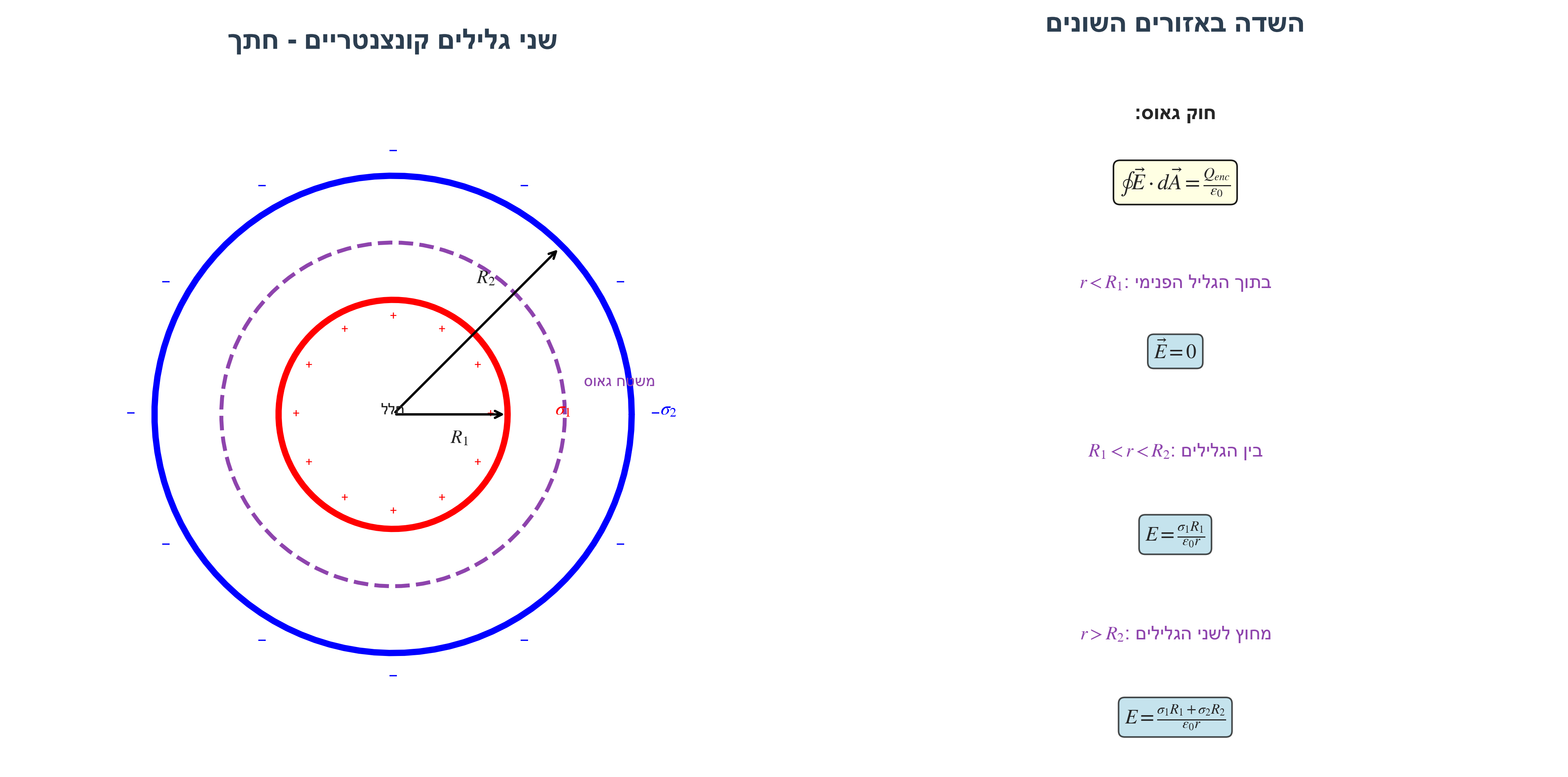
- גליל פנימי ברדיוס $R_1$ עם צפיפות משטחית $\sigma_1$
- גליל חיצוני ברדיוס $R_2$ עם צפיפות משטחית $\sigma_2$
שאלה: מהו השדה בכל המרחב?
פתרון
שלב 1: קביעת כיוון השדה
מסימטריה גלילית: השדה חייב להיות רדיאלי (בכיוון $\hat{r}$).
- אין יתרון לכיוון $\hat{\theta}$ או $\hat{z}$
- השדה יכול להיות רק פנימה או החוצה
שלב 2: בניית מעטפת גאוס
נבנה מעטפת גאוס גלילית ברדיוס $r$ ואורך $L$:
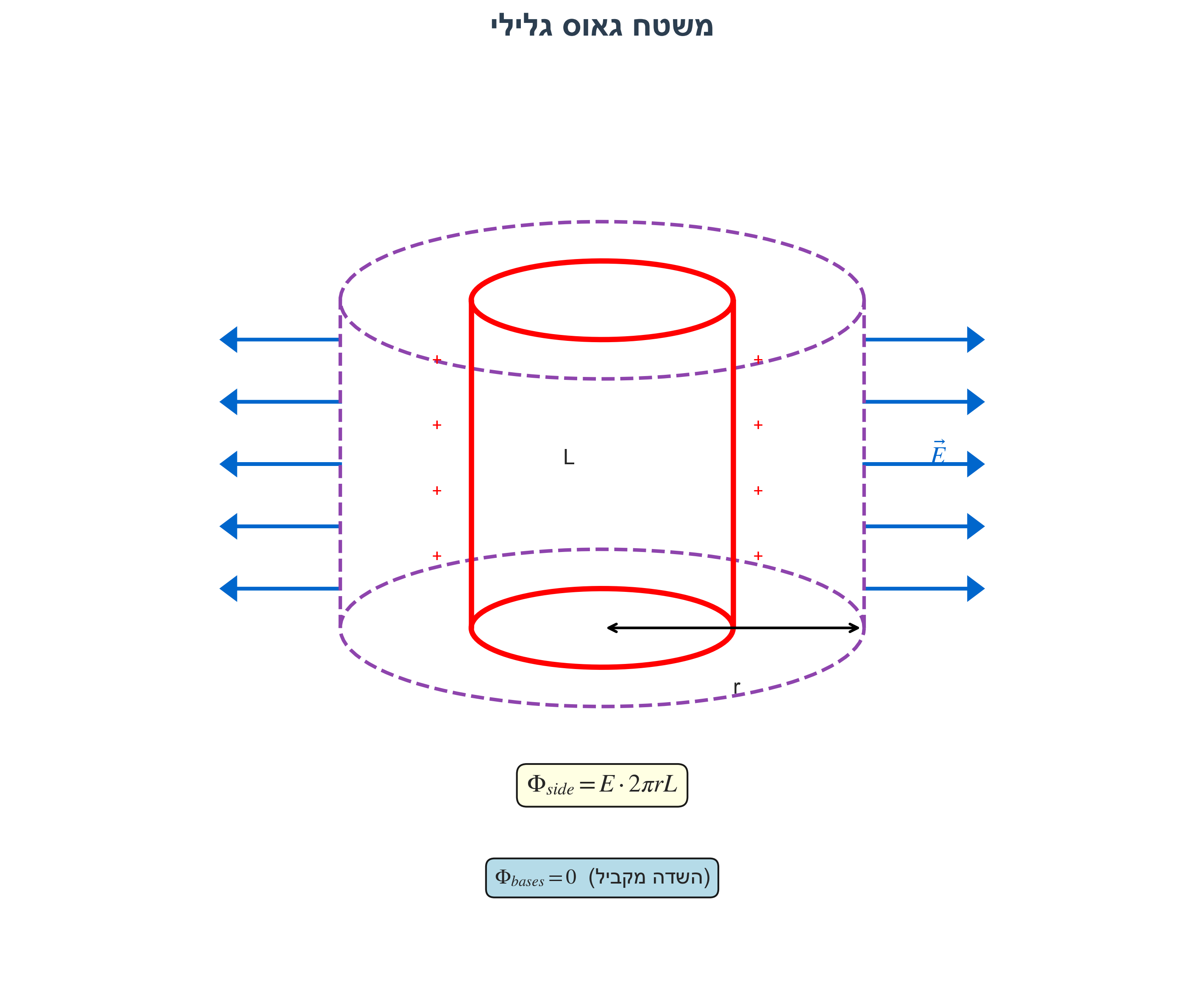
השטף דרך המעטפת:
- דרך המעטפת הצדדית: $\Phi = E \cdot 2\pi r L$
- דרך הבסיסים: $\Phi = 0$ (השדה מקביל לבסיסים)
שלב 3: יישום חוק גאוס לכל אזור
אזור I: $r < R_1$ (בתוך הגליל הפנימי)
המטען הכלוא: $Q_{\text{enc}} = 0$
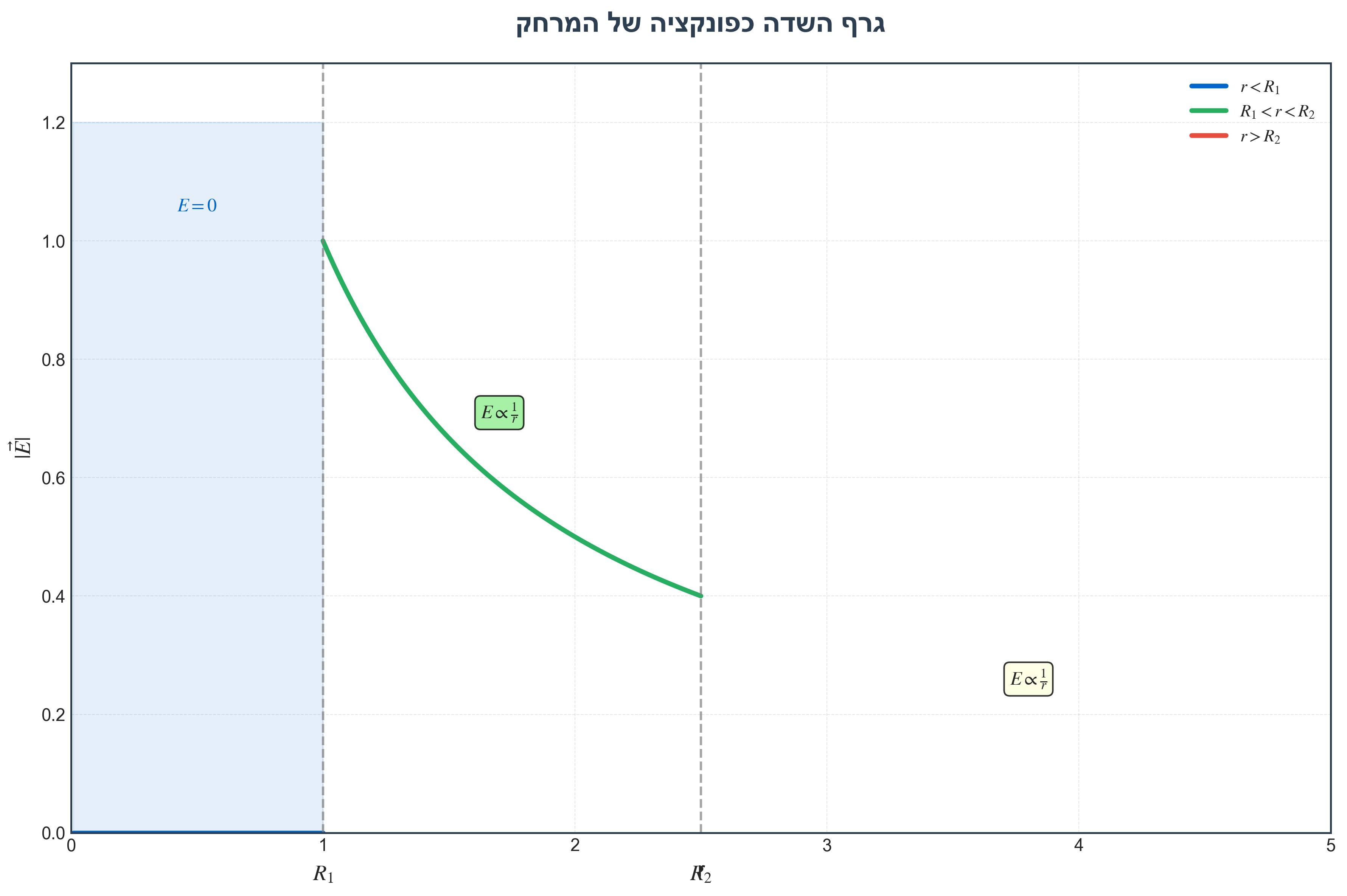
\[E \cdot 2\pi r L = 0\] \[\boxed{E(r < R_1) = 0}\]אזור II: $R_1 < r < R_2$ (בין הגלילים)
המטען הכלוא: רק מהגליל הפנימי
\[Q_{\text{enc}} = \sigma_1 \cdot 2\pi R_1 L\] \[E \cdot 2\pi r L = \frac{\sigma_1 \cdot 2\pi R_1 L}{\epsilon_0}\] \[\boxed{E(R_1 < r < R_2) = \frac{\sigma_1 R_1}{\epsilon_0 r}}\]אזור III: $r > R_2$ (מחוץ לשני הגלילים)
המטען הכלוא: משני הגלילים
\[Q_{\text{enc}} = \sigma_1 \cdot 2\pi R_1 L + \sigma_2 \cdot 2\pi R_2 L\] \[E \cdot 2\pi r L = \frac{2\pi L(\sigma_1 R_1 + \sigma_2 R_2)}{\epsilon_0}\] \[\boxed{E(r > R_2) = \frac{\sigma_1 R_1 + \sigma_2 R_2}{\epsilon_0 r}}\]הערה: האורך $L$ מצטמצם בכל המקרים - התוצאה לא תלויה באורך המעטפת שבחרנו.
סיכום - שיטות לחישוב שדה חשמלי
שיטה 1: אינטגרציה ישירה (סופרפוזיציה)
- לוקחים אלמנט מטען $dQ$
- מחשבים $d\vec{E} = \frac{k \cdot dQ}{r^2}\hat{r}$
- מפרקים לרכיבים
- בודקים סימטריה - אילו רכיבים מתאפסים
- עושים אינטגרל
- יתרון: עובד תמיד
- חיסרון: לפעמים האינטגרל מסובך
שיטה 2: חוק גאוס
- מזהים סימטריה
- בונים מעטפת גאוס מתאימה
- מחשבים שטף: $\Phi = \oint \vec{E} \cdot d\vec{A}$
- מחשבים מטען כלוא: $Q_{\text{enc}}$
- מיישמים: $\Phi = \frac{Q_{\text{enc}}}{\epsilon_0}$
- יתרון: פשוט ומהיר כשיש סימטריה
- חיסרון: עובד רק עם סימטריה מתאימה
טבלת השוואה
| מצב | שיטה מומלצת |
|---|---|
| מטען נקודתי | חוק קולון ישירות |
| מוט/קשת סופיים | אינטגרציה |
| כדור/גליל/מישור אינסופי | חוק גאוס |
| צורה לא סימטרית | אינטגרציה |
 דור פסקל
דור פסקל