הקדמה
להלן שחזור אפשרי ללא אחריות לבחינת הגמר שנערכה ביום 14 ביולי 2025 (מועד א׳). הבחינה לא הייתה קלה, לעניות דעתי, והתשובות שלהלן מובאות כניחוש בלבד.
עדכון: חלק מהשאלות עודכנו לאחר פרסום המבחן הרשמי.
בהצלחה!
\[\frac{t^3}{6} \mathbf{\hat{x}} - \frac{t^2}{2} \mathbf{\hat{y}}\]שאלה 1 - אינטגרציה כפולה
גוף שמסתו אחד קילוגרם נמצא ברגע $t=0$ בראשית הצירים של מישור אופקי חלק. הכוח השקול הפועל על הגוף במישור האופקי הוא:
\[\mathbf{F} = -\alpha \hat{\mathbf{y}} - \beta v_y \hat{\mathbf{x}}\]$v_y$ הוא רכיב ה-$y$ של מהירותו הרגעית. הניחו ש $\alpha=\beta=1$ ביחידות המתאימות.
נתון גם תנאי התחלה $\vec{v}(t=0) = \vec{0} \, \mathrm{m/s}$.
מה וקטור המקום של הגוף?
אינטגרציה כפולה. הייתה רק תשובה אחת שקיימה את הנדרש בציר $x$.
\[-k X - N \sin{\alpha}\]שאלה 2 - מסה מחוברת בקפיץ שמונחת עליה מסה קטנה
שאלה 3 - חישוב מהירות יחסית
מוזמנים להשלים.
שאלה 4 - זוית תנודות מואצת
מסילה מעגלית אנכית חלקה, אשר רדיוסה $R$, מאיצה שמאלה בתאוצה קבועה $a$. חרוז קטן שמסתו $m$ מתנדנד סביב נקודת שיווי המשקל המצוייה בגובה $h$.
תדירות התנודות הקטנות של הקוף מקיימת:
התשובה הנכונה היא ככל הנראה:
\[\omega^2 = \frac{\sqrt{g^2 + a^2}}{R}\]שאלה 5 - מערכת מטוטלת-תיבה
תיבה חלולה אשר מסתה היא $M$ מונחת על משטח אופקי חלק הנמצא במעבדה.
מתקרת מערכת התיבה תלויה מטוטלת עשויה חוט קל שאורכו $L$ ובקצהו השני כדור קטן שמסתו היא $m$. מחזיקים את המטוטלת כך שהחוט המתוח יוצר זווית של $60^\circ$ עם האנך, ומשחררים את המערכת.
מהירות הכדור $v$ ומהירות התיבה $V$ במערכת המעבדה, כאשר הכדור נמצא בנקודה הנמוכה ביותר, היא:
התושבה:
\[\boxed{ \begin{aligned} V &= \sqrt{\frac{mgL}{M(1+M/m)}} \\ v &= -\sqrt{\frac{MgL}{m(1+M/m)}} \end{aligned} }\]נשתמש בחוק שימוש אנרגיה בנקודה הנמוכה ביותר. נקבל שתי משוואות עבור שתי המהירויות.
משימוש תנע (המהירויות בכיוונים נגדיים):
\[0 = mv - MV \implies \boxed{V = \frac{mv}{M}}\]משימור אנרגיה - ברכיב האופקי בלבד:
\[0 + mgL(1-\cos(60)) = \frac{1}{2}mv^2 + \frac{1}{2}MV^2 + 0\] \[mgL = mv^2 + MV^2\]נציב את הביטוי ל $V$ כדי לקבל משוואה רק עם $v$:
\[mv^2 + M\left(\frac{-mv}{M}\right)^2 = mgL\] \[mv^2 + \frac{(mv)^2}{M} = mgL\] \[v^2 + \frac{m(v)^2}{M} = gL\] \[v^2\left(1 + \frac{m}{M}\right) = gL\] \[v = \sqrt{\frac{gL}{\left(1 + \frac{m}{M}\right)}}\] \[v = \sqrt{\frac{MgL}{M\left(1 + \frac{m}{M}\right)}}\]לצערי לא הצלחתי להגיע לפיתוח הסופי, כנראה שבגלל הכיוון של המהירות זה למעשה:
\[v = -\sqrt{\frac{MgL}{\left(M + m\right)}} = - \sqrt{\frac{MgL}{m\left(1 + M/m\right)}}\]באופן דומה מקבלים את הביטוי עבור $V$.
שאלה 6 - התנגשות אלסטית של שתי מסות
מסה $m_2$ במהירות $u$ מתקרבת למסה $m_1$ שנמצאת במנוחה. למסה $m_1$ מחובר קפיץ עם קבוע $k$, בכיוון שממנו מתקרבת המסה $m_1$.
המסה $m_2$ מתנגשת התנשות אלסטית בקפיץ שמחובר למסה $m_1$.
מה התכווצות הקפיץ $d$ המקסימלית? (רמז: מהירות יחסית של המסות).
ככל הנראה:
\[d = \sqrt{\frac{m_1 m_2}{k(m_1 + m_2)}} u\]פתרון מפורט:
משימור תנע:
\[p_i = p_f\] \[m_2 u + 0 = (m_2+m_1)u_f\]מכאן נקבל:
\[u_f = \frac{m_2 u}{m_2 + m_1}\]משימור אנרגיה מכנית:
\[\frac{1}{2}m_2 u^2 + 0 = \frac{1}{2} (m_2 + m_1) u_f^2 + \frac{1}{2}k d^2\]נציב את הביטוי שמצאנו ל $u_f$ ונכפול ב-2:
\[m_2 u^2 = (m_2 + m_1) \left( \frac{m_2 u}{m_2 + m_1}\right)^2 + k d^2\] \[m_2 u^2 = \frac{(m_2 u)^2}{m_2 + m_1} + k d^2\] \[kd^2 = \frac{\cancel{m_2^2 u^2} + m_1 m_2 u^2 - \cancel{m_2^2 u_2^2}}{m_2 +m_1}\] \[\boxed{d = \sqrt{\frac{m_1 m_2}{k(m_1 + m_2)}}u}\]שאלה 7 - באנג׳י
אדם עושה באנג׳י.
מגדירים ב-z(t) את המרחק המתוח של חבל הבאנג׳י (לאחר שקפץ).
כוח הגרר של האוויר מסומן:
\[F_{\text{drag}} = -b \dot{z}\]משוואת התנועה היא:
\[z(t) = \frac{mg}{k} \left(1 - e^{-\alpha t}\right)\]השאלה: איזו משוואה מקיים הפרמטר $\alpha$?
פתרון:
היה ניתן לפסול את רוב התשובות על סמך יחידות מידה בלבד.
משוואת הכוחות:
\[m\ddot{z} = mg - kz - b\dot{z}\]מהפתרון הנתון:
- $\dot{z} = \frac{mg\alpha}{k}e^{-\alpha t}$
- $\ddot{z} = -\frac{mg\alpha^2}{k}e^{-\alpha t}$
הצבה במשוואת הכוחות:
\[m\left(-\frac{mg\alpha^2}{k}e^{-\alpha t}\right) = mg - k\left(\frac{mg}{k}(1 - e^{-\alpha t})\right) - b\left(\frac{mg\alpha}{k}e^{-\alpha t}\right)\]פישוט:
\[-\frac{m^2g\alpha^2}{k}e^{-\alpha t} = mge^{-\alpha t} - \frac{bmg\alpha}{k}e^{-\alpha t}\]חלוקה ב-$e^{-\alpha t}$:
\[-\frac{m^2g\alpha^2}{k} = mg - \frac{bmg\alpha}{k}\]העברת אגפים:
\[\frac{m^2g\alpha^2}{k} - \frac{bmg\alpha}{k} - mg = 0\]חלוקה ב-$mg$:
\[\boxed{\frac{m\alpha^2}{k} - \frac{b\alpha}{k} - 1 = 0}\]בכל מקרה הביטוי המקובל לאלפא הוא בדיעבד:
\[m\alpha^2 - b\alpha - k = 0\]טעיתי בשאלה הזאת בגלל חוסר תשומת לב. סימנתי אותה ושיניתי כיוון שהצבה של $\alpha \to 0$ גרמה לי לחשוב שמדובר בסתירה: $-1\ne 0$.
שאלה 8 - זמן לנפילה של גולה
\[t=\frac{\cosh^{-1}\left(2\right)}{\omega}\]הפתרון זמין בסיכום שיעור התגבור.
למי שמתעצלים לחפש:
ניסוח הבעיה
גליל אופקי באורך $L$ מסתובב נגד כיוון השעון במהירות זוויתית קבועה $\omega$. מסה $m$ מתחילה במרכז הגליל (במיקום $r = L/2$) ממצב מנוחה, ונעה תחת השפעת הכוח הצנטריפוגלי בלבד.
נתונים:
תנאי התחלה:
- $r(t=0) = \frac{L}{2}$ (מיקום התחלתי במרכז הגליל)
- $\dot{r}(t=0) = 0$ (מהירות רדיאלי התחלתי אפס - ממנוחה)
הפרמטרים של המערכת:
- $\omega$ = מהירות זוויתית קבועה של הגליל
- $L$ = אורך הגליל
- $m$ = מסת הגוף
מטרה: למצוא את התנועה $r(t)$ של המסה והזמן ($t$) שבו היא מגיעה לקצה הגליל ($r = L$).
שלב 1: יישום חוק ניוטון השני במערכת ייחוס מסתובבת
במערכת ייחוס מסתובבת עם מהירות זוויתית קבועה $\omega$, הכוח הצנטריפוגלי פועל על מסה הנמצאת במרחק $r$ מהמרכז:
\[\mathbf{F}_{\text{centrifugal}} = m\omega^2 r\]הכוח מכוון החוצה ברכיב הרדיאלי $\hat{r}$.
שלב 2: משוואת התנועה
יישום החוק השני של ניוטון בכיוון הרדיאלי:
\[m\ddot{r} = m\omega^2 r\]המסה מצטמצמת:
\[\ddot{r} = \omega^2 r \tag{1}\]שלב 3: פתרון המשוואה הדיפרנציאלית
משוואה (1) היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני עם מקדמים קבועים.
המשוואה האופיינית:
\[\lambda^2 = \omega^2\]הפתרונות: $\lambda = \pm\omega$
הפתרון הכללי:
\[r(t) = A e^{\omega t} + B e^{-\omega t}\]או בצורה היפרבולית שקולה:
\[r(t) = C \cosh(\omega t) + D \sinh(\omega t) \tag{2}\]שלב 4: יישום תנאי התחלה
תנאי התחלה:
- $r(0) = \frac{L}{2}$
- $\dot{r}(0) = 0$
מהתנאי הראשון:
\[r(0) = C = \frac{L}{2}\]לכן:
\[r(t) = \frac{L}{2} \cosh(\omega t) + D \sinh(\omega t)\]מהתנאי השני:
\[\dot{r}(t) = \frac{L}{2} \omega \sinh(\omega t) + D \omega \cosh(\omega t)\] \[\dot{r}(0) = D \omega = 0\]לכן: $D = 0$
שלב 5: הפתרון הסופי
\[r(t) = \frac{L}{2} \cosh(\omega t) \tag{3}\] \[\dot{r}(t) = \frac{L \omega}{2} \sinh(\omega t) \tag{4}\] \[\ddot{r}(t) = \frac{L \omega^2}{2} \cosh(\omega t) \tag{5}\]שלב 6: חישוב זמן ההגעה לקצה הגליל
המסה מגיעה לקצה הגליל כאשר $r(t) = L$:
\[L = \frac{L}{2} \cosh(\omega t)\] \[2 = \cosh(\omega t)\] \[\omega t = \cosh^{-1}(2)\] \[\boxed{t = \frac{\cosh^{-1}(2)}{\omega}}\]הערה: טעיתי ובחרתי באפשרות של $t = \frac{\sinh^{-1}(2)}{\omega}$ מחוסר תשומת לב.
נתראה במועד הבא, בהצלחה!
שאלות ממועד 2025 ב׳
שאלה עם $\ln$ - תאוצה זוויתית
מיקום גוף נע מתואר בקואורדינטות x ו y באופן הבא (לא זוכר במדיוק):
\[x(t) = A\ln\left(1 + \frac{t}{\tau}\right) \cos\left(2A\omega\left[(t + \tau)\ln\left(1 + \frac{t}{\tau}\right) - t\right]\right)\] \[y(t) = A\ln\left(1 + \frac{t}{\tau}\right) \sin\left(2A\omega\left[(t + \tau)\ln\left(1 + \frac{t}{\tau}\right) - t\right]\right)\]$A, \tau$ הם קבועים ביחידות המתאימות.
מה התאוצה הזוויתית של הגוף? ($a_\theta$)
סימנתי:
\[a_\theta = \frac{2A\omega \tau}{(t + \tau)^2}\]התשובה הנכונה היא אולי:
\[\boxed{a_\theta = \frac{2A\omega}{t + \tau}}\]שאלת קליע - מתיחות בחוט:
\[T = (m + M)g + \frac{m^2v_0^2}{2L(M+m)}\]שאלת כוכב - מהירות יציאה מהפלנטה:
\[\sqrt{v_0 + \frac{2GM(R-a)}{Ra}}\]שאלת קפיץ:
\[\ddot{r} -(\dot{\theta}^2 -\omega^2)r - \omega^2 r_0 = 0\]שאלת חיכוך:
\[\tan{\theta} \leq \frac{\mu g + A}{g-\mu A}\]שאלת אנרגיה:
\[-36 \, \mathrm{J}\]שאלת אמפליטודה של תנודות:
\[A = \frac{m_1 v_1}{\sqrt{k m_2}}\]שאלות נוספות שעלו מבחינת הגמר 2024 א׳
שאלות מתרגיל 3 (החבל המחליק)
שאלה a: מי הוא $A$ אם האורך ההתחלתי של החתיכה המשתלשלת הוא $x_0$? מהו זמן ההשתלשלות במקרה זה?
פתרון:
מתנאי ההתחלה $x(0) = x_0$:
\[x(0) = A \cosh(0) + \frac{\mu L}{1+\mu} = A + \frac{\mu L}{1+\mu} = x_0\]לכן:
\[A = x_0 - \frac{\mu L}{1+\mu}\]זמן ההשתלשלות המלאה מתקבל כאשר $x(t) = L$:
\[L = \left(x_0 - \frac{\mu L}{1+\mu}\right) \cosh(\omega t) + \frac{\mu L}{1+\mu}\]פותרים עבור $t$:
\[t = \frac{1}{\omega} \cosh^{-1}\left(\frac{L - \frac{\mu L}{1+\mu}}{x_0 - \frac{\mu L}{1+\mu}}\right) = \frac{1}{\omega} \cosh^{-1}\left(\frac{L}{x_0(1+\mu) - \mu L}\right)\]כאשר $\omega = \sqrt{\frac{g(1+\mu)}{L}}$
שאלה b: מהו הפתרון הכללי של משוואת התנועה עבור המקרה בו החבל מתחיל את החלקתו ממהירות התחלתית כלשהי $v_0$?
פתרון:
הפתרון הכללי של המשוואה $\ddot{y} = \omega^2 y$ הוא:
\[y(t) = A \cosh(\omega t) + B \sinh(\omega t)\]מתנאי ההתחלה:
- $y(0) = x_0 - \frac{\mu L}{1+\mu} = A$
- $\dot{y}(0) = v_0 = B\omega$
לכן $B = \frac{v_0}{\omega}$ והפתרון הוא:
\[x(t) = \left(x_0 - \frac{\mu L}{1+\mu}\right) \cosh(\omega t) + \frac{v_0}{\omega} \sinh(\omega t) + \frac{\mu L}{1+\mu}\]שאלה מתרגיל 6-4 (החרוז על הקשת)
מהי התאוצה הכוללת בקואורדינטות פולריות?
פתרון:
בקואורדינטות פולריות, התאוצה הכוללת היא:
\[|\vec{a}| = \sqrt{a_r^2 + a_\theta^2}\]מהפתרון שחושב:
- $a_r = -L\omega^2\theta_0^2 \cos^2(\omega t)$
- $a_\theta = -L\omega^2\theta_0 \sin(\omega t)$
לכן:
\[|\vec{a}| = L\omega^2\theta_0\sqrt{\theta_0^2 \cos^4(\omega t) + \sin^2(\omega t)}\]מהי המהירות היחסית חרוז→צופה לכל זמן $t$? מהי המהירות היחסית בנקודה בה החרוז בתחתית הקשת?
פתרון:
וקטור המיקום היחסי:
\[\vec{r}_{rel} = (R\sin\theta - \bar{v}t)\hat{x} + R\cos\theta \hat{y}\]המהירות היחסית:
\[\vec{v}_{rel} = \frac{d\vec{r}_{rel}}{dt} = (R\cos\theta \cdot \dot{\theta} - \bar{v})\hat{x} - R\sin\theta \cdot \dot{\theta} \hat{y}\]בתחתית הקשת ($\theta = 0$):
\[\vec{v}_{rel} = (R\dot{\theta}(0) - \bar{v})\hat{x} = -\bar{v}\hat{x}\]כי בתחתית $\dot{\theta}(0) = 0$ (נקודת קיצון).
שאלה מתרגיל 8-7 (מערכת קפיץ-מסה בנוזל)
אימות תנאי ההתחלה עבור הפתרון של מיימון
עבור $x(t) = Ae^{-\gamma t} + Bte^{-\gamma t}$ עם תנאי התחלה $x(0) = 0$, $\dot{x}(0) = v_0$:
- $x(0) = A = 0$
- $\dot{x}(t) = -\gamma A e^{-\gamma t} + Be^{-\gamma t} - \gamma Bte^{-\gamma t}$
- $\dot{x}(0) = -\gamma A + B = B = v_0$
אכן מקבלים $A = 0$, $B = v_0$ ✓
שאלה מתרגיל 11-9 (הקליע והבול)
מהו וקטור המתיחות בחוט כאשר הבול עם הקליע תקוע בתוכו נמצא בנקודה הנמוכה ביותר?
פתרון:
בנקודה הנמוכה ביותר ($\theta = 0$):
- המהירות מקסימלית: $v = L\omega\theta_0$ (כי $\dot{\theta}_{max} = \omega\theta_0$)
- התאוצה הצנטריפיטלית: $a_c = \frac{v^2}{L} = L\omega^2\theta_0^2$
מאיזון כוחות בכיוון הרדיאלי:
\[T - (m+M)g = (m+M)a_c\]לכן:
\[T = (m+M)(g + L\omega^2\theta_0^2) = (m+M)g(1 + \theta_0^2)\]כי $\omega^2 = \frac{g}{L}$.
וקטור המתיחות:
\[\vec{T} = -(m+M)g(1 + \theta_0^2)\hat{r}\]הסימן השלילי כי המתיחות מכוונת לעבר מרכז המעגל (נגד כיוון $\hat{r}$).
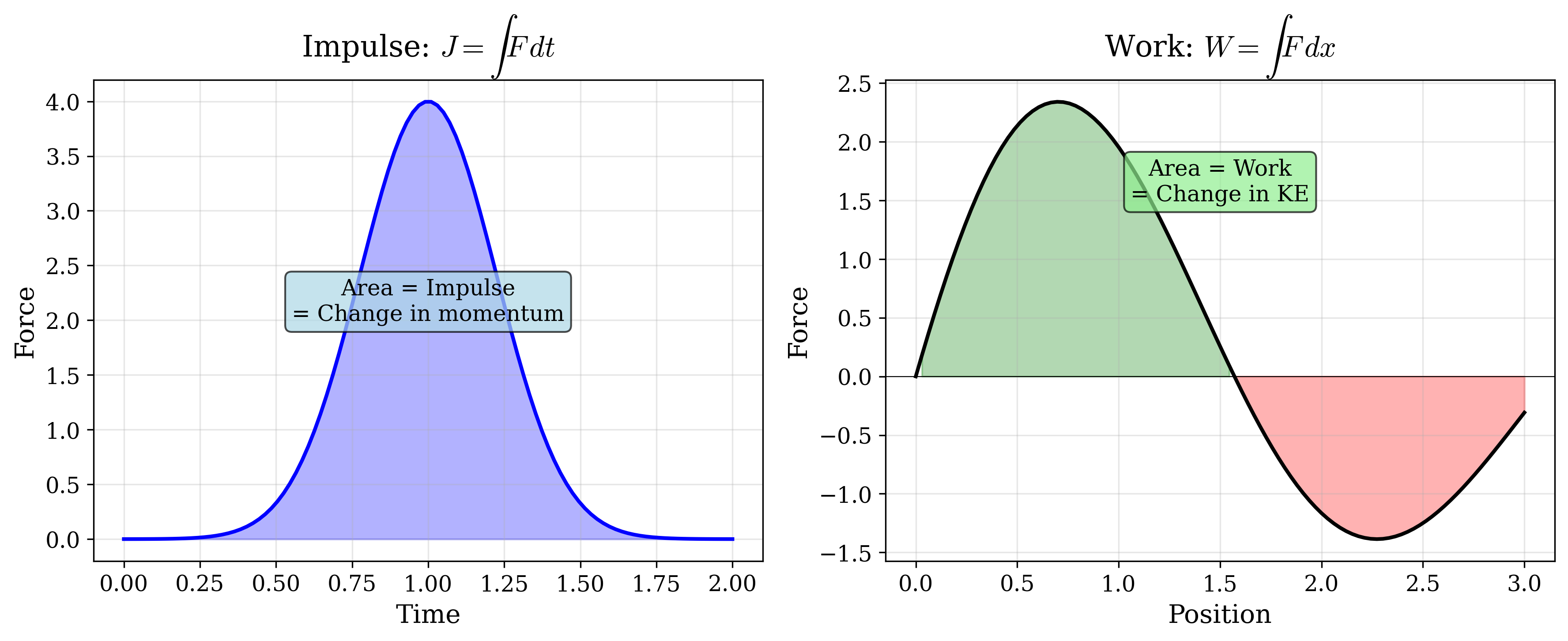
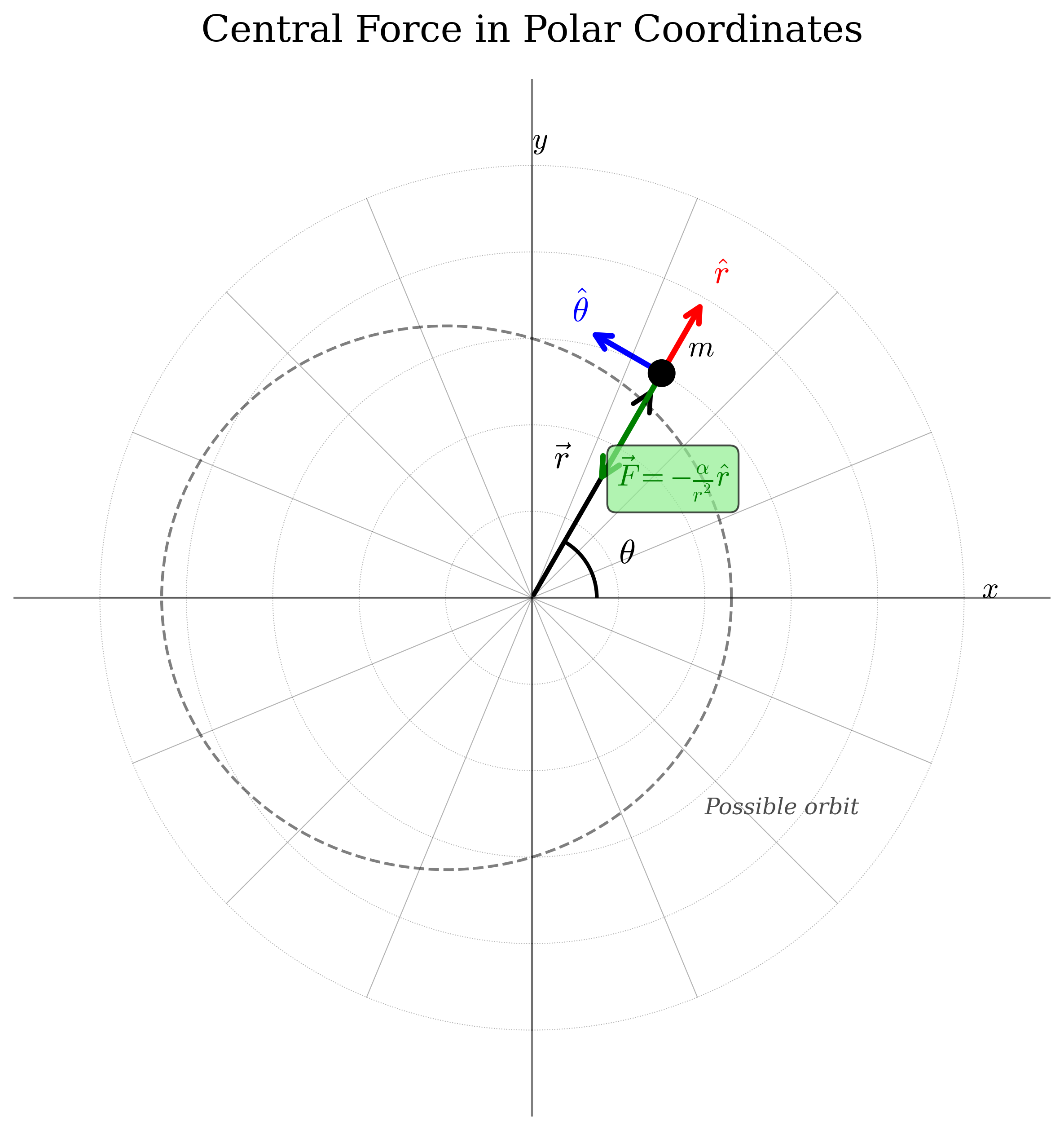
גרפים נחמדים שאולי יסייעו:
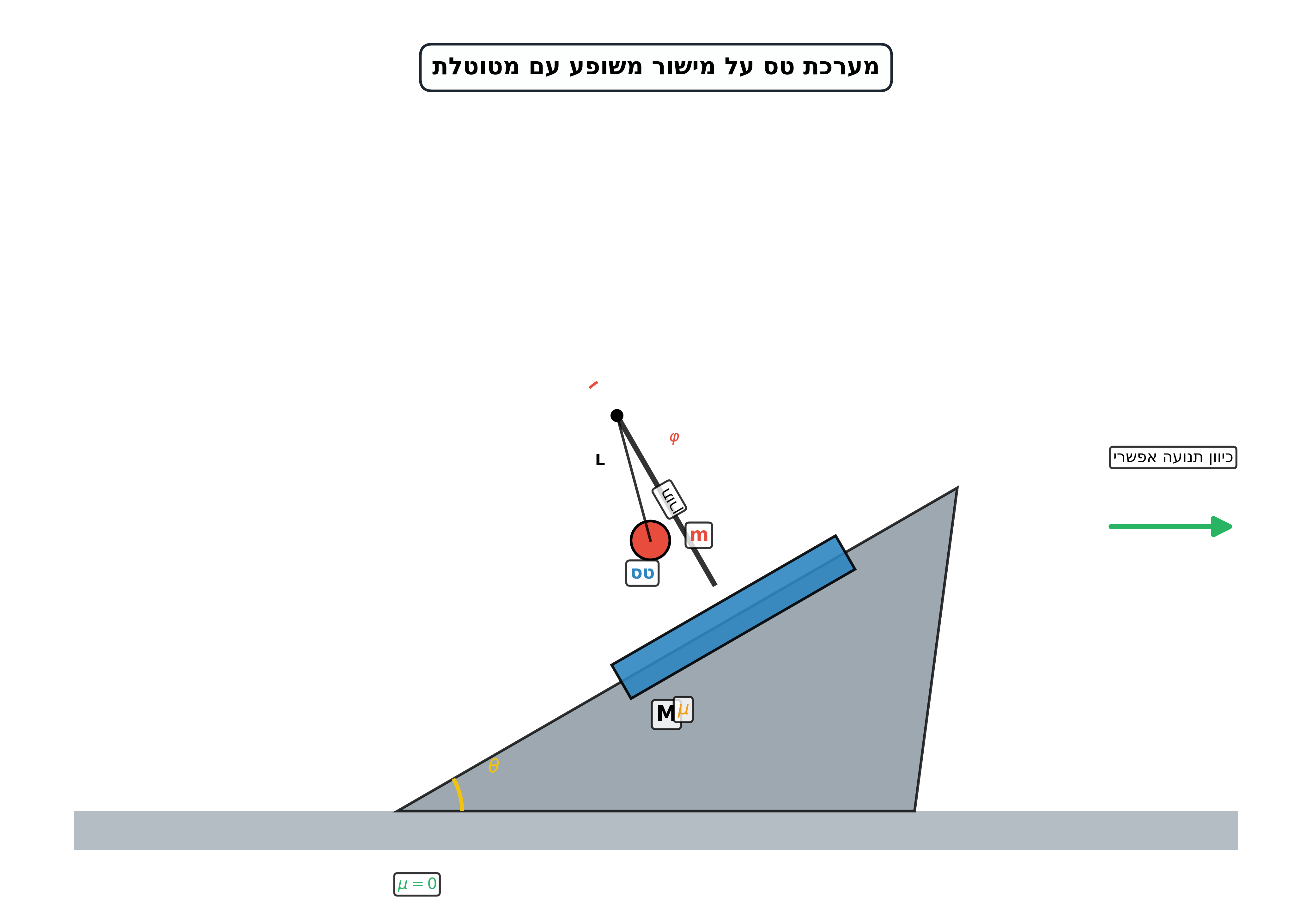
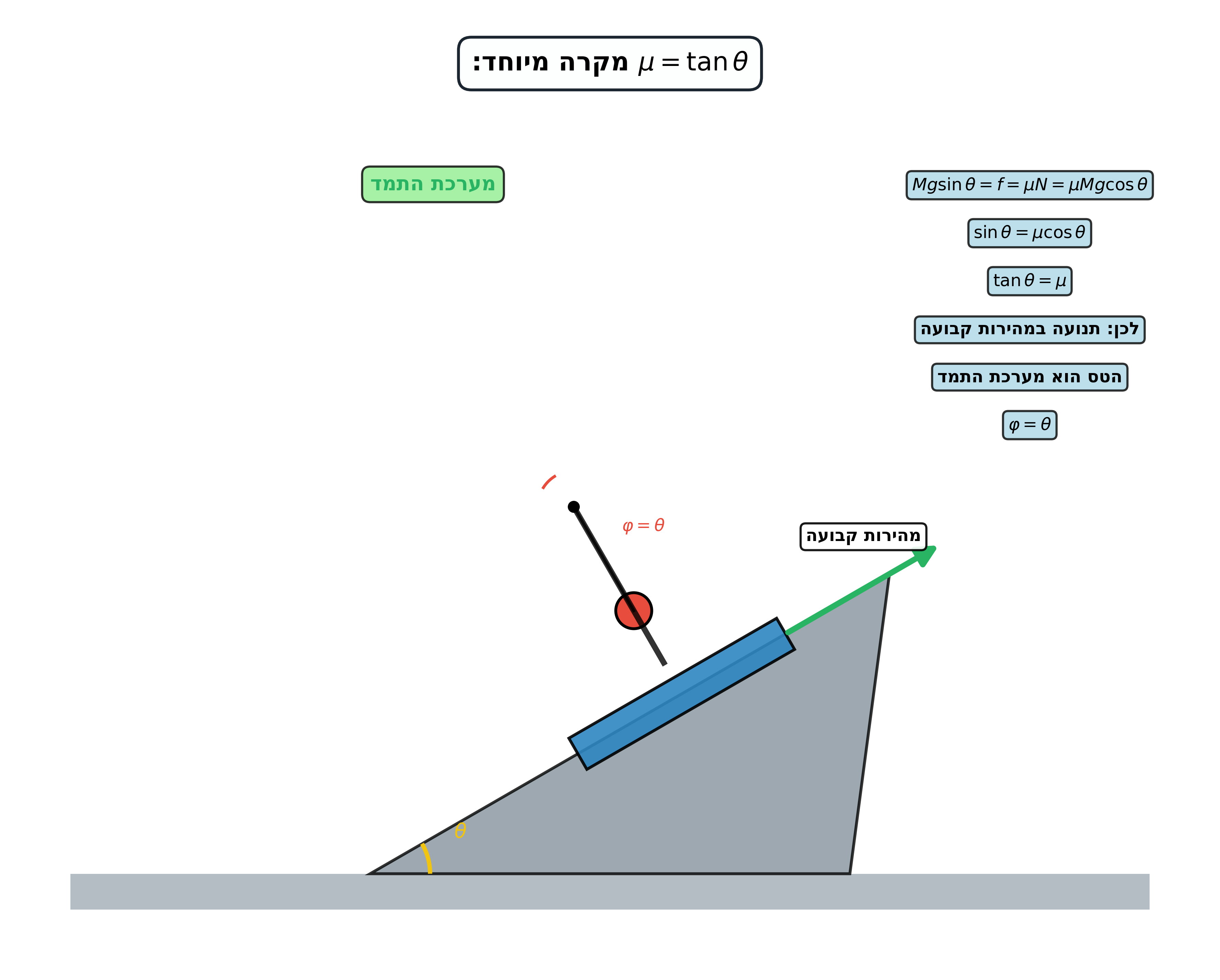
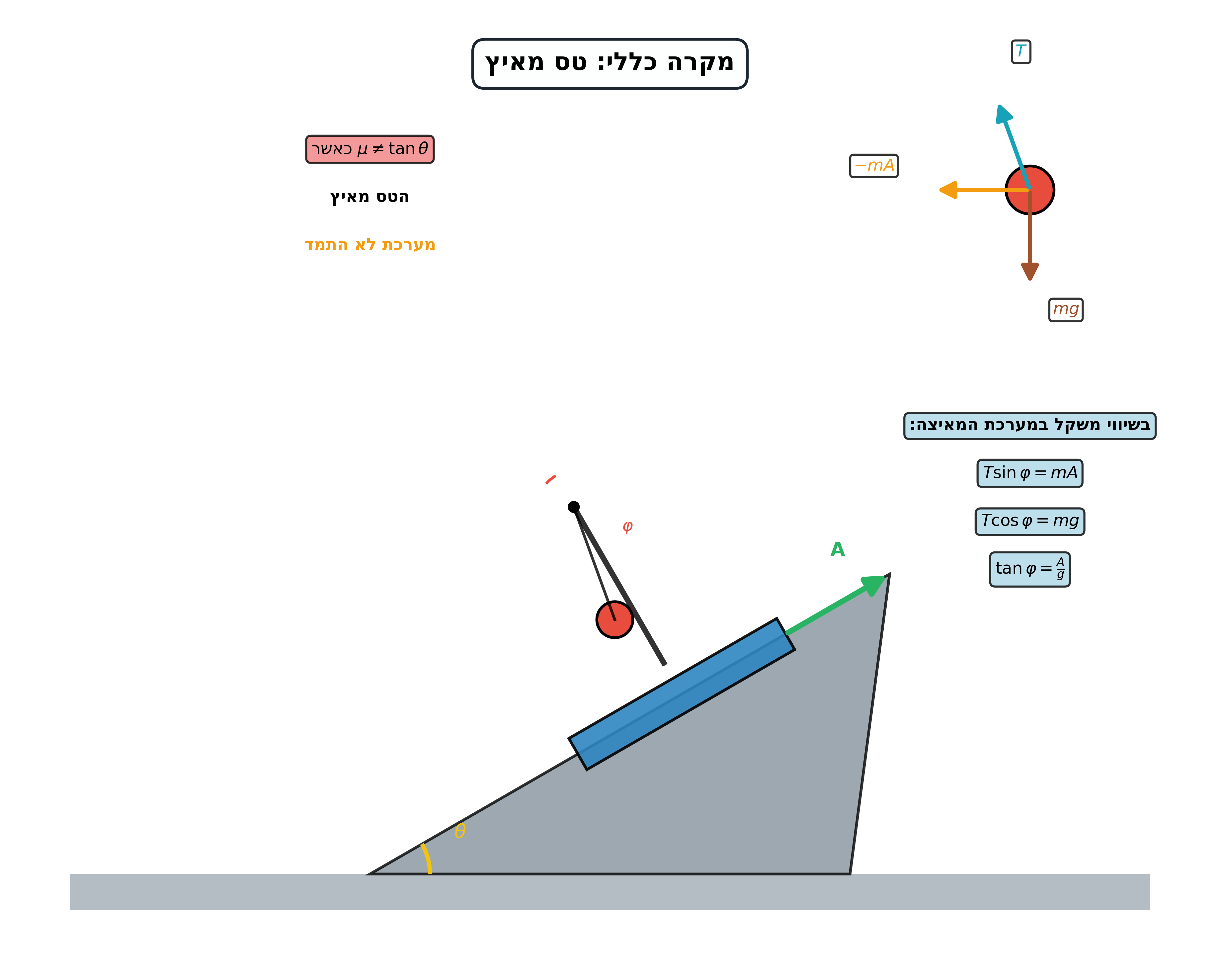
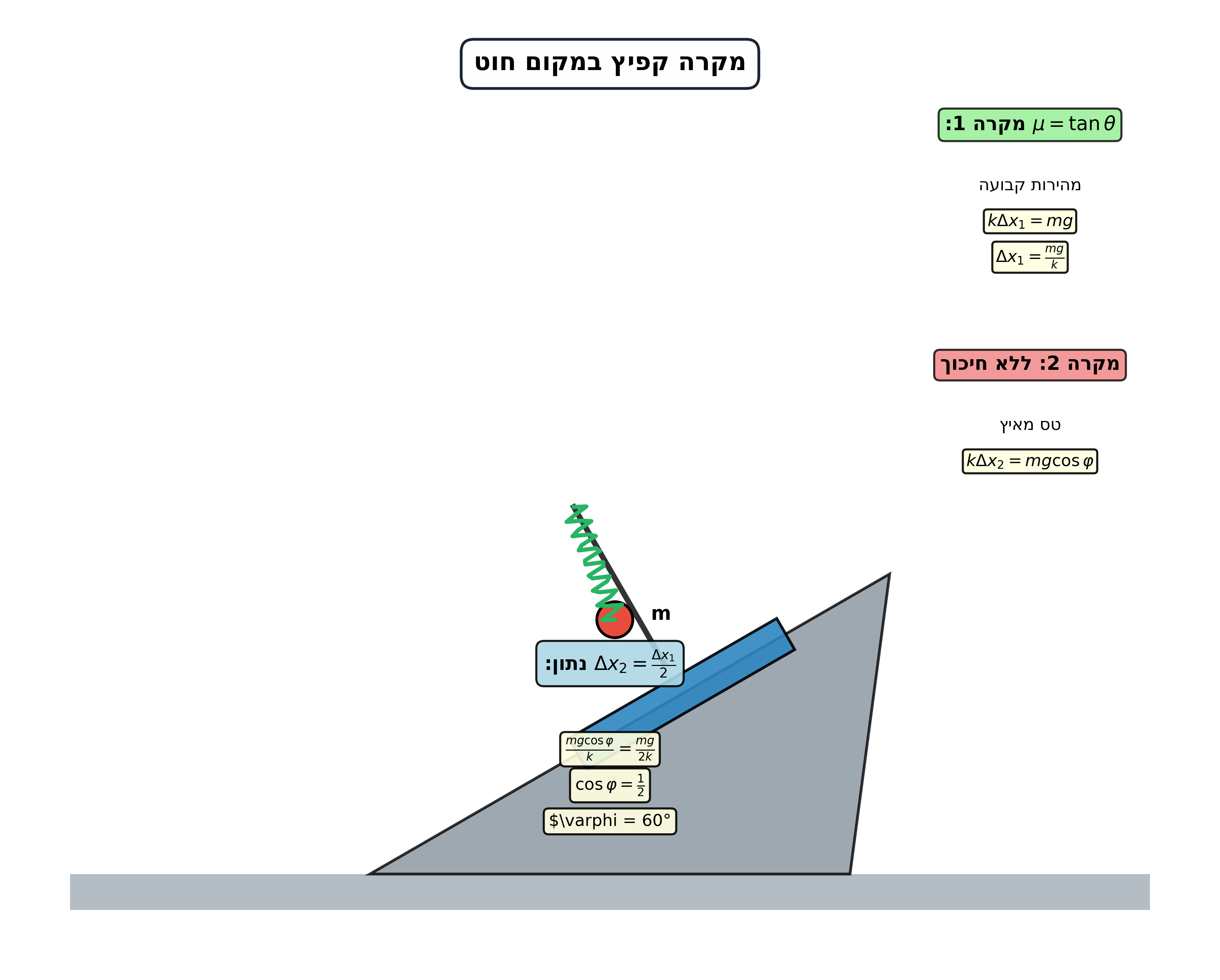
בעיית החבל:
דור פסקל