מעבר מההתפלגות הנורמלית להתפלגות t-Student
התפלגות t-Student: מאפיינים בסיסיים
כאשר גודל המדגם קטן (בדרך כלל $n < 30$), אין באפשרותנו להסתמך על משפט הגבול המרכזי כדי להניח התפלגות נורמלית של ממוצע המדגם. במקרים אלה, אנו פונים להתפלגות t-Student, המאופיינת במספר תכונות חשובות:
מאפיינים מתמטיים:
- התפלגות t-Student דומה להתפלגות הנורמלית אך רחבה יותר
- הרוחב של ההתפלגות תלוי במספר דרגות החופש
- ככל שמספר דרגות החופש גדל, ההתפלגות מתקרבת להתפלגות הנורמלית הסטנדרטית
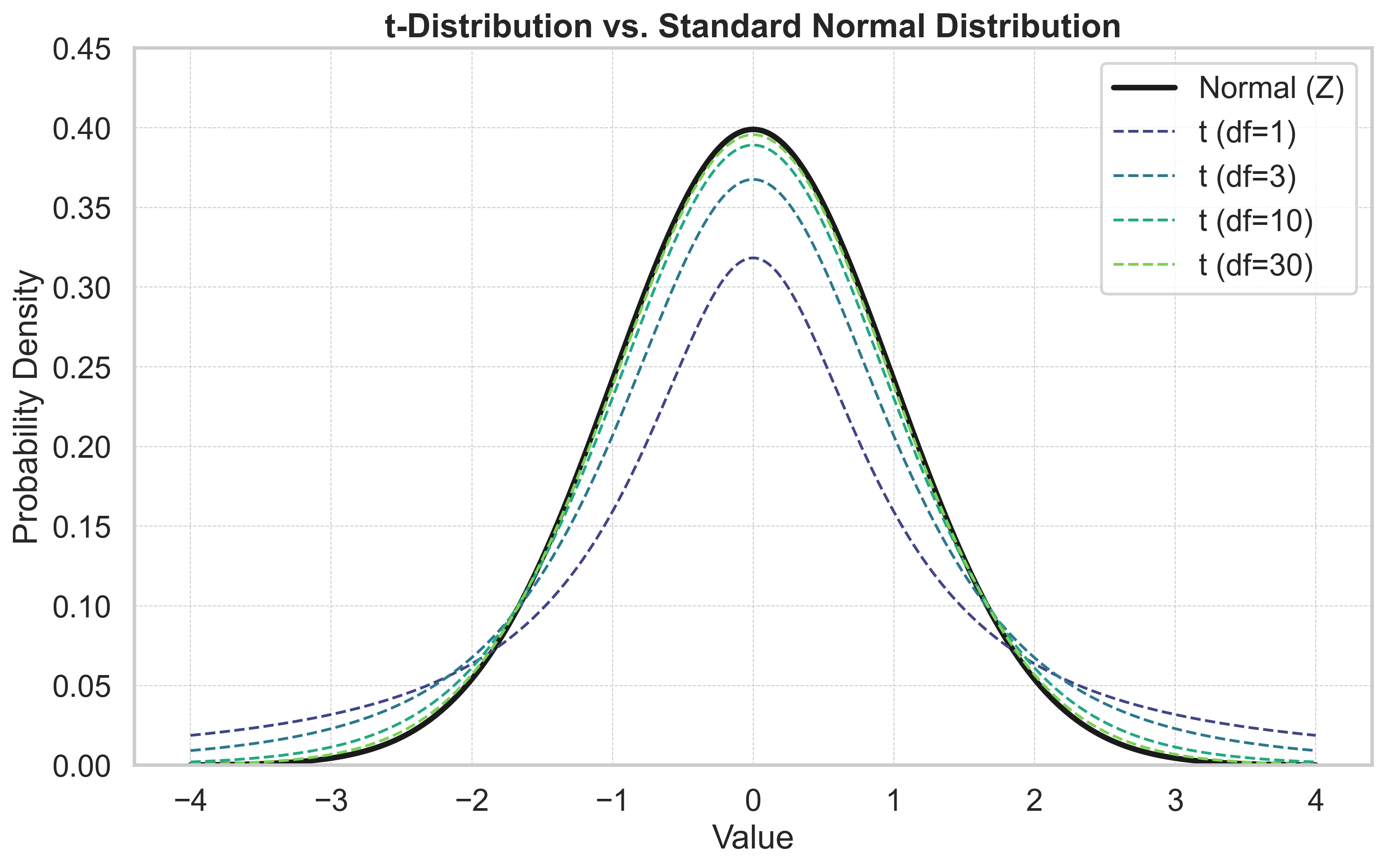
דרגות חופש: הגדרה ומשמעות
דרגות החופש מוגדרות כ-$df = n - 1$, כאשר $n$ הוא גודל המדגם. ההיגיון מאחורי חיסור 1 נובע מהעובדה שכאשר אנו מעריכים את הממוצע מהמדגם, התוצאה האחרונה “מוגבלת” על ידי התוחלת שכבר קבעה, ולכן יש לנו רק $n-1$ ערכים “חופשיים”.
הקשר בין דרגות החופש לחישוב השונות:
\[s^2 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}\]חלוקה ב-$(n-1)$ במקום ב-$n$ מבטיחה שהאמידה של השונות תהיה בלתי מוטה (unbiased).
תנאי יישום וקריטריונים לבחירת התפלגות
מתי להשתמש ב-t-Student לעומת ההתפלגות הנורמלית?
התפלגות t-Student מתאימה כאשר:
- גודל המדגם קטן ($n < 30$)
- השונות של האוכלוסייה אינה ידועה
- ניתן להניח שההתפלגות באוכלוסייה היא נורמלית
התפלגות נורמלית מתאימה כאשר:
- גודל המדגם גדול ($n \geq 30$)
- השונות של האוכלוסייה ידועה
- המשפט הגבול המרכזי מבטיח קירוב נורמלי טוב
חישובים מעשיים ב-Excel ו-Python
לחישוב ערכי t מטבלאות או באמצעות תוכנה:
- ב-Excel: שימוש בפונקציה
T.INVאוTINV - ב-Python: שימוש בספריית
scipy.statsעם הפונקציהt.ppf
לדוגמה, עבור דרגות חופש של 11 ורמת מובהקות של 0.025 (לרווח בטחון דו-צדדי של 95%):
\[t_{11,0.975} = 2.201\]רווחי בטחון: תאוריה ויישום
בניית רווח בטחון עבור ממוצע האוכלוסייה
רווח הבטחון עבור ממוצע האוכלוסייה $\mu$ כאשר השונות אינה ידועה:
\[\bar{x} - t_{\alpha/2,n-1} \cdot \frac{s}{\sqrt{n}} \leq \mu \leq \bar{x} + t_{\alpha/2,n-1} \cdot \frac{s}{\sqrt{n}}\]כאשר:
- $\bar{x}$ - ממוצע המדגם
- $s$ - סטיית התקן של המדגם
- $n$ - גודל המדגם
- $t_{\alpha/2,n-1}$ - הערך הקריטי מהתפלגות t-Student
פרשנות סטטיסטית של רווחי בטחון
רווח בטחון של 95% אינו אומר ש”יש סיכוי של 95% שהממוצע האמיתי נמצא ברווח זה”. הפרשנות הנכונה היא:
“אם נחזור על תהליך הדגימה ובניית רווח הבטחון פעמים רבות, 95% מהרווחים שנבנה יכילו את הממוצע האמיתי של האוכלוסייה.”
דוגמה מפורטת: הערכת צפיפות צדפות בשונית
תיאור הבעיה
סטודנט חוקר רוצה להעריך את תוחלת מספר הצדפות למטר רבוע בשונית מסוימת. לשם כך הוא דוגם 12 קוודרטים (כל אחד בגודל מטר רבוע) ומונה את מספר הצדפות בכל קוודרט.
נתונים:
- גודל מדגם: $n = 12$
- ממוצע המדגם: $\bar{x} = 6.0$ צדפות למטר רבוע
- סטיית תקן של המדגם: $s = 2.985$
- נתון: ניתן להניח שההתפלגות באוכלוסייה נורמלית
- דרישה: בניית רווח בטחון ברמה של 95%
פתרון שלב אחר שלב
שלב 1: זיהוי הבעיה הסטטיסטית מכיוון ש-$n = 12 < 30$ והשונות אינה ידועה, נשתמש בהתפלגות t-Student.
שלב 2: קביעת דרגות החופש
\[df = n - 1 = 12 - 1 = 11\]שלב 3: מציאת הערך הקריטי עבור רווח בטחון של 95%, $\alpha = 0.05$ ולכן $\alpha/2 = 0.025$. מתוך טבלת t-Student או באמצעות תוכנה:
\[t_{11,0.975} = 2.201\]שלב 4: חישוב רווח הבטחון
\[\begin{aligned} \text{Confidence interval} &= \bar{x} \pm t_{\alpha/2,n-1} \cdot \frac{s}{\sqrt{n}} \\ &= 6.0 \pm 2.201 \cdot \frac{2.985}{\sqrt{12}} \\ &= 6.0 \pm 2.201 \cdot \frac{2.985}{3.464} \\ &= 6.0 \pm 2.201 \cdot 0.862 \\ &= 6.0 \pm 1.897 \end{aligned}\]התוצאה הסופית:
\[\boxed{4.103 \leq \mu \leq 7.897}\]פרשנות התוצאות
ניתן לומר ברמת בטחון של 95% שהממוצע האמיתי של מספר הצדפות למטר רבוע בשונית זו נמצא בין 4.1 ל-7.9 צדפות. זוהי הדרך המדעית הנכונה להציג תוצאות מדידה - לא כערך נקודתי אלא כטווח של ערכים אפשריים עם רמת בטחון מוגדרת.
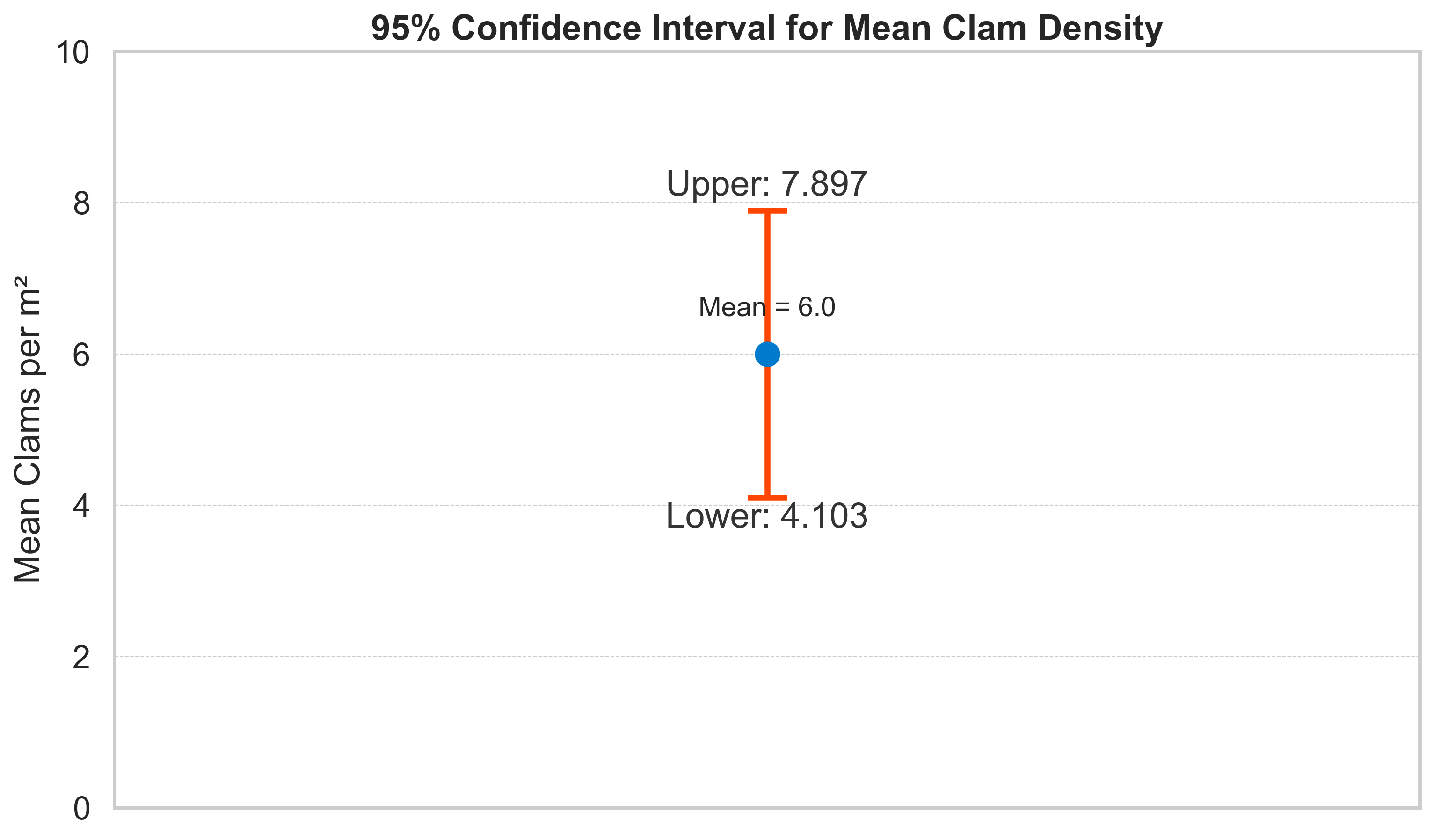
השפעת רמת הבטחון על רוחב הרווח
ככל שמבקשים רמת בטחון גבוהה יותר (למשל 99% במקום 95%), הערך הקריטי $t_{\alpha/2,n-1}$ גדל, וכתוצאה מכך הרווח הופך רחב יותר. זו הדילמה הסטטיסטית הבסיסית בין דיוק (רווח צר) לבין ודאות (רמת בטחון גבוהה).
עבור רמת בטחון של 99%:
\[t_{11,0.995} = 3.106\]הרווח יהיה:
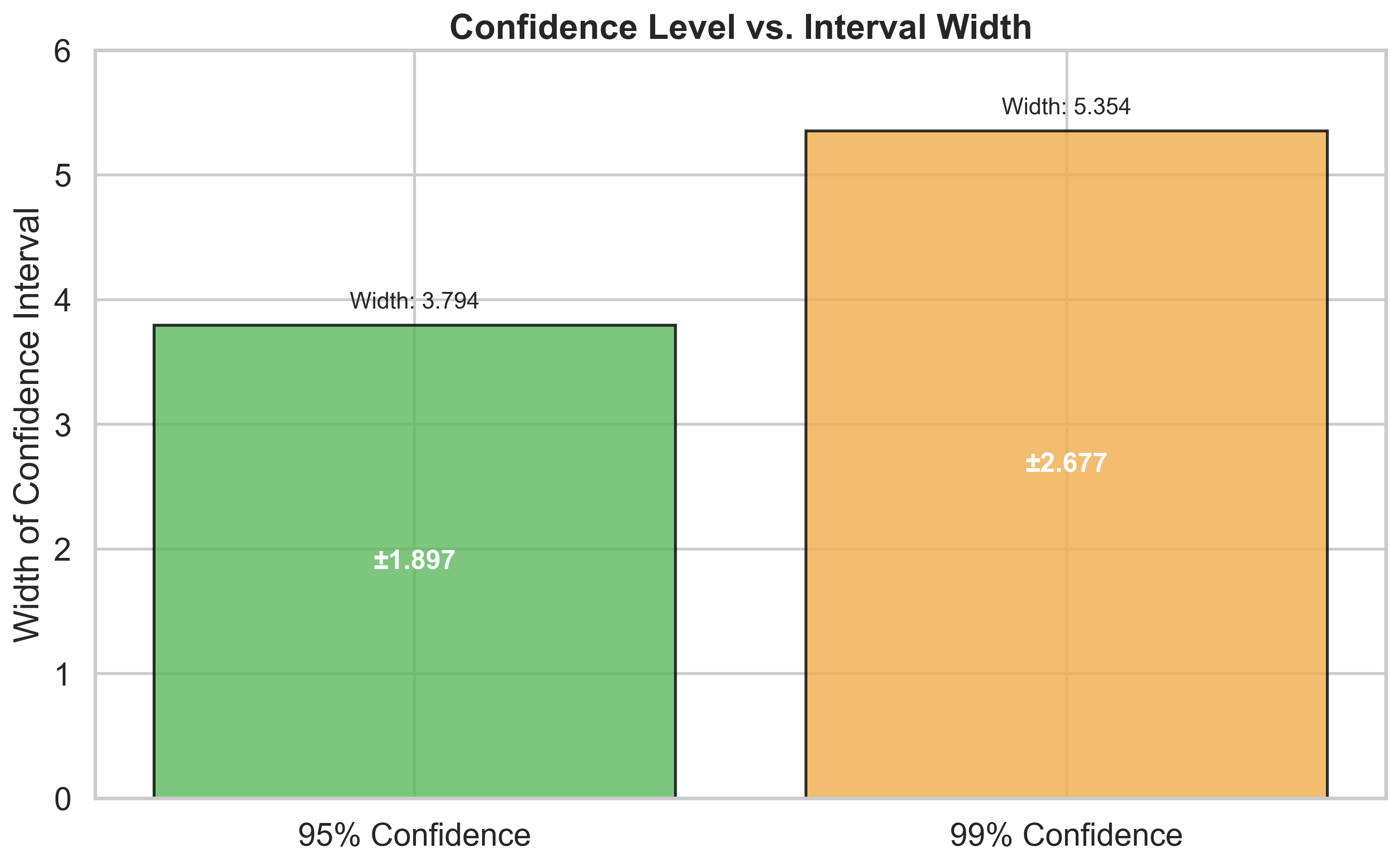
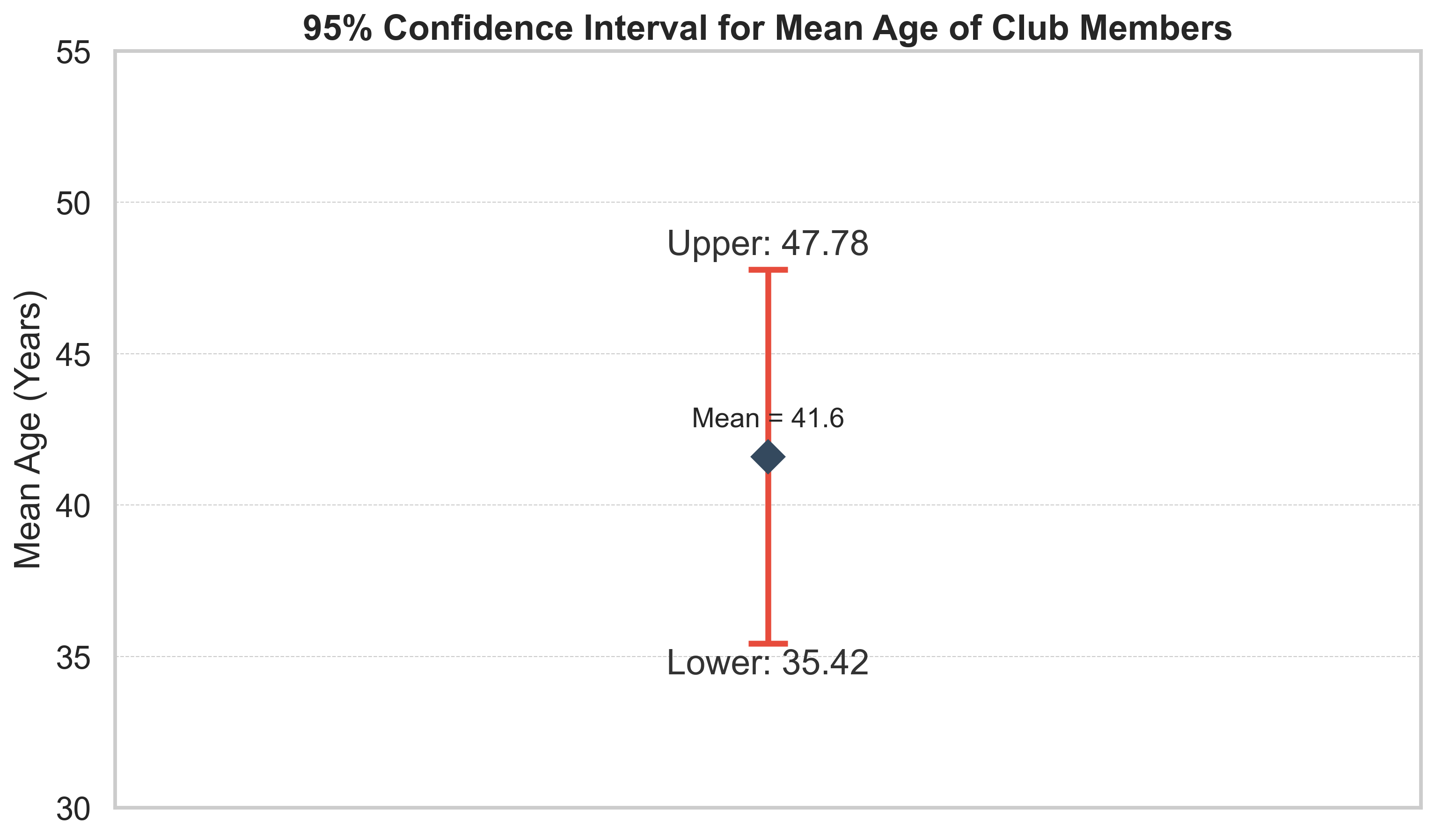
\[6.0 \pm 3.106 \cdot 0.862 = 6.0 \pm 2.677\] \[3.323 \leq \mu \leq 8.677\]דוגמה נוספת: הערכת גיל ממוצע בקרב חברי מועדון
תיאור הבעיה השנייה
מנהל מועדון מעוניין להעריך את הגיל הממוצע של קהל היעד שלו. לשם כך נדגמו 10 חברי מועדון שנבחרו באקראי, והתקבלו הנתונים הבאים:
נתוני המדגם:
- גודל מדגם: $n = 10$
- ממוצע המדגם: $\bar{x} = 41.6$ שנים
- סטיית תקן של המדגם: $s = 8.64$ שנים
- נתון: גיל חברי המועדון מתפלג נורמלית באוכלוסייה
המטרה: בניית רווח בטחון ברמה של 95% לתוחלת הגיל של חברי המועדון.
התמודדות עם הנחת הנורמליות
חשוב לציין כי ההנחה שגיל מתפלג נורמלית היא קירוב בלבד. מבחינה תאורטית, גיל הוא משתנה חיובי בהכרח, בעוד שההתפלגות הנורמלית מתפרשת מ-$-\infty$ עד $+\infty$. עם זאת, כאשר הממוצע גדול מספיק יחסית לסטיית התקן (כלל אצבע: לפחות 3 סטיות תקן מעל האפס), הקירוב הנורמלי נותר תקף למטרות מעשיות.
במקרה הנוכחי: $\frac{\bar{x}}{s} = \frac{41.6}{8.64} \approx 4.8$, מה שמצביע על כך שההנחה סבירה.
פתרון המקרה השני
שלב 1: זיהוי הפרמטרים הסטטיסטיים
- $n = 10 < 30$ ← נשתמש בהתפלגות t-Student
- דרגות חופש: $df = n - 1 = 9$
שלב 2: מציאת הערך הקריטי עבור רווח בטחון של 95% ו-9 דרגות חופש:
\[t_{9,0.975} = 2.262\]שלב 3: חישוב רווח הבטחון
\[\begin{aligned} \text{Confidence interval} &= 41.6 \pm 2.262 \cdot \frac{8.64}{\sqrt{10}} \\ &= 41.6 \pm 2.262 \cdot 2.73 \\ &= 41.6 \pm 6.18 \end{aligned}\]התוצאה: $\boxed{35.42 \leq \mu \leq 47.78}$
ניתוח השגיאה המרבית
השגיאה המרבית בהערכה היא $6.18$ שנים. זה אומר שברמת בטחון של 95%, הגיל הממוצע האמיתי של חברי המועדון נמצא במרחק של לכל היותר 6.18 שנים מהאמידה שלנו (41.6 שנים).
מעבר לרווחי בטחון עבור פרופורציות
הבסיס התאורטי להתפלגות פרופורציות
כאשר עוברים מהערכת ממוצעים להערכת פרופורציות, המבנה המתמטי משתנה באופן מהותי. עבור פרופורציה $p$ באוכלוסייה, המשתנה הבסיסי הוא בינומי עם פרמטרים $n$ ו-$p$.
התכונות הסטטיסטיות של פרופורציית המדגם:
- תוחלת: $E[\hat{p}] = p$
- שונות: $\text{Var}[\hat{p}] = \frac{p(1-p)}{n}$
- סטיית תקן: $\sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}}$
תנאי יישום הקירוב הנורמלי
בעבור מדגמים גדולים, ניתן להשתמש במשפט הגבולי המרכזי כדי לקרב את התפלגות $\hat{p}$ להתפלגות נורמלית. התנאים הנדרשים:
- $np \geq 5$ ו-$n(1-p) \geq 5$
כאשר תנאים אלה מתקיימים, ההתפלגות הבינומית מתקרבת להתפלגות נורמלית, ובכך מאפשרת שימוש בערכי $z$ במקום בערכי $t$.
נוסחת רווח הבטחון לפרופורציות
הנוסחה הכללית לרווח בטחון עבור פרופורציה:
\[\hat{p} - z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p} + z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]כאשר:
- $\hat{p}$ - פרופורציית המדגם
- $z_{\alpha/2}$ - הערך הקריטי מההתפלגות הנורמלית הסטנדרטית
- השורש מבטא את סטיית התקן המוערכת של פרופורציית המדגם
דוגמה מעשית: סקר פוליטי
תיאור הבעיה
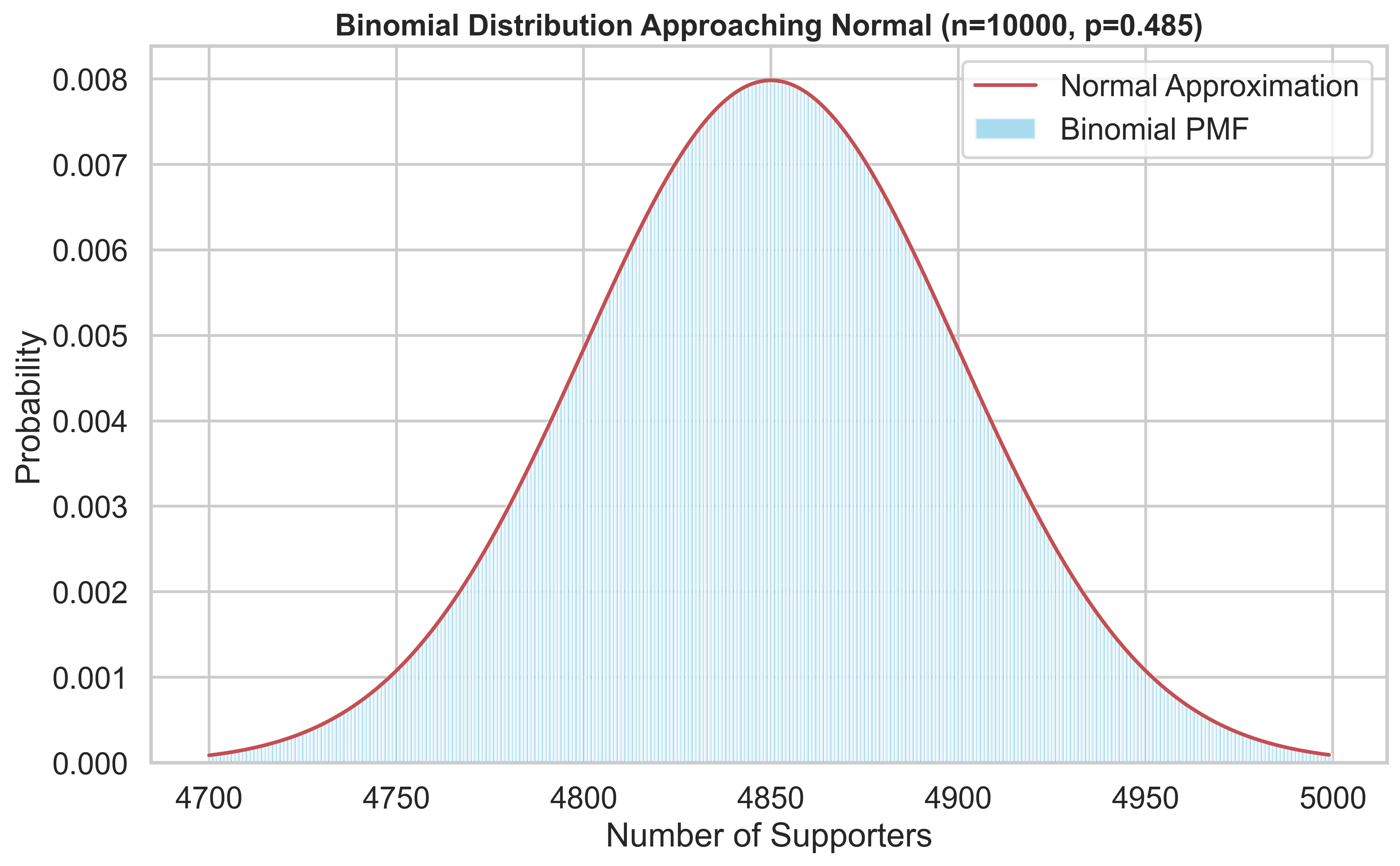
סטטיסטיקאי מדיני רוצה להעריך את שיעור התמיכה במועמד מסוים. נערך סקר בקרב 10,000 מצביעים אקראיים, מתוכם 4,850 הצהירו שהם יצביעו עבור המועמד.
נתוני הסקר:
- גודל מדגם: $n = 10,000$
- מספר תומכים: $x = 4,850$
- פרופורציית המדגם: $\hat{p} = \frac{4,850}{10,000} = 0.485$
- דרישה: רווח בטחון ברמה של 99%
בדיקת תנאי הקירוב הנורמלי
\[n\hat{p} = 10,000 \times 0.485 = 4,850 > 5 \checkmark\] \[n(1-\hat{p}) = 10,000 \times 0.515 = 5,150 > 5 \checkmark\]שני התנאים מתקיימים באופן ברור, ולכן ניתן להשתמש בקירוב הנורמלי.
פתרון הסקר הפוליטי
שלב 1: מציאת הערך הקריטי עבור רווח בטחון של 99%: $\alpha = 0.01$, $\alpha/2 = 0.005$
\[z_{0.005} = z_{0.995} = 2.576\]שלב 2: חישוב סטיית התקן המוערכת
\[\hat{\sigma}_{\hat{p}} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = \sqrt{\frac{0.485 \times 0.515}{10,000}} = \sqrt{\frac{0.2498}{10,000}} = 0.005\]שלב 3: בניית רווח הבטחון
\[0.485 \pm 2.576 \times 0.005 = 0.485 \pm 0.0129\]התוצאה הסופית:
\[0.472 \leq p \leq 0.498\]פרשנות פוליטית של התוצאות
התוצאה מצביעה על כך שברמת בטחון של 99%, שיעור התמיכה האמיתי במועמד נמצא בין 47.2% ל-49.8%. זהו טווח משמעותי מבחינה פוליטית, מכיוון שהוא כולל הן את האפשרות שהמועמד זוכה (מעל 50%) והן את האפשרות שהוא מפסיד (מתחת ל-50%).
התמודדות עם אי-ודאות במקרים של פרופורציה לא ידועה
הבעיה של פרופורציה לא ידועה מראש
במקרים שבהם אין לנו מידע מקדים על הפרופורציה הצפויה, מתעוררת בעיה בחישוב גודל המדגם הנדרש או ברוחב רווח הבטחון. במצבים אלה, נהוג להשתמש בגישה השמרנית של $\hat{p} = 0.5$.
הצדקה מתמטית: הביטוי $p(1-p)$ מגיע לערכו המקסימלי כאשר $p = 0.5$:
\[\max_{p} [p(1-p)] = 0.5 \times 0.5 = 0.25\]שימוש בערך זה מבטיח שרווח הבטחון יהיה רחב מספיק לכסות את כל המקרים האפשריים.
שיקולים מעשיים בסקרים פוליטיים
מקורות הטיה בסקרי דעת קהל
הדיון על הסקר הפוליטי מעלה שאלות חשובות על מהימנות התוצאות. מקורות הטיה עיקריים כוללים:
- הטיית תגובה: מצביעים עשויים לא לחשוף את כוונותיהם האמיתיות
- הטיית דגימה: קושי בהגעה לייצוג אמיתי של כלל האוכלוסייה
- אפקט המרואיין הביישן: נטייה להסתיר תמיכה במועמדים שנויים במחלוקת
- שיקולי אסטרטגיה: מצביעים עשויים לטעון לתמיכה במועמד מסוים כדי להשפיע על תפיסת הציבור
משמעות הרווח הסטטיסטי במציאות הפוליטית
חשוב להבין שרווח הבטחון הסטטיסטי מתייחס אך ורק לשגיאת הדגימה האקראית. הוא אינו לוקח בחשבון הטיות שיטתיות או שגיאות מדידה, המהוות לעתים קרובות מקור שגיאה משמעותי יותר בסקרי דעת קהל.
דור פסקללשיעור בנושא רווח סמך