לחץ על הכרטיסים כדי לנווט בעץ
בחר את סוג הניתוח הסטטיסטי שברצונך לבצע
X̄ ± Zα/2 · σ/√nX̄ ± Zα/2 · s/√nX̄ ± tα/2(n-1) · s/√np̄ ± Zα/2 · √[p̄(1-p̄)/n]P(X=k) = C(n,k)pk(1-p)n-k"]
%% Hypothesis Testing Branch
Hypothesis --> HypPop{"כמה אוכלוסיות?"}
HypPop -->|1️⃣| HypOne["אוכלוסייה אחתZ = (X̄ - μ₀)/(s/√n)Z = (X̄ - μ₀)/(σ/√n)t = (X̄ - μ₀)/(s/√n)Z = (p̄ - p₀)/√[p₀(1-p₀)/n]Di = Xi(1) - Xi(2)Z = D̄/(sD/√n)t = D̄/(sD/√n)Z = (X̄₁ - X̄₂)/(σ√(1/n₁ + 1/n₂))Z = (X̄₁ - X̄₂)/(sp√(1/n₁ + 1/n₂))sp² = [(n₁-1)s₁² + (n₂-1)s₂²]/(n₁+n₂-2)"]
HypTwoUnknownSize -->|לא - לפחות אחד קטן| HypTwoSmallNormal{"נורמלי בשתיt = (X̄₁ - X̄₂)/(sp√(1/n₁ + 1/n₂))למיטב ידיעתנו לא פורסם לקורס סילבוס באתר האוניברסיטה.
נושאי הקורס בהתאם לתכני התרגולים והשיעורים:
פרויקט גמר בסטטיסטיקה לרפואנים תשפ״ה: ניתוח השפעת מגדר על דיכאון בקרב 3,387 סטודנטים לרפואה. המחקר מצא כי אין הבדל מובהק סטטיסטית בין סטודנטיות לסטודנטים ברמות הדיכאון. כולל שיטות מחקר, ניתוחים סטטיסטיים, מסקנות והמלצות להמשך.
מבחן בסטטיסטיקה לרפואה עם פתרונות: רווח סמך, p-value, רגרסיה, הסתברות, בדיקות t, χ², ורגרסיה. כולל חישובים ודוגמאות קוד.
הסבר חזותי ומעשי להסקה סטטיסטית: זיהוי התפלגות מתאימה (Z או t), שימוש ב-ISF לבניית רווח סמך, ודוגמאות עם פסיכומטרי ומשלוחים.
מבחני סטטיסטיקה לרפואה עם פתרונות: רווח סמך, p-value, רגרסיה, הסתברות, בדיקות t, χ², ורגרסיה. כולל חישובים ודוגמאות קוד.
דף נוסחאות לסטטיסטיקה לרפואנים, כולל קירובים, מדדי מרכז ופיזור, טרנספורמציות לינאריות, רגרסיה לינארית ומרובה, התפלגויות דיסקרטיות ורציפות, שגיאות תקן, רווחי סמך, בדיקת השערות ועוד.
סיכום שיעור על רגרסיה לינארית מרובה, כולל חזרה על רגרסיה פשוטה, פירוק שונות, R-squared, ובניית מודל ב-Python עם statsmodels לפירוש מקדמים, רווחי סמך וחישוב p-value.
סקירת יסודות ניתוח הישרדות - פונקציית S(t), חציון ורבעונים, קפלן-מאייר עם צנזורה, מבחן לוג-רנק, דוגמאות רפואיות וטיפים מעשיים למטלות בקורס.
שאלות פתורות על הסקה סטטיסטית, וחישובי הסתברות (בייס, גיאומטרית, מעריכית), רגרסיה, רווח סמך ומבחני t. כולל בחינת מודל רגרסיה לינארית, חישוב רווח סמך, והסקת מסקנות ממבחן t.
סיכום שיעור סטטיסטיקה על משתנים קטגוריאליים, Relative Risk ו-Odds Ratio, כולל רווח סמך לוג-נורמלי ודוגמאות כמו הטיטאניק, הקורונה והאחות הרוצחת קריסטן גילברט.
הקדמה למשתנים קטגוריאליים ולמבחני קשר ביניהם, כולל טבלאות שכיחויות, מבחן חי-ריבוע, תנאי תקפות, טיב התאמה, ודוגמה משפטית מתוקשרת על אחות שרצחה מטופלים.
מבחני השערות למדגמים מזווגים - ההיגיון התיאורטי, פיתוח סטטיסטי של מבחן t, דוגמאות חישוביות, השוואה למדגמים בלתי תלויים, עץ החלטה והמלצות ליישום.
בדיקת השערות עבור פרופורציה, בדיקת השערות עם שונות לא ידועה, חזרה על הבסיס לבדיקות השערות - מבחן Z, חישוב P-value, רווחי סמך, בדיקת פרופורציות, p-hacking, ודגש על שקיפות ומניעת מניפולציות סטטיסטיות.
בדיקת השערות סטטיסטית - ניסוח של השארת האפס, חישוב P-value, קבלת החלטה לפי רמת מובהקות, טעויות מסוג I ו־II, השפעת גודל המדגם ועוצמת המבחן.
מעבר מהתפלגות נורמלית ל-t - שימוש כש-n קטן מ-30 או השונות אינה ידועה. רווחי סמך, דרגות חופש, SF ו-PPF, ודוגמאות עם Python ו-Excel.
הערכת פרופורציות באוכלוסייה, בניית רווחי סמך, בדיקת השערות, חישוב P-value והקשרים בין הערכה לדחיית השערות.
יסודות ההסקה הסטטיסטית - אומדן ובדיקת השערות, תוחלת, שונות, סטיית תקן, משפט הגבול המרכזי ורווחי סמך. כולל דוגמאות רפואיות.
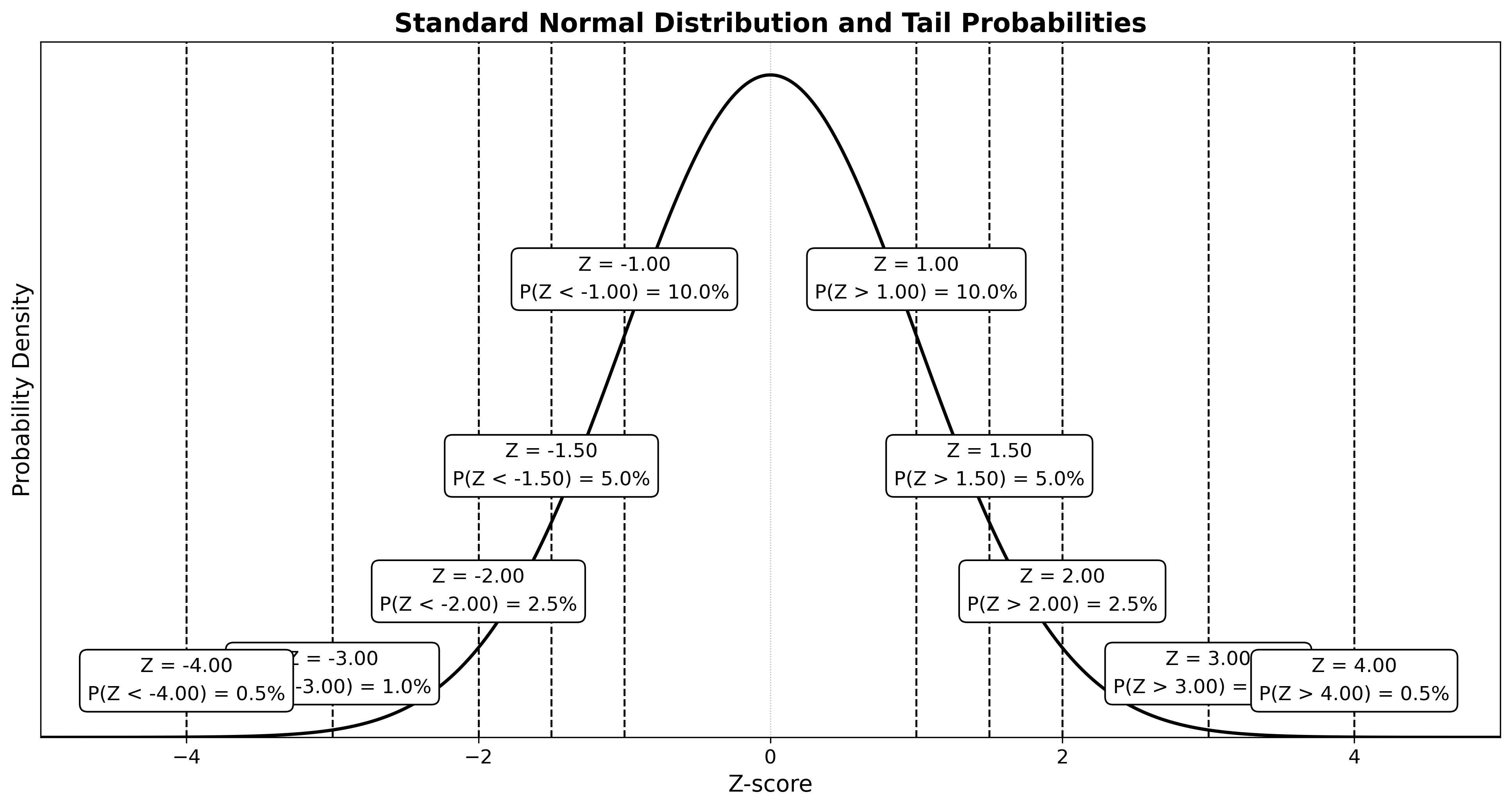
הסבר על התפלגות נורמלית - ערכים קריטיים, הסתברויות, סטיית תקן, דוגמת משקל תינוקות, קירוב לבינומית, ומשמעות סטטיסטית בהשוואת קבוצות.
הסבר על התפלגות נורמלית - ערכים קריטיים, הסתברויות, סטיית תקן, דוגמת משקל תינוקות, קירוב לבינומית, ומשמעות סטטיסטית בהשוואת קבוצות.
פתרון מטלה 1 בקורס סטטיסטיקה לרפואנים. הוכחה של נוסחת רגרסיה לינארית ללא חותך, כולל גזירה ידנית ומימוש ב־Python עם statsmodels, לצד תרגול הסתברות עם כדורים ותרחישי הישרדות.
כלל בייז בדיאגנוסטיקה – בדיקות לסרטן ודוגמות, קיצור חישוב, תוחלת, שונות, משתנים מקריים בדידיים, בינומי וברנולי, חישובי דוגמאות ויישומים ועוד.
מבוא להסתברות, מרחב מדגם, מאורעות, כללי כפל, הסתברות מותנית, שונות משותפת, מקדם מתאם של פירסון ורגרסיה ליניארית לניבוי משתנים.
רגרסיה לינארית בסטטיסטיקה רפואית - ניתוח היחסים בין משתנים, שיטת הריבועים הפחותים, הבנת שאריות ומדד טיב התאמה (R²) לבניית מודלים מדויקים.
מדדי קשר - קריטריונים למדד טוב, שונות משותפת והבנה גרפית, מגבלות המדדים, מקדם המתאם של פירסון, וטכניקות לטיפול בקשרים לא לינאריים.
חישוב טווח, ממוצע, שונות וסטיית תקן באקסל, השפעת טרנספורמציות על מדדים סטטיסטיים, מקדם המתאם של פירסון והקשרים בין משתנים, השוואת קבוצות על בסיס מדדים סטטיסטיים, וניתוח גרפי פיזור. המסמכים מבארים את המשמעות המתמטית של המדדים, מציגים נוסחאות ודוגמאות מספריות, ומדגישים מה ניתן ומה לא ניתן להסיק ממקדמי מתאם.
מדדי מיקום (ממוצע, חציון), מדדי פיזור (טווח, שונות, סטיית תקן), אחוזונים, השפעת טרנספורמציות, זיהוי חריגים ותרשימי קופסה.
מבוא לקורס בסטטיסטיקה לרפואה, כולל מידע אדמיניסטרטיבי, חשיבות הסטטיסטיקה הרפואית, סוגי משתנים, סולמות מדידה, התפלגויות, ודרכי הצגה גרפית.