כל התכנים בעמוד אחד
כל הצעות הפתרון למטלות הבית בקורס פיזיקה ב׳ זמינות כאן להדפסה מרוכזת או לייצוא כ-PDF. התוכן מוצג בסדר כרונולוגי - מהסיכומים המוקדמים ביותר למאוחרים ביותר. אם חלק מהעמודים כוללים נוסחאות מתמטיות, ייתכן שייקח להן מספר שניות להיטען. למידה מהנה!
תוכן העניינים
פתרון תרגיל 2 - מטענים חשמליים, שדות חשמליים וחוק גאוס
תאריך: 10/11/2025שאלה 1: השוואת הכוח החשמלי והכוח הכבידתי בין חלקיקים יסודיים
גודלו של כוח הכבידה בין שתי מסות נתון על ידי:
\[F_G = \frac{G m_1 m_2}{r^2}, \quad G = 6.67 \times 10^{-11} \, \mathrm{N \cdot m^2 / kg^2}\]גודלו של הכוח החשמלי בין שני מטענים חשמליים נתון על ידי:
\[F_E = \frac{K q_1 q_2}{r^2}, \quad K = 9 \times 10^9 \, \mathrm{N \cdot m^2 / C^2}\]
בכמה גדול הכוח החשמלי בין שני פרוטונים לעומת הכוח הכבידתי ביניהם?
האם יחס זה תלוי במרחק בין הפרוטונים?
כיצד הייתה משתנה התשובה אם היה מדובר בשני אלקטרונים?
נתונים:
- מטען הפרוטון והאלקטרון: $q = \pm 1.6 \times 10^{-19} \, \mathrm{C}$
- מסת פרוטון: $m_p = 1.7 \times 10^{-27} \, \mathrm{kg}$
- מסת אלקטרון: $m_e = 9.1 \times 10^{-31} \, \mathrm{kg}$
נחשב את הכוח החמשלי לפי הנוסחה ולפי הנתונים.
\[F_E = -\frac{9 \times 10^9 \, \mathrm{N \cdot m^2 / C^2} (1.6 \times 10^{-19} \, \mathrm{C})^2}{r^2}\]לא צריך את הרדיוס כי הוא יצמצם בהמשך.
\[F_G = \frac{6.67 \times 10^{-11} \, \mathrm{N \cdot m^2 / kg^2} \times (1.7 \times 10^{-27} \, \mathrm{kg})^2}{r^2}\]\[\begin{aligned} \frac{F_E}{F_G} &= \frac{\frac{9 \times 10^9 \, \mathrm{N \cdot m^2 / C^2} (1.6 \times 10^{-19} \, \mathrm{C})^2}{r^2}}{\frac{6.67 \times 10^{-11} \, \mathrm{N \cdot m^2 / kg^2} \times (1.7 \times 10^{-27} \, \mathrm{kg})^2}{r^2}} \\ &= \frac{9\times 10^9 \times (1.6 \times 10^{-19})^2}{6.67 \times 10^{-11} \times (1.7 \times 10^{-27})^2} \\ &= \frac{23.04 \times 10^{36}}{19.276} \end{aligned}\]טעות אפשרית - לערבב בין מסת פרוטון לאלקטרון בחישוב המסות:
\[F_G = \frac{6.67 \times 10^{-11} \, \mathrm{N \cdot m^2 / kg^2} \times 1.7 \times 10^{-27} \, \mathrm{kg} \times 9.1 \times 10^{-31} \, \mathrm{kg}}{r^2}\]
סך הכל:
\[\boxed{\frac{F_E}{F_G} \approx 1.195 \times 10^{36}}\]היחס לא תלוי במרחק ($r$ מצטמצם).
אם היה מדובר בשני אלקטרונים:
\[\begin{aligned} \frac{F_E}{F_G} &= \frac{\frac{9 \times 10^9 \, \mathrm{N \cdot m^2 / C^2} (1.6 \times 10^{-19} \, \mathrm{C})^2}{r^2}}{\frac{6.67 \times 10^{-11} \, \mathrm{N \cdot m^2 / kg^2} \times (9.1 \times 10^{-31} \, \mathrm{kg})^2}{r^2}} \\ &= \frac{9\times 10^9 \times (1.6 \times 10^{-19})^2}{6.67 \times 10^{-11} \times (9.1 \times 10^{-31})^2} \cdots \end{aligned}\]סך הכל - הפער גדל כשהמסה גדלה.
שאלה 2: שדה, כוח ותנועה במערכת סימטרית של שני מטענים נקודתיים
שני מטענים נקודתיים זהים ושליליים, בעלי מטען $-q$ כל אחד, מונחים לאורך ישר במרחק של $2d$ מטר זה מזה, כ״א מטר אחד משני צידי הראשית, $\vec{r}_{1,2}=(\pm d)\hat{x}$.
- האם קיימת נקודה במישור בו נמצא הישר אשר בה השדה מתאפס? אם כן מצאו אותה אם לא הסבירו מדוע.
- מהו השדה החשמלי $\vec{E}$ שיוצרים המטענים בנקודה $\vec{r}=b\hat{y}$?
- איזה כוח $\vec{F}$ יפעל על פרוטון שיוב בנקודה זו?
- אלקטרון משוחרר ממנוחה בנקודה זו. איזו תנועה (אפיון וצרה) יבצע?

סעיף א - נקודה בה השדה מתאפס
השדה מתאפס בנקודה על הראשית משיקולי סימטריה.
סעיף ב - השדה החשמלי בנקודה על ציר $y$
משיקולי סימטריה יתאפסו ההשפעות לכיוון ציר $x$ ותהיה רק השפעה לכיוון ציר וואי למטה.
ההשפעה של כל אחד מהמטענים היא:
\[\frac{k (-q)}{r^2}\]כאשר $r$ מתקבל על ידי:
\[\sqrt{d^2 + b^2}\]בנוסף, הכיוון הוא: $\cos$ והוא שווה ליחס $\frac{b}{r}$
כלומר ששני המטענים יחד נותנים:
\[2\frac{k (-q)}{r^2} \cdot \frac{b}{r}\] \[2\frac{k (-q)}{d^2 + b^2} \cdot \frac{b}{\sqrt{d^2 + b^2}}\] \[-2\frac{kqb}{\left(d^2 + b^2\right)^{\frac{3}{2}}}\]פתרון מדויק יותר לכל הסעיפים ניתן למצוא בתרגול 3.
שאלה 3: שדה חשמלי של טבעת טעונה – צפיפות, סימטריה ואינטגרציה
טבעת מעגלית לא מוליכה שרדיוסה $R$ טעונה באופן אחיד במטען כולל חיובי $Q$.
- מהי צפיפות המטען הקווית על הטבעת?
- מסובבים את הטבעת במהירות זוויתית $\omega$. מהו וקטור צפיפות הזרם על הטבעת?
- ללא חישוב, מהו השדה החשמלי במרכז הטבעת?
- מהו השדה החשמלי $\vec{E}$ על ציר $z$ המאונך למישור הטבעת ומנקב אותה במרכזה?

סעיף 1 - צפיפות מטען קווית
מהגדרה של צפיפות קווית:
\[\lambda = \frac{Q}{L}\]כאשר $L$ הוא אורך הטבעת (היקף המעגל).
נציב ונקבל שהצפיפות הקווית היא:
\[\boxed{\lambda = \frac{Q}{2\pi R} \, \left[ \frac{C}{m} \right]}\]סעיף 2 - צפיפות זרם
טרם למדנו את הנושא (נכון לכתיבת שורות אלו).
סעיף 3 - שדה במרכז
משיקולי סימטריה בלבד, השדה במרכז הטבעת הוא אפס:
\[\boxed{\vec{E} = 0}\]סעיף 4 - שדה על ציר $z$ שמאונך לטבעת
הבחנה מהותית: בגלל סימטריה, רק רכיב $z$ של השדה שורד.
נוסחאות נדרשות:
מדף הנוסחאות, שדה של מטען נקודתי (קטן) נתון על ידי:
\[\boxed{dE = k\frac{dq}{r^2}}\]אלמנט מטען קטן על הטבעת הוא:
\[dq=\lambda dL\]כאשר $dL$ הוא אורך קשת קטנטנה. בקואורדינטות קוטביות:
\[dL = R d \theta\]וסך הכל:
\[dq = \lambda R d \theta\]נמשיך.
מרחק מאלמנט על הטבעת לנקודה על הציר במרחק $z$:
\[r = \sqrt{R^2 + z^2}\]נציב ונקבל:
\[dE = \frac{k \cdot \lambda R d \theta}{R^2 + z^2} \cos \phi\]משיקולי טריגונומטריה:
\[\cos \phi = \frac{z}{\sqrt{R^2+z^2}}\]נציב ונקבל:
\[dE = \frac{k \cdot \lambda R d \theta}{\left(R^2 + z^2\right)^{\frac{3}{2}}}\]נעשה אינטגרל כדי לסכום את כל המטענים הנקודתיים:
\[E = \int_0^{2\pi} dE(\theta)\]\[= \frac{k \lambda R z}{(R^2 + z^2)^{3/2}} \int_0^{2\pi} d\theta = \frac{k \lambda R z}{(R^2 + z^2)^{3/2}} \cdot 2\pi\]הפנמה חשובה שדרושה להמשך: כל מה שבתוך האינטגרל קבוע ביחס ל $\theta$.
סך הכל:
\[E= \frac{2\pi k \lambda R z}{\left(R^2 + z^2\right)^{\frac{3}{2}}} \hat{z}\]ואם נציב $\lambda = \frac{Q}{2\pi R}$ נקבל:
\[\boxed{\vec{E} = \frac{kQz}{\left(R^2 + z^2\right)^{\frac{3}{2}}} \hat{z}}\]הערות:
אם המטען היה מוליך, מטען חיובי מסוים היה מושך אליו את כל המטענים והיה מתקבל קיטוב על הטבעת. לא מוליך = מבודד.
נניח ששמנו מטען $(-q)$ ושמבקשים מאיתנו לצייר את השדה. אם הטבעת מוליכה - יש קיטוב, אחרת אין קיטוב.
המשיק לקווי השדה הוא השקול הווקטורי של השדות שנוצרים מהצטברויות המטען השונות.
אם מדובר בכדור ויש קיטוב על הכדור - השדה לא חייב להיות אפס, אבל השטף כן.
שאלה 4: שדה ושטף במערכת גלילים קונצנטריים טעונים – יישום חוק גאוס
שתי מעטפות גליליות קונצנטריות (בעלות ציר משותף) ברדיוס $R_2, R_1$ ובאורך אינסופי טעונות בצפיפות משטחית $\sigma_1 \sigma_2$ קולון ליחידת שטח, בהתאמה. הגלילים אינם מוליכים.
- מהו וקטור השדה החשמלי בכל המרחב?
- מסירים פס דק באורך אינסופי מהגליל החיצוני (כך שהפס שהוסר מקביל לציר הגלילים) מהו עתה השדה החשמלי על הציר?
- מהו השטף החשמלי דרך הגליל הפנימי במקרה של סעיף ב׳?

סעיף 1 - שדה בכל המרחב
רכיבי השדה על ציר $\hat{z}$ מתאפסים משיקולי סימטריה. נשארנו רק עם הרכיבים שיוצאים בניצב ליריעות הגליל (לכיוון מישור $xy$).
נשתמש בחוק גאוס עבור כל אחת מהיריעות בנפרד. חוק גאוס:
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}\]במילים: שטף השדה דרך אלמנט נפח גלילי שווה לסך כל המטען שכלוא בתוך אלמנט הנפח חלקי $\epsilon_0$.
רמז: צריך לחלק לשלושה אזורים:
- $r < R_1$
- $R_1 < r < R_2$
- $r > R_2$
נבחר משטח גאוסי גלילי לכל אזור - המטען הכלוא תלוי באזור.
תחילה נפתור באופן כללי לשדה חיצוני ולשדה פנימיה ביחס לגליל עם צפיפות משטחית $\sigma$ ורדיוס $R$, ואז ניישם על שני הגלילים.
בתוך הגליל ($r < R$)
אין מטען כלוא בתוך הגליל הפנימי, לפי גאוס השדה הוא אפס:
\[\phi(r < R) = \int_{surface} \vec{E} \cdot d\vec{A} = \int_{surface} | E_{xy} | dA \underbrace{=}_{gauss} \frac{Q_{enc}}{\varepsilon_0} = 0\] \[\implies E_{xy} = 0 \quad \text{for } r < R\]מחוץ לגליל ($r > R$)
השדה החיצוני מקיים:
\[\phi(r > R) = \int_{surface} | \underbrace{E_{xy}}_{\text{constant}} | dA = \frac{Q_{enc}}{\varepsilon_0} \underset{\star}{=} \frac{\sigma \cdot 2\pi R \cdot L}{\varepsilon_0}\]$(\star)$ קשר בין צפיפות משטחית למטען:
\[Q = \sigma \cdot A\]במקרה של גליל:
\[A = 2 \pi R L\]מכאן:
\[Q = \sigma \cdot 2 \pi R L\]
זה מטען אינסופי אך גם השטרף הוא אינסופי כי האינטגרל מכיל שטח אינסופי:
\[\phi (r \ge R) = E_{xy} (r > R) \cdot 2\pi r \cdot L = \frac{\sigma \cdot 2\pi R \cdot L}{\varepsilon_0}\] \[\implies E_{xy} (r > R) = \frac{\sigma R}{\varepsilon_0 r} \cdot \hat{r} \quad \text{for } r > R\]סעיף 2 - הסרת פס מהגליל החיצוני
הבחנה מהותית: נדרש להשתמש בסופרפוזיציה. גליל שלם פחות פס זה כמו גליל שלם ועוד פס עם מטען הפוך.
מה השדה של הגליל השלם על הציר?
תשובה: השדה על הציר הוא אפס.
מה השדה של פס אינסופי טעון?
\[E = \frac{\sigma}{2 \pi \varepsilon_0 r}\]סעיף 3 - שטף דרך הגליל הפנימי
נוסחה:
\[\Phi = \oint \vec{E} \cdot d\vec{A}\]או דרך גאוס:
\[\Phi = \frac{Q_{enc}}{\varepsilon_0}\]הבחנה מהותית: האם יש מטען בתוך הגליל הפנימי? לא.
הערה - בשדה אינסופי רואים מרחוק גליל כקבל, כמו שבמעגלי רואים מעגל כנקודה.
שאלה 5: שדה חשמלי בכדור לא מוליך עם צפיפות מטען נפחית משתנה
כדור לא מוליך ברדיוס $R$ טעון בצפיפות נפחית רדיאלית:
\[\rho(r) = \rho_0/r\]
מהן יחידות $\rho_0$?
מהו השדה החשמלי בתוך הכדור?
עזרה: שטח קליפה כדורית ברדיוס $r$ ועובי $dr$ הוא:
\[dV = 4 \pi r^2 dr\]

צפיפות נפחית של מטען -> מטען לנפח:
\[\left[ \rho \right] = \frac{C}{m^3}\]כדי שהיחידות יסתדרו צריך שהיחידות של $\rho_0$ יהיו:
\[\frac{C}{m^2}\]סעיף 2 - שדה בתוך הכדור
נוסחאות נדרשות:
חוק גאוס:
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}\]שלבים:
- נבחר משטח גאוסי כדורי ברדיוס $r < R$
-
נחשב את המטען הכלוא $Q_{enc}$ על ידי אינטגרציה:
\[Q_{enc} = \int_0^r \rho(r') \cdot dV = \int_0^r \frac{\rho_0}{r'} \cdot 4\pi r'^2 \, dr'\]נפשט (צמצום של $r’$ ):
\[= \int_0^r \rho_0 \cdot 4\pi r' \, dr'\]נוציא קבועים ונפתור:
\[= \rho_0 \cdot 4\pi \int_0^r r' \, dr' = \rho_0 \cdot 4\pi \frac{r^2}{2}\] -
הצד השמאלי של גאוס (מסימטריה כדורית):
\[\oint \vec{E} \cdot d\vec{A} = E \cdot 4\pi r^2\] -
נשווה ונפתור עבור $E$
\[E \cdot 4\pi r^2 = \frac{\rho_0 \cdot 4\pi \frac{r^2}{2}}{\epsilon_0} \implies \boxed{E = \frac{\rho_0}{2\epsilon_0}}\]
שאלה 6: בדיקת עקביות פיזיקלית של קווי שדה חשמלי
נתונה תמונה של ארבעה מטענים וצריך לקבוע את המטען שלהם.
הפתרון הוא שזה לא מצב פיזיקלי אפשרי - בנקודה ג׳ יש קווים נכנסים וגם קווים יוצאים.
קווי שדה חשמלי לא יכולים גם להיכנס וגם לצאת מאותו מטען נקודתי. מטען הוא או מקור (חיובי - רק יוצאים) או בור (שלילי - רק נכנסים).
התשובה: ה. לא ייתכן מצב כזה של קווי שדה הציור מתאר מצב לא פיזיקלי.
שאלה 7: חישוב מטען כלוא מתוך שטף שדה דרך קובייה
נתונה קובייה שאורך מקצועה הוא $a$.
השדה החשמלי דרך הפאות השונות הוא:
- פאה עליונה: $\vec{E} = E_0 \hat{z}$
- פאה תחתונה: $\vec{E} = E_0 \hat{z}$
- פאה ימנית: $\vec{E} = E_1 \hat{x}$
- פאה שמאלית: $\vec{E} = -E_1 \hat{x}$
- פאות קדמית ואחורית: $\vec{E} = \vec{0}$
מהו המטען הכולל הכלוא בקובייה?

צריך:
- לחשב את השטף דרך כל פאה: $\Phi = \vec{E} \cdot \hat{n} \cdot a^2$
- לסכום את כל השטפים
- להשתמש בגאוס: $Q_{enc} = \varepsilon_0 \cdot \Phi_{total}$
ננסה לחשב כל פאה בנפרד.
דרך הפאות העליונות והתחתונות:
\[\vec{E} = E_0 \hat{z} \pm \hat{z}\]אבל מכיוונים מנוגדים ולכן מתבטל. הקדמי והאחרוי אפס מכאן שנשארו רק הפאה הימנית והפעה השמאלית - לשתיהן שטף על מישור איקס.
לימנית שטף חיובי ולמעשה גם לשמאלית (כי היא מינוס אבל מהכיוון השני של ציר איקס).
מכאן שהשטף הוא:
\[2E_1 \hat{x} a^2\]נציב בגאוס ונקבל:
\[2E_1 \hat{x} a^2 = \frac{Q_{enc}}{\epsilon_0}\]טעות - שטף הוא סקלר, לא וקטור. אז:
\[2E_1 a^2 = \frac{Q_{enc}}{\epsilon_0} \implies Q = 2E_1 a^2 \epsilon_0\]נזכור ש-
\[k = \frac{1}{4\pi \epsilon_0}\]אז אפשר גם לרשום:
\[\boxed{Q = \frac{E_1 a^2}{2\pi k}}\]שאלה 8: שיווי משקל בין כוח חשמלי לכוח כבידה – כדור טעון ליד לוח אינסופי
כדור קטן שמסתו אחד גרם טעון במטען של מינוס חצי מיקרוקולון. הכדור מרחף במנוחה מתחת ללוח אופקי, גדול מאוד, טעון בצפיפות מטען אחידה $\sigma$. המערכת נמצאת בריק.
- שרטטו תרשים מתאים למצב הנתון
- חשבו את צפיפות המטען על הלוח

לא הצלחתי את השאלה, להלן פיתרון של קלוד:
נתונים
- $m = 1 \text{ g} = 10^{-3} \text{ kg}$
- $q = -0.5 \times 10^{-6} \text{ C}$
- הכדור מרחף במנוחה מתחת ללוח
חלק א’ - תרשים
+ + + + + + + + לוח (σ > 0)
↓ E
○ כדור (q < 0)
↑ Fₑ
↓ mg
חלק ב’ - חישוב צפיפות המטען
שיווי משקל: הכוח החשמלי כלפי מעלה מאזן את הכבידה כלפי מטה.
קביעת סימן σ: מכיוון ש-$q < 0$ והכוח צריך להיות כלפי מעלה, השדה חייב להיות כלפי מטה. שדה יוצא מלוח חיובי, לכן $\sigma > 0$.
משוואה:
\[|q| \cdot \frac{\sigma}{2\varepsilon_0} = mg\]פתרון:
\[\sigma = \frac{2\varepsilon_0 mg}{|q|} = \frac{2 \times 8.85 \times 10^{-12} \times 10^{-3} \times 10}{0.5 \times 10^{-6}}\] \[\boxed{\sigma = 3.54 \times 10^{-7} \text{ C/m}^2}\]שאלה 9: סטיית חוט בשדה חשמלי אופקי – שיווי משקל כוחות
מסדרים את אותו לוח בשאלה הקודמת במצב אנכי ותולים את אותו כדור בקצהו של חוט מבודד המחובר לתקרה.
- שרטטו תרשים של המצב החדש המתואר בסעיף זה.
- מהי זווית הסטייה של החוט מהאנך במצב זה?

תקרה
+ |
+ | T (מתיחות)
לוח אנכי (σ > 0)+ |θ
+ ○ כדור (q < 0)
+ ↙ ↓
+ Fₑ mg
+ ←
שיווי משקל
יש שלושה כוחות:
- $mg$ למטה
- $F_E = |q| \cdot \frac{\sigma}{2\epsilon_0}$ אופקית (לכיוון הלוח, כי $q < 0$)
- $T$ מתיחות החוט (בזווית)
נציב את כל הנתונים:
\[= \frac{0.5 \times 10^{-6} \cdot \frac{3.54 \times 10^{-7}}{2 \times 8.85 \times 10^{-12}}}{10^{-3} \times 10}\] \[= \frac{0.5 \times 10^{-6} \cdot 2 \times 10^{4}}{10^{-2}} = \frac{10^{-2}}{10^{-2}} = 1\] \[\implies \theta = 45^{\circ}\]זה הגיוני פיזיקלית: הכוח החשמלי שווה בדיוק לכוח הכבידה, ולכן הזווית היא 45°.
(אפשר גם לראות את זה ישירות: בשאלה הקודמת הכוח החשמלי איזן את הכבידה כשהכדור ריחף, אז $F_E = mg$, ולכן $\tan\theta = \frac{F_E}{mg} = 1$)
שאלה 10: כדור טעון בין לוחות מקבילים – חישוב שדה ותנועה איכותית
בין שני לוחות מבודדים גדולים מאוד אשר המרחק ביניהם הוא $d=20 \, \mathrm{cm}$, תלוי בקצה חוט מבודד כדור מוליך קטן, שמסתו $m=10^{-5} \, \mathrm{Kg}$ ומטענו $q=10^{-6} \, \mathrm{C}$.
הכנסת הכדור בין הלוחות גורמת לחוט לסטות בזווית של $\alpha=4^{\circ}$. בהנחה שהמרחק בין הלוחות קטן מאוד יחסית למימדיהם.
________ | | |\ | | | | | \○ | | | | ○ | | | | | | | |<--------->| | d
- מהי צפיפות המטען המשטחי $\sigma$ שעל כל לוח?
- חוזרים על כל התהליך, אך הפעם עם לוחות מוליכים הטעונים באותו מטען משטחי $\sigma$ שחישבנו למעלה. תארו באופן איכותי את תנועת הכדור בין הלוחות.

זכיר משהו מפיזיקה קל: הכדור תלוי על חוט וסוטה בזווית - זה מזכיר משהו מפיזיקה א׳!
שיווי משקל של שלושה כוחות
על הכדור פועלים:
- כוח כבידה $mg$ - כלפי מטה
- כוח חשמלי $F_E = qE$ - אופקית (לכיוון הסטייה)
- מתיחות החוט $T$ - לאורך החוט
\ T
\
\θ
○ ← Fₑ = qE
↓
mg
נוסחת המפתח
בשיווי משקל כזה (כמו מטוטלת בשדה חשמלי):
\[\tan(\alpha) = \frac{F_E}{mg} = \frac{qE}{mg}\]מה השדה בין שני לוחות?
בין שני לוחות מקבילים טעונים הפוכים (קבל), השדות מסתכמים:
\[E_{\text{total}} = \frac{\sigma}{\varepsilon_0}\](לא $\frac{\sigma}{2\varepsilon_0}$ - למה?)
כלומר שאם נציב את השדה בנוסחה מקודם נקבל:
\[\tan(\alpha)=\frac{qE}{mg}=\frac{q\sigma}{mg\epsilon_0}\]תהיות וטעויות שהיו לי:
- המסה כן רלוונטית! היא קובעת את כוח הכבידה
- לא צריך נוסחת $\frac{1}{r^2}$ - זה לוח אינסופי, לא מטען נקודתי
- כן, זה שילוב של כוח חשמלי וכבידה בזווית
נציב ונפתור:
\[\tan(4) = \frac{q \sigma}{mg \epsilon_0}\]$g=10 \, \mathrm{m/}\mathrm{s}^2$ היא תאוצת הכבידה.
\[\sigma = \frac{\tan(4)mg\epsilon_0}{q}\]נציב את המשקל והמטען הנתון וכן $\epsilon_0 \approx 8 \times 10^{-12}$.
\[= \frac{0.06 \cdot 10^{-5} \cdot 10 \cdot 8 \cdot 10^{-12}}{10^{-6}}\] \[= \frac{6 \cdot \cancel{10^{-6}} \cdot 8 \cdot 10^{-12}}{\cancel{10^{-6}}}\]נשאר
\[\boxed{\sigma \approx 4.8 \times 10^{-11} \, \mathrm {C/m}^2}\]כאשר שני הלוחות מוליכים
לא הצלחתי לבד. להלן תשובה מקלוד:
לוחות מוליכים לא אומר שאין שדה ביניהם!
ההבדל: בלוחות מבודדים המטען נשאר במקום. בלוחות מוליכים המטען יכול לזוז בתוך הלוח.
מה יקרה: הכדור הטעון ישפיע על פיזור המטען בלוחות (אינדוקציה), מה שישנה את השדה, מה שיזיז את הכדור, וחוזר חלילה… הכדור יתנדנד או ינוע לכיוון אחד הלוחות.
שאלה 11: אינדוקציה ושימור מטען במערכת כדורים מוליכים ולוח טעון
מצמידים שני כדורים מוליכים שאינם טעונים. מתחת לכדורים מניחים לוח טעון במטען חשמלי חיובי.
○ ○ -------------- ++++++++++++++ --------------
- מפרידים את הכדורים זה מזה. האם לאחר ההפרדה הכדורים טעונים? אם לא מדוע אם כן מה סימן המטען בכל כדור.
- ענה על השאלה כשאר הלוח אנכי:
|+| |+| ○ ○ |+| |+| |+|

תשובה מ-ChatGPT 5.2 Thinking
נשתמש בשני עקרונות:
- אינדוקציה: שדה חיצוני גורם להפרדת מטענים במוליך (קיטוב), ומטענים יכולים לזרום אם שני מוליכים במגע.
- שימור מטען: לשני הכדורים יחד היה מטען כולל (0), אז אחרי כל התהליך סכום המטענים על שניהם חייב להישאר (0).
מצב 1: הלוח אופקי מתחת לשני הכדורים (כמו בציור העליון)
כאן השדה מהלוח החיובי הוא בערך כלפי מעלה. שני הכדורים (כשמחוברים) יתקטבו כך שיצטבר מטען שלילי יותר למטה וחיובי יותר למעלה — אבל בגלל סימטריה מושלמת (שני הכדורים באותו מרחק מהלוח), אין “כדור קרוב יותר” שיקבל עודף אלקטרונים על חשבון השני.
לכן, כשמפרידים את הכדורים (בעוד הלוח שם) מתקבל:
- כל כדור נשאר עם מטען נטו (0) (נייטרלי).
- בזמן שהלוח קרוב הם מקוטבים, אבל זה לא “נטען” נטו לכל כדור.
✅ תשובה מצב 1: אחרי ההפרדה שני הכדורים נייטרליים (אין “+” על אחד ו“-” על השני).
הערה חשובה: אם הלוח לא היה סימטרי ביחס לשני הכדורים (למשל קרוב יותר לאחד מהם), אז כן היה מתקבל מצב של “אחד שלילי ואחד חיובי”.
מצב 2: הלוח אנכי בצד (כמו בציור התחתון)
כאן יש שבירת סימטריה: הכדור השמאלי קרוב יותר ללוח החיובי.
- אלקטרונים נמשכים ללוח החיובי ⇒ זורמים דרך המגע אל הכדור הקרוב.
- לכן הכדור הקרוב מקבל עודף אלקטרונים ⇒ נהיה שלילי.
- הכדור הרחוק נשאר עם מחסור אלקטרונים ⇒ נהיה חיובי.
- המטענים יהיו שווים בגודל והפוכים בסימן (כי הסכום חייב להישאר (0)).
✅ תשובה מצב 2:
- הכדור הקרוב ללוח החיובי: שלילי ((-))
- הכדור הרחוק מהלוח: חיובי ((+))
שאלה 12: ניתוח כיוון שדה חשמלי והיטל רכיבים ממטענים לא סימטריים
נתונים שני מטענים $Q_1$ ו-$Q_2$ . בנקודה $A$ השדה החשמלי $\vec{E}$ מכוון אופקית ימינה.
- איזה מטען הוא חיובי ואיזה שלילי?
- נתון $\vert Q_2 \vert = 5 \vert Q_1 \vert$. מיצאו את $a$.
E A|---> |a Q1 | Q2 -○--------------------○ a 2a

אני חושב ש $Q_2$ כנראה שלילי כי הוא מושך אליו (בולען), אבל השאלה לא לגמרי ברורה לי כי נראה מהציור שהנקודה A גבוהה יותר ושהמשיכה היא לא בכיוון שמתאים בדיוק למערכת (הייתי מצפה לראות קו מA ל Q2).
לגבי סעיף 2, אני חושב שצריך להיעזר בחוק קולון?
נסתכל על נקודה בראשית?
אולי בעזרת $E$?
ביקשתי רמז:
נכון, צריך להשתמש בשדה החשמלי. בנקודה $A$:
רמז: השדה הכולל הוא אופקי בלבד (אין רכיב אנכי).
זה אומר שרכיבי ה-$y$ של השדות מ-$Q_1$ ומ-$Q_2$ חייבים להתאפס.
נסה לרשום את המרחק מכל מטען לנקודה $A$, ואת רכיב ה-$y$ של כל שדה.
תודה לקלוד אופוס 4.5. ננסה להקשיב לעצתו הטובה לרוב.
המרחק מהנקודה הימנית ל$A$ הוא:
\[d_1 = \sqrt{2}a\]משיקולי פיתגורס.
המרחק של $Q_2$ הוא:
\[d_2 = \sqrt{a^2 + 4a^2} = \sqrt{5}a\]רכיבי ה-$y$ הוא המרחק הזה עם היטל שלדעתי יוצר סינוס. מכאן:
\[E_1 = \frac{kQ_1}{2a^2}\sin(45) = \frac{kQ_1}{2a^2}\frac{1}{\sqrt{2}}\]הזוויות החשובות של מעגל היחידה זמינות בסיכום על מעגל היחידה.
\[E_2 = \frac{kQ_2}{5a^2}\sin(26.5) = \frac{kQ_2}{5a^2}\frac{1}{...}\]מסתבר שהיה טעות להשתמש בערך של הסינוס:
טריק לסינוס
לא צריך לחשב זוויות במעלות! הסינוס הוא פשוט:
\[\sin(\theta) = \frac{\text{Nitzav Negdi}}{\text{Yeter}} = \frac{a}{d}\]אז:
\[\sin(\theta_1) = \frac{a}{\sqrt{2}a} = \frac{1}{\sqrt{2}}\] \[\sin(\theta_2) = \frac{a}{\sqrt{5}a} = \frac{1}{\sqrt{5}}\]השוואת רכיבי $y$
\[E_{1y} = \frac{kQ_1}{2a^2} \cdot \frac{1}{\sqrt{2}}\] \[E_{2y} = \frac{kQ_2}{5a^2} \cdot \frac{1}{\sqrt{5}}\]מתאפסים, אז:
\[\frac{kQ_1}{2a^2} \cdot \frac{1}{\sqrt{2}} = \frac{kQ_2}{5a^2} \cdot \frac{1}{\sqrt{5}}\]נציב $|Q_2| = 5|Q_1|$ ונפתור עבור $a$.
\[\frac{Q_1}{2a^2} \cdot \frac{1}{\sqrt{2}} = \frac{Q_1}{a^2} \cdot \frac{1}{\sqrt{5}}\]אוקיי כנראה שיש טעות בשאלה, כי למעשה העובדה שהתנאי מתקיים עדיין לא מסייעת למצוא ערך מסוים של $a$.
שאלה 13: שדה ותאוצה לאורך ציר סימטריה של שני מטענים זהים
נתונים שני מטענים חיוביים זהים $Q$ המרוחקים זה מזה $2d$.
Q ● | | ----------+-----------◯------> x | B | ● Q
הראו שהשדה החשמלי לאורך ציר $x$ החיובי נתון בביטוי:
\[\vec{E}(x) = \frac{2KQx}{(x^2 + d^2)^{3/2}}\hat{x}\]קבלו ביטוי עבור תאוצתו של חלקיק אשר מסתו היא $m$ ומטענו החשמלי הוא $q$ והוא מונח היכנשהו על ציר ה-$x$.

משיקולי סימטרייה ההשפעה על ציר $y$ מתאפסת ויש השפעה רק על ציר $x$.
המרחק של הנקודה B מכל מטען הוא:
\[r=\sqrt{x^2+d^2}\]ההיטל על ציר $x$ הוא קוסינוס (ניצב שליד הווית חלקי היתר)
\[\cancel{\cos(\theta) = \frac{d}{\sqrt{x^2+d^2}}}\]סך הכל כל מטען משפיע:
\[\cancel{\vec{E}(x) = \frac{kQ}{(x^2+d^2)} \cdot \frac{d}{\sqrt{x^2+d^2}}}\]אופס, טעיתי במיקום של הזווית, זה כנראה אמור להיות:
\[\cos(\theta) = \frac{x}{\sqrt{x^2+d^2}}\]Q ● \ | \ r | \ | θ ↘ ----------+-------◯------> x | B | | ● Q
וסך הכל יש שניים אז:
\[\boxed{\vec{E}(x)_{tot} = \frac{2kQx}{(x^2+d^2)^{3/2}} \hat{x}}\]נמצא כעת ביטוי לתאוצה של חלקיק כנדרש.
כוח של חלקיק נתון על ידי:
\[\vec{F} = q\vec{E}\]מהחוק השני של ניוטון:
\[\vec{F}=m\vec{a}\]מכאן:
\[q\vec{E}=m\vec{a} \implies \vec{a} = \frac{q\vec{E}}{m}\]נציב את הביטוי ל $E$:
\[\vec{a} = \frac{q}{m} \cdot \frac{2kQx}{(x^2+d^2)^{3/2}} \hat{x}\]או בצורה מסודרת:
\[\boxed{\vec{a}(x) = \frac{2kQqx}{m(x^2+d^2)^{3/2}} \hat{x}}\]שאלה 14: השוואת התנהגות השדה החשמלי בכדור מבודד ובכדור מוליך

פתרון תרגיל 3 - גאוס, קולון, אנרגיה ועבודה בשדה אלקטרוסטטי
תאריך: 01/12/2025שאלה 1: איפוס שדה וכוחות במערכת מטענים נקודתיים על קו ישר
שני מטענים של 6 קולון (מימין בתרשים מטה) ו-3 קולון (משמאל) נמצאים לאורך קו ישר. המרחק בין המטענים הוא מטר אחד.
+3 C +6 C ---|--------------------|--- |<------- 1 m ------>|
- האם קיימת נקודה לאורך הקו הישר שבה השדה החשמלי מתאס? אם לא, נמקו מדוע לא, אם קיימת נקודה כזו, חשבו את מיקומה לאורך הקו הישר.
- מניחים מטען שלישי במרחק שני מטר משמאל למטען בן שלשת הקולון. מה צריך להיות גודלו ומה מטענו כדי ששקול הכוחות על המטען בן ששת הקולון יתאפס?
- מה גודל הכוח שמפעיל המטען בן ששת הקולון על המטען השלישי שהונח שלשה מטר משמאלו?
סעיף 1
מעקרון הסופרפוזיציה לשדות חשמליים:
\[\vec{E}_{total} = \vec{E}_1 + \vec{E}_2\]נוסחת השדה של מטען נקודתי:
\[E = k \frac{q}{r^2}\]תנאי להתאפסות:
\[E_1 = E_2\]כלומר:
\[k \frac{q_1}{r_1^2} = k \frac{q_2}{r_2^2}\]נציב בנתוני השאלה:
\[q_1 = 3\] \[q_2 = 6\]נמצא את המרחקים. הבעיה חד מימדית, אם המרחק מהנקודה השמאלית הוא $x$ מהנקודה הימנית יהיה $(1-x)$.
\[\frac{3}{r_1^2} = \frac{6}{r_2^2}\]הופך ל:
\[\frac{3}{x^2} = \frac{6}{(1-x)^2}\] \[\frac{x^2}{(1-x)^2} = \frac{1}{2}\]מכאן זה פיתוח מתמטי. נוציא שורש:
\[\frac{x}{1-x} = \frac{1}{\sqrt{2}}\] \[\sqrt{2} x = 1 - x\] \[x (\sqrt{2} + 1) = 1\] \[\boxed{x = \frac{1}{\sqrt{2} + 1} \approx 0.414 \, \mathrm{m}}\]הנקודה במרחק של כ-0.414 מטר מימין למטען השמאלי (בין שני המטענים).
מניחים מטען שלישי במרחק שני מטר משמאל למטען בן שלשת הקולון. מה צריך להיות גודלו ומה מטענו כדי ששקול הכוחות על המטען בן ששת הקולון יתאפס?
להבנתי צריך להשתמש בסופר פוזיציה.
הוא צריך להיות שלילי כנראה.
נציב במשוואה.
שקול הכוחות על המטען בן ששת הכולון הוא:
\[F_{3 \to 6} + F_{? \to 6} = 0\]ניעזר בחוק קולון:
\[k\frac{3 \cdot 6}{1^2} + k \frac{q_3 \cdot 6}{9} = 0\] \[\frac{2q_3}{3} = -18\] \[\boxed{q_3 = -27}\]הכיוון צריך להיות שלילי כי המטען המקורי של 6 היה חיובי.
מה גודל הכוח שמפעיל המטען בן ששת הקולון על המטען השלישי שהונח שלשה מטר משמאלו?
זה לא פשוט 6? מה זה גודל הכוח?
גודל הכוח הכוונה לערך המוחלט של הכוח בניוטונים, לא רק ערך המטען.
צריך להשתמש בחוק קולון:
\[F = k\frac{q_1 \cdot q_2}{r^2}\]הנתונים:
- $q_1 = 6C$
- $q_2 = -27C$ (המטען מהסעיף הקודם)
- $r = 3m$
- $k = 8.99 \times 10^9$
ננסה להציב ולחשב:
\[F = k \frac{-27 \cdot 6}{9} = - 18 k\]בערך מוחלט:
\[18k\]אם נציב את הערך של $k$ כדי לקבל תשובה ביחידות של ניוטון:
\[\boxed{F = 18k = 18 \times 8.99 \times 10^9 \approx 1.62 \times 10^{11} \, \mathrm{N}}\]שאלה 2: שדה, פוטנציאל ועבודה במערכת סימטרית של מטענים על משושה משוכלל
בכל אחד מחמשת הקודקודים $\text{A, B, C, D, E}$ של משושה משוכלל שאורך צלעו $a$ נמצא מטען חיובי $Q$. בקודקוד $\text{F}$ אין מטען.
a B(Q)-----(Q) A / \ / a a \ C(Q)-----O ----- F \ / \ / D(Q)-----E(Q)
מה וקטור השדה החשמלי השקול (גודל וכיוון) במרכזו של המשושה - נקודה O?
מעבירים מטען נוסף $\text{Q}$ ממרחק גדול מאוד (לצורך עניין אינסוף) אל הנקודה $\text{O}$. מהי העבודה שנעשתה נגד כוחות השדה החשמלי?
- מעבירים את המטען מהסעיף הקודם מנקודה O אל נקודה F.
- מה השדה החשמלי בנקודה O כעת?
- האם דרושה עבודה חיצונית כדי להביא מטען כלשהו $q$ מאינסוף אל מרכז המשושה? אם כן חשבו את העבודה.
בכל אחד משלושת קודקודי המשושה $\text{E, C, A}$ מחליפים את המטען החיובי $Q$ במטען שלילי $-Q$. בכל אחד משלושת הקודקודים האחרים נמצא מטען $Q$ ובנקודה $O$ שבמרכז המשושה אין מטען.
האם פעולה זו תגרום לשינוי העבודה הדרושה להבאת אותו מטען $q$ מאינסוף למרכז המשושה?
סעיף א׳ - וקטור השדה החשמלי במרכז
אפשר לזהות שכל המטענים מתבטלים משיקולי סימטריות למעט המעטן שמול הנקודה F.
\[\boxed{E(O) = k\frac{Q}{(a)^2} \hat{x}}\]$a$ כי זה המרחק של צלע המשושה, וזה המרחק מהנקודה O למטען Q שמולה.
השדה מצביע לכיוון ציר $x$ חיובי, כלומר ימינה.
סעיף ב׳ - עבודה להביא מטען מאינסוף
מעבירים מטען נוסף $\text{Q}$ ממרחק גדול מאוד (לצורך עניין אינסוף) אל הנקודה $\text{O}$. מהי העבודה שנעשתה נגד כוחות השדה החשמלי?
נראה שצריך כאן נוסחאות של אנרגיה פוטנציאלית ועבודה.
נוסחאות נדרשות:
פוטנציאל חשמלי של מטען נקודתי:
\[V = k\frac{q}{r}\]עבודה נגד השדה:
\[W = q \cdot \Delta V = q(V_{final} - V_{initial})\]או דרך אנרגיה פוטנציאלית:
\[W = \Delta U = U_{final} - U_{initial}\]רמז מקלוד: הפוטנציאל באינסוף שווה לאפס. צריך לחשב את הפוטנציאל בנקודה O שנוצר מכל 5 המטענים, ואז להכפיל ב-Q.
הפוטנציאל מכל אחד מהמטענים הוא:
\[V_i = \frac{kQ}{a}\]סך הכל:
\[V = \frac{5kQ}{a}\]אז העבודה היא:
\[W = Q(\frac{5kQ}{a} - 0) = \boxed{\frac{5kQ^2}{a}}\]סעיף ג - מזיזים את המטען הנוסף
לאחר ההזזה השדה הוא אפס משיקולי סימטריה.
אכן דרושה עבודה כזאת - בדומה למה שעשינו מקודם רק שהפעם יש שישה מטענים:
\[W = Q(\frac{6kQ}{a} - 0) = \boxed{\frac{6kQ^2}{a}}\]סעיף ד - שינוי המטענים
עכשיו זה אפס.
אפשר לראות מסופרפוזיציה:
\[W = \sum _{i=1}^3 \frac{kQ^2}{a} + \sum _{i=1}^3\frac{k(-Q)\cdot Q}{a} = 0\]שאלה 3: שדה חשמלי בכדור מבודד עם חלל פנימי קונצנטרי – שימוש בחוק גאוס
פתרון מלא נמצא בתרגול 5. להלן ניסיון מענה נוסף.
נתון לנו כדור מבודד עם חלל פנימי כדורי אשר מרכזו מתלכד עם מרכז הכדור. רדיוס החלל הפנימי הוא $R_1$, רדיוס הכדור הוא $R_2$. הכדור טעון בצפיפות מטען חשמלי אחידה, וסך כל המטען עליו הוא $Q$. קבלו את:
- $\vec{E}(r<R_1)$
- $\vec{E}(R_1<r<R_2)$
- $\vec{E}(r>R_2)$
במונחים של הפרמטרים $Q, R_1,R_2,K$ וכתלות במרחק $r$ מן הראשית.

השדה בתוך החלל
בתוך החלל אין מטען כי נתון שזה חלל ריק (לא חומר מבודד). אפשר לראות מחוק גאוס שהשדה חייב להיות אפס.
השדה בין הכדור הפנימי לחיצוני
נשתמש בחוק גאוס - נבנה מעטפת סביב הכדור הפנימי.
צריך למצוא כמה מטען נמצא בתוך משטח גאוס ברדיו $R_1 < r < R_2$.
אפשר לקבל את זה בעזרת צפיפות המטען $\rho$.
המטען $Q$ מפוזר בנפח הכדור פחות נפח החלל, כלומר:
\[\rho = \frac{Q}{\frac{4}{3}\pi R_2^3 - \frac{4}{3}\pi R_1^3}\]\[\rho = \frac{Q}{\frac{4}{3}\pi (R_2 - R_1)} = \frac{3Q}{4\pi (R_2 - R_1)}\]תזכורת - נפח של כדור
\[\frac{4}{3}\pi R^3\]
המטען בתוך משטח גאוסי דמיוני ברדיוס $r$:
\[Q_{enc} = \rho \cdot \underbrace{\frac{4}{3}\pi(r^3 - R_1^3)}_{\text{volume between } R_1 \text{ to } r}\]נציב בחוק גאוס ונמצא את $E$:
חוק גאוס הוא:
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\epsilon_0}\]
צד שמאל (השטף):
\[E \cdot 4\pi r^2\]צד ימין:
\[\frac{\rho \cdot \frac{4}{3}\pi(r^3 - R_1^3)}{\epsilon_0}\]אז:
\[E \cdot 4\pi r^2 = \frac{\rho \cdot \frac{4}{3}\pi(r^3 - R_1^3)}{\epsilon_0}\]נפתור עבור $E$ ונציב את $\rho = \frac{3Q}{4\pi(R_2^3 - R_1^3)}$:
\[E = \frac{\rho \cdot \frac{4}{3}\pi(r^3 - R_1^3)}{\epsilon_0 \cdot 4\pi r^2 }\] \[E = \frac{\frac{\cancel{3}Q}{\cancel{4\pi}(R_2^3 - R_1^3)} \cdot \frac{\cancel{4\pi}}{\cancel{3}}(r^3 - R_1^3)}{\epsilon_0 \cdot 4\pi r^2 }\] \[\boxed{E(R_1 < r < R_2) = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)}\hat{r}}\]השדה מחוץ לכדור החיצוני
אפשר להתייחס כמטען נקודתי להבנתי:
\[E = \frac{kQ}{r^2}\]שאלה 4: שדה חשמלי של מוט טעון אחיד על ציר – חישוב באמצעות אינטגרל
מוט דק באורך $L$ טעון בצפיפות מטען אחידה $\lambda$ קולון למטר. המוט מונח על ציר $y$ השלילי כך שקצהו העליון מתלכד עם ראשית הצירים. מהו השדה החשמלי שיוצר המוט על ציר $y$ החיובי?

לדעתי אינטגרל.
אל אלמנט $dy’$ על המוט יוצר שדה בנקודה $y$ על ציר $y$ החיובי.
המרחק בין אלמנט $y’$, יעני וואי שלילי, לבין החיובי הוא:
\[d= y-y'\]המוט נמצא מ-$y’ = -L$ עד $y’ = 0$, אז:
\[dq = \lambda \, dy'\] \[dE = \frac{k \, dq}{(y - y')^2} = \frac{k\lambda \, dy'}{(y - y')^2}\] \[E = \int_{-L}^{0} \frac{k\lambda \, dy'}{(y - y')^2}\]מכאן הסתבכתי עם האינטגרל, לפי קלוד זה די קל וצריך פשוט הצבה.
שאלה 5: שדה ועבודה של דיסקה עם צפיפות מטען רדיאלית משתנה
דיסקה עגולה ברדיוס $R$ טעונה בצפיפות מטען משטחית רדיאלית $\sigma(r) = \sigma _0 e6{-kr}$
- מהו השדה החשמלי על ציר $y$ החיובי?
- חלקיק שמסתו $m$ ומטענו החשמלי הוא $q$ נופל מטה על ציר $y$ החיובי מגובה $y=b$ לגובה $y=a (b>a)$. קבלו את משוואת שימור האנרגיה של החלקיק בפרמטרים של הבעייה.
זאת צפיפות משתנה , אז נדרש לדעתי אינטגרל.
נוסחה לשדה של טבעת על הציר
השדה בנקודה $y$ מטבעת ברדיוס $r$:
\[dE_y = \frac{k \cdot dq \cdot y}{(r^2 + y^2)^{3/2}}\](רק רכיב $y$ שורד מסימטריה)
המטען על טבעת
\[dq = \sigma(r) \cdot dA = \sigma_0 e^{-kr} \cdot 2\pi r \, dr\]האינטגרל
\[E_y = \int_0^R \frac{k \cdot \sigma_0 e^{-kr} \cdot 2\pi r \cdot y}{(r^2 + y^2)^{3/2}} dr\]זה אינטגרל מסובך. שוין.
אגב היה פוטנציאל של טבעת בשאלה 8 במבחן אמצע תשפה:
\[\int \frac{kdq}{\sqrt{r^2 + z^2}}dA = k \int \frac{dq}{\sqrt{r^2 + z^2}}\]שאלה 6: אטום המימן
אטום המימן
שאלה 7
פתרון מלא נמצא בתרגול 5.
שאלה 8: סופרפוזיציה של שדות - קליפה כדורית טעונה ומישור אינסופי
משטח מישורי אין סופי הטעון בצפיפות מטענים $+\sigma$ קולון למטר מרובע נמצא במרחק $L$ ממרכזה של קליפה כדורית דקה בעלת רדיוס $R$. הקליפה הכדורית טעונה אף היא בצפיפות מטענים $+\sigma$ קולון למטר מרובע.

סעיף 1: שדה בנקודה A
השדה החשמלי בנקודה A בין הקליפה הכדורית למשטח המישורי, במרחק $a$ ממרכז הקליפה הכדורית יהיה (משתמשים במערכת הצירים שבציור לקביעת הכיוון החיובי):
כנראה שצריך לעשות סופר פוזיציה.
הקליפה מבחוץ היא כמו מטען נקודתי אז ההשפעה שלה היא:
\[E = \frac{kQ}{a^2}\]כאשר
\[Q = 4\pi R^2 \sigma\](זאת קליפה כדורית - לשים לב לא להבלבל עם מעגל כמו שקרה לי כבר)
סך הכל:
\[E = \frac{k 4\pi R^2 \sigma}{a^2}\]לכיוון $x$ חיובי.
המשטח לעומת זאת משפיע בכיוון הפוך. משטח אינסופי מתקבל על ידי הנוסחה:
\[E_{plane} = \frac{\sigma}{2\epsilon_0}\]הערה: השדה קבוע ולא תלוי במרחק! והא מצביע הרחק מהמשטח - בכיוון מינוס איקס.
סופרפוזיציה בנקודה A
\[\vec{E}_A = \underbrace{\frac{kQ}{a^2}\hat{x}}_{\text{shell}} + \underbrace{\left(-\frac{\sigma}{2\epsilon_0}\right)\hat{x}}_{\text{plane}}\]ננסה להציב $Q = 4\pi R^2 \sigma$ ולפשט:
\[\vec{E}_A = \frac{k4\pi R^2 \sigma}{a^2}\hat{x} + \left(-\frac{\sigma}{2\epsilon_0}\right)\hat{x}\]קיצור דרך:
\[k = \frac{1}{4\pi\epsilon_0}\]אז:
\[E_{sphere} = \frac{kQ}{a^2} = \frac{1}{4\pi\epsilon_0} \cdot \frac{4\pi R^2 \sigma}{a^2} = \frac{R^2 \sigma}{\epsilon_0 a^2}\]סופרפוזיציה
\[E_A = \frac{R^2 \sigma}{\epsilon_0 a^2} - \frac{\sigma}{2\epsilon_0} = \boxed{\frac{\sigma}{\epsilon_0}\left(\frac{R^2}{a^2} - \frac{1}{2}\right)}\]סעיף 2: עבודה בין הנקודות B ו-A
מהי העבודה הדרושה כדי להעביר מטען חיובי קטן $q$ מהנקודה $B$ לנקודה $A$ שבציור?
יש לנו את השדה החשמלי אולי אפשר לקבל ממנו את הפוטנציאל?
כנראה שצריך להיעזר בהפרש פוטנציאלים כי:
\[W = q\Delta V = q (V_A - V_B) = -q \int _B^A \vec{E}d\vec{l}\]אורך המסלול הוא $2a$.
תרומת הקליפה לעבודה מתבטלת משיקולי סמיטריה ולכן רק המשטח האינסופי תורם:
\[W=-q\int _{-a}^a \left(-\frac{\sigma}{2\epsilon_0}\right)dx = \frac{q \sigma }{2 \epsilon_0} x \bigg{|}_{-a}^{a} = \frac{q \sigma }{2 \epsilon_0} (a - (-a)) = \boxed{\frac{q\sigma a}{\epsilon_0}}\]שאלה 9: שדות, פוטנציאל וכוחות בין לוחות מוליכים מקבילים טעונים
נתונות שטי טבללאות $\text{I}$ ו- $\text{II}$ מישוריות, מוליכות, אינסופיות בעלות עובי של 2 מילימטר כל אחת, ומקבילות זו לזו. המרחק בין הטבלאות הוא $D=0.1$ מטר. הטבלה השמאלית $(\text{I})$ טעונה בצפיפות מטען חיובית $\sigma_1 = +10\cdot 10^{-9}$ קולון למטר בריבוע, והטבלה הימנית $(\text{II})$ טעונה בצפיפות מטען שלילית $\sigma_2 = -6 \cdot 10^{-9}$ מטר לריבוע.
נסמן ב א את המרחב שמשמאלת לטבלה I, ב ב את המרחב שבין שתי הטבלאות וב ג את המרחב שמימין לטבלה II:


סעיף 1: שדה חשמלי משמאל
מהו ערכו של השדה החמשלי (ביחידות של וולט למטר) באזור א?
הפתרון הבא כנראה שגוי אבל הביא לתשובה הנכונה:
חישבתי כך: שדה אינסופי נתון על ידי:
\[\frac{\sigma}{2\epsilon_0}\]בגלל שהלוח מוליך המטען מצטבר על הקצוות, ובגלל שמימין יש לוח עם מטען שלילי, על הדופן הימנית של הלוח השמאלי מצטבר מטען באותו גודל, של $+6 \cdot 10^{-9}$ כך שעל הצד השמאלי נשאר $+4 \cdot 10^{-9}$.
נציב בנוסחה:
\[E_א = \frac{4 \cdot 10^{-9}}{2\epsilon_0}\]נציב:
\[\epsilon_0 \approx 8.854 \cdot 10^{-12}\]אז:
\[E_א = \frac{2 \cdot 10^{3}}{8.854} \approx 226\]הערה: בפתרון הרשמי נראו שהשתמשו דווקא ב $k$:
\[k = \frac{1}{4\pi\varepsilon_0}\]אז:
\[\frac{\sigma}{2\varepsilon_0} = \frac{\sigma \cdot 4\pi k}{2} = 2\pi k \sigma\]גם השתמשו בנוסחה אחרת:
באזור החיצוני (א או ג):
\[E = \frac{|\sigma_1| - |\sigma_2|}{2\varepsilon_0}\]באזור הפנימי (ב):
\[E = \frac{|\sigma_1| + |\sigma_2|}{2\varepsilon_0}\]
סעיף 2: הפרש פוטנציאלים
מהו הפרט הפוטנציאלים (בוולטים) בין שני הלוחות?
נשתמש בנוסחה:
\[\Delta V = E \cdot d\]מסופר פוזיציה:
\[\Delta V = 0.1 \left(\frac{\sigma_1}{2\epsilon_0} + \frac{\sigma_1}{2\epsilon_0}\right)\]כאן יש משהו טריקי, כנראה שלא אמורים לחסר (במקור הצבתי מינוס ויצא לא נכון). זה כנראה בגלל שהם באותו כיוון.
\[\Delta V = \frac{0.1}{2\epsilon_0} \left(+10\cdot 10^{-9} + 6 \cdot 10^{-9} \right) \approx \boxed{90.4}\]בהתחלה גם חשבתי ששואלים רק על האזור של ב׳, אבל כנראה שזה לא היה המצב. הנה התשובה השגויה שלי לתיעוד:
יש לנו את השדה באזור ב (בין הלוחות). הפרש פוטנציאלים קשור לשדה על ידי:
\[\Delta V = E \cdot d\]$d$ הוא המרחק.
אבל קודם צריך לחשב את השדה באזור ב.
כאמור בסעיף 1 על הצד הפנימי של הלוח השמאלי יש $+6 \cdot 10^{-9}$, ועל הצד הפנימי של הלוח הימני יש $-6 \cdot 10^{-9}$.
אז השדה באזור ב נוצר משני המשטחים האלה:
\[E_ב = \frac{6 \cdot 10^{-9}}{2\varepsilon_0} + \frac{6 \cdot 10^{-9}}{2\varepsilon_0} = \frac{6 \cdot 10^{-9}}{\varepsilon_0}\](שני השדות באותו כיוון - מהחיובי לשלילי)
עכשיו אפשר לחשב את הפרש הפוטנציאלים עם $\Delta V = E \cdot D$:
\[\Delta V = \frac{6 \cdot 10^{-9}}{\varepsilon_0} \cdot 0.1\] \[\Delta V = \frac{6 \cdot 10^{-9}}{8.854 \cdot 10^{-12}} \cdot 0.1\] \[= \frac{6 \cdot 10^{-9} \cdot 0.1}{8.854 \cdot 10^{-12}}\] \[= \frac{6 \cdot 10^{-10}}{8.854 \cdot 10^{-12}}\] \[= \frac{600}{8.854} \approx 67.7\]
סעיף 3: כוח חשמלי על לוח 2
מהו הכוח החשמלי (בניוטונים) הפועל על יחידת שטח של לוח $\text{II}$?
הנוסחה לכוח על מטען:
\[F = qE\]במקרה שלנו צריך להתאים ליחידת שטח (לחץ?)
כוח על שטח טעון:
אם יש לנו שטח $A$ עם צפיפות מטען $\sigma$, אז המטען הכולל הוא:
\[q = \sigma \cdot A\]לכן:
\[F = qE = \sigma A \cdot E\]כוח ליחידת שטח:
\[\frac{F}{A} = \sigma \cdot E\]במקרה שלנו:
\[\frac{F}{A} = \sigma_{II} \cdot E_{I} = -6 \cdot 10^{-9} \cdot \frac{10 \cdot 10^{-9}}{2\epsilon_0}\] \[\frac{F}{A} = 6 \cdot 10^{-9} \cdot \frac{10 \cdot 10^{-9}}{2 \cdot 8.854 \cdot 10^{-12}}\] \[= \frac{60 \cdot 10^{-18}}{17.7 \cdot 10^{-12}}\] \[= \frac{60 \cdot 10^{-18}}{1.77 \cdot 10^{-11}}\] \[\approx 3.4 \cdot 10^{-6} \text{ N/m}^2\]סעיף 4: צפיפות המטענים על השפה הימנית של 1
מה צפיפות המטענים (ביחידות של קולון למטר בריבוע) על השפה הימנית של לוח $\text{I}$?
במקור חשבתי שש (כך פתרתי את התרגיל הראשון) אבל זה שגוי.
כלל ידוע למודלי MML: בשני לוחות מוליכים מקבילים, המטען על שני הצדדים החיצוניים שווה ומתחלק:
\[\sigma_{external} = \frac{\sigma_1 + \sigma_2}{2} = \frac{(10-6) \cdot 10^{-9}}{2} = 2 \cdot 10^{-9}\]
אז על הצדדים הפנימיים:
- לוח I פנימי: $10 - 2 = 8 \cdot 10^{-9}$
- לוח II פנימי: $-6 - 2 = -8 \cdot 10^{-9}$
פתרון שיטתי יותר (כמו זה שפורסם).
בתוך לוח 1 השדה הוא אפס, המטענים מצטברים על הדפנות. נסמן $\sigma_1 ‘$ את הצפיפות על דופן ימין (הפנימית), אז הצפיפות בדופן שמאל (החיצונית) היא: $\sigma_1 - \sigma_1 ‘$.
עכשיו החלק שלא הבנתי עד הסוף, למה:
\[\sigma_1 ' = |\sigma_2| +\sigma_1 - \sigma_1 '\]הסבר:
זה מגיע מהתנאי שהשדה בתוך המוליך חייב להיות אפס.
בתוך לוח I, השדה הכולל = 0:
השדות שמשפיעים על נקודה בתוך לוח I:
הצד השמאלי של לוח I ($\sigma_1 - \sigma_1’$): שדה ימינה → $+\frac{\sigma_1 - \sigma_1’}{2\varepsilon_0}$
הצד הימני של לוח I ($\sigma_1’$): שדה שמאלה ← $-\frac{\sigma_1’}{2\varepsilon_0}$
הצד השמאלי של לוח II ($-|\sigma_2|$): שדה ימינה (לכיוון השלילי) → $+\frac{|\sigma_2|}{2\varepsilon_0}$
הצד הימני של לוח II: תורם גם, אבל בגלל סימטריה אפשר להתעלם כאן
התנאי:
\[\frac{\sigma_1 - \sigma_1'}{2\varepsilon_0} + \frac{|\sigma_2|}{2\varepsilon_0} = \frac{\sigma_1'}{2\varepsilon_0}\]נכפיל ב-$2\varepsilon_0$:
\[\sigma_1 - \sigma_1' + |\sigma_2| = \sigma_1'\]

נוסחאות
חוק קולון:
\[F = k \frac{q_1 q_2}{r^2}\]שדה חשמלי של מטען נקודתי:
\[E = k \frac{q}{r^2}\]קבוע קולון:
\[k = 8.99 \times 10^9 \, \frac{N \cdot m^2}{C^2}\]חוק ניוטון השלישי:
\[\vec{F}_{12} = -\vec{F}_{21}\]מונחים
- שדה חשמלי (Electric field) - עוצמה וכיוון הכוח ליחידת מטען
- סופרפוזיציה - שדות/כוחות מסתכמים וקטורית
- מטען נקודתי - מטען שכל מימדיו זניחים ביחס למרחק
- שיווי משקל חשמלי - נקודה בה השדה או שקול הכוחות מתאפס
פתרון תרגיל 4 - שדות אנרגיות ופוטנציאלים
תאריך: 14/12/2025שאלה 1: חשבונות שדה
הפתרונות המלאים זמינים בתרגול 6.
שאלה 2: אנרגיה, פוטנציאל ותנועה במערכת מטענים על משולש שווה־צלעות
על קודקודיו של משולש שווה צלעות שאורך צלעו הוא $a$ ממקמים שלושה מטנים חשמליים. שניים חיובים זהים בגודל $q$ השלישי מטען שלילי $-Q$ ומסתו $m$. המשולש כולו מונח על משטח אופקי כך שהכבידה לא משחק תפקיד בבעייה.
סעיף א: מציאת גודל מטען שנדרש לאיפוס המערכת
מה צריך להיות גודלו של המטען השלילי כדי שהאנגיה האלקטוסטאלית של כל המערכת תהיה בדיוק אפס?
צריך לעשות סופר פוזיציה על כל הזוגות (שלושה):
\[U_{tot} = \frac{kq^2}{a} + \frac{kq(-Q)}{a} + \frac{kq(-Q)}{a}\] \[= \frac{kq}{a}(q-2Q)\]אז בשביל שיתאפס:
\[q-2Q = 0 \implies Q = -\frac{1}{2}\]שאלו על גודל אז עקרונית הסימן לא משנה.
סעיף ב: חישוב הפוטנציאל בנקודת הקודקוד המכילה את המטען השלילי
מהו הפוטנציאל בנקודת הקודקוד המכילה את המטען השלילי?

אלה ההשפעות של שני החיוביים עליה:
\[V = \frac{2kq}{a}\]טעויות אפשריות:
- המטען השלילי $(-Q)$ לא נכנס כאן לחישוב! סוכמים רק את המטענים החיוביים, כאשר הפוטנציאל שלהם הוא פשוט פוטנציאל נקודתי כמו להביא את המטען הנקודתי מאינסוף.
הערה כללית: הפוטנציאל חיובי כי הוא נוצר על ידי מטענים חיוביים.
סעיף ג: חישוב הפוטנציאל במרכז המשולש
מה הפוטנציאל במרכז המשולש הנגרם על ידי שני המטענים החיוביים?
המרחק בין מרכז משולש שווה צלעות עם צלע $a$ לקודקוד הוא:
\[d = \frac{a}{\sqrt{3}}\]אז הפוטנציאל במרכז הוא:
\[V_{center} = \frac{2kq}{\frac{a}{\sqrt{3}}} = \frac{2\sqrt{3}kq}{a}\]סעיף ד: חישוב מהירות, תאוצה ועבודה על המטען השלילי
מאפשרים למטען השלילי חופש תנועה וכתוצאה מכך הוא מאיץ לעבר מרכז המשולש.
1. מה תהיה המהירות שלו במרכז המשלוש?
אפשר להיעזר בפוטנציאלים שמצאנו ובשימור אנרגיה:
\[U_i + \cancel{\frac{1}{2}mv_i^2} = U_f + \frac{1}{2}mv^2\] \[\frac{1}{2}mv^2 = (-Q)V_i - (-Q)V_f\] \[\frac{1}{2}mv^2 = - Q \frac{2kq}{a} + Q \frac{2\sqrt{3}kq}{a}\] \[v^2 = \frac{Q4k}{am}( - 1 + \sqrt{3})\] \[v = \sqrt{\frac{Q4k}{am}(\sqrt{3} - 1)}\]טעויות שהיו לי:
השתמשתי במטען $q$ במקום $-Q$ כשחישבתי את האנרגיה הפוטנציאלית. כלומר, הנה דוגמה לטעות:
\[\frac{1}{2}mv^2 = qV_i - qV_f\] \[\frac{1}{2}mv^2 = q \frac{2kq}{a} - q \frac{2\sqrt{3}kq}{a}\] \[v^2 = \frac{q4k}{am}(1 - \sqrt{3})\] \[v = \sqrt{\frac{q4k}{am}(1 - \sqrt{3})}\]
2. מה תהיה התאוצה שלו במרכז המשולש?
אני חושב שאפשר לפתור עם ניוטון:
\[F = mA\]מצד שני
\[F = QE\]והשדה במרכז דורש חישוב.
משיקולי סימטריה רק הרחיבים בכיוון הציר של המרכז שורדים (נניח מעלה).
בלי הכיוון:
\[E_1 = E_2 = \frac{kq}{d^2} = \frac{kq}{\left(\frac{a}{\sqrt{3}}\right)^2} = \frac{3kq}{a^2}\]לאחר הכיוון הם נסכמים - יש לי כאן טעות, זה לא קוסינוס שישים הזווית כנראה יותר קשורה לשלושים. אתקן בהמשך.
\[E = \frac{6kq}{a^2} \cos(60) = \frac{6kq}{a^2} \cdot \frac{1}{2}\]אז:
\[\frac{6kq}{a^2} = mA\] \[A = \frac{6kq}{ma^2}\]להזהר לא להתבלבל בסימונים: $a$ קטנה משמש כאן לצלע.
3. כמה עבודה נדרשת על מנת להחזירו ממרכז המשולש לקודקוד בו היה ממוקם מראש?
\[W = (-Q)\left(V_f - V_i\right)\] \[W = (-Q)\left(\frac{2kq}{a} - \frac{2\sqrt{3}kq}{a}\right)\] \[W = \frac{-2Qkq}{a}\left(1 - \sqrt{3}\right)\]זאת האנרגיה הקינטית שהרוויח בנפילה, והיא חיובית.
\[\boxed{W = \frac{2Qkq}{a}(\sqrt{3} - 1)}\]שאלה 3: פוטנציאל חשמלי בגליל מוליך עם מעטפת גלילית מוארקת
גליל מוליך ארוך מאוד אשר רדיוסו הוא $a$ טעון בצפיפות מטען אורכית $\lambda$ קולון ליחידת אורך של הגליל. סביב הגליל מונחת מעטפת גלילית דקה ומוארקת ברדיוס $b>a$, כך שציר הגליל וציר המעטפת הגלילית מתלכדים. מהו הפוטנציאל החשמלי בכל המרחב?
הנחייה: מיצאו את השדה והביאו חלקיק מן האינסוף כנגד (או עם) השפעת השדה.

גם לתרגיל הזה קיים פתרון מפורט בתרגול 6. להלן פתרון נוסף:
נתחיל מחישוב פוטנציאל.
בתוך מוליך פוטנציאל אפס:
\[E(r<a) = 0\]על המוליך עצמו יש נוחסה:
בין המוליך למעטפת - יש נוסחה:
\[E(a<r<b) = \frac{\lambda}{2\pi\epsilon_0 r}\]מחוץ - המעטפת מוארקת ולהבנתי השדה מנוטרל:
\[E(r<b)=0\]מציאת הפוטנציאל - מבחוץ לבפנים:
\[V(b)=0\]בגלל הארקה.
אזור $a < r < b$:
\[V(a < r < b) = -\int_b^r E \, dr' = -\int_b^r \frac{\lambda}{2\pi\varepsilon_0 r'} dr' = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{r}\right)\]אזור $r < a$:
פוטנציאל קבוע בתוך מוליך, שווה לערך על השפה:
\[V = V(a) = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right)\]סיכום:
\[V(r) = \begin{cases} \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right) & r < a \\ \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{r}\right) & a < r < b \\ 0 & r > b \end{cases}\]
שאלה 4: כדור מוליך עם הארקות
גם לתרגיל הזה קיים פתרון מפורט בתרגול 6.
שאלה 5: אנרגיה פוטנציאלית של קונפיגורציות מטענים בקובייה
נתונה קוביה אשר אורך צלעה הוא $a$.
במקרה ראשון מניחים מטען חשמלי $+q$ על כל אחד מקוקודי הקוביה. מהי האנרגיה הפוטנציאלית האגורה בקונפיגורציית מטענים זו?
במקרה השני מניחים על ארבעת הקודקודים העליונים מטען חשמלי שלילי שגודלו הוא $-q$ ועל ארבעת הקוקודים התחתונים מטען חשמלי חיובי שגודלו הוא $+q$. מהי האנרגיה הפוטנציאלית האגורה בקונפיגורציית מטענים זו?

סעיף 1 - רק מטענים חיוביים
קצת קומבינטוריקה. בקובייה יש:
- זוגות שנוצרים מהצלעות - 12 כאלה, במרחק $a$
- זוגות שנוצרים מאלכסונים על פאות - 12 כאלה במרחק $\sqrt{2}a$
- זוגות שנוצרים מאלכסונים בתוך הקובייה - 4 כאלה במרחק $\sqrt{3}a$
אפשר לוודא שזה נסכם למספר הזוגות שמתקבלים מבירה של 8 על 2:
\[\binom{8}{2} = \frac{8!}{6!\cdot 2} = 7 \cdot 4 = 28\]
עכשיו נסכום:
\[U_{tot} = 12 \frac{kq^2}{a} + 12 \frac{kq^2}{\sqrt{2}a} + 4 \frac{kq^2}{\sqrt{3}a}\] \[= 4 \frac{kq^2}{a} \left(3 + 3 \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}}\right)\]או בצורה מסודרת:
\[\boxed{U = \frac{4kq^2}{a} \left(3 + \frac{3\sqrt{2}}{2} + \frac{\sqrt{3}}{3}\right)}\]סעיף 2 - שינוי המטען
מסתבר שזה לא מתאפס - למרות שיש ארבעה חיוביים וארבעה שליליים המרחקים שונים.
התאצלתי לסכום, להלן פתרון מג׳ונרט:
בסעיף 2 צריך לבדוק את הסימנים של כל סוג זוג:
צלעות (12 זוגות, מרחק $a$):
- צלעות אופקיות (על הפאה העליונה): 4 זוגות $(-q)(-q) = +q^2$
- צלעות אופקיות (על הפאה התחתונה): 4 זוגות $(+q)(+q) = +q^2$
- צלעות אנכיות: 4 זוגות $(+q)(-q) = -q^2$
סה”כ צלעות: $4 + 4 - 4 = 4$ זוגות “חיוביים”
אלכסוני פאות (12 זוגות, מרחק $\sqrt{2}a$):
- על הפאה העליונה: 2 זוגות $(-q)(-q) = +q^2$
- על הפאה התחתונה: 2 זוגות $(+q)(+q) = +q^2$
- על 4 הפאות האנכיות: 8 זוגות $(+q)(-q) = -q^2$
סה”כ אלכסוני פאות: $2 + 2 - 8 = -4$ זוגות
אלכסוני קובייה (4 זוגות, מרחק $\sqrt{3}a$):
כל אלכסון מחבר קודקוד עליון לתחתון: $(+q)(-q) = -q^2$
סה”כ: $-4$ זוגות
נסכום:
\[U = \frac{kq^2}{a}\left(4 \cdot 1 - 4 \cdot \frac{1}{\sqrt{2}} - 4 \cdot \frac{1}{\sqrt{3}}\right)\] \[= \frac{4kq^2}{a}\left(1 - \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{3}}\right)\]המספר בסוגריים הוא בערך $1 - 0.707 - 0.577 \approx -0.28$
אז האנרגיה שלילית, מה שהגיוני - יש יותר זוגות של מטענים מנוגדים (שמושכים) מאשר זוגות של מטענים זהים (שדוחים).
שאלה 6
גם לתרגיל הזה קיים פתרון מפורט בתרגול 6.
שאלה 7: מטענים ופוטנציאל במערכת כדור מוליך וקליפה כדורית מוליכה קונצנטרית
כדור מוליך בעל רדיוס $a$ טעון במטען חיובי $+3Q$ ומצא בתוך קליפה כדורית מוליכה בעלת רדיוס פנימי $b$ ורדיוס חיצוני $c$, הטעונה במטען $-Q$. לכדור ולקליפה הכדורית יש מרכז משותף.
מהו המטען על השפה החיצונית $(r=c)$ של הקליפה הכדורית?
מהו הפוטנציאל החשמלי על השפה הפנימית $(r=b)$ של הקליפה הכדורית? הנח שהפוטנציאל באינסוף הוא אפס.
מהו הפוטנציאל החמשלי במרכז הכדור $(r=0)$ ? הנח שהפוטנציאל באינסוף הוא אפס.
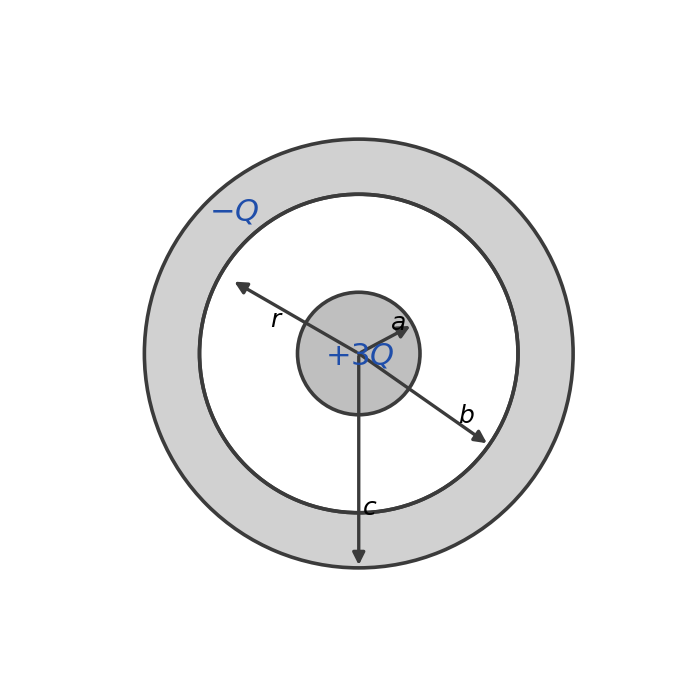
סעיף 1 - המטען על השפה החיצונית של הקליפה
הכדור מוליך אז המטענים יהיו על המעטפת שלו.
גם הקליפה הכדורית אבל להבנתי זה יתחלק כך שחלק אולי יתאזנו עם האמצע?
נכון, בדיוק!
העיקרון: בתוך מוליך השדה חייב להיות אפס. לכן אם ניקח משטח גאוסי בתוך החומר של הקליפה ($b < r < c$), השדה שם אפס, ולכן המטען הכלוא חייב להיות אפס.
מה קורה:
על השפה הפנימית ($r=b$) יישב מטען $-3Q$ כדי לאזן את השדה מהכדור הפנימי.
המטען הכולל על הקליפה הוא $-Q$, אז משימור מטען:
\[Q_{inner} + Q_{outer} = -Q\] \[-3Q + Q_{outer} = -Q\] \[Q_{outer} = +2Q\]
הפוטנציאל החשמלי על השפה הפנימית
דרך מקוצרת:
בתוך מוליך הפוטנציאל קבוע, ושווה לפוטנציאל על השפה החיצונית שלו. במקרים שאין השפעה מבחוץ מה שבפנים כנראה מתבטבל, להבנתי. אולי אפשר לחשוב על זה כעבודה להבאת מטען יחיד מאינסוף לנקודה.
במקרה שלנו השפה החיצונית במרחק $c$ ובמטען $+2Q$, לכן:
\[V(r=b) = \frac{2kQ}{c}\]
להלן גם חישוב מלא.
לחישוב פוטנציאל משתמשים במרחק מהמרכז, לא במרחק מהשפה!
הפוטנציאל בנקודה $r=b$ נוצר מכל התפלגויות המטען. עבור קליפות כדוריות וכדורים:
- מטען על כדור/קליפה ברדיוס $R$: אם אנחנו בחוץ ($r > R$), הפוטנציאל הוא $\frac{kQ}{r}$
- אם אנחנו בפנים ($r < R$), הפוטנציאל הוא $\frac{kQ}{R}$ (קבוע!)
בנקודה $r = b$ יש שלושה תרומות:
-
הכדור הפנימי ($+3Q$ על $r=a$): אנחנו בחוץ, אז $\frac{k(+3Q)}{b}$
-
השפה הפנימית של הקליפה ($-3Q$ על $r=b$): אנחנו בדיוק עליה, אז $\frac{k(-3Q)}{b}$
-
השפה החיצונית ($+2Q$ על $r=c$): אנחנו בפנים, אז $\frac{k(+2Q)}{c}$
דוגמה לטעות שלי - חישוב ההשפעה מהקצה במקום מהמרכז:
יש עליה השפעה מבפנים ומבחוץ וצריך לסכום:
- ההשפעה של הקליפה החיצונית - במרחק של $c-r$ ממנה - טעות! המרחק הוא מהמרכז!
- ההשפעה של הפנימית במרחק של $b-a$ - טעות! רק b.
- גם פספסתי את ההשפעה של הצד הפנימי של הקליפה החיצונית (שלמעשה מתבטל עם הפנימי).
הפוטנציאל החשמלי במרכז הכדור
השדה אפס אבל הפוטנציאל לא. במקרה הזה יש השפעות חיצוניות שלא מתבטלות וצריך לסכום. אפשר לחשוב על להביא חלקיק מהאינסוף?
נסכום:
- החיצונית משפיעה $\frac{2kQ}{c}$
- החלק הפנימי של החיצונית: $\frac{-3kQ}{b}$
- החלק החיצוני של הפנימי: $\frac{3kQ}{a}$
סך הכל:
\[V_{ball} = k\left(\frac{3Q}{a}+\frac{-3Q}{b}+\frac{2Q}{c}\right)\]