פיזיקה ב׳ (חשמל) - כל שיעורי הבית והתרגולים להדפסה

כל התכנים בעמוד אחד

כל סיכומי התרגולים והצעות הפתרון לשיעורי הבית בקורס פיזיקה ב׳ זמינים כאן להדפסה מרוכזת או לייצוא כ-PDF. התוכן מוצג בסדר כרונולוגי - מהסיכומים המוקדמים ביותר למאוחרים ביותר. אם חלק מהעמודים כוללים נוסחאות מתמטיות, ייתכן שייקח להן מספר שניות להיטען. למידה מהנה!

תוכן העניינים

תרגול 1 - וקטורים ומכפלות 26/10/2025
תרגול 2 - גרדיאנט, דיברגנץ ורוטור 02/11/2025
תרגול 3 - שדה חשמלי וחוק גאוס 16/11/2025
תרגול 4 - התפלגות מטען לא אחידה ושדה חשמלי 23/11/2025
תרגול 5 - שדות חשמליים, אנרגיה פוטנציאלית וחוק גאוס 30/11/2025
תרגול 6 - פוטנציאל חשמלי ומוליכים 07/12/2025
פתרון בוחן לדוגמה - גרסת ג׳מני 2025 08/12/2025
הצעת פתרון - בוחן אמצע גרסת קלוד 12/12/2025
הצעת פתרון - בוחן אמצע תשפה 12/12/2025

תרגול 1 - וקטורים ומכפלות

תאריך: 26/10/2025

חזרה על וקטורים

וקטור יחידה
חיבור וקטורי (כבר עבדנו עליו במכניקה - חיבור מהירויות, חיבור כוחות)
כפל סקלרי
מעבר מקורדינטות קרטזיות לפולריות

מכפלה סקלרית (Scalar Product)

הגדרה

המכפלה הסקלרית היא פעולה שלוקחת שני וקטורים והתוצאה היא מספר ממשי (לא וקטור).

תכונות

כאשר מכפילים וקטור בעצמו מכפלה סקלרית: $\vec{a} \cdot \vec{a} \geq 0$

התוצאה תמיד חיובית, אלא אם כן הוקטור עצמו אפס.

נוסחאות

בקורדינטות קרטזיות: סכום המכפלות של הרכיבים
\[\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z\]
ביטוי גיאומטרי:
\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos\theta\]
כאשר $\theta$ היא הזווית המרחבית בין הוקטורים.

שימושים

בדיקת ניצבות: אם $\vec{a} \cdot \vec{b} = 0$ אז הוקטורים ניצבים
חישוב זווית במרחב:
\[\cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}\]
התוצאה תמיד בין $-1$ ל-$1$ (גם במרחב ארבע ממדים, חמש ממדים, ואפילו בפונקציות)

מכפלה וקטורית (Vector Product / Cross Product)

תוצאה ותכונות

התוצאה היא וקטור (בניגוד למכפלה סקלרית)
הוקטור המתקבל ניצב למישור שנפרש על ידי $\vec{a}$ ו-$\vec{b}$
הכיוון נקבע לפי כלל יד ימין

נוסחה

\[\boxed{\vec{a} \times \vec{b} = \hat{x}(y_a z_b - z_a y_b) + \hat{y}(z_a x_b - x_a z_b) + \hat{z}(x_a y_b - y_a x_b)}\]

גודל

\[\boxed{|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| |\sin\theta |}\]

כיוון לפי כלל יד ימין

(מוזמנים לקרוא בהרחבה בשיעור על וקטורים)

שימושים

מציאת וקטור הניצב למישור של שני וקטורים
אם $\vec{a} \times \vec{b} = 0$ אז הוקטורים מקבילים

פונקציות סקלריות במרחב

הגדרה

פונקציה סקלרית: $\phi: \mathbb{R}^3 \to \mathbb{R}$

פונקציה שלוקחת שלושה משתנים $(x, y, z)$ ומחזירה מספר.

דוגמה: פוטנציאל חשמלי - $V(x, y, z)$

הגרדיאנט (Gradient)

הגדרה

\[\nabla\phi = \frac{\partial\phi}{\partial x}\hat{x} + \frac{\partial\phi}{\partial y}\hat{y} + \frac{\partial\phi}{\partial z}\hat{z}\]

כאשר $\frac{\partial\phi}{\partial x}$ היא נגזרת חלקית - נגזרת לפי $x$ כאשר $y$ ו-$z$ קבועים.

פרשנות פיזיקית

כיוון השינוי המרבי: הגרדיאנט מצביע לכיוון שבו הפונקציה משתנה הכי מהר
גודל השינוי: $|\nabla\phi|$ מייצג את קצב השינוי המרבי
ניצב למשטח: הגרדיאנט ניצב למישור המשיק למשטח $\phi = const$

תרגיל מכפלה סקלרית ווקטורית

נתונים שני וקטורים:
\[\vec{A} = 2\hat{x} + 3\hat{y} + 4\hat{z}\] \[\vec{B} = -\hat{x} + 2\hat{y} + 3\hat{z}\]
מיצאו את קוסינוס וסינוס הזווית בין שני הווקטורים.

מצאו את כל הווקטורים הניצבים לווקטור:
\[\vec{C} = e\hat{x} + \pi\hat{y} + \hat{z}\]
רישמו את הווקטור $\vec{C}$ בקורואדינטות כדוריות $(r, \theta, \phi)$.

עבור אילו ערכים של $\alpha$, $\beta$ הווקטורים:
\[\begin{aligned} \vec{A} &= 3\hat{x} + \alpha\hat{y} + 5\hat{z} \\ \vec{B} &= -2\hat{x} + \alpha\hat{y} - 2\beta\hat{z} \end{aligned}\]
מצביעים באותו כיוון (קוליניאריים)?

פתרון תרגיל 1

בשביל הקוסינוס ניעזר בנוסחה של המכפלה הסקלרית:

\[\boxed{\vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos\theta}\]

נבודד ונציב:

\[\begin{aligned} \cos\theta &= \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|} \\ &= \frac{(2)(-1) + (3)(2) + (4)(3)}{\sqrt{2^2 + 3^2 + 4^2} \sqrt{(-1)^2 + 2^2 + 3^2}} \\ &= \frac{-2 + 6 + 12}{\sqrt{4 + 9 + 16} \sqrt{1 + 4 + 9}} \\ &= \frac{16}{\sqrt{29} \sqrt{14}} \\ &= \frac{16}{\sqrt{406}} \approx 0.79 \end{aligned}\]

בשביל הסינוס נשתמש בנוסחה של המכפלה הווקטורית:

\[\boxed{|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin\theta}\]

כדי לפתח את המכפלה הווקטורית נשתמש בדטרמיננטה (בשיעור דווקא נעזרנו בהגדרה המפורטת):

\[\begin{aligned} \vec{A} \times \vec{B} &= \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ 2 & 3 & 4 \\ -1 & 2 & 3 \end{vmatrix} \\ &= \hat{x}(3 \cdot 3 - 4 \cdot 2) - \hat{y}(2 \cdot 3 - 4 \cdot -1) + \hat{z}(2 \cdot 2 - 3 \cdot -1) \\ &= \hat{x}(9 - 8) - \hat{y}(6 + 4) + \hat{z}(4 + 3) \\ &= \hat{x}(1) - \hat{y}(10) + \hat{z}(7) \\ &= \hat{x} - 10\hat{y} + 7\hat{z} \end{aligned}\]

כדי למצוא את גודל הווקטור המתקבל:

\[\begin{aligned} |\vec{A} \times \vec{B}| &= \sqrt{1^2 + (-10)^2 + 7^2} \\ &= \sqrt{1 + 100 + 49} = \sqrt{150} = 5\sqrt{6} \end{aligned}\]

נציב את גודל המכפלה הווקטורית ואת גודל הווקטורים בזהות:

\[\begin{aligned} \sin\theta &= \frac{|\vec{A} \times \vec{B}|}{|\vec{A}| |\vec{B}|} = \frac{5\sqrt{6}}{\sqrt{29} \sqrt{14}} = \frac{5\sqrt{6}}{\sqrt{406}} \approx 0.608 \end{aligned}\]

סך הכל:

\[\boxed{\cos\theta \approx 0.79, \quad \sin\theta \approx 0.608}\]

אפשר לבדוק בעזרת זהויות טריגונומטריות (גם ניתן לקבל את הסינוס ישירות מהקוסינוס):

\[\sin\theta = \sqrt{1 - \cos^2\theta} = \sqrt{1 - (0.79)^2} \approx 0.608\]

או לחלופין:

\[\sin^2\theta + \cos^2\theta = 1 \implies 0.608^2 + 0.79^2 \approx 1\]

לא הספקנו לפתור את תרגילים 2 ו-3 בכתה.

פתרון תרגיל 2

וקטור ניצב למישור חייב לקיים:

\[\vec{C} \cdot \vec{D} = 0\]

נגדיר את הווקטור הניצב כ:

\[\vec{D} = d_x \hat{x} + d_y \hat{y} + d_z \hat{z}\]

נחשב את המכפלה הסקלרית:

\[\begin{aligned} \vec{C} \cdot \vec{D} &= (e)(d_x) + (\pi)(d_y) + (1)(d_z) = 0 \\ &\Rightarrow ed_x + \pi d_y + d_z = 0 \\ &\Rightarrow d_z = -ed_x - \pi d_y \end{aligned}\]

כל זוג ערכים של $d_x$ ו-$d_y$ ייתן לנו ערך יחיד של $d_z$. לכן יש אינסוף וקטורים ניצבים ל-$\vec{C}$.

רישום בקורדינטות כדוריות:

\[\begin{aligned} r &= \sqrt{e^2 + \pi^2 + 1^2} \\ \theta &= \arccos\left(\frac{1}{r}\right) \\ \phi &= \arctan\left(\frac{\pi}{e}\right) \end{aligned}\]

פתרון תרגיל 3

מוזמנים להשלים.

תרגילי גרדיאנט

הבהרה: הגרדיאנט ניצב למשטח המשיק לשדה $f(x,y,z)=const$ בנקודה נתונה.

מהו וקטור היחידה הניצב למישור המשיק למשטח $xyz=6$ בנקודה $(2,-1, -3)$?

מהי הזווית בין הוקטור היצב למישור המשיק למשטח $x^2y = z$ בנקודה $(-2,1,4)$ לבין הוקטור הניצב למישור המשיק למשטח $x^3y^4 = z+2$ בנקודה $(2,-1,6)$?

נתון שדה הלחץ: $A(x,y,z,t)=x^2+y^2t-2z$ כך ש-$x,y,z$ במטרים ו-$t$ בשניות.

מהו הגרדיאנט של $A$?

מהו גודל הגרדיאנט בנקודה $(4,1,10)$ לאחר 2 שניות?

מהו הרכיב (ההיטל) של הגרדיאנט בכיוון $r=6x\hat{x}-\hat{y}+y\hat{z}$?

תלות בזמן

פונקציה יכולה להיות תלויה לא רק ב-$x, y, z$ אלא גם בזמן $t$
כל הפרמטרים (כולל הפוטנציאל) יכולים להשתנות בזמן ובמקום
כאשר מחשבים נגזרת חלקית לפי זמן, מציבים את הזמן כקבוע (לא גוזרים לפי זמן)

דוגמה לפונקציה

\[\phi(x,y,z,t) = 2x + x^3 + 2y + y^3 - 2z\]

הערה: הזמן $t$ הוא פרמטר נוסף של הפונקציה

הגרדיאנט ותלות בזמן

הגרדיאנט הוא שיפוע מרחבי בלבד - לא שיפוע הקשור בזמן
גם אם המשטח עצמו משתנה בזמן, הגרדיאנט עדיין מחושב רק לפי הקוורדינטות המרחביות
הזמן הוא פרמטר שמשפיע על הפונקציה, אך אינו חלק מהגרדיאנט

שאלה: האם זמן הוא ממד מרחבי?

במובן מסוים, המרחב יכול להיות ארבעה ממדי (כולל זמן)
אבל: זה לא רלוונטי לחישוב הגרדיאנט
הגרדיאנט מתייחס רק לשיפוע המרחבי, לא לשינויים בזמן

הבהרה:

כאשר כותבים $\phi(x,y,z,t)$, הזמן $t$ הוא פרמטר נוסף
ניתן לכתוב זאת באופן מפורש יותר כ-$\phi(x,y,z; t)$ כדי להבהיר שהזמן הוא פרמטר ולא קוורדינטה מרחבית

בעיית יחידות

שאלה: איך מודדים זמן ביחידות של מרחב (שניות במטרים)?

זוהי בעיה של יחידות - זמן ומרחב נמדדים ביחידות שונות

פתרון תרגיל 1

נחשב את הגרדיאנט של הפונקציה:

\[f(x,y,z) = xyz\] \[\nabla f = \frac{\partial f}{\partial x}\hat{x} + \frac{\partial f}{\partial y}\hat{y} + \frac{\partial f}{\partial z}\hat{z}\] \[\begin{aligned} \frac{\partial f}{\partial x} &= yz \\ \frac{\partial f}{\partial y} &= xz \\ \frac{\partial f}{\partial z} &= xy \end{aligned}\] \[\nabla f = yz\hat{x} + xz\hat{y} + xy\hat{z}\]

נחשב את הגרדיאנט בנקודה $(2,-1,-3)$:

\[\begin{aligned} \nabla f(2,-1,-3) &= (-1)(-3)\hat{x} + (2)(-3)\hat{y} + (2)(-1)\hat{z} \\ &= 3\hat{x} - 6\hat{y} - 2\hat{z} \end{aligned}\]

כדי למצוא את וקטור היחידה, נחלק את הווקטור בגודלו:

\[|\nabla f(2,-1,-3)| = \sqrt{3^2 + (-6)^2 + (-2)^2} = \sqrt{9 + 36 + 4} = \sqrt{49} = 7\]

וקטור היחידה הוא:

\[\hat{n} = \frac{1}{7}(3\hat{x} - 6\hat{y} - 2\hat{z}) = \frac{3}{7}\hat{x} - \frac{6}{7}\hat{y} - \frac{2}{7}\hat{z}\]

פתרון תרגיל 2

נחשב את הגרדיאנט של הפונקציה הראשונה:

\[f_1(x,y,z) = x^2 y - z\] \[\nabla f_1 = \frac{\partial f_1}{\partial x}\hat{x} + \frac{\partial f_1}{\partial y}\hat{y} + \frac{\partial f_1}{\partial z}\hat{z}\] \[\begin{aligned} \frac{\partial f_1}{\partial x} &= 2xy \\ \frac{\partial f_1}{\partial y} &= x^2 \\ \frac{\partial f_1}{\partial z} &= -1 \end{aligned}\] \[\nabla f_1 = 2xy\hat{x} + x^2\hat{y} - \hat{z}\]

נחשב את הגרדיאנט בנקודה $(-2,1,4)$:

\[\begin{aligned} \nabla f_1(-2,1,4) &= 2(-2)(1)\hat{x} + (-2)^2\hat{y} - \hat{z} \\ &= -4\hat{x} + 4\hat{y} - \hat{z} \end{aligned}\]

נחשב את הגרדיאנט של הפונקציה השנייה:

\[f_2(x,y,z) = x^3 y^4 - (z + 2)\] \[\nabla f_2 = \frac{\partial f_2}{\partial x}\hat{x} + \frac{\partial f_2}{\partial y}\hat{y} + \frac{\partial f_2}{\partial z}\hat{z}\] \[\begin{aligned} \frac{\partial f_2}{\partial x} &= 3x^2 y^4 \\ \frac{\partial f_2}{\partial y} &= 4x^3 y^3 \\ \frac{\partial f_2}{\partial z} &= -1 \end{aligned}\] \[\nabla f_2 = 3x^2 y^4\hat{x} + 4x^3 y^3\hat{y} - \hat{z}\]

נחשב את הגרדיאנט בנקודה $(2,-1,6)$:

\[\begin{aligned} \nabla f_2(2,-1,6) &= 3(2^2)(-1)^4\hat{x} + 4(2^3)(-1)^3\hat{y} - \hat{z} \\ &= 3(4)(1)\hat{x} + 4(8)(-1)\hat{y} - \hat{z} \\ &= 12\hat{x} - 32\hat{y} - \hat{z} \end{aligned}\]

כדי למצוא את הזווית בין שני הווקטורים הניצבים, נשתמש במכפלה הסקלרית:

\[\cos\theta = \frac{\nabla f_1 \cdot \nabla f_2}{|\nabla f_1| |\nabla f_2|}\]

נחשב את המכפלה הסקלרית:

\[\begin{aligned} \nabla f_1 \cdot \nabla f_2 &= (-4)(12) + (4)(-32) + (-1)(-1) \\ &= -48 - 128 + 1 \\ &= -175 \end{aligned}\]

נחשב את גדלי הווקטורים:

\[\begin{aligned} |\nabla f_1| &= \sqrt{(-4)^2 + 4^2 + (-1)^2} = \sqrt{16 + 16 + 1} = \sqrt{33} \\ |\nabla f_2| &= \sqrt{12^2 + (-32)^2 + (-1)^2} = \sqrt{144 + 1024 + 1} = \sqrt{1169} \end{aligned}\]

נציב בנוסחה של הקוסינוס:

\[\begin{aligned} \cos\theta &= \frac{-175}{\sqrt{33} \sqrt{1169}} \\ &= \frac{-175}{\sqrt{38577}} \approx -0.89 \end{aligned}\]

סך הכל:

\[\boxed{\cos\theta \approx -0.89}\]

תרגול 2 - גרדיאנט, דיברגנץ ורוטור

תאריך: 02/11/2025

שאלה 1

חשבו את הגרדיאנט של:
\[\phi(r)=\frac{e^{-\lambda r}}{r}\]
$r$ הקואורדינטה הרדיאלית במישור.

מה היחידות של $\lambda$?

אנחנו לא מכירים את הנוסחה של גרדיאנט בקואורדינטות פולריות. ניתן להמיר לקרטזיות ואז לפתח את הביטוי:

\[\phi(\sqrt{x^2 + y^2})\]

אבל זה מבלבל. מגוגל מקבלים שהנוסחה של הגרדיאנט בקואורדינטות פולאריות היא:

\[\nabla \phi = \frac{\partial \phi}{\partial r} \hat{r} + \cancel{\frac{1}{r} \frac{\partial \phi}{\partial \theta} \hat{\theta}}\]

לפונקציה אין ביטוי במישור אנגולרי $\theta$ ולכן החלק השני מתאפס.

נגזור חלקית לפי $r$:

\[\frac{\partial \phi}{\partial r} = -\frac{1}{r^2} e^{-\lambda r} + \frac{1}{r} (-\lambda )e^{-\lambda r}\]

נוסיף את הכיוון הרדיאלי:

\[\boxed{\nabla \phi = \frac{\partial \phi}{\partial r} \hat{r} = \left(-\frac{1}{r^2} e^{-\lambda r} - \frac{\lambda}{r} e^{-\lambda r}\right) \hat{r}}\]

לפי נגזרת של מכפלה.

הבהרה: השתמשנו בכלל המכפלה:
\[(f g)' = f'g + g'f\]
וכן בכלל השרשרת לגבי נגזרת של פונקציה מורכבת (באקספוננט):
\[(e^{-\lambda r})' = (-\lambda r)'e^{-\lambda r} = -\lambda e^{-\lambda r}\]
עקרונית היה ניתן גם בעזרת נגזרת של מנה.

טעויות אפשריות - לשכוח לגזור את הפונקציה באקספוננט:
\[\nabla \phi = \frac{\partial \phi}{\partial r} \hat{r} = -\frac{1}{r^2} e^{-\lambda r} + \frac{1}{r} (-\lambda \textcolor{red}{r})e^{-\lambda r}\]

היחידות של שלמדה הן $\frac{1}{\ell}$ כאשר $\ell$ היא האורך הרלוונטי, למשל מטרים. זה בכלכל שהארגומנט של פונקציית האקספוננט חייב להיות חסר יחידות.

שאלה 2

נתון השדה הוקטורי:
\[\vec{E}(x,y,z) = yz\hat{x} + xz\hat{y} + xy\hat{z}\]
חשבו את הדיברגנץ ואת הרוטור של $\vec{E}$.

נתחיל מהדיברנץ - נגזור את השינוי בכל ציר ונסכום לקבלת סקאלר. כדי שיתאים לדף הנוסחאות נניח ש $E=V$.

\[\frac{\partial V_x}{\partial x} = 0\] \[\frac{\partial V_y}{\partial y} = 0\] \[\frac{\partial V_z}{\partial z} = 0\]

סך הכל:

\[\boxed{\nabla \cdot \vec{E} = 0}\]

נמשיך עם חישוב הרוטור.

\[\text{curl}\,\vec{E} = \vec{\nabla} \times \vec{E} = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_x & E_y & E_z \end{vmatrix}\] \[\begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_x & E_y & E_z \end{vmatrix} = \hat{x}(x -x) - \hat{y}(y -y) + \hat{z}(z - z) = 0\]

שאלה 3

משפט הדיברגנץ:
\[\int_V (\nabla \cdot \vec{F}) \, dV = \int_S (\vec{F} \cdot \hat{n}) \, da = \Phi\]

נתון השדה הוקטורי הקבוע:
\[\vec{V} = 2\hat{x} +3\hat{y} + 4\hat{z}\]
חשבו את השטף של שדה זה דרך:

הרצפה של תיבה ריבועית אשר צלעה באורך 1מ׳, והיא מונחת על מישור $xy$ כך ששתיים מצלעותיה מתלכדות עם הצירים.

המשולש אשר קודקודיו הן הנקודות $(1,0,0),(0,1,0),(0,0,1)$. רמז: משוואת המישור של המשולש היא $x+y+z=1$, בנו שדה נורמלי למשטח.

ניעזר במשפט הדיברגנץ. $\hat{n}$ של התיבה הוא מינוס. $da$ של התיבה הוא שטח התיבה. נחשב את האינטגרל:

\[\int_S (\vec{F} \cdot \hat{n}) \, da = \vec{F} \cdot (-\hat{z}) \cdot 1m^2 = -4 m^2\]

נחשב את השטף דרך המשולש. נחשב את וקטור הנורמל למישור…

תרגול 3 - שדה חשמלי וחוק גאוס

תאריך: 16/11/2025

חזרה על מושגי יסוד

שטף חשמלי

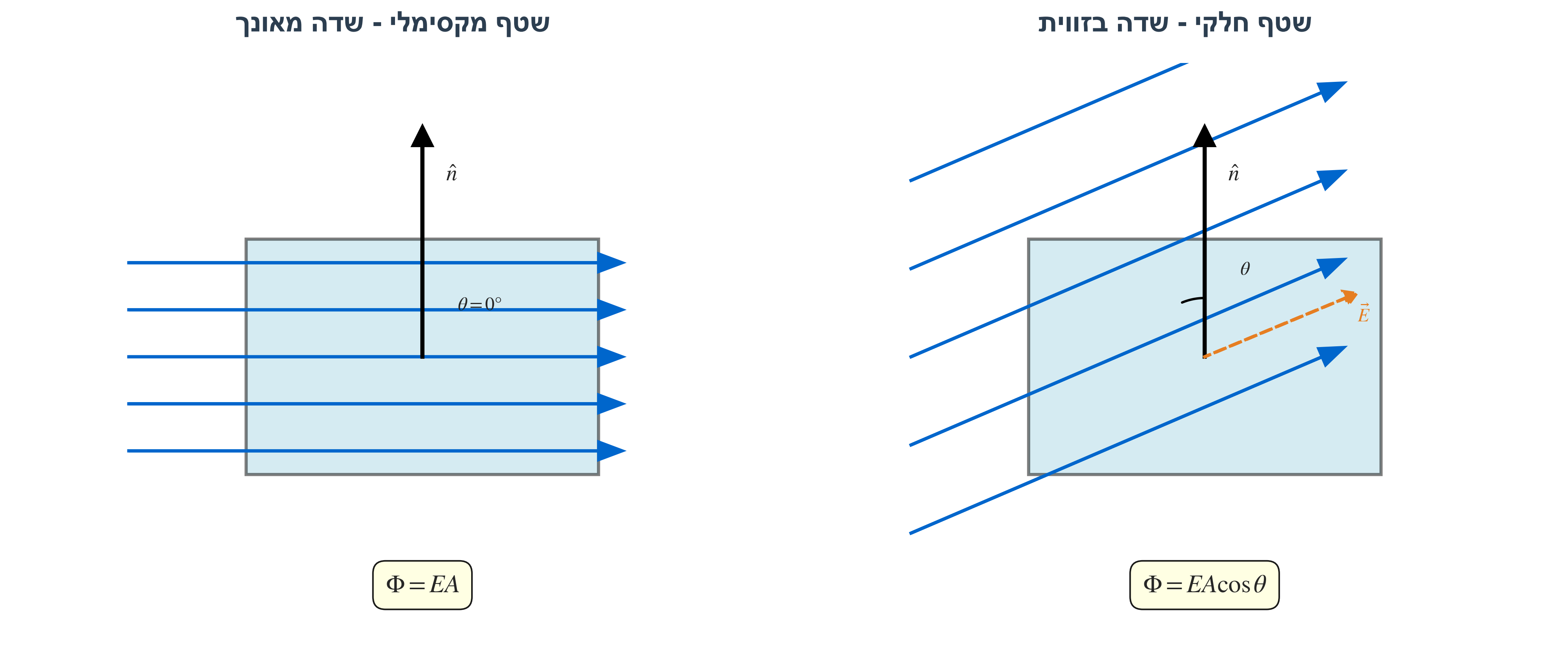
שטף מתאר כמה שדה חשמלי עובר דרך משטח.

כאשר יש שדה חשמלי $\vec{E}$ ומשטח, מפרקים את השדה ל:

רכיב מאונך למשטח - תורם לשטף
רכיב משיק למשטח - לא תורם לשטף

\[\Phi = \oint \vec{E} \cdot d\vec{A} = \oint E \cos\theta \, dA\]

רק הרכיב המאונך יוצא מהמשטח ותורם לשטף.

שדה חשמלי - מקור והשפעה

מי מייצר שדה?

מטען חשמלי $Q$ מייצר סביבו שדה חשמלי.

מי מרגיש שדה?

מטען אחר $q$ שנמצא בשדה מרגיש כוח:

\[\vec{F} = q\vec{E}\]

מטען חיובי ← כוח בכיוון השדה
מטען שלילי ← כוח נגד כיוון השדה

שדה של מטען נקודתי

\[\vec{E} = \frac{kq_1}{r^2}\hat{r}\]

$k \approx 9 \times 10^9 \, \text{N·m}^2/\text{C}^2$ - קבוע קולון
השדה דועך כמו $\frac{1}{r^2}$
מטען חיובי ← שדה יוצא (מעיין)
מטען שלילי ← שדה נכנס (בולען)

צפיפויות מטען

צפיפות קווית $\lambda$

\[\lambda = \frac{dq}{dl} \quad \text{[C/m]}\]

מטען ליחידת אורך.

צפיפות משטחית $\sigma$

\[\sigma = \frac{dq}{dA} \quad \text{[C/m²]}\]

מטען ליחידת שטח.

צפיפות נפחית $\rho$

\[\rho = \frac{dq}{dV} \quad \text{[C/m³]}\]

מטען ליחידת נפח.

עקרון הסופרפוזיציה

כאשר יש רצף של מטענים:

לוקחים אלמנט מטען קטן $dq$
מחשבים את השדה שהוא מייצר: $d\vec{E} = \frac{k \cdot dq}{r^2}\hat{r}$
סוכמים (אינטגרל) על כל המטענים

\[\vec{E} = \int d\vec{E} = \int \frac{k \cdot dq}{r^2}\hat{r}\]

תרגיל 1: שני מטענים שליליים

נתונים שני מטענים נקודתיים זהים $-q$ כל אחד, נמצאים במרחק $2d$ זה מזה על ציר $x$ (אחד ב-$+d$ ואחד ב-$-d$).

האם קיימת נקודה במרחב שבה השדה מתאפס?

מהו השדה ב- $\vec{r}=b\hat{y}$?

מהו הכוח על הפרוטון בנקודה הזו?

סעיף א’: נקודה שבה השדה מתאפס

שאלה: האם קיימת נקודה במרחב שבה השדה מתאפס?

פתרון:

שני המטענים שליליים ← השדה נכנס לכל אחד מהם.

בנקודה בדיוק באמצע (בראשית):

השדה מ-$-q$ הימני מכוון שמאלה
השדה מ-$-q$ השמאלי מכוון ימינה
המרחקים שווים ← הגדלים שווים ← השדות מתבטלים

\[\boxed{\vec{E}(0,0) = 0}\]

בכל נקודה אחרת השדה לא מתאפס.

סעיף ב’: השדה על ציר Y

שאלה: מהו השדה בנקודה $(0, b)$ על ציר $y$?

פתרון:

בנקודה על ציר $y$, כל מטען מייצר שדה לכיוונו (כי הם שליליים).

ניתוח סימטריה:

רכיבי $X$ מתבטלים (סימטריה)
רכיבי $Y$ מתחברים (שניהם כלפי מטה)

\[E_y = - 2 | E | \cos\theta = -2 \cdot \frac{kq}{r^2} \cos\theta = -2 \cdot \frac{kqb}{r^3}\]

כאשר:

\[r = \sqrt{d^2 + b^2}, \quad \cos\theta = \frac{b}{r}\] \[\boxed{E_y = -\frac{2kqb}{(d^2 + b^2)^{3/2}}}\]

(הסימן השלילי מציין כיוון $-\hat{y}$)

סעיף ג’: כוח על פרוטון

שאלה: מהו הכוח על פרוטון בנקודה $(0, Y)$?

פתרון:

\[\vec{F} = q\vec{E} = e \cdot \vec{E}\]

הפרוטון חיובי, לכן הכוח בכיוון השדה (כלפי מטה).

סעיף ד’: תנועת הפרוטון

שאלה: איזו תנועה תהיה לפרוטון?

פתרון:

הכוח פועל כלפי מטה (לכיוון $-Y$). הפרוטון יואץ כלפי מטה.

הערה: התנועה אינה הרמונית פשוטה כי הכוח אינו פרופורציונלי להעתק באופן לינארי.

תרגיל 2: שדה חשמלי של טבעת טעונה

נתונה טבעת ברדיוס $R$ טעונה במטען $Q$ בצפיפות אחידה $\lambda$.

מהו השדה במרכז הטבעת?

מהו השדה בנקודה על ציר הטבעת במרחק $Z$ מהמרכז?

מה קורה לשדה כאשר $Z \gg R$?

מה קורה לשדה כאשר $Z \ll R$?

סעיף א’: השדה במרכז הטבעת

פתרון:

מסימטריה: בכל כיוון שמסתכלים מהמרכז, רואים את אותה תמונה.

לכל אלמנט מטען יש אלמנט מנוגד בצד השני שמבטל את השדה שלו.

\[\boxed{\vec{E}(0) = 0}\]

סעיף ב’: השדה על הציר (בגובה $Z$)

פתרון:

ניתוח סימטריה:

רכיבי $X$ ו-$Y$ מתבטלים
השדה השקול בכיוון $Z$ בלבד

חישוב:

אלמנט מטען $dq$ תורם:

\[dE = \frac{k \cdot dq}{r^2}\]

כאשר $r = \sqrt{R^2 + Z^2}$.

הרכיב בכיוון $Z$:

\[dE_z = dE \cos\theta = \frac{k \cdot dq}{r^2} \cdot \frac{Z}{r} = \frac{kZ \cdot dq}{(R^2 + Z^2)^{3/2}}\]

סכימה על כל הטבעת:

\[E_z = \int dE_z = \frac{kZ}{(R^2 + Z^2)^{3/2}} \int dq = \frac{kQZ}{(R^2 + Z^2)^{3/2}}\] \[\boxed{\vec{E}(Z) = \frac{kQZ}{(R^2 + Z^2)^{3/2}}\hat{z}}\]

טריק: במקום לעבור לזוויות ולעשות אינטגרל מ-$0$ עד $2\pi$, ניתן להוציא את כל הקבועים מהאינטגרל ולהישאר עם $\int dQ = Q$.

חוק גאוס

הניסוח

\[\Phi = \oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]

משמעות: השטף של השדה החשמלי דרך מעטפת סגורה שווה למטען הכלוא בתוכה חלקי $\epsilon_0$.

מתי משתמשים?

חוק גאוס שימושי כאשר יש סימטריה:

סימטריה כדורית
סימטריה גלילית
סימטריה מישורית

עקרונות

מטען בתוך המעטפת ← תורם לשטף
מטען מחוץ למעטפת ← השטף שנכנס = השטף שיוצא ← תרומה כוללת אפס
בוחרים מעטפת גאוס שמתאימה לסימטריה

תרגיל 3: שני גלילים קונצנטריים

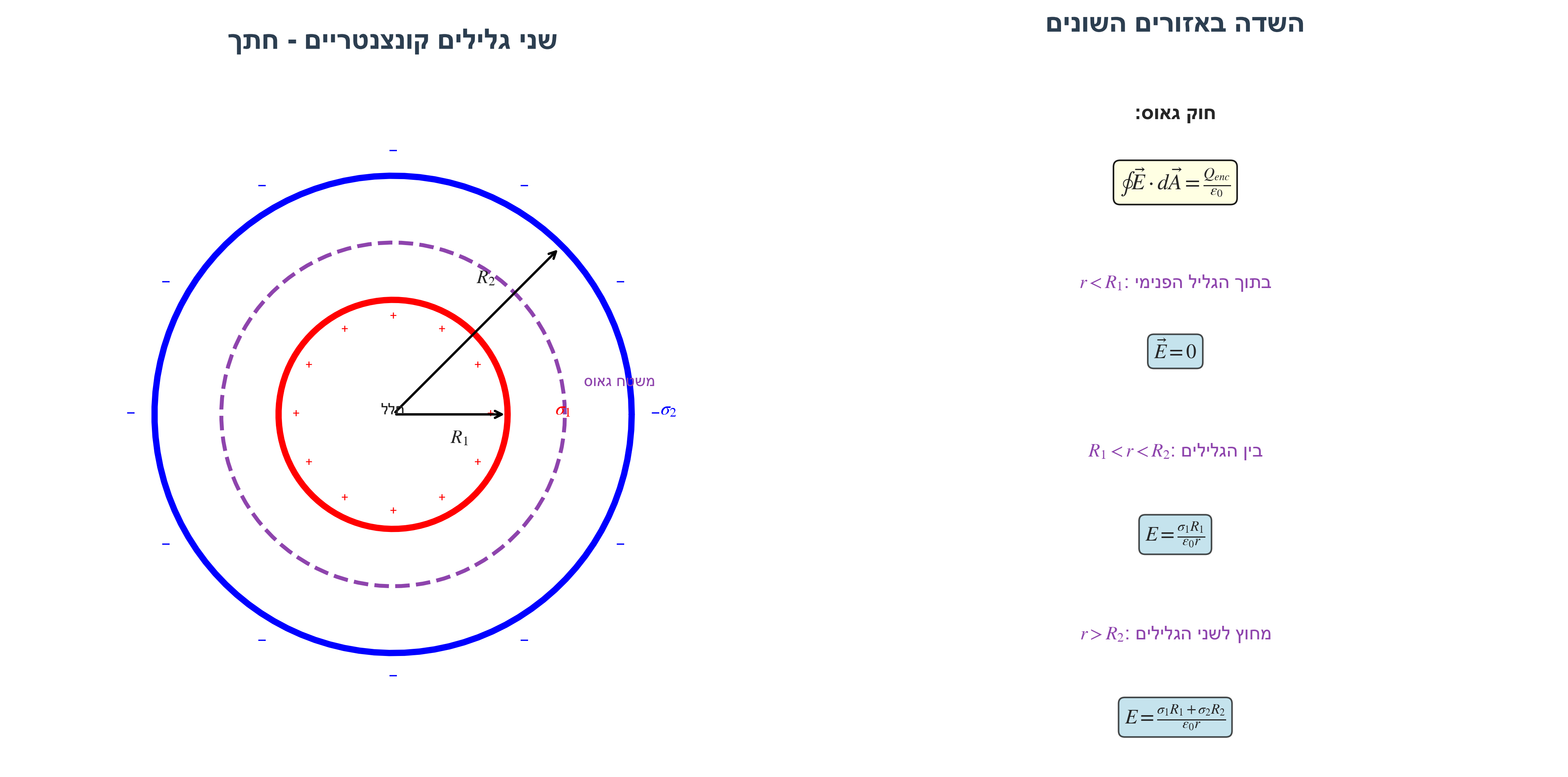
נתונים:

שני גלילים אינסופיים קונצנטריים (בעלי ציר משותף):

גליל פנימי ברדיוס $R_1$ עם צפיפות משטחית $\sigma_1$

גליל חיצוני ברדיוס $R_2$ עם צפיפות משטחית $\sigma_2$

שאלה: מהו השדה בכל המרחב?

פתרון

שלב 1: קביעת כיוון השדה

מסימטריה גלילית: השדה חייב להיות רדיאלי (בכיוון $\hat{r}$).

אין יתרון לכיוון $\hat{\theta}$ או $\hat{z}$
השדה יכול להיות רק פנימה או החוצה

שלב 2: בניית מעטפת גאוס

נבנה מעטפת גאוס גלילית ברדיוס $r$ ואורך $L$:

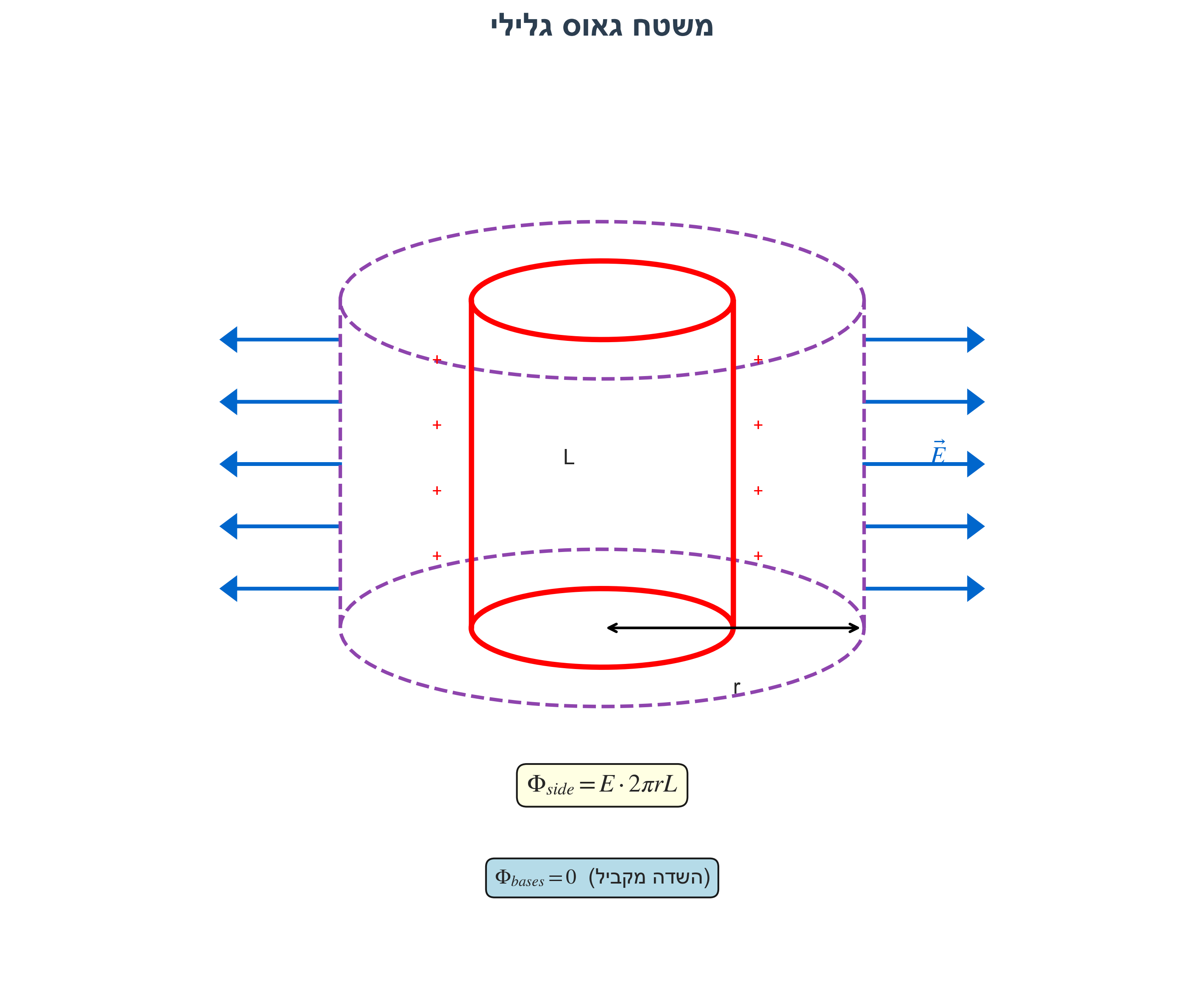
השטף דרך המעטפת:

דרך המעטפת הצדדית: $\Phi = E \cdot 2\pi r L$
דרך הבסיסים: $\Phi = 0$ (השדה מקביל לבסיסים)

שלב 3: יישום חוק גאוס לכל אזור

אזור I: $r < R_1$ (בתוך הגליל הפנימי)

המטען הכלוא: $Q_{\text{enc}} = 0$

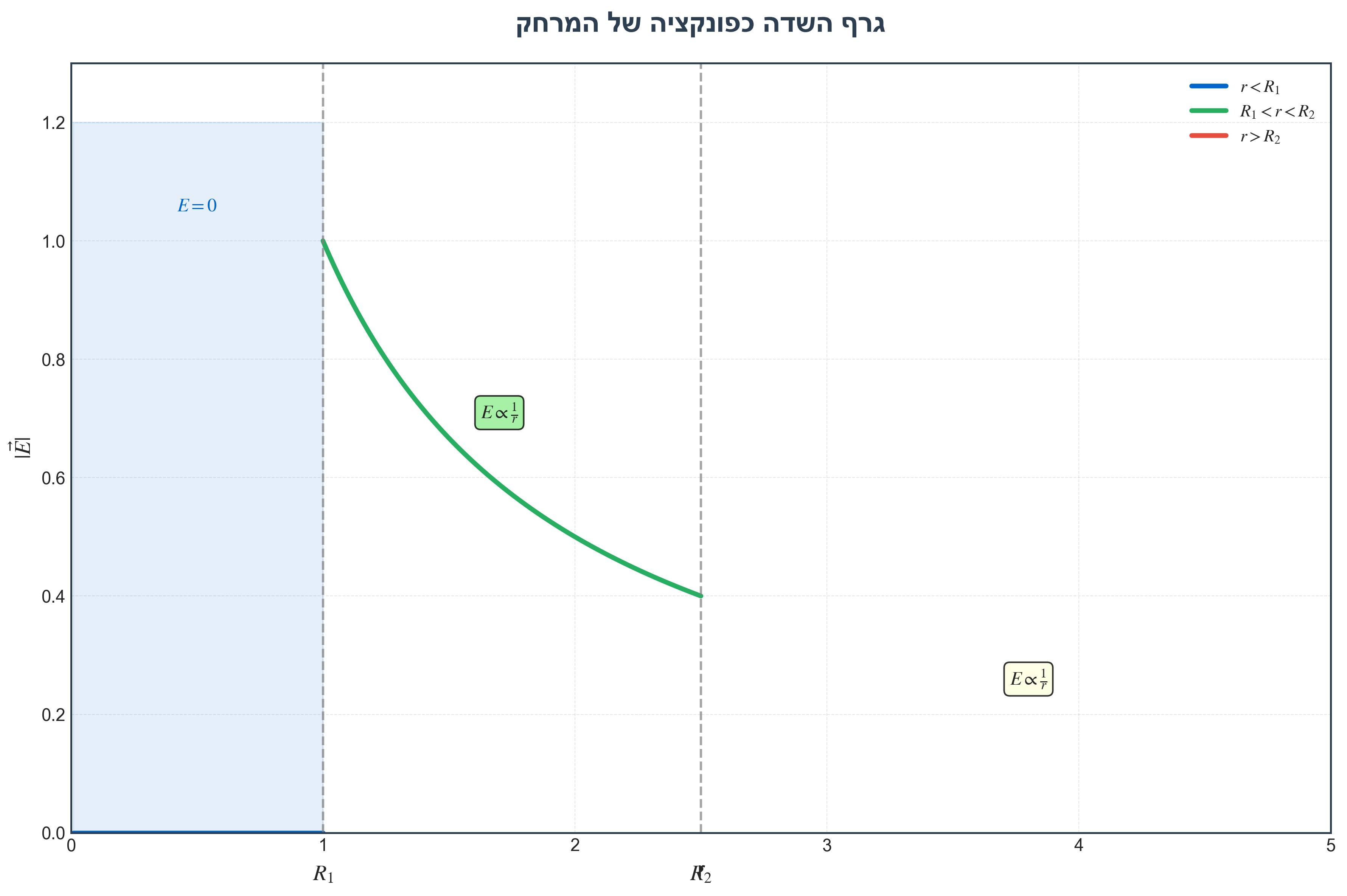
\[E \cdot 2\pi r L = 0\] \[\boxed{E(r < R_1) = 0}\]

אזור II: $R_1 < r < R_2$ (בין הגלילים)

המטען הכלוא: רק מהגליל הפנימי

\[Q_{\text{enc}} = \sigma_1 \cdot 2\pi R_1 L\] \[E \cdot 2\pi r L = \frac{\sigma_1 \cdot 2\pi R_1 L}{\epsilon_0}\] \[\boxed{E(R_1 < r < R_2) = \frac{\sigma_1 R_1}{\epsilon_0 r}}\]

אזור III: $r > R_2$ (מחוץ לשני הגלילים)

המטען הכלוא: משני הגלילים

\[Q_{\text{enc}} = \sigma_1 \cdot 2\pi R_1 L + \sigma_2 \cdot 2\pi R_2 L\] \[E \cdot 2\pi r L = \frac{2\pi L(\sigma_1 R_1 + \sigma_2 R_2)}{\epsilon_0}\] \[\boxed{E(r > R_2) = \frac{\sigma_1 R_1 + \sigma_2 R_2}{\epsilon_0 r}}\]

הערה: האורך $L$ מצטמצם בכל המקרים - התוצאה לא תלויה באורך המעטפת שבחרנו.

סיכום - שיטות לחישוב שדה חשמלי

שיטה 1: אינטגרציה ישירה (סופרפוזיציה)

לוקחים אלמנט מטען $dQ$
מחשבים $d\vec{E} = \frac{k \cdot dQ}{r^2}\hat{r}$
מפרקים לרכיבים
בודקים סימטריה - אילו רכיבים מתאפסים
עושים אינטגרל

יתרון: עובד תמיד
חיסרון: לפעמים האינטגרל מסובך

שיטה 2: חוק גאוס

מזהים סימטריה
בונים מעטפת גאוס מתאימה
מחשבים שטף: $\Phi = \oint \vec{E} \cdot d\vec{A}$
מחשבים מטען כלוא: $Q_{\text{enc}}$
מיישמים: $\Phi = \frac{Q_{\text{enc}}}{\epsilon_0}$

יתרון: פשוט ומהיר כשיש סימטריה
חיסרון: עובד רק עם סימטריה מתאימה

טבלת השוואה

מצב	שיטה מומלצת
מטען נקודתי	חוק קולון ישירות
מוט/קשת סופיים	אינטגרציה
כדור/גליל/מישור אינסופי	חוק גאוס
צורה לא סימטרית	אינטגרציה

תרגול 4 - התפלגות מטען לא אחידה ושדה חשמלי

תאריך: 23/11/2025

יחידות וצפיפויות מטען

יחידות מטען חשמלי

יחידת המטען החשמלי: קולון (C)

סוגי צפיפות מטען

סוג	סימון	הגדרה	יחידות
צפיפות קווית	$\lambda$	מטען ליחידת אורך	C/m
צפיפות משטחית	$\sigma$	מטען ליחידת שטח	C/m²
צפיפות נפחית	$\rho$	מטען ליחידת נפח	C/m³

צפיפות אחידה לעומת לא אחידה

צפיפות אחידה:

\[\lambda = \frac{Q}{L}, \quad \sigma = \frac{Q}{A}, \quad \rho = \frac{Q}{V}\]

צפיפות לא אחידה: הצפיפות היא פונקציה של המיקום במרחב, למשל $\lambda(x)$, $\sigma(\theta, \phi)$, $\rho(r)$.

אלמנטי מטען

\[dq = \lambda \cdot dl \quad \text{(linear)}\] \[dq = \sigma \cdot dA \quad \text{(surface)}\] \[dq = \rho \cdot dV \quad \text{(volume)}\]

אלמנטים בקואורדינטות שונות

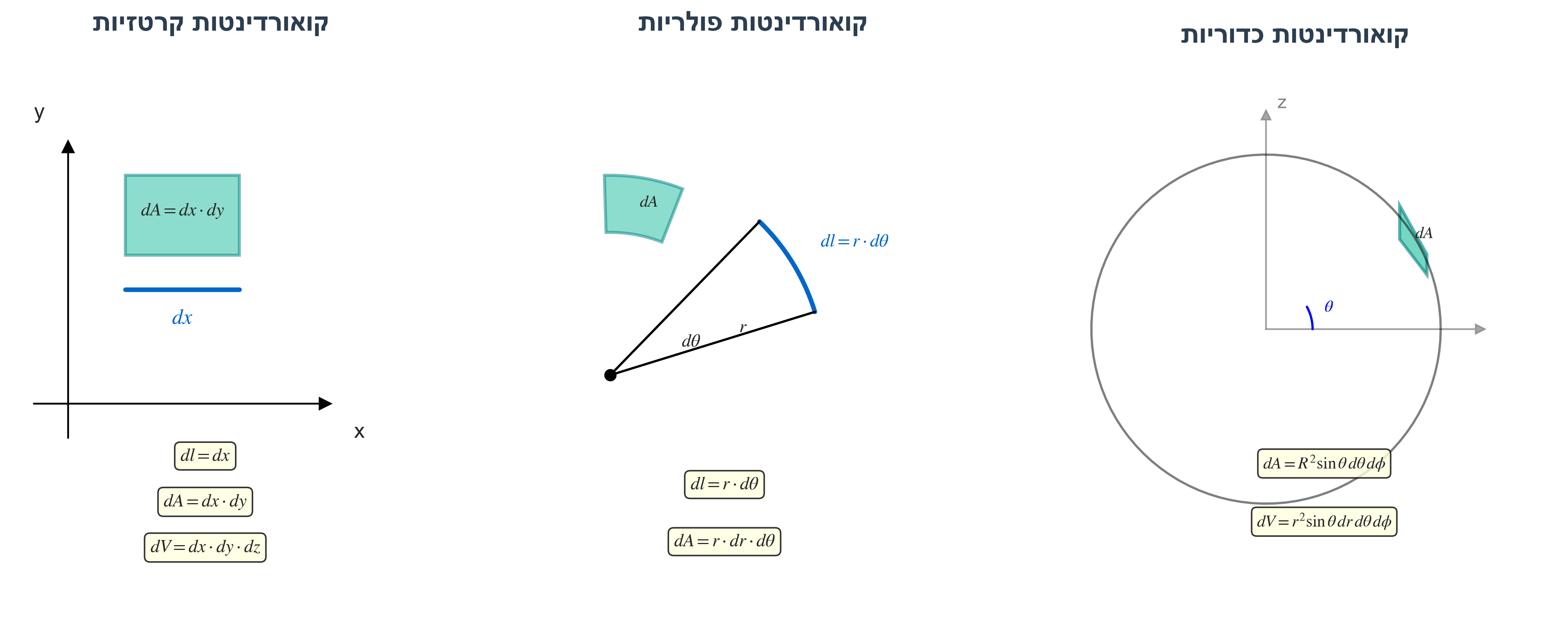
קואורדינטות קרטזיות

אלמנט	ביטוי
אורך	$dl = dx$
שטח	$dA = dx \cdot dy$
נפח	$dV = dx \cdot dy \cdot dz$

קואורדינטות פולריות (דו-ממד)

אלמנט	ביטוי
אורך קשת	$dl = r \cdot d\theta$
שטח	$dA = r \cdot dr \cdot d\theta$

קואורדינטות כדוריות (תלת-ממד)

אלמנט	ביטוי
שטח מעטפת כדור	$dA = R^2 \sin\theta \, d\theta \, d\phi$
נפח	$dV = r^2 \sin\theta \, dr \, d\theta \, d\phi$

תחומי האינטגרציה:

$\theta$: מ-$0$ עד $\pi$ (מקוטב לקוטב)
$\phi$: מ-$0$ עד $2\pi$ (סיבוב מלא)
$r$: מ-$0$ עד $R$ (מהמרכז לשפה)

תרגיל 1: מטען כולל על מוט עם צפיפות לא אחידה

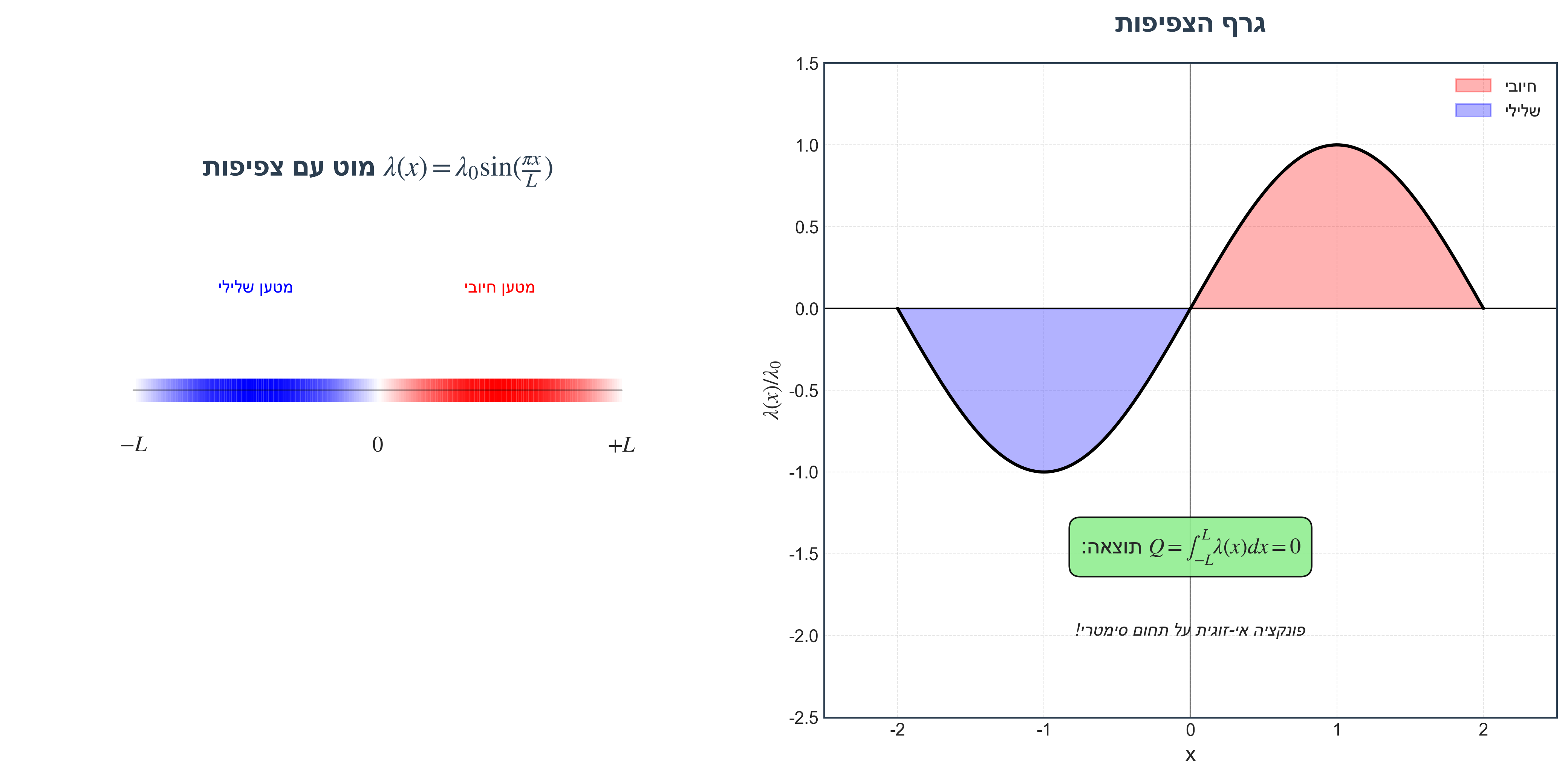
מוט באורך $2L$ (מ-$(-L)$ עד $(+L)$) עם צפיפות מטען:
\[\lambda(x) = \lambda_0 \sin\left(\frac{\pi x}{L}\right)\]
מהו המטען הכולל?

פתרון בעזרת אינטגרל על אורך המוט

\[Q = \int dq = \int_{-L}^{L} \lambda(x) \, dx = \int_{-L}^{L} \lambda_0 \sin\left(\frac{\pi x}{L}\right) dx\] \[Q = \lambda_0 \left[-\frac{L}{\pi} \cos\left(\frac{\pi x}{L}\right)\right]_{-L}^{L}\] \[Q = -\frac{\lambda_0 L}{\pi} \left[\cos(\pi) - \cos(-\pi)\right] = -\frac{\lambda_0 L}{\pi} \left[-1 - (-1)\right] = 0\]

תוצאה: $Q = 0$

הסבר: הפונקציה $\sin\left(\frac{\pi x}{L}\right)$ היא פונקציה אי-זוגית - חיובית בצד אחד ושלילית בצד השני. לכן האינטגרל על תחום סימטרי מתאפס.

תרגיל 2: מטען כולל על מעטפת כדור

מעטפת כדור ברדיוס $R$ עם צפיפות מטען משטחית:
\[\sigma(\phi) = \sigma_0 \cos\phi\]
מהו המטען הכולל?

פתרון בעזרת אינטגרל על שטח כדור

\[Q = \int dq = \iint \sigma \, dA = \int_0^{\pi} \int_0^{2\pi} \sigma_0 \cos\phi \cdot R^2 \sin\theta \, d\phi \, d\theta\] \[Q = \sigma_0 R^2 \int_0^{\pi} \sin\theta \, d\theta \int_0^{2\pi} \cos\phi \, d\phi\]

האינטגרל על $\phi$:

\[\int_0^{2\pi} \cos\phi \, d\phi = [\sin\phi]_0^{2\pi} = 0\]

תוצאה: $Q = 0$

הסבר: כאשר $\phi = 0$ הצפיפות חיובית (צד אחד של הכדור), וכאשר $\phi = \pi$ הצפיפות שלילית (הצד הנגדי). המטענים מתקזזים.

תרגיל 3: מטען כולל על קשת (חצי מעגל)

קשת (חצי מעגל) ברדיוס $r$ עם צפיפות מטען:
\[\lambda(\theta) = \lambda_0 \theta^2\]
כאשר $\theta$ רץ מ-$0$ עד $\pi$.

מהו המטען הכולל?

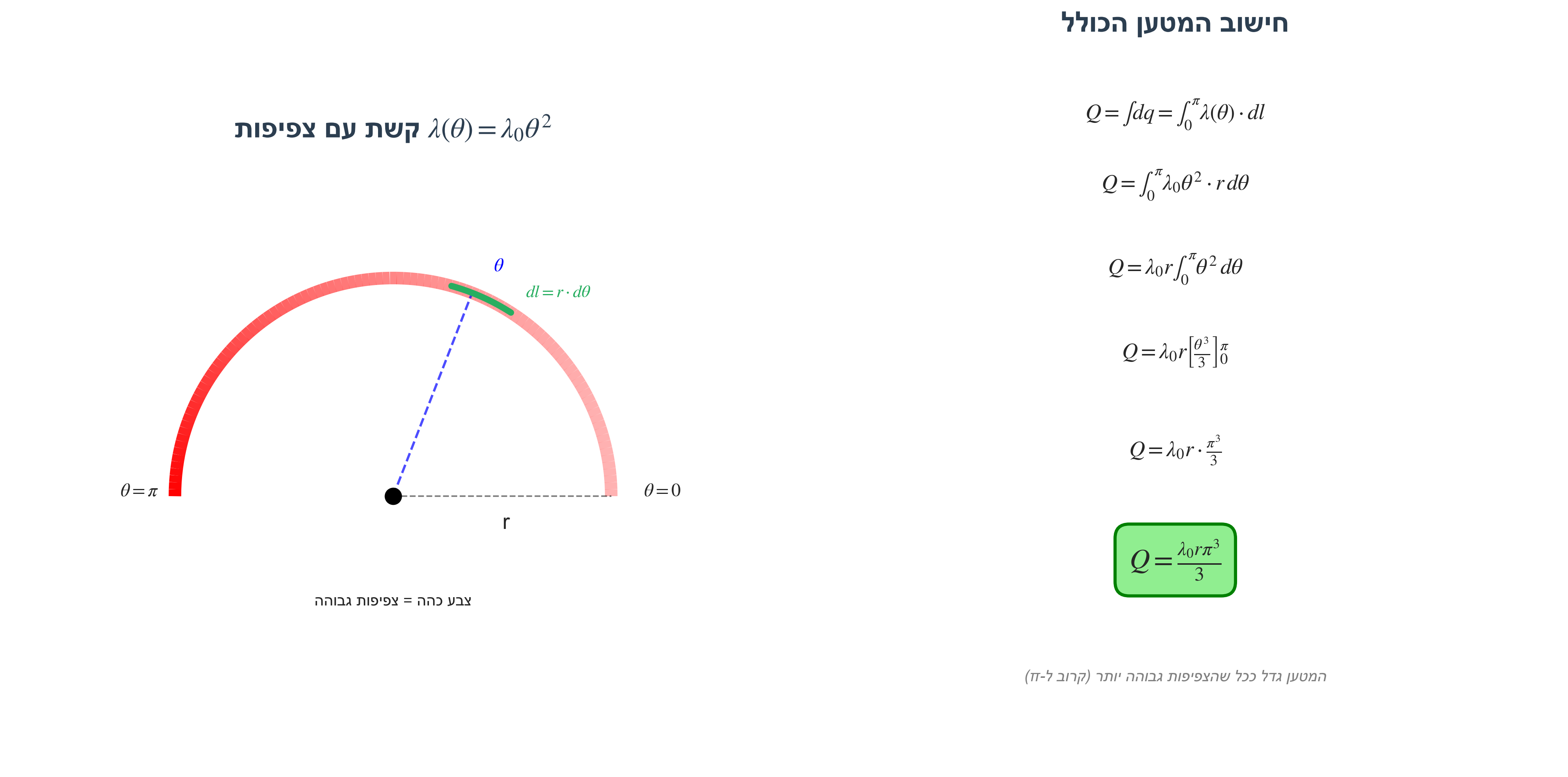
פתרון בעזרת אינטגרל על אורך הקשת

\[Q = \int dq = \int_0^{\pi} \lambda(\theta) \cdot dl = \int_0^{\pi} \lambda_0 \theta^2 \cdot r \, d\theta\] \[Q = \lambda_0 r \int_0^{\pi} \theta^2 \, d\theta = \lambda_0 r \left[\frac{\theta^3}{3}\right]_0^{\pi}\] \[\boxed{Q = \frac{\lambda_0 r \pi^3}{3}}\]

שדה חשמלי - שיטת החישוב

העיקרון

בחר אלמנט מטען קטן $dq$
חשב את השדה $d\vec{E}$ שהוא יוצר בנקודה הרצויה
פרק לרכיבים ($x$, $y$, $z$)
בדוק סימטריות - אילו רכיבים מתאפסים?
בצע אינטגרציה על הרכיבים שנותרו

נוסחת השדה מאלמנט מטען

\[d\vec{E} = \frac{k \cdot dq}{r^2} \hat{r}\]

תרגיל 4: שדה חשמלי של דיפול (מוט עם צפיפות משתנה)

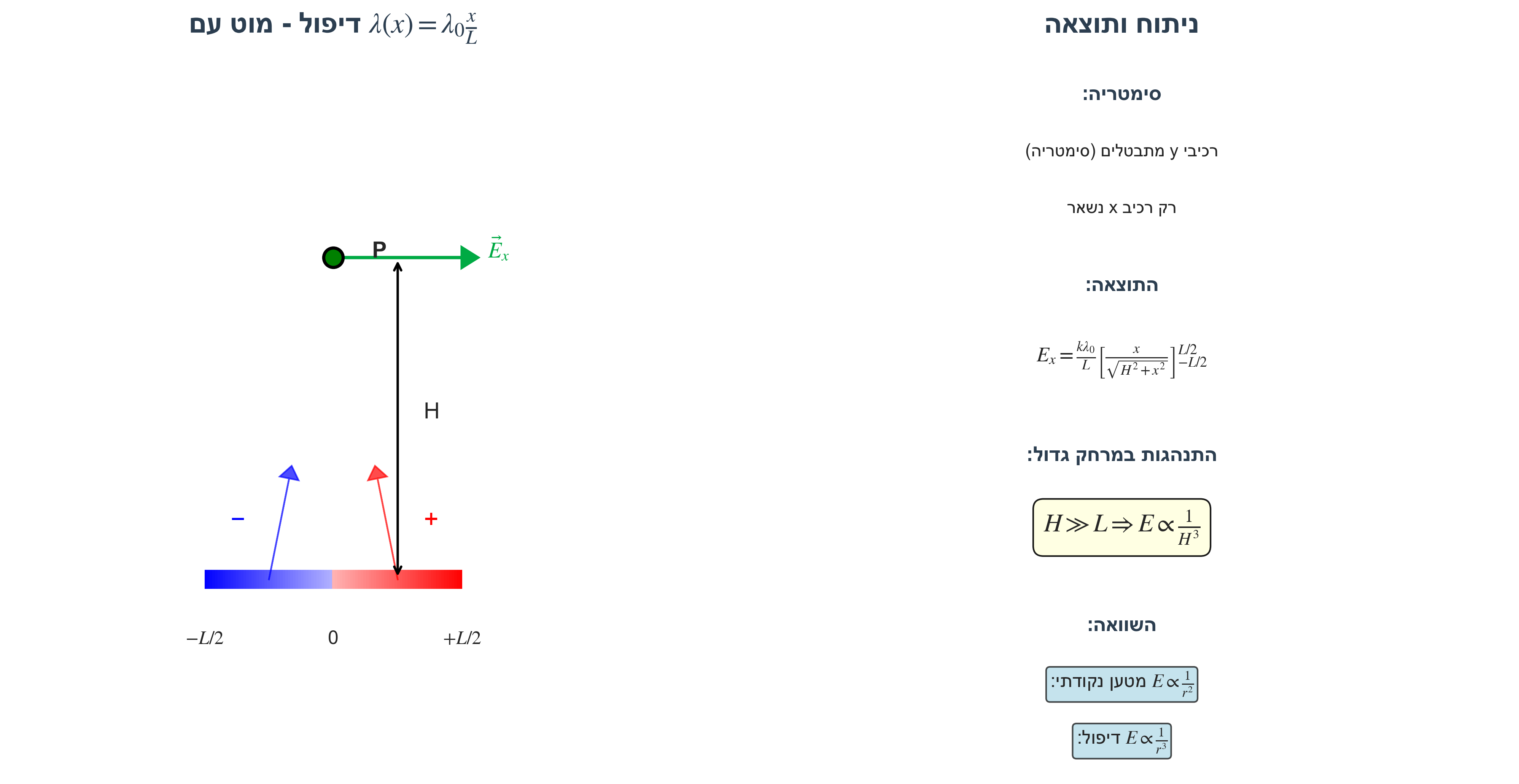
מוט באורך $L$ (מ-$-L/2$ עד $+L/2$) עם צפיפות מטען:
\[\lambda(x) = \lambda_0 \frac{x}{L}\]
נקודת התצפית בגובה $H$ מעל מרכז המוט.

מהו השדה החשמלי בנקודה זו?

ניתוח הבעיה

התנהגות הצפיפות:

ב-$x > 0$: צפיפות חיובית (מטען חיובי)
ב-$x < 0$: צפיפות שלילית (מטען שלילי)
המטען הכולל: $Q = 0$

זהו דיפול - מערכת עם מטען כולל אפס אך פיזור לא אחיד.

סימטריה

מניתוח סימטריה: השדה הכולל יהיה בכיוון $x$ בלבד.

הסבר: לכל מטען חיובי בצד ימין יש מטען שלילי מקביל בצד שמאל. רכיבי ה-$y$ מתבטלים, ורכיבי ה-$x$ מתחברים.

פתרון

\[E_x = \int dE_x = \int dE \cos\theta\]

כאשר:

\[dE = \frac{k \cdot dq}{r^2} = \frac{k \lambda(x) dx}{r^2}\] \[\cos\theta = \frac{x}{r}, \quad r = \sqrt{H^2 + x^2}\] \[E_x = \int_{-L/2}^{L/2} \frac{k \lambda_0 \frac{x}{L} \cdot x}{(H^2 + x^2)^{3/2}} dx\] \[E_x = \frac{k \lambda_0}{L} \int_{-L/2}^{L/2} \frac{x^2}{(H^2 + x^2)^{3/2}} dx\]

תוצאה

\[\boxed{E_x = \frac{k \lambda_0}{L} \left[\frac{x}{\sqrt{H^2 + x^2}}\right]_{-L/2}^{L/2}}\]

התנהגות במרחק גדול

כאשר $H \gg L$ (רחוק מהמוט):

\[E \propto \frac{1}{H^3}\]

מסקנה חשובה: שדה של דיפול דועך כמו $\frac{1}{r^3}$, לעומת שדה של מטען נקודתי שדועך כמו $\frac{1}{r^2}$.

תרגיל 5: שדה חשמלי של מלבן טעון

מלבן בממדים $a \times b$ עם צפיפות מטען משטחית אחידה $\sigma$.

נקודת התצפית בגובה $H$ מעל מרכז המלבן.

מהו השדה החשמלי בנקודה זו?

ניתוח סימטריה

מסימטריית הבעיה: השדה הכולל יהיה בכיוון $z$ בלבד (ניצב למשטח).

הסבר: הנקודה נמצאת במרכז המלבן, ולכל אלמנט מטען יש אלמנט מקביל בצד הנגדי שמבטל את רכיבי $x$ ו-$y$.

פתרון:

\[E_z = \int dE_z = \int dE \cos\alpha\]

כאשר:

\[dE = \frac{k \cdot dq}{R^2} = \frac{k \sigma \, dx \, dy}{R^2}\] \[\cos\alpha = \frac{H}{R}, \quad R = \sqrt{H^2 + x^2 + y^2}\] \[E_z = \int_{-a/2}^{a/2} \int_{-b/2}^{b/2} \frac{k \sigma H}{(H^2 + x^2 + y^2)^{3/2}} dx \, dy\]

תוצאה סופית:

\[\boxed{E_z = 4k\sigma \arctan\left(\frac{ab}{4H\sqrt{H^2 + \frac{a^2}{4} + \frac{b^2}{4}}}\right)}\]

בדיקת גבולות

1. מרחק גדול ($H \gg a, b$):

\[E_z \approx \frac{kQ}{H^2}\]

כמו מטען נקודתי! (כאשר $Q = \sigma \cdot a \cdot b$)

2. מרחק קטן ($H \to 0$):

כאשר $H$ קטן מאוד (קרוב למשטח), המלבן נראה כמו משטח אינסופי:

\[E_z \to \frac{\sigma}{2\epsilon_0}\]

זהו השדה של משטח אינסופי (ניתן לחשב בעזרת חוק גאוס).

סיכום - שיטת חישוב שדה חשמלי מהתפלגות מטען

שלבי הפתרון

זיהוי סוג הצפיפות - קווית ($\lambda$), משטחית ($\sigma$), או נפחית ($\rho$)
בחירת אלמנט מטען - $dq = \lambda \, dl$ או $dq = \sigma \, dA$ או $dq = \rho \, dV$
בחירת מערכת קואורדינטות מתאימה - קרטזית, פולרית, כדורית
ניתוח סימטריה - אילו רכיבים מתאפסים מראש?
רישום השדה מאלמנט מטען: $d\vec{E} = \frac{k \cdot dq}{r^2} \hat{r}$
פירוק לרכיבים - שימוש בטריגונומטריה
ביטוי הכל במשתנה אינטגרציה אחד - כל המשתנים צריכים להיות מבוטאים במשתנה האינטגרציה
ביצוע האינטגרל - במבחן יינתנו נוסחאות לאינטגרלים מורכבים

טבלת השוואה - התנהגות שדה במרחק גדול

מקור השדה דעיכת השדה

מטען נקודתי $E \propto \frac{1}{r^2}$

דיפול $E \propto \frac{1}{r^3}$

משטח אינסופי $E = \text{const}$

מקור השדה	דעיכת השדה
מטען נקודתי	$E \propto \frac{1}{r^2}$
דיפול	$E \propto \frac{1}{r^3}$
משטח אינסופי	$E = \text{const}$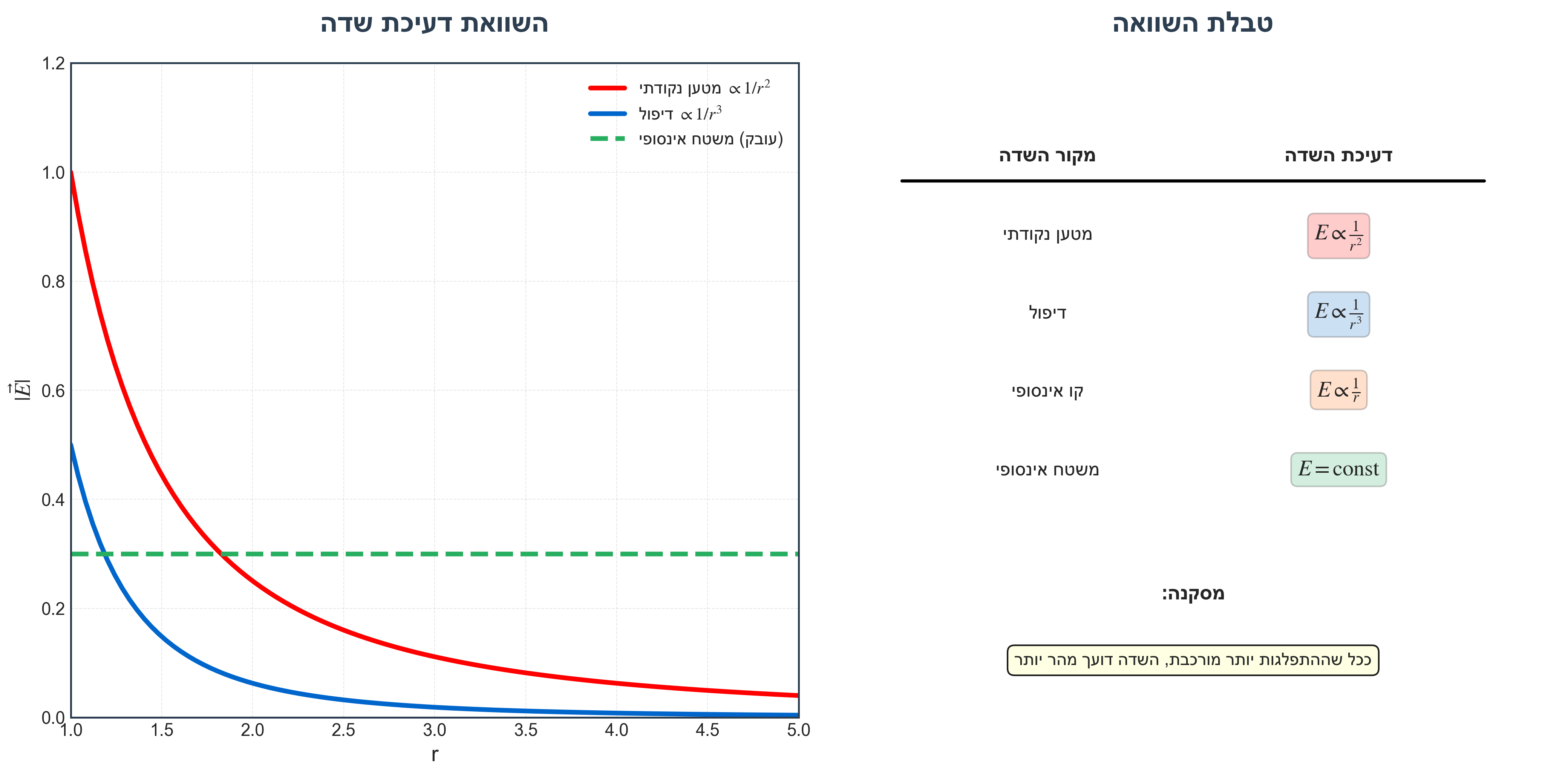

תרגול 5 - שדות חשמליים, אנרגיה פוטנציאלית וחוק גאוס

תאריך: 30/11/2025

סיכום חומר קודם

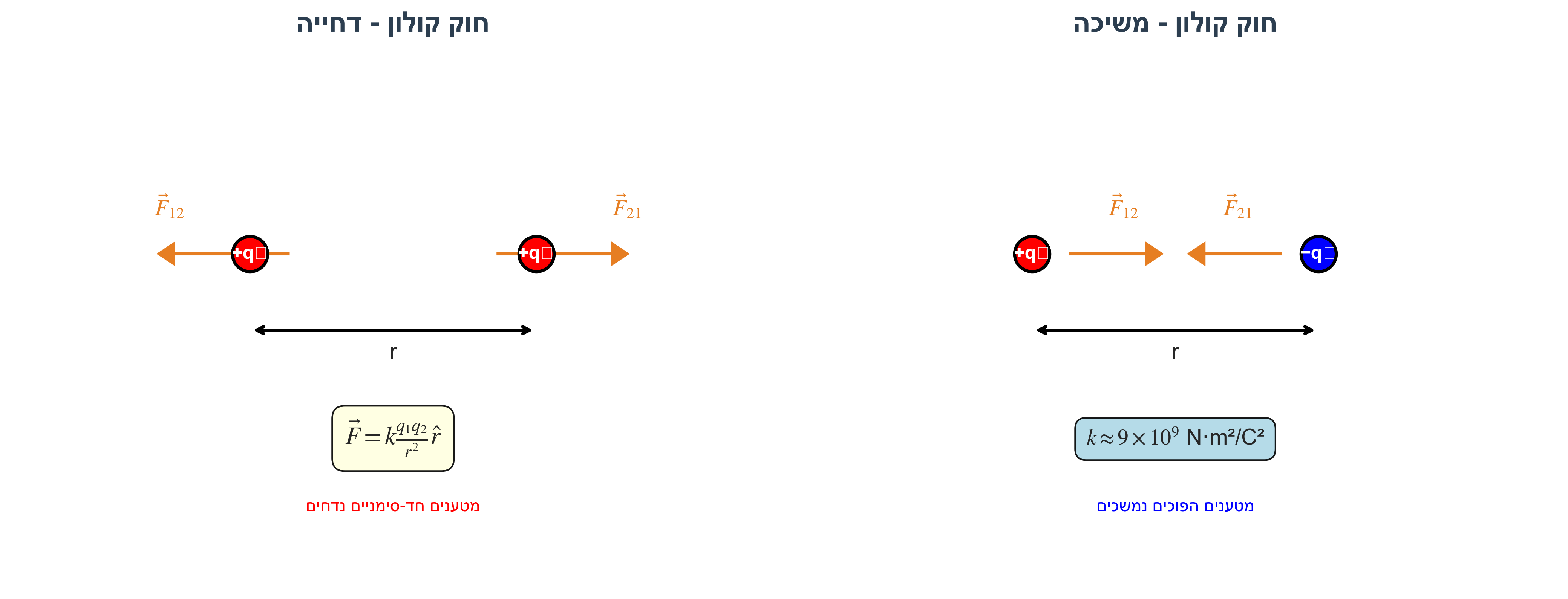
חוק קולון

הכוח בין שני מטענים נקודתיים:

\[\vec{F} = k \frac{q_1 q_2}{r^2} \hat{r}\]

$k \approx 9 \times 10^9 \, \text{N·m}^2/\text{C}^2$ - קבוע קולון
מטענים שווי סימן נדחים, מטענים בעלי סימנים הפוכים נמשכים

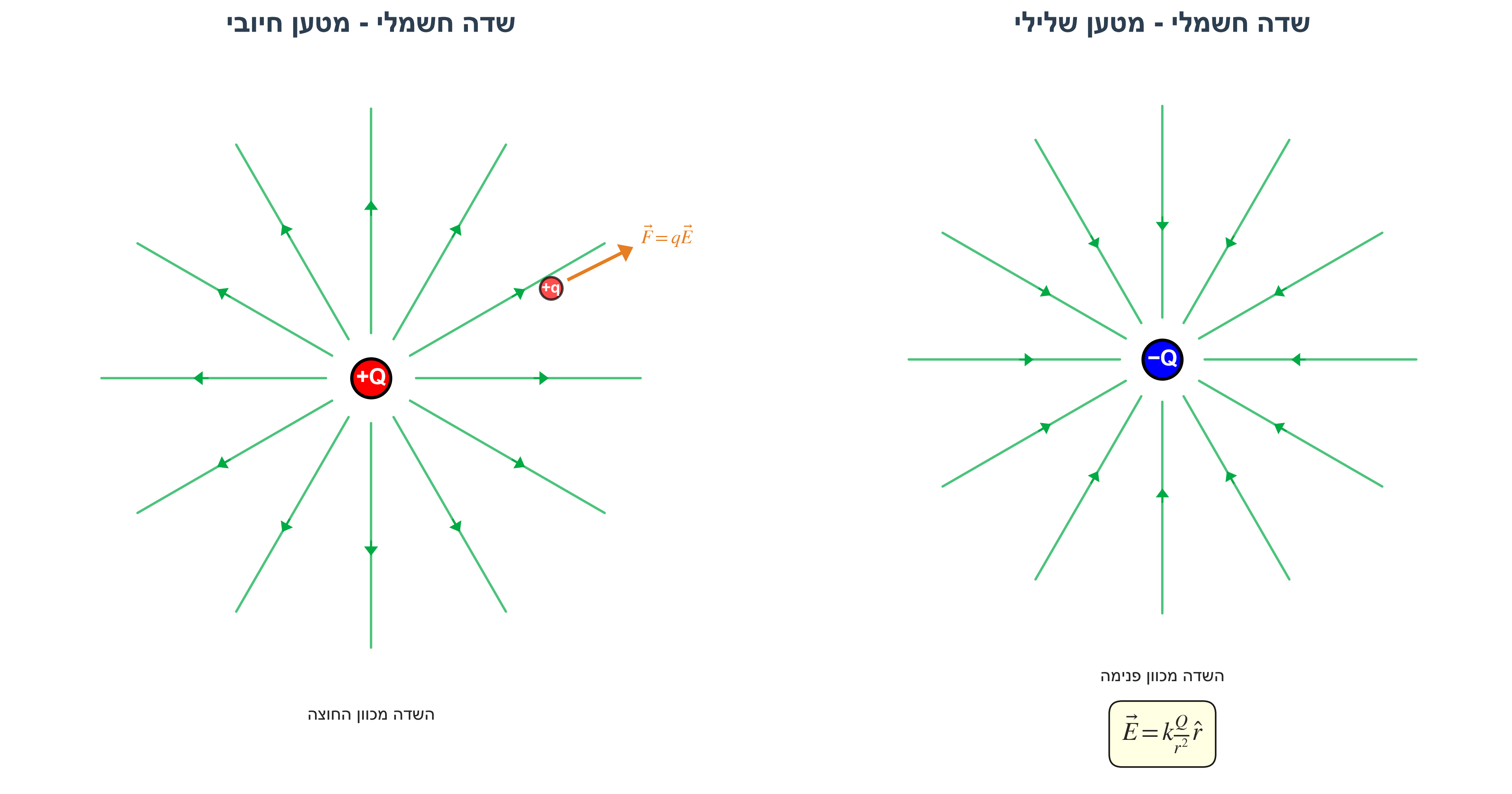
שדה חשמלי

שדה חשמלי נוצר על ידי מטענים קבועים במרחב:

\[\vec{E} = \frac{\vec{F}}{q} = k\frac{Q}{r^2}\hat{r}\]

הכוח על מטען $q$ בשדה חשמלי:

\[\vec{F} = q\vec{E}\]

מטען חיובי ← כוח בכיוון השדה
מטען שלילי ← כוח נגד כיוון השדה

עקרון הסופרפוזיציה

השדה הכולל הוא סכום וקטורי של השדות מכל המטענים:

\[\vec{E}_{\text{total}} = \sum_i \vec{E}_i\]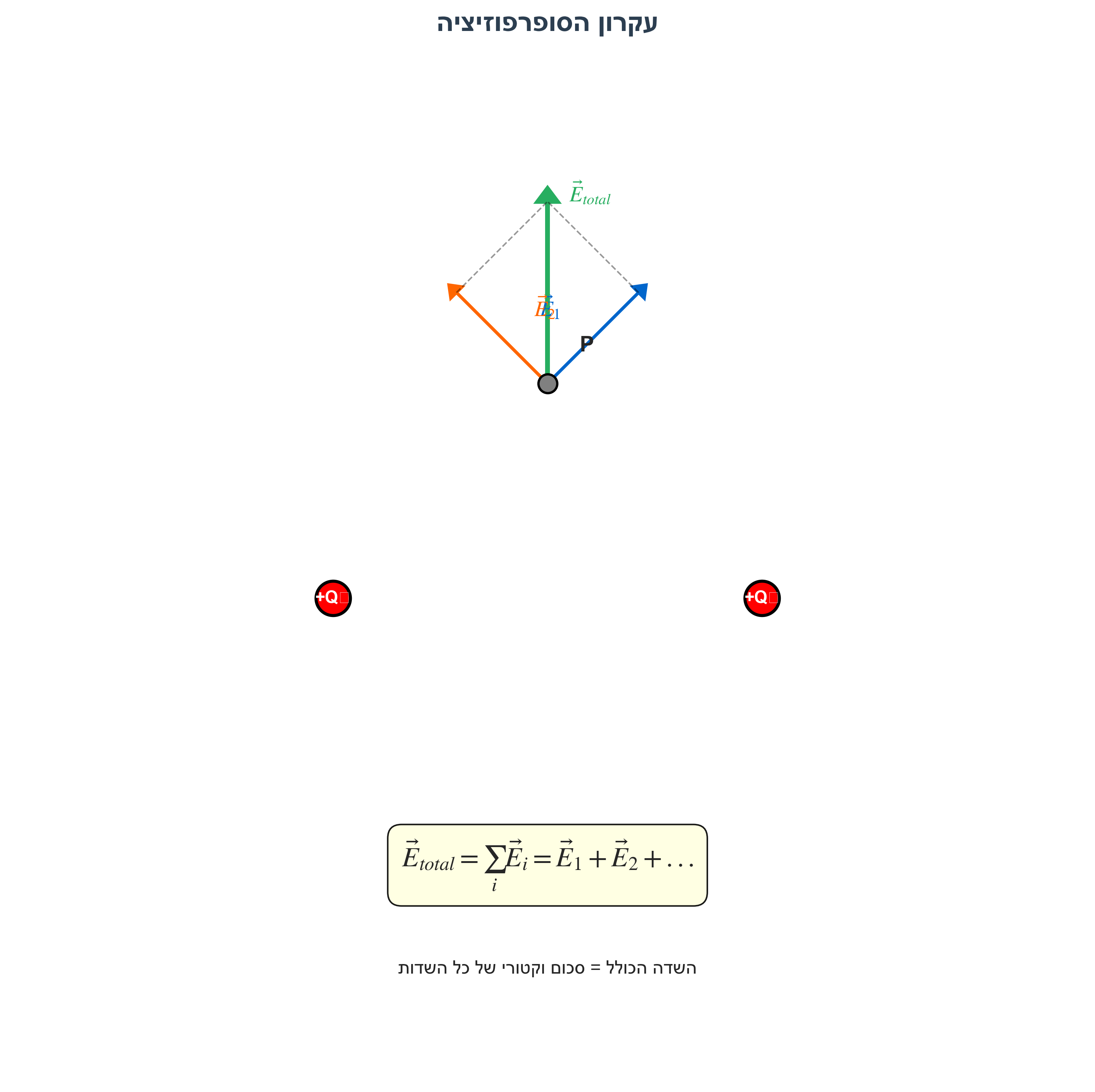 superposition

שדה משמר

שדה חשמלי הוא שדה משמר:

העבודה במעגל סגור שווה לאפס
העבודה בין שתי נקודות אינה תלויה במסלול

אנרגיה פוטנציאלית חשמלית

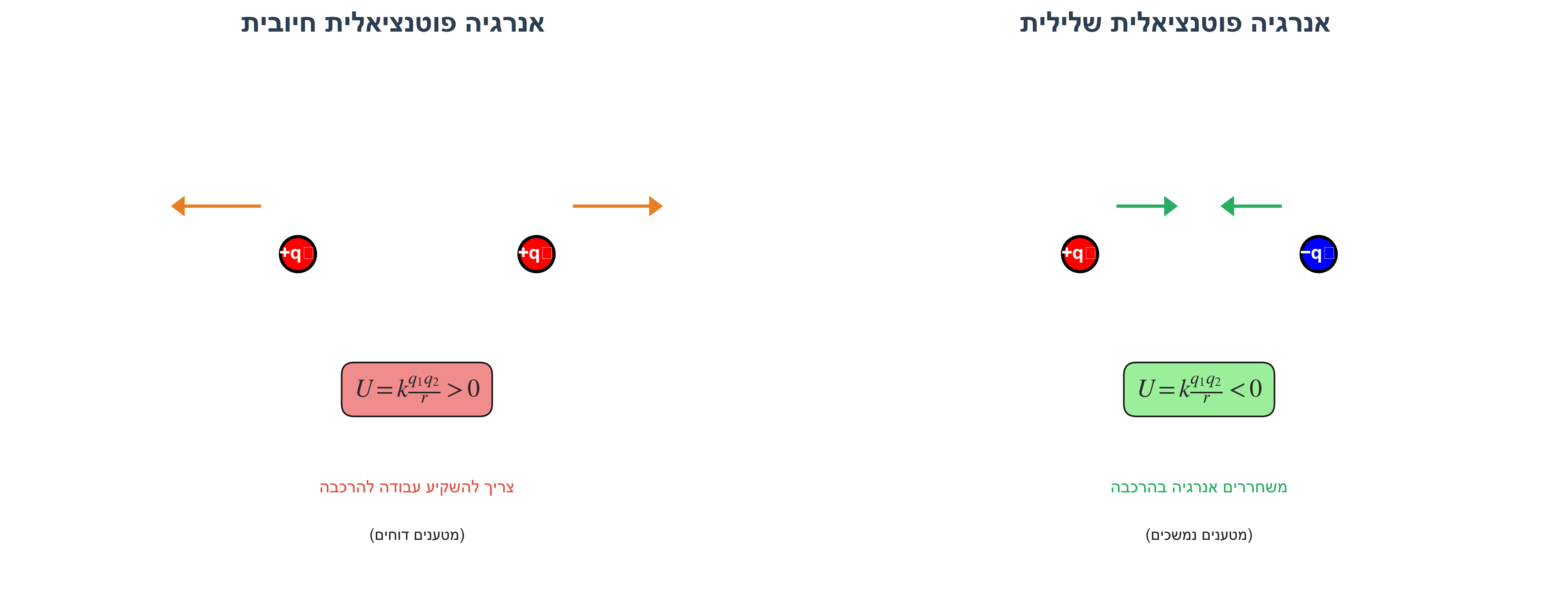
\[U = k\frac{q_1 q_2}{r}\]

$U > 0$ (חיובית) ← המטענים דוחים זה את זה, נדרשה עבודה להרכבת המערכת
$U < 0$ (שלילית) ← המטענים נמשכים זה לזה, התקבלה אנרגיה בהרכבת המערכת

תרגיל 1: משושה עם מטענים

נתון משושה משוכלל עם אורך צלע $a$. בחמישה מתוך שישה קודקודים (A, B, C, D, E) נמצא מטען נקודתי חיובי $+Q$. בקודקוד F אין מטען.

חשב את השדה החשמלי בנקודה O (מרכז המשושה).

מהי העבודה שנדרשת להבאת מטען נוסף $+Q$ ממרחק אינסופי לנקודה O?

אם נוסיף מטען $+Q$ גם בקודקוד F, מהו השדה החשמלי בנקודה O? ומהי העבודה להבאת מטען $+Q$ מאינסוף לנקודה O?

אם נשנה את סימני המטענים בקודקודים A, C, E ל-$-Q$, האם תשתנה העבודה להבאת מטען $+Q$ לנקודה O?

סעיף א’: השדה החשמלי במרכז המשושה

שאלה: מהו וקטור השדה החשמלי השקול בנקודה O (מרכז המשושה)?

פתרון:

משיקולי סימטריה, מטענים הנמצאים בקודקודים מנוגדים יוצרים שדות שמבטלים זה את זה:

השדה מ-A מבטל את השדה מ-D
השדה מ-B מבטל את השדה מ-E

נשאר רק התרומה של המטען ב-C:

\[\vec{E}_O = \vec{E}_C = \frac{kQ}{a^2}\hat{x}\]

סעיף ב’: עבודה להבאת מטען נוסף למרכז

שאלה: מעבירים מטען נוסף $Q$ ממרחק אינסופי לנקודה O. מהי העבודה שנעשתה?

פתרון:

העבודה שווה לאנרגיה הפוטנציאלית של המערכת (סכום התרומות מכל הזוגות):

\[W = U = \sum_{i} k\frac{Q \cdot Q}{r_i}\]

המרחק מכל קודקוד למרכז הוא $a$, ויש 5 מטענים:

\[W = 5 \cdot \frac{kQ^2}{a}\]

הערה: בחישוב זה התעלמנו מהאנרגיה שנדרשה לבניית המערכת המקורית (5 המטענים).

סעיף ג’: הוספת מטען לקודקוד F

שאלה:

(א) מהו השדה החשמלי במרכז כעת?
(ב) מהי העבודה להבאת מטען $Q$ מאינסוף למרכז?

פתרון:

(א) השדה במרכז:

כעת יש סימטריה מלאה - כל המטענים מבטלים זה את זה:

\[\vec{E}_O = 0\]

(ב) העבודה:

\[W = 6 \cdot \frac{kQ^2}{a}\]

סעיף ד’: החלפת סימני מטענים

שאלה: בקודקודים A, C, E מחליפים את המטען החיובי במטען שלילי $-Q$. האם תשתנה העבודה להבאת מטען למרכז?

פתרון:

כעת יש שלושה מטענים $+Q$ ושלושה מטענים $-Q$:

\[W = 3 \cdot \frac{kQ \cdot Q}{a} + 3 \cdot \frac{kQ \cdot (-Q)}{a} = 0\]

התשובה: אפס - התרומות מתבטלות בסופרפוזיציה.

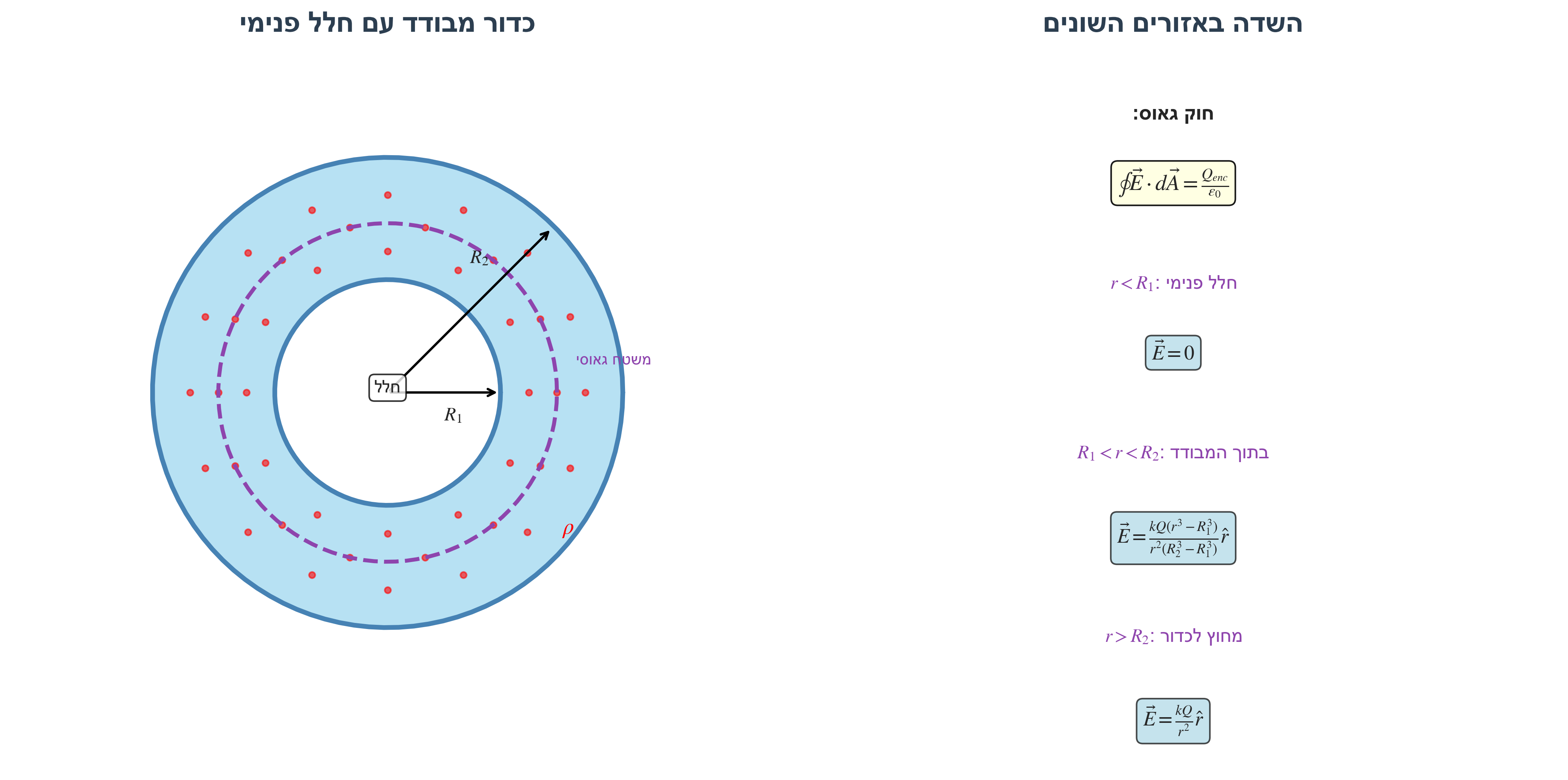
תרגיל 2: חוק גאוס - כדור מבודד עם חלל פנימי

כדור מבודד עם חלל פנימי כדורי (קונצנטרי):

רדיוס החלל הפנימי: $R_1$

רדיוס הכדור החיצוני: $R_2$

צפיפות מטען אחידה $\rho$ בחומר המבודד

סך המטען: $Q$

חשב את השדה החשמלי באזורים השונים:

בתוך החלל הפנימי ($r < R_1$)

בתוך החומר המבודד ($R_1 < r < R_2$)

מחוץ לכדור ($r > R_2$)

חוק גאוס

\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]

כאשר $\frac{1}{4\pi\epsilon_0} = k$

סעיף א’: השדה באזור $r < R_1$ (בתוך החלל)

פתרון:

נבחר מעטפת גאוסית כדורית ברדיוס $r < R_1$.

המטען הכלוא בתוך המעטפת: $Q_{\text{enclosed}} = 0$ (אין מטען בחלל הפנימי)

לפי חוק גאוס:

\[E \cdot 4\pi r^2 = \frac{0}{\epsilon_0}\] \[\boxed{\vec{E}(r < R_1) = 0}\]

סעיף ב’: השדה באזור $R_1 < r < R_2$ (בתוך החומר המבודד)

פתרון:

נבחר מעטפת גאוסית כדורית ברדיוס $r$.

המטען הכלוא הוא חלק יחסי מהמטען הכולל:

\[Q_{\text{enclosed}} = Q \cdot \frac{V(R_1 \to r)}{V(R_1 \to R_2)} = Q \cdot \frac{\frac{4}{3}\pi r^3 - \frac{4}{3}\pi R_1^3}{\frac{4}{3}\pi R_2^3 - \frac{4}{3}\pi R_1^3}\] \[Q_{\text{enclosed}} = Q \cdot \frac{r^3 - R_1^3}{R_2^3 - R_1^3}\]

לפי חוק גאוס:

\[E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0} \cdot \frac{r^3 - R_1^3}{R_2^3 - R_1^3}\] \[\boxed{\vec{E}(R_1 < r < R_2) = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)}\hat{r}}\]

פתרון אחר, משיעור תגבור:

השימוש בחוק גאוס כאן הוא הכדור הגדול, פחות הכדור הקטן (למעשה סופר פוזיציה).
\[Q_{in} = \underbrace{\frac{4\pi r^3}{3}\rho}_{\text{full ball}} - \underbrace{\frac{4\pi R_1^3}{3}\rho}_{\text{full negative ball with R radius}}=\frac{4\pi \rho}{3\epsilon_0}\left(r^3-R_1^3\right)\]
מצד אחד

כאשר לפי שיעור 4:
\[Q = \rho \cdot \frac{4\pi R^3}{3} \implies \rho = \frac{3Q}{4\pi R^3}\]
כלומר:
\[\rho = \frac{3Q}{4\pi (R_2^3 - R_1^3)}\]
נציב חזרה:
\[Q_{in} = \frac{4\pi }{3\epsilon_0}\left(r^3-R_1^3\right) \cdot \frac{3Q}{4\pi (R_2^3 - R_1^3)} = \frac{Q(r^3 - R_1^3)}{(R_2^3 - R_1^3)}\]
וכל זה לחלק לאפסילון 0 שווה לאינטגרל של השדה על המעטפת:
\[E \cdot 4\pi r^2 = \frac{Q(r^3 - R_1^3)}{\epsilon_0 (R_2^3 - R_1^3)} \implies E = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)} \hat{r}\]

סעיף ג’: השדה באזור $r > R_2$ (מחוץ לכדור)

פתרון:

המטען הכלוא הוא כל המטען: $Q_{\text{enclosed}} = Q$

\[E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0}\] \[\boxed{\vec{E}(r > R_2) = \frac{kQ}{r^2}\hat{r}}\]

מסקנה: מחוץ לכדור, השדה זהה לשדה של מטען נקודתי $Q$ במרכז.

תרגיל 3: משולש ישר-זווית עם מטענים

נתון משולש ישר-זווית שווה-שוקיים עם:

קודקודים A ו-C: מטען $+q$

קודקוד B (בזווית הישרה): מטען $-q$

אורך הניצבים: $a$

אורך היתר: $a\sqrt{2}$
            B(-q)
            /|\
     a√2  /  |  \ a√2
         /   |a   \
       /  a  |  a   \
      -------|--------
    C(+q)    O     A(+q)

סעיף א’: הכוח על המטען ב-B

פתרון:

הכוח על $-q$ ב-B הוא סכום הכוחות מ-A ומ-C.

כיוון x (לאורך הניצב): הרכיבים מתאפסים. פורמאלית:

הכוח מ-A בכיוון x:

\[F_{A,x} = -\frac{kq^2}{2a^2} \cos(45°) = -\frac{kq^2}{2a^2} \cdot \frac{1}{\sqrt{2}}\]

הכוח מ-C בכיוון x:

\[F_{C,x} = \frac{kq^2}{2a^2} \cos(45°) = \frac{kq^2}{2a^2} \cdot \frac{1}{\sqrt{2}}\]

סך הכל אפס:

\[F_x = F_{A,x} + F_{C,x} = 0\]

כיוון y:

שני הכוחות פועלים באותו כיוון:

\[F_y = 2 \cdot \frac{kq^2}{2a^2} \sin(45°) = \frac{kq^2}{\sqrt{2}a^2}\]

הכוח הכולל:

\[\boxed{\vec{F}_B = \frac{kq^2}{\sqrt{2}a^2}\hat{y}}\]

סעיף ב’: האנרגיה הפוטנציאלית של המערכת

פתרון:

נסכום את האנרגיה של כל זוגות המטענים:

\[U = U_{AB} + U_{BC} + U_{AC}\] \[U_{AB} = k\frac{(+q)(-q)}{\sqrt{2}a} = -\frac{kq^2}{a\sqrt{2}} = U_{BC}\] \[U_{AC} = k\frac{(+q)(+q)}{2a} = \frac{kq^2}{2a}\]

סך הכל:

\[U = -\frac{kq^2}{a\sqrt{2}} - \frac{kq^2}{a\sqrt{2}} + \frac{kq^2}{2a} = -\frac{2kq^2}{a\sqrt{2}} + \frac{kq^2}{2a}\] \[\boxed{U = k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right)}\]

סעיף ג’: מהירות המטען B בנקודה O

שאלה: משחררים את המסה B (בעלת מסה $m$) ומחזיקים את שני המטענים האחרים במקומם. מהי מהירות B כשעוברת דרך נקודה O (מרכז היתר)?

גילוי נאות - לא הבנתי עד הסוף את הפתרון לסעיף הזה.

פתרון:

משימור אנרגיה:

\[U_{\text{initial}} + K_{\text{initial}} = U_{\text{final}} + K_{\text{final}}\] \[U_1 + 0 = U_0 + \frac{1}{2}mv^2\]

ממה שקיבלנו בסעיף הקודם:

\[U_0 = k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right)\]

כמו כן:

\[U_1 = U_{AO} + U_{CO} + U_{AC} = \frac{-2kq^2}{a} + \frac{kq^2}{2a} = k\frac{q^2}{2a}\left(1 - 4\right) = -\frac{3kq^2}{2a}\]

נעבור לחישוב האנרגיה:

\[\underbrace{E_{k_0}}_{=0} + E_{p_0} = E_{kf} + E_{pf}\] \[E_{kf} = E_{p_0} - E_{pf} = U_0 - U_1\] \[= k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right) - \left(-\frac{3kq^2}{2a}\right) = k\frac{q^2}{2a}\left(4 - 2\sqrt{2}\right)\]

כמו כן:

\[E_{kf} = \frac{1}{2}mv^2 \implies v = \sqrt{\frac{2E_{kf}}{m}} = \sqrt{\frac{kq^2}{am}\left(4 - 2\sqrt{2}\right)}\] \[\boxed{v = \sqrt{\frac{kq^2}{am}\left(4 - 2\sqrt{2}\right)}}\]

או בגרסה שבתשובות:

\[\boxed{v = \sqrt{\frac{4kq^2}{am}\left(1 - \frac{\sqrt{2}}{2}\right)} = \sqrt{\frac{4kq^2}{am}\left(1 - \frac{1}{\sqrt{2}}\right)}}\]

נקודות שחשוב לזכור

סופרפוזיציה - תקפה רק במערכות לינאריות
אנרגיה פוטנציאלית - גודל סקלרי (לא וקטור), יש לו סימן
חוק גאוס - שימושי כשיש סימטריה (כדורית, גלילית, מישורית)
שדה בתוך חלל במבודד - תלוי רק במטען הכלוא בתוך המעטפת הגאוסית
שימור אנרגיה - $K_i + U_i = K_f + U_f$ (בכוח משמר)
מחוץ להתפלגות כדורית - השדה זהה לשדה של מטען נקודתי במרכז

תרגול 6 - פוטנציאל חשמלי ומוליכים

תאריך: 07/12/2025

חזרה על מושגי יסוד

שדה חשמלי ממטען נקודתי

\[\vec{E} = \frac{kQ}{r^2}\hat{r}\]

השדה דועך כמו $\frac{1}{r^2}$
מטען חיובי ← שדה יוצא החוצה
מטען שלילי ← שדה נכנס פנימה

נוסחאות אנרגיה פוטנציאלית חשמלית

גודל נוסחה וסימון

אנרגיה פוטנציאלית חשמלית $U^{elec}(A) = -\int_\infty^A \vec{F}d\vec{s} \, \mathrm{(J)}$

אנרגיה פוטנציאלית חשמלית
בין שני מטענים נקודתיים
במרחק $r$ אחד מהשני $U^{elec} = k \frac{q_1 q_2}{r} \, \mathrm{(J)}$

מבטאת את העבודה החיצונית שנדרשת בשביל להביא מטען מהאינסוף

אם המטענים שווי סימן ← עבודה חיובית (דחייה)

אם המטענים הפוכי סימן ← עבודה שלילית (משיכה)

גודל	נוסחה וסימון
אנרגיה פוטנציאלית חשמלית	\(U^{elec}(A) = -\int_\infty^A \vec{F}d\vec{s} \, \mathrm{(J)}\)
אנרגיה פוטנציאלית חשמלית בין שני מטענים נקודתיים במרחק $r$ אחד מהשני	\(U^{elec} = k \frac{q_1 q_2}{r} \, \mathrm{(J)}\)

פוטנציאל חשמלי - הגדרה

פוטנציאל חשמלי הוא אנרגיה פוטנציאלית ליחידת מטען:

\[V = \frac{U^{elec}}{q} = \frac{-W_{\infty}^{elec}}{q}\]

יחידות:

\[[V] = \frac{\text{J}}{\text{C}} = \text{Volt}\]

1 ג’אול לקולון = 1 וולט
מתח = הפרש פוטנציאלים (למשל 220V בחשמל ביתי)

הקשר בין שדה לפוטנציאל

הכוח הוא מינוס הגרדיאנט של האנרגיה הפוטנציאלית:

\[\vec{F} = -\nabla U\]

בחילוק ב-$q$:

\[\vec{E} = -\nabla V\]

נוסחאות הפרש פוטנציאל חשמלי

גודל הערות יחידות

הפרש פוטנציאל $\Delta V = V_2 - V_1$ העבודה ליחידת מטען הנדרשת להעביר יחידת מטען מנקודה 1 ל-2 וולט (V)

חישוב הפרש פוטנציאל בעזרת שדה חשמלי $\Delta V = -\int_1^2 \vec{E} \cdot d\vec{s}$ וולט (V)

והפוך - בהינתן הפוטנציאל השדה הוא $\vec{E} = -\nabla V$ וולט למטר (V/m)

פוטנציאל חשמלי ממטען נקודתי הוא $V=\frac{kq}{r}$ לעומתו השדה הוא $\vec{E}=\frac{kq}{r^2}\hat{r}$ והאנרגיה הפוטנציאלית ממטענים נקודתיים היא $U^{elec} = k \frac{q_1 q_2}{r}$ וולט (V)

גודל	הערות	יחידות
הפרש פוטנציאל $\Delta V = V_2 - V_1$	העבודה ליחידת מטען הנדרשת להעביר יחידת מטען מנקודה 1 ל-2	וולט (V)
חישוב הפרש פוטנציאל בעזרת שדה חשמלי	\(\Delta V = -\int_1^2 \vec{E} \cdot d\vec{s}\)	וולט (V)
והפוך - בהינתן הפוטנציאל השדה הוא	\(\vec{E} = -\nabla V\)	וולט למטר (V/m)
פוטנציאל חשמלי ממטען נקודתי הוא $V=\frac{kq}{r}$	לעומתו השדה הוא $\vec{E}=\frac{kq}{r^2}\hat{r}$ והאנרגיה הפוטנציאלית ממטענים נקודתיים היא $U^{elec} = k \frac{q_1 q_2}{r}$	וולט (V)

חישוב הפרש פוטנציאלים

\[\Delta V = V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\]

הערה: הפוטנציאל הוא גודל סקלרי, למרות שהאינטגרל כולל וקטורים.

פוטנציאל ממטען נקודתי

\[V = \frac{kQ}{r}\]

הפוטנציאל דועך כמו $\frac{1}{r}$ (לא $\frac{1}{r^2}$ כמו השדה!)
נקודת הייחוס: $V(\infty) = 0$

סופרפוזיציה להמונים (?)

הפוטנציאל שמושרה על ידי מספר מטענים:
\[V_{total} = \sum_i V_i = \sum_i \frac{kQ_i}{r_i}\]
הפוטנציאל השקול בנקודה שנוצר כתוצאה ממספר מטענים הוא סכום הפוטנציאלים.

אם יש רצף של מטענים אז יש לתרגם הסכום לאינטגרל:
\[V_{total} = \int \frac{k \, dQ}{r} = k \int \frac{\rho(\vec{r'}) dV'}{|\vec{r} - \vec{r'}|}\]

תכונות של מוליכים

שדה בתוך מוליך

בתוך מוליך, השדה החשמלי שווה לאפס:
\[\vec{E}_{\text{inside}} = 0\]

הסיבה הפיזיקלית:

שדה מפעיל כוח על מטענים
במוליך, המטענים יכולים לזוז בחופשיות
המטענים זזים עד שסכום הכוחות עליהם שווה לאפס
מגיעים לשיווי משקל אלקטרוסטטי

פוטנציאל בתוך מוליך

אם $\vec{E} = 0$ בתוך המוליך, אז:

\[\vec{E} = -\nabla V = 0 \quad \Rightarrow \quad V = \text{const}\]

הפוטנציאל בתוך מוליך קבוע (אך לא בהכרח אפס!)

הארקה (Grounding)

מהי הארקה?

הארקה = חיבור פיזי לכדור הארץ.

כאשר מוליך מוארק:

הפוטנציאל שלו שווה לפוטנציאל כדור הארץ
כדור הארץ נחשב כמאגר אינסופי עם $V = 0$
לכן: פוטנציאל על מוליך מוארק = 0

הסבר פיזי

כדור הארץ הוא כדור מוליך ענק. אם יש הפרש פוטנציאלים בין המוליך המוארק לכדור הארץ:

מטענים יזרמו עד שהפוטנציאלים ישתוו
בגלל שכדור הארץ ענק, הפוטנציאל שלו נשאר כמעט קבוע (אפס)

חשיבות בטיחותית

בבית, יש שלושה חורים בשקע:

שניים לפאזה ולאפס (220V)
השלישי מחובר להארקה

למה זה חשוב?

אם חוט חשמל נוגע במסגרת מתכתית של מכשיר
בלי הארקה: הזרם עובר דרך האדם לכדור הארץ
עם הארקה: הזרם הולך ישר לכדור הארץ דרך חוט ההארקה

תרגיל 1: חשבונות שדה

תרגיל 1א - חצי מעגל

חשבו את השדה החשמלי בראשית הצירים עבור מטען $Q = 4 \mu \, \mathrm{C}$ המפולג באופן אחיד על חצי מעגל ברדיוס $R=0.74 \, \mathrm{m}$.

חצי המעגל על ציר $y$ כך שהחצי רק על החלק השלישי של ציר $x$. להלן תמונה:

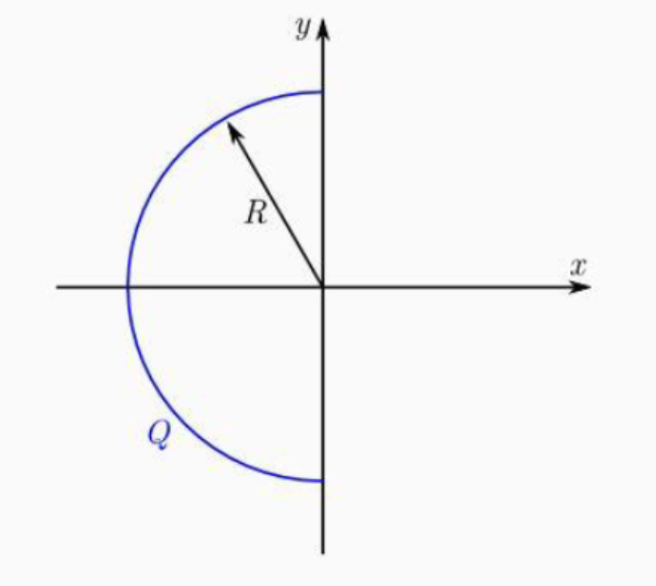
שימו לב: זה חצי מעגל, לא חצי דיסקה (חצי מעגל - משתמשים בהיקף לא בשטח).

להבנתי פחות רלוונטי לסופרפוציפיה. במקרה כזה צריך אינטגרל. כן צריך להבין משיקולי סימטריה מה מתאפס (לא הכל!).

נסתכל על הראשית. נראה שרק בכיוון ציר $x$ יש משהו כי ההשפעות בכיוון ציר $y$ מתאפסות?

ניקח יחידת מטען קטנה (חילקתי את המטען הכולל בהיקף של חצי מעגל):

\[\textcolor{green}{dq} = \frac{Q}{\pi R} d \theta\]

נשתמש בגאוס? לא! גאוס לא מתאים כאן כי חסרה סימטריה. צריך לעשות אינטגרל על השדה ישירות! כל אלמנט קטן עושה על הראשית שדה חשמלי קטנטן של:

\[dE = \frac{K \cdot \textcolor{green}{dq}}{R^2}\]

צריך לפרק לרכיבים מהסימטריה כדי להשיאר רק עם ההיטל על ציר $x$:

\[dE_x = dE \cdot \cos(\theta) = \frac{K}{R^2} \cdot \frac{Q}{\pi R} \cos(\theta)d\theta\]

גבולות האינטגרסיה על $\theta$ הם מ$\frac{\pi}{2}$ אל $\frac{3\pi}{2}$ (ניסיתי לחשוב על מעגל היחידה ועל הציור):

\[\int_{\pi/2}^{3\pi/2} \frac{K}{R^2} \cdot \frac{Q}{\pi R} \cos(\theta)d\theta = \frac{K}{R^2} \cdot \frac{Q}{\pi R} \int_{\pi/2}^{3\pi/2} \cos(\theta)d\theta\] \[= \frac{K}{R^2} \cdot \frac{Q}{\pi R} \sin(\theta)\Big|_{\pi/2}^{3\pi/2} = \boxed{-2 \frac{K}{R^2} \cdot \frac{Q}{\pi R}}\]

\[\sin\left(\frac{\pi}{2}\right) = 1\] \[\sin\left(\frac{3\pi}{2}\right) = -1\]

נציב את המספרים כדי לקבל תשובה מספרית:

\[E_x = -\frac{2 \cdot (9 \times 10^9) \cdot (4 \times 10^{-6})}{\pi \cdot (0.74)^2} \approx -4.16 \, \mathrm{N / C}\]

דוגמה לטעות:
\[E_x = - \frac{2KQ}{\pi R^2} = - \frac{8K}{\pi \cdot 0.5476} = - \frac{8K}{\sim 1.72} \approx -4.65 K\]
שכחתי להציב את ה-$\mu$ (מיקרו) של המטען.
\[Q = 4\mu C = 4 \times 10^{-6} \, \mathrm{C}\]
וגם צריך להציב את הערך של $K$:
\[K = 9 \times 10^9 \frac{\mathrm{Nm}^2}{\mathrm{C}^2}\]

תרגיל 1ב - חלל גלילי בתוך גליל מלא

גליל אינסופי מלא טעון בצפיפות מטען נפחית אחידה $\rho_0$. בגליל נקדח חור כמוראה בציור. מהו השדה החשמלי בתוך החור?

רדיוס הגליל הוא $a$, רדיוס החור $b$ החור נקדח בנקודה $(c,0)$.

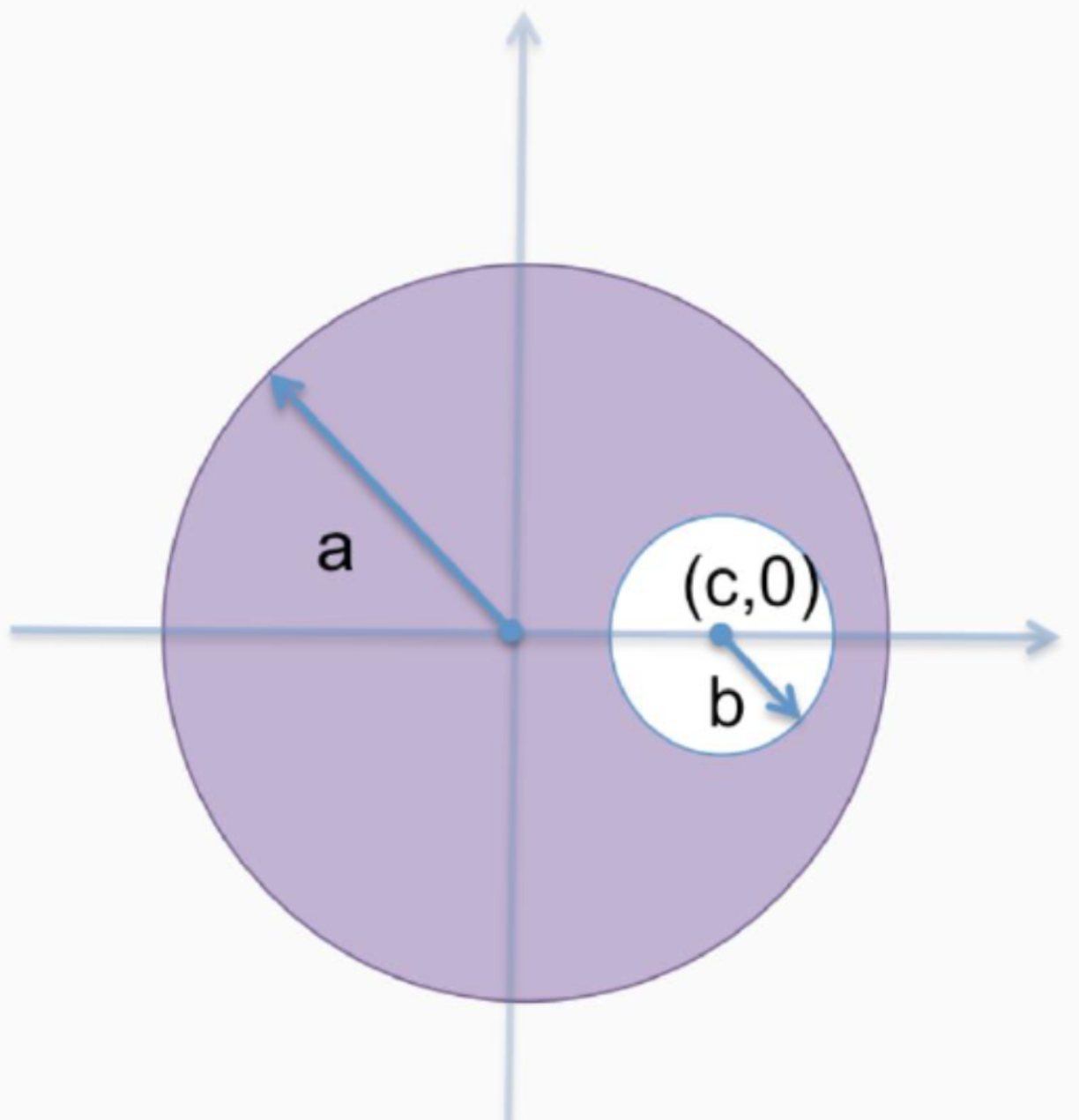
לדעתי צריך להיעזר בסופר פוזיציה ובחוק גאוס: השדה הוא כמו גליל מלא פחות שדה של הגליל הקטן (החור).

החור הוא לא מטען נקודתי!

מה השדה של כל חלק?

גליל מלא ברדיוס $a$ וצפיפות $\rho_0$:

בתוך הגליל ($r < a$): מה השדה? (נשתמש בגאוס)

המטען בתוך הגליל הוא לא אפס!

להיזהר לא להתבלבל עם מוליך. במוליך אין מטען בפנים.

אבל כאן יש צפיפות מטען נפחית $\rho_0$ - כל הנפח מלא במטען!

חישוב נכון עם גאוס

משטח גאוס גלילי ברדיוס $r$ ואורך $L$:

\[E \cdot 2\pi r L = \frac{Q_{inside}}{\epsilon_0}\]

מה המטען בתוך הגליל?

\[Q_{inside} = \rho_0 \cdot V = \rho_0 \cdot \pi r^2 L\]

אז:

\[E_1 \cdot 2\pi r L = \frac{\rho_0 \pi r^2 L}{\epsilon_0}\] \[\boxed{\hat{E}_1\left(r\right) = \frac{\rho_0 \hat{r}}{2\epsilon_0}}\]

זה השדה בתוך גליל מלא. תובנה חשובה: הוא גדל עם $r$, לא קבוע!

הערה: זה היה המטען בתוך גליל טעון - מחוץ לגליל טעון ככל הנראה:
\[\vec{E} = \frac{\lambda}{2\pi \epsilon_0 r}\hat{r}\]

גליל קטן ברדיוס $b$ וצפיפות $\rho_0$ שמרכזו ב-$(c, 0)$:

זה גם גליל, לא מטען נקודתי!
מה השדה שלו בתוכו?

באופן דומה זה לא אפס.

משטח גאוס גלילי ברדיוס מטעים נותן פעם נוספת נוסחה דומה. המטען בגליל הקטן אבל שונה - הוא הפוך בכיוון לצפיפות של הגדול (כי להחסיר זה כמו להוסיף מטען הפוך). וגם הרדיוס כאן להבנתי שונה:

\[\hat{E}_2\left(r\right) = \frac{(-\rho_0) \hat{r'}}{2\epsilon_0}\]

הטריק עכשיו זה לזהות ש:
\[\vec{r'} = \vec{r} - \vec{c}\]
או ברישום שקול:
\[\vec{r'} = \vec{r} - c \hat{x}\]

סך הכל:

\[\hat{E}_2\left(r\right) = \frac{(-\rho_0) \cdot (\vec{r} - c \hat{x})}{2\epsilon_0}\]

השדה הכולל:

\[E = E_1 + E_2 = \frac{\rho_0 \hat{r}}{2\epsilon_0} + \frac{(-\rho_0) \cdot (\vec{r} - c \hat{x})}{2\epsilon_0} = \cancel{\frac{\rho_0 \hat{r}}{2\epsilon_0}} + \cancel{\frac{(-\rho_0) \cdot \vec{r}}{2\epsilon_0}} - \frac{ (-\rho_0) \cdot c \hat{x}}{2\epsilon_0}\] \[= \frac{ \rho_0 \cdot c \hat{x}}{2\epsilon_0}\]

תובנה חשובה

שני הגלילים נותנים שדה אחיד בתוכם (לא תלוי ב-$r$, רק בוקטור המיקום מהמרכז). אז כשמחסרים (או מחברים אותם) מקבלים גם כן שדה אחיד, לא משנה איפה בתוך החור.

דילגנו על תרגיל 2 - הוא זמין בפתרון תרגיל 4.

תרגיל 3: מציאת פוטנציאל חשמלי

גליל מוליך ארוך מאוד אשר רדיוסו הוא $a$ טעון בצפיפות מטען אורכית $\lambda$ קולון ליחידת אורך של הגליל. סביב הגליל מונחת מעטפת גלילית דקה ומוארקת ברדיוס $b>a$, כך שציר הגליל וציר המעטפת הגלילית מתלכדים. מהו הפוטנציאל החשמלי בכל המרחב?

הנחייה: מיצאו את השדה והביאו חלקיק מן האינסוף כנגד (או עם) השפעת השדה.

ננסה להיעזר ברמז - נמצא תחילה את השדה. צריך לפצל לשלושה אזורים:

בתוך המוליך $(r<a)$
בין הגליל למעטפת $(a < r < b)$
מחוץ למטעפת $(r>b)$

בתוך מוליך השדה הוא אפס:

\[\vec{E_1} = \vec{0}\]

בין הגליל למעטפת - נבנה מעטפת גאוסית גלילית.

בגדול הנוסחה לשדה מחוץ לגלליל טעון היא כאמור:

\[\vec{E_2} = \frac{\lambda}{2\pi \epsilon_0 r}\hat{r}\]

מחוץ למעטפת - אפשר להיעזר בכך שהמטעפת מוארקת: המעטפת המוארקת “רואה” מטען $+\lambda$ על הגליל הפנימי, אז היא תיטען ב-$-\lambda$ (מטענים נשאבים מהאדמה).

סך המטען הכלוא במשטח גאוס ב-$r > b$:

\[Q_{inside} = (+\lambda L) + (-\lambda L) = 0\]

לכן:

\[\vec{E_3}(r > b) = 0\]

חישוב הפוטנציאל

יש לנו את השדה בכל מקום. עכשיו צריך לחשב:

\[V(r) = -\int_{\infty}^{r} \vec{E} \cdot d\vec{r}\]

נתחיל מ-$r > b$ (שם $V = 0$ כי מוארק), ונתקדם פנימה.

האינטגרל רץ על המסלול מנקודת הייחוס (אינסוף) עד לנקודה שבה רוצים למצוא את הפוטנציאל.

בין המטעפת לגליל - נפרק לאזורים (כי השדה משתנה באזורים שונים)

באזור $a < r < b$:

\[V(r) = -\int_{\infty}^{b} \vec{E_3} \cdot dr - \int_{b}^{r} \vec{E_2} \cdot dr\] \[= -\int_{\infty}^{b} 0 \cdot dr - \int_{b}^{r} \frac{\lambda}{2\pi\epsilon_0 r'} dr'\] \[= 0 - \frac{ \lambda }{2 \pi \epsilon_0} \ln \left(r'\right) \bigg|_b^r\] \[= -\frac{\lambda}{2\pi\epsilon_0} \left[\ln(r) - \ln(b)\right]\] \[= \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right)\]

עכשיו ננסה לחשב את $V(r)$ עבור $r < a$ (בתוך המוליך).

באזור $r < a$:

\[V(r) = -\int_{\infty}^{b} \vec{E_3} \cdot dr - \int_{b}^{a} \vec{E_2} \cdot dr - -\int_{a}^{r} \vec{E_1} \cdot dr\] \[= -\int_{\infty}^{b} 0 \cdot dr - \int_{b}^{a} \frac{\lambda}{2\pi\epsilon_0 r'} dr' -\int_{a}^{r} 0 \cdot dr\] \[= 0 - \frac{ \lambda }{2 \pi \epsilon_0} \ln \left(r'\right) \bigg|_b^a + 0\] \[= \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right)\]

סך הכל:

\[V(r) = \begin{cases} \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right) \, & \text{for } r<a \\ \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right) \, & \text{for } a<r<b \\ 0 \, & \text{for } r< b \\ \end{cases}\]

פתרון כתה - מציאת הפוטנציאל במרחב

להלן הפתרון לאותה השאלה לפי התרגול בכתה.

פתרון בעזרת חוק גאוס ואינטגרציה

שלב 1: מציאת השדה בין הגלילים ($a < r < b$)

משתמשים בחוק גאוס עם מעטפת גלילית ברדיוס $r$ ואורך $L$:

\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enc}}}{\epsilon_0}\] \[E \cdot 2\pi r L = \frac{\lambda L}{\epsilon_0}\] \[E(a < r < b) = \frac{\lambda}{2\pi\epsilon_0 r}\]

שלב 2: מציאת הפוטנציאל

הפוטנציאל על המעטפת המוארקת:

\[V(b) = 0\]

הפוטנציאל בנקודה $r$ (בין $a$ ל-$b$):

\[V(r) - V(b) = -\int_b^r E \, dr'\] \[V(r) = -\int_b^r \frac{\lambda}{2\pi\epsilon_0 r'} dr'\] \[V(r) = -\frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{r}{b}\right)\] \[\boxed{V(a < r < b) = \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right)}\]

שלב 3: פוטנציאל בתוך הגליל הפנימי ($r < a$)

השדה בתוך מוליך הוא אפס, לכן הפוטנציאל קבוע:

\[V(r < a) = V(a) = \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right)\]

שלב 4: פוטנציאל מחוץ למעטפת ($r > b$)

המעטפת מוארקת ולכן $V(b) = 0$.

מחוץ למעטפת, צריך לחשב את השדה ולבצע אינטגרציה.

תרגיל 4: כדור מוליך עם הארקות

נתון כדור מוליך $A$ שרדיוסו הוא $R$ ומטענו הוא $+Q$.

שרטטו באופן איכותי גרף של הפוטנציאל $V(r)$ כתלות במרחק $r$ ממרכז הכדור, בתחום $0 \le r \le 3R$.

מקיפים את הכדור $A$ בקליפה מוליכה כדורית דקה $B$ שרדיוסה הוא $2R$, כך שלשני הגופים יש מרכז משותף. הקליפה טעונה במטען חשמלי $-2Q$.

מהו הפוטנציאל החשמלי בכל המרחב? (רמז: סופרפוזיציה)

מהי העבודה הנדרשת להביא מטען $q$ כלשהו מהאינסוף אל הקליפה החיצונית? (רמז: אין צורך לחשב אינטגרל)

עתה מאריקים את הקליפה החיצונית. מהו המטען המצטבר על הכדור המוליך ועל הקליפה במצב זה?

מנתקים את ההארקה ומחברים את שני הגופים במוליך דק. מהו המטען עתה על כל מוליך? (הניחו שלא מצטברים מטענים על המוליך הדק).

סעיף א - כדור מוליך טעון: גרף איכותי של הפוטנציאל החשמלי

נתון כדור מוליך ברדיוס $R$ טעון במטען $Q$.

מהו הפוטנציאל החשמלי בכל המרחב?

מוליך - המטענים יכולים לזוז. צריך להפריד לאזורים.

אזור 1: בתוך הכדור ($r < R$)

השדה בתוך מוליך הוא אפס:

\[E(r < R) = 0\]

לכן הפוטנציאל קבוע:

\[V(r < R) = \text{const}\]

אזור 2: מחוץ לכדור ($r > R$)

מחוץ לכדור, הוא נראה כמו מטען נקודתי:

\[E(r > R) = \frac{kQ}{r^2}\]

הפוטנציאל:

\[V(r > R) = \frac{kQ}{r}\]

מציאת הקבוע בתוך הכדור

הפוטנציאל רציף, לכן:

\[V(r < R) = V(R) = \frac{kQ}{R}\]

סיכום

\[V(r) = \begin{cases} \frac{kQ}{R} & r \leq R \\ \frac{kQ}{r} & r > R \end{cases}\]

גרף איכותי

V
│
│████████████  ← קבוע בתוך הכדור
│            ╲
│             ╲
│              ╲  ← דועך כמו 1/r
│               ╲
│                ╲___
└─────────────────────── r
         R

הערה: יש קפיצה בנגזרת (בשדה) על פני המעטפת, אבל הפוטנציאל עצמו רציף.

סעיף ב - חישוב בעזרת סופרפוזיציה

כדור מוליך ברדיוס $R$ טעון במטען $+Q$

מקיפים את הכדור בקליפה מוליכה כדורית דקה ברדיוס $2R$

הקליפה טעונה במטען $-2Q$

מרכז משותף

מהו הפוטנציאל החשמלי בכל המרחב?

נפתור בנפרד עבור כל גוף ואז נסכום.

תרומת הכדור הפנימי (ירוק) - מטען $+Q$

בתוך הכדור ($r < R$):

\[V_{\text{green}}(r < R) = \frac{kQ}{R} \quad \text{(const)}\]

מחוץ לכדור ($r > R$):

\[V_{\text{green}}(r > R) = \frac{kQ}{r}\]

תרומת הקליפה החיצונית (אדום) - מטען $-2Q$

בתוך הקליפה ($r < 2R$):

\[V_{\text{red}}(r < 2R) = \frac{k(-2Q)}{2R} = -\frac{kQ}{R} \quad \text{(const)}\]

מחוץ לקליפה ($r > 2R$):

\[V_{\text{red}}(r > 2R) = \frac{k(-2Q)}{r} = -\frac{2kQ}{r}\]

סופרפוזיציה - סיכום כל האזורים

אזור 1: $r < R$ (בתוך הכדור הפנימי)

\[V = V_{\text{green}} + V_{\text{red}} = \frac{kQ}{R} + \left(-\frac{kQ}{R}\right) = 0\]

אזור 2: $R < r < 2R$ (בין הכדור לקליפה)

\[V = \frac{kQ}{r} + \left(-\frac{kQ}{R}\right) = \frac{kQ}{r} - \frac{kQ}{R}\] \[\boxed{V(R < r < 2R) = kQ\left(\frac{1}{r} - \frac{1}{R}\right)}\]

אזור 3: $r > 2R$ (מחוץ לקליפה)

\[V = \frac{kQ}{r} + \left(-\frac{2kQ}{r}\right) = -\frac{kQ}{r}\] \[\boxed{V(r > 2R) = -\frac{kQ}{r}}\]

הסבר שיטת הסופרפוזיציה

מחשבים את הפוטנציאל מכל גוף בנפרד
מתייחסים לכל גוף כאילו האחר לא קיים
סוכמים את התרומות (חיבור או חיסור לפי הסימן)

יתרון: מפשט בעיות עם מספר גופים טעונים

סעיף ב(2) העבודה הנדרשת להביא מטען $q$ כלשהו מהאינסוף אל הקליפה החיצונית

מצאנו את הפונציאל אז העבודה קשורה להפרש פוטנציאלים. באינסוף הפוטנציאל הוא 0, מכאן שהעבודה להזיז מטען $q$ היא:

\[W = q \cdot \Delta V = q \cdot \left(V_{final \implies r=2R}-V_{initial}\right)\] \[= q ((-\frac{kQ}{r}) - 0) = \boxed{-\frac{qkQ}{2R}}\]

להיזהיר לא להתבלבל בסימנים! זאת העבודה הסופית פחות ההתחלתית.

למה העבודה יוצאת שלילית?

הפוטנציאל בקליפה החיצונית הוא שלילי, כלומר מושך מטענים, מכאן שלמעשה השדה עושה עבודה חיובית ואנחנו לא צריכים לעשות מבחוץ עבודה (זה נמשך לבד).

סעיף ג - מטען מצטבר כשמאריקים

נתון שמאריקים את הקליפה החיצונית ושואלים מה המטען המצטבר על הכדור המוליך ועל הקליפה במצב הזה.

כשמאריקים את הקליפה, הפוטנציאל שלה הופך לאפס. אבל זה לא אומר שהמטען נשאר אותו דבר! הקליפה מחוברת לאדמה, אז מטענים יכולים לזרום אליה או ממנה עד שהפוטנציאל שלה יהיה אפס.

שאלות מנחות:

הכדור הפנימי - האם הוא מחובר למשהו? האם המטען שלו יכול להשתנות?

המטען שלו לא משתנה!
הקליפה - מה צריך להיות המטען עליה כדי שהפוטנציאל ב-$r = 2R$ יהיה אפס?

צריך להשתוות לזה של הכדור? כן!

תובנה מהותית: צריך להשתמש בסופרפוזיציה. הפוטנציאל בקליפה ($r = 2R$) הוא סכום התרומות מהכדור ($+Q$) ומהקליפה עצמה (מטען לא ידוע $Q_{shell}$).

נחשב את הפוטנציאל בקליפה (צריך להיות אפס):

\[V(2R) = \underbrace{\frac{kQ}{2R}}_{\text{inner ball}} + \underbrace{\frac{kQ_{shell}}{2R}}_{\text{shell}} = 0\]

נפתור עבור $Q_{shell}$:

\[\frac{kQ}{2R} + \frac{kQ_{shell}}{2R} = 0 \implies \boxed{Q_{shell} = -Q}\]

סעיף ד - מטען על כל מוליך לאחר חיבור

לאחר מוליך המטענים מתחלקים עד שנשארים במקום באיזון.

המצב ההתחלתי - אפס

אחרי סעיף ג (הארקה):

הכדור הפנימי: $+Q$
הקליפה: $-Q$ (חישבנו בסעיף ג)

סך המטען במערכת: $Q + (-Q) = 0$

כשמחברים מוליך - תנועת מטענים

כשמחברים שני מוליכים, המטענים נעים עד שהפוטנציאל שווה בשניהם.

למה הכל מתאפס?

סך המטען במערכת הוא אפס, והמערכת סימטרית (כדור בתוך קליפה עם מרכז משותף).

אם סך המטען אפס ואין כוחות חיצוניים, המטענים יתפלגו כך שהפוטנציאל אחיד בכל המערכת. הדרך היחידה לעשות זאת היא:

מטען על הכדור: $0$
מטען על הקליפה: $0$

(כל חלוקה אחרת תיצור הפרש פוטנציאלים בין המוליכים)

[דילגנו על תרגיל 5]

תרגיל 6: קליפות וכדורים

נתונה קליפה כדורית $B$ דקה ומוליכה, בעלת רדיוס $2R$, ובתוכה כדור מוליך $A$ בעל רדיוס $R$. הקליפה והכדור בעלי מרכז משותף. הכדור $A$ טעון במטען $+Q$ והכדור $B$ נייטרלי (אינו טעון). כדור שלישי $C$, שרדיוסו $R$ ומטענו $+3Q$ נמצא רחוק משני הראשונים. מחברים את הכדורים $B$ ו-$C$ בתיל מוליך.

מה יהיה מטענה של הקליפה הכדורית $B$, אחרי שהמערכת הגיעה למצב של שיווי משקל?

מהו פוטנציאל הכדור $A$ לאחר שהמערכת הגיעה למצב שיווי משקל?

סעיף 1 - מטען הקליפה B בשיווי משקל

נחשב!

הקליפה בהתחלה היא אולי $-Q$ כי היא מאזנת את הכדור הפנימי?

אבל הקליפה $B$ היא בסך הכל נייטרלית, אז בצד החיצוני שלה כנראה נמצא $Q$?

כשמחברים את $B$ ו $C$ הפוטנציאל שלהם צריך להיות שווה, סך המטען שמתחלק ביניהם הוא כנראה $4Q$, אז על כל חלק יש $2Q$? לא! יש כאן הבדלים ברדיוסים.

הפוטנציאל על פני כדור הוא:

\[V = \frac{kQ}{R}\]

אז על פני הקליפה הגדולה:

\[V_{big} = \frac{kQ_b}{2R}\]

ואילו על הקטנה:

\[V_{small} = \frac{kQ_s}{R}\]

הפוטנציאלים אבל שווים, כלומר:

\[V_{small} = V_{big} \implies Q_b = 2Q_s \implies Q_s = \frac{Q_b}{2}\]

סך המטען הוא שווה ל-$4Q$, אז:

\[Q_b + Q_s = Q_b + \frac{Q_b}{2} = 4Q\] \[\frac{3Q_b}{2} = 4Q \implies Q_b = \frac{8Q}{3}\]

תובנה קריטית: זה לא מספיק! צריך לחבר גם את ההשפעה של הצד הפנימי של הקליפה $B$ בשביל לכל את המטן הכולל!

המטען על הקליפה $B$ כולל:

צד פנימי: $-Q$
צד חיצוני: $\frac{8Q}{3}$

סה”כ על $B$:

\[Q_B = -Q + \frac{8Q}{3} = \frac{-3Q + 8Q}{3} = \boxed{\frac{5Q}{3}}\]

פתרון כתה - שימור מטען

בפתרון הרשמי הגיעו לתוצאה הזאת בדרך אחרת:

הפוטנציאל על B, בדומה למה שמצאנו, הוא סכום הפוטנציאלים

\[V_B = \frac{kQ_B}{2R} + \underbrace{\frac{kQ}{2R}}_{\text{from inner ball}}\]

ועל הכדור החיצוני:

\[V_C=\frac{kQ_C}{R}\]

מהשוויון בין הפוטנציאלים נקבל:

\[\frac{\cancel{k}Q_B}{\cancel{2R}} + \frac{\cancel{k}Q}{\cancel{2R}} = \frac{\cancel{k}Q_C}{\cancel{R}}\] \[Q_B = 2Q_C - Q\]

ומשימור מטען ניתן לקבל:

\[Q_B + Q_C = 3Q \implies 2Q_c = 6Q - 2Q_B\]

נציב ונקבל:

\[Q_B = 6Q - 2Q_B - Q\] \[3Q_B = 5Q \implies \boxed{Q_B = \frac{5Q}{3}}\]

סעיף 2 - פוטנציאל הכדור $A$ בשיווי משקל

צריך לחשב כנראה את ההשפעה שלש לקילפה החיצונית, לפי המטען שמצאנו בסעיף הקודם.

הפוטנציאל של כדור $A$ (שנמצא ב-$r \leq R$) מורכב מסופרפוזיציה של:

תרומת הכדור $A$ עצמו: $\frac{kQ}{R}$
תרומת הקליפה $B$: הפוטנציאל בתוך קליפה הוא קבוע ושווה ל-$\frac{kQ_B}{2R}$

אז:

\[V_A = \frac{kQ}{R} + \frac{kQ_B}{2R} = \frac{kQ}{R} + \frac{k \cdot \frac{5Q}{3}}{2R} = \boxed{\frac{11kQ}{6R}}\]

סיכום - נקודות חשובות

פוטנציאל vs שדה

תכונה	שדה $\vec{E}$	פוטנציאל $V$
סוג	וקטור	סקלר
דעיכה ממטען נקודתי	$\frac{1}{r^2}$	$\frac{1}{r}$
בתוך מוליך	אפס	קבוע
קשר	$\vec{E} = -\nabla V$	$V = -\int \vec{E} \cdot d\vec{l}$

מוליכים

שדה בתוך מוליך = 0
פוטנציאל בתוך מוליך = קבוע
מטענים מתפלגים על פני השטח

הארקה

מוליך מוארק: $V = 0$
מטענים יכולים לזרום מ/אל כדור הארץ

סופרפוזיציה

פוטנציאל כולל = סכום הפוטנציאלים מכל מטען
עובד כי פוטנציאל הוא גודל סקלרי (פשוט לסכום!)

טיפים לפתרון

זהה את האזורים - בתוך מוליך, בין מוליכים, מחוץ
מצא את השדה בכל אזור (חוק גאוס)
בצע אינטגרציה למציאת הפוטנציאל
השתמש בתנאי שפה (הארקה, רציפות)
בדוק סופרפוזיציה כשיש מספר גופים

פתרון בוחן לדוגמה - גרסת ג׳מני 2025

תאריך: 08/12/2025

להלן פתרונות שלי לבוחן מג׳ונרט שהועלה לתרגול. קחו את הדברים בערבון מוגבל. בהצלחה!

שאלה 3-1: טבעת ״פגומה״ (סופרפוזיציה וסימטריה)

נתונה טבעת דקה מחומר מבודד ברדיוס $R$, המונחת במישור $xy$ ומרכזה בראשית הצירים. הטבעת טעונה בצפיפות מטען אורכית אחידה וחיובית $\lambda$. מחסירים (חותכים החוצה) מהטבעת קשת קטנה מאוד באורך $L (L \ll R)$ הנמצאת בדיוק בראש הטבעת (על צירך ה-$y$ החיובי, בנקודה $(0,R)$).

1. מהו כיוון וגודל השדה החשמלי בראשית הצירים (מרכז הטבעת)?

משיקולי סימטרייה כל המטענים מתאפסים למעט המטען מכיוון מטה, שכעת יכול לצאת דרך הקשת העליונה שהחסרנו (זה כמו להוסיף מטען הפוך).

אפשר אולי לחשב מסופר פוזיציה.

ברגיל זה אפס. כדי לחשב את השדה החשמלי של המטען שהוספנו (החסרנו) ניעזר בדף הנוחסאות.

הנוסחה לחישוב שדה חשמלי של מטען נקודתי היא:

\[\vec{E} = \frac{kq_1}{r^2}\hat{r}\]

או בצורה סקלרית בלי וקטור הכיוון.

במקרה הזה הכיוון הוא במעלה ציר $\hat{y}$.

המטען שלנו מתקבל בעזרת הנוסחה לחישוב מטען נקודתי:

\[\lambda = \frac{q}{\ell} \implies q = \lambda \cdot L\]

סך הכל:

\[\boxed{\vec{E} = \frac{k \lambda L}{R^2} \hat{y}}\]

כלפי מעלה.

מהו הפוטנציאל החשמלי בראשית הצירים?

הניחו ש $L$ קטן מאוד כך שהמטען הכולל כמעט לא השתנה, או חשבו במדויק $Q_{\text{tot}} = \lambda (2 \pi R - L)$.

הנוסחה של פוטנציאל מטען נקודתי היא:

\[V = \frac{kq}{r}\]

נציב את הרמז $Q_{\text{tot}} = \lambda (2 \pi R - L)$. אפשר לקבל אותו מהנוסחה של צפיפות מטען אורכית $(q=\lambda \cdot L)$: במקור האורך היה שני פאי אר אבל הורדנו ממנו קשת באורך $L$.

\[V = \frac{kQ_{tot}}{R} = \frac{k\lambda(2\pi R - L)}{R}\]

אם $L \ll R$, אפשר לקרב ל-$V \approx \frac{2\pi k\lambda R}{R} = 2\pi k\lambda$

הערה: בפתרון הרשמי פתרו בעזרת אינטגרל. להבנתי ניתן להשתמש כאן בנוסחה ישירות בגלל המערכת בשאלה.

בשיעור התגבור הובהר שדווקא האינטגרל הוא הדרך הנכונה, ושהוא נדרש בצד סופרפוזיצה.

מניחים אלקטרון (מטען $-e$) במנוחה במרכז הטבעת. לאן הוא ינוע מיד לאחר השחרור?

לדעתי למטה - יתרחק מהמטען השלילי שכאילו הוספנו מעליו.

פורמאלית, זה נובע מהכוח שפועל על מטען בשדה חשמלי:

\[\vec{F} = q \vec{E}\]

השדה במרכב הוא כאמור

\[\boxed{\vec{E} = \frac{k \lambda L}{R^2} \hat{y}}\]

כלפי מעלה.

לאלקטרון מטען שלילי אז הוא יהיה בכיוון הפוך - כלפי מטה (לכיוון מינוס וואי).

שאלות 5-4: מוליכים מחוברים (השוואת פוטנציאלים)

שתי קליפות כדוריות מוליכות נמצאות רחוק מאוד זו מזו (ניתן להזניח השפעה הדדית). רדיוס הקליפה הראשונה $R_1 = R$ והיא טעונה במטען $Q$. רדיוס הקליפה השנייה $R_2 = 3R$ והיא ניטרלית (מטען 0). מחברים את שתי הקליפות באמצעות תיל מוליך דק וארוך.

מהו המטען הסופי $q_1$ שיישאר על הקליפה הקטנה $(R)$?

תובנה מהותית: כשמחברים קליפות מוליכות עם תיל מוליך המטענים נעים מהקליפה הטעונה לנייטרלית עד שיהיה ביניהם שוויון פוטנציאלים (ואז לא יופעלו כוחות על מטענים לזוז ממקומם).

הפוטנציאל על מעטפת כדורית באופן כללי נתון על ידי:

\[V_{\text{on Ma'atefet Kadurit}} = k \int_{\text{HaMa'atefet}}\frac{\sigma ds}{r} = \frac{k \cdot \sigma \cdot 4 \pi r^2}{r} = \frac{kQ}{r}\]

נציב בקליפות של השאלה. על קליפה 2:

\[V_2 = \frac{k \cdot Q_2}{R_2} = \frac{k \cdot Q_2}{3R}\]

על קליפה 1:

\[V_1 = \frac{k \cdot Q_1}{R_1} = \frac{k \cdot Q_1}{R}\]

נשווה:

\[\frac{k \cdot Q_1}{R} = \frac{k \cdot Q_2}{3R} \implies Q_2 = 3Q_1\]

משימוש מטען מתקיים ש:

\[Q_1 + Q_2 = Q \implies Q_1 + 3Q_1 = Q \implies 4Q_1 = Q \implies \boxed{Q_1 = \frac{Q}{4}}\]

מהו הפוטנציאל המשותף של שתי הקליפות לאחר החיבור (ביחס לאינסוף)?

נחשב את הפוטנציאל במצב הסופי.

\[V = \frac{k \cdot Q_1}{R_1} = \frac{k \cdot \frac{Q}{4}}{R} = \boxed{\frac{kQ}{4R}}\]

הסבר מקלוד: הפוטנציאל המשותף

מה קורה פיזיקלית?

אחרי שהמטענים מתחלקים בין הקליפות, שתיהן נמצאות באותו פוטנציאל (זו הסיבה שהמטענים הפסיקו לזוז).

אז אפשר לחשב את הפוטנציאל המשותף דרך כל אחת מהקליפות — התוצאה תהיה זהה.

חישוב דרך קליפה 1
\[V = \frac{kQ_1}{R_1} = \frac{k \cdot \frac{Q}{4}}{R} = \frac{kQ}{4R}\]

בדיקה דרך קליפה 2
\[V = \frac{kQ_2}{R_2} = \frac{k \cdot \frac{3Q}{4}}{3R} = \frac{3kQ}{4 \cdot 3R} = \frac{kQ}{4R}\]
אותה תוצאה — וזה הגיוני כי הפוטנציאלים שווים.

למה “ביחס לאינסוף”?

הפוטנציאל תמיד נמדד ביחס לנקודת ייחוס. הנוסחה $V = \frac{kq}{r}$ מניחה ש-$V(\infty) = 0$.

זה פשוט אומר שאנחנו משתמשים בקונבנציה הסטנדרטית.

שאלות 7-6: קובייה חסרה (גיאומטריה וסופרפוזיציה)

נתונה קבוייה דמיונית שאורך צלעה $d$. ב-7 מתוך 8 קודקודי הקוביה מקובעים מטענים חיוביים זהים $+q$. הקודקוד השמיני (נניח בראשית הצירים) ריק.

מהו גודל השדה החשמלי במרכז הקוביה?

זה דומה לשאלות הקודמות רק מורכב יותר.

נחשב כאילו יש מטען חיובי על הכל ואז סופר פוזיציה עם מטען שלילי במקום שאין בו מטען.

התרומות של כל הפאות מבטלות זו את זו אז ברגיל יש במרכז אפס?

פאה אחת שלילית משפיעה על המרכז כך:

\[|E| = \frac{kq}{(R)^2}\]

נחשב את המרחק $R$ מהקודקוד למרכז:

האלכסון של קוביה עם צלע באורך $d$ נתון על ידי:

\[\sqrt{d^2 + d^2 +d^2} = \sqrt{3}d\]

המרחק מהפינה למרכז הוא חצי מהאלכסון:

\[R = \frac{\sqrt{3}d}{2}\]

מכאן שהשדה מהמטען ה״חסר״ (השלילי הדמיוני) הוא:

\[|E| = \frac{kq}{(R)^2} = \frac{kq}{\left(\frac{\sqrt{3}d}{2}\right)^2} = \boxed{\frac{4kq}{3d^2}}\]

מהי האנרגיה הפוטנציאלית החשמלית הדרושה כדי להביא מטען נוסף $+q$ מאינסוף ולהושיב אותו בקודקוד השמיני הריק (כך שתושלם קובייה מלאה)?

נתון עזר: הפוטנציאל שיוצרת קובייה מלאה של 8 מטענים במרכזה הוא $V_{center}$. זה לא עוזר כאן. חישבו על סכום הפוטנציאלים בקוקוד הריק. נתון כי המקדם הגיאומטרי $\alpha = \left( 3 + \frac{3}{\sqrt{2}} + \frac{1}{\sqrt{3}} \right) \approx 5.7$.

זה דומה לתרגיל המשושה החד מימדי שפתרנו להבנתי.

האנרגיה הדרושה להביא מטען $+q$ לנקודה היא:

\[U = qV\]

כאשר $V$ הוא הפוטנציאל בנקודה לפני הכנסת המטען.

תחילה נחשב את הפוטנציאל בפינה הריקה, זה מתקבל מההשפעה של כל שבעת המטענים האחרים. יש שלושה סוגים של מרחקים מהפינה הריקה לפינות אחרות (צלע, אלכסון פאה ואלכסון קובייה), המקדם שברמז כבר מסכם את הגאומטריה.

\[V = 5.7\frac{kq}{d}\]

מכאן (סופרפוזיציה של כל התרומות לאנרגיה החשמלית הנדרשת):

\[U = 5.7\frac{kq^2}{d}\]

הבהרה - מקור הרמז

אפשר לקבל את המקדמים מחישובים טריגונומטריים של משולשים ישרי זווית.
\[\begin{aligned} V_{\text{E tot}} &= \underbrace{V_{EA} + V_{EG} + V_{EH}}_{\frac{3kq}{d}} + \underbrace{V_{EB} + V_{EF} + V_{ED}}_{\frac{3kq}{d\sqrt{2}}} + \underbrace{V_{EC}}_{\frac{kq}{d\sqrt{3}}} \\ &= \left(3 + \frac{3}{\sqrt{2}} + \frac{1}{\sqrt{3}}\right)\frac{kq}{d} \\ &= \alpha \frac{kq}{d} \end{aligned}\]

שאלות 9-8: מוט עם צפיפות משתנה (אינטגרציה)

מוט מבודד באורך $L$ מונח על ציר $x$ בין הנקודה $x=0$ ל-$x=L$. צפיפות המטען האורכית של המוט משתנה לפי הנוסחה: $\lambda(x) = A \cdot x^2$ (כאשר $A$ קבוע חיובי).

מהו המטען הכולל $Q$ על המוט?

הצפיפות לא אחידה אז נראה שנדרשת כאן אינטגרציה.

ליחידה קטנה על המוט:

\[dq = A \cdot x^2 dx\]

נסכום בעזרת אינטגרל:

\[\int_0^L A \cdot x^2 dx = A \frac{x^3}{3} |^L = \boxed{A \frac{L^3}{3}}\]

חשבו את השדה החשמלי בנקודה $x=2L$ (מימין למוט)?

נחשב את התרומה של כל אלמנט קטן $dq$ על המוט לשדה בנקודה.

כמו מקודם, אלמנט קטן הוא:

\[dq=\lambda(x)dx = Ax^2dx\]

תובנה מהותית: המרחק בן כל אלמנט קטן על המוט לבן הנקודה משתנה לפי:

\[r = 2L-x\]

הבנה נוספת: צריך להיעזר בנוסחה של שדה חשמלי, ולסכום עם אינטגרל:

\[dE = \frac{kdq}{r^2} = \frac{kAx^2dx}{\left(2L-x\right)^2}\]

אינטגרל חביב:

\[E = \int_0^L dE dx\]

נוציא קבועים:

\[= kA \int \frac{x^2dx}{\left(2L-x\right)^2}\]

מסתבר שזה מספיק טוב, ומופיע כאחת התשובות.

הצעת פתרון - בוחן אמצע גרסת קלוד

תאריך: 12/12/2025

להלן מבחן מג׳ונרט שנוצר על ידי קלוד, יחד עם הצעת פתרון מפורטת לכל שאלה. לא בטוח שהשאלות או התשובות נכונות. בהצלחה!

הנחיות

משך הבחינה: שעתיים וחצי
השימוש בכל חומר עזר כתוב או מצולם מותר
בבחינה 9 שאלות ברירה, יש לענות על כולן
בכל שאלת ברירה יש ארבע תשובות לבחירה. יש לבחור תשובה אחת בלבד

שאלות 3-1

חצי כדור מוליך חלול בעל רדיוס $R$ טעון במטען כולל $+Q$ המפוזר באופן אחיד על פניו. מרכז בסיס חצי הכדור נמצא בראשית הצירים, וציר הסימטריה של חצי הכדור מונח לאורך ציר $z$ החיובי.

נקודה $A$ נמצאת על ציר $z$ במרחק $\frac{R}{2}$ מהראשית (בתוך החלל הפנוי של חצי הכדור).

נקודה $B$ נמצאת על ציר $z$ במרחק $2R$ מהראשית (מחוץ לחצי הכדור).

שאלה 1

הפוטנציאל החשמלי בנקודה $B$ הוא בקירוב:

$V = \frac{KQ}{2R}$

$V = \frac{KQ}{R}$

$V = \frac{2KQ}{R}$

$V = 0$

שאלה 2

אם מציבים מטען נקודתי $-q$ בראשית הצירים, הכוח הפועל עליו יהיה:

בכיוון $+\hat{z}$

בכיוון $-\hat{z}$

$\vec{F} = 0$

בכיוון רדיאלי כלפי חוץ

שאלה 3

מטען קטן $+q$ בעל מסה $m$ משתחרר ממנוחה מנקודה $B$. מה תהא מהירותו כאשר יגיע לאינסוף?

$v = \sqrt{\frac{KQq}{mR}}$

$v = \sqrt{\frac{2KQq}{mR}}$

$v = \sqrt{\frac{KQq}{2mR}}$

$v = 0$

שאלות 5-4

שני גלילים מוליכים קואקסיאליים (בעלי ציר משותף) אינסופיים: הגליל הפנימי בעל רדיוס $a$ טעון בצפיפות מטען אורכית $+\lambda$, והגליל החיצוני בעל רדיוס $b$ טעון בצפיפות מטען אורכית $-\lambda$.

שאלה 4

השדה החשמלי באזור $a < r < b$ הוא:

$\boxed{E = \frac{\lambda}{2\pi\varepsilon_0 r}}$

$E = \frac{\lambda}{\pi\varepsilon_0 r^2}$

$E = \frac{2\lambda}{\pi\varepsilon_0 r}$

$E = 0$

בהתחלה חשבתי שהתשובה היא ד׳ מפני שבתוך מוליך אין שדה חשמלי, אבל אז הבנתי שהאזור שנשאל לא נחשב ״בתוך מוליך״ אלא בין המוליכים.

צריך להשתמש כאן בחוק גאוס.

תובנה חשובה: המשטח שכלוא בחלל הגאוסי שאנחנו צריכים לבנות הוא רק הגליל הפנימי!

\[E_r \cdot 2\pi r L = \frac{\lambda L}{\epsilon_0} \implies E_r = \frac{\lambda}{2\pi \epsilon_0 r}\]

התשובה הנכונה היא א.

למה הגליל החיצוני לא משפיע?

התשובה הקצרה

באזור $a < r < b$, משטח גאוס לא מקיף את הגליל החיצוני, ולכן המטען שלו לא נכלל ב-$Q_{inside}$.

הסבר עם חוק גאוס

כשבונים משטח גאוס גלילי ברדיוס $r$ (כאשר $a < r < b$):
        ─────────────────────
       |                     | ← גליל חיצוני (רדיוס b), מטען −λ
       |   ┌─────────────┐   |
       |   |             |   |
       |   |   ┌─────┐   |   |
       |   |   |  +  | ← גליל פנימי (רדיוס a), מטען +λ
       |   |   └─────┘   |   |
       |   |             | ← משטח גאוס (רדיוס r)
       |   └─────────────┘   |
       |                     |
        ─────────────────────
\[Q_{inside} = +\lambda L \text{ (Only the Inner Flux!)}\]
הגליל החיצוני נמצא מחוץ למשטח גאוס, אז הוא לא תורם ל-$Q_{inside}$.

עקרון חשוב

חוק גאוס מתייחס רק למטען שבתוך המשטח הסגור. מטענים מבחוץ יוצרים שדה שנכנס ויוצא מהמשטח, אבל התרומה הכוללת שלהם לשטף היא אפס.

שאלה 5

הפרש הפוטנציאלים בין הגליל הפנימי לחיצוני הוא:

$\boxed{\Delta V = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right)}$

$\Delta V = \frac{\lambda}{2\pi\varepsilon_0} \left(\frac{1}{a} - \frac{1}{b}\right)$

$\Delta V = \frac{\lambda}{4\pi\varepsilon_0} \ln\left(\frac{a}{b}\right)$

$\Delta V = \frac{\lambda}{\pi\varepsilon_0} \left(\frac{1}{a} + \frac{1}{b}\right)$

תובנה חשובה: אלה לא כדורים! להזהר מקיצורי דרך מוכרים.

פוטנציאל על גליל מתקבל על ידי הנוסחה:

\[V(r) = -\int E \, dr = -\int \frac{\lambda}{2\pi\epsilon_0 r} \, dr = -\frac{\lambda}{2\pi\epsilon_0} \ln(r) + C\]

נציב בנתוני השאלה ונקבל:

\[V_{big}= -\frac{(-\lambda)}{2\pi \epsilon_0}\ln(b)\] \[V_{small}= - \frac{\lambda}{2\pi \epsilon_0}\ln(a)\]

אז ההפרש בין הפנימי לחיצוני הוא:

\[- \frac{\lambda}{2\pi \epsilon_0}\ln(a) - \frac{(-\lambda)}{2\pi \epsilon_0}\ln(b) = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right)\]

התשובה הנכונה היא לדעתי א.

שאלות 7-6

שלושה מטענים נקודתיים שווים $+q$ ממוקמים בקודקודי משולש שווה צלעות שאורך צלעו $a$. מרכז המשולש נמצא בראשית הצירים.

נתון:

המרחק ממרכז משולש שווה צלעות לכל קודקוד הוא $\frac{a}{\sqrt{3}}$

שאלה 6

הפוטנציאל החשמלי במרכז המשולש הוא:

$\boxed{V = \frac{3\sqrt{3}Kq}{a}}$

$V = \frac{Kq\sqrt{3}}{a}$

$V = \frac{3Kq}{a}$

$V = 0$

צריך לעשות סופרפוזיציה של הפוטנציאלים.

כל מטען תורם:

\[V = \frac{kq}{\frac{a}{\sqrt{3}}} = \frac{\sqrt{3}kq}{a}\]

ויש שלושה כאלה, אז התשובה היא א:

\[V = \frac{3\sqrt{3}Kq}{a}\]

שאלה 7

רוצים לשתול מטען $Q$ במרכז המשולש כך שהאנרגיה הפוטנציאלית הכוללת של המערכת תהיה אפס. ערכו של $Q$ הוא:

$\boxed{Q = -\frac{q}{\sqrt{3}}}$

$Q = -\sqrt{3}q$

$Q = -\frac{3q}{2}$

$Q = -q$

טעיתי כאן. חישבתי לפני הנוסחאות של פוטנציאל במקום אנרגיה פוטנציאלית וקביבלתי שהתשובה היא 4.

להלן פתרון מתוקן של קלוד:

פתרון - מטען נדרש לאיפוס אנרגיה פוטנציאלית

יש כאן בלבול בין פוטנציאל לבין אנרגיה פוטנציאלית.

מה ההבדל?

פוטנציאל $V$ = אנרגיה ליחידת מטען (סקלר של הנקודה)

אנרגיה פוטנציאלית $U$ = האנרגיה הדרושה להרכבת המערכת

חישוב האנרגיה הפוטנציאלית

האנרגיה הכוללת של המערכת כוללת את כל הזוגות:

לפני הוספת $Q$ (3 זוגות של $q$-$q$, מרחק $a$):
\[U_{initial} = 3 \cdot \frac{Kq^2}{a}\]
אחרי הוספת $Q$ (מוסיפים 3 זוגות של $Q$-$q$, מרחק $\frac{a}{\sqrt{3}}$):
\[U_{new} = 3 \cdot \frac{KQq}{\frac{a}{\sqrt{3}}} = \frac{3\sqrt{3}KQq}{a}\]
דרישה: $U_{total} = 0$
\[\frac{3Kq^2}{a} + \frac{3\sqrt{3}KQq}{a} = 0\] \[q + \sqrt{3}Q = 0\] \[Q = -\frac{q}{\sqrt{3}}\]
התשובה הנכונה היא א.

שאלות 9-8

טבעת דקה בעלת רדיוס $R$ עשויה מחומר מבודד וטעונה במטען כולל $Q$ המפוזר באופן אחיד. מרכז הטבעת נמצא בראשית הצירים, והטבעת מונחת במישור $xy$.

שאלה 8

הפוטנציאל החשמלי לאורך ציר $z$ הוא:

$V(z) = \frac{KQ}{z}$

$V(z) = \frac{KQ}{\sqrt{R^2 + z^2}}$

$V(z) = \frac{KQz}{(R^2 + z^2)^{3/2}}$

$V(z) = \frac{KQ}{R} \cdot \frac{z}{\sqrt{R^2 + z^2}}$

שואלים על הפוטנציאל. הטבעת רציפה כנראה נצטרך כאן אינטגרל.

\[\int \frac{kdq}{\sqrt{r^2 + z^2}}dA = k \int \frac{dq}{\sqrt{r^2 + z^2}}\]

בשלה הזה נתקעתי וביקשתי רמז מהקלוד.

רמז

שים לב: כל נקודה על הטבעת נמצאת באותו מרחק מנקודה על ציר $z$.

מה המרחק הזה? (רמז: משפט פיתגורס)

אם המרחק קבוע, מה זה אומר על האינטגרל?

אפשר להוציא קבועים מהאינטגרל!

אם המרחק $\sqrt{R^2 + z^2}$ קבוע, אז:

\[V = \frac{K}{\sqrt{R^2 + z^2}} \int dq = \text{?}\]

מה שווה $\int dq$ על כל הטבעת? $Q$! סך הכל נקבל:

\[\boxed{V(z) = \frac{KQ}{\sqrt{R^2 + z^2}}}\]

התשובה היא ב.

רשמים:

ניסיתי בשלב מסוים גם להציב $dq = \frac{Q}{2\pi R}$ אבל זה לא סייע, כי למעשה זה רק $\lambda = \frac{Q}{2\pi R}$ . עקרונית היה אפשר אולי:

\[dq = \lambda \cdot dl = \frac{Q}{2\pi R} \cdot dl\]

ואז הייתי מקבל:

\[\int dq = \frac{Q}{2\pi R} \int dl = \frac{Q}{2\pi R} \cdot 2\pi R = Q\] \[\implies \frac{K}{\sqrt{R^2 + z^2}} \int dq = \frac{KQ}{\sqrt{R^2 + z^2}}\]

שאלה 9

מחליפים את התפלגות המטען בטבעת כך שצפיפות המטען הזוויתית תהיה:
\[\lambda(\theta) = \lambda_0 \cos(\theta)\]
כאשר $\theta$ היא הזווית מציר $x$ החיובי.

הפוטנציאל החשמלי במרכז הטבעת (בראשית) הוא:

$V = \frac{K\lambda_0 \cdot 2\pi R}{R}$

$V = \frac{K\lambda_0}{R}$

$V = 0$

$V = \frac{K\lambda_0 \pi}{R}$

זה אפס.

הסבר מלא שהתאצלתי לכתוב:

\[V = \int \frac{K \cdot dq}{R} = \frac{K}{R} \int_0^{2\pi} \lambda_0 \cos(\theta) \cdot R \, d\theta = \frac{K\lambda_0}{1} \int_0^{2\pi} \cos(\theta) \, d\theta = 0\]

כי $\int_0^{2\pi} \cos(\theta) \, d\theta = 0$ (מחזור שלם של קוסינוס).

נוסחאות עזר

\[K = \frac{1}{4\pi\varepsilon_0} = 9 \times 10^9 \, \frac{N \cdot m^2}{C^2}\] \[\int \frac{dx}{\sqrt{x^2 + a^2}} = \ln\left(x + \sqrt{x^2 + a^2}\right) + C\] \[\int_0^{2\pi} \cos(\theta) \, d\theta = 0\]

בהצלחה!

הצעת פתרון - בוחן אמצע תשפה

תאריך: 12/12/2025

שאלות 3-1

מרצפים קליפה כדורית חלולה אשר רדיוסה הוא $R$ באלף אריחים מבודדים, כל אחד מהם טעון במטען משטחי חיובי $\sigma$. מרכז הקליפה מתלכד עם ראשית הצירים, הקוטב הצפוני של הקליפה יושב על ציר $z$ החיובי. מסירים את האריח היושב על הקוטב הצפוני.

ניתן להניח שהמימדים של כל אריח מאוד קטנים מספיק להתייחס אליו כמטען נקודתי.

ניתן להיעזר בכך שהיעדר מטען הוא סופרפוזיציה של שני מטענים שווים בגודלם והפוכים בסימנם.

שאלה 1 - מה השדה החשמלי בראשית הצירים

הבנה מהותית: בחומר מבודד המטענים אינם ניידים, ולכן צפיפות המטען קבועה.

משיקולי סימטריה כל המטענים מתבטלים למעט זה מלמטה, למרות שהכל חיובי - הסרה של משהו חיובי זה כמו להוסיף משהו שלילי.

אז המטען השלילי שלכאורה הוספנו מושך אליו את ראשית הצירים.

הנוסחה:

\[E = \frac{Kq}{R^2}\hat{n}\]

אז הרדיוס אר, נציב את המטען ההפוך ששמנו $\sigma$ הטריק לדעתי קשור לכיוונים. זה מושך את הראשית למעלה אז להבנתי:

\[\boxed{\vec{E} = \left(\frac{K\sigma}{R^2}\right)\hat{z}}\]

שאלה 2 - מה הפוטנציאל בקוטב הדרומי

צריך שוב להיעזר בסופר פוזיציה. הנוסחה לפוטנציאל בתוך (ועל) כדור היא:

\[V_{full} = \frac{kQ}{R}\]

תובנה חשובה: $Q = 1000 \sigma$. גם לא משנה המרחק כשמדובר בפוטנציאל של כדור - זה קבוע לכל מקום בפנים ועל הקליפה.

\[V_{north} = \frac{k(-\sigma)}{2R}\]

תובנה חשובה: לשים לב שהמרחק בין הצפון לדרום הוא פעמיים הרדיוס.

נסכום:

\[V_{tot}= V_{full} + V_{north} = \frac{2000\sigma k}{2R} - \frac{k\sigma}{2R} = \boxed{\frac{1999k\sigma}{2R}}\]

שאלה 3 - מהירות של מטען משוחרר

מטען קטן $q \ll \sigma$ אשר מסתו היא $m$ משתחרר מהאריח היושב על הקוטב הדרומי. מה תהא מהירותו ברגע שיעבור דרך רשאית הצירים?

אפשר לפתור בעזרת אנרגיה פוטנציאלית ומשוואת שימור האנרגיה.

המצב ההתחחלתי הוא מנוחה - מהירות אפס.

מצאנו את הפוטנציאל ההתחלתי בסעיף הקודם:

\[V_{init} = \frac{1999k\sigma}{2R}\]

צריך למצוא את הפוטנציאל בסוף:

\[V_{final} = ?\]

בסוף זה למעשה למצוא את האנרגיה הפוטנציאלית בראשית. בניגוד לשאלה הקודמת המרחק כעת מהצפון הוא $R$ במקום $2R$:

\[V_{final} = \frac{1000\sigma k}{R} + \frac{k(-\sigma)}{R} = \frac{999\sigma k}{R} = \frac{1998\sigma k}{2R}\]

המשוואה:

\[\cancel{\frac{1}{2}mv_i^2} + qV_{init} = \frac{1}{2}mv_f^2 + qV_{f}\] \[v_f = \sqrt{\frac{2qV_i-2qVf}{m}} = \sqrt{\frac{2qk\sigma}{2Rm}} = \boxed{\sqrt{\frac{qk\sigma}{Rm}}}\]

תכלס יצא יפה.

רמזים מקלוד לפתרון שאלות 5-4: קליפות כדוריות מוליכות

נוסחאות יסוד שצריך לזכור

פוטנציאל של קליפה כדורית טעונה:

בתוך הקליפה ועליה (r ≤ R) - האר של הקליפה:
\[V = \frac{kQ}{R}\]
(קבוע!)

מחוץ לקליפה (r > R):
\[V = \frac{kQ}{r}\]

עקרון הסופרפוזיציה: הפוטנציאל הכולל הוא סכום התרומות מכל המטענים

גישה לשאלה 4

שלב 1: חשב את הפוטנציאל בנקודה על הקליפה הפנימית ($r = R_1$)

כל קליפה תורמת לפוטנציאל:

קליפה 1 (אנחנו עליה): $V_1 = \frac{kQ_1}{R_1}$

קליפה 2 (אנחנו בתוכה): $V_2 = \frac{kQ_2}{R_2}$

קליפה 3 (אנחנו בתוכה): $V_3 = \frac{kQ_3}{R_3}$

שלב 2: השווה את הסכום לאפס ובודד את $Q_2$

גישה לשאלה 5

מה קורה בהארקה?

הפוטנציאל על הקליפה המוארקת הופך ל-0

מטען זורם מ/אל האדמה עד שזה קורה

שלב 1: חשב את הפוטנציאל על הקליפה החיצונית ($r = R_3$) לפני ההארקה

שלב 2: קבע מה צריך להיות המטען החדש $Q_3’$ כדי שהפוטנציאל יהיה 0

שלב 3: ההפרש $\Delta Q = Q_3’ - Q_3$ הוא המטען שזרם מהאדמה

טיפ חשוב

בקליפה מוליכה, הפוטנציאל קבוע בכל הנפח הפנימי שלה - זה נובע מכך ששדה חשמלי בתוך מוליך הוא אפס.

שאלות 5-4

נתונות שלוש קליפות קונצרטיות מוליכות אשר רדיוסיהן הם $R_1 < R_2 < R_3$. הקליפה הפנימית טעונה במטען $Q_1$ וזו החיצונית טעונה במטען $Q_3$.

שאלה 4

מה צריך להיות המטען על הקליפה האמצעית כדי שהפוטנציאל על הקליפה הפנימית יתאפס?

תובנה חשובה: הם רוצים שהפוטנציאל של הפנימית יתאפס וצריך למצוא מטען של האמצעית.

צריך למצוא את כל ההשפעות בשביל לקבל את הפוטנציאל בפנימית:

\[V_{tot} = V_{inner} + V_{middle} + V_{out}\]

נקודת המבט תהיה לעמוד על הקליפה הפנימית אז:

\[V_{inner} = \frac{kQ_1}{R_1}\] \[V_{middle} = \frac{kQ_?}{R_2}\] \[V_{out} = \frac{kQ_3}{R_3}\] \[V_{inner} + V_{middle} + V_{out} = 0\] \[\frac{kQ_1}{R_1} + \frac{kQ_?}{R_2} + \frac{kQ_3}{R_3} = 0\] \[\frac{Q_?}{R_2} = - \frac{Q_1}{R_1} - \frac{Q_3}{R_3}\] \[Q_? = \boxed{- \frac{R_2 Q_1}{R_1} - \frac{R_2 Q_3}{R_3}}\]

שאלה 5

במצב זה, שבו הפוטנציאל על הקליפה הפנימית הוא אפס, מאריקים את הקליפה החיצונית. האדמה הזרימה אל הקליפה החיצונית (או לקחה מן הקליפה החיצונית) מטען בשיעור?

כדי היא תתאפס היא צריכה להיות שווה להשפעות של שתי הפנימיות כלומר:

\[(V_1(3) + V_2(3)) + V_3 = 0\] \[\begin{aligned} V_1(3) + V_2(3) &= \frac{kQ_1}{R_3} + \frac{kQ_2}{R_3} \\ &= \frac{k}{R_3} \left(Q_1 + Q_2 \right) \\ &=\frac{k}{R_3} \left(Q_1 - \frac{R_2 Q_1}{R_1} - \frac{R_2 Q_3}{R_3} \right) \end{aligned}\]

ומנגד נרצה שכל זה יהי שווה ל:

\[-\frac{Q_3}{R_3}\]

כלומר:

\[\frac{k}{R_3} \left(Q_1 - \frac{R_2 Q_1}{R_1} - \frac{R_2 Q_3}{R_3} \right) = -\frac{kQ_3}{R_3}\] \[Q_1 - \frac{R_2 Q_1}{R_1} - \frac{R_2 Q_3}{R_3} = -Q_3\] \[Q_1\left(1 - \frac{R_2}{R_1}\right) - \frac{R_2 Q_3}{R_3} = -Q_3\] \[Q_1\left(1 - \frac{R_2}{R_1}\right) + Q_3 \left( 1 - \frac{R_2}{R_3} \right)\]

ככל הנראה יש לי איפשהו טעות בסימנים.

שאלות 7-6

יון מולקולרי מסוים מורכב מארבעה יונים חד אטומיים הטעונים במטען $q$, אשר יושבים על קודקודיו של ארבעון משוכלל אשר אורך צלעו היא $a$.

שאלה 6

מה גודלו של מרכיב הכוח החשמלי הפועל על כל יון בכיוון המשך אחת הצלעות של הארבעון?

לא הצלחתי, לצערי. מומזנים להשלים.

שאלה 7

מה צריך להיות מטען של יון נוסף ששותלים במרכז הארבעון, כדי שהאנרגיה הפוטנציאלית החשמלית הכוללת תהיה אפס.

כנ״ל.

שאלות 9-8

מוט דק אשר אורכו הוא $2L$ עשוי מחומר מבודד. מניחים את המוט על ציר ה-$x$ כך שמרכזו של המוט מתלכד עם הרשית.

שאלה 8

טוענים את המוט בצפיפות מטען אורכית $\lambda$ קולון ליחידת אורך. מה הפוטנציאל החשמלי הנגרם ע״י המוט לאורך ציר $y$?

הפוטנציאל ביחידה הוא:

\[V = \frac{K\lambda}{R}\]

במקרה הזה צריך לסכום את כל ההשפעות לאורך המוט. בנוסף, במקרה של השפעה רציפה צריך להשתמש באינטגרל:

\[V_{total} = \int \frac{k \, dQ}{r} = k \int \frac{\rho(\vec{r'}) dV'}{R}\]

\[R = \sqrt{x^2 + y^2}\]

מכאן:

\[V(y) = k \int_{-L}^{L} \frac{\lambda dx}{\sqrt{x^2 + y^2}} = \boxed{k\lambda \int_{-L}^{L} \frac{dx}{\sqrt{x^2 + y^2}}}\]

תוספות מקלוד:

זה אינטגרל סטנדרטי (מופיע בטבלאות):
\[\int \frac{dx}{\sqrt{x^2 + a^2}} = \ln\left(x + \sqrt{x^2 + a^2}\right) + C\]
כאן $a = y$, אז:
\[V(y) = k\lambda \left[\ln\left(x + \sqrt{x^2 + y^2}\right)\right]_{-L}^{L}\] \[V(y) = k\lambda \ln\left(\frac{L + \sqrt{L^2 + y^2}}{-L + \sqrt{L^2 + y^2}}\right)\]

שאלה 9

מסירים את המטען הקודם וטוענים את המוט מחדש בצפיפות מטען תלוית מקום על פי הקשר:
\[\lambda(x) = \lambda_0 \sin (\pi x / L)\]
מה הפוטנציאל לאורך ציר $y$ כעת?

האינטגרל להבנתי טריקי יותר. יש גם סימטריות. יש מצב שמתאפס? נחשב ישירות כדי לבדוק:

\[V(y) = k \int_{-L}^{L} \frac{\lambda_0 \sin (\pi x / L) dx}{\sqrt{x^2 + y^2}} = k\lambda_0 \int_{-L}^{L} \frac{ \sin (\pi x / L) dx}{\sqrt{x^2 + y^2}}\]

טוב זה כנראה לא פתרון לרמתנו.

למה זה מתאפס?

הסתכל על הפונקציה $\sin(\pi x / L)$:

היא אי-זוגית: $\sin(-\theta) = -\sin(\theta)$

הסתכל על $\frac{1}{\sqrt{x^2 + y^2}}$:

היא זוגית: תלויה ב-$x^2$

הכלל
\[\int_{-a}^{a} (\text{Zugit}) \times (\text{E-Zugit}) \, dx = 0\]
כי המכפלה אי-זוגית, והאינטגרל על תחום סימטרי מתאפס.

התשובה
\[\boxed{V(y) = 0}\]
פיזיקלית: המטען החיובי בצד $x > 0$ מתקזז בדיוק עם המטען השלילי בצד $x < 0$.

דור פסקל

15 בדצמבר 2025