כל שיעורי הבית - מוכן להדפסה

דף נוסחאות ופתרונות תרגילים

תאריך: 20/03/2025

תוכן עניינים

1. מתמטיקה בסיסית וטריגונומטריה
2. וקטורים ומערכות צירים
3. קינמטיקה - תורת התנועה
4. דינמיקה - חוקי ניוטון וכוחות
5. תנועה הרמונית ואוסצילציות
6. בעיות מרכזיות ודוגמאות
7. טכניקות פתרון ואלגוריתמים
8. נוסחאות מהירות לבחינה

---

מתמטיקה בסיסית וטריגונומטריה

זוויות נפוצות

\[\boxed{ \begin{aligned} \sin(30°) &= \frac{1}{2} = 0.5 \\[5pt] \cos(30°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\[5pt] \tan(30°) &= \frac{1}{\sqrt{3}} \approx 0.577 \\[5pt] \\[5pt] \sin(45°) &= \cos(45°) = \frac{1}{\sqrt{2}} \approx 0.707 \\[5pt] \tan(45°) &= 1 \\[5pt] \\[5pt] \sin(60°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\[5pt] \cos(60°) &= \frac{1}{2} = 0.5 \\[5pt] \tan(60°) &= \sqrt{3} \approx 1.732 \end{aligned}}\]

זהויות טריגונומטריות

\[\boxed{ \begin{aligned} \sin(90° - \theta) &= \cos\theta \\[5pt] \cos(90° - \theta) &= \sin\theta \end{aligned}}\] \[\boxed{ \begin{aligned} \sin^2\theta + \cos^2\theta &= 1 \\[5pt] 1 + \tan^2\theta &= \frac{1}{\cos^2\theta} \\[5pt] \\[5pt] \sin(2\theta) &= 2\sin\theta\cos\theta \\[5pt] \cos(2\theta) &= \cos^2\theta - \sin^2\theta \\[5pt] &= 2\cos^2\theta - 1 \\[5pt] &= 1 - 2\sin^2\theta \\[5pt] \\[5pt] \tan(2\theta) &= \frac{2\tan\theta}{1 - \tan^2\theta} \end{aligned}}\]

פונקציות היפרבוליות

\[\boxed{ \begin{aligned} \sinh(x) &= \frac{e^x - e^{-x}}{2} \\[5pt] \cosh(x) &= \frac{e^x + e^{-x}}{2} \\[5pt] \tanh(x) &= \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\[5pt] \end{aligned}}\]

קירוב בזוויות קטנות (ברדיאנים)

\[\boxed{ \begin{aligned} \sin\theta &\approx \theta \\[5pt] \tan\theta &\approx \theta \\[5pt] \cos\theta &\approx 1 - \frac{\theta^2}{2} \end{aligned}}\]

נוסחאות טריגונומטריות שימושיות

חיבור זוויות:

\[\boxed{ \begin{aligned} \sin(a + b) &= \sin a \cos b + \cos a \sin b \\[5pt] \cos(a + b) &= \cos a \cos b - \sin a \sin b \end{aligned}}\]

חוקי הסינוסים והקוסינוסים:

\[\boxed{ \begin{aligned} \sin A &= \frac{a \sin B}{b} \\[5pt] \sin B &= \frac{b \sin A}{a} \\[5pt] \sin C &= \frac{c \sin A}{a} \\[5pt] \cos C &= \frac{a^2 + b^2 - c^2}{2ab} \end{aligned}}\]

יחידות והמרות

יחידות סטדנרטיות:

\[\boxed{ \begin{aligned} \left[\mathrm{m}\right] &= \mathrm{meter} \\[5pt] \left[\mathrm{s}\right] &= \mathrm{second} \\[5pt] \left[\mathrm{kg}\right] &= \mathrm{kilogram} \\[5pt] \left[\mathrm{N}\right] &= \mathrm{Newton} = \mathrm{kg \cdot m/s^2} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} \left[\omega\right] &= \mathrm{rad/s} \\[5pt] \left[\theta\right] &= \mathrm{rad} \\[5pt] \left[\alpha\right] &= \mathrm{rad/s^2} \\[5pt] \left[\tau\right] &= \mathrm{N \cdot m} = \mathrm{J} \\[5pt] \left[\mathrm{F}\right] &= \mathrm{N} = \mathrm{kg \cdot m/s^2} \\[5pt] \left[\mathrm{p}\right] &= \mathrm{kg \cdot m/s} \\[5pt] \left[\mathrm{E}\right] &= \mathrm{J} = \mathrm{N \cdot m} = \mathrm{kg \cdot m^2/s^2} \\[5pt]\left[\mathrm{V}\right] &= \mathrm{m^3} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} 1 \, \mathrm{N} &= 1 \, \mathrm{kg} \cdot \mathrm{m/s^2} \\[5pt] 1 \, \mathrm{J} &= 1 \, \mathrm{N} \cdot \mathrm{m} = 1 \, \mathrm{kg} \cdot \mathrm{m^2/s^2} \\[5pt] g &\approx 10 \, \mathrm{m/s^2} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} 1 \mathrm{ m} &= 100 \, \mathrm{ cm} \\[5pt] &= 1000 \, \mathrm{ mm} \\[5pt] &= 10^6 \, \mathrm{ μm} \\[5pt] &= 10^9 \, \mathrm{ nm} \\[5pt] \\[5pt] 1 \mathrm{ km} &= 1000\, \mathrm{ m} = 10^3 \mathrm{ m} \\[5pt] \\[5pt] 1 \mathrm{ m} &= 1000 \, \mathrm{ mm} \\[5pt] 1 \mathrm{ m} &= 10^9 \, \mathrm{ nm} \\[5pt] 1 \mathrm{ m} &= 0.001\, \mathrm{ km} \\[5pt] \\[5pt] 1 \mathrm{ s} &= 1000 \, \mathrm{ ms} \\[5pt] &= 10^6 \, \mathrm{ μs} \\[5pt] &= 10^9 \, \mathrm{ ns} \\[5pt] \\[5pt] 1 \mathrm{ min} &= 60 \, \mathrm{ s} \\[5pt] 1 \mathrm{ h} &= 3600 \, \mathrm{ s} = 3.6 \times 10^3 \, \mathrm{ s} \\[5pt] \\[5pt] 1 \mathrm{ knot} &= 1.852 \, \mathrm{ km/h} \\[5pt] \end{aligned}}\]

---

וקטורים ומערכות צירים

פעולות בסיסיות על וקטורים

גודל (אורך) וקטור

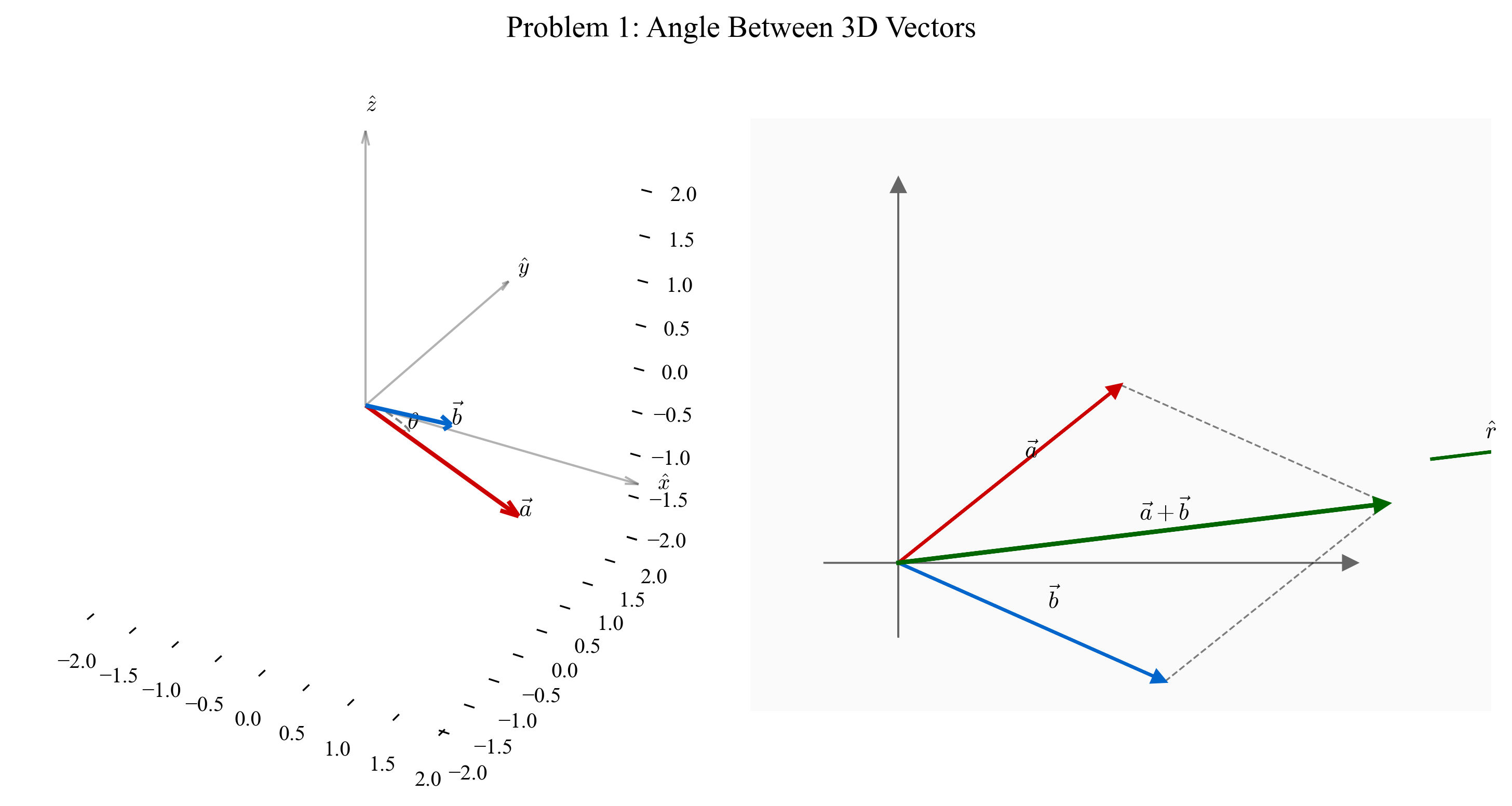
\[\vert\vec{v}\vert = \sqrt{v_x^2 + v_y^2 + v_z^2}\]

נרמול וקטור (יצירת וקטור יחידה)

\[\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert}\]

מכפלה סקלרית

\[\mathbf{a} \cdot \mathbf{\vec{b}} = \vert\mathbf{a}\vert\vert\mathbf{\vec{b}}\vert\cos\theta = a_xb_x + a_yb_y + a_zb_z\]

זווית בין וקטורים

\[\cos\theta = \frac{\mathbf{a} \cdot \mathbf{\vec{b}}}{\vert\mathbf{a}\vert\vert\mathbf{\vec{b}}\vert}\]

תנאי ניצבות

\[\mathbf{a} \perp \mathbf{\vec{b}} \Leftrightarrow \mathbf{a} \cdot \mathbf{\vec{b}} = 0\]

חיבור וקטורים (שקול כוחות)

\[\mathbf{F}_{\text{net}} = \mathbf{F}_1 + \mathbf{F}_2 + \ldots + \mathbf{F}_n\]

זווית של וקטור במישור

זווית בין וקטור לבין ציר ה-$x$ (נגד כיוון השעון):

\[\boxed{ \theta = \atan 2(y,x) = \begin{cases} \arctan \left(\frac{v_y}{v_x}\right) & \text{if } v_x > 0 \\[5pt] \arctan \left(\frac{v_y}{v_x}\right) + \pi & \text{if } v_x < 0 \text{ and} v_y \geq 0 \\[5pt] \arctan \left(\frac{v_y}{v_x}\right) - \pi & \text{if } v_x < 0 \text{ and} v_y < 0 \\[5pt] \frac{\pi}{2} & \text{if } v_x = 0 \text{ and } v_y > 0 \\[5pt] -\frac{\pi}{2} & \text{if } v_x = 0 \text{ and } v_y < 0 \\[5pt] \text{undefined} & \text{if } v_x = 0 \text{ and } v_y = 0 \end{cases} }\]

מערכות קואורדינטות

קואורדינטות קרטזיות

\[\vec{r} = x\mathbf{\hat{x}} + y\mathbf{\hat{y}} + z\mathbf{\hat{z}}\]

קואורדינטות פולריות (2D)

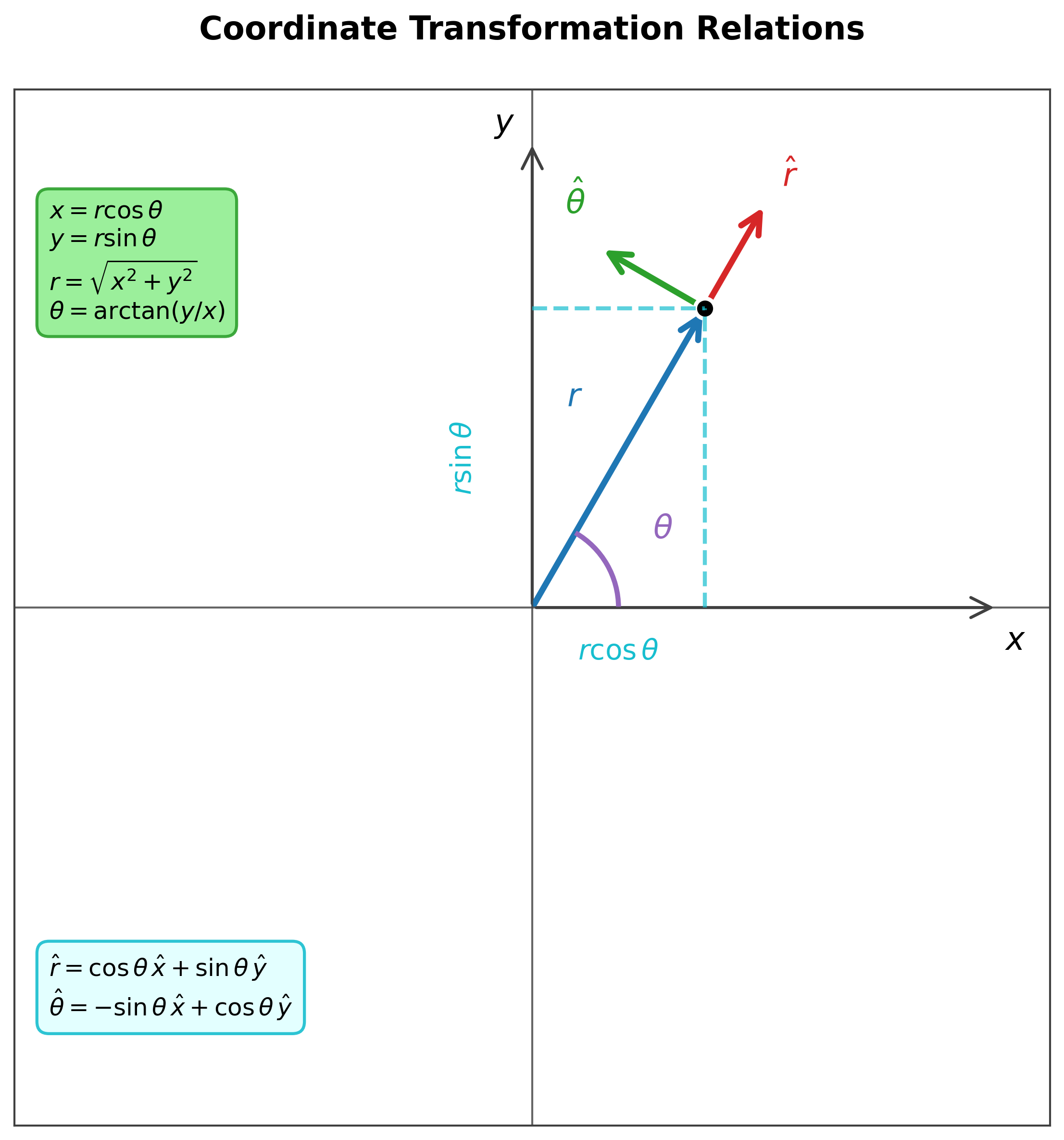
המרה מקרטזיות לפולריות:

\[\boxed{ \begin{aligned} r &= \sqrt{x^2 + y^2} \\[5pt] \theta &= \atan 2(y,x) \end{aligned}}\]

המרה מפולריות לקרטזיות:

\[\boxed{ \begin{aligned} x &= r\cos\theta \\[5pt] y &= r\sin\theta \end{aligned}}\]

וקטורי יחידה פולריים:

\[\boxed{ \begin{aligned} \mathbf{\hat{r}} &= \cos\theta \mathbf{\hat{x}} + \sin\theta \mathbf{\hat{y}} \\[5pt] \mathbf{\hat{\theta}} &= -\sin\theta \mathbf{\hat{x}} + \cos\theta \mathbf{\hat{y}} \end{aligned}}\]

נגזרות וקטורי היחידה:

\[\boxed{ \begin{aligned} \dot{\mathbf{\hat{r}}} &= \dot{\theta}\mathbf{\hat{\theta}} \\[5pt] \dot{\mathbf{\hat{\theta}}} &= -\dot{\theta}\mathbf{\hat{r}} \end{aligned}}\]

מהירות ותאוצה בפולריות:

\[\boxed{ \begin{aligned} \vec{v} &= \dot{r}\mathbf{\hat{r}} + r\dot{\theta}\mathbf{\hat{\theta}} \\[5pt] \mathbf{a} &= (\ddot{r} - r\dot{\theta}^2)\mathbf{\hat{r}} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}} \end{aligned}}\]

קואורדינטות גליליות (3D)

המרה מקרטזיות לגליליות:

\[\boxed{ \begin{aligned} x &= r\cos\theta \\[5pt] y &= r\sin\theta \\[5pt] z &= z \end{aligned}}\] \[\boxed{ \begin{aligned} r &= \sqrt{x^2 + y^2} \\[5pt] \theta &= \arctan\left(\frac{y}{x}\right) \text{adjusted for quadrant} \\[5pt] z &= z \end{aligned}}\]

קואורדינטות כדוריות (3D)

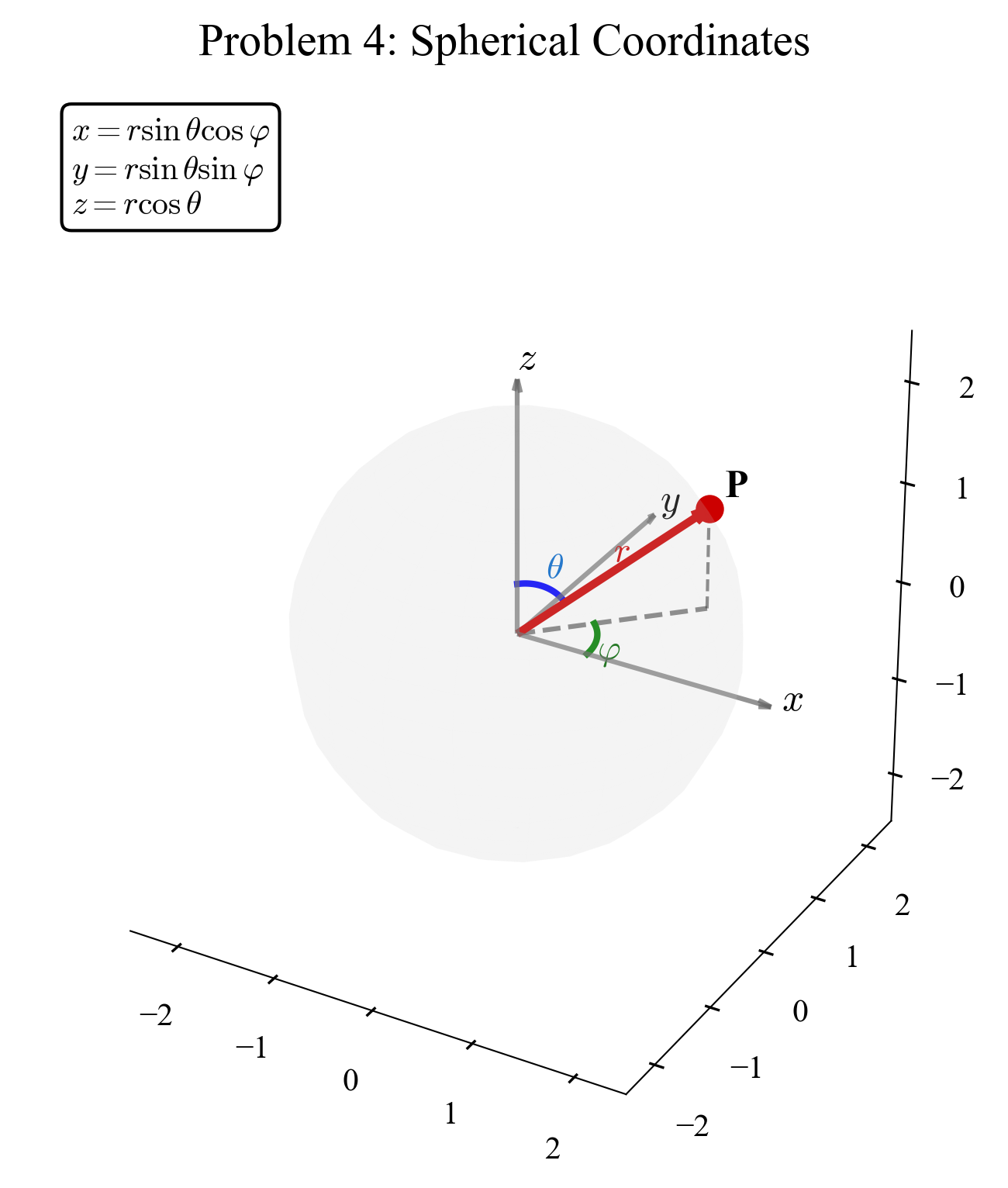
המרה מקרטזיות לכדוריות:

• $r = \sqrt{x^2 + y^2 + z^2}$
• $\theta$ = זווית מציר z
• $\varphi$ = זווית במישור xy

המרה מכדוריות לקרטזיות:

• $x = r\sin\theta\cos\varphi$
• $y = r\sin\theta\sin\varphi$
• $z = r\cos\theta$

---

קינמטיקה - תורת התנועה

הגדרות בסיסיות

וקטור מיקום

\[\vec{r} = x\mathbf{\hat{x}} + y\mathbf{\hat{y}} + z\mathbf{\hat{z}}\]

וקטור העתק

\[\boxed{ \begin{aligned} \Delta \vec{r} &= \vec{r}_2 - \vec{r}_1 \\[5pt] &=\vec{r}(t + \Delta t) - \vec{r}(t) \\[5pt] &= \Delta x\mathbf{\hat{x}} + \Delta y\mathbf{\hat{y}} + \Delta z\mathbf{\hat{z}} \end{aligned}}\]

מהירות ממוצעת

\[\vec{v}_{\text{avg}} = \frac{\Delta \vec{r}}{\Delta t} = \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t}\]

מהירות רגעית

\[\vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t} = \frac{d\vec{r}}{dt}\]

גודל המהירות (סקלר)

\[v = \vert\vec{v}\vert = \sqrt{v_x^2 + v_y^2 + v_z^2} \, \mathrm{m/s}\]

תאוצה

\[\mathbf{a} = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} = \frac{\Delta \vec{v}}{\Delta t} = \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t}\]

מהירות יחסית

איך גוף $A$ רואה את גוף $B$:

\[\vec{v}_{A\to B} = \vec{v}_B - \vec{v}_A\]

תנועה בקו ישר עם תאוצה קבועה

\[\boxed{ \begin{aligned} x(t) &= x_0 + v_0t + \frac{1}{2}at^2 \\[5pt] v(t) &= v_0 + at \\[5pt] v^2 &= v_0^2 + 2a\Delta x \end{aligned}}\]

צניחה חופשית (תנועה אנכית)

\[\boxed{ \begin{aligned} y(t) &= y_0 + v_0t - \frac{1}{2}gt^2 \\[5pt] v_y(t) &= v_0 - gt \\[5pt] v_y^2 &= v_0^2 - 2g\Delta y \end{aligned}}\]

תנועה בליסטית (תנועת קליע)

רכיב אופקי (ללא תאוצה):

\[x(t) = x_0 + v_{0x}t\]

רכיב אנכי (עם תאוצת כובד):

\[y(t) = y_0 + v_{0y}t - \frac{1}{2}gt^2\]

טווח מקסימלי:

\[R = \frac{v_0^2\sin(2\alpha)}{g}\]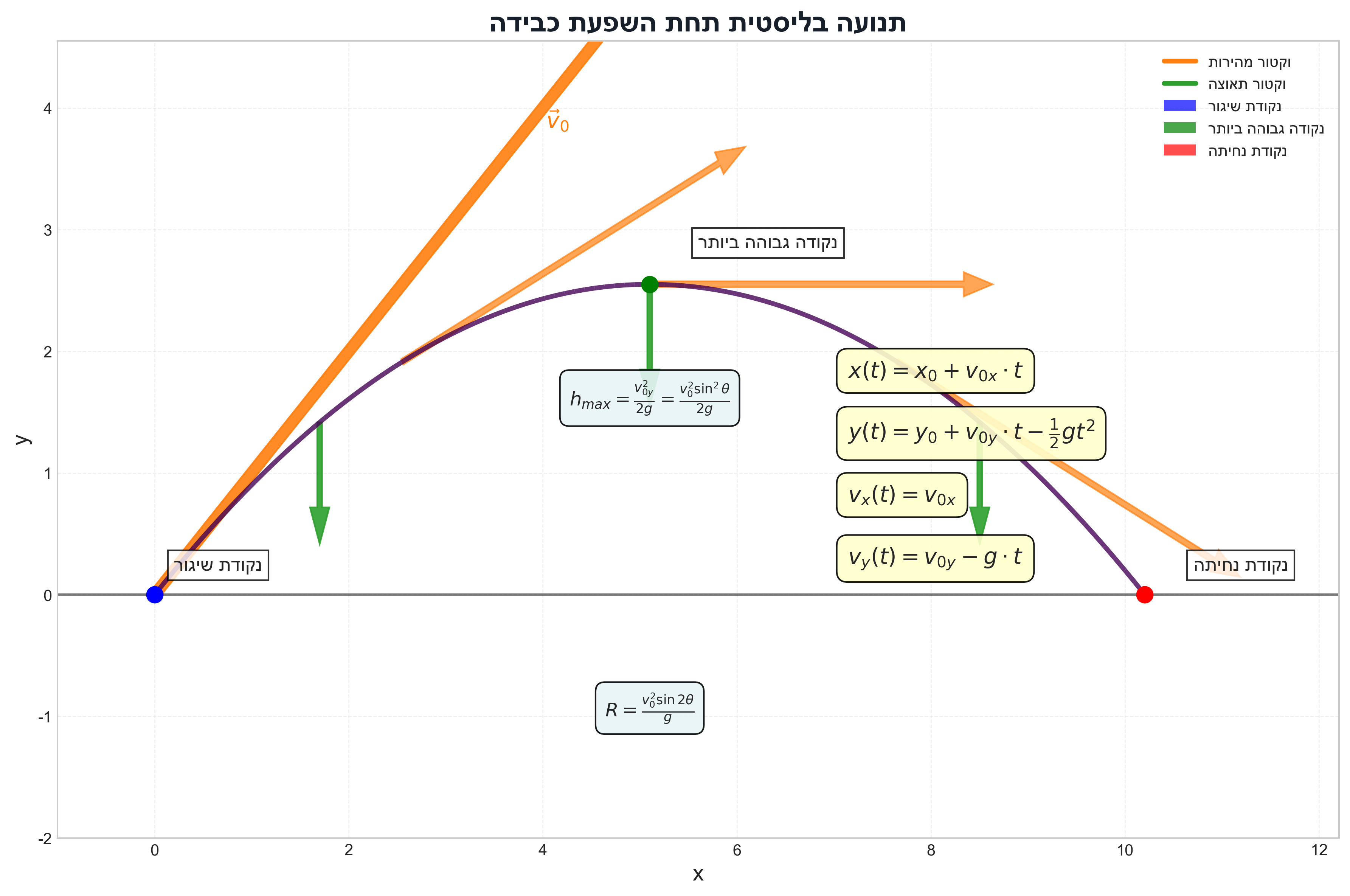

תנועה מעגלית

תנועה מעגלית קצובה (מהירות זוויתית קבועה)

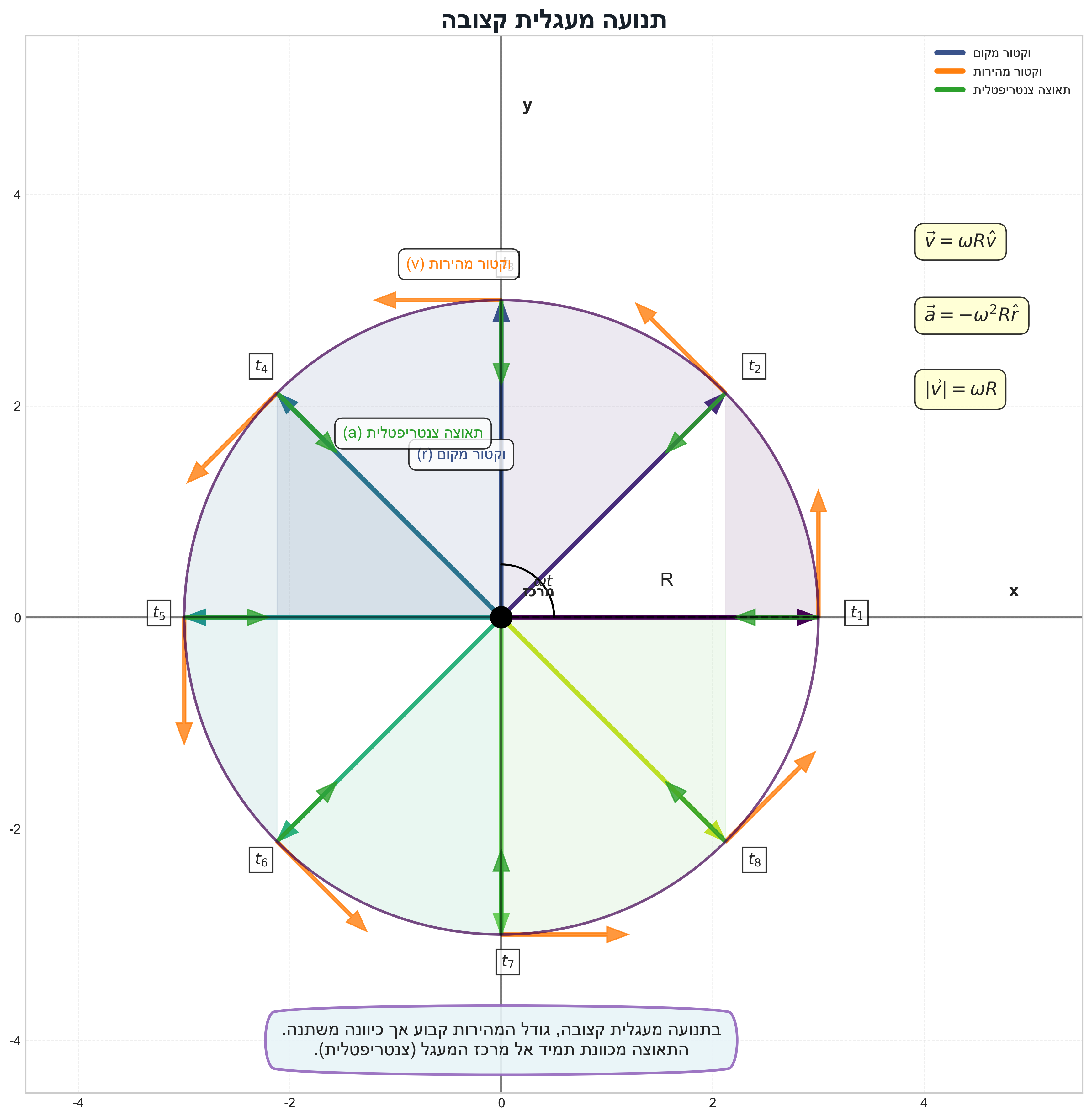
וקטור המיקום:

\[\vec{r}(t) = r[\cos(\omega t)\mathbf{\hat{x}} + \sin(\omega t)\mathbf{\hat{y}}]\]

מהירות זוויתית:

\[\omega = \frac{d\theta}{dt} = \frac{2\pi}{T}\]

מהירות משיקית:

\[v = r\omega\]

תאוצה צנטריפטלית (כלפי המרכז):

\[a_c = \frac{v^2}{r} = r\omega^2\]

כוח צנטריפוגלי - מהמרכז החוצה:

תנועה מעגלית כללית

תאוצה זוויתית:

\[\alpha = \frac{d\omega}{dt} = \frac{d^2\theta}{dt^2}\]

תאוצה משיקית:

\[a_t = r\alpha\]

תאוצה כוללת:

\[\mathbf{a} = -a_c\mathbf{\hat{r}} + a_t\mathbf{\hat{\theta}}\]

תנועה ספירלית

תנועה מעגלית עם רדיוס משתנה (למשל אקספוננציאלית):

\[r(t) = r_0 e^{\alpha t}\]

• אם $\alpha > 0$ — התנועה מתפשטת החוצה
• אם $\alpha < 0$ — התנועה מתכווצת פנימה

---

דינמיקה - חוקי ניוטון וכוחות

חוקי ניוטון

חוק ראשון (חוק ההתמדה)

גוף יישאר במנוחה או בתנועה ישרה קצובה כל עוד לא פועל עליו כוח שקול

\[\sum \mathbf{F} = 0 \Rightarrow \vec{v} = \text{const}\]

חוק שני (חוק התנועה)

התאוצה של גוף פרופורציונית לכוח השקול הפועל עליו

\[\sum \mathbf{F} = m\mathbf{a}\]

דוגמה - מישור משופע:

• ציר ניצב למישור: $N = mg\cos\alpha$ (אין תאוצה)
• ציר מקביל למישור: $mg\sin\alpha = ma$ (יש תאוצה)

חוק שלישי (חוק הפעולה והתגובה)

לכל פעולה יש תגובה שווה בגודלה והפוכה בכיוונה

\[\mathbf{F}_{12} = -\mathbf{F}_{21}\]

סוגי כוחות

כוח כבידה (משקל)

\[\mathbf{F}_g = -mg\hat{j}\]

כיוון: תמיד כלפי מטה

כוח נורמלי

\[N\]

כיוון: תמיד ניצב למשטח המגע

כוח חיכוך

חיכוך סטטי (מנוחה):

\[f_s \leq \mu_s N\]

חיכוך קינטי (תנועה):

\[f_k = \mu_k N\]

כיוון: תמיד מנוגד לכיוון התנועה (או התנועה הצפויה)

כוח קפיץ (חוק הוק)

\[F = -kx\]

• $k$ - קבוע הקפיץ [N/m]
• $x$ - הסטייה ממצב שיווי משקל
• הסימן השלילי מציין כוח מחזיר

כוח גרר (התנגדות תווך)

גרר ליניארי (מהירויות נמוכות):

\[F_d = -\beta v\]

גרר ריבועי (מהירויות גבוהות):

\[F_d = -\beta v^2\]

כוחות מדומים (במערכות לא אינרציאליות)

\[\mathbf{F}_{\text{pseudo}} = -m\mathbf{a}_{\text{frame}}\]

• מערכת לא אינרציאלית: מערכת ייחוס שנמצאת בתאוצה (ליניארית או זוויתית), ולכן יש בה צורך להוסיף כוחות מדומים (פסאודו-כוחות) כדי שחוקי ניוטון “יעבדו” בה.
• מערכת אינרציאלית: מערכת ייחוס שאינה מואצת (כלומר נעה במהירות קבועה או נחה), ובה חוקי ניוטון תקפים כפי שהם – בלי להוסיף כוחות מדומים.

מערכת, מבחינתנו, היא מערכת הצירים הרלוונטית.

תנע ודחף

תנע:

\[\vec{p} = m\vec{v}\]

דחף:

\[\vec{J} = \int \mathbf{F} dt = \Delta \vec{p}\]

שימור תנע:

\[\sum \vec{p}_{\text{before}} = \sum \vec{p}_{\text{after}}\]

בדרך כלל תסייע לנו לנתח התנגשויות בין גופים. נניח שיש שני גופים במסות של $m$ ו-$M$ אז אם הגוף הקטן מתנגש פלסטית במהירות $v_0$ עם הגוף הגדול במנוחה, אז:

\[mv_0 = (m + M)V \implies V = \frac{mv_0}{m + M}\]

הערה חשובה: המהירות של הדבוקה קטנה יותר כי התנע נשמר אבל האנרגיה הקינטית לא נשמרת בהתנגשות פלסטית. חלק מהאנרגיה הקינטית הופכת לחום, עיוות ורעש.

השוואת אנרגיות:

• אנרגיה התחלתית: $K_i = \frac{1}{2}mv_0^2$
• אנרגיה סופית: $K_f = \frac{1}{2}(m + M)V^2 = \frac{1}{2}\frac{m^2v_0^2}{m + M}$
• תמיד: $K_f < K_i$ (אובדן אנרגיה!)

סוגי התנגשויות:

• אלסטית: נשמרים תנע ואנרגיה קינטית
• פלסטית: נשמר תנע בלבד, אנרגיה קינטית לא נשמרת

עבודה ואנרגיה

עבודה בסיסית:

\[W = \int \mathbf{F} \cdot d\vec{r}\]

עבודה במימד אחד (כוח קבוע):

\[W = F \cdot d \cdot \cos\theta\]

אנרגיה קינטית:

\[K = \frac{1}{2}mv^2\]

אנרגיה פוטנציאלית כבידתית:

\[U_g = mgh\]

אנרגיה מכנית כוללת:

\[E = K + U\]

---

משפטי עבודה-אנרגיה

משפט עבודה-אנרגיה הבסיסי:

\[W_{\text{net}} = \Delta K = K_f - K_i\]

משפט עבודה-אנרגיה עם כוחות משמרים ולא משמרים:

\[W_{\text{non-conservative}} = \Delta E = E_f - E_i\]

כאשר:

• $W_{\text{non-conservative}}$ = עבודת כוחות לא משמרים (כמו חיכוך)
• $E = K + U$ = אנרגיה מכנית כוללת

---

שימור אנרגיה

עם כוחות משמרים בלבד:

\[E_i = E_f \quad \text{or} \quad K_i + U_i = K_f + U_f\]

עם כוחות לא משמרים (חיכוך):

\[E_i + W_{\text{non-conservative}} = E_f\]

או בצורה מפורשת:

\[K_i + U_i + W_{\text{friction}} = K_f + U_f\]

---

עבודת חיכוך

עבודת חיכוך (תמיד שלילית):

\[W_{\text{friction}} = -f_k \cdot d = -\mu_k mg \cdot d\]

חישוב עבודת חיכוך מאנרגיות:

\[W_{\text{friction}} = E_f - E_i = (K_f + U_f) - (K_i + U_i)\]

אנרגיה שאבדה בחיכוך:

\[\Delta E_{\text{lost}} = |W_{\text{friction}}\vert = E_i - E_f\]

---

דוגמאות יישום

גוף גולש במדרון עם חיכוך:

• אנרגיה התחלתית: $E_i = mgh_i$ (אם מתחיל ממנוחה)
• אנרגיה סופית: $E_f = \frac{1}{2}mv_f^2 + mgh_f$
• עבודת חיכוך: $W_{\text{friction}} = E_f - E_i$

התנגשויות:

• אלסטית: נשמרת אנרגיה קינטית ותנע
• פלסטית: נשמר תנע בלבד, אנרגיה קינטית לא נשמרת

---

נוסחאות נוספות

עבודה מגרף כוח-מקום:

\[W = \text{area under the curve } F(x)\]

כוח ממשיק עקומת אנרגיה פוטנציאלית:

\[F = -\frac{dU}{dx}\]

אנרגיה פוטנציאלית כללית:

\[\Delta U = -W_{\text{conservative}}\]

---

עקרונות חשובים

1. כוחות משמרים: עבודתם לא תלויה במסלול (כבידה, אלסטי)
2. כוחות לא משמרים: עבודתם תלויה במסלול (חיכוך, התנגדות אוויר)
3. חיכוך תמיד מקטין אנרגיה מכנית: $W_{\text{friction}} < 0$
4. שימור תנע: תמיד נשמר כאשר אין כוחות חיצוניים נטו

---

תנועה הרמונית ואוסצילציות

אוסצילטור הרמוני פשוט

משוואת התנועה

\[m\ddot{x} + kx = 0\]

או בצורה סטנדרטית:

\[\ddot{x} + \omega^2 x = 0\]

פתרון כללי

\[x(t) = A\cos(\omega t + \phi)\]

כאשר:

• $A$ - משרעת התנודה
• $\omega$ - תדירות זוויתית
• $\phi$ - פאזה התחלתית

פתרון ברישום נוסף:

\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]

כאשר $A$ ו-$B$ הם קבועים שנקבעים על פי תנאי ההתחלה.

תדירות זוויתית

\[\omega = \sqrt{\frac{k}{m}}\]

זמן מחזור

\[T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{m}{k}}\]

תדירות

\[f = \frac{1}{T} = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{k}{m}}\]

אנרגיה באוסצילטור הרמוני

אנרגיה קינטית:

\[K = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2 A^2 \sin^2(\omega t + \phi)\]

אנרגיה פוטנציאלית:

\[U = \frac{1}{2}kx^2 = \frac{1}{2}kA^2 \cos^2(\omega t + \phi)\]

אנרגיה כוללת (קבועה):

\[E = K + U = \frac{1}{2}kA^2\]

מטוטלת מתמטית

משוואת תנועה (זוויות קטנות)

\[\ddot{\theta} + \frac{g}{L}\theta = 0\]

תדירות זוויתית

\[\omega = \sqrt{\frac{g}{L}}\]

זמן מחזור

\[T = 2\pi\sqrt{\frac{L}{g}}\]

אוסצילטור במערכות מואצות

במעלית מואצת כלפי מעלה בתאוצה $A$

• תאוצה אפקטיבית: $g_{\text{eff}} = \sqrt{g^2 + A^2}$
• תדירות זוויתית: $\omega = \sqrt{\frac{g + A}{L}}$
• זמן מחזור: $T = 2\pi\sqrt{\frac{L}{g + A}}$

ברכבת מואצת אופקית בתאוצה $A$

• זווית שיווי משקל: $\theta_0 = \arctan\left(\frac{A}{g}\right)$
• תדירות: $\omega = \sqrt{\frac{g}{L\cos\theta_0}}$

---

בעיות מרכזיות ודוגמאות

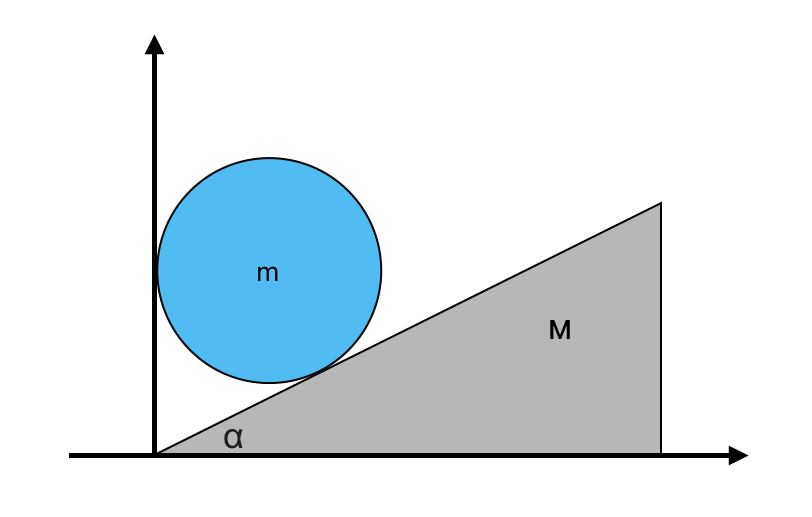
1. בעיית הטריז והגליל

נתונים:

• גליל מסה $m$ על טריז מסה $M$
• זווית הטריז $\alpha = 30°$
• אין חיכוך

פתרון:

\[N_m = \frac{2gMm\sqrt{3}}{3M + m}\] \[a_x = \frac{10m\sqrt{3}}{3M + m}\] \[a_y = \frac{10m}{3M + m}\]

2. צנחנית עם התנגדות אוויר

כוח גרר: $F = \beta v^2$

משוואת התנועה:

\[mg - \beta v^2 = m\frac{dv}{dt}\]

מהירות טרמינלית:

\[v_T = \sqrt{\frac{mg}{\beta}}\]

פתרון כללי:

\[v(t) = v_T \tanh\left(\frac{gt}{v_T}\right)\]

3. גוף על מישור משופע

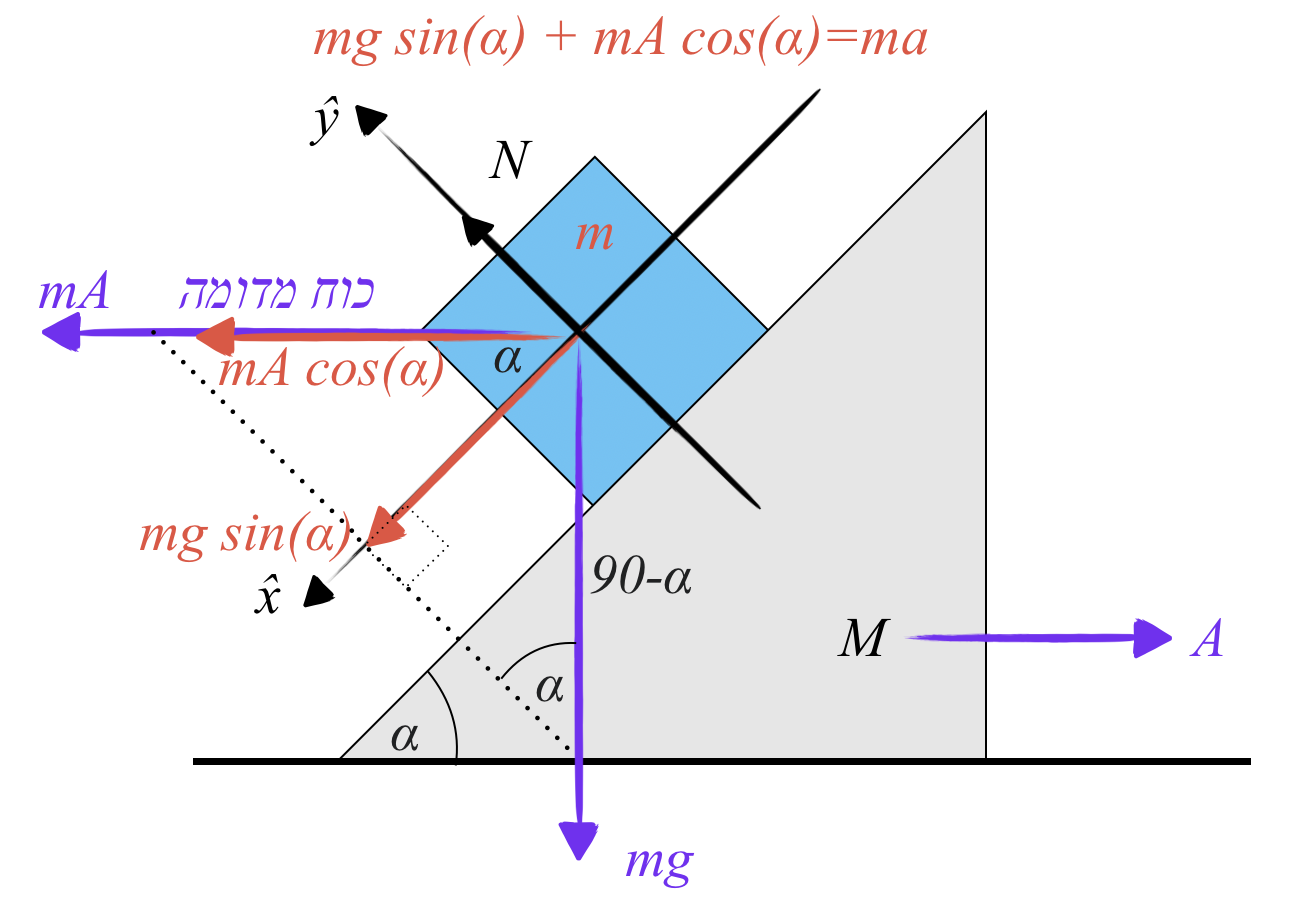
זווית קריטית (ללא החלקה):

\[\theta_{\max} = \arctan(\mu_s)\]

תאוצה בהחלקה:

\[a = g(\sin\theta - \mu_k\cos\theta)\]

תנועה במהירות קבועה:

\[\theta = \arctan(\mu_k)\]

4. מכונת אטווד עם זבוב

תאוצה כשהזבוב על מסה:

\[a = \frac{mg}{2M+m}\]

תאוצה ללא זבוב:

\[a = 0\]

5. תנועה יחסית - הולך רגל וקרוסלה

• הולך רגל: $x(t) = 4 + 4t$ (תנועה ישרה)
• נער על קרוסלה: $\vec{r}(t) = (2\sin(3t), 2\cos(3t))$ (תנועה מעגלית)

• מהירות יחסית:

  \[\vec{v}_{\text{rel}} = \vec{v}_{\text{boy}} - \vec{v}_{\text{man}}\]

טרנספורמציית גליליית:

6. תנועה ספירלית מתכנסת

דוגמה: $\vec{r}(t) = e^{-\alpha t}[\cos(\omega t)\mathbf{\hat{x}} + \sin(\omega t)\mathbf{\hat{y}}]$

• המרחק דועך: $\vert\vec{r}(t)\vert = e^{-\alpha t}$
• הזווית גדלה: $\theta(t) = \omega t$
• גודל המהירות: $\vert\vec{v}(t)\vert = e^{-\alpha t}\sqrt{\alpha^2 + \omega^2}$

7. מערכות מצומדות

שתי מסות עם קפיץ על מישור משופע:

תדירות מותאמת:

\[\omega = \sqrt{\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}}\]

---

טכניקות פתרון ואלגוריתמים

אלגוריתם כללי לפתרון בעיות

1. תרשים כוחות
   • צייר דיאגרמת גוף חופשי לכל גוף
   • סמן את כל הכוחות הפועלים
   • ודא שלא שכחת כוחות
2. בחירת מערכת צירים
   • בחר צירים נוחים (לרוב לאורך התנועה)
   • במישור משופע: ציר אחד לאורך המישור
   • בתנועה מעגלית: צירים פולריים
3. כתיבת משוואות תנועה
   • כתוב $\sum F_x = ma_x$ לכל ציר
   • כתוב עבור כל גוף בנפרד
   • שים לב לסימנים
4. הוספת אילוצים
   • קשרים גיאומטריים (חוט לא נמתח)
   • קשרים קינמטיים (תאוצות זהות)
   • תנאי התחלה
5. פתרון מערכת המשוואות
   • ספור משתנים ומשוואות
   • פתור באלגברה או דיפרנציאלית
   • בדוק סבירות התוצאה

משוואות דיפרנציאליות נפוצות ופתרונותיהן

אוסצילטור הרמוני

משוואה: $\ddot{x} + \omega^2 x = 0$

פתרון: $x(t) = A\cos(\omega t) + B\sin(\omega t)$

אוסצילטור עם הסטה

משוואה: $\ddot{x} + \omega^2 x = C$

פתרון: $x(t) = A\cos(\omega t) + B\sin(\omega t) + \frac{C}{\omega^2}$

דעיכה אקספוננציאלית

משוואה: $\dot{x} = -\gamma x$

פתרון: $x(t) = x_0 e^{-\gamma t}$

גידול אקספוננציאלי

משוואה: $\ddot{x} = \omega^2 x$

פתרון: $x(t) = A\cosh(\omega t) + B\sinh(\omega t)$

בדיקות חשובות

1. בדיקת יחידות
   • ודא שהיחידות מתאימות בשני צדי המשוואה
   • כוח: [N] = [kg⋅m/s²]
   • אנרגיה: [J] = [kg⋅m²/s²]
2. בדיקת גבולות
   • מה קורה כש $m \to 0$ או $m \to \infty$?
   • מה קורה כש $\theta \to 0$ או $\theta \to 90°$?
3. בדיקת סימטריות
   • האם הבעיה סימטרית?
   • האם אפשר לפשט?
4. בדיקת שימור
   • האם האנרגיה נשמרת?
   • האם התנע נשמר?

---

נוסחאות מהירות לבחינה

כוחות וחוקי ניוטון

\[\boxed{ \begin{aligned} \sum \mathbf{F} &= m\mathbf{a} \\[5pt] \mathbf{F}_g &= mg \\[5pt] f_s &\leq \mu_s N \\[5pt] f_k &= \mu_k N \\[5pt] \mathbf{F}_{\text{spring}} &= -kx \end{aligned}}\]

קינמטיקה - תאוצה קבועה

\[\boxed{ \begin{aligned} v &= v_0 + at \\[5pt] x &= x_0 + v_0t + \frac{1}{2}at^2 \\[5pt] v^2 &= v_0^2 + 2a\Delta x \end{aligned}}\]

תנועה מעגלית

\[\boxed{ \begin{aligned} v &= r\omega \\[5pt] a_c &= \frac{v^2}{r} = r\omega^2 \\[5pt] T &= \frac{2\pi}{\omega} \end{aligned}}\]

תנועה הרמונית

\[\boxed{ \begin{aligned} \omega &= \sqrt{\frac{k}{m}} \\[5pt] T &= 2\pi\sqrt{\frac{m}{k}} \\[5pt] E &= \frac{1}{2}kA^2 \end{aligned}}\]

מטוטלת

\[\boxed{ \begin{aligned} \omega &= \sqrt{\frac{g}{L}} \\[5pt] T &= 2\pi\sqrt{\frac{L}{g}} \end{aligned}}\]

---

• קרא את השאלה פעמיים לפני שמתחיל
• צייר תמיד דיאגרמת כוחות
• בדוק יחידות בכל שלב
• השתמש בערכי קירוב: $g = 10$, $\pi \approx 3$, $\sqrt{3} \approx 1.7$
• רשום תשובות ביניים

טעויות נפוצות להימנע מהן

• אל תשכח לפרק וקטורים לרכיבים
• שים לב לכיוון הכוחות (סימנים!)
• חיכוך תמיד נגד כיוון התנועה
• בתנועה מעגלית, תאוצה צנטריפטלית פנימה
• אל תערבב בין מסה למשקל

אסטרטגיה לפתרון

1. 5 דקות ראשונות: קרא את כל המבחן
2. התחל מהקל: פתור קודם שאלות שאתה בטוח בהן
3. הקצה זמן: חלק את הזמן לפי ניקוד
4. בדיקה: השאר 10 דקות בסוף לבדיקה

פתרון תרגיל מס׳ 1 - וקטורים

תאריך: 24/03/2025

שאלה 1 וקטורים דו-מימדיים

נתונים שני וקטורים דו-מימדיים:

\[\begin{aligned} \vec{a} &= 3\hat{x} - 3\hat{y} \\[10pt] \vec{b} &= -2\hat{x} + \hat{y} \end{aligned}\]

נתון:

\[\vec{c} = -2\vec{a} + 3\vec{b}\]

א. חישוב וקטור $\vec{c}$

נציב את הערכים:

\[\begin{aligned} \vec{c} &= -2(3\hat{x} - 3\hat{y}) + 3(-2\hat{x} + \hat{y}) \\[10pt] &= (-6\hat{x} + 6\hat{y}) + (-6\hat{x} + 3\hat{y}) \\[10pt] &= -12\hat{x} + 9\hat{y} \end{aligned}\]

ב. חישוב וקטורי היחידה

וקטור יחידה מוגדר כוקטור בעל אותו כיוון כמו הוקטור המקורי, אך באורך 1. כדי לחשב וקטור יחידה, מחלקים את הוקטור באורכו (נורמה).

עבור $\vec{a}$:

\[\vert \vec{a}\vert = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}\]

וקטור היחידה:

\[\begin{aligned} \hat{a} = \frac{\vec{a}}{\vert \vec{a}\vert} &= \frac{3\hat{x} - 3\hat{y}}{3\sqrt{2}} \\[10pt] &= \frac{1}{\sqrt{2}}\hat{x} - \frac{1}{\sqrt{2}}\hat{y} \end{aligned}\]

עבור $\vec{b}$:

\[\vert \vec{b}\vert = \sqrt{(-2)^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}\]

וקטור היחידה:

\[\begin{aligned} \hat{b} = \frac{\vec{b}}{\vert \vec{b}\vert} &= \frac{-2\hat{x} + \hat{y}}{\sqrt{5}} \\[10pt] &= -\frac{2}{\sqrt{5}}\hat{x} + \frac{1}{\sqrt{5}}\hat{y} \end{aligned}\]

עבור $\vec{c}$:

\[\vert \vec{c}\vert = \sqrt{(-12)^2 + 9^2} = \sqrt{144 + 81} = \sqrt{225} = 15\]

וקטור היחידה:

\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{-12\hat{x} + 9\hat{y}}{15} = -\frac{4}{5}\hat{x} + \frac{3}{5}\hat{y}\]

ג. ציור הוקטור השקול ווקטור ההפרש

הוקטור השקול $\vec{a} + \vec{b}$:

\[\vec{a} + \vec{b} = (3\hat{x} - 3\hat{y}) + (-2\hat{x} + \hat{y}) = \hat{x} - 2\hat{y}\]

וקטור ההפרש $\vec{a} - \vec{b}$:

\[\begin{aligned} \vec{a} - \vec{b} &= (3\hat{x} - 3\hat{y}) - (-2\hat{x} + \hat{y}) \\[10pt] &= 3\hat{x} - 3\hat{y} + 2\hat{x} - \hat{y} \\[10pt] &= 5\hat{x} - 4\hat{y} \end{aligned}\]

לציור הוקטורים על נייר משבצות, יש לסמן את מערכת הצירים ולשרטט:

• את $\vec{a}$ מראשית הצירים לנקודה $(3, -3)$
• את $\vec{b}$ מראשית הצירים לנקודה $(-2, 1)$
• את $\vec{a} + \vec{b}$ מראשית הצירים לנקודה $(1, -2)$
• את $\vec{a} - \vec{b}$ מראשית הצירים לנקודה $(5, -4)$

ד. ציור הוקטור השקול $\vec{a} + \vec{b} + \vec{c}$

נחשב תחילה את הסכום:

\[\begin{aligned} \vec{a} + \vec{b} + \vec{c} &= (3\hat{x} - 3\hat{y}) + (-2\hat{x} + \hat{y}) + (-12\hat{x} + 9\hat{y}) \\[10pt] &= (3 - 2 - 12)\hat{x} + (-3 + 1 + 9)\hat{y} \\[10pt] &= -11\hat{x} + 7\hat{y} \end{aligned}\]

לציור הוקטור השקול, יש לסמן את מערכת הצירים ולשרטט את הוקטור מראשית הצירים לנקודה $(-11, 7)$.

ה. חישוב הזוויות

הזווית שוקטור יוצר עם ציר ה-$x$ (נגד כיוון השעון) ניתנת על ידי הביטוי: $\theta = \tan^{-1}(\frac{y}{x})$

כאשר צריך לקחת בחשבון את הרביע שבו נמצא הוקטור:

עבור $\vec{a} = 3\hat{x} - 3\hat{y}$:

מכיוון שהוקטור נמצא ברביע הרביעי ($x > 0$, $y < 0$), נחשב:

\[\theta_a = \tan^{-1}(\frac{-3}{3}) = \tan^{-1}(-1) = -45°\]

ומכיוון שאנו מודדים נגד כיוון השעון, נוסיף $360°$:

\[\theta_a = 360° - 45° = 315°\]

עבור $\vec{b} = -2\hat{x} + \hat{y}$:

מכיוון שהוקטור נמצא ברביע השני ($x < 0$, $y > 0$), נחשב:

\[\theta_b = \tan^{-1}(\frac{1}{-2}) = \tan^{-1}(-0.5) \approx -26.57°\]

ונוסיף $180°$:

\[\theta_b = 180° - 26.57° = 153.43°\]

עבור $\vec{c} = -12\hat{x} + 9\hat{y}$:

מכיוון שהוקטור נמצא ברביע השני ($x < 0$, $y > 0$), נחשב:

\[\theta_c = \tan^{-1}(\frac{9}{-12}) = \tan^{-1}(-0.75) \approx -36.87°\]

ונוסיף $180°$:

\[\theta_c = 180° - 36.87° = 143.13°\]

שאלה 2: וקטורים תלת-מימדיים

נתונים שלושת הוקטורים התלת-מימדיים:

\[\begin{aligned} \vec{a} &= (2,2,0) \\[10pt] \vec{b} &= (2,0,2) \\[10pt] \vec{c} &= (0,2,2) \end{aligned}\]

א. ציור הוקטורים במערכת צירים קרטזית

לציור וקטורים תלת-מימדיים, יש לסמן מערכת צירים תלת-מימדית ולשרטט:

• את $\vec{a}$ מראשית הצירים לנקודה $(2, 2, 0)$
• את $\vec{b}$ מראשית הצירים לנקודה $(2, 0, 2)$
• את $\vec{c}$ מראשית הצירים לנקודה $(0, 2, 2)$

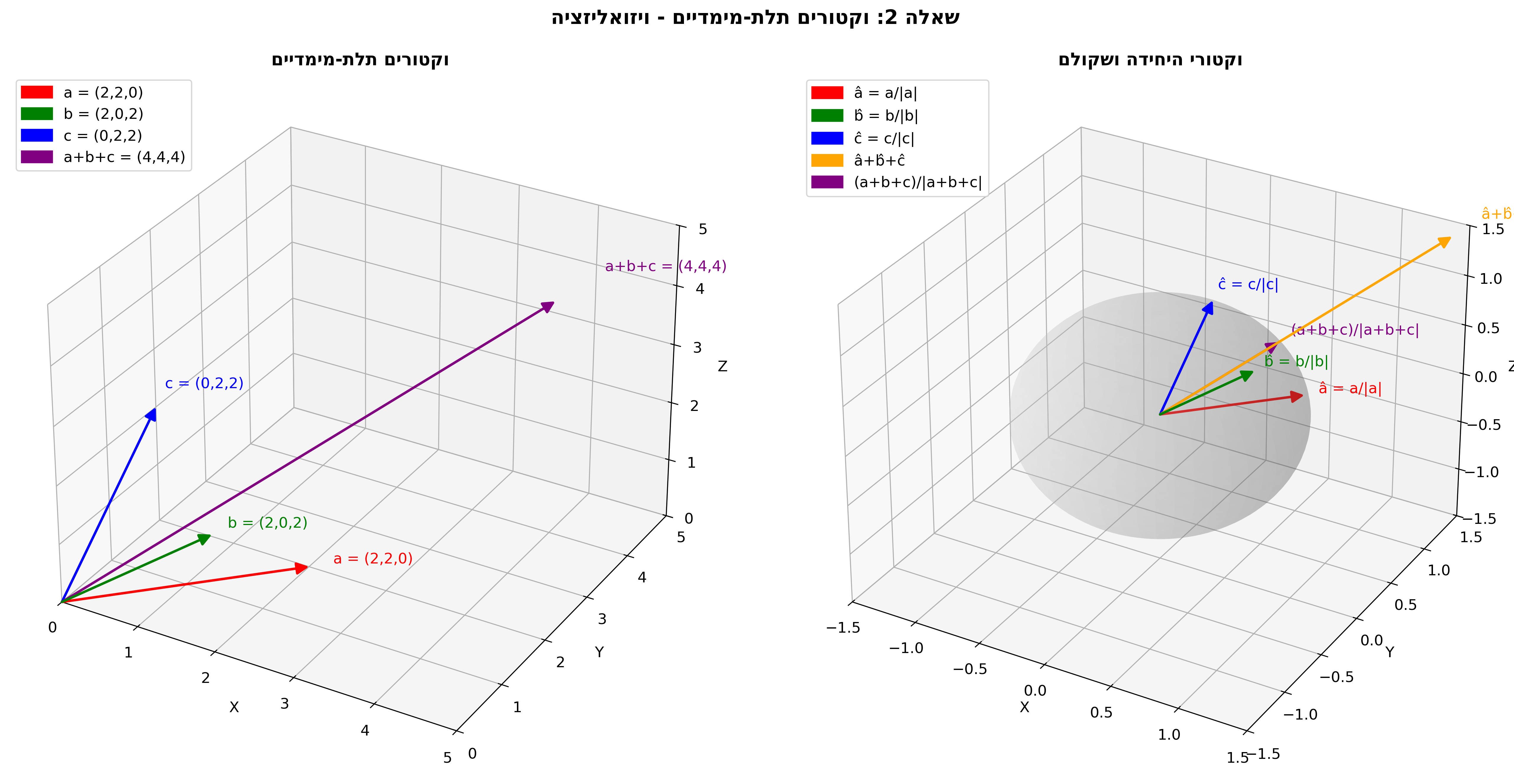איור של הוקטורים במערכת צירים תלת-מימדית	הדמיה של הפרמטריזציה הלינארית של שלושת הוקטורים

ב. ציור השקול הוקטורי

השקול הוקטורי של שלושת הוקטורים הוא:

\[\begin{aligned} \vec{a} + \vec{b} + \vec{c} &= (2,2,0) + (2,0,2) + (0,2,2) \\[10pt] &= (2+2+0, 2+0+2, 0+2+2) \\[10pt] &= (4, 4, 4) \end{aligned}\]

לציור השקול הוקטורי, יש לשרטט וקטור מראשית הצירים לנקודה $(4, 4, 4)$.

ג. נרמול הוקטורים

נרמול וקטור פירושו חישוב וקטור היחידה בכיוון הוקטור המקורי.

עבור $\vec{a}$:

\[\vert \vec{a}\vert = \sqrt{2^2 + 2^2 + 0^2} = \sqrt{8} = 2\sqrt{2}\]

הוקטור המנורמל:

\[\hat{a} = \frac{\vec{a}}{\vert \vec{a}\vert} = \frac{(2,2,0)}{2\sqrt{2}} = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0)\]

עבור $\vec{b}$:

\[\vert \vec{b}\vert = \sqrt{2^2 + 0^2 + 2^2} = \sqrt{8} = 2\sqrt{2}\]

הוקטור המנורמל:

\[\hat{b} = \frac{\vec{b}}{\vert \vec{b}\vert} = \frac{(2,0,2)}{2\sqrt{2}} = (\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}})\]

עבור $\vec{c}$:

\[\vert \vec{c}\vert = \sqrt{0^2 + 2^2 + 2^2} = \sqrt{8} = 2\sqrt{2}\]

הוקטור המנורמל:

\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{(0,2,2)}{2\sqrt{2}} = (0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\]

ד. בדיקת התלכדות

נבדוק האם השקול של שלושת הוקטורים המנורמלים מתלכד עם וקטור היחידה של השקול הוקטורי.

סכום הוקטורים המנורמלים:

\[\hat{a} + \hat{b} + \hat{c} = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0) + (\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}) + (0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\] \[\begin{aligned} &= (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} + 0, \frac{1}{\sqrt{2}} + 0 + \frac{1}{\sqrt{2}}, 0 + \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}) \\[10pt] &= (\frac{2}{\sqrt{2}}, \frac{2}{\sqrt{2}}, \frac{2}{\sqrt{2}}) \\[10pt] &= \sqrt{2} \cdot (1, 1, 1) \end{aligned}\]

וקטור היחידה של השקול:

השקול הוקטורי:

\[\vec{a} + \vec{b} + \vec{c} = (4, 4, 4)\]

האורך שלו:

\[\vert \vec{a} + \vec{b} + \vec{c}\vert = \sqrt{4^2 + 4^2 + 4^2} = \sqrt{48} = 4\sqrt{3}\]

וקטור היחידה:

\[\frac{\vec{a} + \vec{b} + \vec{c}}{\vert \vec{a} + \vec{b} + \vec{c}\vert} = \frac{(4, 4, 4)}{4\sqrt{3}} = \frac{1}{\sqrt{3}} \cdot (1, 1, 1)\]

מכיוון ש-$\hat{a} + \hat{b} + \hat{c} = \sqrt{2} \cdot (1, 1, 1)$ והוקטור היחידה של השקול הוא $\frac{1}{\sqrt{3}} \cdot (1, 1, 1)$, הם אינם מתלכדים. הסכום של הוקטורים המנורמלים גדול פי $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ מוקטור היחידה של השקול.

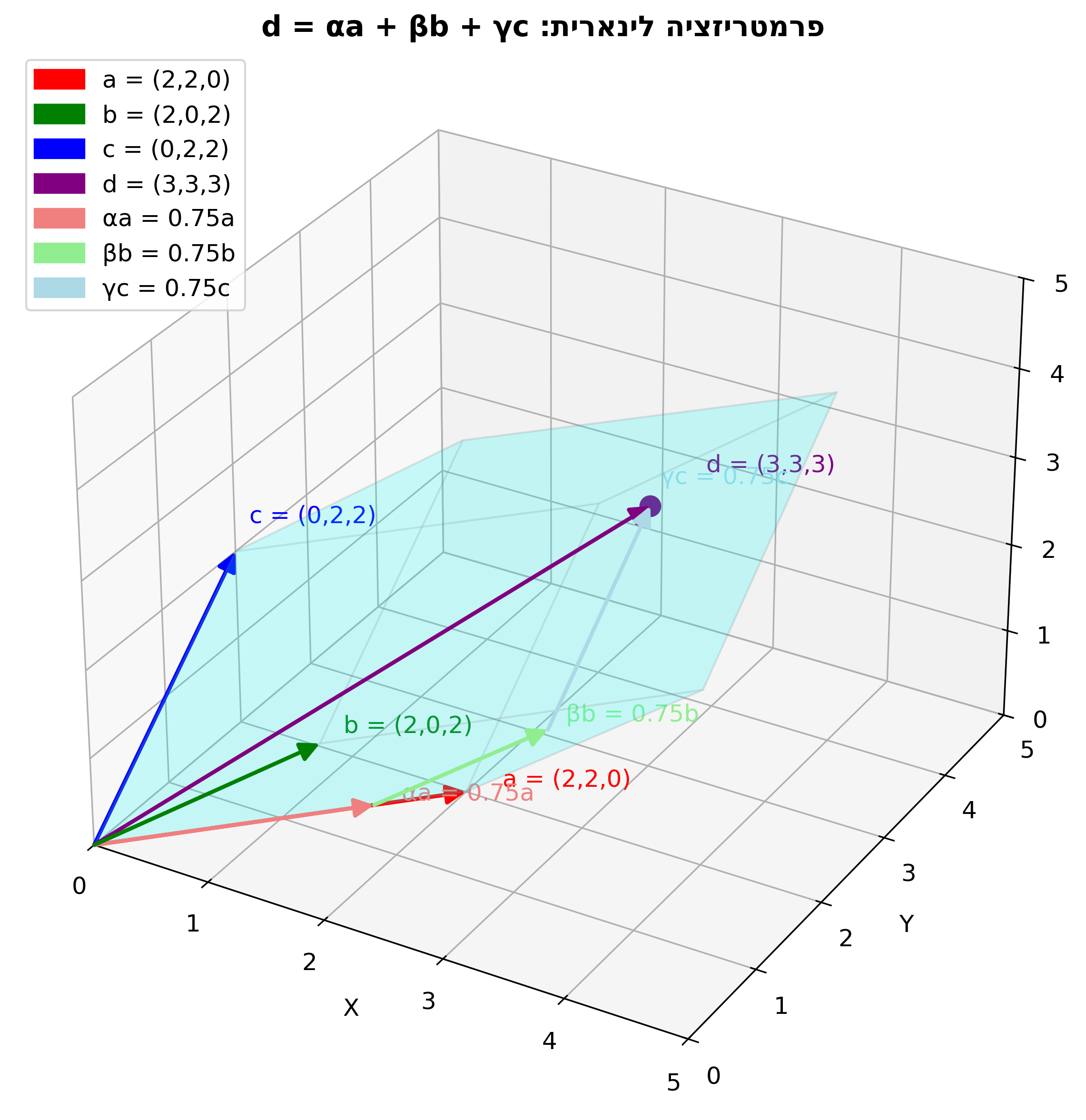
ה. מציאת המקדמים בצרוף הלינארי

נתון הוקטור

\[\vec{d} = (3, 3, 3)\]

ואנו מחפשים את הערכים $\alpha, \beta, \gamma$ כך ש:

\[\vec{d} = \alpha\vec{a} + \beta\vec{b} + \gamma\vec{c}\]

נציב את הוקטורים הנתונים:

\[\vec{d} = \alpha(2,2,0) + \beta(2,0,2) + \gamma(0,2,2)\]

נפרק לרכיבים:

\[\begin{aligned} 3 &= 2\alpha + 2\beta \\[10pt] 3 &= 2\alpha + 2\gamma \\[10pt] 3 &= 2\beta + 2\gamma \end{aligned}\]

מהשוואת המשוואה הראשונה והשנייה, מקבלים: $\beta = \gamma$

נסכם את שלוש המשוואות:

\[9 = 4\alpha + 4\beta + 4\gamma\]

מכיוון ש-$\beta = \gamma$, מקבלים:

\[9 = 4\alpha + 8\beta\] \[\frac{9}{4} = \alpha + 2\beta\]

מהמשוואה הראשונה:

\[\frac{3}{2} = \alpha + \beta\]

נפתור את המערכת:

\[\alpha + 2\beta = \frac{9}{4}\] \[\alpha + \beta = \frac{3}{2}\]

נחסר את המשוואה השנייה מהראשונה:

\[\beta = \frac{9}{4} - \frac{3}{2} = \frac{9 - 6}{4} = \frac{3}{4}\]

נציב בחזרה:

\[\alpha + \frac{3}{4} = \frac{3}{2}\] \[\alpha = \frac{3}{2} - \frac{3}{4} = \frac{6 - 3}{4} = \frac{3}{4}\]

כיוון ש-$\beta = \gamma$, מקבלים: $\alpha = \beta = \gamma = \frac{3}{4}$

נבדוק את התוצאה:

\[\alpha\vec{a} + \beta\vec{b} + \gamma\vec{c} = \frac{3}{4}(2,2,0) + \frac{3}{4}(2,0,2) + \frac{3}{4}(0,2,2)\] \[= \frac{3}{4}(4, 4, 4) = (3, 3, 3) = \vec{d}\]

הערה: יש שיטה מתודולוגית יותר לפתור את הבעיה של מציאת מקדמים בצירוף לינארי באמצעות מטריצות. זוהי למעשה השיטה הסטנדרטית בעולם האלגברה הלינארית. יש שיטות נוספות לפתרון, כמו מטריצה הפוכה.

---

שאלה 3: קואורדינטות גליליות

קואורדינטות גליליות מורכבות משלושה מרכיבים: $(ρ, \theta, z)$, כאשר:

• $ρ$ הוא המרחק מציר ה-$z$ (ולא מהראשית)
• $\theta$ היא הזווית במישור $x$-$y$, הנמדדת מציר ה-$x$ (נגד כיוון השעון)
• $z$ היא הקואורדינטה לאורך ציר ה-$z$

א. נוסחאות המעבר

המעבר מקואורדינטות קרטזיות לגליליות:

$ρ = \sqrt{x^2 + y^2}$ (המרחק מציר ה-$z$) $\theta = \tan^{-1}(y/x)$ (הזווית במישור $x$-$y$) $z$ נשאר זהה

המעבר מקואורדינטות גליליות לקרטזיות:

$x = ρ \cos \theta$ $y = ρ \sin \theta$ $z$ נשאר זהה

ב. הקשר הפיתגוראי

המרחק של נקודה מהראשית בקואורדינטות קרטזיות הוא:

\[r = \sqrt{x^2 + y^2 + z^2}\]

בקואורדינטות גליליות, הקשר הפיתגוראי הוא:

\[r^2 = ρ^2 + z^2 = x^2 + y^2 + z^2\]

שאלה 4: יישומי וקטורים בגיאומטריה

בשאלה זו מובאות דוגמאות לשימושים של וקטורים לפתרון בעיות גיאומטריות:

1. הוכחה שאלכסוני מקבילית חוצים זה את זה:

   במקבילית ABCD עם אלכסונים הנפגשים בנקודה P, ניתן לייצג את הוקטורים מהראשית:

   • $\vec{P} = \frac{1}{2}(\vec{A} + \vec{C}) = \frac{1}{2}(\vec{B} + \vec{D})$

   כלומר, P היא נקודת האמצע של שני האלכסונים, מה שמוכיח שהם חוצים זה את זה.

2. הוכחת משפט על קו המחבר את נקודות האמצע של שתי צלעות במשולש:

   במשולש ABC, אם D היא נקודת האמצע של AB ו-E היא נקודת האמצע של AC, אז:

   • $\vec{DE} = \vec{E} - \vec{D} = \frac{1}{2}\vec{C} - \frac{1}{2}\vec{B} = \frac{1}{2}(\vec{C} - \vec{B}) = \frac{1}{2}\vec{BC}$

   מכאן, הקו DE מקביל לצלע BC ואורכו מחצית מאורך BC.

פתרון תרגיל מס׳ 2 בפיזיקה - וקטורים ותנועה

תאריך: 28/03/2025

שאלה 1 - וקטורים תלת-ממדיים וזווית ביניהם

נתונים שני הווקטורים:

\[\vec{a} = \hat{x} + (\sqrt{2})\hat{y} - (\sqrt{3})\hat{z}\] \[\vec{b} = (\sqrt{3})\hat{x} - (\sqrt{2})\hat{y} + \hat{z}\]

1. היעזרו במחשבון בלבד כדי למצוא את הזווית בין שני הווקטורים.
2. קבלו וקטור יחידה המצביע בכיוון השקול הווקטורי של שני הווקטורים.

סעיף א: זווית בין וקטורים

הזווית בין שני וקטורים מחושבת באמצעות המכפלה הסקלרית:

\[\cos\theta = \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}|\vert \vec{b}\vert}\]

שלב 1: חישוב המכפלה הסקלרית

\[\vec{a} \cdot \vec{b} = (1)(\sqrt{3}) + (\sqrt{2})(-\sqrt{2}) + (-\sqrt{3})(1)\] \[= \sqrt{3} - 2 - \sqrt{3} = -2\]

שלב 2: חישוב גודל הווקטורים

\[\vert \vec{a}\vert = \sqrt{1^2 + (\sqrt{2})^2 + (-\sqrt{3})^2} = \sqrt{1 + 2 + 3} = \sqrt{6}\] \[\vert \vec{b}\vert = \sqrt{(\sqrt{3})^2 + (-\sqrt{2})^2 + 1^2} = \sqrt{3 + 2 + 1} = \sqrt{6}\]

שלב 3: חישוב הזווית

\[\cos\theta = \frac{-2}{\sqrt{6} \cdot \sqrt{6}} = \frac{-2}{6} = -\frac{1}{3}\] \[\boxed{\theta = \arccos\left(-\frac{1}{3}\right) \approx 109.47^\circ}\]

הערה: זווית גדולה מ-90° מעידה על כך שהווקטורים יוצרים זווית קהה ביניהם. המכפלה הסקלרית השלילית מאששת זאת.

סעיף ב: וקטור יחידה בכיוון השקול

שלב 1: מציאת השקול

\[\begin{aligned} \vec{a} + \vec{b} &= (1 + \sqrt{3})\hat{x} + (\sqrt{2} - \sqrt{2})\hat{y} + (-\sqrt{3} + 1)\hat{z} \\[10pt] &= (1 + \sqrt{3})\hat{x} + 0\hat{y} + (1 - \sqrt{3})\hat{z} \end{aligned}\]

שלב 2: חישוב גודל השקול

\[\vert \vec{a} + \vec{b}\vert = \sqrt{(1 + \sqrt{3})^2 + 0^2 + (1 - \sqrt{3})^2}\]

פיתוח הביטויים:

\[(1 + \sqrt{3})^2 = 1 + 2\sqrt{3} + 3 = 4 + 2\sqrt{3}\] \[(1 - \sqrt{3})^2 = 1 - 2\sqrt{3} + 3 = 4 - 2\sqrt{3}\]

לכן:

\[\vert \vec{a} + \vec{b}\vert = \sqrt{4 + 2\sqrt{3} + 4 - 2\sqrt{3}} = \sqrt{8} = 2\sqrt{2}\]

שלב 3: וקטור היחידה

\[\begin{aligned} \hat{r} &= \frac{\vec{a} + \vec{b}}{\vert \vec{a} + \vec{b}\vert} \\[10pt] &= \frac{1}{2\sqrt{2}}[(1 + \sqrt{3})\hat{x} + (1 - \sqrt{3})\hat{z}] \\[10pt] &= \frac{1 + \sqrt{3}}{2\sqrt{2}}\hat{x} + \frac{1 - \sqrt{3}}{2\sqrt{2}}\hat{z} \end{aligned}\]

---

שאלה 2: פעולות על וקטורים דו-ממדיים

נתונים שני וקטורים דו-ממדיים:

\[\vec{a} = 3\hat{x} - 3\hat{y}, \quad \vec{b} = -2\hat{x} + \hat{y}\]

1. קבלו את הסינוס והקוסינוס של הזווית של הווקטור $2\vec{a} - 3\vec{b}$ ביחס לציר האיקס (אין צורך לחשב את הזווית עצמה).
2. נתון הווקטור $\vec{c} = \pi\hat{x} + e\hat{y}$. קבלו את כל הווקטורים שבעולם הניצבים לו.
3. רישמו את הווקטור $\vec{c}$ בבסיס שנפרש ע”י הווקטורים $\vec{a}, \vec{b}$.

סעיף א: סינוס וקוסינוס של זווית

שלב 1: חישוב הווקטור

\[2\vec{a} - 3\vec{b} = 2(3\hat{x} - 3\hat{y}) - 3(-2\hat{x} + \hat{y})\] \[= 6\hat{x} - 6\hat{y} + 6\hat{x} - 3\hat{y}\] \[= 12\hat{x} - 9\hat{y}\]

שלב 2: גודל הווקטור

\[|2\vec{a} - 3\vec{b}\vert = \sqrt{12^2 + (-9)^2} = \sqrt{144 + 81} = \sqrt{225} = 15\]

שלב 3: הסינוס והקוסינוס

עבור וקטור $\vec{v} = v_x\hat{x} + v_y\hat{y}$:

• $\cos\theta = \frac{v_x}{\vert \vec{v}\vert }$ (רכיב x מנורמל)
• $\sin\theta = \frac{v_y}{\vert \vec{v}\vert }$ (רכיב y מנורמל)

לכן:

\[\cos\theta = \frac{12}{15} = \frac{4}{5}\] \[\sin\theta = \frac{-9}{15} = -\frac{3}{5}\]

הערה: שימו לב שמתקיים $\cos^2\theta + \sin^2\theta = \frac{16}{25} + \frac{9}{25} = 1$ כנדרש.

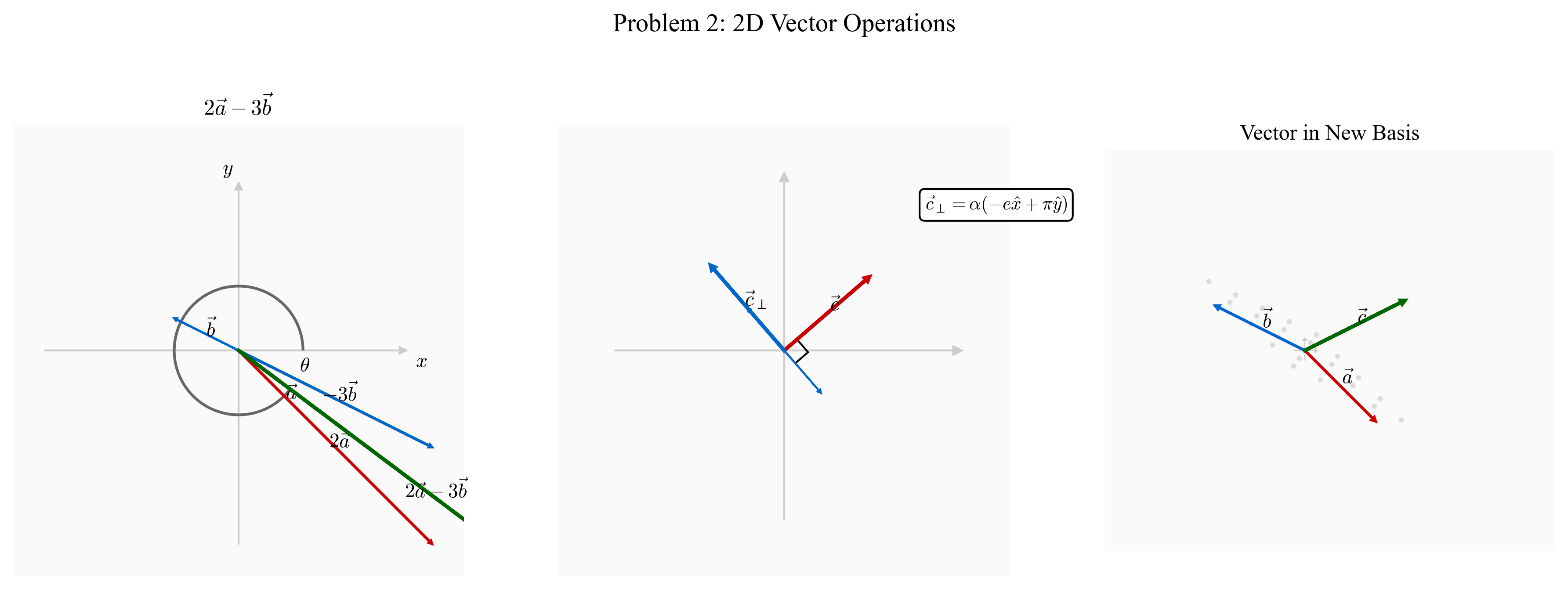
סעיף ב: וקטורים ניצבים

עיקרון: וקטור $\vec{v}$ ניצב ל-$\vec{c}$ אם ורק אם $\vec{v} \cdot \vec{c} = 0$.

אם $\vec{v} = x\hat{x} + y\hat{y}$, אז:

\[\vec{v} \cdot \vec{c} = x\pi + ye = 0\]

מכאן:

\[x\pi = -ye\] \[x = -\frac{e}{\pi}y\]

התשובה: כל הווקטורים הניצבים ל-$\vec{c}$ הם מהצורה:

\[\vec{v}_\perp = \alpha(-e\hat{x} + \pi\hat{y})\]

כאשר $\alpha$ הוא סקלר כלשהו.

בדיקה:

\(\vec{v}_\perp \cdot \vec{c} = \alpha(-e\pi + \pi e) = 0\) ✓

סעיף ג: ייצוג בבסיס חדש

מטרה: למצוא סקלרים $\lambda, \mu$ כך ש:

\[\vec{c} = \lambda\vec{a} + \mu\vec{b}\]

הצבה:

\[\pi\hat{x} + e\hat{y} = \lambda(3\hat{x} - 3\hat{y}) + \mu(-2\hat{x} + \hat{y})\]

השוואת רכיבים:

• רכיב x: $\pi = 3\lambda - 2\mu$
• רכיב y: $e = -3\lambda + \mu$

פתרון מערכת המשוואות:

מהמשוואה השנייה: $\mu = e + 3\lambda$

הצבה בראשונה:

\[\pi = 3\lambda - 2(e + 3\lambda) = 3\lambda - 2e - 6\lambda = -3\lambda - 2e\] \[\lambda = -\frac{\pi + 2e}{3}\] \[\mu = e + 3\left(-\frac{\pi + 2e}{3}\right) = e - \pi - 2e = -\pi - e\]

התשובה:

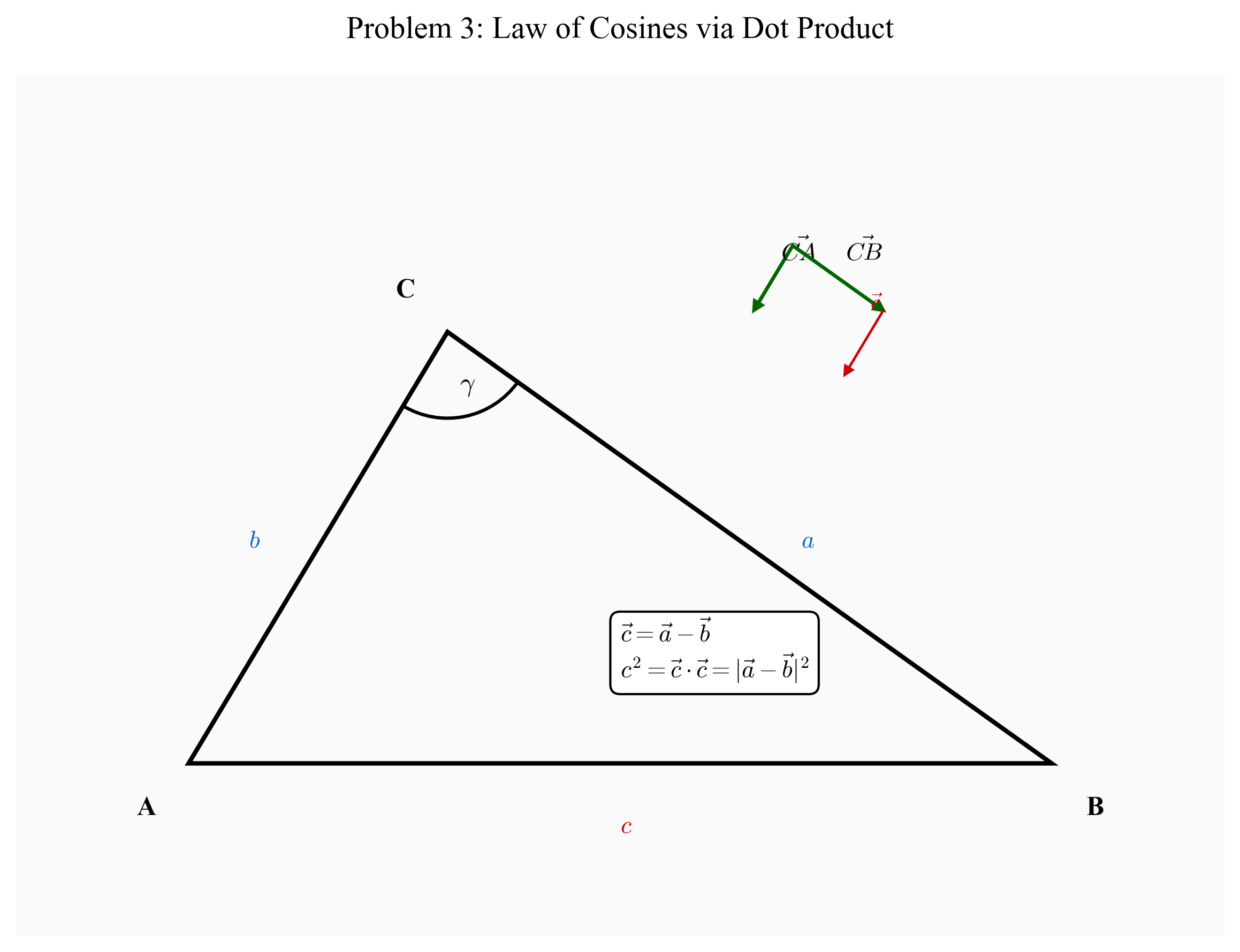
\[\vec{c} = -\frac{\pi + 2e}{3}\vec{a} - (\pi + e)\vec{b}\]

---

שאלה 3: הוכחת משפט הקוסינוסים

נתון משולש עם צלעות a, b, c וזווית γ מול הצלע c. הוכיחו את משפט הקוסינוסים:

\[c^2 = a^2 + b^2 - 2ab\cos\gamma\]

באמצעות שימוש טריוויאלי במכפלה הסקלרית.

רעיון מרכזי: נייצג את צלעות המשולש כווקטורים ונשתמש בתכונות המכפלה הסקלרית.

שלב 1: הגדרת הווקטורים

נסמן את קודקודי המשולש כ-A, B, C. נגדיר:

• $\vec{a}$ = וקטור מ-C ל-B (אורכו a)
• $\vec{b}$ = וקטור מ-C ל-A (אורכו b)
• $\vec{c}$ = וקטור מ-A ל-B (אורכו c)

שלב 2: קשר בין הווקטורים מסגירת המשולש:

\[\vec{c} = \vec{a} - \vec{b}\]

שלב 3: חישוב $c^2$ באמצעות מכפלה סקלרית

\[c^2 = \vert \vec{c}|^2 = \vec{c} \cdot \vec{c}\]

הצבת הקשר מצעד 2:

\[c^2 = (\vec{a} - \vec{b}) \cdot (\vec{a} - \vec{b})\]

שלב 4: פיתוח המכפלה הסקלרית

תכונת הדיסטריביוטיביות של המכפלה הסקלרית:

\[c^2 = \vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b}\]

מכיוון שהמכפלה הסקלרית קומוטטיבית: $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$

\[c^2 = \vert \vec{a}|^2 - 2\vec{a} \cdot \vec{b} + \vert \vec{b}|^2\]

שלב 5: שימוש בהגדרת המכפלה הסקלרית

\[\vec{a} \cdot \vec{b} = \vert \vec{a}|\vert \vec{b}|\cos\gamma\]

כאשר γ היא הזווית בין $\vec{a}$ ו-$\vec{b}$ (שהיא הזווית בקודקוד C).

שלב 6: הצבה וסיום

\[c^2 = a^2 - 2ab\cos\gamma + b^2\] \[c^2 = a^2 + b^2 - 2ab\cos\gamma\]

✓

תובנה: ההוכחה הווקטורית אלגנטית יותר מההוכחה הגיאומטרית הקלאסית ומדגישה את הקשר בין אלגברה וגיאומטריה.

---

שאלה 4: קואורדינטות כדוריות

הביטו באיור בנקודה P אשר מרחקה מהראשית הוא r. הווקטור היוצא מהראשית ומצביע אל הנקודה נתון בביטוי:

\[\vec{r} = x\hat{x} + y\hat{y} + z\hat{z}\]

כאשר (x, y, z) הם הקואורדינטות של הנקודה P. תהיינה (r, θ, φ) קואורדינטות חדשות כמוראה באיור. שלושה זו מכונה קואורדינטות כדוריות.

א. הראו שמתקיים:

\[x = r\sin\theta\cos\varphi, \quad y = r\sin\theta\sin\varphi, \quad z = r\cos\theta\]

ב. עשו שימוש בביטויים מעלה וקבלו במפורש:

\[x^2 + y^2 + z^2 = r^2\]

סעיף א: נוסחאות ההמרה

הבנת המערכת:

• r: המרחק מהראשית לנקודה P
• θ: הזווית מציר z החיובי (זווית קוטבית, 0 ≤ θ ≤ π)
• φ: הזווית בהיטל על מישור xy מציר x החיובי (זווית אזימוטלית, 0 ≤ φ < 2π)

גזירת הנוסחאות:

שלב 1: רכיב z

מהגדרת θ כזווית מציר z:

\[z = r\cos\theta\]

שלב 2: היטל על מישור xy

אורך ההיטל של $\vec{r}$ על מישור xy:

\[\rho = r\sin\theta\]

שלב 3: רכיבי x ו-y

בהיטל על מישור xy, הזווית φ נמדדת מציר x:

\[x = \rho\cos\varphi = r\sin\theta\cos\varphi\] \[y = \rho\sin\varphi = r\sin\theta\sin\varphi\]

סעיף ב: אימות הקשר

חישוב ישיר:

\[\begin{aligned} x^2 + y^2 + z^2 &= (r\sin\theta\cos\varphi)^2 + (r\sin\theta\sin\varphi)^2 + (r\cos\theta)^2 \\[10pt] &= r^2\sin^2\theta\cos^2\varphi + r^2\sin^2\theta\sin^2\varphi + r^2\cos^2\theta \\[10pt] &= r^2\sin^2\theta(\cos^2\varphi + \sin^2\varphi) + r^2\cos^2\theta \end{aligned}\]

מהזהות הטריגונומטרית $\cos^2\varphi + \sin^2\varphi = 1$:

\[= r^2\sin^2\theta + r^2\cos^2\theta\] \[= r^2(\sin^2\theta + \cos^2\theta)\]

\(= r^2 \cdot 1 = r^2\) ✓

משמעות פיזיקלית: התוצאה מאשרת שהמרחק מהראשית נשמר בהמרה בין מערכות הקואורדינטות.

---

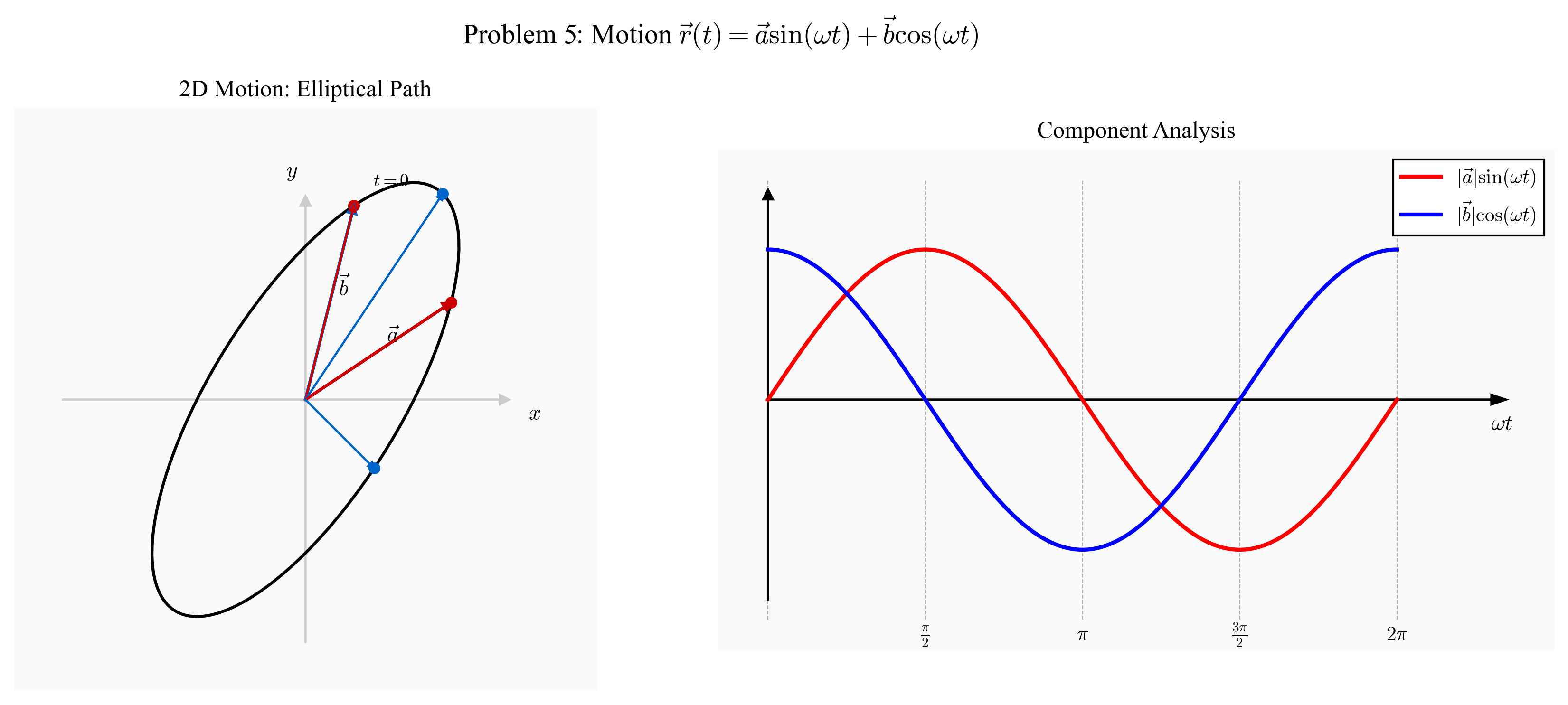
שאלה 5: תנועה סינוסואידלית משולבת

וקטור המקום של גוף מסוים המבצע תנועה כלשהי מתואר באמצעות:

\[\vec{r}(t) = \vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)\]

כאשר $\vec{a}, \vec{b}$ הם וקטורים קבועים.

1. קבלו את המרחק של הגוף מהראשית כפונקציה של הזמן.
2. קבלו ביטוי עבור וקטור המהירות של הגוף.
3. קבלו ביטוי עבור וקטור היחידה תלוי-הזמן המתאר את כיוון תנועתו של הגוף.
4. קבלו את המכפלה $\vec{r}(t) \cdot \vec{v}(t)$.

הערה: השאלה הופיעה בבלוג של המרצה, עם החלפה בין $\sin$ ל-$\cos$, וסקאלרים $a, b$ במקום וקטורים. הפתרון כאן מתייחס לגרסה המקורית עם וקטורים.

סעיף א: מרחק מהראשית

\[\begin{aligned} \vert \vec{r}(t)| &= \sqrt{(\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)) \cdot (\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t))} \\[10pt] &= \sqrt{\vert \vec{a}|^2\sin^2(\omega t) + 2(\vec{a} \cdot \vec{b})\sin(\omega t)\cos(\omega t) + \vert \vec{b}|^2\cos^2(\omega t)} \end{aligned}\] \[= \vert \vec{a}|^2\sin^2(\omega t) + 2(\vec{a} \cdot \vec{b})\sin(\omega t)\cos(\omega t) + \vert \vec{b}|^2\cos^2(\omega t)\]

שימוש בזהות: $\sin(\omega t)\cos(\omega t) = \frac{1}{2}\sin(2\omega t)$

\[\vert \vec{r}(t)|^2 = \vert \vec{a}|^2\sin^2(\omega t) + \vert \vec{b}|^2\cos^2(\omega t) + (\vec{a} \cdot \vec{b})\sin(2\omega t)\]

המרחק:

\[\boxed{\vert \vec{r}(t)| = \sqrt{\vert \vec{a}\vert ^2\sin^2(\omega t) + \vert \vec{b}\vert ^2\cos^2(\omega t) + (\vec{a} \cdot \vec{b})\sin(2\omega t)}}\]

מקרה פרטי: אם $\vec{a} \perp \vec{b}$ (כלומר $\vec{a} \cdot \vec{b} = 0$) ו-$\vert \vec{a}\vert = \vert \vec{b}\vert = R$, אז:

\[\boxed{\vert \vec{r}(t)| = R}\]

והתנועה היא מעגלית ברדיוס קבוע.

סעיף ב: וקטור המהירות

\[\vec{v}(t) = \frac{d\vec{r}}{dt} = \frac{d}{dt}[\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)]\] \[= \vec{a}\omega\cos(\omega t) - \vec{b}\omega\sin(\omega t)\] \[= \omega[\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)]\]

סעיף ג: וקטור יחידה בכיוון התנועה

וקטור היחידה בכיוון המהירות:

\[\hat{v}(t) = \frac{\vec{v}(t)}{\vert \vec{v}(t)|}\]

תחילה נחשב את גודל המהירות:

\[\vert \vec{v}(t)|^2 = \omega^2[\vert \vec{a}|^2\cos^2(\omega t) - 2(\vec{a} \cdot \vec{b})\cos(\omega t)\sin(\omega t) + \vert \vec{b}|^2\sin^2(\omega t)]\] \[= \omega^2[\vert \vec{a}|^2\cos^2(\omega t) + \vert \vec{b}|^2\sin^2(\omega t) - (\vec{a} \cdot \vec{b})\sin(2\omega t)]\]

לכן:

\[\hat{v}(t) = \frac{\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)}{\sqrt{\vert \vec{a}|^2\cos^2(\omega t) + \vert \vec{b}|^2\sin^2(\omega t) - (\vec{a} \cdot \vec{b})\sin(2\omega t)}}\]

סעיף ד: מכפלה סקלרית

\[\vec{r}(t) \cdot \vec{v}(t) = [\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)] \cdot \omega[\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)]\] \[= \omega[\vert \vec{a}|^2\sin(\omega t)\cos(\omega t) - (\vec{a} \cdot \vec{b})\sin^2(\omega t) + (\vec{a} \cdot \vec{b})\cos^2(\omega t) - \vert \vec{b}|^2\sin(\omega t)\cos(\omega t)]\] \[= \omega\sin(\omega t)\cos[\omega t](\vert \vec{a}|^2 - \vert \vec{b}|^2) + \omega[\vec{a} \cdot \vec{b}](\cos^2(\omega t) - \sin^2(\omega t))\]

שימוש בזהויות:

\[\cos^2(\omega t) - \sin^2(\omega t) = \cos(2\omega t)\]

ובזהות הטריגונומטרית:

\[\sin(\omega t)\cos(\omega t) = \frac{1}{2}\sin(2\omega t)\] \[\vec{r}(t) \cdot \vec{v}(t) = \frac{\omega}{2}[\vert \vec{a}|^2 - \vert \vec{b}|^2]\sin(2\omega t) + \omega(\vec{a} \cdot \vec{b})\cos(2\omega t)\]

תובנה פיזיקלית: כאשר $\vert \vec{a}\vert = \vert \vec{b}\vert $ ו-$\vec{a} \perp \vec{b}$, מתקבל $\vec{r}(t) \cdot \vec{v}(t) = 0$, כלומר המהירות תמיד ניצבת למיקום - תנועה מעגלית!

---

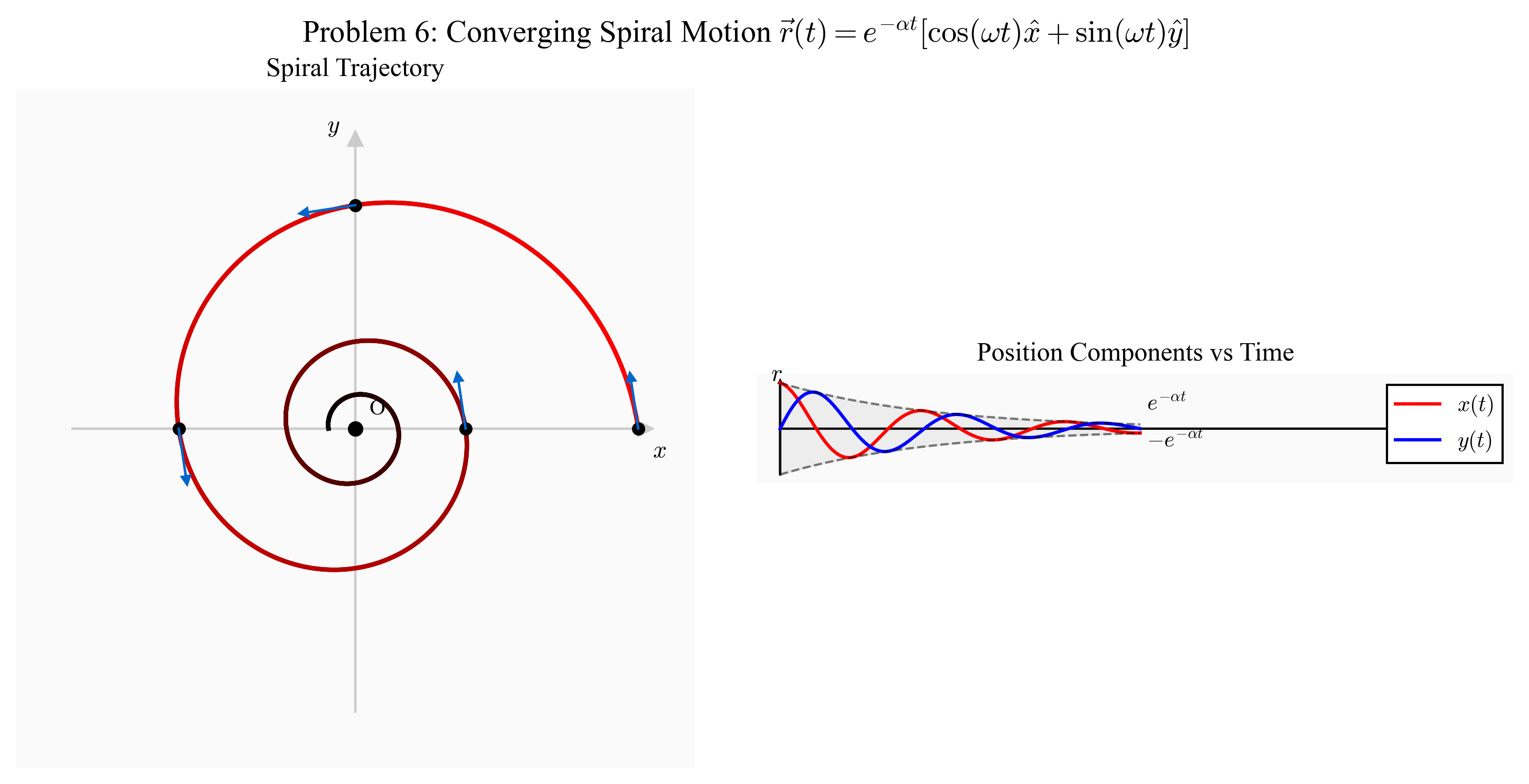
שאלה 6: תנועה ספירלית מתכנסת

וקטור המקום של חלקיק כלשהו הנע במישור נתון ע”י:

\[\vec{r}(t) = e^{-\alpha t}\cos(\omega t)\hat{x} + e^{-\alpha t}\sin(\omega t)\hat{y}\]

כאשר α, ω הם פרמטרים כלשהם.

1. מהן היחידות של הפרמטרים α, ω?
2. הראו שהחלקיק נע בספירלה מעגלית שמתכנסת לעבר המרכז.
3. קבלו את וקטור המהירות של החלקיק כתלות בזמן.
4. מהו גודל וקטור המהירות של החלקיק כתלות בזמן?

סעיף א: יחידות הפרמטרים

עקרון: הארגומנט של פונקציות אקספוננציאליות וטריגונומטריות חייב להיות חסר יחידות.

• עבור $e^{-\alpha t}$: הביטוי $\alpha t$ חייב להיות חסר יחידות. מכיוון ש-$[t] = \text{s}$ (שניות), נדרש: $[\alpha] = \text{s}^{-1}$

• עבור $\cos(\omega t)$ ו-$\sin(\omega t)$: הביטוי $\omega t$ חייב להיות חסר יחידות (רדיאנים). לכן: $[\omega] = \text{rad/s} = \text{s}^{-1}$

משמעות פיזיקלית:

• $\alpha$: קצב הדעיכה (decay rate)
• $\omega$: תדירות זוויתית של הסיבוב

סעיף ב: הוכחת תנועה ספירלית מתכנסת

שלב 1: מרחק מהראשית

\[\begin{aligned} \vert \vec{r}(t)| &= \sqrt{(e^{-\alpha t}\cos(\omega t))^2 + (e^{-\alpha t}\sin(\omega t))^2} \\[10pt] &= e^{-\alpha t}\sqrt{\cos^2(\omega t) + \sin^2(\omega t)} \\[10pt] &= e^{-\alpha t} \cdot 1 = e^{-\alpha t} \end{aligned}\]

מכיוון ש-$\alpha > 0$ (פיזיקלית), המרחק דועך אקספוננציאלית עם הזמן.

שלב 2: זווית הקוטב

\[\tan\phi = \frac{y}{x} = \frac{e^{-\alpha t}\sin(\omega t)}{e^{-\alpha t}\cos(\omega t)} = \tan(\omega t)\]

לכן: $\phi = \omega t$

הזווית גדלה ליניארית עם הזמן - החלקיק מסתובב.

מסקנה: החלקיק נע על ספירלה המתלפפת פנימה, כאשר המרחק מהראשית דועך אקספוננציאלית והזווית גדלה ליניארית - ספירלה לוגריתמית מתכנסת.

סעיף ג: וקטור המהירות

\[\vec{v}(t) = \frac{d\vec{r}}{dt}\]

נגזור כל רכיב בנפרד באמצעות כלל המכפלה:

רכיב x:

\[\begin{aligned} v_x &= \frac{d}{dt}[e^{-\alpha t}\cos(\omega t)] \\[10pt] &= -\alpha e^{-\alpha t}\cos(\omega t) - \omega e^{-\alpha t}\sin(\omega t) \\[10pt] &= -e^{-\alpha t}[\alpha\cos(\omega t) + \omega\sin(\omega t)] \end{aligned}\]

רכיב y:

\[v_y = \frac{d}{dt}[e^{-\alpha t}\sin(\omega t)]\] \[= -\alpha e^{-\alpha t}\sin(\omega t) + \omega e^{-\alpha t}\cos(\omega t)\] \[= e^{-\alpha t}[\omega\cos(\omega t) - \alpha\sin(\omega t)]\]

וקטור המהירות:

\[\vec{v}(t) = e^{-\alpha t}[-(\alpha\cos(\omega t) + \omega\sin(\omega t))\hat{x} + (\omega\cos(\omega t) - \alpha\sin(\omega t))\hat{y}]\]

סעיף ד: גודל המהירות

\[\vert \vec{v}(t)|^2 = v_x^2 + v_y^2\] \[= e^{-2\alpha t}[(\alpha\cos(\omega t) + \omega\sin(\omega t))^2 + (\omega\cos(\omega t) - \alpha\sin(\omega t))^2]\]

פיתוח הסוגריים:

\[= e^{-2\alpha t}[\alpha^2\cos^2(\omega t) + 2\alpha\omega\cos(\omega t)\sin(\omega t) + \omega^2\sin^2(\omega t)\] \[+ \omega^2\cos^2(\omega t) - 2\alpha\omega\cos(\omega t)\sin(\omega t) + \alpha^2\sin^2(\omega t)]\]

האיברים המעורבים מתבטלים:

\[\begin{aligned} \vert \vec{v}(t)|^2 &= e^{-2\alpha t}[\alpha^2(\cos^2(\omega t) + \sin^2(\omega t)) + \omega^2(\cos^2(\omega t) + \sin^2(\omega t))] \\[10pt] &= e^{-2\alpha t}[\alpha^2 + \omega^2(\cos^2(\omega t) + \sin^2(\omega t))] \\[10pt] &= e^{-2\alpha t}[\alpha^2 + \omega^2] \end{aligned}\]

גודל המהירות:

\[\vert \vec{v}(t)| = e^{-\alpha t}\sqrt{\alpha^2 + \omega^2}\]

תובנות פיזיקליות:

1. המהירות דועכת באותו קצב כמו המרחק מהראשית

2. היחס בין גודל המהירות למרחק קבוע:

   \[\frac{\vert \vec{v}(t)|}{\vert \vec{r}(t)|} = \sqrt{\alpha^2 + \omega^2}\]
3. במקרה הגבולי $\alpha = 0$, מתקבלת תנועה מעגלית במהירות קבועה

פתרון תרגיל מס׳ 3 בפיזיקה - קינמטיקה

תאריך: 06/04/2025

שאלה 1: הולך רגל ונער על קרוסלה

הולך רגל נע בקו ישר כך שאורך ציר האיקס כתלות בזמן הוא:

\[x(t) = 4 + 4t\]

נער יושב על קרוסלה שמסתובבת כך שוקטור המקום שלו נתון על ידי:

\[\vec{r}(t) = \left( 2 \sin(3t),\ 2 \cos(3t) \right)\]

א. מהן היחידות של שתי הספרות ארבע בביטוי $x(t) = 4 + 4t$?

ב. מהן מהירות ותאוצת הולך הרגל כפונקציה של הזמן?

ג. קבלו את וקטור ההעתק $\Delta \vec{r}(t)$ בין הולך הרגל לבין הנער בכל זמן. מה המרחק ביניהם בזמן $t = 0$?

ד. קבלו את וקטור המהירות היחסית:

\[\vec{v}_{P \to B}(t)\]

מהו גודל המהירות היחסית בכל רגע כפי שנראה על ידי הולך הרגל?

א. מציאת היחידות של המקדמים בפונקציית המיקום

נתון: $x(t) = 4 + 4t$

• $x(t)$ מייצג מיקום, לכן היחידות שלו הן מטרים [m]
• $t$ מייצג זמן, יחידות של שניות [s]

עבור האיבר הראשון $4$:

• מכיוון ש-$x(t)$ הוא במטרים, המקדם $4$ חייב להיות גם במטרים $[m]$

עבור האיבר השני $4t$:

• $[4t] = [4] \times [t] = [4] \times [s]$
• אם $[4t]$ צריך להיות במטרים, אז $[4]$ חייב להיות ביחידות של $\mathrm{[m/s]}$

תשובה: המקדם 4 בביטוי הקבוע $4$ הוא ביחידות של $[m]$, והמקדם 4 בביטוי $4t$ הוא ביחידות של $\mathrm{[m/s]}$.

ב. מציאת מהירות ותאוצה של הולך הרגל

מהירות היא הנגזרת הראשונה של המיקום ביחס לזמן:

\[v(t) = \frac{dx(t)}{dt} = 4 \; \mathrm{[m/s]}\]

תאוצה היא הנגזרת השנייה של המיקום (או הנגזרת הראשונה של המהירות):

\[a(t) = \frac{dv(t)}{dt} = 0 \; [m/s^2]\]

מסקנה: הולך הרגל נע במהירות קבועה של 4 מטרים לשנייה, ללא תאוצה.

ג. וקטור ההעתק בין הולך הרגל לנער

וקטור המקום של הולך הרגל:

\[\vec{r}_{\text{Pedestrian}}(t) = (4 + 4t, 0)\]

[הולך רק על ציר ה-x]

וקטור המקום של הנער:

\[\vec{r}_{\text{Boy}}(t) = (2\sin(3t), 2\cos(3t))\]

וקטור ההעתק מהולך הרגל לנער:

\[\begin{aligned} \Delta\vec{r} &= \vec{r}_{\text{Pedestrian}}(t) - \vec{r}_{\text{Boy}}(t) \\[10pt] &= (4 + 4t - 2\sin(3t), -3\cos(3t)) \end{aligned}\]

בזמן $t = 0$:

• $\vec{r}_{\text{Pedestrian}}(0) = (4 + 4 \times 0, 0) = (4, 0)$
• $\vec{r}_{\text{Boy}}(0) = (2\sin(0), 2\cos(0)) = (0, 2)$

לכן, $\Delta\vec{r}(0) = (4, -2)$

המרחק ביניהם בזמן $t = 0$ הוא

\[|\Delta\vec{r}(0)| = \sqrt{4^2 + (-2)^2} = \sqrt{16 + 4} = \sqrt{20} = 2\sqrt{5} \approx 4.47\]

מטרים.

ד. וקטור המהירות היחסית

וקטור המהירות של הולך הרגל: $\vec{v}_{\text{Pedestrian}}(t) = (4, 0)$

וקטור המהירות של הנער (נגזרת של וקטור המקום שלו):

\[\vec{v}_{\text{Boy}}(t) = (6\cos(3t), -6\sin(3t))\]

המהירות היחסית שבה רואה הולך הרגל את הנער:

\[\vec{v}_{P \to B} = \vec{v}_{\text{Boy}}(t) - \vec{v}_{\text{Pedestrian}}(t) = (6\cos(3t) - 4, -6\sin(3t))\]

גודל המהירות היחסית:

\[\begin{aligned} \vert \vec{v}_{P \to B}| &= \sqrt{(6\cos(3t) - 4)^2 + (-6\sin(3t))^2} \\[10pt] &= \sqrt{(6\cos(3t) - 4)^2 + 36\sin^2(3t)} \\[10pt] &= \sqrt{(6\cos(3t) - 4)^2 + 36(1 - \cos^2(3t))} \\[10pt] &= \sqrt{(6\cos(3t) - 4)^2 + 36 - 36\cos^2(3t)} \\[10pt] &= \sqrt{36\cos^2(3t) - 48\cos(3t) + 16 + 36 - 36\cos^2(3t)} \\[10pt] &= \sqrt{-48\cos(3t) + 52} \\[10pt] &= \sqrt{52 - 48\cos(3t)} \end{aligned}\]

זהו גודל המהירות היחסית בכל רגע ורגע, כפונקציה של הזמן $t$.

שאלה 2: חלקיק הנע לאורך מסלול

חלקיק מסויים נע לאורך מסלול שמתואר ע”י וקטור המקום:

\[\vec{r}(t) = x_0 e^{-\alpha t}\cos(\alpha t)\hat{x} + y_0 e^{-\alpha t}\hat{y}\]

כאשר $x_0$, $y_0$, $\alpha$ הם פרמטרים קבועים.

א. מהן היחידות של שלושת הפרמטרים הללו?

ב. מה מרחק החלקיק מהראשית בזמן $t = 0$?

ג. היכן ממוקם החלקיק בזמן:

\[t = \frac{2\pi}{\omega}\]

ד. מהו וקטור מהירות החלקיק בזמן $t = 0$?

ה. מה גודל וכיוון וקטור המהירות (וקטור יחידה) בזמן $t = 0$?

ו. מהו וקטור מהירות החלקיק בזמן:

\[t = \frac{2\pi}{\omega}\]

ז. מהו וקטור תאוצת החלקיק בזמן $t = 0$?

ח. מהו גודל וכיוון התאוצה (וקטור יחידה) בזמן $t = 0$?

ט. מהו וקטור תאוצת החלקיק בזמן:

\[t = \frac{2\pi}{\omega}\]

י. מהו כיוון תאוצת החלקיק (וקטור יחידה) בזמן:

\[t = \frac{2\pi}{\omega}\]

---

א. יחידות הפרמטרים

נתון:

\[\vec{r}(t) = x_0 e^{-\alpha t}\cos(\alpha t)\hat{x} + y_0 e^{-\alpha t}\hat{y}\]

וקטור המקום $\vec{r}$ נמדד במטרים $\mathrm{[m]}$. נבדוק את היחידות של כל פרמטר:

• $e^{-\alpha t}$ חייב להיות חסר יחידות (ספרה טהורה). לכן $\alpha t$ חייב להיות חסר יחידות, מה שאומר ש-$\alpha$ צריך להיות ביחידות של $[1/s]$ או $[s^{-1}]$.

• עבור הרכיב $x_0 e^{-\alpha t}\cos(\alpha t)$, מאחר ש-$e^{-\alpha t}\cos(\alpha t)$ הוא חסר יחידות, $x_0$ חייב להיות ביחידות של $\mathrm{[m]}$ כדי שהרכיב יהיה במטרים.

• באופן דומה, $y_0$ גם חייב להיות ביחידות של $\mathrm{[m]}$.

תשובה: $x_0$ ו-$y_0$ הם ביחידות של מטרים $\mathrm{[m]}$, ו-$\alpha$ הוא ביחידות של $[s^{-1}]$.

ב. מרחק החלקיק מהראשית בזמן $t = 0$

בזמן $t = 0$:

\[\begin{aligned} \vec{r}(0) &= x_0 e^0 \cos(0)\hat{x} + y_0 e^0 \hat{y} \\[10pt] &= x_0 (1)(1)\hat{x} + y_0 (1)\hat{y} \\[10pt] &= x_0 \hat{x} + y_0 \hat{y} = (x_0, y_0) \end{aligned}\]

המרחק מהראשית:

\[\vert \vec{r}(0)| = \sqrt{x_0^2 + y_0^2}\]

ג. מיקום החלקיק בזמן $t = \frac{2\pi}{\omega}$

\[\vec{r}\left(\frac{2\pi}{\omega}\right) \overset{\star}{=} \vec{r}\left(\frac{2\pi}{\alpha}\right) = x_0 e^{-\alpha \cdot \frac{2\pi}{\alpha}}\cos\left(\alpha \cdot \frac{2\pi}{\alpha}\right)\hat{x} + y_0 e^{-\alpha \cdot \frac{2\pi}{\alpha}}\hat{y}\]

$\star$ הבהרה בנוגע לסימונים: בסעיף המקורי של השאלה, שאלו על $t = \frac{2\pi}{\omega}$, אך מכיוון ש-$\omega = \alpha$, השתמשנו ב-$t = \frac{2\pi}{\alpha}$.

• המשתנה $\alpha$ בדרך כלל מסמן קצב דעיכה, ומופיע בחזקה של $e^{-\alpha t}$.
• המשתנה $\omega$ מסמן תדירות זוויתית, כלומר, בכמה מעלות משתנה הזווית במחזור, ובדרך כלל מופיע בתוך הפונקציה $\cos(\omega t)$ או $\sin(\omega t)$. הנוסחה הכללי של זמן המחזור $T$ היא:

\[T = \frac{2\pi}{\omega}\]

לאחר פישוט:

\[\vec{r}\left(\frac{2\pi}{\alpha}\right) = x_0 e^{-2\pi}\cos(2\pi)\hat{x} + y_0 e^{-2\pi}\hat{y} = e^{-2\pi}(x_0\hat{x} + y_0\hat{y})\]

מכיוון ש-$\cos(2\pi) = 1$, נקבל:

\[\vec{r}\left(\frac{2\pi}{\alpha}\right) = e^{-2\pi}(x_0, y_0)\]

החלקיק ממוקם באותו כיוון כמו בזמן $t = 0$, אבל במרחק קטן יותר מהראשית.

ד. וקטור מהירות החלקיק בזמן $t = 0$

המהירות היא הנגזרת של וקטור המקום:

\[\vec{v}(t) = \frac{d\vec{r}}{dt}\]

לרכיב ה-x:

\[\begin{aligned} \frac{dx}{dt} &= \frac{d}{dt}[x_0 e^{-\alpha t}\cos(\alpha t)] \\[10pt] &= x_0[(-\alpha)e^{-\alpha t}\cos(\alpha t) + e^{-\alpha t}(-\alpha\sin(\alpha t))] \\[10pt] &= -x_0 \alpha e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)] \end{aligned}\]

לרכיב ה-y:

\[\begin{aligned} \frac{dy}{dt} &= \frac{d}{dt}[y_0 e^{-\alpha t}] \\[10pt] &= y_0(-\alpha)e^{-\alpha t} \\[10pt] &= -y_0 \alpha e^{-\alpha t} \end{aligned}\]

בזמן $t = 0$:

\[\begin{aligned} \vec{v}(0) &= (-x_0 \alpha[\cos(0) + \sin(0)], -y_0 \alpha e^0) \\[10pt] &= (-x_0 \alpha[1 + 0], -y_0 \alpha) \\[10pt] &= (-x_0 \alpha, -y_0 \alpha) \end{aligned}\]

ה. גודל וכיוון המהירות בזמן $t = 0$

גודל המהירות בזמן $t = 0$:

\[\begin{aligned} \vert \vec{v}(0)| &= \sqrt{(-x_0 \alpha)^2 + (-y_0 \alpha)^2} \\[10pt] &= \sqrt{x_0^2 \alpha^2 + y_0^2 \alpha^2} \\[10pt] &= \alpha\sqrt{x_0^2 + y_0^2} \end{aligned}\]

כיוון המהירות (וקטור יחידה) בזמן $t = 0$:

\[\begin{aligned} \hat{v}(0) &= \frac{\vec{v}(0)}{\vert \vec{v}(0)|} \\[10pt] &= \frac{(-x_0 \alpha, -y_0 \alpha)}{\alpha\sqrt{x_0^2 + y_0^2}} \\[10pt] &= \frac{(-x_0, -y_0)}{\sqrt{x_0^2 + y_0^2}} \end{aligned}\]

ו. וקטור מהירות החלקיק בזמן $t = \pi/(2\alpha)$

בזמן $t = \pi/(2\alpha)$:

\[\vec{v}(\pi/(2\alpha)) = (-x_0 \alpha e^{-\pi/2}[\cos(\pi/2) + \sin(\pi/2)], -y_0 \alpha e^{-\pi/2})\]

מכיוון ש-$\cos(\pi/2) = 0$ ו-$\sin(\pi/2) = 1$:

\[\vec{v}(\pi/(2\alpha)) = (-x_0 \alpha e^{-\pi/2}[0 + 1], -y_0 \alpha e^{-\pi/2})\] \[= (-x_0 \alpha e^{-\pi/2}, -y_0 \alpha e^{-\pi/2})\]

ז. וקטור תאוצת החלקיק בזמן $t = 0$

התאוצה היא הנגזרת של וקטור המהירות:

\[\vec{a}(t) = \frac{d\vec{v}}{dt}\]

לרכיב ה-x, נגזור את $v_x = -x_0 \alpha e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)]$:

\[\begin{aligned} a_x(t) &= \frac{d}{dt}(-x_0 \alpha e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)]) \\[10pt] &= -x_0 \alpha[(-\alpha)e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)] + e^{-\alpha t}[(-\alpha)\sin(\alpha t) + \alpha\cos(\alpha t)]] \\[10pt] &= x_0 \alpha^2 e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)] - x_0 \alpha e^{-\alpha t}[\alpha\cos(\alpha t) - \alpha\sin(\alpha t)] \\[10pt] &= x_0 \alpha^2 e^{-\alpha t}[\cos(\alpha t) + \sin(\alpha t)] - x_0 \alpha^2 e^{-\alpha t}[\cos(\alpha t) - \sin(\alpha t)] \\[10pt] &= 2x_0 \alpha^2 e^{-\alpha t}\sin(\alpha t) \end{aligned}\]

לרכיב ה-y, נגזור את $v_y = -y_0 \alpha e^{-\alpha t}$:

\[\begin{aligned} a_y(t) &= \frac{d}{dt}(-y_0 \alpha e^{-\alpha t}) \\[10pt] &= -y_0 \alpha[(-\alpha)e^{-\alpha t}] \\[10pt] &= y_0 \alpha^2 e^{-\alpha t} \end{aligned}\]

בזמן $t = 0$:

\[\begin{aligned} \vec{a}(0) &= (2x_0 \alpha^2 \sin(0), y_0 \alpha^2 e^0) \\[10pt] &= (0, y_0 \alpha^2) \end{aligned}\]

ח. גודל וכיוון התאוצה בזמן $t = 0$

גודל התאוצה בזמן $t = 0$:

\[\vert \vec{a}(0)| = \sqrt{0^2 + (y_0 \alpha^2)^2} = |y_0 \alpha^2|\]

כיוון התאוצה (וקטור יחידה) בזמן $t = 0$:

\[\hat{a}(0) = \frac{\vec{a}(0)}{\vert \vec{a}(0)|} = \frac{(0, y_0 \alpha^2)}{|y_0 \alpha^2|} = (0, \text{sgn}(y_0))\]

כאשר $\text{sgn}(y_0)$ הוא הסימן של $y_0$ (1 אם $y_0 > 0$, -1 אם $y_0 < 0$).

ט. וקטור תאוצת החלקיק בזמן $t = \pi/(2\alpha)$

בזמן $t = \pi/(2\alpha)$:

\[\vec{a}(\pi/(2\alpha)) = (2x_0 \alpha^2 e^{-\pi/2}\sin(\pi/2), y_0 \alpha^2 e^{-\pi/2})\]

מכיוון ש-$\sin(\pi/2) = 1$:

\[\vec{a}(\pi/(2\alpha)) = (2x_0 \alpha^2 e^{-\pi/2}, y_0 \alpha^2 e^{-\pi/2})\]

י. כיוון תאוצת החלקיק בזמן $t = \pi/(2\alpha)$

כיוון התאוצה (וקטור יחידה) בזמן $t = \pi/(2\alpha)$:

\[\begin{aligned} \hat{a}(\pi/(2\alpha)) &= \frac{\vec{a}(\pi/(2\alpha))}{\vert \vec{a}(\pi/(2\alpha))|} \\[10pt] &= \frac{(2x_0 \alpha^2 e^{-\pi/2}, y_0 \alpha^2 e^{-\pi/2})}{\sqrt{(2x_0 \alpha^2 e^{-\pi/2})^2 + (y_0 \alpha^2 e^{-\pi/2})^2}} \\[10pt] &= \frac{(2x_0 \alpha^2 e^{-\pi/2}, y_0 \alpha^2 e^{-\pi/2})}{(\alpha^2 e^{-\pi/2})\sqrt{4x_0^2 + y_0^2}} \\[10pt] &= \frac{(2x_0, y_0)}{\sqrt{4x_0^2 + y_0^2}} \end{aligned}\]

---

שאלה 3: גוף שמבצע תנועה

גוף מסויים נע כך שוקטור המקום שלו נתון על ידי:

\[\vec{r}(t) = \vec{a} \cos(\omega t) + \vec{b} \sin(\omega t)\]

כאשר $\vec{a}$ ו-$\vec{b}$ הם וקטורים קבועים כלשהם.

א. הראו שוקטור המקום מקיים את המשוואה הדיפרנציאלית:

\[\ddot{\vec{r}} + \omega^2 \vec{r} = \vec{0}\]

ב. נתון:

\[\vec{a} = (1, -1),\quad \vec{b} = (0, 1)\]

חשבו את $\vec{r}(t = \pi/3\ \, \mathrm{s})$ ואת $\vec{v}(t = \pi/3\ \, \mathrm{s})$.

א. הוכחת משוואה דיפרנציאלית

נחשב את הנגזרת הראשונה (מהירות):

\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -\vec{a}\omega\sin(\omega t) + \vec{b}\omega\cos(\omega t)\]

נחשב את הנגזרת השנייה (תאוצה):

\[\vec{a}(t) = \frac{d\vec{v}}{dt} = -\vec{a}\omega^2\cos(\omega t) - \vec{b}\omega^2\sin(\omega t)\] \[= -\omega^2\left[\vec{a}\cos(\omega t) + \vec{b}\sin(\omega t)\right]\] \[= -\omega^2\vec{r}(t)\]

כלומר:

\[\boxed{\ddot{\vec{r}}(t) = -\omega^2\vec{r}(t)}\]

לכן:

\[\ddot{\vec{r}} + \omega^2\vec{r} = -\omega^2\vec{r} + \omega^2\vec{r} = \vec{0}\]

זה מוכיח שוקטור המקום מקיים את המשוואה הדיפרנציאלית.

ב. חישוב $\vec{r}(t = \pi/3)$ ו-$\vec{v}(t = \pi/3)$

נתון: $\vec{a} = (1, -1)$, $\vec{b} = (0, 1)$

נחשב $\vec{r}(\pi/3)$:

\[\begin{aligned} \vec{r}\left(\frac{\pi}{3}\right) &= \vec{a} \cos\left(\frac{\pi}{3}\right) + \vec{b} \sin\left(\frac{\pi}{3}\right) \\[10pt] &= (1, -1) \cdot \frac{1}{2} + (0, 1) \cdot \frac{\sqrt{3}}{2} \\[10pt] &= \left( \frac{1}{2}, -\frac{1}{2} \right) + \left( 0, \frac{\sqrt{3}}{2} \right) \\[10pt] &= \left( \frac{1}{2}, -\frac{1}{2} + \frac{\sqrt{3}}{2} \right) \\[10pt] &= \left( \frac{1}{2}, \frac{\sqrt{3} - 1}{2} \right) \end{aligned}\]

נחשב $\vec{v}\left(t = \frac{\pi}{3}\right)$:

\[\begin{aligned} \vec{v}(t) &= -\vec{a} \, \omega \sin(\omega t) + \vec{b} \, \omega \cos(\omega t) \\[10pt] \vec{v}\left( \frac{\pi}{3} \right) &= - (1, -1) \cdot \omega \cdot \frac{\sqrt{3}}{2} + (0, 1) \cdot \omega \cdot \frac{1}{2} \\[10pt] &= \left( -\omega \frac{\sqrt{3}}{2}, \, \omega \frac{\sqrt{3}}{2} \right) + \left( 0, \, \frac{\omega}{2} \right) \\[10pt] &= \left( -\omega \frac{\sqrt{3}}{2}, \, \omega \left( \frac{\sqrt{3}}{2} + \frac{1}{2} \right) \right) \\[10pt] &= \omega \left( -\frac{\sqrt{3}}{2}, \, \frac{\sqrt{3} + 1}{2} \right) \end{aligned}\]

---

שאלה 3 מהבלוג - בעיית הקליע

קליע נורה ממקור הצירים במהירות התחלתית

\[v_0 = 2\;\mathrm{m/s}, \qquad \theta_0 = 30^{\circ}.\]

המערכת ללא התנגדות אוויר; הציר $x$ אופקי, הציר $y$ אנכי כלפי מעלה, והאצת הכובד $g \approx 9.81\;\mathrm{m/s}^2$.

נוסחאות התנועה הבליסטית מופיעות בתרגיל 2 של החוברת:

\[\begin{aligned} x(t) &= v_{0x}\,t,\\[10pt] y(t) &= v_{0y}\,t-\frac12gt^{2}. \end{aligned}\]

קבלו את מרחקו של הקליע מהראשית ואת זווית נטייתו מעל האופק בכל רגע ורגע.

---

1. פירוק המהירות לגורמים

\[\begin{aligned} v_{0x} &= v_0\cos\theta_0 = 2\cdot\frac{\sqrt3}{2}=1.732\;\mathrm{m/s},\\[10pt] v_{0y} &= v_0\sin\theta_0 = 2\cdot\frac12 =1.000\;\mathrm{m/s}. \end{aligned}\]

---

2. משוואות המקום כפונקציה של הזמן

\[\boxed{\; \begin{aligned} x(t) &= v_{0x}\,t = 1.732\,t,\\[10pt] y(t) &= v_{0y}\,t-\frac12gt^{2}=t-4.905\,t^{2}. \end{aligned}}\tag{1}\]

הנגזרת לפי $t$ תֵּתן לנו את רכיבי המהירות; הנגזרת השנייה את התאוצה ($-g\hat y$) – בדיוק כמתואר בתרגיל 3 .

---

3. זמן המעוף הכולל

הקליע נוחת כאשר $y(t)=0$ (מעבר מלבד $t=0$):

\[t_{\!\text{land}}=\frac{2v_{0y}}{g}=\frac{2}{9.81}=0.2039\;\text{s}.\]

---

4. טווח אופקי (range)

\[R = x(t_{\!\text{land}})= v_{0x}t_{\!\text{land}} =1.732\cdot 0.2039 = 0.353\;\text{m}.\]

---

5. גובה מירבי

ה‐$y$ ‑מהירות מתאפסת בשיא:

\[t_{h}=\frac{v_{0y}}{g}=0.1019\;\text{s}.\]

גובה:

\[y_{\max}=v_{0y}t_h-\tfrac12gt_h^{2} =0.102-4.905\cdot(0.102)^{2}=0.051\;\text{m}.\]

מיקום אופקי בשיא: $x_h=v_{0x}t_h=1.732\cdot0.102=0.177\;\text{m}$.

---

6. מרחק מהראשית וזווית הנטייה בזמן כלשהו

עבור כל $t$:

\[\begin{aligned} r(t) &= \sqrt{x^{2}(t)+y^{2}(t)},\\[10pt] \varphi(t) &= \tan^{-1}\!\Bigl(\tfrac{y(t)}{x(t)}\Bigr). \end{aligned}\tag{2}\]

לדוגמה בשיא הגובה:

\[r_h=\sqrt{0.177^{2}+0.051^{2}}=0.184\;\text{m},\qquad \varphi_h=\tan^{-1}\!\Bigl(\tfrac{0.051}{0.177}\Bigr)=16.0^{\circ}.\]

---

שאלה 5 מהבלוג - הולך‑רגל וקרוסלה (2)

נתוני השאלה

• הולך‑רגל:

  \[\boxed{\;\vec r_1(t)=\bigl(4t,\;0\bigr)\;}\]

  כלומר מהירות קבועה $v_p=4\;\text{m/s}$ לאורך ציר $x$.

• הנער על הקרוסלה:

  \[\boxed{\;\vec r_2(t)=\bigl(2\sin 3t,\;2\cos 3t\bigr)\;}\]

  תנועה מעגלית ברדיוס $R=2\;\text{m}$ ומהירות זוויתית $\omega=3\;\text{rad/s}$.

1. מה מייצגתת כאן הספרה $4$ ומה יחידותיה?
2. מה מייצגתת כאן הספרה $2$ ומה יחידותיה, מה מייצגת הספרה $3$ ומה יחידותיה?
3. קבלו את הוקטור $r_{2\to1}$ (מ‑$2$ אל $1$) המייצג את האופן שבו רואה הנער את הולך הרגל.
4. קבלו את הזווית שבה רואה הולך הרגל את הנער בכל רגע ורגע.

א-ב. פירוש הקבועים ויחידותיהם

קבוע	משמעות	יחידות
$4$	מהירות קווית של ההולך‑רגל $v_p$	$\text{m·s}^{-1}$
$2$	רדיוס מסלול הקרוסלה $R$	$\text{m}$
$3$	מהירות זוויתית של הנער $\omega$	$\text{rad·s}^{-1}$

טיפ מה-AI: הפונקציות $\sin,\cos$ “מצפות” לארגומנט ברדיאנים, ולכן $\omega$ ב‑$\mathrm{rad/s}$.

---

ג. וקטור המקום היחסי — “איך רואה הנער (2) את הולך-הרגל (1)”

הגדרה והמשמעות הפיזיקלית

וקטור המקום היחסי $\vec{r}_{2\to1}$ מתאר את המיקום של גוף אחד ביחס לגוף אחר. הוא מוגדר כדלקמן:

\[\boxed{\vec{r}_{2\to1}(t) = \vec{r}_1(t) - \vec{r}_2(t)}\]

כאשר:

• $\vec{r}_{2\to1}$ הוא וקטור המקום מהנער (2) אל הולך-הרגל (1)
• קצה החץ בנער ← ראשו בהולך-הרגל

יישום על המקרה שלנו

בהינתן וקטורי המקום של שני הגופים:

• הולך-הרגל (1) נע בקו ישר: $\vec{r}_1(t) = (4t, 0)$
• הנער (2) נע במסלול מעגלי: $\vec{r}_2(t) = (2\sin(3t), 2\cos(3t))$

נחשב את וקטור המקום היחסי:

\[\begin{aligned} \vec{r}_{2\to1}(t) &= \vec{r}_1(t) - \vec{r}_2(t) \\[10pt] &= (4t, 0) - (2\sin(3t), 2\cos(3t)) \\[10pt] &= (4t - 2\sin(3t), -2\cos(3t)) \end{aligned}\]

ניתוח רכיבי הווקטור היחסי

\[\boxed{\vec{r}_{2\to1}(t) = (4t - 2\sin(3t), -2\cos(3t))}\]

רכיב וקטורי	ביטוי מתמטי	המשמעות הפיזיקלית
$x_{2\to1}(t)$	$4t - 2\sin(3t)$	שילוב של תנועה קווית ותנודה מחזורית
$y_{2\to1}(t)$	$-2\cos(3t)$	תנודה מחזורית טהורה (מעלה-מטה)

הדגמה חזותית

וקטור המקום היחסי מתאר כיצד הולך-הרגל נראה מנקודת המבט של הנער. כפי שניתן לראות באיור, הוא מחושב על ידי החסרת וקטור המקום של הנער מווקטור המקום של הולך-הרגל.

---

ד. פתרון: הזווית שבה רואה הולך-הרגל את הנער

א. הגדרת הבעיה

עלינו לחשב את הזווית שבה רואה הולך-הרגל את הנער בכל רגע נתון. כזכור:

• הולך-הרגל (1) נמצא במיקום: $\vec{r}_1(t) = (4t, 0)$
• הנער (2) נמצא במיקום: $\vec{r}_2(t) = (2\sin(3t), 2\cos(3t))$

ב. גישה לפתרון

בדומה לחישוב הקודם, נצטרך למצוא את וקטור המקום היחסי, אבל הפעם מנקודת המבט של הולך-הרגל:

\[\vec{r}_{1\to2}(t) = \vec{r}_2(t) - \vec{r}_1(t)\]

הזווית שאנו מחפשים היא הזווית בין וקטור זה לבין הכיוון החיובי של ציר ה-$x$ (שהוא כיוון הייחוס מנקודת מבטו של הולך-הרגל).

ג. חישוב וקטור המקום היחסי

מציבים את וקטורי המקום של שני הגופים:

\[\begin{aligned} \vec{r}_{1\to2}(t) &= \vec{r}_2(t) - \vec{r}_1(t) \\[10pt] &= (2\sin(3t), 2\cos(3t)) - (4t, 0) \\[10pt] &= (2\sin(3t) - 4t, 2\cos(3t)) \end{aligned}\]

ד. חישוב הזווית

הזווית בין וקטור לציר ה-$x$ החיובי נתונה על ידי:

\[\theta(t) = \arctan2(y, x) = \arctan2(2\cos(3t), 2\sin(3t) - 4t)\]

כאשר הפונקציה $\arctan2$ מחזירה זווית בטווח $[-\pi, \pi]$ בהתאם לרביע שבו נמצא הוקטור.

הנוסחה הכללית לחישוב הזווית בכל זמן t:

\[\theta(t) = \arctan2(2\cos(3t), 2\sin(3t) - 4t)\]

פתרון תרגיל מס׳ 4 בפיזיקה - קינמטיקה

תאריך: 25/04/2025

שאלה 1: מציאת כוח קבוע

מצאו את הכוח הקבוע הדרוש כדי להאיץ מסה של 10 טון מ־54 קמ״ש ל־108 קמ״ש לאורך קו ישר, במשך 5 דקות.

שלב 1: המרת יחידות

• נמיר את המסה מטונות לק”ג: 10 טון = 10,000 ק”ג

• נמיר את המהירויות מקילומטר לשעה למטרים לשנייה:

  \[\boxed{ \begin{aligned} 54 \, \mathrm{km/h} &= 54 \times \frac{1000}{3600} = 15 \, \mathrm{m/s} \\ 108 \, \mathrm{km/h} &= 108 \times \frac{1000}{3600} = 30 \, \mathrm{m/s} \end{aligned} }\]

• נמיר את הזמן מדקות לשניות:

  \[\boxed{ \begin{aligned} 5 \, \mathrm{minutes} &= 5 \times 60 = 300 \, \mathrm{seconds} \end{aligned} }\]

שלב 2: חישוב התאוצה

התאוצה היא קצב השינוי במהירות. נשתמש בנוסחה:

\[a = \frac{v_f - v_i}{t}\]

כאשר:

• $v_f$ היא המהירות הסופית
• $v_i$ היא המהירות ההתחלתית
• $t$ הוא הזמן שעבר

נציב:

\[a = \frac{30 - 15}{300} = \frac{15}{300} = 0.05 \left[\frac{\text{m}}{\text{s}^2}\right]\]

שלב 3: חישוב הכוח

לפי החוק השני של ניוטון, הכוח שווה למסה כפול התאוצה:

\[F = m \times a\]

נציב:

\[F = 10,000 \times 0.05 = 500 \left[\text{N}\right]\]

הסבר: הכוח הדרוש הוא 500 ניוטון. כוח זה צריך להיות מופעל באופן קבוע במשך 5 דקות כדי להגדיל את מהירות העצם מ-54 קמ״ש ל-108 קמ״ש. בפיזיקה, כוח הוא מה שגורם לשינוי במצב התנועה של גוף. ככל שהמסה גדולה יותר, יש צורך בכוח גדול יותר כדי לייצר את אותה התאוצה.

---

שאלה 2: נושאת מטוסים מול זבוב

א. איזה כוח נדרש לעצור נושאת מטוסים של 100,000 טון מ־40 קמ״ש לעצירה תוך 10 דקות?

שלב 1: המרת יחידות לנושאת המטוסים

• נמיר את המסה מטונות לק”ג: 100,000 טון = 100,000,000 ק”ג
• נמיר את המהירות מק”מ/שעה למ’/שנייה: $40 \, \mathrm{km/h} = 40 \times \frac{1000}{3600} \approx 11.11$ מ’/שנייה
• נמיר את הזמן מדקות לשניות: 10 דקות = $10 \times 60 = 600$ שניות

שלב 2: חישוב התאוצה של נושאת המטוסים

מכיוון שאנחנו מעוניינים לעצור את נושאת המטוסים, המהירות הסופית היא אפס:

\[a = \frac{v_f - v_i}{t} = \frac{0 - 11.11}{600} = \frac{-11.11}{600} \approx -0.01852 \left[\frac{\text{m}}{\text{s}^2}\right]\]

הסימן השלילי מציין האטה (תאוצה שלילית).

שלב 3: חישוב הכוח לעצירת נושאת המטוסים

\[F = m \times a = 100,000,000 \times (-0.01852) = -1,852,000 \left[\text{N}\right]\]

מכיוון שאנחנו מחפשים את גודל הכוח, נתייחס לערך המוחלט: 1,852,000 ניוטון.

הסבר: נדרש כוח של כ-1.85 מיליון ניוטון כדי לעצור נושאת מטוסים ענקית. זהו כוח עצום! דמיינו כאילו אתם דוחפים 185,000 ק”ג (משקל של כ-185 מכוניות) כנגד כוח הכבידה.

ב. כמה זמן ייקח לעצור זבוב של גרם אחד באותה מהירות, עם אותו כוח?

שלב 1: המרת יחידות לזבוב

• נמיר את מסת הזבוב מגרמים לק”ג: 1 גרם = 0.001 ק”ג

שלב 2: חישוב התאוצה של הזבוב

כאשר אותו כוח (1,852,000 ניוטון) פועל על הזבוב, התאוצה תהיה:

\[a = \frac{F}{m} = \frac{1,852,000}{0.001} = 1,852,000,000 \left[\frac{\text{m}}{\text{s}^2}\right]\]

שלב 3: חישוב הזמן לעצירת הזבוב

\[t = \frac{v_f - v_i}{a} = \frac{0 - 11.11}{1,852,000,000} \approx -6 \times 10^{-9} \left[\text{s}\right]\]

הסימן השלילי מציין את כיוון התנועה. לכן, הזמן הנדרש הוא כ-6 ננו-שניות.

הסבר: עם אותו כוח שנדרש לעצור נושאת מטוסים, זבוב קטן ייעצר כמעט מיידית - תוך פחות מאחד חלקי מיליארד של שנייה! זוהי המחשה מדהימה של החוק השני של ניוטון: $F = ma$. ככל שהמסה קטנה יותר, התאוצה גדולה יותר כאשר מפעילים אותו כוח.

---

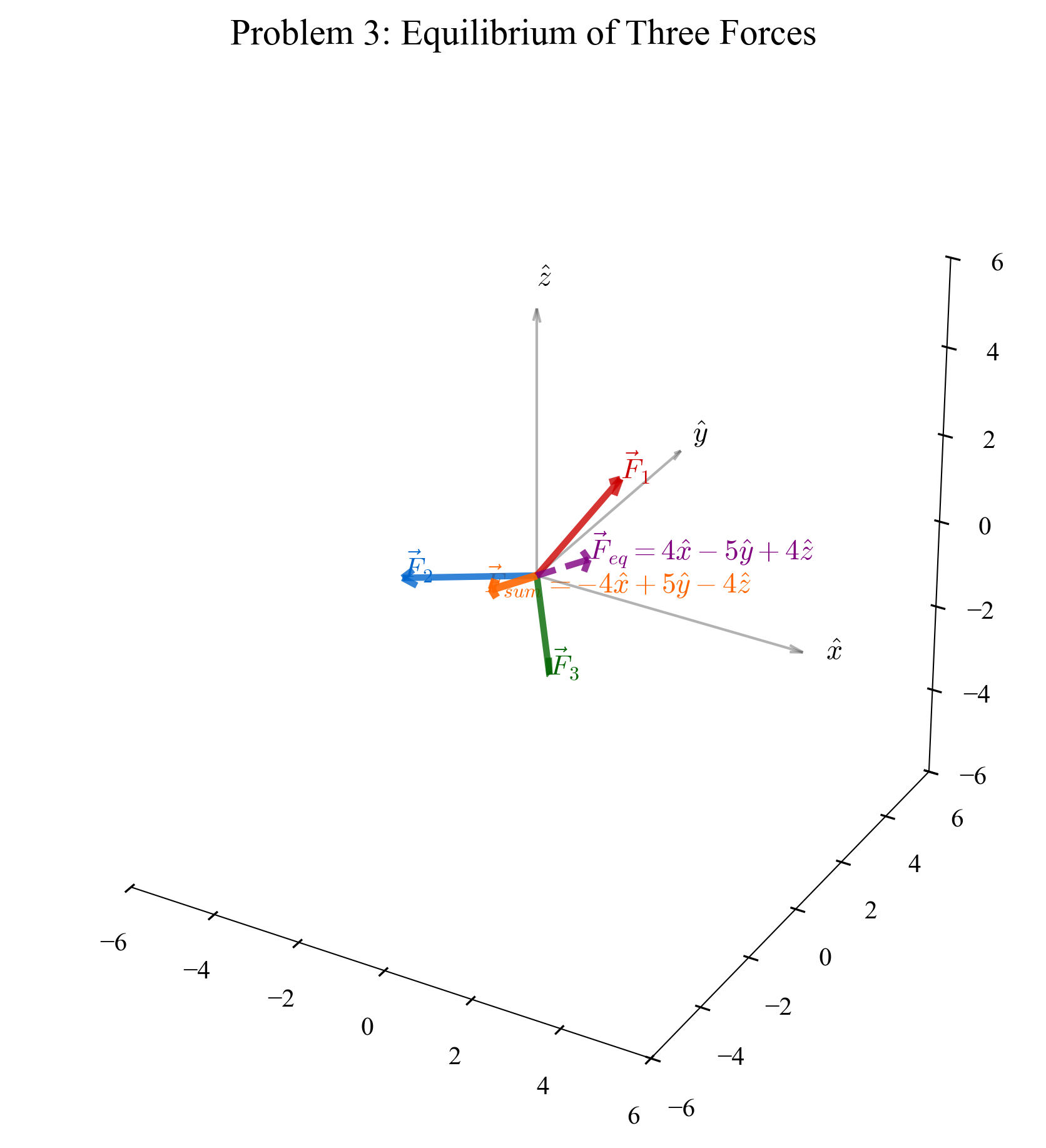
שאלה 3: סכום כוחות

נתון חלקיק עליו פועלים שלושת הכוחות:

\[\begin{aligned} \vec{F}_1 &= 3\hat{x} - 2\hat{y} + 4\hat{z} \\[10pt] \vec{F}_2 &= -5\hat{x} + 3\hat{y} - 3\hat{z} \\[10pt] \vec{F}_3 &= -2\hat{x} + 4\hat{y} - 5\hat{z} \end{aligned}\]

1. א. איזה כוח יש להפעיל על החלקיק כדי שוקטור המהירות שלו יישאר קבוע?
2. בהנחה שהכוח הזה לא מופעל, מה יהיה וקטור התאוצה של החלקיק? ומה גודלו?

הפתרון לחלק א’ - מציאת הכוח הנדרש

שלב 1: הבנת העיקרון הפיזיקלי

לפי החוק הראשון של ניוטון, אם החלקיק נע במהירות קבועה (כלומר, וקטור המהירות שלו אינו משתנה), סכום הכוחות הפועלים עליו חייב להיות אפס.

שלב 2: חישוב סכום הכוחות הנתונים

נחשב את סכום שלושת הכוחות הנתונים:

\[\vec{F}_{sum} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3\]

נחבר את המרכיבים בכל אחד מהכיוונים בנפרד:

• בכיוון $\hat{x}$: $3 + (-5) + (-2) = 3 - 5 - 2 = -4$
• בכיוון $\hat{y}$: $(-2) + 3 + 4 = -2 + 3 + 4 = 5$
• בכיוון $\hat{z}$: $4 + (-3) + (-5) = 4 - 3 - 5 = -4$

מכאן:

\[\vec{F}_{sum} = -4\hat{x} + 5\hat{y} - 4\hat{z}\]

שלב 3: מציאת הכוח הנדרש

כדי שסכום הכוחות יהיה אפס, עלינו להפעיל כוח שהוא ההופכי של סכום הכוחות הנתונים:

\[\begin{aligned} \vec{F}_{neended} &= -\vec{F}_{sum} \\[10pt] &= -(-4\hat{x} + 5\hat{y} - 4\hat{z}) \\[10pt] &= 4\hat{x} - 5\hat{y} + 4\hat{z} \end{aligned}\]

הסבר: כדי לשמור על מהירות קבועה, עלינו להפעיל כוח שיבטל בדיוק את השפעת כל הכוחות האחרים. זהו יישום ישיר של החוק הראשון של ניוטון, הקובע שגוף ישמור על מצב התנועה שלו אלא אם כן פועל עליו כוח חיצוני.

הפתרון לחלק ב’ - חישוב התאוצה

שלב 1: הבנת העיקרון הפיזיקלי

אם הכוח שמצאנו בחלק א’ אינו מופעל, אז לפי החוק השני של ניוטון, סכום הכוחות יגרום לתאוצה של החלקיק.

שלב 2: חישוב וקטור התאוצה

בהנחה שמסת החלקיק היא $m$, וקטור התאוצה יהיה: $\vec{a} = \frac{\vec{F}_{sum}}{m} = \frac{-4\hat{x} + 5\hat{y} - 4\hat{z}}{m}$

במקרה זה, אם לא נתונה המסה, נניח $m = 1$ ק”ג לשם פשטות:

\[\vec{a} = -4\hat{x} + 5\hat{y} - 4\hat{z} \left[\frac{\text{m}}{\text{s}^2}\right]\]

שלב 3: חישוב גודל וקטור התאוצה

גודל וקטור התאוצה מחושב לפי נוסחת המרחק במרחב תלת-ממדי:

\[\begin{aligned} \vert \vec{a}| &= \sqrt{a_x^2 + a_y^2 + a_z^2} \\[10pt] &= \sqrt{(-4)^2 + 5^2 + (-4)^2} \\[10pt] &= \sqrt{16 + 25 + 16} = \sqrt{57} \approx 7.55 \left[\frac{\text{m}}{\text{s}^2}\right] \end{aligned}\]

הסבר: אם לא נפעיל את הכוח המאזן, החלקיק יאיץ בכיוון שנקבע על ידי סכום הכוחות. התאוצה תהיה בעוצמה של כ-7.55 מ’/שנייה². זה אומר שבכל שנייה, מהירות החלקיק תשתנה ב-7.55 מ’/שנייה בכיוון שחישבנו. אפשר לדמיין זאת כמו מכונית שמאיצה מ-0 ל-100 קמ״ש בכ-3.7 שניות - זוהי תאוצה משמעותית!

---

שאלה 4: תנועה בנפילה חופשית

נניח שגוף שמסתו $m$ נופל בקרבת פני כדור הארץ בתאוצה קבועה של:

\[g \approx 10~\left[\frac{\text{m}}{\text{s}^2}\right]\]

נבחר את ציר x להיות אנכי כלפי מטה.

• א. הראו שמהירותו בכל זמן $t$ לאחר מכן היא:

  \[v(t) = v_0 + g(t - t_0)\]

  כאשר:

  • $v_0 = v(t_0)$
  • רמז: $\frac{\Delta v}{\Delta t} = g$

• ב. הראו:

  \[x(t) = x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2\]

  כאשר:

  • $x_0 = x(t_0)$
  • $\frac{dx}{dt} = v(t)$

• ג. לתוך פיר בעומק 500 מטר, הושלכה אבן במהירות התחלתית של שני מטר לשנייה. בשעה 10:00 בבוקר (נניח $t_0 = 0$). חשבו:

  1. מהי מהירות האבן בשנייה השלישית?
  2. איפה היא נמצאת בזמן זה?
  3. מה הדרך שהיא עברה בין השנייה הרביעית לחמישית?
  4. כמה זמן ייקח לה להגיע לתחתית?

א. הוכחת נוסחת המהירות $v(t)=v_0 + g(t - t_0)$

שלב 1: הבנת ההגדרות הבסיסיות

תאוצה מוגדרת כקצב השינוי של המהירות ביחס לזמן:

\[a = \frac{\Delta v}{\Delta t}\]

במקרה של נפילה חופשית, התאוצה קבועה ושווה ל-$g$:

\[\frac{\Delta v}{\Delta t} = g\]

שלב 2: ניסוח משוואה דיפרנציאלית ואינטגרציה

אם התאוצה קבועה, נוכל לכתוב:

\[\frac{dv}{dt} = g\]

נבצע אינטגרציה על שני צדי המשוואה:

\[\int_{t_0}^{t} \frac{dv}{dt} dt = \int_{t_0}^{t} g dt\]

מימין נקבל:

\[\int_{t_0}^{t} g dt = g(t - t_0)\]

משמאל נקבל:

\[\int_{t_0}^{t} \frac{dv}{dt} dt = \int_{v_0}^{v(t)} dv = v(t) - v_0\]

נשלב את התוצאות:

\[v(t) - v_0 = g(t - t_0)\] \[v(t) = v_0 + g(t - t_0)\]

הסבר: נוסחה זו מראה כיצד המהירות משתנה עם הזמן תחת תאוצה קבועה. היא אומרת לנו שהמהירות בזמן $t$ שווה למהירות ההתחלתית $v_0$ בתוספת המהירות שנוספה כתוצאה מהתאוצה. המהירות הנוספת היא מכפלה של התאוצה $g$ בזמן שחלף $(t - t_0)$.

ב. הוכחת נוסחת המיקום $x(t)=x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2$

שלב 1: שימוש בקשר בין מהירות למיקום

לפי ההגדרה, מהירות היא קצב השינוי של המיקום ביחס לזמן:

\[v(t) = \frac{dx}{dt}\]

שלב 2: הצבת נוסחת המהירות ואינטגרציה

נציב את הנוסחה שמצאנו בחלק א’:

\[\frac{dx}{dt} = v_0 + g(t - t_0)\]

נבצע אינטגרציה על שני צדי המשוואה:

\[\int_{t_0}^{t} \frac{dx}{dt} dt = \int_{t_0}^{t} [v_0 + g(t - t_0)] dt\]

משמאל נקבל:

\[\int_{t_0}^{t} \frac{dx}{dt} dt = \int_{x_0}^{x(t)} dx = x(t) - x_0\]

מימין נקבל:

\[\begin{aligned} \int_{t_0}^{t} [v_0 + g(t - t_0)] dt &= v_0 \int_{t_0}^{t} dt + g \int_{t_0}^{t} (t - t_0) dt \\[10pt] &= v_0 (t - t_0) + g \int_{t_0}^{t} (t - t_0) dt \end{aligned}\]

נחשב את האינטגרל השני:

\[\begin{aligned} \int_{t_0}^{t} (t - t_0) dt &= \int_{t_0}^{t} t dt - t_0 \int_{t_0}^{t} dt = \left[\frac{t^2}{2}\right]_{t_0}^{t} - t_0 (t - t_0) \\[10pt] &= \frac{t^2}{2} - \frac{t_0^2}{2} - t_0 (t - t_0) = \frac{t^2 - t_0^2}{2} - t_0 (t - t_0) \\[10pt] &= \frac{(t + t_0)(t - t_0)}{2} - t_0 (t - t_0) = (t - t_0) \left[\frac{t + t_0}{2} - t_0 \right] \\[10pt] &= (t - t_0) \frac{t + t_0 - 2t_0}{2} = (t - t_0) \frac{t - t_0}{2} = \frac{(t - t_0)^2}{2} \end{aligned}\]

נשלב את התוצאות:

\[x(t) - x_0 = v_0 (t - t_0) + g \frac{(t - t_0)^2}{2}\] \[x(t) = x_0 + v_0 (t - t_0) + \frac{1}{2} g (t - t_0)^2\]

הסבר: נוסחה זו מתארת את המיקום של גוף בזמן $t$ כתלות במיקום ההתחלתי $x_0$, המהירות ההתחלתית $v_0$, והתאוצה $g$. היא מורכבת משלושה חלקים: המיקום ההתחלתי, המרחק שהיה נעבר במהירות קבועה $v_0$, והתוספת עקב התאוצה הקבועה.

ג. פתרון הבעיה המעשית

נתונים:

• עומק הפיר: $500$ מטר
• מהירות התחלתית: $v_0 = 2$ מ’/שנייה (כלפי מטה)
• זמן התחלתי: $t_0 = 0$
• תאוצת הכבידה: $g = 10$ מ’/שנייה²
• מיקום התחלתי: $x_0 = 0$ (נקבע את ראשית הצירים בפתח הפיר)

1. מהירות האבן בשנייה השלישית

נשתמש בנוסחה מחלק א’ כדי למצוא את המהירות בזמן $t = 3$ שניות:

\[\begin{aligned} v(3) &= v_0 + g(3 - 0) \\[10pt] &= 2 + 10 \cdot 3 = 32 \mathrm{[m/s]} \end{aligned}\]

הסבר: האבן מתחילה עם מהירות של 2 מ’/שנייה ומאיצה עקב הכבידה. לאחר 3 שניות, היא צברה 30 מ’/שנייה נוספים, כך שהמהירות הכוללת היא 32 מ’/שנייה.

2. מיקום האבן בשנייה השלישית

נשתמש בנוסחה מחלק ב’ כדי למצוא את המיקום בזמן $t = 3$ שניות:

\[\begin{aligned} x(3) &= x_0 + v_0(3 - 0) + \frac{1}{2}g(3 - 0)^2 \\[10pt] &= 0 + 2 \cdot 3 + \frac{1}{2} \cdot 10 \cdot 3^2 \\[10pt] &= 6 + 5 \cdot 9 = 6 + 45 = 51 \mathrm{[m]} \end{aligned}\]

הסבר: לאחר 3 שניות, האבן נמצאת במרחק של 51 מטר מפתח הפיר. מתוך זה, 6 מטרים הם תוצאה של המהירות ההתחלתית, ו-45 מטרים נוספים הם תוצאה של התאוצה עקב הכבידה.

3. הדרך שנעברה בין השנייה הרביעית לחמישית

נמצא את המיקום בזמן $t = 4$ שניות:

\[\begin{aligned} x(4) &= 0 + 2 \cdot 4 + \frac{1}{2} \cdot 10 \cdot 4^2 \\[10pt] &= 8 + 5 \cdot 16 = 8 + 80 = 88 \left[\text{m}\right] \end{aligned}\]

נמצא את המיקום בזמן $t = 5$ שניות:

\[\begin{aligned} x(5) &= 0 + 2 \cdot 5 + \frac{1}{2} \cdot 10 \cdot 5^2 \\[10pt] &= 10 + 5 \cdot 25 = 10 + 125 = 135 \left[\text{m}\right] \end{aligned}\]

הדרך שנעברה בין השנייה הרביעית לחמישית היא:

\[\Delta x = x(5) - x(4) = 135 - 88 = 47 \mathrm{[m]}\]

הסבר: בין השנייה הרביעית לחמישית, האבן עברה מרחק של 47 מטר. זה יותר מהמרחק שהיא עברה בשנייה הקודמת, כי האבן מאיצה ונעה מהר יותר עם כל שנייה שחולפת.

4. הזמן שייקח לאבן להגיע לתחתית הפיר

נרצה למצוא את הזמן $t$ כך שהמיקום $x(t) = 500$ (עומק הפיר):

\[500 = 0 + 2t + \frac{1}{2} \cdot 10 \cdot t^2 = 2t + 5t^2\] \[5t^2 + 2t - 500 = 0\]

נפתור את המשוואה הריבועית באמצעות נוסחת השורשים:

\[t = \frac{-2 \pm \sqrt{4 + 4 \cdot 5 \cdot 500}}{2 \cdot 5} = \frac{-2 \pm \sqrt{4 + 10000}}{10} = \frac{-2 \pm \sqrt{10004}}{10}\] \[t = \frac{-2 \pm 100.02}{10} \approx \frac{-2 + 100.02}{10} \approx 9.8 \mathrm{[s]}\]

(הפתרון השני, עם הסימן שלילי, אינו פיזיקלי כי אנחנו מחפשים זמן חיובי.)

הסבר: ייקח לאבן כ-9.8 שניות להגיע לתחתית הפיר בעומק 500 מטר. בזמן זה, האבן תאיץ בהדרגה עקב הכבידה ותגביר את מהירותה, עד שתגיע לתחתית.

---

שאלה 5: קשר בין העתק למהירות

הראו שאם גוף נע בתאוצה קבועה, מתקיים:

\[v^2(t) = v_0^2 + 2g\Delta x\]

זהו קשר שימושי כאשר אין מידע על הזמן, אלא רק על מהירויות והעתקים.

שלב 1: שימוש בנוסחאות הקיימות

מהשאלה הקודמת, יש לנו את הנוסחאות הבאות עבור גוף הנופל בתאוצה קבועה:

• מהירות: $v(t) = v_0 + g(t - t_0)$
• מיקום: $x(t) = x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2$

לשם פשטות, נניח $t_0 = 0$. אז הנוסחאות הופכות ל:

\[v(t) = v_0 + gt\] \[x(t) = x_0 + v_0t + \frac{1}{2}gt^2\]

שלב 2: הגדרת ההעתק

ההעתק $\Delta x$ הוא השינוי במיקום:

\[\Delta x = x(t) - x_0 = v_0t + \frac{1}{2}gt^2\]

שלב 3: מציאת הזמן $t$ מנוסחת המהירות

מהנוסחה של המהירות, אנחנו יכולים לבטא את הזמן $t$:

\[v(t) = v_0 + gt\] \[t = \frac{v(t) - v_0}{g}\]

שלב 4: הצבת הזמן בנוסחת ההעתק

נציב את $t$ בנוסחת ההעתק:

\[\begin{aligned} \Delta x &= v_0 \cdot \frac{v(t) - v_0}{g} + \frac{1}{2}g \cdot \left(\frac{v(t) - v_0}{g}\right)^2 \\[10pt] &= \frac{v_0(v(t) - v_0)}{g} + \frac{1}{2} \cdot \frac{(v(t) - v_0)^2}{g} \\[10pt] &= \frac{1}{g} \left[v_0(v(t) - v_0) + \frac{1}{2}(v(t) - v_0)^2\right] \end{aligned}\]

שלב 5: פיתוח אלגברי

נפתח את הסוגריים בביטוי האחרון:

\[\begin{aligned} \Delta x &= \frac{1}{g} \left[v_0v(t) - v_0^2 + \frac{1}{2}v(t)^2 - v_0v(t) + \frac{1}{2}v_0^2\right] \\[10pt] &= \frac{1}{g} \left[\frac{1}{2}v(t)^2 - \frac{1}{2}v_0^2\right]\\[10pt] &= \frac{1}{2g} \left[v(t)^2 - v_0^2\right] \end{aligned}\]

שלב 6: אלגברה סופית

נכפיל את שני הצדדים ב-$2g$:

\[2g \cdot \Delta x = v(t)^2 - v_0^2\] \[v(t)^2 = v_0^2 + 2g\Delta x\]

הסבר: נוסחה זו מקשרת בין ריבוע המהירות, ריבוע המהירות ההתחלתית, וההעתק (השינוי במיקום). היא מאפשרת לנו לחשב את המהירות הסופית ללא צורך לדעת את הזמן שעבר. זוהי נוסחה שימושית במיוחד בבעיות מעשיות, כמו חישוב מהירות גוף לאחר שנפל ממגדל בגובה ידוע, או מהירות רכב לאחר שעבר מרחק מסוים בתאוצה קבועה.

יתרונה הגדול של נוסחה זו הוא שהיא מאפשרת לנו לקשר ישירות בין מהירויות והעתקים, ללא התייחסות לזמן. במקרים רבים, קל יותר למדוד מרחקים ומהירויות מאשר זמנים מדויקים, ולכן זוהי נוסחה פרקטית מאוד בפיזיקה יישומית ובהנדסה.

---

שאלה 6: תנועה אנכית כלפי מעלה

זורקים אבן כלפי מעלה במהירות התחלתית של $v_0 = 17~$ מטר לשנייה.

• א. מהי התאוצה בנקודת שיא הגובה?
• ב. מהי המהירות בנקודת שיא הגובה?
• ג. לאיזה גובה תגיע האבן?
• ד. באיזו מהירות תחזור האבן לידיו של הזורק?
• ה. אם היא פוגעת בקרקע מטר אחד מתחת לידו — באיזו מהירות היא פוגעת?

א. התאוצה בנקודת שיא הגובה

שלב 1: הבנת הכוחות הפועלים

כאשר זורקים אבן כלפי מעלה, הכוח היחיד הפועל עליה הוא כוח הכבידה. כוח זה פועל תמיד כלפי מטה, ללא קשר למיקום האבן או למהירותה.

שלב 2: יישום החוק השני של ניוטון

לפי החוק השני של ניוטון, התאוצה שווה לכוח חלקי מסה:

\[a = \frac{F}{m} = \frac{\cancel{m}g}{\cancel{m}} = g\]

כיוון שגוף הנמצא בקרבת פני כדור הארץ חווה תאוצת כבידה של כ-10 מ’/שנייה² כלפי מטה, התאוצה של האבן בכל נקודה, כולל נקודת שיא הגובה, היא:

\[a = -g = -10~\left[\frac{\text{m}}{\text{s}^2}\right]\]

(הסימן השלילי מציין שהתאוצה פועלת בכיוון ההפוך לציר החיובי, שהוא כלפי מעלה במקרה זה)

הסבר: גם כאשר האבן מגיעה לשיא הגובה ו”עוצרת” לרגע, כוח הכבידה ממשיך לפעול עליה. לכן התאוצה אינה משתנה ונשארת $-10 \mathrm{[m/s^2]}$ לאורך כל המסלול.

ב. המהירות בנקודת שיא הגובה

שלב 1: הבנת מה מאפיין את נקודת שיא הגובה

בנקודת שיא הגובה, האבן מגיעה למצב שבו היא משנה את כיוון תנועתה - מתנועה כלפי מעלה לתנועה כלפי מטה. בנקודה זו, המהירות האנכית חייבת להיות אפס.

שלב 2: המסקנה לגבי המהירות

\[v = 0~\mathrm{[m/s]}\]

הסבר: במצב של תנועה אנכית, בנקודת שיא הגובה האבן “עוצרת” באופן רגעי לפני שהיא מתחילה לרדת. זהו מצב שבו המהירות האנכית שווה לאפס. אם הייתה לאבן מהירות שאינה אפס בנקודה זו, היא הייתה ממשיכה לעלות גבוה יותר.

ג. הגובה שאליו תגיע האבן

שלב 1: שימוש בנוסחת הקשר בין מהירות להעתק

נשתמש בנוסחה שהוכחנו בשאלה 5:

\[v^2 = v_0^2 - 2g\Delta x\]

(הסימן התחלף מ”+” ל”-“ כי התאוצה במקרה הזה בכיוון ההפוך לתנועה ההתחלתית)

שלב 2: הצבת הנתונים וחישוב הגובה

בנקודת שיא הגובה, המהירות היא אפס ($v = 0$). נציב:

\[\begin{aligned} 0 &= v_0^2 - 2g\Delta x \\[10pt] 2g\Delta x &= v_0^2 \\[10pt] \Delta x &= \frac{v_0^2}{2g} = \frac{17^2}{2 \cdot 10} = \frac{289}{20} = 14.45~\mathrm{[m]} \end{aligned}\]

הסבר: כאשר זורקים אבן כלפי מעלה, האנרגיה הקינטית (שקשורה למהירות) הופכת לאנרגיה פוטנציאלית (שקשורה לגובה). נוסחה זו מבטאת את שימור האנרגיה - האבן תעלה עד לגובה שבו כל האנרגיה הקינטית ההתחלתית שלה הפכה לאנרגיה פוטנציאלית.

ד. מהירות האבן בחזרה לידיו של הזורק

שלב 1: שימוש בעקרון שימור האנרגיה

במערכת שבה אין חיכוך או התנגדות אוויר, האנרגיה המכנית נשמרת. זה אומר שכאשר האבן חוזרת לגובה ההתחלתי, מהירותה (בערך מוחלט) תהיה זהה למהירות ההתחלתית.

שלב 2: קביעת הכיוון

מכיוון שהאבן חוזרת לידיו של הזורק, היא נעה כלפי מטה, כלומר בכיוון ההפוך למהירות ההתחלתית.

שלב 3: המסקנה

המהירות שבה האבן תחזור לידיו של הזורק היא:

\[v = -v_0 = -17~\text{m/s}\]

(הסימן השלילי מציין שהמהירות היא בכיוון ההפוך לציר החיובי)

הסבר: בתנועה אנכית תחת השפעת הכבידה בלבד (ללא התנגדות אוויר), המהירות בחזרה לנקודת המוצא תהיה שווה בגודלה למהירות ההתחלתית אך בכיוון הפוך. זוהי תוצאה ישירה של שימור האנרגיה.

ה. מהירות הפגיעה בקרקע מטר אחד מתחת ליד

שלב 1: שימוש בנוסחת הקשר בין מהירות להעתק

נשתמש שוב בנוסחה:

\[v^2 = v_0^2 + 2g\Delta x\]

הפעם הסימן הוא חיובי כי התאוצה והתנועה הן באותו כיוון (כלפי מטה).

שלב 2: הצבת הנתונים

• $v_0 = 17~\mathrm{[m/s]}$ (המהירות ההתחלתית)
• $g = 10~\left[\frac{\text{m}}{\text{s}^2}\right]$ (תאוצת הכבידה)
• $\Delta x = 1~\mathrm{[m]}$ (העתק נוסף מתחת לנקודת הזריקה)

$v^2 = 17^2 + 2 \cdot 10 \cdot 1 = 289 + 20 = 309$ $v = \sqrt{309} \approx 17.58~\mathrm{[m/s]}$

מכיוון שהאבן נעה כלפי מטה, המהירות היא שלילית:

\[v \approx -17.58~\text{m/s}\]

הסבר: כאשר האבן ממשיכה מעבר לנקודת הזריקה, היא צוברת אנרגיה קינטית נוספת עקב הכבידה, ולכן מהירותה גדלה. ככל שהאבן נופלת למרחק גדול יותר, מהירותה תגדל בהתאם.

---

שאלה 7: תנועה היפרבולית במישור

וקטור המהירות:

\[\vec{v}(t) = 2\cosh(3t)\hat{x} + 2\sinh(3t)\hat{y}\]

• א. מהי מהירותו ההתחלתית של הגוף ותאוצתו בזמן $t = 0$?
• ב. הניחו כי: $\vec{r}(0) = 3\hat{x} + 3\hat{y}$ מצאו ביטוי לוקטור המקום $\vec{r}(t)$.
• ג. מה גודלו של הכוח הפועל על הגוף בכל רגע? \(\vert \vec{F}(t)\vert = m\vert \vec{a}(t)\vert\), \(m = 10~\text{kg}\)
• ד. מה כיוון הכוח בכל רגע?

א. המהירות ההתחלתית והתאוצה בזמן $t = 0$

שלב 1: חישוב המהירות ההתחלתית:

המהירות ההתחלתית היא וקטור המהירות בזמן $t = 0$:

\[\begin{aligned} \vec{v}(0) &= 2\cosh(3 \cdot 0)\hat{x} + \cancel{2\sinh(3 \cdot 0)\hat{y}} \\[10pt] &= 2 \cdot 1 \cdot \hat{x} + 2 \cdot 0 \cdot \hat{y} \\[10pt] &= 2\hat{x} \end{aligned}\]

כלומר, מהירותו ההתחלתית של הגוף היא $\boxed{2~\text{m/s}}$ בכיוון ציר ה-$x$ החיובי.

שלב 2: חישוב התאוצה:

התאוצה היא הנגזרת של וקטור המהירות ביחס לזמן:

\[\vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d}{dt}[2\cosh(3t)\hat{x} + 2\sinh(3t)\hat{y}]\]

נגזור כל רכיב:

\[\frac{d}{dt}[2\cosh(3t)] = 2 \cdot 3 \cdot \sinh(3t) = 6\sinh(3t)\] \[\frac{d}{dt}[2\sinh(3t)] = 2 \cdot 3 \cdot \cosh(3t) = 6\cosh(3t)\]

לכן הביטוי הכללי לתאוצה הוא:

\[\boxed{\vec{a}(t) = 6\sinh(3t)\hat{x} + 6\cosh(3t)\hat{y}}\]

נחשב את התאוצה בזמן $t = 0$:

\[\begin{aligned} \vec{a}(0) &= 6\sinh(0)\hat{x} + 6\cosh(0)\hat{y} \\[10pt] &= 6 \cdot 0 \cdot \hat{x} + 6 \cdot 1 \cdot \hat{y} \\[10pt] &= 6\hat{y} \end{aligned}\]

כלומר, התאוצה בזמן $t = 0$ היא $\boxed{6~\text{m/s}^2}$ בכיוון ציר ה-$y$ החיובי.

הסבר: בזמן $t = 0$, הגוף נע במהירות של 2 מטר לשנייה בכיוון ציר ה-$x$ החיובי. באותו רגע, התאוצה שלו היא 6 מטר לשנייה בריבוע בכיוון ציר ה-$y$ החיובי. זה מצביע על כך שהגוף יתחיל לשנות את כיוון התנועה שלו, עם נטייה גוברת בכיוון ציר ה-$y$.

ב. מציאת וקטור המקום $\vec{r}(t)$

המהירות היא הנגזרת של המיקום ביחס לזמן:

\[\vec{v}(t) = \frac{d\vec{r}}{dt}\]

אז כדי למצוא את וקטור המקום, נפעיל אינטגרל על וקטור המהירות. אפשר לפתור ישירות בעזרת אינטגרלת בלתי מסוים, או לחלופין להשתמש באינטגרל מסוים עם גבולות מ-0 עד $t$.

פתרון בעזרת אינטגרל בלתי מסוים

דרך ישירה עם אינטגרל בלתי מוגדר:

\[\vec{r}(t) = \int \vec{v}(t) \, dt = \int [2\cosh(3t)\hat{x} + 2\sinh(3t)\hat{y}] \, dt\]

עבור כל רכיב:

• רכיב x: $\int 2\cosh(3t) \, dt = \frac{2}{3}\sinh(3t) + C_1$
• רכיב y: $\int 2\sinh(3t) \, dt = \frac{2}{3}\cosh(3t) + C_2$

אז:

\[\vec{r}(t) = \left[\frac{2}{3}\sinh(3t) + C_1\right]\hat{x} + \left[\frac{2}{3}\cosh(3t) + C_2\right]\hat{y}\]

עכשיו נשתמש בתנאי ההתחלתי $\vec{r}(0) = 3\hat{x} + 3\hat{y}$:

\[\vec{r}(0) = [0 + C_1]\hat{x} + \left[\frac{2}{3} + C_2\right]\hat{y} = 3\hat{x} + 3\hat{y}\]

לכן:

• $C_1 = 3$
• $\frac{2}{3} + C_2 = 3 \Rightarrow C_2 = \frac{7}{3}$

התוצאה הסופית::

\[\boxed{\vec{r}(t) = \left(3 + \frac{2}{3}\sinh(3t)\right)\hat{x} + \left(\frac{7}{3} + \frac{2}{3}\cosh(3t)\right)\hat{y}}\]

פתרון בעזרת אינטגרל מסוים

נשתמש באינטגרל מסוים כדי למצוא את וקטור המקום $\vec{r}(t)$, כאשר ידוע לנו וקטור המהירות $\vec{v}(t)$.

\[\begin{aligned} \vec{r}(t) &= \vec{r}(0) + \int_{0}^{t} \vec{v}(s) ds \\[10pt] &= \vec{r}(0) + \int_{0}^{t} [2\cosh(3s)\hat{x} + 2\sinh(3s)\hat{y}] ds \end{aligned}\]

נעזר באינטגרלים המוכרים, עבור כל רכיב:

\[\begin{aligned} \int \cosh(ax) dx &= \frac{1}{a} \sinh(ax) + C \\[10pt] \int \sinh(ax) dx &= \frac{1}{a} \cosh(ax) + C \end{aligned}\]

עבור הרכיב בכיוון $\hat{x}$:

\[\begin{aligned} \int_{0}^{t} 2\cosh(3s) ds &= 2 \int_{0}^{t} \cosh(3s) ds \\[10pt] &= 2 \cdot \frac{1}{3}[\sinh(3s)]_{0}^{t} \\[10pt] &= \frac{2}{3}[\sinh(3t) - \sinh(0)] \\[10pt] &= \frac{2}{3}\sinh(3t) \end{aligned}\]

עבור הרכיב בכיוון $\hat{y}$:

\[\begin{aligned} \int_{0}^{t} 2\sinh(3s) ds &= 2 \int_{0}^{t} \sinh(3s) ds \\[10pt] &= 2 \cdot \frac{1}{3}[\cosh(3s)]_{0}^{t} \\[10pt] &= \frac{2}{3}[\cosh(3t) - \cosh(0)] \\[10pt] &= \frac{2}{3}[\cosh(3t) - 1] \end{aligned}\]

נחבר את התוצאות שקיבלנו ונציב $\vec{r}(0) = 3\hat{x} + 3\hat{y}$:

\[\begin{aligned} \vec{r}(t) &= \vec{r}(0) + \frac{2}{3}\sinh(3t)\hat{x} + \frac{2}{3}[\cosh(3t) - 1]\hat{y} \\[10pt] &= 3\hat{x} + 3\hat{y} + \frac{2}{3}\sinh(3t)\hat{x} + \frac{2}{3}[\cosh(3t) - 1]\hat{y} \\[10pt] &= (3 + \frac{2}{3}\sinh(3t))\hat{x} + (3 + \frac{2}{3}\cosh(3t) - \frac{2}{3})\hat{y} \\[10pt] &= (3 + \frac{2}{3}\sinh(3t))\hat{x} + (3 - \frac{2}{3} + \frac{2}{3}\cosh(3t))\hat{y} \\[10pt] &= (3 + \frac{2}{3}\sinh(3t))\hat{x} + (\frac{7}{3} + \frac{2}{3}\cosh(3t))\hat{y} \end{aligned}\]

הסבר: וקטור המקום $\vec{r}(t)$ מתאר את מיקום הגוף בכל רגע. הביטוי שקיבלנו מראה כיצד הגוף נע במישור, עם רכיבים שמשתנים באופן היפרבולי עם הזמן. התנועה מתחילה מהנקודה $(3,3)$ ומתפתחת בהתאם לפונקציות היפרבוליות $\sinh$ ו-$\cosh$.

ג. גודל הכוח בכל רגע

מסעיף 1 מצאנו כי וקטור התאוצה הכללי הוא:

\[\vec{a}(t) = 6\sinh(3t)\hat{x} + 6\cosh(3t)\hat{y}\]

גודלו של וקטור התאוצה הוא:

\[\vert \vec{a}(t)| = \sqrt{(6\sinh(3t))^2 + (6\cosh(3t))^2} = 6\sqrt{\sinh^2(3t) + \cosh^2(3t)}\]

נזכור את הזהות ההיפרבולית:

\[\cosh^2(x) - \sinh^2(x) = 1\]

לכן:

\[\sinh^2(x) + \cosh^2(x) = 2\cosh^2(x) - 1\]

נציב:

\[\vert \vec{a}(t)| = 6\sqrt{2\cosh^2(3t) - 1}\]

נחשב את גודל הכוח לפי החוק השני של ניוטון. נתון כי המסה של הגוף היא $m = 10~\text{kg}$. לפי החוק השני של ניוטון:

\[\begin{aligned} \vert \vec{F}(t)| &= m\vert \vec{a}(t)| \\[10pt] &= 10 \cdot 6\sqrt{2\cosh^2(3t) - 1} \\[10pt] &= 60\sqrt{2\cosh^2(3t) - 1}~\left[\text{N}\right] \end{aligned}\]

הסבר: גודל הכוח גדל עם הזמן, כיוון שהפונקציה $\cosh(3t)$ גדלה עם $t$. ככל שהזמן חולף, הגוף חווה כוח הולך וגדל, מה שגורם לו להאיץ בקצב גובר.

ד. כיוון הכוח בכל רגע

שלב 1: התבוננות בקשר בין כוח לתאוצה

לפי החוק השני של ניוטון, וקטור הכוח ווקטור התאוצה נמצאים באותו כיוון:

\[\vec{F} = m\vec{a}\]

שלב 2: מציאת כיוון התאוצה

כיוון התאוצה נקבע על ידי הווקטור היחידה בכיוון התאוצה:

\[\hat{a}(t) = \frac{\vec{a}(t)}{\vert \vec{a}(t)|} = \frac{6\sinh(3t)\hat{x} + 6\cosh(3t)\hat{y}}{6\sqrt{\sinh^2(3t) + \cosh^2(3t)}} = \frac{\sinh(3t)\hat{x} + \cosh(3t)\hat{y}}{\sqrt{\sinh^2(3t) + \cosh^2(3t)}}\]

שלב 3: מסקנה לגבי כיוון הכוח

כיוון שהכוח והתאוצה הם באותו כיוון, כיוון הכוח בכל רגע יהיה:

\[\hat{F}(t) = \hat{a}(t) = \frac{\sinh(3t)\hat{x} + \cosh(3t)\hat{y}}{\sqrt{\sinh^2(3t) + \cosh^2(3t)}}\]

הסבר: כיוון הכוח משתנה עם הזמן, מתחיל בכיוון ציר ה-$y$ החיובי (כאשר $t = 0$) ומשנה את עצמו בהתאם ליחס בין הפונקציות $\sinh(3t)$ ו-$\cosh(3t)$. ככל ש-$t$ גדל, הרכיב בכיוון $\hat{x}$ גדל, והכוח נוטה יותר לכיוון הראשון של המישור (צפון-מזרח).

---

שאלה 8: טריז וגליל

טריז מסה $M$, גליל מסה $m$, שיפוע $\alpha = 30^\circ$, אין חיכוך.

1. א. כאשר הטריז מקובע

   • מהם הכוחות הנורמליים על הגליל? על הטריז?

2. ב. כאשר הטריז חופשי לנוע

   • הגליל מחליק, הטריז מאיץ ימינה. מצאו את התאוצות $a$ ו־$A$ בהתחשב בקשר: $a = A \tan(\alpha)$

א. כאשר הטריז מקובע - כוחות נורמליים

שלב 1: ניתוח הכוחות על הגליל:

על הגליל פועלים הכוחות הבאים:

1. כוח הכבידה $\vec{W}_g = m\vec{g} = mg\hat{y}$, כלפי מטה בכיוון הציר השלילי של $y$
2. כוח נורמלי $\vec{N}$ מהטריז, בכיוון ניצב למשטח השיפוע

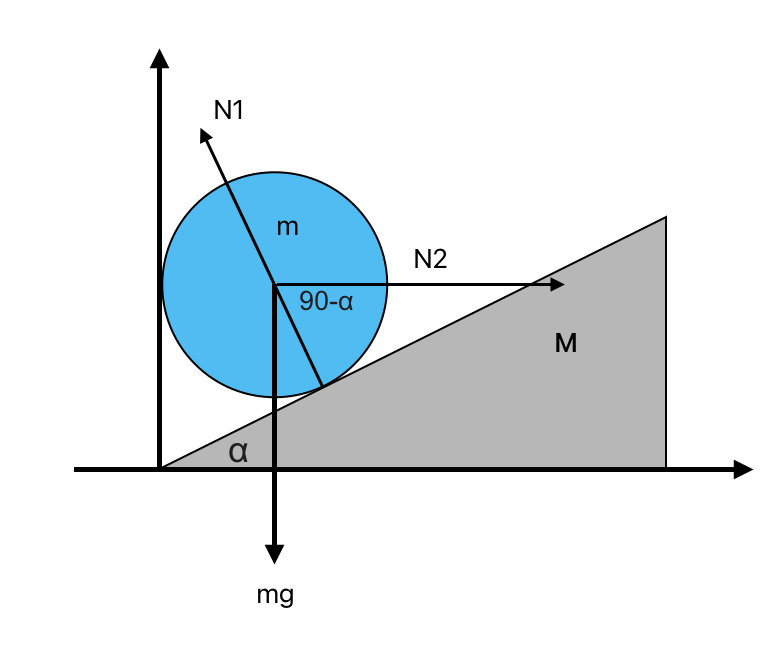
שלב 2: פירוק הכוחות לרכיבים במערכת צירים מתאימה:

נגדיר מערכת צירים כך ש:

• ציר $x’$ מקביל למשטח השיפוע
• ציר $y’$ ניצב למשטח השיפוע

פירוק כוח הכבידה:

• הרכיב במקביל למשטח: $mg\sin\alpha$
• הרכיב בניצב למשטח: $mg\cos\alpha$

שלב 3: יישום החוק השני של ניוטון:

כאשר הטריז מקובע, הגליל ינוע במורד המדרון בתאוצה. בכיוון הניצב למשטח, אין תאוצה:

\[N - mg\cos\alpha = 0\] \[N = mg\cos\alpha = mg\cos(30^\circ) = mg \cdot \frac{\sqrt{3}}{2} \approx 0.866mg\]

שלב 4: כוח נורמלי על הטריז:

על פי החוק השלישי של ניוטון, הכוח שהגליל מפעיל על הטריז שווה בגודלו והפוך בכיוונו לכוח שהטריז מפעיל על הגליל:

\[N_{\text{on }\Delta} = N = mg\cos\alpha \approx 0.866mg\]

הסבר: הכוח הנורמלי על הגליל הוא הכוח שמונע ממנו לחדור לתוך משטח הטריז. גודלו שווה לרכיב כוח הכבידה הניצב למשטח. לפי החוק השלישי של ניוטון, כוח התגובה הזה פועל גם על הטריז, בכיוון ההפוך.

ב. כאשר הטריז חופשי לנוע - מציאת התאוצות

שלב 1: ניתוח הכוחות והתנועה:

כאשר הטריז חופשי לנוע:

• הגליל מחליק במורד השיפוע בתאוצה $a$ (בכיוון $x’$ היחסי לטריז)
• הטריז נע ימינה בתאוצה $A$ (בכיוון $x$ הגלובלי)

נתון שיש קשר בין התאוצות: $a = A \tan(\alpha)$

שלב 2: יישום החוק השני של ניוטון לגליל:

בכיוון המקביל למשטח השיפוע, הכוח היחיד הוא רכיב הכבידה:

\[mg\sin\alpha = m(a_{\text{יחסי}} + A\cos\alpha)\]

כאן $a_{\text{יחסי}}$ היא התאוצה של הגליל ביחס לטריז, ו-$A\cos\alpha$ היא התאוצה הנובעת מתנועת הטריז.

שלב 3: שימוש בקשר בין התאוצות:

מהנתון: $a_{\text{יחסי}} = a = A\tan\alpha$

נציב:

\[\begin{aligned} mg\sin\alpha &= m(A\tan\alpha + A\cos\alpha) \\[10pt] &= mA(\tan\alpha + \cos\alpha) \\[10pt] &= A(\tan\alpha + \cos\alpha) \\[10pt] &= A(\frac{\sin\alpha}{\cos\alpha} + \cos\alpha) \\[10pt] &= A(\frac{\sin\alpha + \cos^2\alpha}{\cos\alpha}) \\[10pt] &= A\frac{\sin\alpha + 1 - \sin^2\alpha}{\cos\alpha} \\[10pt] \end{aligned}\] \[g\sin\alpha \cdot \cos\alpha = A(\sin\alpha + 1 - \sin^2\alpha)\]

שלב 4: פתרון המשוואה:

\[\begin{aligned} A &= \frac{g\sin\alpha \cdot \cos\alpha}{\sin\alpha + 1 - \sin^2\alpha} \\[10pt] &= \frac{g\sin\alpha \cdot \cos\alpha}{1 + \sin\alpha - \sin^2\alpha} \\[10pt] &= \frac{g\sin\alpha \cdot \cos\alpha}{1 + \sin\alpha(1 - \sin\alpha)} \end{aligned}\]

לערך המספרי של $\alpha = 30^\circ$:

\[\sin(30^\circ) = 0.5\] \[\cos(30^\circ) = \frac{\sqrt{3}}{2} \approx 0.866\] \[A = \frac{g \cdot 0.5 \cdot 0.866}{1 + 0.5(1 - 0.5)} = \frac{0.433g}{1 + 0.25} = \frac{0.433g}{1.25} \approx 0.346g\]

שלב 5: חישוב תאוצת הגליל:

מהקשר הנתון:

\[a = A\tan\alpha = 0.346g \cdot \tan(30^\circ) = 0.346g \cdot 0.577 \approx 0.2g\]

הסבר: כאשר הטריז חופשי לנוע, חלק מאנרגיית התנועה של הגליל מועברת לטריז, ולכן הגליל מאיץ בקצב איטי יותר בהשוואה למקרה שבו הטריז מקובע. תאוצת הגליל ביחס לקרקע היא סכום וקטורי של תאוצתו ביחס לטריז ותאוצת הטריז עצמו.

שאלה 9: תנועה בקואורדינטות קוטביות

א. מהן קואורדינטות קוטביות?

• $r(t)$: מרחק מהראשית.
• $\theta(t)$: הזווית עם ציר $x$.

ב. וקטורי היחידה

\[\hat{r}(t) = \cos\theta\hat{x} + \sin\theta\hat{y}\] \[\hat{\theta}(t) = -\sin\theta\hat{x} + \cos\theta\hat{y}\]

הראו כי זוהי מערכת אורתונורמלית.

ג. וקטור המהירות והתאוצה

\[\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta}\] \[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}\]

ד. אם שקול הכוחות הוא

$\vec{F} = F_r\hat{r} + F_\theta\hat{\theta}$

אז לפי חוק שני של ניוטון:

\[F_r\hat{r} + F_\theta\hat{\theta} = m\vec{a}\]

ה. מה קורה כשמסת הגוף משתנה בזמן?

א. הסבר קואורדינטות קוטביות

שלב 1: הגדרת קואורדינטות קוטביות

קואורדינטות קוטביות הן שיטה אלטרנטיבית לתיאור מיקום של נקודה במישור, באמצעות:

1. $r(t)$ - המרחק מהראשית (נקודת המקור של מערכת הצירים)
2. $\theta(t)$ - הזווית בין הקו המחבר את הנקודה לראשית לבין הציר האופקי החיובי (ציר $x$)

שלב 2: הקשר לקואורדינטות קרטזיות

אם נסמן את הקואורדינטות הקרטזיות של נקודה כ-$(x, y)$, אז הקשר לקואורדינטות הקוטביות $(r, \theta)$ הוא:

\[x = r \cos\theta , \qquad y = r \sin\theta\]

לחילופין:

\[r = \sqrt{x^2 + y^2} , \qquad \theta = \tan^{-1}(\frac{y}{x})\]

הסבר: קואורדינטות קוטביות שימושיות במיוחד כאשר מתארים תנועה מעגלית או תנועה שבה המרחק מנקודה מרכזית משחק תפקיד חשוב, כגון בבעיות הקשורות לכבידה, תנועה פלנטרית, או תנועה בשדות כוח מרכזיים.

ב. הוכחת המערכת האורתונורמלית

שלב 1: הגדרת מערכת אורתונורמלית

מערכת אורתונורמלית של וקטורים מורכבת מווקטורים יחידה שניצבים זה לזה. עלינו להוכיח ששני וקטורי היחידה בקואורדינטות קוטביות - $\hat{r}$ ו-$\hat{\theta}$ - מקיימים:

1. הם וקטורי יחידה: \(\vert \hat{r}\vert = \vert \hat{\theta}\vert = 1\)
2. הם ניצבים זה לזה: \(\hat{r} \cdot \hat{\theta} = 0\)

שלב 2: בדיקת תנאי וקטורי יחידה

לבדוק אם $\hat{r}$ הוא וקטור יחידה:

\[|\hat{r}|^2 = (\cos\theta)^2 + (\sin\theta)^2 = \cos^2\theta + \sin^2\theta = 1\]

מכאן

\[|\hat{r}\vert = 1\]

לבדוק אם $\hat{\theta}$ הוא וקטור יחידה:

\[|\hat{\theta}|^2 = (-\sin\theta)^2 + (\cos\theta)^2 = \sin^2\theta + \cos^2\theta = 1\]

מכאן

\[|\hat{\theta}\vert = 1\]

שלב 3: בדיקת תנאי הניצבות

\[\begin{aligned} \hat{r} \cdot \hat{\theta} &= \cos\theta \cdot (-\sin\theta) + \sin\theta \cdot \cos\theta \\[10pt] &= -\cos\theta \sin\theta + \sin\theta \cos\theta = 0 \end{aligned}\]

הסבר: הוכחנו שזוהי מערכת אורתונורמלית. וקטור $\hat{r}$ מצביע תמיד בכיוון היוצא מהראשית לנקודה, כלומר בכיוון הרדיאלי, בעוד שווקטור $\hat{\theta}$ ניצב לו ומצביע בכיוון התנועה המעגלית סביב הראשית.

ג. הסבר וקטור המהירות והתאוצה

שלב 1: וקטור המהירות בקואורדינטות קוטביות

\[\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta}\]

הביטוי הזה מורכב משני רכיבים:

1. $\dot{r}\hat{r}$ - רכיב רדיאלי של המהירות, המייצג את קצב השינוי של המרחק מהראשית
2. $r\dot{\theta}\hat{\theta}$ - רכיב טנגנציאלי של המהירות, המייצג את התנועה הסיבובית סביב הראשית

שלב 2: וקטור התאוצה בקואורדינטות קוטביות

\[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}\]

הביטוי מורכב משני רכיבים:

1. רכיב רדיאלי: $(\ddot{r} - r\dot{\theta}^2)\hat{r}$
   • $\ddot{r}$ - תאוצה רדיאלית ישירה (שינוי בקצב השינוי של $r$)
   • $-r\dot{\theta}^2$ - תאוצה צנטריפטלית (הנובעת מהתנועה הסיבובית)
2. רכיב טנגנציאלי: $(2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}$
   • $2\dot{r}\dot{\theta}$ - אפקט קוריוליס (הנובע משינוי בו-זמני של $r$ ו-$\theta$)
   • $r\ddot{\theta}$ - תאוצה זוויתית (שינוי בקצב הסיבוב)

הסבר: יתרון גדול בשימוש בקואורדינטות קוטביות הוא שהן מאפשרות לבטא באופן ישיר וטבעי תנועה מעגלית או ספירלית. הביטויים שקיבלנו למהירות ולתאוצה כוללים את כל האפקטים הדינמיים החשובים, כמו תאוצה צנטריפטלית ואפקט קוריוליס, שקשה יותר לראות בקואורדינטות קרטזיות.

ד. יישום החוק השני של ניוטון

שלב 1: הצגת וקטור הכוח בקואורדינטות קוטביות

\[\vec{F} = F_r\hat{r} + F_\theta\hat{\theta}\]

כוח ניתן לפרק לרכיב רדיאלי $F_r$ (בכיוון $\hat{r}$) ורכיב טנגנציאלי $F_\theta$ (בכיוון $\hat{\theta}$).

שלב 2: יישום החוק השני של ניוטון

$\vec{F} = m\vec{a}$

\[(F_r\hat{r} + F_\theta\hat{\theta}) = m((\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta})\]

שלב 3: השוואת רכיבים

מכיוון ש-$\hat{r}$ ו-$\hat{\theta}$ הם וקטורים עצמאיים, אנו יכולים להשוות את הרכיבים משני צדי המשוואה:

רכיב רדיאלי:

\[F_r = m(\ddot{r} - r\dot{\theta}^2)\]

רכיב טנגנציאלי:

\[F_\theta = m(2\dot{r}\dot{\theta} + r\ddot{\theta})\]

הסבר: משוואות אלו מתארות את הדינמיקה של גוף הנע במישור בקואורדינטות קוטביות. הן מאפשרות לנו לחשב את תנועת הגוף כאשר ידועים הכוחות הפועלים עליו, או לחילופין לקבוע את הכוחות הדרושים כדי לייצר תנועה מסוימת.

ה. משמעות שינוי המסה עם הזמן

שלב 1: הצגת בעיה עם מסה משתנה

כאשר מסת הגוף $m(t)$ משתנה עם הזמן, החוק השני של ניוטון בצורתו הפשוטה $\vec{F} = m\vec{a}$ אינו תקף יותר.

שלב 2: עדכון החוק השני של ניוטון

הניסוח הכללי יותר של החוק השני של ניוטון הוא:

\[\vec{F} = \frac{d\vec{p}}{dt}\]

כאשר $\vec{p} = m\vec{v}$ הוא התנע של הגוף.

במקרה של מסה משתנה:

\[\vec{F} = \frac{d(m\vec{v})}{dt} = \frac{dm}{dt}\vec{v} + m\frac{d\vec{v}}{dt} = \dot{m}\vec{v} + m\vec{a}\]

שלב 3: השלכות על התנועה בקואורדינטות קוטביות

הרכיב הרדיאלי:

\[F_r = \dot{m}v_r + m(\ddot{r} - r\dot{\theta}^2)\]

כאשר $v_r = \dot{r}$ הוא רכיב המהירות בכיוון $\hat{r}$.

הרכיב הטנגנציאלי:

\[F_\theta = \dot{m}v_\theta + m(2\dot{r}\dot{\theta} + r\ddot{\theta})\]

כאשר $v_\theta = r\dot{\theta}$ הוא רכיב המהירות בכיוון $\hat{\theta}$.

הסבר: כאשר מסת הגוף משתנה, יש לקחת בחשבון גם את קצב שינוי המסה. דוגמה מעשית היא תנועת רקטה, שמסתה פוחתת ככל שהיא צורכת דלק. השינוי במסה תורם לכוח נוסף, הנקרא “תגובת סילון” (jet reaction), המשפיע על תנועת הגוף. ניתוח התנועה במקרה כזה דורש את הצורה הכללית יותר של החוק השני של ניוטון, שלוקחת בחשבון את שינוי התנע במלואו.

פתרון תרגיל מס׳ 5 בפיזיקה - דינמיקות מתקדמות

תאריך: 03/05/2025

בעיה 1: תנועה תחת כוח משתנה בזמן

חלקיק נע תחת השפעת כוח הנתון בביטוי:

\[\vec{F}(t) = a \cos(\omega t) \hat{x} + b \sin(\omega t) \hat{y}\]

כאשר $a$, $b$, $\omega$ הם פרמטרים.

1. מה יחידות הפרמטרים $a$, $b$, $\omega$?

2. אם בהתחלת התנועה החלקיק נמצא במנוחה בראשית, הראו שוקרטור מהירותו בכל זמן $t$ מאוחר יותר נתון בביטוי:

   \[\vec{v}(t) = \frac{a}{m\omega}\sin(\omega t)\hat{x} + \frac{b}{m\omega}(1-\cos(\omega t))\hat{y}\]
3. מהו וקטור התאוצה של החלקיק ב-$t=0$?
4. מהו גודל המהירות של החלקיק בכל זמן $t$?
5. מצאו את וקטור המקום של החלקיק בכל זמן $t$.

סעיף א: מה יחידות הפרמטרים $a$, $b$, $\omega$?

טיפ: יחידות בפיזיקה נקבעות על פי העקרון שכל איברי משוואה חייבים להיות בעלי אותן יחידות (ממדים).

מכיוון ש-$\vec{F}$ הוא כוח, יחידותיו הן ניוטון [N] או [kg⋅m/s²].

• יחידות של $a$ ו-$b$: מכיוון ש-$\cos(\omega t)$ ו-$\sin(\omega t)$ הם חסרי יחידות (מספרים טהורים), הפרמטרים $a$ ו-$b$ חייבים להיות ביחידות של כוח:

\[[a] = [b] = [\mathrm{N}] = \mathrm{kg⋅m/s²}\]

• יחידות של $\omega$: הארגומנט של פונקציות טריגונומטריות חייב להיות חסר יחידות. מכיוון ש-$t$ נמדד בשניות [s], נדרש:

\[[\omega t] = \text{without\ units} \implies [\omega] \cdot [t] = 1\] \[[\omega] \cdot [t] = [\omega] \cdot \text{s} = 1\]

לכן: $\omega = \, [\mathrm{s}^{-1}]$ (רדיאנים לשנייה)

סעיף ב: מציאת וקטור המהירות

החוק השני של ניוטון: $\vec{F} = m\vec{a} = m\frac{d\vec{v}}{dt}$

מכאן:

\[\frac{d\vec{v}}{dt} = \frac{\vec{F}}{m} = \frac{a}{m}\cos(\omega t)\hat{x} + \frac{b}{m}\sin(\omega t)\hat{y}\]

כדי למצוא את $\vec{v}(t)$, נבצע אינטגרציה:

\[\vec{v}(t) = \int_0^t \frac{d\vec{v}}{dt'} dt' = \int_0^t \left[\frac{a}{m}\cos(\omega t')\hat{x} + \frac{b}{m}\sin(\omega t')\hat{y}\right] dt'\]

חישוב האינטגרל:

• רכיב x:

  \[\int_0^t \frac{a}{m}\cos(\omega t') dt' = \frac{a}{m\omega}\sin(\omega t)\]

• רכיב y:

  \[\int_0^t \frac{b}{m}\sin(\omega t') dt' = -\frac{b}{m\omega}\cos(\omega t')\Big{\vert}_0^t = \frac{b}{m\omega}(1-\cos(\omega t))\]

תוצאה סופית:

\[\vec{v}(t) = \frac{a}{m\omega}\sin(\omega t)\hat{x} + \frac{b}{m\omega}(1-\cos(\omega t))\hat{y}\]

(מתקיים כי $\vec{v}(0) = \vec{0}$ כנדרש מתנאי ההתחלה)

סעיף ג: וקטור התאוצה ב-$t=0$

התאוצה היא:

\[\vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{\vec{F}(t)}{m}\]

ב-$t=0$:

\[\vec{a}(0) = \frac{\vec{F}(0)}{m} = \frac{a\cos(0)\hat{x} + b\sin(0)\hat{y}}{m} = \frac{a}{m}\hat{x}\]

סעיף ד: גודל המהירות

גודל המהירות:

\[\vert \vec{v}(t)| = \sqrt{v_x^2 + v_y^2}\]

כאשר:

• $v_x = \frac{a}{m\omega}\sin(\omega t)$
• $v_y = \frac{b}{m\omega}(1-\cos(\omega t))$

לכן:

\[\vert \vec{v}(t)| = \frac{1}{m\omega}\sqrt{a^2\sin^2(\omega t) + b^2(1-\cos(\omega t))^2}\]

סעיף ה: וקטור המקום

אינטגרציה של וקטור המהירות:

\[\vec{r}(t) = \int_0^t \vec{v}(t') dt'\]

חישוב האינטגרלים:

• רכיב x: $\int_0^t \frac{a}{m\omega}\sin(\omega t’) dt’ = -\frac{a}{m\omega^2}\cos(\omega t’)\Big{\vert}_0^t = \frac{a}{m\omega^2}(1-\cos(\omega t))$
• רכיב y: $\int_0^t \frac{b}{m\omega}(1-\cos(\omega t’)) dt’ = \frac{b}{m\omega}\left[t - \frac{\sin(\omega t)}{\omega}\right]$

תוצאה סופית:

\[\vec{r}(t) = \frac{a}{m\omega^2}(1-\cos(\omega t))\hat{x} + \frac{b}{m\omega}\left(t - \frac{\sin(\omega t)}{\omega}\right)\hat{y}\]

---

בעיה 2: תנועת קליע בתווך עם התנגדות

קליע נע אופקית בתוך תווך, התנגדות התווך לקליע פרופורציונית למהירותו עם קבוע פרופורציה $\gamma$, כלומר $f(v) = \gamma v$. נתון: $\gamma = 10$.

1. מה היחידות של $\gamma$?
2. קבלו משוואה עבור התנועה האופקית של הקליע בעזרת החוק השני של ניוטון.
3. מיצאו ביטוי כלל עבור מהירותו הרגעית.
4. מיצאו ביטוי עבור תאוטתו הרגעית.
5. הקליע יצא את הלוע במהירות של 200 מטר לשנייה. כמה זמן ייקח לו להאט למהירות של מטר לשנייה בתוך התווך?
6. מה הייתה תאוטתו הממוצעת של הקליע בזמן זה?

סעיף א: יחידות של $\gamma$

כוח ההתנגדות: $f = \gamma v$

מכיוון ש-$[f] = \mathrm{N}$ ו-$[v] = \mathrm{m/s}$:

\[[\gamma] = \frac{[f]}{[v]} = \frac{\mathrm{N}}{\mathrm{m/s}} = \frac{\mathrm{kg⋅m/s²}}{\mathrm{m/s}} = \, \mathrm{kg/s}\]

לכן:

\[\boxed{\gamma = 10 \, \mathrm{kg/s}}\]

סעיף ב: משוואת התנועה

החוק השני של ניוטון: הכוח היחיד הוא כוח ההתנגדות (בכיוון הפוך למהירות):

\[F = -\gamma v = ma\]

לכן:

\[ma = -\gamma v\]

ברישום דיפרנציאלי:

\[\ddot{v} = -\frac{\gamma}{m}v \tag{1}\]

סעיף ג: ביטוי למהירות הרגעית

משוואה $(1)$ היא משוואה דיפרנציאלית מסדר ראשון שהפתרון האקספוננציאלי שלה הוא:

\[v(t) = v_0 e^{-\frac{\gamma}{m}t}\]

כאשר $v_0$ היא המהירות ההתחלתית.

המשוואה הזאת היא למעשה הפתרון של משוואת התנועה, כאשר $v_0$ הוא המהירות ההתחלתית של הקליע. מגיעים אליה בעזרת הפרדת משתנים:

\[\frac{dv}{v} = -\frac{\gamma}{m} dt\]

אינטגרציה נותנת:

\[\begin{aligned} \int \frac{dv}{v} &= -\frac{\gamma}{m} \int dt \\[10pt] \ln|v| &= -\frac{\gamma}{m}t + C_1 \end{aligned}\]

נוציא אקספוננט לשני הצדדים:

\[\begin{aligned} v &= e^{-\frac{\gamma}{m}t + C_1} \\[10pt] v &= e^{C_1} e^{-\frac{\gamma}{m}t} \\[10pt] &= v_0 e^{-\frac{\gamma}{m}t} \end{aligned}\]

השוויון האחרון מתקבל על ידי קביעת $e^{C_1} = v_0$, כלומר המהירות ההתחלתית.

סעיף ד: תאוטה רגעית

התאוטה היא:

\[a(t) = \frac{dv}{dt} = -\frac{\gamma}{m}v_0 e^{-\frac{\gamma}{m}t} = -\frac{\gamma}{m}v(t)\]

סעיף ה: זמן להאטה

נתון: $v_0 = 200 \, \mathrm{m/s}$, ומחפשים זמן שבו $v = 1 \, \mathrm{m/s}$.

מהמשוואה:

\[1 = 200e^{-\frac{10}{m}t}\] \[\frac{1}{200} = e^{-\frac{10}{m}t}\] \[\ln\left(\frac{1}{200}\right) = -\frac{10}{m}t\] \[t = \frac{m}{10}\ln(200) = \frac{m}{10} \times 5.298 \approx 0.53m \mathrm{s}\]

(התשובה תלויה במסת הקליע $m$ בק”ג)

סעיף ו: תאוטה ממוצעת

שואלים על התאוטה הממוצעת במהלך הזמן בסעיף הקודם, לצורך העניין בין $t=0$ ל-$t=t^*$, כאשר $t^* \approx 0.53m \, \mathrm{s}$.

\[\bar{a} = \frac{\Delta v}{\Delta t} = \frac{1-200}{0.53m} = \frac{-199}{0.53m} \approx -\frac{375.5}{m} \, \mathrm{ m/s²}\]

---

בעיה 3: צניחה חופשית עם התנגדות אוויר

מומחית לצניחה חופשית צונחת בשדה הכבידה של כדור הארץ. תאוצת הכבידה $g \approx 10 \, \mathrm{m/s^2}$, וכוח התנגדות האוויר פרופורציוני לריבוע המהירות: $f = \beta v^2$.

1. מהי המהירות הטרמינלית של הצנחנית?
2. מיצאו את גודלה $\beta$ אם משקלה של הצנחנית הוא $600 \mathrm{N}$, כלומר $m \approx 60 \, \mathrm{kg}$, ומהירותה הטרמינלית היא $216 \, \mathrm{km/h}$.
3. מהו החוק השני של ניוטון במקרה זה?

4. הראו שהחוק השני של ניוטון במקרה זה מוביל למשוואה דיפרנציאלית:

   \[\frac{dv}{dt} = g(1- \alpha^2 v^2)\]

   מה היחידות של $\alpha = \sqrt{\frac{\beta}{mg}}$?

5. בהנחה שהצנחנית החלה ממהירות אפס, כלומר $v(0) = 0$, הראו שמהירותה הרגעית של הצנחנית בכל זמן $t$ נתונה בביטוי:

   \[v(t) = \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]
6. מהו הגבול האסימפטוטי של המהירות הרגעית כאשר $t \to \infty$?
7. חשבו את המהירויות של הצנחנית ב-$t = 6 \, \mathrm{s}$ ו-$t = 12 \, \mathrm{s}$.

8. מהו המיקום של הצנחנית בכל זמן $t$? הראו שהמיקום הוא:

   \[z(t) = \frac{m}{\beta}\ln\left[\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right]\]
9. מהו המיקום של הצנחנית ב-$t = 6 \, \mathrm{s}$ ו-$t = 12 \, \mathrm{s}$?

סעיף א: מהירות טרמינלית

הגדרה: מהירות טרמינלית היא המהירות שבה הכוחות מאוזנים והתאוצה מתאפסת.

במצב שיווי משקל:

\[mg = \beta v_{\text{terminal}}^2\]

לכן:

\[v_{\text{terminal}} = \sqrt{\frac{mg}{\beta}}\]

סעיף ב: מציאת $\beta$

נתון:

• משקל: $W = mg = 600 \, \mathrm{N}$, לכן $m = 60 \, \mathrm{kg}$
• מהירות טרמינלית: $v_{\text{terminal}} = 216 \mathrm{km/h} = 60 \, \mathrm{m/s}$

מהנוסחה:

\[60 = \sqrt{\frac{600}{\beta}}\] \[3600 = \frac{600}{\beta}\] \[\beta = \frac{600}{3600} = \frac{1}{6} \text{ N⋅s²/m²}\]

סעיף ג: החוק השני

הכוחות הפועלים:

• כוח כבידה למטה: $mg$
• התנגדות אוויר למעלה: $\beta v^2$

החוק השני (כיוון חיובי כלפי מטה):

\[m\frac{dv}{dt} = mg - \beta v^2\]

סעיף ד: משוואה דיפרנציאלית

מהחוק השני:

\[\frac{dv}{dt} = g - \frac{\beta}{m}v^2 = g\left(1 - \frac{\beta v^2}{mg}\right)\]

נגדיר $\alpha^2 = \frac{\beta}{mg}$:

\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]

יחידות של $\alpha$: $[\alpha^2] = \frac{[\beta]}{[mg]} = \frac{\text{N⋅s²/m²}}{\text{N}} = \text{s²/m²}$

לכן: $[\alpha] = \text{s/m}$

סעיף ה: פתרון המשוואה הדיפרנציאלית

טכניקה: הפרדת משתנים ושימוש באינטגרל של $\frac{1}{1-u^2}$.

לאחר אינטגרציה ושימוש בתנאי התחלה $v(0) = 0$:

\[v(t) = \frac{1}{\alpha}\tanh(\alpha g t)\]

כאשר $\alpha = \sqrt{\frac{\beta}{mg}}$, נקבל:

\[v(t) = \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]

סעיף ו: גבול אסימפטוטי

\[\lim_{t \to \infty} v(t) = \sqrt{\frac{mg}{\beta}}\lim_{t \to \infty}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right) = \sqrt{\frac{mg}{\beta}} \cdot 1 = v_{\text{terminal}}\]

(מכיוון ש-$\lim_{x \to \infty}\tanh(x) = 1$)

סעיף ז: חישוב מהירויות

עם הנתונים:

\[m = 60 \, \mathrm{kg}, \qquad \beta = 1/6 \, \mathrm{N⋅s^2/m^2}, \qquad g = 10 \, \mathrm{m/s}^2\]

נחשב את $\sqrt{\frac{\beta g}{m}}$:

\[\sqrt{\frac{\beta g}{m}} = \sqrt{\frac{(1/6) \cdot 10}{60}} = \sqrt{\frac{1}{36}} = \frac{1}{6} \text{ s}^{-1}\]

• ב-$t = 6$ s: $v(6) = 60\tanh(1) \approx 60 \times 0.762 = 45.7 \, \mathrm{m/s}$
• ב-$t = 12$ s: $v(12) = 60\tanh(2) \approx 60 \times 0.964 = 57.8 \, \mathrm{m/s}$

(המהירויות מתקרבות ל-$60 \, \mathrm{m/s}$, המהירות הטרמינלית)

סעיף ח: מיקום הצונחת

אינטגרציה של המהירות:

\[z(t) = \int_0^t v(t') dt' = \int_0^t \sqrt{\frac{mg}{\beta}}\tanh\left(\sqrt{\frac{\beta g}{m}}t'\right) dt'\]

תוצאה:

\[z(t) = \frac{m}{\beta}\ln\left[\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right]\]

סעיף ט: חישוב מיקומים

• ב-$t = 6$ s: $z(6) = 360\ln[\cosh(1)] \approx 360 \times 0.433 = 156 \, \mathrm{m}$
• ב-$t = 12$ s: $z(12) = 360\ln[\cosh(2)] \approx 360 \times 1.317 = 474 \, \mathrm{m}$

---

בעיה 4: חבל מחליק מעל מסמר

חבל מסיבי חסר חיכוך באורך $L=1 \, \mathrm{m}$ משתלשל משני צידיו של מסמר חסר חיכוך התקוע אופקית בקיר אנכי. בזמן $t = 0$, החבל ממוקם כך ששליש מאורכו ($L/3$) משתלשל מצידו האחד של המסמר, ושני שליש ($2L/3$) מצידו השני.

כמה זמן ייקח לחבל כולו להחליק מהמסמר?

תנאי ההתחלה:

• בזמן $t = 0$, החבל ממוקם כך ששליש מאורכו ($L/3$) משתלשל מצידו האחד של המסמר (שמאל), ושני שליש ($2L/3$) מצידו השני (ימין). כלומר, $y(t=0) = \frac{2L}{3}$.
• בזמן $t = 0$, החבל לא נע, כלומר מהירותו $v(0) = \dot{y}(0) = 0$.

פתרון בעיית החבל המשתלשל על מסמר

ככל שחולף הזמן, יותר מאסה של החבל עוברת מצד אחד של המסמר לצד השני, מה שמשנה את התאוצה של המערכת.

נקבע ציר $y$ שכיוונו החיובי כלפי מטה. בזמן $t = 0$, הקצה הקצר של החבל (שליש מאורכו) נמצא בצד שמאל של המסמר.

הערה: המתרגל העדיף להשתמש בסימון $z$ במקום $y$. לא קריטי.

בכל רגע נתון, הכוח המניע את החבל הוא ההפרש במשקל בין שני צידי המסמר. ככל שיותר חבל עובר לצד הארוך, הכוח המאיץ את התנועה גדל:

• בצד שמאל של המסמר המסה היא $\frac{L-y}{L}M$, כאשר $y$ הוא אורך החבל המשתלשל מהמסמר בצד שמאל.
• בצד ימין של המסמר המסה היא $\frac{y}{L}M$.

הביטוי לכוח המניע את החבל הוא:

\[\sum F = \frac{y}{L}M \cdot g - \frac{L-y}{L}M \cdot g = M\ddot{y}\] \[\begin{aligned} M\ddot{y} &= \frac{Mg}{L} \times \left[y - (L-y)\right] \\[5pt] &= \frac{Mg}{L} \times \left[y - L + y\right] \\[5pt] &= \frac{Mg}{L} \times \left[2y - L \right] \\[5pt] &= \left(\frac{2y}{L}\right)Mg - Mg \\[5pt] \end{aligned}\]

נחלק ב-$M$ ונקבל ונסדר:

\[\boxed{\ddot{y} = \underbrace{\frac{2g}{L}}_{\omega^2} y - g}\]

זה ביטוי מהצורה:

\[\ddot{y} = \omega^2 y - g\]

כאשר $\omega^2 = \frac{2g}{L}$.

כדי להיעזר בפתרון המוכר (של $\ddot{y} = \omega^2 y$), ניעזר בהזזה: נגדיר מתשנה חדש $z = y - \frac{L}{2}$, כך ש:

\[\ddot{z} = \ddot{y} = \frac{2g}{L}y - g = \frac{2g}{L}\left(z + \frac{L}{2}\right) - g = \frac{2g}{L}z + g - g = \frac{2g}{L}z\]

השוויון השמאלי מתקיים מכיוון שהמשתנים שונים בקבוע, ומכאן שהנגזרת השנייה שלהם שקולה.

הפתרון הוא:

\[\boxed{z(t) = A \cosh(\omega t) + B \sinh(\omega t)}\]

הערה: שימו לב לפונקציות ההיפרבוליות $\cosh$ ו-$\sinh$, ולא לפונקציות הטריגונומטריות $\cos$ ו-$\sin$, בגלל המקדם של אומגה.

כעת נציב חזרה את $y$:

\[y(t) = z(t) + \frac{L}{2} = A \cosh(\omega t) + B \sinh(\omega t) + \frac{L}{2}\]

נציב את תנאי ההתחלה:

1. בזמן $t = 0$, $y(0) = \frac{2}{3}L$:

\[\frac{2L}{3} = A \cosh(0) + B \sinh(0) + \frac{L}{2}\] \[\frac{2L}{3} = A + 0 + \frac{L}{2}\]

נציב $L = 1 \, \mathrm{m}$:

\[\boxed{A = \frac{2}{3} - \frac{1}{2} = \frac{4}{6} - \frac{3}{6} = \frac{1}{6}}\]

1. בזמן $t = 0$, $\dot{y}(0) = 0$:

נגזור את הפתרון כדי לקבל את המהירות:

\[\dot{y}(t) = -A \omega \sinh(\omega t) + B \omega \cos(\omega t)\] \[\dot{y}(0) = -A \omega \sinh(0) + B \omega \cos(0) = B \omega\]

מכאן נקבל:

\[B = 0\]

נציב את $A$ ו-$B$ בחזרה:

\[y(t) = \frac{1}{6} \cosh(\omega t) + \frac{1}{2}\]

כעת נציב את $\omega = \sqrt{\frac{2g}{L}}$:

\[y(t) = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right) + \frac{1}{2}\]

מציאת הזמן שבו החבל כולו משתלשל

כדי למצוא את הזמן שבו החבל כולו משתלשל, נציב $y(t) = L$:

\[L = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right) + \frac{1}{2}\] \[L - \frac{1}{2} = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right)\]

$L=1 \, \mathrm{m}$, ולכן:

\[\frac{1}{2} = \frac{1}{6} \cosh\left(\sqrt{\frac{2g}{L}} t\right)\] \[\cosh\left(\sqrt{\frac{2g}{L}} t\right) = 3\] \[\sqrt{\frac{2g}{L}} t = \cosh^{-1}(3)\] \[t = \frac{\cosh^{-1}(3)}{\sqrt{\frac{2g}{L}}}\]

נחשב את הערך:

\[t = \frac{\cosh^{-1}(3)}{\sqrt{\frac{2 \cdot 10}{1}}} = \frac{\cosh^{-1}(3)}{\sqrt{20}} \approx \frac{1.7627}{4.472} \approx 0.394 \, \mathrm{s}\]

לסיכום, הזמן שייקח לחבל כולו להחליק מהמסמר הוא:

\[\boxed{0.394 \, \mathrm{s}}\]

הערה: בתרגול המתרגל פתר את הבעיה בעזרת טור טיילור, אך הפתרון המוצג כאן הוא פתרון מדויק יותר בעזרת משוואות דיפרנציאליות.

---

בעיה 5: פתרונות של משוואות דיפרנציאליות

סוגי המשוואות הדיפרנציאליות בקורס:

1. משוואה מסדר ראשון מהצורה $\dot{v} = \alpha v$.

   מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למהירות.

   הפתרון מהצורה:

   \[\boxed{v(t) = A e^{\alpha t}}\]

2. משוואה מסדר ראשון מהצורה $\dot{v} = -\alpha v$.

   מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למהירות בכיוון ההפוך.

   הפתרון מהצורה:

   \[\boxed{v(t) = A e^{-\alpha t}}\]

3. משוואה מסדר שני מהצורה $\ddot{x} = -\omega^2 x$ (תנועה הרמונית).

   הפתרון מהצורה:

   \[\boxed{x(t) = A\cos(\omega t) + B\sin(\omega t) = C\cos\left(\omega t + \phi\right)}\]

4. משוואה היפרבולית מהצורה $\ddot{x} = \omega^2 x$.

   מתקבלת מהחוק השני של ניוטון עם כוח פרופורציונלי למיקום בכיוון ההפוך.

   הפתרון מהצורה:

   \[\boxed{x(t) = A\cosh(\omega t) + B\sinh(\omega t)}\]

נתון:

\[\alpha = 3 \, \mathrm{Hz}, \qquad \omega = 9 \, \mathrm{Hz}\]

הערה: $\omega$ ו-$\alpha$ הם קבועים של תדירות, כלומר שהיחידות שלהם הן $\mathrm{[Hz]}$ או $\mathrm{[1/s]}$.

סעיף א: פתרון משוואות מסדר ראשון

מיצאו את $A$ עבור שני המקרים הראשונים כאשר נתון:

\[x(0) = 1 \, \mathrm{m}. \qquad v(1) = -1 \, \mathrm{m/s}\]

עבור $\dot{v} = \alpha v$ (כאשר $\alpha = 3 \mathrm{Hz}$):

\[\begin{aligned} v(t) &= A e^{3t} \\[5pt] v(t=1) &= A e^{3} = -1 \\[5pt] \implies A &= -\frac{1}{e^{3}} \, \mathrm{m} \end{aligned}\]

הערה: לא מובן לי מדוע ניתן גם הנתון לגבי $x(0) = 1 \, \mathrm{m}$, מכיוון שמהירות היא נגזרת של מיקום, ולכן תנאי ההתחלה של המהירות מספיק כדי לקבוע את $A$.

לשלמות התמונה אפשר גם לקבל את משוואת המיקום $x(t)$. מהפתרון הכללי של מהירות ומיקום ($v(t) = \dot{x}(t)$):

\[x(t) = \int v(t) dt = \int A e^{3t} dt = \frac{A}{3} e^{3t} + C\]

נציב את תנאי ההתחלה $x(0) = 1 \, \mathrm{m}$ ואת $A$ שמצאנו:

\[1 = \frac{-\frac{1}{e^{3}}}{3} e^{0} + C\] \[\boxed{C = 1 + \frac{1}{3e^{3}} \, \mathrm{m}}\]

לכן:

\[x(t) = \frac{-\frac{1}{e^{3}}}{3} e^{3t} + 1 + \frac{1}{3e^{3}} = -\frac{1}{3e^{3}} e^{3t} + 1 + \frac{1}{3e^{3}}\]

נסדר את התוצאה:

\[\boxed{x(t) = 1 + \frac{1}{3e^{3}} - \frac{1}{3e^{3}} e^{3t}}\]

הערה: אפשר להיעזר בווקטור המקום בנקודת ההתחלה בשביל לתא את וקטור המקום הכללי:

\[x(t) = x_0 + \int_0^t v(t') dt' = 1 + \int_0^t A e^{3t'} dt' = 1 + A\left[e^{3t'}\right]_0^t = 1 + A\left(e^{3t} - e^{0}\right) = 1 + A\left(e^{3t} - 1\right)\]

נציב את $A$ שמצאנו:

\[x(t) = 1 -\frac{1}{3e^{3}}\left(e^{3t} - 1\right) = 1 - \frac{1}{3e^{3}} e^{3t} + \frac{1}{3e^{3}}\] \[\boxed{x(t) = 1 + \frac{1}{3e^{3}} - \frac{1}{3e^{3}} e^{3t}}\]

---

עבור $\dot{v} = -\alpha v$ (כאשר $\alpha = 3$ Hz):

\[v(t) = A e^{-3t}\]

באופן דומה למקודם, נשתמש בתנאי ההתחלה של המהירות:

\[\begin{aligned} v(t=1) &= A e^{-3} = -1 \\[5pt] A &= -e^{3} \, \mathrm{m} \end{aligned}\]

לכן:

\[\boxed{A = -e^{3} \, \mathrm{m}}\]

---

סעיף ב: תנועה הרמונית

משוואה:

\[\ddot{x} = -\omega^2 x\]

פתרון כללי:

\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]

נתון:

\[x(0) = 2 \, \mathrm{m}, \qquad v(\pi/\omega) = 2 \, \mathrm{m/s}\]

נדרש: מצאו את $A, \, B, \, C, \, \phi$.

פתרון

מ-$x(0) = 2$:

\[\boxed{A = 2 \, \mathrm{m}}\]

המהירות (נגזרת הפתרון):

\[v(t) = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\]

מ-$v(\pi/\omega) = 2 \, \mathrm{m/s}$:

\[2 = -2\omega \cdot 0 + B\omega \cdot (-1) = -B\omega\]

נציב $\omega = 3 \, \mathrm{Hz}$:

\[\boxed{B = -\frac{2 \, \mathrm{[m/s]}}{\omega \, \mathrm{[1/s]}} = -\frac{2}{3} \, \mathrm{m}}\]

ניעזר בנוסחה הנוספת למציאת $C$ ו-$\phi$:

---

סעיף ג: משוואה היפרבולית

משוואה:

\[\ddot{x} = \omega^2 x\]

פתרון כללי:

\[x(t) = A\cosh(\omega t) + B\sinh(\omega t)\]

נתון:

\[x(0) = 0 \, \mathrm{m}, \qquad v(1) = \ln 3\, \, \mathrm{m/s}\]

מ-$x(0) = 0$:

\[\boxed{A = 0 \, \mathrm{m}}\]

המהירות:

\[v(t) = B\omega\cosh(\omega t)\]

מ-$v(1) = \ln 3$:

\[\ln 3 = B\omega\cosh(\omega)\] \[B = \frac{\ln 3}{\omega\cosh(\omega)}\]

נציב $\omega = 3 \, \mathrm{Hz}$:

\[\boxed{B = \frac{\ln 3}{3\cosh(3)} = \frac{\ln 3}{3\cdot 10.0677} \approx 0.109 \, \mathrm{m}}\]

---

פתרון תרגיל מס׳ 6

תאריך: 08/06/2025

הערה חשובה: תשובות מפורטות יותר לרוב התרגילים כאן נמצאות בסיכומי השיעורים והתרגולים, כולל סיכומי שיעורי התגבור. התשובות שלהלן לקוחות מתוך טיוטה ישנה שמצאתי ושאלי תסייע למישהו, אך מומלץ לעבור על התשובות בסיכומי השיעורים, התרגולים והתגבורים.

שאלה 1: מסה על מישור משופע עם קפיץ

נתון: על גבי מישור משופע חסר חיכוך מונחת מסה $m$ המחוברת אל ראשו של המישור בקפיץ. המישור המשופע יכול להחליק ללא חיכוך על גבי רצפה אופקית. שיפוע המישור המשופע הוא $\alpha$, קבוע הכוח של הקפיץ הוא $k$, אורכו הרפוי של הקפיץ הוא $\ell$. מסת המישור המשופע היא $M$.

נכנה ב-$x(t)$ את מרחקה של $m$ מראש המישור המשופע. תנאי התחלה: $x(t=0) = \ell$ (הקפיץ רפוי), ומשחררים ממנוחה.

מושגים חשובים

• מערכת ייחוס לא אינרציאלית: מערכת המישור המשופע מאיצה, לכן נצטרך להתחשב בכוחות מדומים
• כוח מדומה (פסאודו-כוח): \(\vec{F}_{pseudo} = -m\vec{a}_{frame}\) כאשר \(\vec{a}_{frame}\) היא תאוצת מערכת הייחוס

סעיף א: דיאגרמת כוחות

על המסה $m$ (במערכת המישור המשופע):

• כוח הכבידה: $mg$ (כלפי מטה)
• כוח הקפיץ: $F_s = k(\ell-x)$ (לאורך המישור)
• כוח נורמלי: $N_1$ (ניצב למישור)
• כוח מדומה: $F_{pseudo} = mA$ (כאשר $A$ היא תאוצת המישור)

על המישור המשופע $M$:

• כוח הכבידה: $Mg$ (כלפי מטה)
• כוח נורמלי מהרצפה: $N_2$ (כלפי מעלה)
• כוח תגובה מהמסה: $-N_1$ (בכיוון הפוך לנורמל על $m$)
• כוח תגובה מהקפיץ: $k(\ell-x)$ (בכיוון הפוך לכוח על $m$)

סעיף ב: משוואות תנועה

עבור המישור המשופע $M$ (בכיוון אופקי):

\[MA = N_1\sin\alpha + k(\ell-x)\cos\alpha\]

עבור המסה $m$ במערכת המישור המשופע:

לאורך המישור (ציר x):

\[ma = mg\sin\alpha - k(\ell-x) + mA\cos\alpha\]

ניצב למישור:

\[0 = N_1 - mg\cos\alpha - mA\sin\alpha\]

מהמשוואה האחרונה:

\[N_1 = mg\cos\alpha + mA\sin\alpha\]

סעיף ג: משוואה דיפרנציאלית עבור $x$

נציב את $N_1$ במשוואת התנועה של $M$:

\[MA = (mg\cos\alpha + mA\sin\alpha)\sin\alpha + k(\ell-x)\cos\alpha\]

נפתור עבור $A$:

\[MA = mg\cos\alpha\sin\alpha + mA\sin^2\alpha + k(\ell-x)\cos\alpha\] \[A(M - m\sin^2\alpha) = mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha\] \[A = \frac{mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha}{M + m\cos^2\alpha}\]

נציב במשוואת התנועה של $m$ לאורך המישור:

\[m\ddot{x} = mg\sin\alpha - k(\ell-x) + m\cos\alpha \cdot \frac{mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha}{M + m\cos^2\alpha}\]

לאחר פישוט:

\[\ddot{x} = -\frac{k(M + m)}{m(M + m\cos^2\alpha)}x + \frac{k(M + m)\ell + Mmg\sin\alpha}{m(M + m\cos^2\alpha)}\]

זאת משוואה מהצורה:

\[\ddot{x} = -\omega^2 x + x_0\]

כאשר:

\[\omega^2 = \frac{k(M + m)}{m(M + m\cos^2\alpha)}\] \[x_0 = \frac{k(M + m)\ell + Mmg\sin\alpha}{k(M + m)}\]

סעיף ד: זמן עד עצירה ראשונה

בתנועה הרמונית, הזמן עד עצירה ראשונה הוא רבע מחזור:

\[t^* = \frac{T}{4} = \frac{\pi}{2\omega} = \frac{\pi}{2}\sqrt{\frac{m(M + m\cos^2\alpha)}{k(M + m)}}\]

סעיף ה: פתרון עבור $x(t)$

הפתרון הכללי למשוואה הדיפרנציאלית:

\[x(t) = x_{eq} + A\cos(\omega t) + B\sin(\omega t)\]

כאשר $x_{eq} = x_0/\omega^2$ היא נקודת שיווי המשקל.

מתנאי ההתחלה:

• $x(0) = \ell$: נותן $x_{eq} + A = \ell$
• $\dot{x}(0) = 0$: נותן $B = 0$

לכן:

\[x(t) = x_{eq} + (\ell - x_{eq})\cos(\omega t)\]

סעיף ו: תיאור תנועת המישור המשופע

המישור המשופע מבצע תנועה מחזורית:

• בהתחלה הוא מאיץ ימינה (כשהקפיץ דחוס)
• מהירותו גדלה עד שהמסה $m$ מגיעה לנקודת שיווי המשקל
• אז הוא ממשיך בתנועה אך מאט
• בנקודה שבה $m$ נעצרת לראשונה, גם המישור נעצר רגעית
• התנועה מתהפכת והמחזור חוזר

סעיף ז: משוואה דיפרנציאלית עבור המישור המשופע

מיקום המישור המשופע: $X(t)$

ממשוואת התנועה של $M$:

\[M\ddot{X} = N_1\sin\alpha + k(\ell-x)\cos\alpha\]

כאשר $x$ הוא המיקום היחסי של $m$ ביחס למישור.

סעיף ח: מהירות המישור המשופע

אינטגרציה של התאוצה:

\[V(t) = \int_0^t A(\tau)d\tau\]

עם הפתרון שמצאנו עבור $x(t)$, ניתן לחשב את $A(t)$ ולאנטגר.

---

שאלה 2: מטוטלת בקרון מאיץ

נתון: מתקרתו של קרון המאיץ ימינה תלויה מטוטלת. החוט באורך $\ell$, המסה $m$.

סעיף א: תאוצת הקרון בשיווי משקל

בשיווי משקל בזווית $\theta_0$:

כוחות על המסה:

• כוח הכבידה: $mg$ (כלפי מטה)
• מתיחות החוט: $T$ (לאורך החוט)
• כוח מדומה: $ma$ (שמאלה, כאשר $a$ היא תאוצת הקרון)

תנאי שיווי משקל:

\[T\sin\theta_0 = ma\] \[T\cos\theta_0 = mg\]

מחלוקת המשוואות:

\[\tan\theta_0 = \frac{a}{g}\]

לכן:

\[a = g\tan\theta_0\]

סעיף ב: תדירות תנודות קטנות

עבור תנודות קטנות סביב $\theta_0$, נסמן $\theta = \theta_0 + \phi$ כאשר $\phi$ קטנה.

משוואת התנועה:

\[m\ell\ddot{\phi} = -mg\sin(\theta_0 + \phi) + ma\cos(\theta_0 + \phi)\]

לזוויות קטנות ועם $a = g\tan\theta_0$:

\[\ddot{\phi} = -\frac{g}{\ell\cos\theta_0}\phi\]

תדירות זוויתית:

\[\omega = \sqrt{\frac{g}{\ell\cos\theta_0}}\]

משרעת: אם מסיטים למצב אנכי ($\theta = 0$), המשרעת היא $\theta_0$.

סעיף ג: חרק על דופן הקרון

החרק נצמד לדופן הימנית ומחליק מטה בתאוצה $g/2$.

כוחות על החרק:

• כוח כבידה: $mg$ (מטה)
• כוח נורמלי מהדופן: $N$ (שמאלה)
• כוח חיכוך: $f = \mu N$ (מעלה)
• כוח מדומה: $ma$ (שמאלה)

משוואות תנועה:

• אופקי: $N = ma$
• אנכי: $mg - \mu N = m(g/2)$

נציב:

\[mg - \mu ma = mg/2\] \[1 - \mu\tan\theta_0 = 1/2\] \[\tan\theta_0 = \frac{1}{2\mu}\]

סעיף ד: מסלול נפילה במערכת העגלה

כשהחוט נקרע בזווית $\theta = 0°$, המסה נופלת בתאוצה יחסית:

• אופקית: $-a$ (שמאלה ביחס לעגלה)
• אנכית: $g$ (מטה)

המסלול הוא פרבולה עם ציר סימטריה בזווית $\arctan(a/g) = \theta_0$ ביחס לאנך.

---

שאלה 3: שאלת הזבוב - מערכת גלגלת

נתון: שתי מסות זהות $m_1 = m_2 = 99$ גרם קשורות בחוט על גלגלת. זבוב במסה $m = 2$ גרם נוחת על $m_1$ ב-$t=0$, מתעופף ב-$t=2s$, ונוחת על $m_2$ ב-$t=4s$.

מצב התחלתי	הזבוב מגיע ל-$m_2$

סעיף א: סקיצת המערכת ב-$t=0$

בזמן נחיתת הזבוב:

• שתי המסות במנוחה באותו גובה
• הזבוב נוחת על $m_1$ (הימנית)
• $m_1$ מתחילה לרדת עם תאוצה $a$ כלפי מטה
• $m_2$ עולה עם אותה תאוצה

סעיף ב: תיאור התנועה

$0 \leq t < 2s$: $m_2$ מאיצה מעלה בתאוצה קבועה ממהירות התחלתית אפס

$2s \leq t < 4s$: הזבוב מעופף, המערכת בהתמדה, $m_2$ ממשיכה במהירות קבועה מעלה

$t \geq 4s$: הזבוב על $m_2$, התאוצה מתהפכת, $m_2$ מאטה ואז יורדת

סעיף ג: חישוב התאוצות

שלב א ($0 \leq t < 2s$):

\[(m_1 + m)g - T = (m_1 + m)a\] \[T - m_2g = m_2a\]

פתרון:

\[a = \frac{mg}{2M + m} = \frac{2 \times 10}{2 \times 99 + 2} = 0.1 \text{ m/s}^2\]

שלב ב: $a = 0$ (התמדה)

שלב ג: $a = -0.1$ m/s² (סימטרי לשלב א)

סעיף ד: מהירות כפונקציה של הזמן

\[v(t) = \begin{cases} 0.1t & 0 \leq t < 2s \\ 0.2 & 2s \leq t < 4s \\ 0.2 - 0.1(t-4) & t \geq 4s \end{cases}\]

סעיף ה: גרף מהירות-זמן

גרף ליניארי למקוטעין:

• עולה מ-0 ל-0.2 m/s בין $t=0$ ל-$t=2s$
• קבוע ב-0.2 m/s בין $t=2s$ ל-$t=4s$
• יורד מ-0.2 ל-(-0.4) m/s בין $t=4s$ ל-$t=10s$

סעיף ו: העתק כולל

ההעתק הוא השטח מתחת לגרף מהירות-זמן:

• משולש: $\frac{1}{2} \times 2 \times 0.2 = 0.2$ m
• מלבן: $2 \times 0.2 = 0.4$ m
• טרפז: $\frac{1}{2} \times 6 \times (0.2 - 0.4) = -0.6$ m

סה”כ: $0.2 + 0.4 - 0.6 = 0$ m

המערכת חוזרת למצבה ההתחלתי!

---

שאלה 4: טס על מישור משופע

נתון: על מישור משופע מחליק טס ועליו תורן. בראש התורן קשור חוט ובקצהו משקולת במסה $m$.

סעיף א: הגדרת מערכת התמד

מערכת התמד (אינרציאלית): מערכת ייחוס שבה לא מורגשים כוחות מדומים. זאת מערכת שאינה מאיצה ביחס למערכת אינרציאלית אחרת.

סעיף ב: זווית פרישה כאשר $\mu = \tan\theta$

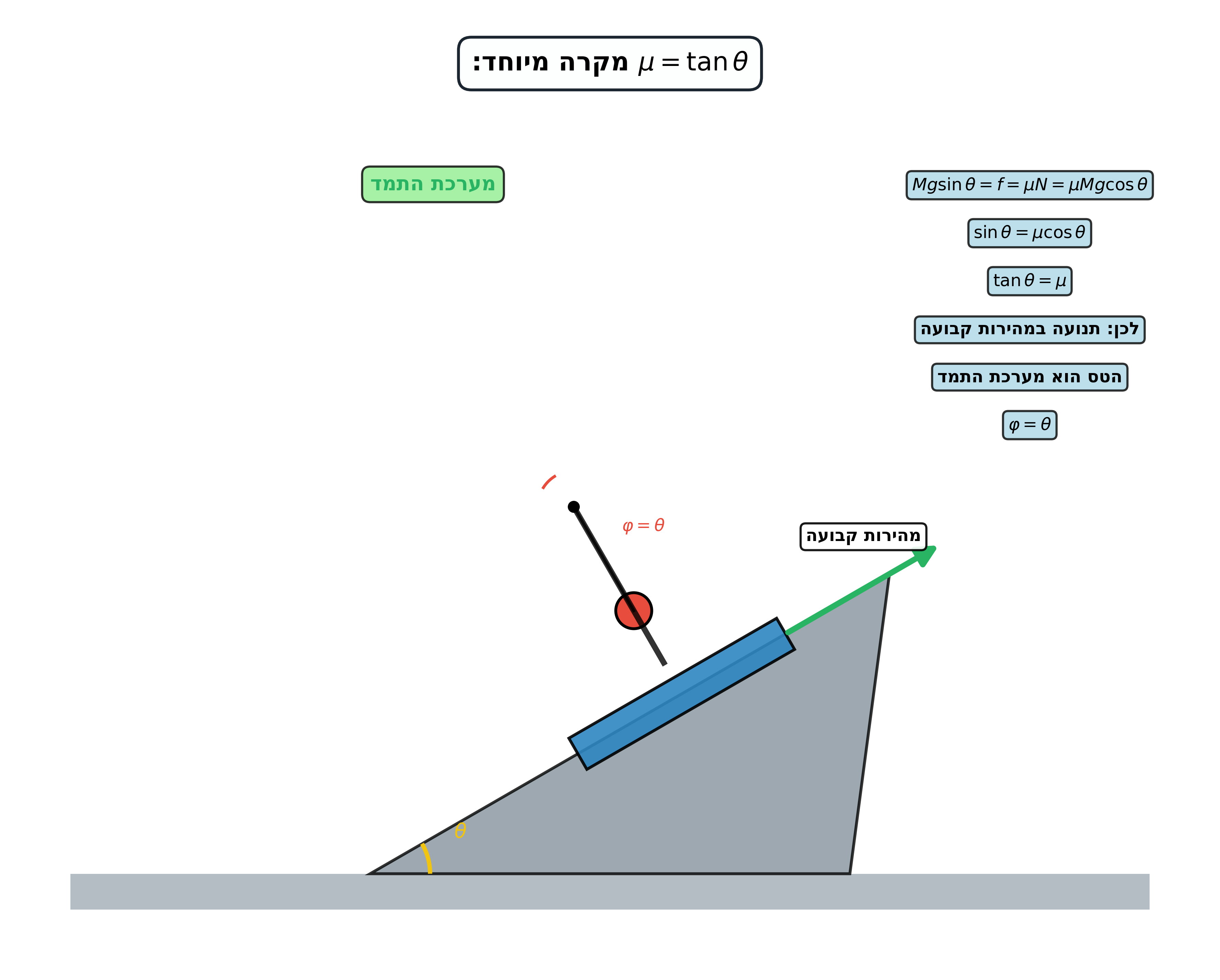
כאשר $\mu = \tan\theta$, הטס גולש במהירות קבועה (ללא תאוצה).

במערכת הטס (שהיא מערכת התמד במקרה הזה):

• כוח הכבידה: $mg$ (אנכית מטה)
• מתיחות החוט: $T$ (לאורך החוט)

בשיווי משקל, החוט אנכי: $\varphi = 0$

סעיף ג: תנועה ללא חיכוך

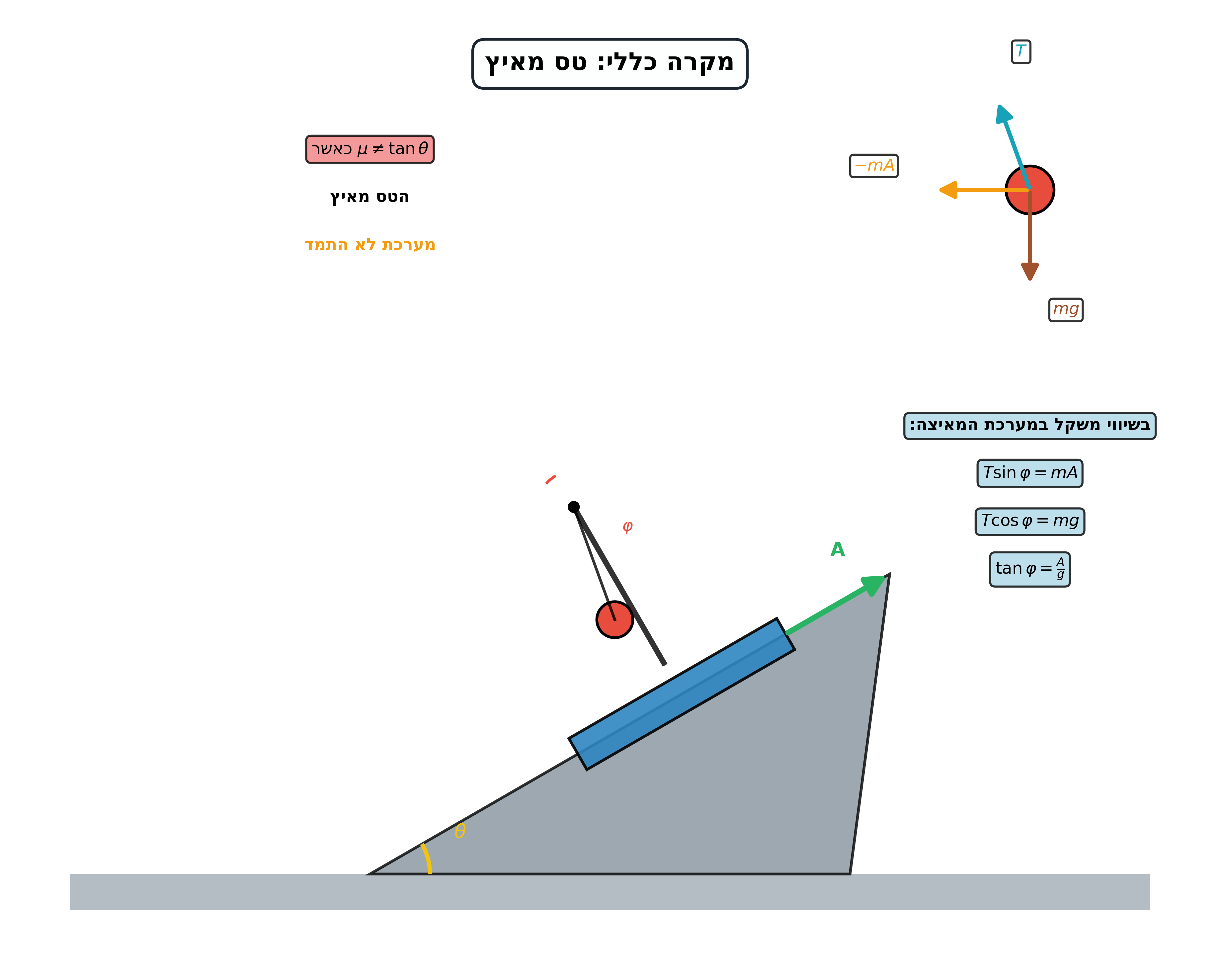
ללא חיכוך, הטס מאיץ עם $a = g\sin\theta$.

במערכת הטס:

• כוח כבידה: $mg$
• כוח מדומה: $ma = mg\sin\theta$ (במעלה המישור)

זווית הפרישה:

\[\tan\varphi = \frac{a}{g\cos\theta} = \tan\theta\]

לכן: $\varphi = \theta$

לפי הדרישה $\Delta x_2 = \frac{1}{2}\Delta x_1$:

\[\frac{mg\cos\varphi}{k} = \frac{mg}{2k}\] \[\cos\varphi = \frac{1}{2}\] \[\varphi = 60°\]

סעיף ד: מסלול נפילה

כשהחוט נקרע ב-$\theta = 0°$, במערכת העגלה:

• תאוצה אופקית: $-a$ (שמאלה)
• תאוצה אנכית: $g$ (מטה)

המסלול הוא פרבולה עם ציר סימטריה בזווית $\theta$ ביחס לאנך.

---

שאלה 5: שתי מסות מחוברות בקפיץ

נתון: מסה $m_1$ על מסה $m_2$, מחוברות בקפיץ עם קבוע $k$. אורך רפוי אפס. מושכים את $m_1$ שמאלה מרחק $\ell$ ומשחררים.

נוסחאות חשובות

• מסה מצומצמת: $\mu = \frac{m_1m_2}{m_1 + m_2}$
• תדירות זוויתית: $\omega = \sqrt{\frac{k}{\mu}}$

סעיף א: בדיקת יחידות

\[t^* = \frac{\pi}{2}\sqrt{\frac{\mu}{k}} = \frac{\pi}{2}\sqrt{\frac{[kg]}{[N/m]}} = \frac{\pi}{2}\sqrt{\frac{[kg]}{[kg \cdot m/s^2]/[m]}} = [s]\]

סעיף ב: פונקציית מקום-זמן

מתנאי ההתחלה $x(0) = -\ell$, $\dot{x}(0) = 0$:

\[x(t) = -\ell\cos(\omega t)\]

סעיף ג: הפרש מהירויות

\[v_1(t) = \dot{x}(t) = \ell\omega\sin(\omega t)\] \[v_2(t) = -\frac{m_1}{m_2}v_1(t)\] \[\Delta v = v_1 - v_2 = v_1\left(1 + \frac{m_1}{m_2}\right) = v_1\frac{m_1 + m_2}{m_2}\]

סעיף ד: העתק של $m_2$

משימור תנע:

\[X(t) = \frac{m_1}{m_1 + m_2}\ell[1 - \cos(\omega t)]\]

סעיף ה: תנועת זבוב ללא חיכוך

הזבוב נע בקו ישר במערכת התמד. מיקומו משתנה בין שתי המסות באופן מחזורי.

סעיף ו: זמן התנתקות זבוב עם חיכוך

הזבוב מתנתק כאשר:

\[|ma_{rel}| > \mu mg\]

כאשר $a_{rel} = \omega^2 \ell\cos(\omega t)$ היא התאוצה היחסית.

זמן התנתקות:

\[t_{detach} = \frac{1}{\omega}\arccos\left(\frac{\mu g}{\omega^2 \ell}\right)\]

סעיף ז: משוואות עם חיכוך בין המסות

עם חיכוך $\mu$ בין המסות:

\[m_1\ddot{x} = -kx - \mu m_1 g \cdot \text{sgn}(\dot{x})\] \[m_2\ddot{X} = -kx + \mu m_1 g \cdot \text{sgn}(\dot{x})\]

כאשר $\text{sgn}$ היא פונקציית הסימן.

פתרון תרגיל מספר 7 - תנועה, כוחות ושימור

תאריך: 15/06/2025

שאלה 1: תנועה על מסלול אליפטי

וקטור המקום של חלקיק מסיבי נתון על ידי:

\[\vec{r}(t) = a\cos(\omega t)\hat{x} + b\sin(\omega t)\hat{y}\]

1. משוואת אליפסה קנונית (זוהי אליפסה אשר מרכזה יושב על ראשית הצירים ושני ציריה מתלכדים עם ציר ה-x וציר ה-y) נתונה על ידי:

   \[\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1\]

   הוכיחו כי החלקיק נע על גבי אליפסה קנונית.

2. הראו שמתקיים:

   \[\vec{r} \cdot \vec{p} = \frac{1}{2}m(b^2 - a^2)\sin(2\omega t)\]

3. כפי שראינו בכיתה, האנרגיה הקינטית של גוף שמסתו m הנע במהירות v היא גודל סקלרי המוגדר דרך:

   \[E_k = \frac{p^2}{2m} = \frac{1}{2}mv^2\]

   קבוע של התנועה הוא קומבינציה (בדרך כלל מכפלה) של משתנים דינמיים שכל אחד מהם תלוי בזמן, אך הקומבינציה בכללותה אינה תלויה בזמן.

   קבלו את האנרגיה הקינטית של החלקיק הנע על גבי האליפסה כתלות בזמן. הראו שבמקרה של תנועה מעגלית (a = b), האנרגיה הקינטית היא קבוע של התנועה ומצאו אותו.

סעיף א - הוכחת תנועה על אליפסה

מוקטור המקום נתון:

\[\vec{r}(t) = a\cos(\omega t)\hat{x} + b\sin(\omega t)\hat{y}\]

מכאן נקבל את רכיבי המיקום:

• $x(t) = a\cos(\omega t)$
• $y(t) = b\sin(\omega t)$

כדי להוכיח שהחלקיק נע על אליפסה, נחשב:

\[\frac{x^2}{a^2} = \frac{a^2\cos^2(\omega t)}{a^2} = \cos^2(\omega t)\] \[\frac{y^2}{b^2} = \frac{b^2\sin^2(\omega t)}{b^2} = \sin^2(\omega t)\]

לכן:

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = \cos^2(\omega t) + \sin^2(\omega t) = 1\]

קיבלנו את משוואת האליפסה הקנונית, מכאן שהחלקיק אכן נע על מסלול אליפטי.

סעיף ב - מכפלה סקלרית של מיקום ותנע

ראשית, נמצא את וקטור המהירות על ידי גזירת וקטור המקום:

\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -a\omega\sin(\omega t)\hat{x} + b\omega\cos(\omega t)\hat{y}\]

וקטור התנע:

\[\vec{p}(t) = m\vec{v}(t) = -ma\omega\sin(\omega t)\hat{x} + mb\omega\cos(\omega t)\hat{y}\]

כעת נחשב את המכפלה הסקלרית:

\[\begin{aligned} \vec{r} \cdot \vec{p} &= [a\cos(\omega t)][-ma\omega\sin(\omega t)] + [b\sin(\omega t)][mb\omega\cos(\omega t)] \\ &= -ma^2\omega\cos(\omega t)\sin(\omega t) + mb^2\omega\sin(\omega t)\cos(\omega t) \\ &= m\omega\sin(\omega t)\cos(\omega t)(b^2 - a^2) \end{aligned}\]

תזכורת: $\sin(2\alpha) = 2\sin(\alpha)\cos(\alpha)$, לכן $\sin(\alpha)\cos(\alpha) = \frac{1}{2}\sin(2\alpha)$

\[\vec{r} \cdot \vec{p} = \frac{1}{2}m\omega(b^2 - a^2)\sin(2\omega t)\]

כפי שנדרשנו.

משמעות פיזיקלית: המכפלה הסקלרית בין מיקום לתנע מתנדנדת בתדירות כפולה (2ω) ומתאפסת כאשר a = b (תנועה מעגלית).

---

סעיף ג - אנרגיה קינטית וקבועי תנועה

האנרגיה הקינטית מוגדרת כך:

\[\boxed{E_k = \frac{1}{2}m v^2 = \frac{1}{2}m(\vec{v} \cdot \vec{v})}\]

נחשב את גודל המהירות בריבוע:

\[v^2 = v_x^2 + v_y^2 = \boxed{a^2\omega^2\sin^2(\omega t) + b^2\omega^2\cos^2(\omega t)}\]

נציב בנוסחה לאנרגיה קינטית:

\[E_k(t) = \frac{1}{2}m\omega^2\left[a^2\sin^2(\omega t) + b^2\cos^2(\omega t)\right]\]

למקרה של תנועה מעגלית (a = b):

\[E_k = \frac{1}{2}m\omega^2a^2[\sin^2(\omega t) + \cos^2(\omega t)] = \boxed{\frac{1}{2}m\omega^2a^2}\]

זה אכן קבוע. מכאן שהאנרגיה הקינטית במקרה של תנועה מעגלית אינה תלויה בזמן.

הסבר: בתנועה מעגלית אחידה, גודל המהירות קבוע (רק הכיוון משתנה), ולכן האנרגיה הקינטית נשארת קבועה. לעומת זאת, בתנועה אליפטית כללית, גודל המהירות משתנה לאורך המסלול - מקסימלי בציר הקצר ומינימלי בציר הארוך.

---

שאלה 2: מתקף וכוחות

1. על מסה של חמישה טון הנעה בקו ישר פעל כוח שהאיץ אותה ממהירות של 500 קמ”ש למהירות של 700 קמ”ש במשך שתי דקות. מהו המתקף שהכוח הפעיל על המסה? מהו המתקף שהמסה מפעילה על הכוח?

2. בתום הזמן הזה המסה התרסקה על הארץ בתהליך שארך עשירית השנייה. מהו הכוח הממוצע שכדור הארץ הפעיל על המסה בזמן זה?

3. כמה אנרגיה קינטית הרוויחה המסה בתהליך ההאצה?

המתקף מוגדר כשינוי בתנע:

\[J = \Delta p = m(v_2 - v_1) \, \mathrm{N \cdot s}\]

נמיר את היחידות ליחידות סטנדרטיות:

• מסה:

  \[m = 5000 \, \mathrm{kg}\]

• מהירות התחלתית:

  \[v_1 = 500 \, \mathrm{km/h} = \frac{500 \times 1000}{3600} \approx 138.89 \, \mathrm{m/s}\]

• מהירות סופית:

  \[v_2 = 700 \,\mathrm{km/h} = \frac{700 \times 1000}{3600} \approx 194.44 \, \mathrm{m/s}\]

• זמן:

  \[\Delta t = 2 \mathrm{min} = 2 \times 60 = 120 \, \mathrm{s}\]

נציב את הערכים לחישוב המתקף:

סעיף א - חישוב המתקף

\[\begin{aligned} J &= m(v_2 - v_1) \\[5pt] &= 5000 \times (194.44 - 138.89)\\[5pt] &\approx \boxed{277,750 \, \mathrm{N \cdot s}} \end{aligned}\]

ביחס למתקף שהמסה מפעילה על הכוח, נשתמש בחוק השלישי של ניוטון:

לפי החוק השלישי של ניוטון: המתקף שהמסה מפעילה על הכוח שווה בגודלו והפוך בכיוונו:

\[\boxed{J_{\text{mass on force}} = -277,750 \text{ N·s}}\]

---

סעיף ב - כוח ממוצע בהתרסקות

הנוסחה לכוח ממוצע היא:

\[F_{\text{avg}} = \frac{\Delta p}{\Delta t}\]

בהתרסקות נתוני המערכת:

• מהירות התחלתית (המהירות לפני ההתרסקות):

  \[v_i = 194.44 \,\mathrm{m/s}\]

• מהירות סופית: (המסה נעצרת)

  \[v_f = 0\]

• זמן התרסקות:

  \[\Delta t = 0.1 \mathrm{s}\]

שינוי התנע:

\[\Delta p = m(v_f - v_i) = 5000 \times (0 - 194.44) = -972,200 \text{ kg·m/s}\]

הכוח הממוצע:

\[F_{\text{avg}} = \frac{\Delta p}{\Delta t} = \frac{-972,200}{0.1} = -9,722,000 \text{ N} = \boxed{-9.72 \text{ MN}}\]

הסימן השלילי מציין שהכוח פועל בכיוון ההפוך לתנועה (כוח בלימה).

זה כוח עצום - אל תתרסקו במהירות גבוהה.

---

סעיף ג - שינוי באנרגיה קינטית

נחשב את ההפרש באנרגיה הקינטית לפני ואחרי ההאצה.

אנרגיה קינטית התחלתית:

\[E_{k1} = \frac{1}{2}mv_1^2 = \frac{1}{2} \times 5000 \times (138.89)^2 = 48,229,167 \text{ J} \approx 48.23 \text{ MJ}\]

אנרגיה קינטית סופית:

\[E_{k2} = \frac{1}{2}mv_2^2 = \frac{1}{2} \times 5000 \times (194.44)^2 = 94,618,519 \text{ J} \approx 94.62 \text{ MJ}\]

השינוי באנרגיה הקינטית:

\[\begin{aligned} \Delta E_k &= E_{k2} - E_{k1} \\[5pt] &= 94.62 - 48.23 \\[5pt] &= \boxed{46.39 \text{ MJ}} \end{aligned}\]

הסבר: האנרגיה שהושקעה בהאצת המסה (46.39 מגה-ג’אול) הופכת לאנרגיה קינטית. בהתרסקות, כל האנרגיה הזו (94.62 MJ) הופכת לחום, עיוות, וצורות אנרגיה אחרות.

---

שאלה 3: כוחות מרכזיים

על חלקיק מסיבי פועל כוח מרכזי מהצורה:

\[\vec{F}(r) = f(r)\hat{r}\]

1. הסבירו מה פירוש כוח מרכזי ומדוע הביטוי למעלה הוא הביטוי הכללי ביותר שאפשר לרשום עבור כוח מרכזי.

2. הראו שאפשר לרשום את הביטוי עבור כוח מרכזי גם כ:

   \[\vec{F}(r) = \frac{f(r)}{r}\vec{r}\]

3. הראו שבשני מימדים אפשר לרשום את הכוח המרכזי גם כך:

   \[\vec{F}(x,y) = f(\sqrt{x^2 + y^2})\cos(\tan^{-1}(y/x))\hat{x} + f(\sqrt{x^2 + y^2})\sin(\tan^{-1}(y/x))\hat{y}\]

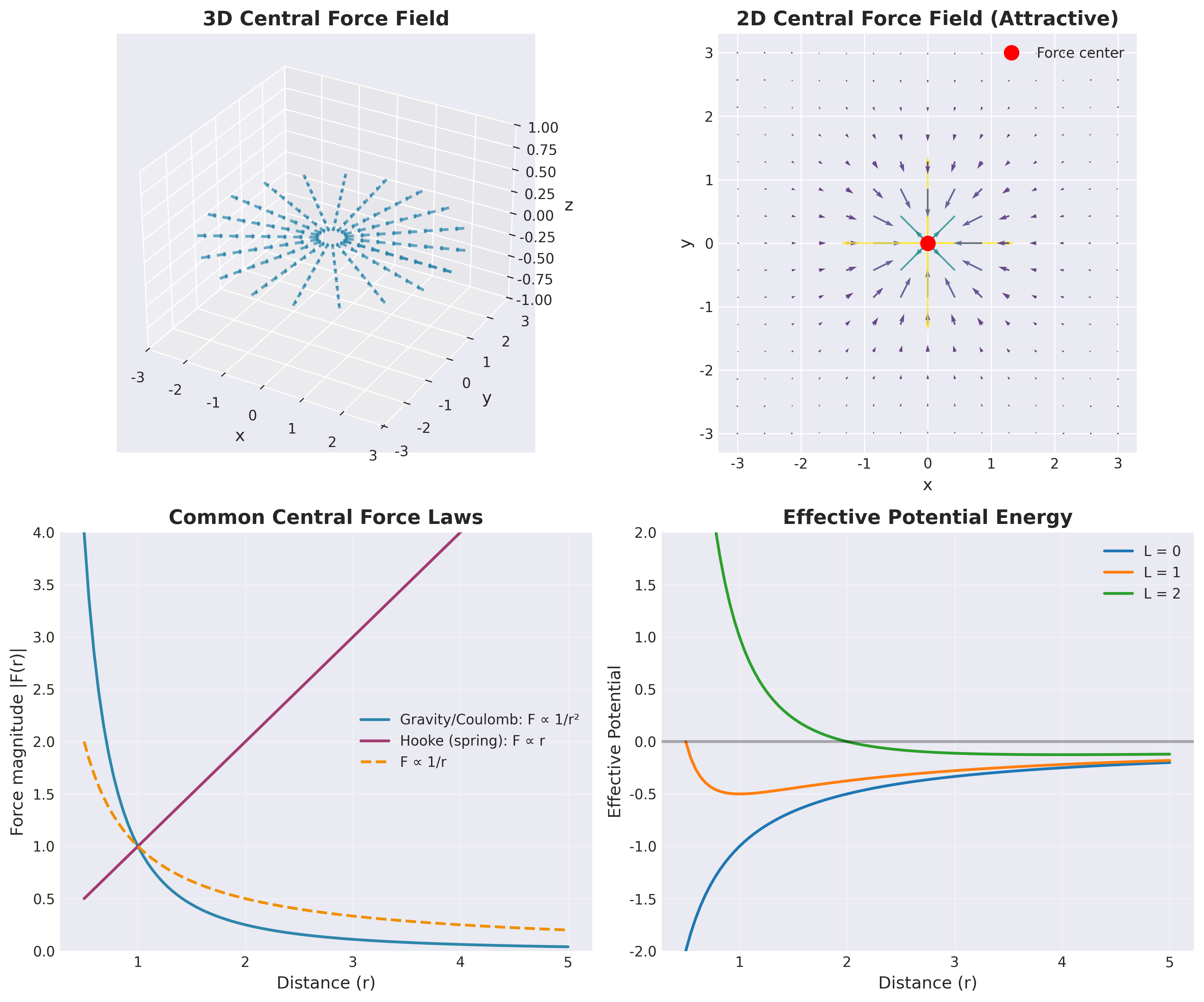
(תודה למודל החדש של Anthropic על הפתרון הבא)

סעיף א - הגדרת כוח מרכזי

כוח מרכזי הוא כוח שמקיים שני תנאים:

1. כיוון הכוח: הכוח פועל תמיד לאורך הקו המחבר בין החלקיק למרכז הכוח (בדרך כלל הראשית)
2. גודל הכוח: גודל הכוח תלוי רק במרחק מהמרכז, לא בכיוון

הביטוי $\vec{F}(r) = f(r)\hat{r}$ הוא הכללי ביותר כי:

• $\hat{r}$ מבטיח שהכיוון תמיד רדיאלי (מהמרכז החוצה או פנימה)
• $f(r)$ היא פונקציה כללית של המרחק בלבד (יכולה להיות חיובית או שלילית)
• אין תלות בזוויות - רק במרחק

דוגמאות לכוחות מרכזיים:

• כוח הכבידה: $f(r) = -\frac{GMm}{r^2}$
• כוח קולון: $f(r) = \frac{kq_1q_2}{r^2}$
• כוח הוק (קפיץ רדיאלי): $f(r) = -k(r-r_0)$

סעיף ב - ייצוג חלופי

נזכור ש:

\[\hat{r} = \frac{\vec{r}}{r}\]

לכן:

\[\vec{F}(r) = f(r)\hat{r} = f(r) \cdot \frac{\vec{r}}{r} = \frac{f(r)}{r}\vec{r}\]

זה ייצוג שקול - במקום להשתמש בווקטור היחידה הרדיאלי, משתמשים בווקטור המיקום עצמו ומנרמלים אותו.

סעיף ג - ייצוג בקואורדינטות קרטזיות

בקואורדינטות קרטזיות:

• $r = \sqrt{x^2 + y^2}$
• $\theta = \tan^{-1}(y/x)$

וקטור היחידה הרדיאלי בקואורדינטות קרטזיות:

\[\hat{r} = \cos\theta\hat{x} + \sin\theta\hat{y}\]

כאשר:

• $\cos\theta = \cos(\tan^{-1}(y/x)) = \frac{x}{\sqrt{x^2 + y^2}}$
• $\sin\theta = \sin(\tan^{-1}(y/x)) = \frac{y}{\sqrt{x^2 + y^2}}$

לכן:

\[\vec{F}(x,y) = f(r)\hat{r} = f[\sqrt{x^2 + y^2}](\cos(\tan^{-1}(y/x))\hat{x} + \sin(\tan^{-1}(y/x))\hat{y})\]

הערה: בפועל, נוח יותר להשתמש בביטוי:

\[\vec{F}(x,y) = f(\sqrt{x^2 + y^2}) \cdot \frac{x\hat{x} + y\hat{y}}{\sqrt{x^2 + y^2}}\]

---

שאלה 4: התנגשות וחוקי שימור

הראו שחוק שימור האנרגיה וחוק שימור התנע הקווי בהתנגשות מצחית של שתי מסות $m_1, m_2$ הנעות על קו ישר מובילים אל הקשר:

\[v_2 - v_1 = -(u_2 - u_1)\]

או:

\[\Delta v = -\Delta u\]

כאשר $v_1, v_2$ הן מהירויות המסות (בהתאמה) לפני ההתנגשות, ו-$u_1, u_2$ הן מהירויות המסות (בהתאמה) אחרי ההתנגשות.

נשתמש בשני חוקי השימור:

1. שימור תנע:

\[m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2\]

נסדר מחדש:

\[m_1(u_1 - v_1) = m_2(v_2 - u_2) \quad \tag{1}\]

2. שימור אנרגיה (התנגשות אלסטית):

\[\frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2\]

נסדר:

\[m_1(u_1^2 - v_1^2) = m_2(v_2^2 - u_2^2)\]

נפרק לגורמים:

\[m_1(u_1 - v_1)(u_1 + v_1) = m_2(v_2 - u_2)(v_2 + u_2) \tag{2}\]

נחלק משוואה $(2)$ במשוואה $(1)$:

\[\frac{m_1(u_1 - v_1)(u_1 + v_1)}{m_1(u_1 - v_1)} = \frac{m_2(v_2 - u_2)(v_2 + u_2)}{m_2(v_2 - u_2)}\]

נקבל:

\[u_1 + v_1 = v_2 + u_2\]

נסדר מחדש:

\[v_2 - v_1 = -(u_2 - u_1)\]

או:

\[\Delta v = -\Delta u\]

המשמעות הפיזיקלית: בהתנגשות אלסטית חד-ממדית, המהירות היחסית בין שני הגופים הופכת את כיוונה אך שומרת על גודלה. נראה שזה תנאי הכרחי לשימור האנרגיה הקינטית בהתנגשות.

---

שאלה 5: התנגשות פלסטית ומסה מצומצמת

שני גופים שמסתם $m_1, m_2$ נעים זה לעבר זה במהירויות $v_1, v_2$ בהתאמה, ומתנגשים זה בזה בהתנגשות פלסטית. לאחר ההתנגשות הם ממשיכים לנוע יחדיו במהירות $v$.

הראו שהאנרגיה הקינטית שאובדת בתהליך ההתנגשות ניתנת בביטוי:

\[\Delta E_k = \frac{1}{2}\mu(m_1, m_2)(\Delta v)^2\]

כאשר $\Delta v = v_1 - v_2$ וכן:

\[\mu(m_1, m_2) = \frac{m_1m_2}{m_1 + m_2}\]

היא המסה המצומצמת של שני הגופים.

שלב 1: מציאת המהירות הסופית

משימור התנע:

\[m_1v_1 + m_2v_2 = (m_1 + m_2)v\]

לכן:

\[v = \frac{m_1v_1 + m_2v_2}{m_1 + m_2}\]

שלב 2: חישוב האנרגיה הקינטית ההתחלתית

\[E_{k,i} = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2\]

שלב 3: חישוב האנרגיה הקינטית הסופית

\[E_{k,f} = \frac{1}{2}(m_1 + m_2)v^2 = \frac{1}{2}(m_1 + m_2)\left(\frac{m_1v_1 + m_2v_2}{m_1 + m_2}\right)^2\] \[= \frac{(m_1v_1 + m_2v_2)^2}{2(m_1 + m_2)}\]

שלב 4: חישוב האובדן באנרגיה

\[\Delta E_k = E_{k,f} - E_{k,i}\]

אחרי אלגברה מפורטת (שכוללת פיתוח ריבועים וסידור מחדש) אפשר לכאורה להגיע לביטוי:

\[\Delta E_k = -\frac{1}{2}\frac{m_1m_2}{m_1 + m_2}(v_1 - v_2)^2\]

הסימן השלילי מציין אובדן אנרגיה. בערך מוחלט:

\[|\Delta E_k| = \frac{1}{2}\mu(\Delta v)^2\]

כאשר $\mu = \frac{m_1m_2}{m_1 + m_2}$ היא המסה המצומצמת.

הסבר פיזיקלי: המסה המצומצמת מייצגת את “המסה האפקטיבית” של מערכת שני הגופים כאשר בוחנים את התנועה היחסית ביניהם. האנרגיה שאובדת תלויה במהירות היחסית ההתחלתית ובמסה המצומצמת.

---

שאלה 6: החזרה אלסטית מרצפה

הסבירו לעצמכם: מדוע כדור אלסטי לחלוטין הפוגע ברצפה בזווית α ביחס לאנך לרצפה, חייב לנתר מהרצפה בדיוק באותה זווית ובדיוק באותו גודל של מהירות?

פתרון והסבר

נפרק את המהירות לרכיבים:

• רכיב מאוזן (מקביל לרצפה): $v_x = v\sin\alpha$
• רכיב מאונך (ניצב לרצפה): $v_y = v\cos\alpha$

בהתנגשות אלסטית מושלמת עם רצפה:

1. הרכיב המאוזן ($v_x$):
   • לא פועל כוח בכיוון המאוזן
   • לכן: $v’_x = v_x = v\sin\alpha$
2. הרכיב המאונך ($v_y$):
   • בהתנגשות אלסטית מושלמת, הרכיב המאונך מתהפך בכיוון
   • גודלו נשמר (שימור אנרגיה)
   • לכן: $v’_y = -v_y = -v\cos\alpha$ (כיוון למעלה)

חישוב הזווית והמהירות אחרי ההחזרה:

גודל המהירות:

\[v' = \sqrt{ {v'_x}^2 + {v'_y}^2 } = \sqrt{ (v\sin\alpha)^2 + (v\cos\alpha)^2 } = v\]

הזווית ביחס לאנך:

\[\tan \alpha' = \frac{v'_x}{\vert v'_y\vert } = \frac{v\sin \alpha}{v \cos \alpha} = \tan \alpha\]

לכן: $\alpha’ = \alpha$

סיכום: בהתנגשות אלסטית מושלמת:

• גודל המהירות נשמר (שימור אנרגיה)
• זווית הפגיעה שווה לזווית ההחזרה (חוק ההחזרה)

מסתבר שזה עיקרון בסיסי באופטיקה גיאומטרית (החזרת אור) ובמכניקה. לא למדתי את הדברים האלה מעולם אבל ככה עולה מגוגל.

---

שאלה 7: התפוצצות פצצה ושימור תנע

פצצה מתפוצצת בנקודה מסוימת באוויר.

הסבירו מדוע - למרות שפועל כוח חיצוני על הפצצה (כוח הכבידה) - אפשר לומר במידה רבה של אמת שווקטור התנע השקול של כל חלקי הפצצה אחרי ההתפוצצות שווה בקירוב מצוין לווקטור התנע השקול של הפצצה לפני ההתפוצצות?

ניתוח הכוחות:

1. כוחות פנימיים (הפיצוץ):
   • כוחות עצומים בין חלקי הפצצה
   • פועלים לזמן קצר מאוד (מילישניות)
   • לפי החוק השלישי של ניוטון - מבטלים זה את זה בסכום הכולל
2. כוח חיצוני (כבידה):
   • $\mathbf{F}_{\text{gravity}} = Mg$ (כאשר M מסת הפצצה)
   • פועל באופן רציף

השוואת המתקפים:

המתקף מכוח הכבידה במשך זמן הפיצוץ $\Delta t$:

\[J_{\text{gravity}} = Mg \cdot \Delta t\]

כאשר $\Delta t \approx 0.001$ שניות (אופייני לפיצוץ), המתקף זניח.

לעומת זאת, השינוי בתנע של חלקי הפצצה עקב הפיצוץ הוא עצום:

\[\Delta p_{\text{fragments}} \gg J_{\text{gravity}}\]

מסקנה: בזמן הקצר של הפיצוץ, אפשר להזניח את השפעת הכבידה ולהתייחס למערכת כמבודדת. לכן:

\[\vec{P}_{i} \approx \vec{P}_{f}\]

הסבר מתמטי מפורט:

נניח שהפצצה בעלת מסה $M$ נעה במהירות $\vec{V}$ לפני הפיצוץ.

התנע לפני הפיצוץ:

\[\vec{P}_{i} = M\vec{V}\]

אחרי הפיצוץ, הפצצה מתפרקת ל-n חלקים עם מסות $m_i$ ומהירויות $\vec{v}_i$:

\[\vec{P}_{f} = \sum_{i=1}^{n} m_i\vec{v}_i\]

עקרון הקירוב:

• זמן הפיצוץ:

  \[\Delta t \approx 10^{-3} \, \mathrm{s}\]

• שינוי התנע מכבידה:

  \[\Delta P_g = Mg\Delta t \approx 10^{-2}M\]

• שינוי תנע טיפוסי של רסיס:

  \[\Delta P_{\text{frag}} \approx m_i \times 1000 \, \mathrm{m/s}\]

היחס:

\[\frac{\Delta P_g}{\Delta P_{\text{frag}}} \approx \frac{10^{-2}M}{m_i \times 1000} \ll 1\]

דוגמה מספרית:

• פצצה במסה 100 ק”ג
• זמן פיצוץ: 0.001 שניות

• מתקף הכבידה:

  \[J_g = 100 \times 10 \times 0.001 = 1 \, \mathrm{kg \cdot m/s}\]

• שינוי תנע טיפוסי של רסיס:

  \[\Delta P_{\text{frag}} \approx 0.1 \, \mathrm{kg} \times 1000 \, \mathrm{m/s} = 100 \, \mathrm{kg \cdot m/s}\]

היחס: $\frac{1}{1000} = 0.001$ - זניח לחלוטין!

יישומים מעשיים:

1. בליסטיקה: חישוב מסלולי רסיסים
2. בטיחות: הערכת טווח סיכון
3. פירוטכניקה: תכנון זיקוקים (תבנית סימטרית)

---

סיכום עקרונות מרכזיים מהתרגיל

1. תנועה הרמונית ומסלולים

• שילוב של תנועות הרמוניות בכיוונים מאונכים יוצר מסלולים אליפטיים
• במקרה המיוחד של משרעות שוות - מתקבלת תנועה מעגלית

2. חוקי שימור בהתנגשויות

• התנגשות אלסטית: נשמרים תנע ואנרגיה קינטית
• התנגשות פלסטית: נשמר רק התנע, אנרגיה “אובדת” (הופכת לחום ולעיוות)

3. כוחות מרכזיים

• כוחות שהכיוון שלהם רדיאלי והגודל שלהם תלוי רק במרחק
• חשובים מאוד בפיזיקה: כבידה, כוחות חשמליים, ועוד

4. מתקף וכוחות

• מתקף = שינוי בתנע = $\int F dt$
• בזמנים קצרים, כוחות גדולים יוצרים מתקפים משמעותיים (הדוגמה בשיעור הייתה לגבי קפיצה ממגדל - מזרן עבה מאריך את זמן ההתרסקות - אם הזמן גדל פי 100, הכוח הממוצע קטן פי 100)

---

טיפים שספק יעזרו

1. המרת יחידות: תמיד וודאו שכל הגדלים באותן יחידות (SI עדיף)
2. בדיקת ממדים: וודאו שהתוצאה הסופית ביחידות הנכונות
3. בדיקת סבירות: האם התוצאה הגיונית? (למשל, אנרגיה חיובית)
4. ציור דיאגרמות: במיוחד בבעיות התנגשות וכוחות
5. שימוש בחוקי שימור: לעתים קרובות הדרך הקלה ביותר לפתרון

פתרון תרגיל מספר 8 - תנועה, כוחות ושימור

תאריך: 24/06/2025

הקדמה: מושגי יסוד בעבודה ואנרגיה

עבודה (Work) היא גודל סקלרי המתאר את האנרגיה המועברת לגוף או ממנו כאשר כוח פועל עליו לאורך מסלול מסוים. מתמטית, העבודה מוגדרת כמכפלה הסקלרית של הכוח וההעתק:

\[W = \mathbf{F} \cdot \Delta\mathbf{r} = F \cdot \Delta r \cdot \cos\alpha\]

כאשר $\alpha$ היא הזווית בין כיוון הכוח לכיוון ההעתק. שימו לב שרק הרכיב של הכוח בכיוון התנועה תורם לעבודה - זו הסיבה שאנחנו משתמשים במכפלה סקלרית.

כאשר הכוח משתנה לאורך המסלול, אנחנו צריכים לחשב את העבודה כאינטגרל:

\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F} \cdot d\mathbf{r}\]

משפט עבודה-אנרגיה הוא אחד המשפטים החשובים ביותר במכניקה. הוא קובע שהעבודה הכוללת שמבצעים כל הכוחות על גוף שווה לשינוי באנרגיה הקינטית שלו:

\[W_{\text{total}} = \Delta E_k = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\]

משפט זה מאפשר לנו לפתור בעיות מורכבות בלי לדעת את כל פרטי התנועה - מספיק לדעת את המצב ההתחלתי ואת המצב הסופי.

הספק (Power) מתאר את קצב ביצוע העבודה (לפי ההגדרה בכתה: ״השינוי הרגעי בעבודה שמבצע כוח $\mathbf{F}$ על גוף במהלך תנועתו״). הוא מוגדר כנגזרת של העבודה לפי הזמן:

\[P = \frac{dW}{dt} = \mathbf{F} \cdot \mathbf{v}\]

---

שאלה 1: גרירת מזוודה

מזוודה אשר מסתה 20 קילוגרם נגררת על רצפת הטרמינל בכוח של 50 ניוטון ובזווית של 45 מעלות מעל האופק לאורך דרך של מאה מטר.

1. מה משקל המזוודה במהלך גרירתה?
2. כמה עבודה ביצע הגורר לאורך מסלול הגרירה?
3. בהנחה שמהירות המזוודה קבועה לאורך כל הדרך, כמה עבודה ביצע כוח החיכוך על המזוודה לאורך מסלול הגרירה?
4. מהו מקדם החיכוך אם ידוע שהוא מתכונתי לגודלו של הכוח הנורמלי?

פתרון מפורט

נתונים:

• מסה: $m = 20 \, \mathrm{kg}$
• כוח גרירה: $F = 50 \, \mathrm{N}$
• זווית: $\alpha = 45°$
• מרחק: $\Delta x = 100 \, \mathrm{m}$

סעיף א: משקל המזוודה

המשקל של גוף הוא הכוח שמפעיל עליו כדור הארץ, והוא תמיד נתון על ידי:

\[\mathbf{W} = m\mathbf{g} \approx 20 \times 10 = 200 \, \mathrm{N}\]

שימו לב: המשקל אינו תלוי בכוחות אחרים הפועלים על הגוף. גם אם מישהו מרים את המזוודה או גורר אותה, המשקל שלה נשאר קבוע (כל עוד אנחנו באותו מקום על פני כדור הארץ).

הערה נוספת: לא ברור לי למרי האם המשקל בקורס הוא וקטור (עם כיוון) או סקאלר. נראה שקבוע הכבידה הוא בדרך כלל סקאלר, ובכל מקרה פועל כלפי מטה.

סעיף ב: העבודה שביצע הגורר

כשמחשבים עבודה, רק הרכיב של הכוח בכיוון התנועה תורם לתוצאה. במקרה שלנו, הכוח פועל בזווית של 45° לאופק, אבל התנועה היא אופקית. לכן:

\[W = F \cos\alpha \cdot \Delta x = 50 \times \cos(45°) \times 100\]

נחשב את הקוסינוס:

\[\cos(45°) = \frac{\sqrt{2}}{2} \approx 0.707\]

לכן:

\[W = 50 \times 0.707 \times 100 = 3535 \text{ J}\]

סעיף ג: עבודת כוח החיכוך

כשגוף נע במהירות קבועה התאוצה שלו היא אפס. לפי החוק השני של ניוטון, זה אומר שסכום הכוחות שפועלים עליו הוא אפס.

בציר האופקי (כיוון x):

\[\sum F_x = 0\] \[F\cos\alpha + f_{\text{friction}} = 0\]

כאן $f_{\text{friction}}$ הוא כוח החיכוך (שלילי כי הוא מתנגד לתנועה):

\[f_{\text{friction}} = -F\cos\alpha = -50 \times 0.707 = -35.35 \, \mathrm{N}\]

העבודה של כוח החיכוך:

\[W_f = f_{\text{friction}} \cdot \Delta x = -35.35 \times 100 = -3535 \text{ J}\]

שימו לב: העבודה של כוח החיכוך שלילית כי הוא פועל בכיוון הפוך לתנועה. זה אומר שכוח החיכוך “גוזל” אנרגיה מהמערכת (הופך אותה לחום).

דרך נוספת להגיע לתוצאה הזאת (שבאופן מעניין הבינה המלאכותית לא הציעה לי אותה), היא בעזרת משפט עבודה אנרגיה:

\[W_{\text{total}} = \Delta E_k\]

מכיוון שהמהירות קבועה, אין שינוי באנרגיה הקינטית:

\[\Delta E_k = 0\]

לכן:

\[W_{\text{total}} = W + W_f = 0\]

מכאן:

\[W = -W_f \implies W_f = -W = -3535 \text{ J}\]

סעיף ד: מקדם החיכוך

כדי למצוא את מקדם החיכוך, נמצא קודם את הכוח הנורמלי. נשתמש בשיווי משקל בציר האנכי (כיוון y):

\[\sum F_y = 0\] \[N + F\sin\alpha - mg = 0\]

מכאן:

\[\begin{aligned} N &= mg - F\sin\alpha \\[10pt] &\approx 200 - 50 \times 0.707 \\[10pt] &= 200 - 35.35 = 164.65 \, \mathrm{N} \end{aligned}\]

עכשיו נוכל לחשב את מקדם החיכוך הקינטי:

\[\mu_k = \frac{|f_{\text{friction}}\vert}{N} \approx \frac{35.35}{160.65} = 0.22 \, \text{ (unitless)}\]

לפי גוגל זה ערך סביר למקדם חיכוך בין מזוודה לרצפת טרמינל.

תזכורת: מקדם החיכוך הוא היחס בין שני כוחות - כוח החיכוך לבין הכוח הנורמלי. מכאן שהוא חסר יחידות.

---

שאלה 2: כוח כבידה על פלנטה

כוח הכבידה בין גוף מאוד מסיבי כמו כוכב לבין גוף הרבה פחות מסיבי כמו פלנטה הסובבת אותו, נתון בביטוי:

\[\mathbf{F}(r) = -\frac{\alpha}{r^3}\mathbf{r}\]

באשר $\mathbf{r}$ הוא וקטור המקום של הפלנטה במערכת צירים אשר ראשיתה יושבת במרכז הכוכב, $\alpha$ הוא פרמטר כלשהו שתלוי במסות של שני הגופים.

עוד ידוע שהפלנטה סובבת את הכוכב במסלול אליפטי כך ש-

\[\mathbf{r}(t) = a\cos(\omega t)\mathbf{\hat{x}} + b\sin(\omega t)\mathbf{\hat{y}}\]

1. אם $\omega = 2 \times 10^{-7} \text{ sec}^{-1}$ כמה ימים אורכת שנה אחת על פני הפלנטה?
2. הסבירו מדוע $d\mathbf{r} = \mathbf{v}dt$
3. קבלו ביטוי עבור העבודה כאינטגרל על הזמן
4. חשבו כמה עבודה מבצע הכוכב על הפלנטה בארבעה חודשים
5. חשבו כמה עבודה מבצע הכוכב על הפלנטה בשנה שלמה

פתרון מפורט

זו שאלה מגניבה לעניות דעתי. הכוח הנתון הוא כוח מרכזי (פועל לכיוון המרכז - ראו פתרון תרגיל 7) והמסלול הוא אליפטי - בדיוק כפי שחזה קפלר וניסח ניוטון.

סעיף א: משך השנה

התדירות הזוויתית $\omega$ קשורה לזמן המחזור $T$ על ידי:

\[T = \frac{2\pi}{\omega}\]

נציב את הנתון:

\[T = \frac{2\pi}{2 \times 10^{-7}} = \pi \times 10^7 \text{ seconds}\]

כדי להמיר לימים, נחלק במספר השניות ביממה:

\[T = \frac{\pi \times 10^7}{86400} \approx 363.6 \text{ days}\]

זה קרוב מאוד לשנה ארצית!

סעיף ב: הקשר $d\mathbf{r} = \mathbf{v}dt$

זאת למעשה ההגדרה הבסיסית של מהירות. המהירות היא קצב השינוי של המיקום:

\[\mathbf{v} = \frac{d\mathbf{r}}{dt}\]

כאשר אנחנו מסדרים מחדש:

\[d\mathbf{r} = \mathbf{v}dt\]

זה אומר שהשינוי האינפיניטסימלי במיקום שווה למהירות כפול השינוי האינפיניטסימלי בזמן.

סעיף ג: העבודה כאינטגרל על הזמן

נתחיל מההגדרה הבסיסית של עבודה:

\[dW = \mathbf{F} \cdot d\mathbf{r}\]

נשתמש בתוצאה מסעיף ב:

\[dW = \mathbf{F} \cdot \mathbf{v}dt\]

לכן העבודה הכוללת היא:

\[W = \int_{t_1}^{t_2} \mathbf{F} \cdot \mathbf{v} dt\]

זאת נוסחה שימושית כשיודעים את הכוח והמהירות כפונקציות של הזמן.

סעיף ד: עבודה בארבעה חודשים

כדי לחשב את העבודה, נצטרך למצוא קודם את המהירות:

\[\mathbf{v} = \frac{d\mathbf{r}}{dt} = -a\omega\sin(\omega t)\mathbf{\hat{x}} + b\omega\cos(\omega t)\mathbf{\hat{y}}\]

עכשיו נחשב את המכפלה הסקלרית $\mathbf{F} \cdot \mathbf{v}$. ראשית, נמצא את $r^3$:

\[r^2 = a^2\cos^2(\omega t) + b^2\sin^2(\omega t)\] \[r^3 = [a^2\cos^2(\omega t) + b^2\sin^2(\omega t)]^{3/2}\]

המכפלה הסקלרית:

\[\mathbf{F} \cdot \mathbf{v} = -\frac{\alpha}{r^3}(\mathbf{r} \cdot \mathbf{v})\]

נחשב את $\mathbf{r} \cdot \mathbf{v}$:

\[\mathbf{r} \cdot \mathbf{v} = a\cos(\omega t) \cdot (-a\omega\sin(\omega t)) + b\sin(\omega t) \cdot (b\omega\cos(\omega t))\] \[= -a^2\omega\cos(\omega t)\sin(\omega t) + b^2\omega\sin(\omega t)\cos(\omega t)\] \[= \omega\sin(\omega t)\cos(\omega t)(b^2 - a^2)\]

תוצאה מעניינת: אם $a = b$ (מסלול מעגלי), אז $\mathbf{r} \cdot \mathbf{v} = 0$, מה שאומר שהכוח תמיד ניצב למהירות והעבודה היא אפס!

סעיף ה: עבודה בשנה שלמה

זוהי תוצאה כללית חשובה: בכל תנועה מחזורית סגורה תחת כוח משמר (כמו כוח הכבידה), העבודה הכוללת במחזור שלם היא תמיד אפס. הסיבה פשוטה: הגוף חוזר לאותה נקודה עם אותה מהירות, ולכן האנרגיה הקינטית שלו לא השתנתה. לפי משפט עבודה-אנרגיה, העבודה חייבת להיות אפס.

---

שאלה 3: עבודה לאורך משולש

חשבו את העבודה שמבצע הכוח

\[\mathbf{F}(x,y) = 2\sinh(x+y)\mathbf{\hat{x}} + 2\cosh(x-y)\mathbf{\hat{y}}\]

על גוף כלשהו הנגרר לאורך צלעות המשולש ישר-הזווית אשר קודקודיו הם הנקודות:

\[(0,0), (\ln 2, 0), (\ln 2, \ln 2)\]

וקטור השדה	היטלי הכוח על צלעות המשולש

פתרון - חישוב עבודה לאורך משולש

נחלק את החישוב לשלוש צלעות המשולש.

צלע 1: מ-$(0,0)$ ל-$(\ln 2, 0)$

לאורך צלע זו, $y = 0$ ו-$dy = 0$. לכן:

\[W_1 = \int_0^{\ln 2} F_x(x,0)dx = \int_0^{\ln 2} 2\sinh(x)dx\]

נחשב את האינטגרל:

\[W_1 = 2[\cosh(x)]_0^{\ln 2} = 2(\cosh(\ln 2) - \cosh(0))\]

נשתמש בהגדרה: $\cosh(x) = \frac{e^x + e^{-x}}{2}$

עבור $x = \ln 2$:

\[\cosh(\ln 2) = \frac{e^{\ln 2} + e^{-\ln 2}}{2} = \frac{2 + 1/2}{2} = 1.25\]

כמו כן, $\cosh(0) = 1$.

לכן:

\[\boxed{W_1 = 2(1.25 - 1) = 0.5 \text{ J}}\]

צלע 2: מ-$(\ln 2, 0)$ ל-$(\ln 2, \ln 2)$

לאורך צלע זו, $x = \ln 2$ ו-$dx = 0$. לכן:

\[W_2 = \int_0^{\ln 2} F_y(\ln 2, y)dy = \int_0^{\ln 2} 2\cosh(\ln 2 - y)dy\]

נבצע החלפת משתנים: $u = \ln 2 - y$, אז $du = -dy$:

\[W_2 = -\int_{\ln 2}^0 2\cosh(u)du = \int_0^{\ln 2} 2\cosh(u)du = 2[\sinh(u)]_0^{\ln 2}\]

כאשר $\sinh(\ln 2) = \frac{e^{\ln 2} - e^{-\ln 2}}{2} = \frac{2 - 1/2}{2} = 0.75$

לכן:

\[\boxed{W_2 = 2(0.75 - 0) = 1.5 \text{ J}}\]

צלע 3: מ-$(\ln 2, \ln 2)$ ל-$(0,0)$ לאורך היתר

על היתר של משולש ישר-זווית שווה-שוקיים מתקיים $x = y$. נוכל להגדיר:

• $x = y = t$
• $t$ משתנה מ-$\ln 2$ ל-$0$
• $dx = dy = dt$

העבודה לאורך צלע זו:

\[\begin{aligned} W_3 &= \int_{\ln 2}^0 [F_x(t,t)dt + F_y(t,t)dt] \\[10pt] &= \int_{\ln 2}^0 [2\sinh(2t) + 2\cosh(0)]dt \\[10pt] &= \int_{\ln 2}^0 [2\sinh(2t) + 2]dt \end{aligned}\]

נחשב:

\[\begin{aligned} W_3 &= [2 \cdot \frac{1}{2}\cosh(2t) + 2t]_{\ln 2}^0 \\[10pt] &= [\cosh(2t) + 2t]_{\ln 2}^0 \\[10pt] &= (1 + 0) - (\cosh(2\ln 2) + 2\ln 2) \end{aligned}\]

כאשר $\cosh(2\ln 2) = \cosh(\ln 4) = \frac{4 + 1/4}{2} = 2.125$

לכן:

\[\boxed{W_3 = 1 - 2.125 - 2\ln 2 = 1 - 2.125 - 1.386 = -2.511 \text{ J}}\]

העבודה הכוללת:

\[\boxed{W_{\text{total}} = W_1 + W_2 + W_3 = 0.5 + 1.5 - 2.511 = -0.511 \text{ J}}\]

העובדה שהעבודה לאורך המסלול הסגור אינה אפס מעידה על כך שהכוח אינו משמר.

---

שאלה 4: הספק

ההספק P (Power) מוגדר כשינוי הרגעי בעבודה שמבצע כוח על גוף במהלך תנועתו.

1. הוכיחו: $P = \mathbf{F} \cdot \mathbf{v}$
2. קבלו ביטוי עבור ההספק הרגעי של עבודת הכוכב על הפלנטה מהשאלה הקודמת
3. טורבינת רוח בחוות עמק הבכא שברמת הגולן עובדת בהספק של 3.2 מגה-ואט. כמה אנרגיה מייצרת החווה כולה בשעת עבודה אחת, אם ידוע שיש בה 36 טורבינות פעילות?

4. באזור מסוים ע”פ כדור הארץ הספק טורבינת הרוח הוא פונקציה של הזמן כך ש-

   \[P(t) = 3.2\sin\left(\frac{2\pi}{\text{day}}t\right)\]

   כמה אנרגיה מייצרת הטורבינה הנ”ל ביממה אחת?

פתרון מפורט

סעיף א: הוכחת הנוסחה להספק

נתחיל מההגדרה של הספק:

\[P = \frac{dW}{dt}\]

נזכור שהעבודה האינפיניטסימלית היא:

\[dW = \mathbf{F} \cdot d\mathbf{r}\]

לכן:

\[P = \frac{dW}{dt} = \frac{\mathbf{F} \cdot d\mathbf{r}}{dt} = \mathbf{F} \cdot \frac{d\mathbf{r}}{dt} = \mathbf{F} \cdot \mathbf{v}\]

זוהי נוסחה אינטואיטיבית: ההספק גדל כאשר הכוח גדל וכאשר המהירות בכיוון הכוח גדלה.

סעיף ב: הספק רגעי של הכוכב על הפלנטה

משאלה 2, מצאנו ש:

\[\mathbf{F} \cdot \mathbf{v} = -\frac{\alpha\omega\sin(\omega t)\cos(\omega t)(b^2 - a^2)}{r^3}\]

זהו ההספק הרגעי. שימו לב שהוא מחליף סימן - לפעמים הכוכב מבצע עבודה חיובית על הפלנטה (מאיץ אותה) ולפעמים שלילית (מאט אותה).

סעיף ג: אנרגיה מחוות טורבינות

ההספק הכולל של החווה:

\[P_{\text{total}} = 36 \times 3.2 = 115.2 \text{ MW}\]

האנרגיה המיוצרת בשעה:

\[E = P \times t = 115.2 \text{ MW} \times 1 \text{ hour} = 115.2 \text{ MWh}\]

זו כמות אנרגיה משמעותית - מספיקה לכ-100,000 בתים ליום אחד! (מקור מפוקפק)

סעיף ד: אנרגיה עם הספק משתנה

כאשר ההספק משתנה בזמן, האנרגיה הכוללת היא האינטגרל של ההספק:

\[E = \int_0^T P(t)dt = \int_0^{24} 3.2\sin\left(\frac{2\pi}{24}t\right)dt\]

נבצע החלפת משתנים: $u = \frac{2\pi}{24}t$, אז $du = \frac{2\pi}{24}dt$:

\[E = 3.2 \times \frac{24}{2\pi}\int_0^{2\pi} \sin(u)du\]

האינטגרל של סינוס על מחזור שלם הוא אפס:

\[\int_0^{2\pi} \sin(u)du = [-\cos(u)]_0^{2\pi} = -\cos(2\pi) + \cos(0) = -1 + 1 = 0\]

לכן $E = 0$.

תוצאה זו אולי מפתיעה, אבל היא הגיונית: במחצית היממה הטורבינה מייצרת אנרגיה (הספק חיובי) ובמחצית השנייה היא צורכת אנרגיה (הספק שלילי), והסכום הכולל הוא אפס. במציאות, כמובן, טורבינות לא צורכות אנרגיה - זו רק דוגמה מתמטית.

---

שאלה 5: עבודה ממשפט עבודה-אנרגיה

כתוצאה מעבודתו של כוח כלשהו, מבצע גוף שמסתו $m = 4$ ק”ג תנועה לאורך המסלול

\[\mathbf{r}(t) = (3t^2 - 2t)\mathbf{\hat{x}} + t^3\mathbf{\hat{y}} - t^4\mathbf{\hat{z}}\]

חשבו את העבודה שמבצע הכוח על הגוף במהלך השנייה השנייה לתנועתו.

פתרון - חישוב עבודה בעזרת משפט עבודה-אנרגיה

משפט עבודה-אנרגיה מאפשר לחשב את העבודה בלי לדעת את הכוח עצמו! כל שעלינו לעשות הוא למצוא את המהירויות בתחילת פרק הזמן ובסופו.

ראשית, נמצא את וקטור המהירות על ידי גזירה:

\[\mathbf{v}(t) = \frac{d\mathbf{r}}{dt} = (6t - 2)\mathbf{\hat{x}} + 3t^2\mathbf{\hat{y}} - 4t^3\mathbf{\hat{z}}\]

עבור השנייה השנייה, אנחנו מסתכלים על הפרק זמן מ-$t = 1$ עד $t = 2$.

ב-$t = 1$:

\[\mathbf{v}_1 = (6 - 2)\mathbf{\hat{x}} + 3\mathbf{\hat{y}} - 4\mathbf{\hat{z}} = 4\mathbf{\hat{x}} + 3\mathbf{\hat{y}} - 4\mathbf{\hat{z}}\]

גודל המהירות:

\[v_1 = \sqrt{4^2 + 3^2 + (-4)^2} = \sqrt{16 + 9 + 16} = \sqrt{41} \text{ m/s}\]

ב-$t = 2$:

\[\mathbf{v}_2 = (12 - 2)\mathbf{\hat{x}} + 12\mathbf{\hat{y}} - 32\mathbf{\hat{z}} = 10\mathbf{\hat{x}} + 12\mathbf{\hat{y}} - 32\mathbf{\hat{z}}\]

גודל המהירות:

\[v_2 = \sqrt{10^2 + 12^2 + (-32)^2} = \sqrt{100 + 144 + 1024} = \sqrt{1268} \text{ m/s}\]

נחשב את האנרגיות הקינטיות:

האנרגיה הקינטית ב-$t = 1$:

\[E_{k1} = \frac{1}{2}mv_1^2 = \frac{1}{2} \times 4 \times 41 = 82 \text{ J}\]

האנרגיה הקינטית ב-$t = 2$:

\[E_{k2} = \frac{1}{2}mv_2^2 = \frac{1}{2} \times 4 \times 1268 = 2536 \text{ J}\]

לפי משפט עבודה-אנרגיה:

\[W = E_{k2} - E_{k1} = 2536 - 82 = \boxed{2454 \text{ J}}\]

זוהי עבודה חיובית גדולה מאוד - הכוח האיץ את הגוף באופן משמעותי במהלך השנייה השנייה.

---

שאלה 6: ניתוח גרף כוח

הערה: השאלה גם הופיעה בדף התרגול הנוסף עם פתרון רשמי של המרצה. הפיתרון כאן הוא לא אותו פיתרון, אבל מגיע לאותן תוצאות.

הגרף המצורף מתאר את הכוח השקול הפועל על גוף שמסתו $m = 2 \, \mathrm{kg}$.

ידוע כי הגוף החל את תנועתו בראשית הצירים במהירות של ארבעה מטרים לשנייה $v(x = 0) = 4 \mathrm{m/s}$.

1. איזה גודל פיסיקלי מתואר ע”י השטח הכלוא בין הגרף ובין ציר ה-X?
2. חשבו את האנרגיה הקינטית של הגוף בנקודה $x = 3.0 \, \mathrm{m}$.
3. מהו שיעור הנקודה $x$ שבה יש לגוף אנרגיה קינטית של $8 \, \mathrm{J}$?
4. מהי האנרגיה הקינטית המקסימלית שהגוף מקבל בין הנקודה $x=0$ ל-$x=5$?
5. האם שינה הגוף את כיוון תנועתו בין $x=0$ ל-$x=5$?

פתרון מפורט

סעיף א: משמעות השטח מתחת לגרף

כאשר יש לנו גרף של כוח כפונקציה של מיקום, השטח מתחת לגרף מייצג את העבודה:

\[W = \int_{x_1}^{x_2} F(x)dx\]

זהו עיקרון חשוב: השטח החיובי (מעל ציר ה-x) מייצג עבודה חיובית, והשטח השלילי (מתחת לציר ה-x) מייצג עבודה שלילית.

סעיף ב: אנרגיה קינטית ב-x = 3 מטר

מהגרף, אנחנו רואים שהכוח יורד ליניארית מ-4 ניוטון ב-x=0 ל-0 ב-x=1, ואז ממשיך לרדת ל-(-4) ניוטון ב-$x=2$.

העבודה מ-x=0 עד x=3 היא השטח של משולש חיובי (מ-0 עד 1) ועוד שטח של משולש שלילי (מ-1 עד 2) ועוד שטח מלבן שלילי (מ-2 עד 3):

\[W_{0\to3} = -4 \text{ J}\]

האנרגיה הקינטית ההתחלתית:

\[E_{k0} = \frac{1}{2}mv_0^2 = \frac{1}{2} \times 2 \times 16 = 16 \text{ J}\]

לכן האנרגיה הקינטית ב-x=3:

\[E_{k3} = E_{k0} + W_{0\to3} = 16 - 4 = 12 \text{ J}\]

סעיף ג: נקודה עם אנרגיה קינטית של 8 ג’אול

נחפש נקודה שבה העבודה המצטברת היא:

\[W = 16 - 8 = 8 \text{ J}\]

מהגרף, נצטרך להמשיך מעבר ל-x=3 כדי להגיע לעבודה שלילית של 8 ג’אול. בין x=3 ל-x=4, הכוח קבוע ושווה ל-($-4$) ניוטון, כך שהעבודה היא:

\[W_{0\to 4} = 16 - 8 = 8 \text{ J}\]

סעיף ד: אנרגיה קינטית מקסימלית

האנרגיה הקינטית מקסימלית תהיה בנקודה שבה העבודה המצטברת החיובית היא מקסימלית. מהגרף, זה קורה ב-x=1, שם:

\[W_{0\to1} = \frac{1}{2} \times 1 \times 4 = 2 \text{ J}\]

לכן:

\[E_{k,\text{max}} = 16 + 2 = 18 \text{ J}\]

סעיף ה: שינוי כיוון

הגוף משנה כיוון כאשר המהירות שלו מתאפסת. זה קורה כאשר כל האנרגיה הקינטית נעלמת, כלומר כאשר $E_k = 0$.

נצטרך עבודה של:

\[W = 0 - 16 = -16 \text{ J}\]

כפי שחישבנו, העבודה הכוללת עד x=5 היא $-8$ ג’אול.

מכיוון שהעבודה הכוללת עד x=5 היא רק $-8$ ג’אול, ואנחנו צריכים $-16$ ג’אול כדי לעצור את הגוף, המסקנה היא שהגוף לא הגיע למצב של מהירות אפס בתחום הנתון. לכן, הגוף לא שינה את כיוון תנועתו.

זו דוגמה טובה לכך שכוח שלילי (מתנגד לתנועה) לא בהכרח גורם לגוף לעצור - זה תלוי בגודל האנרגיה הקינטית ההתחלתית ובגודל העבודה השלילית.