כל השיעורים בעמוד אחד
כל סיכומי השיעורים בקורס פיזיקה לרפואנים זמינים כאן להדפסה מרוכזת או ייצוא כ-PDF. התוכן מוצג בסדר כרונולוגי - מהסיכומים המוקדמים ביותר למאוחרים ביותר. אם חלק מהעמודים כוללים נוסחאות מתמטיות, ייתכן שייקח להן מספר שניות להיטען. למידה מהנה!
שיעור 1
תאריך: 16/03/2025רקע היסטורי
המכניקה הניוטונית, נושא הלימוד בקורס זה, פותחה במאה ה-17 על ידי שני ענקי המדע: גוטפריד וילהלם לייבניץ ואיזק ניוטון. שני אישים אלה, שהיו יריבים מפורסמים, תרמו כל אחד בדרכו להתפתחות הפיזיקה המודרנית.
לייבניץ (1716-1646) היה איש אשכולות במלוא מובן המילה - פילוסוף דגול שרעיונותיו נלמדים עד היום, מתמטיקאי שפיתח את החשבון האינפיניטסימלי, ואף המציא את רוב הסימונים המתמטיים שבהם אנו משתמשים כיום.
ניוטון (1727-1643), יריבו הגדול, היה לא רק מדען אלא גם תיאולוג שעסק רבות בפרשנות המקרא, במיוחד בנבואות אחרית הימים. הוא שלט בעברית והותיר אחריו כתבים רבים העוסקים בפענוח ספרי דניאל ויחזקאל. מעניין לציין שניוטון עסק גם באלכימיה וניסה להפוך חומרים פשוטים לזהב - משימה שהטבע אכן מבצע בליבות כוכבים כבדים, שם יסודות קלים הופכים ליסודות כבדים יותר.
 |  |
|---|---|
| ניוטון (1727-1643) | לייבניץ (1716-1646) |
המכניקה הניוטונית בפרספקטיבה
ניוטון הצליח לנסח את הדינמיקה והקינמטיקה של גופים באמצעות מערכת חוקים ומשוואות דיפרנציאליות. הישגו המרכזי היה ההבנה שאותם חוקים פיזיקליים השולטים בתנועת גופים במעבדה שולטים גם בתנועת גרמי השמיים.
כעבור כ-200 שנה, איינשטיין הראה שהמכניקה הניוטונית היא קירוב מצוין לתיאור הטבע, אך לא התיאור המלא. באנלוגיה: כשם שהסביבה הקרובה נראית לנו שטוחה אף שאנו חיים על כדור, כך המכניקה הניוטונית היא קירוב מצוין למציאות ברוב המצבים היומיומיים, אך היא חלק מתיאוריה רחבה יותר - תורת היחסות.
למרות שתורת היחסות היא “הדבר האמיתי והיפה”, כל פיזיקאי מתחיל את דרכו בלימוד המכניקה הניוטונית, שמהווה את הבסיס להבנת הפיזיקה המודרנית.
כלים מתמטיים נדרשים
לימוד הפיזיקה דורש כלים מתמטיים מתקדמים מעבר לחשבון האינפיניטסימלי הבסיסי. בקורס זה נזדקק למשוואות דיפרנציאליות ברמת מבוא, אלגברה לינארית, פונקציות מרובות משתנים, משוואות דיפרנציאליות חלקיות, ואופרטורי גזירה דיפרנציאליים וקטוריים. כלים אלה יילמדו תוך כדי הקורס בהתאם לצורך.
המרחב התלת-ממדי וחשבון וקטורים
המציאות הפיזיקלית שלנו היא תלת-ממדית. כדי לקבוע מיקום מדויק של נקודה במרחב, נדרשים שלושה מספרים. לשם כך אנו משתמשים במערכת של שלושה צירים ניצבים זה לזה, עם ראשית משותפת המשמשת כנקודת ייחוס.
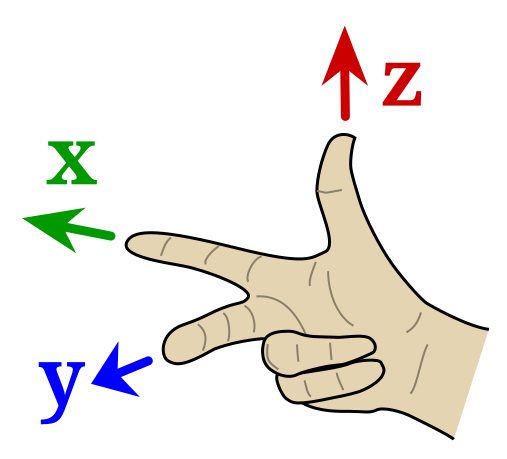
מערכת צירים ימנית
מערכת הצירים הסטנדרטית בפיזיקה מאורגנת כ”שלשה ימנית” על פי כלל יד ימין (כלל בורג ימני): כאשר אצבעות יד ימין מתכופפות מציר x לציר y, האגודל מצביע בכיוון ציר z.
 | |
|---|---|
| כלל יד ימין | מערכת צירים תלת-ממדית ימנית (מימין) ושמאלית (משמאל) |
הגדרת וקטור
וקטור הוא ישות מתמטית שמתארת גודל וכיוון במרחב. ברמה האלמנטרית, וקטור מסומן באמצעות אות עם חץ מעליה (למשל $\vec{v}$), ובספרות מקצועית לעתים משתמשים באות מודגשת ($\mathbf{v}$).
במרחב תלת-ממדי, וקטור מיוצג על ידי שלשה סדורה של מספרים, למשל $(2,1,3)$, כאשר כל מספר מייצג את הרכיב בכיוון הציר המתאים.
מאפייני וקטור
וקטור מאופיין על ידי שני גדלים בסיסיים:
- גודל - אורך הוקטור
- כיוון - האוריינטציה שלו במרחב
ייצוג גרפי של וקטור
וקטור מיוצג גרפית כחץ. לדוגמה, הוקטור $(2,1,3)$ מתקבל על ידי תזוזה של 2 יחידות בכיוון ציר $x$, יחידה אחת בכיוון ציר $y$, ו-3 יחידות בכיוון ציר $z$. החץ המייצג את הוקטור נמתח מראשית הצירים לנקודה הסופית.
וקטורי יחידה
וקטור יחידה הוא וקטור שאורכו שווה בדיוק לאחד. לכל וקטור $\vec{r}$ ניתן להגדיר וקטור יחידה בכיוונו:
\[\hat{r} = \frac{\vec{r}}{\vert\vec{r}\vert}\]כאשר $\vert\hat{r}\vert = 1$.
במערכת צירים קרטזית מוגדרים שלושה וקטורי יחידה בסיסיים:
- $\hat{x}$ (או $\hat{i}$) = $(1,0,0)$ - וקטור יחידה בכיוון ציר x
- $\hat{y}$ (או $\hat{j}$) = $(0,1,0)$ - וקטור יחידה בכיוון ציר y
- $\hat{z}$ (או $\hat{k}$) = $(0,0,1)$ - וקטור יחידה בכיוון ציר z
וקטורי יחידה אלה מהווים בסיס סטנדרטי למרחב התלת-ממדי. כל וקטור ניתן לפירוק לרכיביו באמצעותם:
\[\vec{a} = a_x\hat{x} + a_y\hat{y} + a_z\hat{z}\]שיטות לתיאור וקטורים
תיאור קרטזי
בתיאור קרטזי, וקטור מיוצג על ידי הקואורדינטות שלו ביחס לצירים:
\[\vec{a} = (a_x, a_y, a_z)\]תיאור פולרי (דו-ממדי)
במישור דו-ממדי, ניתן לתאר וקטור באמצעות אורכו והזווית שהוא יוצר עם ציר $x$ החיובי. הקשר בין שני התיאורים נתון על ידי:
- $\tan \theta = \frac{a_y}{a_x}$
- $\theta = \arctan(\frac{a_y}{a_x})$
- $\vert\vec{a}\vert = \sqrt{a_x^2 + a_y^2}$
אורך וקטור
אורך (או גודל) של וקטור מחושב באמצעות הכללה של משפט פיתגורס:
\[\vert \vec{a}\vert = \sqrt{a_x^2 + a_y^2 + a_z^2}\]נוסחה זו ניתנת להכללה למרחב $n$-ממדי:
\[\vert \vec{a}\vert = \sqrt{a_1^2 + a_2^2 + \ldots + a_N^2}\]פעולות על וקטורים
מכפלת סקלר בווקטור
סקלר הוא גודל המתואר על ידי מספר בלבד, ללא כיוון. כאשר כופלים סקלר $\alpha$ בווקטור $\vec{a} = (a_x, a_y, a_z)$, מתקבל:
\[\alpha \vec{a} = (\alpha a_x, \alpha a_y, \alpha a_z)\]המשמעות הגיאומטרית של פעולה זו:
- אם $\alpha > 1$: מתיחת הוקטור
- אם $0 < \alpha < 1$: כיווץ הוקטור
- אם $\alpha < 0$: היפוך כיוון הוקטור (בנוסף לשינוי האורך)
דוגמה 1
נתון $\vec{a} = (3, 2, -1)$. נחשב:
- $2\vec{a} = 2(3, 2, -1) = (6, 4, -2)$
- $\vert\vec{a}\vert = \sqrt{3^2 + 2^2 + (-1)^2} = \sqrt{14}$
- $\vert2\vec{a}\vert = \sqrt{6^2 + 4^2 + (-2)^2} = \sqrt{56} = 2\sqrt{14}$
שימו לב שאורך הוקטור הוכפל בדיוק באותו גורם.
חיבור וחיסור וקטורים
חיבור וקטורים מבוצע רכיב-רכיב:
\[\vec{a} + \vec{b} = (a_x + b_x, a_y + b_y, a_z + b_z)\]באופן דומה, חיסור וקטורים:
\[\vec{a} - \vec{b} = (a_x - b_x, a_y - b_y, a_z - b_z)\]דוגמה 2
נתונים:
- $\vec{a} = (2, 2) = 2\hat{x} + 2\hat{y}$
- $\vec{b} = (1, 3) = \hat{x} + 3\hat{y}$
חיבורם:
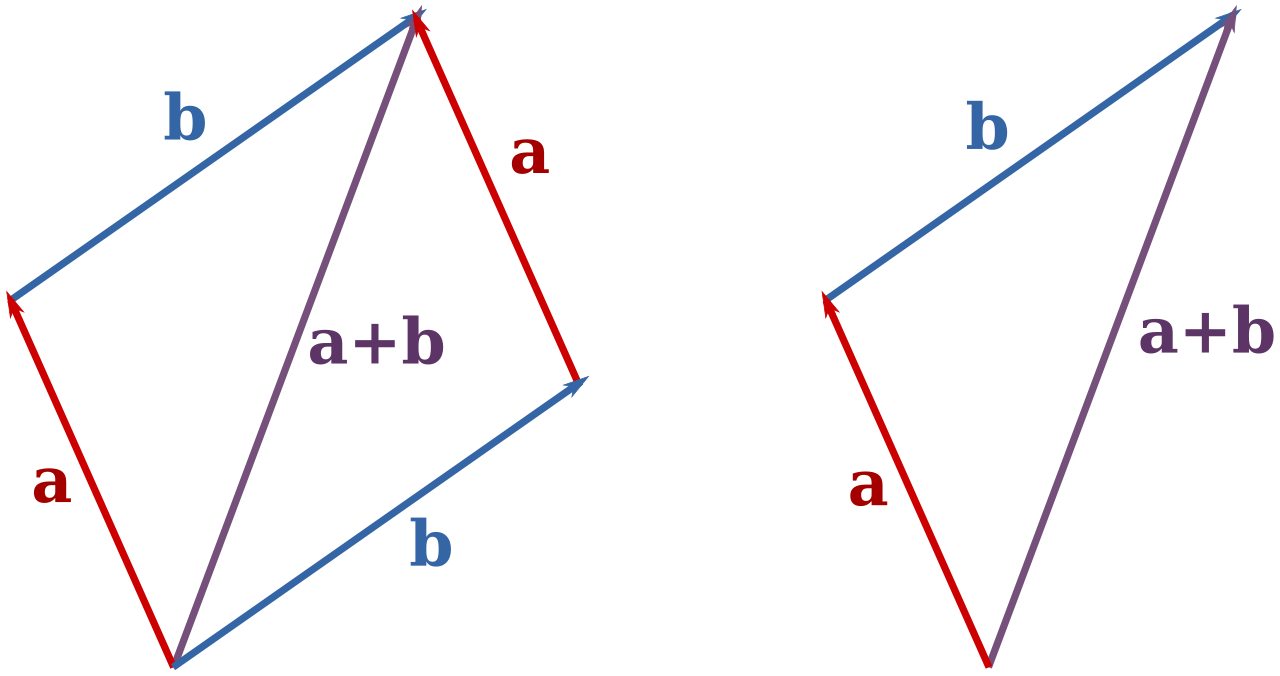
\[\vec{a} + \vec{b} = (2,2) + (1,3) = (3,5)\]המשמעות הגיאומטרית של חיבור וקטורים
גיאומטרית, סכום של שני וקטורים הוא האלכסון הגדול במקבילית ששני הווקטורים פורשים. הסכום הזה נקרא השקול הווקטורי. האלכסון הקטן במקבילית מייצג את ההפרש בין הוקטורים.
 |
|---|
| מקבילית הוקטורים - הסכום הוא האלכסון הגדול |
משפט פיתגורס במרחב תלת-ממדי
נרחיב את משפט פיתגורס למרחב תלת-ממדי:
\[\vert \vec{a}\vert = \sqrt{a_x^2 + a_y^2 + a_z^2}\]ניתן לצייר נקודה במרחב תלת-ממדי ולהשתמש במשפט פיתגורס פעמיים כדי לחשב את המרחק שלה מהראשית.
\[\begin{aligned} \vec{a} &= (a_x, a_y, a_z) \\[10pt] \vert \vec{a}| &= \sqrt{a_x^2 + a_y^2 + a_z^2} \end{aligned}\]אפשר להרחיב את משפט פיתגורס לכל מספר ממדים:
“ב-N ממדים, הגודל של $\vec{a}$… יהיה שווה ל-$\sqrt{a_1^2 + a_2^2 + \ldots + a_N^2}$”
שיעור 2 - חשבון וקטורי
תאריך: 24/03/2025חזרה על פעולות בסיסיות בווקטורים
בשיעור הקודם למדנו על הפעולות הבסיסיות בווקטורים. עבור וקטור $\vec{v}$ וסקלר $\alpha$, פעולת הכפל מוגדרת:
\[\alpha \vec{v} = (\alpha v_x, \alpha v_y, \alpha v_z)\]עבור שני וקטורים $\vec{v}$ ו-$\vec{w}$, פעולות החיבור והחיסור מתבצעות רכיב-רכיב:
\[\vec{v} \pm \vec{w} = (v_x \pm w_x, v_y \pm w_y, v_z \pm w_z)\]הבסיס הסטנדרטי במרחב התלת-ממדי
הבסיס הסטנדרטי של המרחב התלת-ממדי מורכב משלושה וקטורי יחידה ניצבים זה לזה:
\[\hat{x} = \begin{pmatrix} 1 \\[10pt] 0 \\[10pt] 0 \end{pmatrix}, \quad \hat{y} = \begin{pmatrix} 0 \\[10pt] 1 \\[10pt] 0 \end{pmatrix}, \quad \hat{z} = \begin{pmatrix} 0 \\[10pt] 0 \\[10pt] 1 \end{pmatrix}\]כל אחד מווקטורי הבסיס הללו הוא וקטור יחידה (באורך 1) המצביע בכיוון אחד הצירים הקרטזיים.
ייצוג וקטורים: שורה ועמודה
וקטור ניתן לייצוג בשתי צורות שקולות:
-
וקטור שורה:
\[(3, 2, 1)\] -
וקטור עמודה:
\[\begin{pmatrix} 3 \\[10pt] 2 \\[10pt] 1 \end{pmatrix}\]
במסגרת החשבון הווקטורי במרחב האוקלידי, אין הבדל עקרוני בין שני הייצוגים. הבחירה ביניהם נקבעת בדרך כלל על פי הנוחות החישובית בהקשר הספציפי.
פריסת וקטור בבסיס
פריסה בבסיס הסטנדרטי
כל וקטור במרחב התלת-ממדי ניתן לביטוי כקומבינציה לינארית של וקטורי הבסיס הסטנדרטי. לדוגמה, הוקטור $\vec{a} = (3, 2, 1)$ ניתן לכתיבה כך:
\[\vec{a} = 3\hat{x} + 2\hat{y} + \hat{z}\]פירוש גיאומטרי: כדי להגיע לנקודה המייצגת את הוקטור, נלך 3 צעדים בכיוון ציר $x$, 2 צעדים בכיוון ציר $y$, וצעד אחד בכיוון ציר $z$.
הביטוי הזה נקרא הפריסה של הוקטור $\vec{a}$ בבסיס הסטנדרטי. המקדמים 3, 2, 1 הם הקואורדינטות שלו במערכת הצירים הקרטזית.
בסיס לא סטנדרטי
ניתן להגדיר בסיסים אחרים למרחב התלת-ממדי. לדוגמה, הקבוצה:
\[\vec{e}_1 = (1, 1, 0), \quad \vec{e}_2 = (1, 0, 1), \quad \vec{e}_3 = (0, 1, 1)\]מהווה בסיס חוקי למרחב התלת-ממדי.
תנאי לקבוצת בסיס
קבוצת וקטורים מהווה בסיס אם ורק אם הווקטורים בלתי תלויים לינארית - כלומר, אף וקטור בקבוצה אינו ניתן לביטוי כקומבינציה לינארית של האחרים.
ניתן להדגים שהווקטורים $\vec{e}_1, \vec{e}_2, \vec{e}_3$ אכן בלתי תלויים על ידי ניסיון לבטא את $\vec{e}_1$ כקומבינציה לינארית של $\vec{e}_2$ ו-$\vec{e}_3$:
\[\vec{e}_1 = \alpha \vec{e}_2 + \beta \vec{e}_3\]פיתוח המשוואה:
\[\begin{pmatrix} 1 \\[10pt] 1 \\[10pt] 0 \end{pmatrix} = \alpha \begin{pmatrix} 1 \\[10pt] 0 \\[10pt] 1 \end{pmatrix} + \beta \begin{pmatrix} 0 \\[10pt] 1 \\[10pt] 1 \end{pmatrix} = \begin{pmatrix} \alpha \\[10pt] \beta \\[10pt] \alpha + \beta \end{pmatrix}\]השוואת הרכיבים נותנת את מערכת המשוואות:
\[\begin{aligned} \alpha &= 1 \\[10pt] \beta &= 1 \\[10pt] \alpha + \beta &= 0 \end{aligned}\]מערכת זו סותרת (מהמשוואות הראשונות נובע ש-$\alpha + \beta = 2$, בעוד המשוואה השלישית דורשת $\alpha + \beta = 0$). לכן אין ערכים של $\alpha$ ו-$\beta$ המקיימים את המשוואה, והווקטורים אכן בלתי תלויים לינארית.
פריסת וקטור בבסיס לא סטנדרטי
כעת נרצה לפרוס את הוקטור $\vec{a} = (3, 2, 1)$ בבסיס החדש ${\vec{e}_1, \vec{e}_2, \vec{e}_3}$. אנו מחפשים מקדמים $\alpha, \beta, \gamma$ כך ש:
\[\vec{a} = \alpha \vec{e}_1 + \beta \vec{e}_2 + \gamma \vec{e}_3\]הצבת הווקטורים:
\[\begin{pmatrix} 3 \\[10pt] 2 \\[10pt] 1 \end{pmatrix} = \alpha \begin{pmatrix} 1 \\[10pt] 1 \\[10pt] 0 \end{pmatrix} + \beta \begin{pmatrix} 1 \\[10pt] 0 \\[10pt] 1 \end{pmatrix} + \gamma \begin{pmatrix} 0 \\[10pt] 1 \\[10pt] 1 \end{pmatrix}\]פיתוח אגף ימין:
\[\begin{pmatrix} 3 \\[10pt] 2 \\[10pt] 1 \end{pmatrix} = \begin{pmatrix} \alpha + \beta \\[10pt] \alpha + \gamma \\[10pt] \beta + \gamma \end{pmatrix}\]השוואת הרכיבים מניבה מערכת של שלוש משוואות בשלושה נעלמים:
\[\begin{aligned} \alpha + \beta &= 3 \\[10pt] \alpha + \gamma &= 2 \\[10pt] \beta + \gamma &= 1 \end{aligned}\]פתרון מערכת משוואות זו ייתן את המקדמים $\alpha, \beta, \gamma$ - הקואורדינטות של הוקטור $\vec{a}$ בבסיס החדש. שימו לב שאותו וקטור מיוצג על ידי קואורדינטות שונות בבסיסים שונים, אך הוא נשאר אותו וקטור גיאומטרי במרחב.
המכפלה הסקלרית
המכפלה הסקלרית היא פעולה מתמטית בסיסית וחשובה בחשבון וקטורי. בניגוד לפעולות שראינו עד כה (חיבור וקטורים, כפל בסקלר), המכפלה הסקלרית מקבלת כקלט שני וקטורים ומחזירה כפלט סקלר - גודל המתואר על ידי מספר יחיד ללא כיוון. לדוגמה, הטמפרטורה (37.2 מעלות) היא גודל סקלרי טיפוסי.
הגדרה מתמטית
המכפלה הסקלרית בין שני וקטורים $\vec{a}$ ו-$\vec{b}$ מוגדרת כך:
\[\vec{a} \cdot \vec{b} = \vert \vec{a}|\vert \vec{b}|\cos\theta\]כאשר:
- $\vert\vec{a}\vert$ ו-$\vert\vec{b}\vert$ הם אורכי הווקטורים
- $\theta$ היא הזווית בין הווקטורים
- הנקודה (·) מסמנת מכפלה סקלרית (להבדיל ממכפלה רגילה בין מספרים)
תכונות המכפלה הסקלרית עבור וקטורי הבסיס
נבחן את התנהגות המכפלה הסקלרית עבור וקטורי היחידה של הבסיס הסטנדרטי:
מכפלה של וקטור יחידה בעצמו
עבור וקטור יחידה כמו $\hat{x}$:
\[\hat{x} \cdot \hat{x} = |\hat{x}||\hat{x}|\cos(0°) = 1 \cdot 1 \cdot 1 = 1\]הזווית בין וקטור לעצמו היא אפס, ו-$\cos(0°) = 1$.
באופן דומה:
\[\hat{x} \cdot \hat{x} = \hat{y} \cdot \hat{y} = \hat{z} \cdot \hat{z} = 1\]מכפלה בין וקטורי יחידה שונים
עבור וקטורי יחידה ניצבים:
\[\hat{x} \cdot \hat{y} = |\hat{x}||\hat{y}|\cos(90°) = 1 \cdot 1 \cdot 0 = 0\]מכיוון שהזווית בין $\hat{x}$ ל-$\hat{y}$ היא 90 מעלות, ו-$\cos(90°) = 0$.
באופן כללי, לכל זוג וקטורי בסיס שונים:
\[\hat{x} \cdot \hat{y} = \hat{x} \cdot \hat{z} = \hat{y} \cdot \hat{z} = 0\]התנאי לניצבות וקטורים
המכפלה הסקלרית מספקת לנו כלי אלגנטי לזיהוי ניצבות בין וקטורים. אם המכפלה הסקלרית בין שני וקטורים מתאפסת, אחת משלוש האפשרויות הבאות מתקיימת:
- הווקטור הראשון הוא וקטור האפס (כל רכיביו אפס)
- הווקטור השני הוא וקטור האפס
- שני הווקטורים שונים מאפס וניצבים זה לזה
מכיוון שווקטור האפס הוא מקרה טריוויאלי, אנו מתמקדים במקרה השלישי ומגדירים:
\[\vec{a} \perp \vec{b} \iff \vec{a} \cdot \vec{b} = 0\]כלומר, שני וקטורים (שאינם וקטור האפס) ניצבים זה לזה אם ורק אם המכפלה הסקלרית ביניהם היא אפס.
חישוב מכפלה סקלרית ברכיבים קרטזיים
נפתח כעת נוסחה לחישוב המכפלה הסקלרית באמצעות הרכיבים הקרטזיים של הווקטורים. נתונים שני וקטורים:
\[\vec{a} = a_x\hat{x} + a_y\hat{y} + a_z\hat{z}\] \[\vec{b} = b_x\hat{x} + b_y\hat{y} + b_z\hat{z}\]המכפלה הסקלרית ביניהם:
\[\vec{a} \cdot \vec{b} = (a_x\hat{x} + a_y\hat{y} + a_z\hat{z}) \cdot (b_x\hat{x} + b_y\hat{y} + b_z\hat{z})\]בפיתוח הביטוי, נקבל תשעה איברים. כל איבר מהצורה $(a_i\hat{i}) \cdot (b_j\hat{j})$ ייתן:
- $a_ib_i$ כאשר $i = j$ (כי $\hat{i} \cdot \hat{i} = 1$)
- 0 כאשר $i \neq j$ (כי וקטורי הבסיס ניצבים)
לכן, רק שלושה איברים שורדים:
\[\vec{a} \cdot \vec{b} = a_xb_x + a_yb_y + a_zb_z\]זוהי נוסחה פשוטה ויעילה: המכפלה הסקלרית בין שני וקטורים שווה לסכום מכפלות רכיביהם המתאימים.
חישוב אורך וקטור באמצעות מכפלה סקלרית
יישום מיוחד וחשוב של המכפלה הסקלרית הוא חישוב אורך וקטור. כאשר מכפילים וקטור בעצמו:
\[\vec{a} \cdot \vec{a} = a_xa_x + a_ya_y + a_za_z = a_x^2 + a_y^2 + a_z^2\]אך לפי הגדרת המכפלה הסקלרית:
\[\vec{a} \cdot \vec{a} = \vert \vec{a}|\vert \vec{a}|\cos(0°) = \vert \vec{a}|^2\]לכן:
\[\vert \vec{a}|^2 = a_x^2 + a_y^2 + a_z^2\]ומכאן:
\[\vert \vec{a}\vert = \sqrt{\vec{a} \cdot \vec{a}}\]נוסחה זו מספקת דרך אלגנטית לחישוב אורך וקטור באמצעות המכפלה הסקלרית, ומקשרת בין הגדרה גיאומטרית (אורך) לחישוב אלגברי (מכפלה סקלרית).
נרמול וקטור
נרמול וקטור הוא תהליך של יצירת וקטור יחידה (באורך 1) המצביע באותו כיוון של הווקטור המקורי. תהליך זה מתבצע על ידי חלוקת הווקטור באורכו:
\[\hat{a} = \frac{\vec{a}}{\vert \vec{a}\vert} = \frac{\vec{a}}{\sqrt{\vec{a} \cdot \vec{a}}}\]דוגמה לנרמול וקטור
נבחן את וקטורי הבסיס הלא-סטנדרטי שהגדרנו קודם. עבור הווקטור $\vec{e}_1 = (1, 1, 0)$:
ראשית נחשב את אורכו באמצעות המכפלה הסקלרית:
\[\vec{e}_1 \cdot \vec{e}_1 = 1^2 + 1^2 + 0^2 = 2\]לכן:
\[\vert \vec{e}_1| = \sqrt{2}\]כעת נוכל לבנות וקטור יחידה בכיוון $\vec{e}_1$:
\[\hat{e}_1 = \frac{\vec{e}_1}{\vert \vec{e}_1|} = \frac{1}{\sqrt{2}}(1, 1, 0)\]באופן דומה, עבור $\vec{e}_2 = (1, 0, 1)$:
\[\hat{e}_2 = \frac{1}{\sqrt{2}}(1, 0, 1)\]מציאת הזווית בין וקטורים
המכפלה הסקלרית מאפשרת לנו לחשב את הזווית בין כל שני וקטורים במרחב. מההגדרה של המכפלה הסקלרית:
\[\vec{a} \cdot \vec{b} = \vert \vec{a}|\vert \vec{b}|\cos\theta\]נוכל לבודד את הזווית:
\[\cos\theta = \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}|\vert \vec{b}\vert}\]ולכן:
\[\theta = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}|\vert \vec{b}\vert}\right)\]דוגמה מפורטת למציאת זווית
נתונים שני וקטורים:
\[\vec{a} = 3\hat{x} - 3\hat{y} + \hat{z} = (3, -3, 1)\] \[\vec{b} = 2\hat{x} + \hat{y} - 3\hat{z} = (2, 1, -3)\]השאלה: מהי הזווית בין הווקטורים $\vec{a}$ ו-$\vec{b}$?
שלב 1: חישוב המכפלה הסקלרית
\[\vec{a} \cdot \vec{b} = 3(2) + (-3)(1) + 1(-3) = 6 - 3 - 3 = 0\]שלב 2: חישוב אורכי הווקטורים
\[\vert \vec{a}\vert = \sqrt{3^2 + (-3)^2 + 1^2} = \sqrt{9 + 9 + 1} = \sqrt{19}\] \[\vert \vec{b}\vert = \sqrt{2^2 + 1^2 + (-3)^2} = \sqrt{4 + 1 + 9} = \sqrt{14}\]שלב 3: חישוב הזווית
\[\cos\theta = \frac{0}{\sqrt{19}\sqrt{14}} = 0\]לכן:
\[\boxed{\theta = \arccos(0) = 90°}\]המסקנה: הווקטורים ניצבים זה לזה.
| וקטורים ניצבים - המכפלה הסקלרית ביניהם היא אפס |
בדיקת ניצבות בין וקטורים
כפי שראינו, תנאי הכרחי ומספיק לניצבות בין שני וקטורים (שאינם וקטור האפס) הוא שהמכפלה הסקלרית ביניהם תתאפס. נבדוק האם וקטורי הבסיס הלא-סטנדרטי שהגדרנו ניצבים זה לזה:
\[\vec{e}_1 \cdot \vec{e}_2 = (1, 1, 0) \cdot (1, 0, 1) = 1(1) + 1(0) + 0(1) = 1\]מכיוון שהמכפלה הסקלרית אינה אפס, הווקטורים $\vec{e}_1$ ו-$\vec{e}_2$ אינם ניצבים. חשוב להבחין: וקטורים יכולים להיות בלתי תלויים לינארית (כפי שהוכחנו קודם) מבלי להיות ניצבים זה לזה.
וקטורים חשובים בפיזיקה
וקטור המקום
וקטור המקום (position vector) הוא אחד הווקטורים הבסיסיים ביותר בפיזיקה. הוא מוגדר כווקטור המצביע מראשית הצירים אל מיקומו של חלקיק במרחב. בחירת ראשית הצירים נתונה לבחירתנו, ובדרך כלל נבחר אותה במקום שיפשט את פתרון הבעיה.
בעולם הפיזיקלי, כל דבר נמצא בתנועה, ולכן וקטור המקום הוא פונקציה של הזמן:
\[\vec{r}(t) = x(t)\hat{x} + y(t)\hat{y} + z(t)\hat{z}\]כל אחד מרכיבי הווקטור הוא פונקציה של הזמן, ולכן $\vec{r}(t)$ הוא פונקציה וקטורית - פונקציה שמחזירה וקטור עבור כל ערך של $t$.
וקטור ההעתק
כאשר חלקיק נע במרחב, הוא משנה את מיקומו מרגע לרגע. וקטור ההעתק $\Delta\vec{r}$ מתאר את השינוי במיקום החלקיק בין שני רגעי זמן.
אם ברגע $t$ החלקיק נמצא במיקום $\vec{r}(t)$, וברגע $t + \Delta t$ הוא נמצא במיקום $\vec{r}(t + \Delta t)$, אז וקטור ההעתק מוגדר:
\[\Delta\vec{r} = \vec{r}(t + \Delta t) - \vec{r}(t)\]| וקטור ההעתק מחבר בין שתי נקודות על מסלול התנועה |
המהירות הממוצעת במהלך פרק הזמן $\Delta t$ היא:
\[\vec{v}_{avg} = \frac{\Delta\vec{r}}{\Delta t} = \frac{\vec{r}(t + \Delta t) - \vec{r}(t)}{\Delta t}\]וקטור המהירות הרגעית
המהירות הרגעית מתקבלת כאשר אנו לוקחים את הגבול של המהירות הממוצעת כאשר $\Delta t$ שואף לאפס:
\[\vec{v}(t) = \lim_{\Delta t \to 0} \frac{\Delta\vec{r}}{\Delta t} = \frac{d\vec{r}}{dt}\]וקטור המהירות הרגעית הוא הנגזרת של וקטור המקום לפי הזמן. זוהי פונקציה וקטורית המורכבת משלושה רכיבים:
\[\vec{v}(t) = v_x(t)\hat{x} + v_y(t)\hat{y} + v_z(t)\hat{z}\]חשוב להבחין בין שני מושגים:
- Velocity (מהירות): גודל וקטורי הכולל גודל וכיוון
- Speed (מהירות סקלרית): הגודל בלבד, $\vert\vec{v}\vert$
לדוגמה, “נוסע במהירות 100 קמ”ש צפונה” מתאר velocity, בעוד “נוסע במהירות 100 קמ”ש” מתאר רק speed.
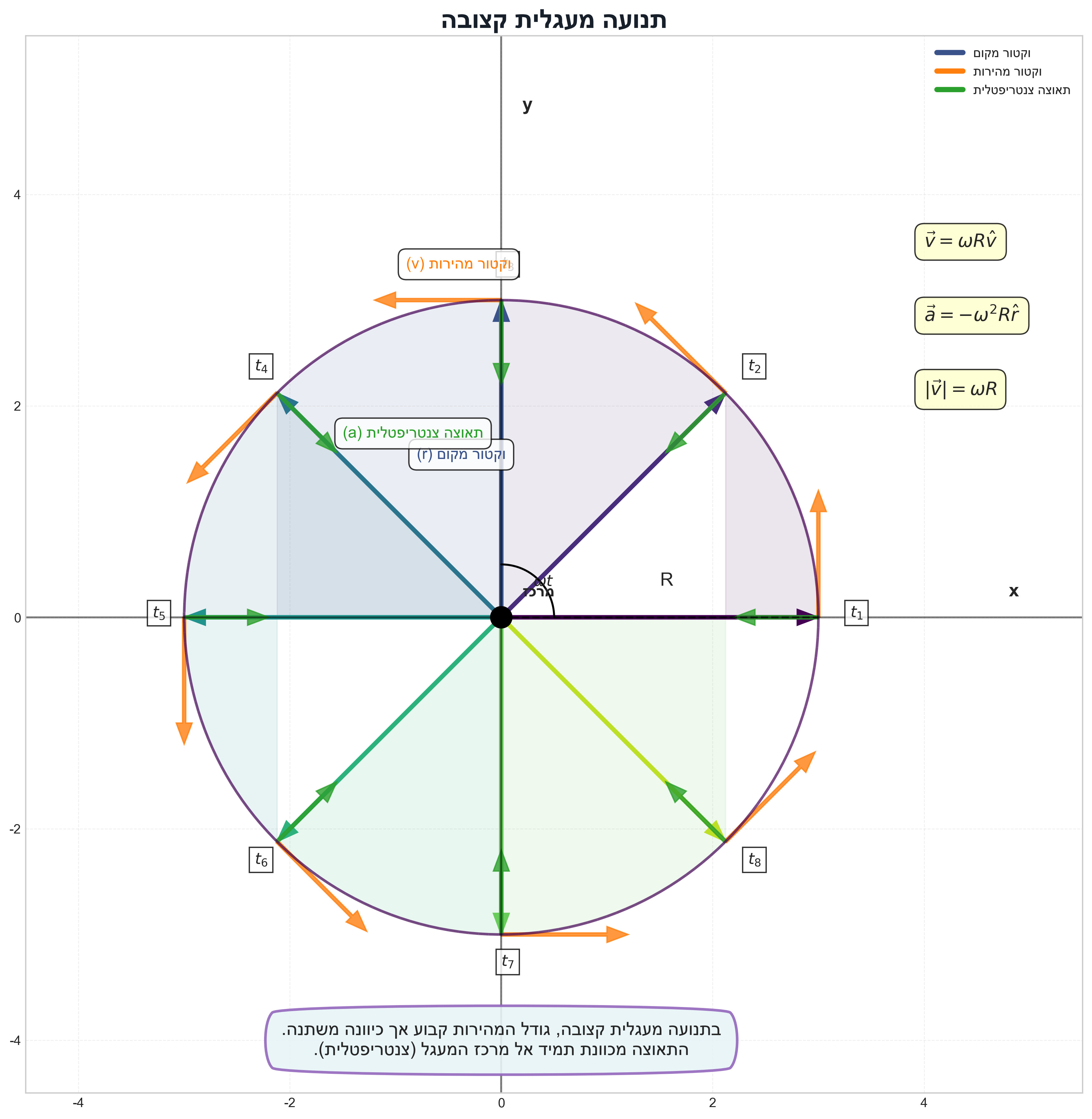
תנועה מעגלית קצובה
תנועה מעגלית קצובה היא תנועה שבה חלקיק נע במסלול מעגלי בקצב זוויתי קבוע. המאפיין המרכזי של תנועה זו הוא שהזווית משתנה באופן לינארי עם הזמן:
\[\theta(t) = \omega t\]כאשר $\omega$ היא המהירות הזוויתית, ביחידות של רדיאנים לשנייה.
| תנועה מעגלית קצובה - החלקיק נע על מסלול מעגלי |
| הזווית גדלה באופן לינארי עם הזמן |
וקטור המקום בתנועה מעגלית
עבור חלקיק הנע במעגל ברדיוס $r$, וקטור המקום נתון על ידי:
\[\vec{r}(t) = r\cos(\omega t)\hat{x} + r\sin(\omega t)\hat{y}\]נוכל לוודא שהחלקיק אכן נע במסלול מעגלי על ידי חישוב אורך וקטור המקום:
\[\begin{aligned} \vert \vec{r}|^2 &= \vec{r} \cdot \vec{r} \\[10pt] &= (r\cos(\omega t)\hat{x} + r\sin(\omega t)\hat{y}) \cdot (r\cos(\omega t)\hat{x} + r\sin(\omega t)\hat{y}) \\[10pt] &= r^2\cos^2(\omega t) + r^2\sin^2(\omega t) \end{aligned}\]לכן $\vert\vec{r}\vert = r$ - קבוע לכל זמן $t$. החלקיק נשאר תמיד במרחק $r$ מהראשית.
וקטור המהירות בתנועה מעגלית
וקטור המהירות מתקבל מגזירת וקטור המקום:
\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -\omega r\sin(\omega t)\hat{x} + \omega r\cos(\omega t)\hat{y}\]גודל המהירות:
\[\vert \vec{v} \vert^2 = \omega^2r^2\sin^2(\omega t) + \omega^2r^2\cos^2(\omega t) = \omega^2r^2\]לכן:
\[\vert \vec{v} \vert = \omega r\]גודל המהירות קבוע, אך כיוונה משתנה כל הזמן.
הוכחה שהמהירות משיקה למסלול
כדי להוכיח שוקטור המהירות משיק למסלול המעגלי, נראה שהוא ניצב לוקטור המקום:
\[\begin{aligned} \vec{r} \cdot \vec{v} &= r\cos(\omega t) \cdot (-\omega r\sin(\omega t)) + r\sin(\omega t) \cdot (\omega r\cos(\omega t)) \\[10pt] &= -\omega r^2\cos(\omega t)\sin(\omega t) + \omega r^2\sin(\omega t)\cos(\omega t) \\[10pt] &= 0 \end{aligned}\]מכיוון שהמכפלה הסקלרית מתאפסת, הווקטורים ניצבים. וקטור המקום מצביע מהמרכז אל החלקיק (בכיוון הרדיוס), ולכן וקטור המהירות חייב להיות משיק למעגל.
| וקטור המהירות (אדום) תמיד ניצב לוקטור המקום (כחול) |
שלבים שונים בתנועה המעגלית
הטבלה הבאה מציגה את התנועה המעגלית בארבע נקודות זמן שונות:
| t = 0 | t = T/8 | t = T/4 | t = 3T/8 |
|---|---|---|---|
בכל רגע, וקטור המהירות משיק למסלול וניצב לוקטור המקום.
כיוון המהירות
וקטור היחידה בכיוון המהירות הוא:
\[\hat{v} = \frac{\vec{v}}{\vert \vec{v}\vert} = \frac{\vec{v}}{\omega r} = -\sin(\omega t)\hat{x} + \cos(\omega t)\hat{y}\]כיוון המהירות משתנה ברציפות עם הזמן, אך גודלה נשאר קבוע. זוהי תכונה מאפיינת של תנועה מעגלית קצובה - התאוצה כולה מופנית למרכז המעגל (תאוצה צנטריפטלית) ומשנה רק את כיוון המהירות, לא את גודלה.
שיעור 3 - קינמטיקה ותנועה מעגלית
תאריך: 02/04/2025קינמטיקה ופונקציות וקטוריות
הגדרות בסיסיות
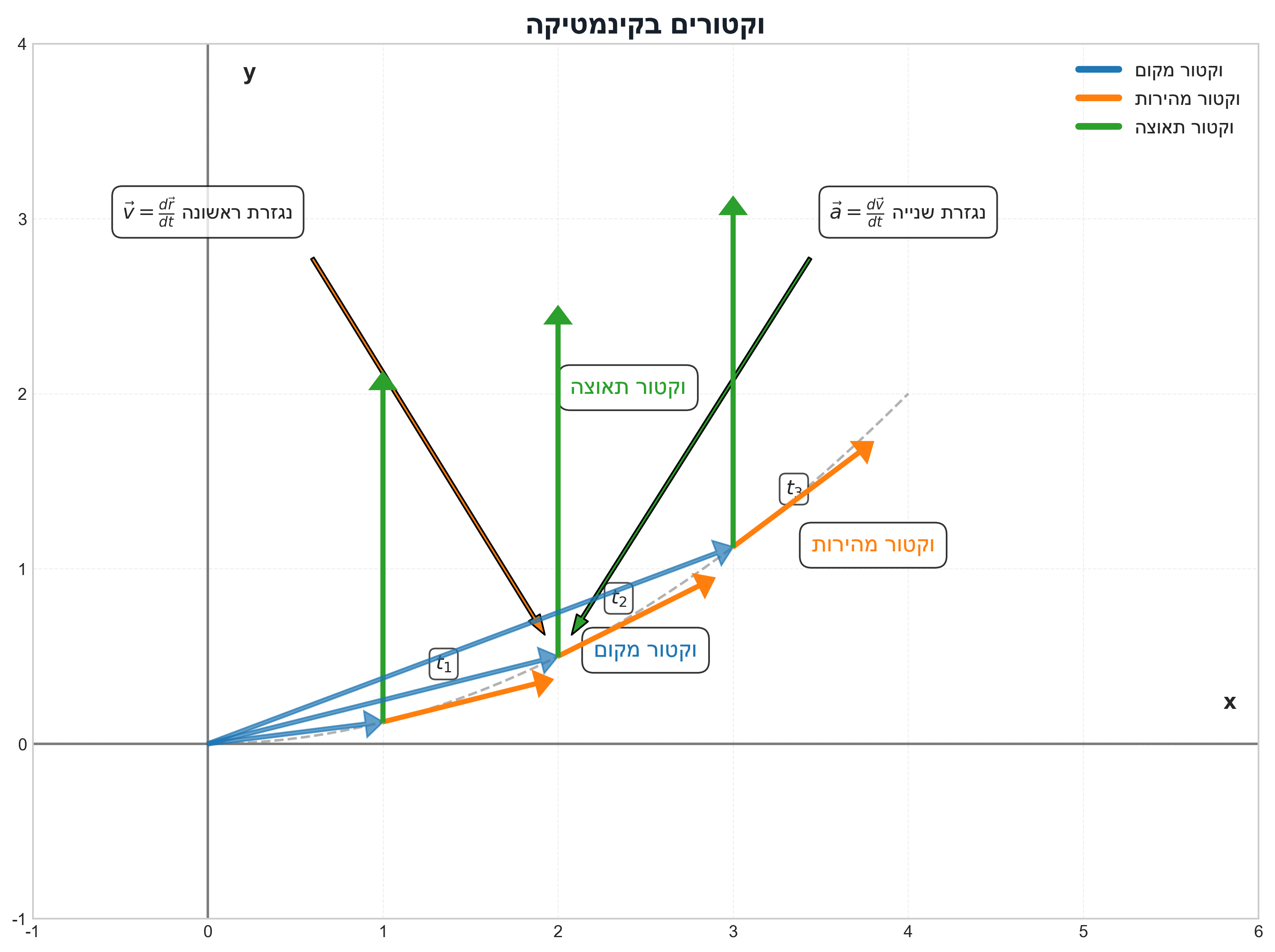
כדי לתאר את תנועת גוף במרחב או במישור, נדרש אובייקט מתמטי הנקרא “פונקציה וקטורית”. פונקציה וקטורית היא וקטור שהרכיבים שלו הם פונקציות התלויות בזמן.
 |
|---|
| וקטורים |
וקטור המקום
- וקטור המקום מתאר את מיקום הגוף בכל רגע $t$.
- מסומן כ-$\vec{r}(t)$.
- הביטוי המתמטי בקואורדינטות קרטזיות: $\vec{r}(t) = x(t)\hat{x} + y(t)\hat{y} + z(t)\hat{z}$.
- שלוש הפונקציות $x(t)$, $y(t)$, ו-$z(t)$ הן הקואורדינטות של הגוף בכל רגע $t$.
- ניתן לרשום גם כשלשה סדורה: $\vec{r}(t) = (x(t), y(t), z(t))$.
וקטור העתק
הגדרה
- בזמן $t$ הגוף נמצא במיקום המתואר על ידי $\vec{r}(t)$.
- בזמן $t + \Delta t$ הגוף נמצא במיקום המתואר על ידי $\vec{r}(t + \Delta t)$.
- וקטור ההעתק $\Delta\vec{r}$ מוגדר כהפרש בין שני וקטורי המיקום: \(\Delta\vec{r} = \vec{r}(t + \Delta t) - \vec{r}(t)\)
- וקטור ההעתק מתאר את השינוי במיקום הגוף בפרק הזמן $\Delta t$.
דוגמה: המרצה צייר על הלוח מערכת צירים תלת-ממדית והראה כיצד ניתן לייצג מיקום של גוף בזמן $t$ ובזמן $t + \Delta t$ ולהגדיר את וקטור ההעתק כהפרש ביניהם.
וקטור מהירות
הגדרה
- המהירות היא קצב שינוי המקום לפי הזמן.
-
מהירות ממוצעת (וקטור) בפרק זמן $\Delta t$:
\[\mathbf{v}_{\text{avg}} = \frac{\Delta\mathbf{r}}{\Delta t}\]
כאשר $\Delta\mathbf{r}$ הוא וקטור ההעתק ו-$\Delta t$ הוא סקלר הזמן.
דוגמה: “אם בשעה 7 בבוקר הייתי בתל אביב ובשעה 8 בבוקר הייתי בירושלים, וקטור ההעתק $\Delta\mathbf{r}$ בין תל אביב לירושלים חלקי פרק הזמן $\Delta t = 1$ שעה נותן את וקטור המהירות הממוצעת.”
מהירות רגעית
-
וקטור המהירות הרגעית הוא הגבול של וקטור המהירות הממוצעת כאשר $\Delta t$ שואף לאפס:
\[\mathbf{v}(t) = \lim_{\Delta t \to 0} \frac{\Delta\mathbf{r}}{\Delta t} = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}}\] -
הביטוי בקואורדינטות קרטזיות:
\[\mathbf{v}(t) = \frac{dx}{dt}\hat{\mathbf{x}} + \frac{dy}{dt}\hat{\mathbf{y}} + \frac{dz}{dt}\hat{\mathbf{z}} = v_x(t)\hat{\mathbf{x}} + v_y(t)\hat{\mathbf{y}} + v_z(t)\hat{\mathbf{z}}\]
כאשר:
- $v_x(t)$, $v_y(t)$, $v_z(t)$ הם רכיבי המהירות (סקלרים)
- $\hat{\mathbf{x}}$, $\hat{\mathbf{y}}$, $\hat{\mathbf{z}}$ הם וקטורי יחידה
הבחנה בין וקטור לסקלר
- וקטור המהירות $\mathbf{v}$: כמות וקטורית עם גודל וכיוון
-
גודל המהירות (speed) $\vert\mathbf{v}\vert$ או $v$: כמות סקלרית חיובית
\[|\mathbf{v} \vert = \sqrt{\mathbf{v} \cdot \mathbf{v}} = \sqrt{v_x^2 + v_y^2 + v_z^2}\]
הערת המרצה: כשמדברים על מהירות, לא מספיק להגיד מהו ה-speed. Speed זה הגודל הסקלרי $\vert\mathbf{v}\vert$ של וקטור המהירות. צריך להגיד גם מהו הכיוון, והכיוון נקבע על ידי שלושת הרכיבים הסקלריים $v_x, v_y, v_z$.
תכונות וקטור המהירות
- וקטור המהירות $\mathbf{v}(t)$ תמיד משיק למסלול התנועה (מצביע בכיוון התנועה).
-
וקטור יחידה בכיוון המהירות:
\[\hat{\mathbf{v}} = \frac{\mathbf{v}}{|\mathbf{v}\vert}\]כאשר $\hat{\mathbf{v}}$ הוא וקטור יחידה ו-$\vert\mathbf{v}\vert$ הוא הגודל הסקלרי.
- וקטור היחידה $\hat{\mathbf{v}}$ מתאר את כיוון התנועה בכל רגע $t$.
סיכום: וקטורים לעומת סקלרים במהירות
| כמות | סוג | סימון | יחידות |
|---|---|---|---|
| וקטור המהירות | וקטור | $\mathbf{v}$ | $\mathrm{m/s}$ בכיוון מסוים |
| גודל המהירות (speed) | סקלר | $\vert\mathbf{v}\vert$ או $v$ | $\mathrm{m/s}$ |
| רכיבי המהירות | סקלרים | $v_x, v_y, v_z$ | $\mathrm{m/s}$ |
| וקטור יחידה של המהירות | וקטור | $\hat{\mathbf{v}}$ | ללא יחידות |
וקטור תאוצה
הגדרה
- התאוצה היא קצב שינוי המהירות לפי הזמן.
-
תאוצה ממוצעת בפרק זמן $\Delta t$:
\[\vec{a}_{\text{avg}} = \frac{\Delta\vec{v}}{\Delta t} = \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t}\] -
התאוצה הרגעית היא הגבול של התאוצה הממוצעת כאשר $\Delta t$ שואף לאפס:
\[\vec{a}(t) = \lim_{\Delta t \to 0} \frac{\Delta\vec{v}}{\Delta t} = \frac{d\vec{v}}{dt} = \dot{\vec{v}} = \frac{d^2\vec{r}}{dt^2} = \ddot{\vec{r}}\]
שאלה מסטודנט: מהו בדיוק $\Delta\vec{v}$?
תשובה המרצה: “$\Delta\vec{v}$ זה וקטור המהירות בזמן $t + \Delta t$ פחות וקטור המהירות בזמן $t$. כלומר, זה הפרש וקטורי של מהירויות.”
דוגמה להמחשה
- “אם בשעה 7 בבוקר נעתי במהירות של 40 קמ״ש ובשעה 8 בבוקר נעתי במהירות של 80 קמ״ש, אז התאוצה הממוצעת במשך השעה הזאת היא 80 קמ״ש פחות 40 קמ״ש, חלקי שעה אחת, שזה 40 קמ״ש לשעה בריבוע.”
שאלה מסטודנט: האם זו תאוצה ממוצעת או רגעית?
תשובה המרצה: “זאת תאוצה ממוצעת. התאוצה הרגעית תתקבל כאשר $\Delta t$ שואף לאפס.”
שאלה מסטודנט: מה כיוון התאוצה?
תשובה המרצה: “התאוצה היא הפרש וקטורי של המהירויות חלקי הזמן. אין שום התחייבות שכיוון וקטור התאוצה יהיה בכיוון המהירות או בכיוון המקום. התאוצה תהיה בכיוון של $\Delta\vec{v}$.”
תנועה מעגלית קצובה
 |
|---|
| תנועה מעגלית קצובה |
הגדרה
- תנועה על מסלול מעגלי בגודל מהירות קבוע.
-
המסלול מתואר על ידי וקטור המקום $\vec{r}(t)$, בהצגה קרטזית:
\[\vec{r}(t) = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}\] - $R$ הוא רדיוס המעגל (קבוע).
- $\omega$ היא המהירות הזוויתית (נמדדת ברדיאנים לשנייה).
- $\theta(t) = \omega t$ היא הזווית, המשתנה לינארית עם הזמן.
הערת המרצה: “כשאני אומר תנועה קצובה אני מתכוון שאני מכסה קשתות שוות במרווחי זמן שווים.”
הערה (דור): אני חושב שיעזור להבין את ההבדל בין קואורדינטות קרטזיות לפולריות. זה מופיע בשיעורים הבאים. בקצרה, ההצגה שלמעלה היא בקואורדינטות קרטזיות $(x, y)$. לעומת זאת, קואורדינטות פולריות מתארות מיקום באמצעות רדיוס וזווית $(R, \theta)$.
הערה נוספת: שימו לב שהנוסחה תלויה בבחירת מערכת הצירים. אם למשל הזווית $\theta$ נמדדת מציר ה-$y$ ולא מציר ה-$x$, הנוסחה תשתנה:
\[\vec{r}(t) = R\sin(\omega t)\hat{x} + R\cos(\omega t)\hat{y}\]אפשר לעבור בין הנוסחאות בעזרת זהויות טריגונומטריות.
וקטור המהירות בתנועה מעגלית
-
נגזור את וקטור המקום לפי הזמן:
\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}\] -
גודל המהירות:
\[\vert\vec{v}\vert = \sqrt{(-\omega R\sin(\omega t))^2 + (\omega R\cos(\omega t))^2} = \sqrt{\omega^2 R^2(\sin^2(\omega t) + \cos^2(\omega t))} = \omega R\] -
גודל המהירות המשיקית קבוע ושווה ל-$v = \omega R$.
הערה: “המהירות המשיקית היא $\omega R$. $\omega$ במקרה שלנו הוא קבוע. היחידות של $\omega$ הן רדיאנים לשנייה. כאשר $\omega$ (רדיאן/שנייה) כפול $R$ (מטר) נותן מהירות במטר/שנייה.”
תכונות מיוחדות
- המהירות ניצבת תמיד לוקטור המקום: $\vec{v} \cdot \vec{r} = 0$.
- המהירות משיקה למעגל.
-
וקטור יחידה בכיוון המהירות:
\[\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert} = -\sin(\omega t)\hat{x} + \cos(\omega t)\hat{y}.\]
הערת המרצה: “אם וקטור המקום הוא בכיוון הרדיוס, ווקטור המהירות ניצב לו, הרי שווקטור המהירות משיק למעגל. הוא בזווית של 90 מעלות מהרדיוס.”
תאוצה צנטריפטלית
 |
|---|
| תאוצה צנטריפטלית |
וקטור התאוצה בתנועה מעגלית
-
נגזור את וקטור המהירות לפי הזמן:
\[\vec{a}(t) = \frac{d\vec{v}}{dt} = -\omega^2 R\cos(\omega t)\hat{x} - \omega^2 R\sin(\omega t)\hat{y}\] -
ניתן לראות שזהו פשוט $-\omega^2$ כפול וקטור המקום המקורי:
\[\vec{a}(t) = -\omega^2 \vec{r}(t)\]
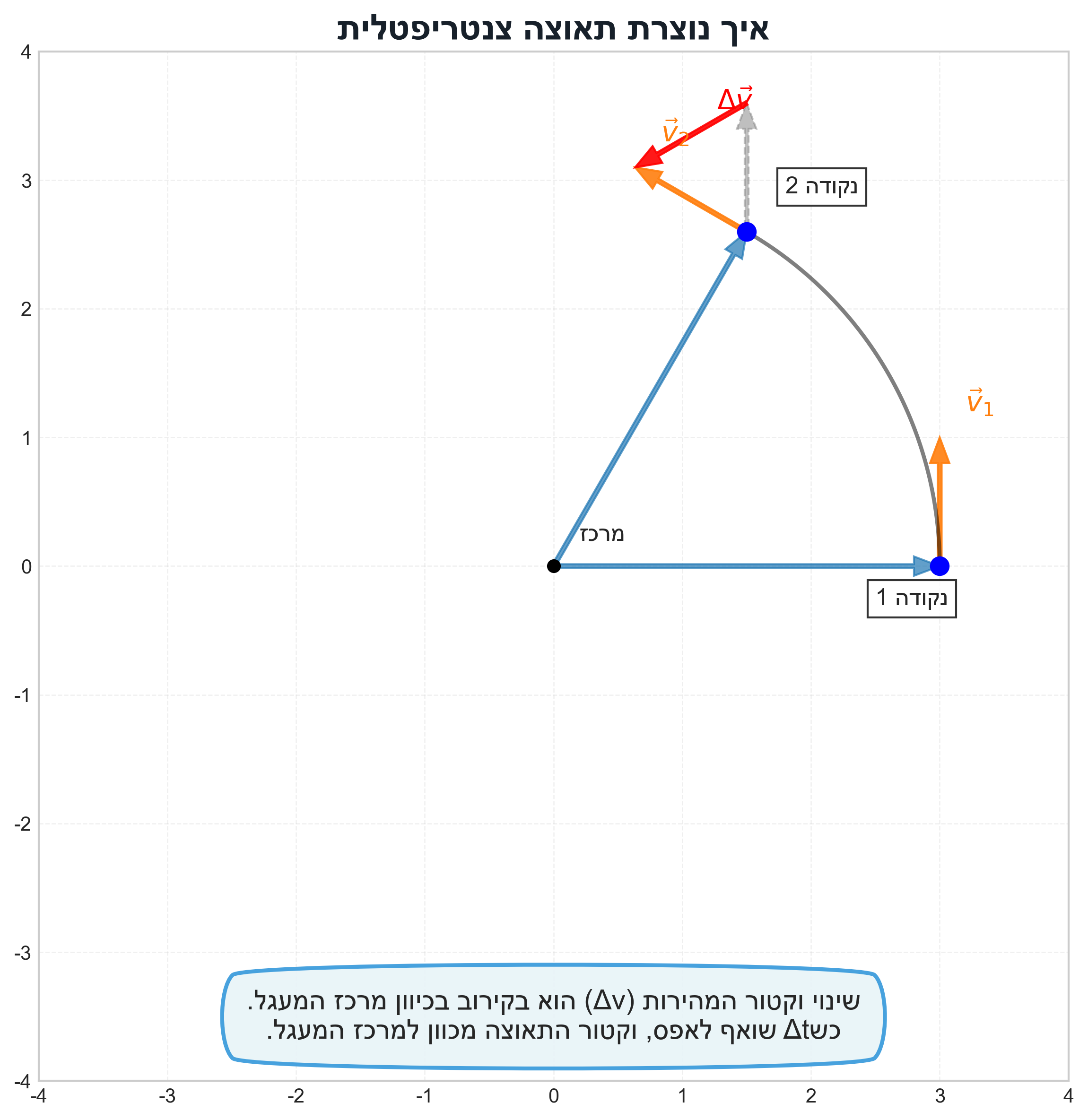
תוצאה חשובה: בתנועה מעגלית קצובה, התאוצה מכוונת תמיד בכיוון הפוך לוקטור המקום, כלומר לעבר מרכז המעגל.
הערה: שימו לב שהתוצאה ($\vec{a}=-\omega^2 \vec{r}$) נכונה בתנועה מעגלית קצובה, כלומר כאשר המהירות הזוויתית $\omega$ קבועה. אם גודל המהירות היה משתנה, הייתה קיימת גם תאוצה משיקית.
תשובת המרצה: “אני מזכיר לכם שאנחנו עוסקים כאן בוקטורים. וקטור המהירות לא מאופיין רק על ידי גודל אלא גם על ידי כיוון. כשאני נע על פני המעגל, אומנם גודל וקטור המהירות קבוע, אבל כיוון המהירות משתנה כל הזמן. אם כיוון המהירות משתנה, יש לי תאוצה, משום שיש שינוי בוקטור המהירות.”
תכונות התאוצה בתנועה מעגלית
- התאוצה מכוונת תמיד לעבר מרכז המעגל.
- גודל התאוצה: $\vert\vec{a}\vert = \omega^2 R$. מאחר ו-$v = \omega R$, ניתן לכתוב גם $\vert\vec{a}\vert = \frac{v^2}{R}$.
- תאוצה זו נקראת “תאוצה צנטריפטלית” (centripetal acceleration).
המחשה גרפית: המרצה צייר על הלוח שני וקטורי מהירות $\vec{v}(t)$ ו-$\vec{v}(t+\Delta t)$ בתנועה מעגלית, והראה שוקטור ההפרש ביניהם $\Delta\vec{v}$ תמיד יצביע לכיוון מרכז המעגל.
סיכום סימונים חשובים
- $\vec{v} = \dot{\vec{r}}$ (נגזרת ראשונה של המקום לפי הזמן)
- $\vec{a} = \dot{\vec{v}} = \ddot{\vec{r}}$ (נגזרת שנייה של המקום לפי הזמן)
- נגזרת שלישית מסומנת בשלוש נקודות ($\dddot{\vec{r}}$) ונקראת “Jerk”, אך השימוש בה במכניקה קלאסית נדיר.
תנועה בתאוצה קבועה
הגדרת המצב
- נניח שהתאוצה קבועה: $\vec{a}(t) = \vec{a}_0 = \text{const}$.
- דוגמה נפוצה היא נפילה חופשית בקרבת פני כדור הארץ, שם $\vec{a} = -g\hat{z}$ (כאשר ציר $z$ מצביע כלפי מעלה).
- $g$ הוא קבוע תאוצת הכובד (בקירוב $g \approx 9.8 \mathrm{ m/s^2}$).
הערת המרצה: “אתם בטח שמעתם שבהיעדר התנגדות אוויר ובקרבת פני כדור הארץ, גופים נופלים בתאוצה קבועה $g$. זה קירוב, ונתקן אותו בהמשך, אבל כרגע נניח שזה נכון.”
מציאת וקטור המהירות באמצעות אינטגרציה
\[\vec{v}(t) = \int \vec{a}(t) dt = \int \vec{a}_0 dt = \vec{a}_0 t + \vec{C}\]הקבוע הווקטורי $\vec{C}$ נקבע על פי תנאי התחלה. אם נתונה המהירות $\vec{v}_0$ בזמן $t=0$:
\[\vec{v}(0) = \vec{a}_0 \cdot 0 + \vec{C} = \vec{v}_0 \implies \vec{C} = \vec{v}_0\]ולכן, משוואת המהירות היא:
\[\vec{v}(t) = \vec{v}_0 + \vec{a}_0 t\]מציאת וקטור המקום באמצעות אינטגרציה
\[\vec{r}(t) = \int \vec{v}(t) dt = \int (\vec{v}_0 + \vec{a}_0 t) dt = \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2 + \vec{D}\]הקבוע הווקטורי $\vec{D}$ הוא וקטור המקום בזמן $t=0$, כלומר $\vec{r}_0$. לכן, משוואת המיקום היא:
\[\vec{r}(t) = \vec{r}_0 + \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2\]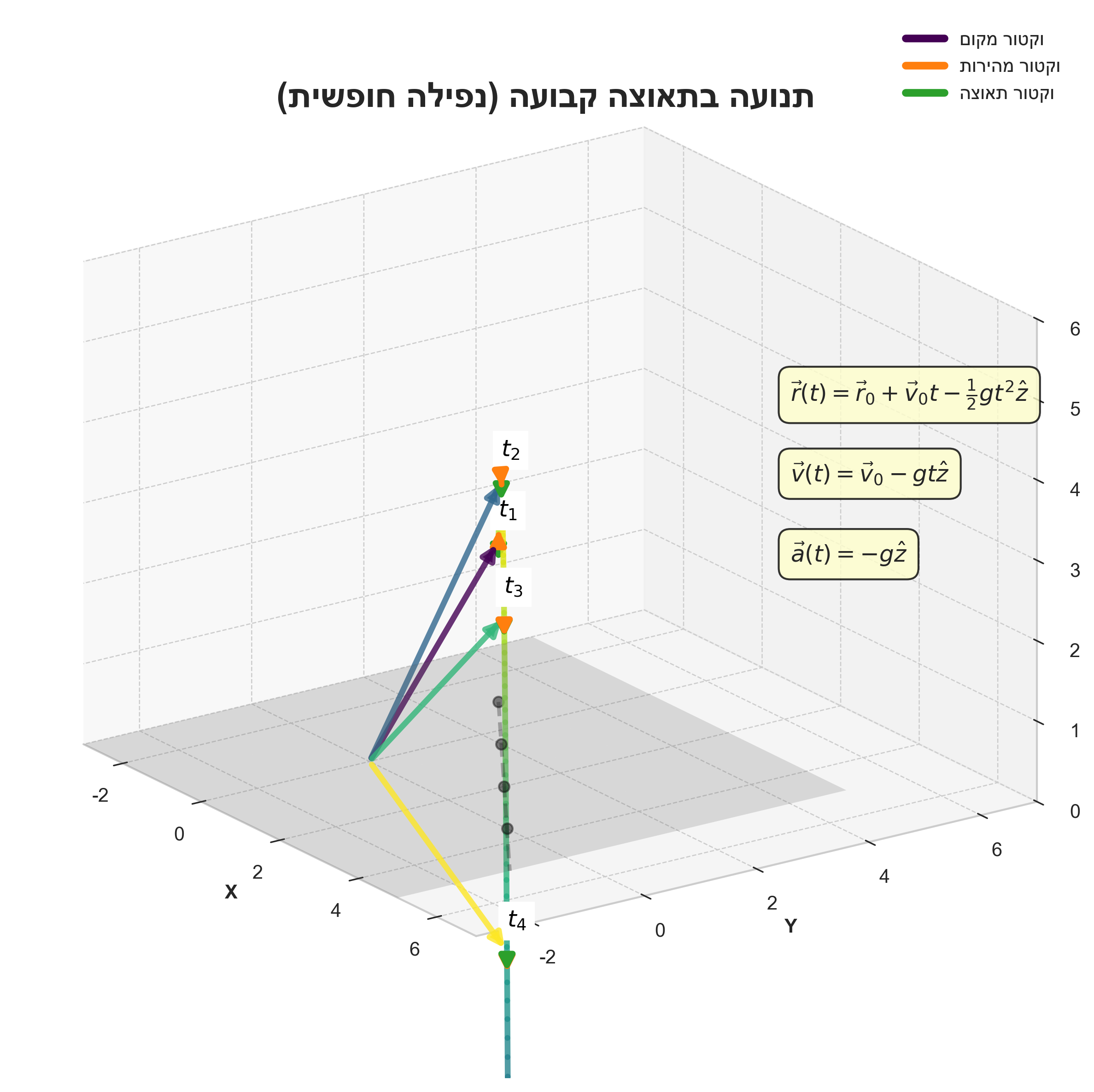 |
|---|
| תנועת קליע (Projectile Motion) |
דוגמה מפורטת
- נתון:
- מיקום התחלתי: $\vec{r}_0 = -\hat{x} + 3\hat{y} + 2\hat{z}$
- מהירות התחלתית: $\vec{v}_0 = 3\hat{x} - 2\hat{y}$
- תאוצה קבועה: $\vec{a}_0 = -g\hat{z}$
-
נציב במשוואת המיקום:
\[\vec{r}(t) = (-\hat{x} + 3\hat{y} + 2\hat{z}) + (3\hat{x} - 2\hat{y})t + \frac{1}{2}(-g\hat{z})t^2\] -
נקבץ איברים לפי רכיבים:
\[\vec{r}(t) = (3t-1)\hat{x} + (-2t+3)\hat{y} + (-\frac{1}{2}gt^2+2)\hat{z}\] - זהו וקטור המיקום בכל רגע $t$.
הערת המרצה: “תנו לי איזה $t$ שאתם רוצים, ואני אגיד לכם בדיוק איפה יהיה הגוף. זו עוצמה גדולה מאוד, יש לי פה יכולת חיזוי פנטסטית.”
תנועה יחסית
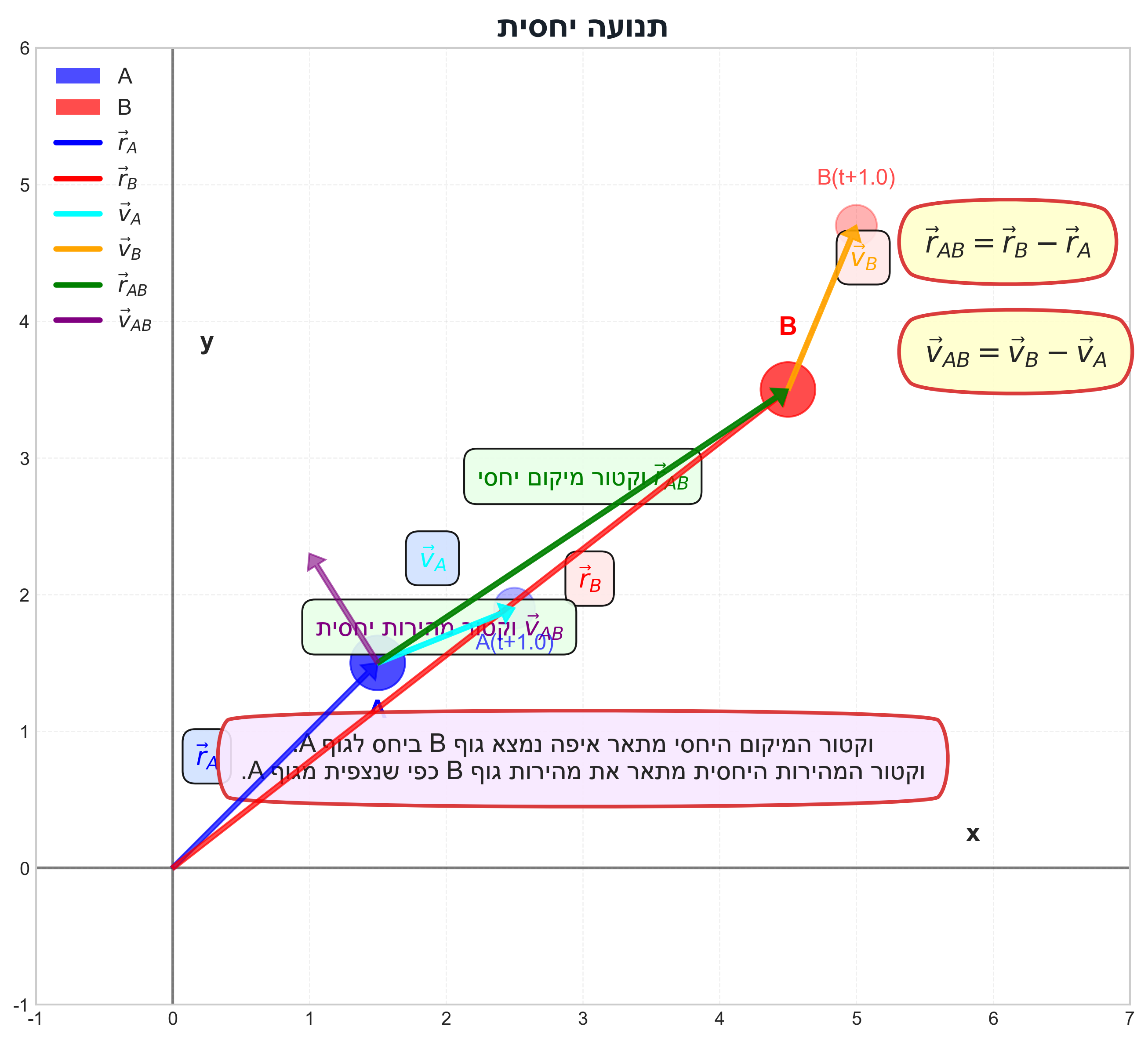
מיקום יחסי
- נניח שיש שני גופים $A$ ו-$B$ עם וקטורי מקום $\vec{r}_A$ ו-$\vec{r}_B$ ביחס לאותה ראשית צירים.
-
וקטור המקום של $B$ ביחס ל-$A$ הוא:
\[\vec{r}_{B/A} = \vec{r}_B - \vec{r}_A\] - המיקום היחסי מתאר איפה נמצא גוף $B$ מנקודת המבט של גוף $A$.
הערת המרצה: “הבחירה של ראשית הצירים היא שרירותית, אבל מרגע שבחרנו אותה, אנחנו צריכים להיות עקביים.”
מהירות יחסית
-
על ידי גזירת המיקום היחסי לפי הזמן, נקבל את המהירות היחסית:
\[\vec{v}_{B/A} = \frac{d\vec{r}_{B/A}}{dt} = \frac{d\vec{r}_B}{dt} - \frac{d\vec{r}_A}{dt} = \vec{v}_B - \vec{v}_A\]
 |
|---|
| תנועה יחסית |
דוגמה 1: מהירות יחסית בתנועה בקו ישר
- “אני נע במהירות של 50 קמ״ש צפונה ($\vec{v}_A = 50\hat{x}$) ויותם נע במהירות של 100 קמ״ש צפונה ($\vec{v}_B = 100\hat{x}$).”
- “מה המהירות שלי יחסית ליותם? $\vec{v}_{A/B} = \vec{v}_A - \vec{v}_B = 50\hat{x} - 100\hat{x} = -50\hat{x}$.”
- “מנקודת מבטו של יותם, אני נע דרומה (בכיוון השלילי) במהירות של 50 קמ״ש.”
דוגמה 2: תנועה מורכבת
- “אם אני נע במסלול מסובך על פני כדור הארץ, וחייזר על הירח רוצה לדעת מה המהירות שלי ביחס אליו…”
- “כל מה שהוא צריך לעשות הוא למדוד את המהירות שלו (\(\vec{v}_B\)) ואת המהירות שלי (\(\vec{v}_A\)) ביחס לאותה ראשית צירים (למשל, השמש), ואז לחשב את ההפרש \(\vec{v}_{A/B} = \vec{v}_A - \vec{v}_B\).”
הערת המרצה על יישומים: “כך פועל למשל טיל ‘חץ’. אם יש לי מכ”ם טוב, אני יכול לשחזר את מסלול המטרה, לדעת את $\vec{v}(t)$ שלה, לחשב את המהירות היחסית, ובהתאם לכך לכוון את טיל היירוט.”
נוסחאות מרכזיות:
- וקטור מקום: $\vec{r}(t) = x(t)\hat{x} + y(t)\hat{y} + z(t)\hat{z}$
- וקטור מהירות: $\vec{v}(t) = \frac{d\vec{r}}{dt} = \dot{\vec{r}}$
- וקטור תאוצה: $\vec{a}(t) = \frac{d\vec{v}}{dt} = \ddot{\vec{r}}$
- תנועה מעגלית קצובה (רדיוס $R$, מהירות זוויתית $\omega$):
- מקום: $\vec{r}(t) = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}$
- מהירות: $\vec{v}(t) = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}$
- גודל מהירות: $\vert\vec{v}\vert = \omega R$
- תאוצה: $\vec{a}(t) = -\omega^2 \vec{r}(t)$
- גודל תאוצה: $\vert\vec{a}\vert = \omega^2 R = \frac{\vert\vec{v}\vert^2}{R}$
- תנועה בתאוצה קבועה $\vec{a}_0$:
- מהירות: $\vec{v}(t) = \vec{v}_0 + \vec{a}_0 t$
- מקום: $\vec{r}(t) = \vec{r}_0 + \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2$
- תנועה יחסית (של B יחסית ל-A):
- מיקום: $\vec{r}_{B/A} = \vec{r}_B - \vec{r}_A$
- מהירות: $\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A$
- תאוצה: $\vec{a}_{B/A} = \vec{a}_B - \vec{a}_A$
הערות חשובות:
- התאוצה הצנטריפטלית קיימת גם כאשר גודל המהירות קבוע, כי כיוון המהירות משתנה.
- תאוצה מתארת שינוי בוקטור המהירות - שינוי בגודל, בכיוון, או בשניהם.
- בתנועה עם תאוצה קבועה, ניתן לחזות את המיקום והמהירות בכל זמן עתידי בהינתן תנאי התחלה.
- אינטגרציה של תאוצה נותנת מהירות (עד כדי קבוע אינטגרציה), ואינטגרציה של מהירות נותנת מיקום (עד כדי קבוע). הקבועים נקבעים מתנאי ההתחלה.
- המרצה מקפיד להבחין בין speed (גודל המהירות) לבין וקטור המהירות (velocity).
- הבחירה של ראשית הצירים היא שרירותית, אך יש להיות עקביים בשימוש בה.
שיעור 4 - פיזיקה ניוטונית
תאריך: 07/04/2025חלק 1: סיכום השיעור הקודם - וקטורים ותנועה
וקטור התאוצה ומשמעותו
בשיעור שעבר נראה כי וקטור התאוצה, שהוא הנגזרת לפי הזמן של וקטור המהירות, מבטא את קצב שינוי המהירות. כשם שהמהירות היא קצב שינוי המקום, כך וקטור התאוצה הוא קצב שינוי קצב שינוי המקום.
כאשר נאמר שגוף נע בתאוצה של $X$ מטר לשנייה בריבוע, הכוונה היא שהגוף משנה את מהירותו בכל שנייה ב-$X$ מטר לשנייה. למשל, גוף הנופל בתאוצה של $10$ מטר לשנייה בריבוע (תאוצת הנפילה החופשית בקרבת פני כדור הארץ), פירוש הדבר שבכל שנייה גדלה מהירותו ב-$10$ מטר לשנייה.
לדוגמה, גוף הנופל מגג מגדל גבוה:
- ברגע $t = 0$ מהירותו היא $0$ מטר לשנייה
- ברגע $t = 1$ שנייה מהירותו היא $10$ מטר לשנייה
- ברגע $t = 2$ שניות מהירותו היא $20$ מטר לשנייה
- ברגע $t = 3$ שניות מהירותו היא $30$ מטר לשנייה
זוהי המשמעות של תאוצת נפילה חופשית של $10$ מטר לשנייה בריבוע.
אופי וקטורי של מהירות ותאוצה
חשוב להזכיר שוקטור המקום הוא וקטור ולא סקלר. המשמעות היא שקצב שינוי וקטור המקום לפי הזמן, וקטור המהירות, הוא בעל גודל וכיוון. כך גם לגבי וקטור התאוצה - יש לו גודל וכיוון.
בתנועה מעגלית קצובה, וקטור המקום תלוי בזמן, משום שהגוף נמצא בכל רגע ורגע בנקודה אחרת על פני המעגל. וקטור המהירות משיק למסלול המעגלי וגם הוא תלוי בזמן. העובדה שגודל המהירות הוא קבוע אינה אומרת שוקטור המהירות הוא קבוע - הוא משתנה בכיוונו ללא הרף.
לכן, כאשר נגזור את וקטור המהירות לפי הזמן בתנועה מעגלית, לא נקבל אפס. כפי שנראה, בתנועה מעגלית, וקטור התאוצה שונה מאפס והוא מכוון לעבר מרכז המעגל.
סיכום מתמטי
\[\mathbf{r}(t) = \text{position vector}\] \[\mathbf{v}(t) = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}} = \text{velocity vector}\] \[\mathbf{a}(t) = \frac{d\mathbf{v}}{dt} = \ddot{\mathbf{r}} = \text{acceleration vector}\]בתנועה מעגלית קצובה מתקיים:
\[\mathbf{a}(t) = -\omega^2 \mathbf{r}(t)\]משמעות הקשר הזה היא שהתאוצה מכוונת לעבר מרכז המעגל (הסימן השלילי). $\mathbf{r}$ יוצא ממרכז המעגל החוצה, ולכן $-\mathbf{r}$ מכוון לעבר מרכז המעגל. $\omega^2$ הוא המהירות הזוויתית בריבוע, שהוא גודל סקלרי חיובי.
עוד נראה כי מתקיים:
\[\mathbf{v} \cdot \mathbf{r} = 0\]כלומר, המהירות תמיד ניצבת לוקטור המקום.
קשר בין תאוצה, מהירות ומיקום באמצעות אינטגרלים
אם נתון $\mathbf{a}(t)$, ניתן לקבל את $\mathbf{v}(t)$ באמצעות אינטגרציה:
\[\mathbf{v}(t) = \int \mathbf{a}(t) dt + \mathbf{v}_0\]כאשר $\mathbf{v}_0$ הוא וקטור קבוע (לדוגמה, המהירות בזמן $t=0$).
באופן דומה:
\[\mathbf{r}(t) = \int \mathbf{v}(t) dt + \mathbf{r}_0\]כאשר $\mathbf{r}_0$ הוא המיקום בזמן $t=0$.
במקרה של תנועה בתאוצה קבועה, האינטגרציות פשוטות (אינטגרל על קבוע).
חלק 2: מבוא לפיזיקה ניוטונית
המעבר מקינמטיקה לפיזיקה
מה שנעשה עד כה הוא למעשה קינמטיקה - אין בזה פיזיקה, אלא רק מתמטיקה. זהו חשבון אינפיניטסימלי שבו משווים פונקציות וקטוריות. כל מה שנעשה היו הגדרות של מושגים:
- הגדרת וקטור המקום בצורה אינטואיטיבית
- הגדרת קצב שינוי המקום, אשר נקרא מהירות
- הגדרת קצב שינוי המהירות, אשר נקרא תאוצה
מהי פיזיקה?
כאשר עוסקים בפיזיקה, נשאלת השאלה: מהי החוקיות שלפיה מתנהלת המציאות? לאיזו חוקיות מצייתת המציאות הפיזיקלית שסובבת אותנו?
אם לא הייתה שום חוקיות, המציאות הייתה קאוטית לחלוטין, ושום דבר מסודר לא היה יכול להתקיים בה. המציאות היא מסודרת ביותר. כל גוף הוא דוגמה חיה לעולם מסודר - אוסף אדיר של גופיפים מסודרים מאוד, וכל גופיף כזה מכיל מבנה פנימי מסודר מאוד. ניתן לרדת לרמה של גרעיני אטומים, וגם שם מתקיימת חוקיות וסדר.
חשיבות הסדר והמידול המתמטי
בפיזיקה, המטרה היא להתחקות אחרי הסדר הזה. אם עושים זאת בצורה מדויקת, מתקבל לא רק תיאור של המציאות, אלא גם תיאור של האופן שבו היא מתפתחת בזמן. הכרת החוקיות מאפשרת לראות איך מצב מתפתח למצב אחר.
אם ניתנת מערכת פיזיקלית וחוקיותה ידועה, ניתן לבנות למערכת מודל מתמטי שמבטא את החוקיות הזו, והמודל המתמטי הזה יאפשר לדעת את מצב המערכת בכל זמן עתידי. הישג זה הושג לראשונה בתקופתו של ניוטון עם שלושת החוקים שלו.
מרגע שפוענחה החוקיות ונוסחה בשפה מתמטית מדויקת, ניתן להשתמש בשפה המתמטית הזו כדי לגזור אמיתות על המציאות, לגזור תובנות עליה, ויותר מכך - לגזור ניבויים (פרדיקציות) לגביה.
חלק 3: מושגי יסוד בפיזיקה ניוטונית
לתיאור מדויק של חוקי ניוטון, נגדיר כמה מושגי יסוד:
מערכת ייחוס
מערכת ייחוס היא מושג בסיסי ביותר בפיזיקה. בשלב ראשון, מערכת ייחוס היא מערכת צירים עם ראשית שנבחרת באופן שרירותי.
לדוגמה, ניתן לבחור את הכיתה כמערכת ייחוס - למקם את הראשית במקום כלשהו, ולפרוס ממנה שלוש קואורדינטות במרחב התלת-מימדי. כל נקודה בכיתה ובעולם ניתנת לתיאור במערכת הייחוס הזו.
ניתן גם לחשוב על מערכת ייחוס אחרת - למשל, מערכת שצמודה למכונית הנוסעת ברחוב. הראשית יכולה להיות, למשל, מרכז המכונית, וממנו יוצאים שלושה צירים.
חשוב לציין: המציאות כשלעצמה אינה תלויה בבחירת מערכת הייחוס. תיאור של תופעות במערכת הייחוס של הכיתה צריך להיות ניתן לתרגום, באמצעות חוקי טרנספורמציה, למערכת הייחוס שצמודה לנהג.
אינטראקציה
אינטראקציה היא השפעה שמתרחשת בין שני גופים כלשהם הממוקמים במרחב. הם לא חייבים לגעת זה בזה, הם יכולים להיות רחוקים זה מזה, אך החשוב הוא שבאינטראקציה מתקיימת פעולת גומלין - כל גוף משפיע על משנהו.
יש הרבה סוגים של אינטראקציות. בכימיה מוכרות אינטראקציות כימיות, שהן פעולות גומלין בין אטומים ומולקולות. האינטראקציה במקרה של הכימיה מתבצעת באמצעות כוחות חשמליים.
ארבע האינטראקציות היסודיות בטבע
בטבע יש ארבע אינטראקציות אלמנטריות המוכרות כיום:
- אינטראקציה כבידתית - קשורה בכוח המשיכה בין מסות.
- אינטראקציה אלקטרומגנטית - קשורה בכל התהליכים הכימיים, יצירת אור וכל התופעות החשמליות.
- אינטראקציה גרעינית חלשה - מתרחשת בליבות של כוכבים, משנה את זהותם של חלקיקים אלמנטריים ואחראית לקרינה רדיואקטיבית.
- אינטראקציה גרעינית חזקה - מקורה בגרעיני אטומים, ומתבצעת בין חלקיקים הנקראים קוורקים.
כוחות אפקטיביים
בעולם המכניקה, העיסוק הוא פחות באינטראקציות היסודיות (למעט אולי האינטראקציה הכבידתית) ויותר בכוחות אפקטיביים.
דוגמה לכוח אפקטיבי: כאשר גוף עומד על הרצפה, הרצפה מפעילה עליו כוח כלפי מעלה. כוח זה נקרא הכוח הנורמלי. כל שני גופים שבאים במגע חווים כוח שאחד מפעיל על השני, והכוח הזה ניצב למישור המגע בין שני הגופים.
הערות סיום
בהמשך נדון ב:
- מערכת מנוחה
- מסה
- טרנספורמציית גלילאו
- שלושת חוקי ניוטון
- סוגי כוחות מעולם המעבדה
אינטראקציות אלקטרומגנטיות
כל כוח בסיסי בטבע או כוח אפקטיבי מקורו למעשה באינטראקציה אלקטרומגנטית. פחות או יותר, מבלי להיכנס לדקויות, רוב הכוחות הנחווים ביומיום הם תוצאה של אינטראקציה אלקטרומגנטית.
מבנה האטום והריק
האטומים הם בבסיסם ריק כמעט מושלם. קוטר האטום גדול פי 100,000 מקוטר גרעין האטום. מכיוון שנפח של כדור תלוי ברדיוס בשלישית, נפח האטום גדול ב-15 סדרי גודל מנפח הגרעין:
- רדיוס האטום גדול בחמישה סדרי גודל (פי 100,000) מגרעין האטום.
- נפח האטום גדול ב-15 סדרי גודל: $(10^5)^3 = 10^{15}$.
- $10^{15}$ זה מיליון מיליארדים.
לסבר את האוזן, אם נבחן את הנפח האמיתי של החומר שנמצא בגוף אנושי:
- נניח שמסת הגוף היא $100\ \mathrm{kg}$ והוא מורכב בעיקר ממים.
- $100\ \mathrm{kg}$ מים הם $0.1\ \mathrm{m}^3$ (עשירית קוב).
- הנפח האמיתי של החומר (ללא הריק) הוא 15 סדרי גודל קטן יותר.
-
כלומר:
\[\frac{0.1\ \mathrm{m}^3}{10^{15}} = 10^{-16}\ \mathrm{m}^3\] - $10^{-16}\ \mathrm{m}^3 = 100 \times 10^{-18}\ \mathrm{m}^3 = 100\ \mathrm{\mu m}^3$
כל אדם, מבחינת החומר הממשי שבו, הוא בגודל של בקטריה גדולה - רק שזו “בקטריה” שמסתה 70-100 ק”ג.
מדוע גופים תופסים נפח?
מה הופך אותנו לגוף בסדר גודל של מטר? מדוע כאשר דוחפים קיר, היד אינה חודרת לתוכו, אם הקיר והיד הם כמעט לגמרי חלל ריק?
הסיבה היא שהאטומים עטופים בשדות אלקטרומגנטיים. גם בקיר וגם ביד יש שדות אלקטרומגנטיים שמונעים מהיד לחדור לתוך הקיר - יש התנגדות של אינטראקציה אלקטרומגנטית שמונעת זאת.
אם האינטראקציה הזאת לא הייתה קיימת, ניתן היה לדחוף את היד לתוך הקיר בלי כל קושי, וגם ליפול לעבר מרכז כדור הארץ. אלו האינטראקציות האלקטרומגנטיות שמונעות מחומר להיכנס בחומר.
כוח נורמלי
מנקודת המבט של המעבדה, אנו רואים לא יותר מאשר כוח נורמלי. הוא מסומן באות $N$ מהמילה “נורמלי”.
הכוח הנורמלי תמיד:
- נובע ממגע בין גופים.
- ניצב למשטח המגע ביניהם.
חשוב להבין שכאשר מדובר על כוח נורמלי, מקורו בכוח האלקטרומגנטי, אבל מתייחסים אליו באופן אפקטיבי כאל כוח ששני גופים מפעילים זה על זה כשהם נוגעים זה בזה.
עוד כוח שנובע מהאינטראקציה האלקטרומגנטית הוא כוח החיכוך, שגם הוא סוג של כוח מגע, ועליו נדבר בהמשך.
אינטראקציות יסודיות נוספות
האינטראקציות הגרעיניות החלשות והחזקות פחות רלוונטיות לקורס זה, למרות שבעקיפין נעשה בהן שימוש ברפואה (למשל, בשימוש בקרינה רדיואקטיבית לאבחונים).
רוב האינטראקציות שנדון בהן מקורן באינטראקציות אלקטרומגנטיות, ואולי גם נדבר קצת על אינטראקציות כבידתיות (הקשורות בעובדה שגופים נושאים מסות).
מסת התמדה
לכל חלקיק אלמנטרי יש תכונה יסודית המגדירה אותו, והתכונה הזאת נקראת התמדה.
מסת התמדה היא:
- ההתנגדות של הגוף לשינוי במצבו תחת פעולת כוח.
- מידת ה”התמדה” ב”אישיות” של הגוף.
- מידת האינרציה, ההתנגדות לשינוי במצב התנועה.
חוקי ניוטון
כעת יוצגו שלושת חוקי ניוטון, המשמשים בסיס לכל המכניקה הניוטונית ששלטה בכיפה המדעית במשך כ-250 שנה, ובאמצעותם ניתן להסביר תופעות רבות.
מושג התנע (Momentum)
נגדיר גודל וקטורי דינמי שנקרא תנע (באנגלית: “מומנטום”):
\[\mathbf{p} = m\mathbf{v}\]כאשר:
- $\mathbf{p}$ הוא התנע
- $m$ היא המסה של הגוף או של מערכת הגופים
- $\mathbf{v}$ הוא וקטור המהירות של הגוף
המסה נמדדת ביחידות של קילוגרם, והיא מבטאת את מידת ההתמדה של הגוף:
- מסה של אדם היא כ-80 קילוגרם (זו לא משקלו, זו מסתו).
- מידת ההתמדה של זבוב היא כחצי גרם.
- מידת ההתמדה של נושאת מטוסים היא כ-200 מיליון קילוגרם.
יש הבדל גדול בין מסה למשקל:
- משקל זה כוח.
- מסה זה מידת התמדה.
ניסיון לעצור נושאת מטוסים ביד בזמן שהיא שטה באוקיינוס יהיה קשה מאוד - יש לה המון התמדה. לעומת זאת, עצירת אדם או זבוב קלה יותר בהתאם למסתם הקטנה יותר.
התנע מבטא במידה רבה את המדד הווקטורי לתנועתיות הקווית של הגוף - גם את כמות התנועתיות וגם את כיוונה.
שימו לב שהתנע תלוי במערכת ייחוס. אם גוף נמצא בתנועה במהירות מסוימת, יש לו תנע ששונה מאפס. אם הוא נמצא במנוחה, התנע שלו שווה לאפס. אבל זה תלוי במערכת הייחוס שבה הוא נמדד. התנע אינו גודל אבסולוטי, אלא גודל שבכל מערכת ייחוס מקבל ערך אחר.
החוק הראשון של ניוטון
החוק הראשון של ניוטון קובע:
בהיעדר השפעות חיצוניות (או בהיעדר אינטראקציות), התנע נשמר בזמן:
\[\mathbf{p} = \text{constant}\]
בהקשר מסוים, חוק זה נקרא “חוק שימור התנע”.
המשמעות היא שאם גוף נמצא בתנועה בכיוון מסוים ובמהירות מסוימת, ולא פועלים עליו כוחות חיצוניים, הגוף ימשיך לנוע באותה מהירות ובאותו כיוון לנצח (כל עוד לא פועלים עליו כוחות חיצוניים).
החוק הראשון נקרא גם “חוק ההתמדה”.
זה מנוגד לחלוטין לאינטואיציה של אריסטו, שסבר שאם הוא מקנה מהירות לגוף מסוים, הגוף יקבל תנופה, אבל לאט לאט התנופה תדעך והוא יעצור. לפי ניוטון, בהיעדר השפעות חיצוניות, הגוף ימשיך לנוע עם התנופה שהוקנתה לו מלכתחילה עד אין קץ.
בהמשך נשתמש בחוק זה במקרה שהמערכת במנוחה (כולל מהירות קבועה). כלומר, כאשר הכוח השקול הפועל על הגוף הוא אפס, נקבל:
\[\sum \mathbf{F} = 0\]כי $\sum \mathbf{F} = 0 \implies \frac{d\mathbf{p}}{dt} = 0 \implies \mathbf{p} = \text{constant}$. החוק הראשון הוא בעצם מקרה פרטי של החוק השני, כאשר הכוח השקול הוא אפס.
החוק השני של ניוטון
נגדיר כוח כהשפעה חיצונית ונסמן אותו ב-$\mathbf{F}$.
כוח הוא וקטור, כי השפעה חיצונית יכולה להיות בעלת גודל וכיוון מסוימים. גוף יכול לדחוף גוף אחר בכיוון מסוים ובכוח מסוים, או בכיוון אחר ובכוח אחר.
יכולות להיות השפעות חיצוניות רבות. נסמן כוחות בודדים ב-$\mathbf{F}_i$ כאשר $i$ הוא אינדקס ($\mathbf{F}_1$, $\mathbf{F}_2$, $\mathbf{F}_3$, וכו’).
שקול הכוחות יסומן ב-$\mathbf{F}$ ויהיה:
\[\mathbf{F} = \mathbf{F}_1 + \mathbf{F}_2 + ... + \mathbf{F}_n\]החוק השני של ניוטון קובע:
שקול הכוחות שווה לקצב השינוי של התנע:
\[\mathbf{F} = \frac{d\mathbf{p}}{dt}\]
שימו לב לעובדה המעניינת הבאה: כאשר שקול הכוחות שווה לאפס, קצב השינוי בתנע שווה לאפס, ואינטגרציה לפי הזמן נותנת $\mathbf{p} = \text{constant}$, וכך חוזרים אל החוק הראשון של ניוטון.
כאשר $\mathbf{F} = 0$, אז $\frac{d\mathbf{p}}{dt} = 0$, ומכאן $\mathbf{p}$ אינו תלוי בזמן.
בהקשר זה, החוק הראשון הוא חוק שימור התנע. כלומר, כאשר מבינים שבמערכת שקול הכוחות מתאפס, ידוע שהתנע נשמר בזמן.
הקשר בין כוח ותאוצה
נזכור ש-$\mathbf{p} = m\mathbf{v}$, ולכן:
\[\mathbf{F} = \frac{d\mathbf{p}}{dt} = \frac{d(m\mathbf{v})}{dt} = \frac{dm}{dt}\mathbf{v} + m\frac{d\mathbf{v}}{dt} = \frac{dm}{dt}\mathbf{v} + m\mathbf{a}\]כאשר $\frac{d\mathbf{v}}{dt} = \mathbf{a}$ (התאוצה).
ברוב המקרים נטפל בבעיות שבהן המסה היא גודל קבוע, ולכן כאשר המסה אינה משתנה בזמן:
\[\mathbf{F} = m\mathbf{a}\]
זוהי הצורה המוכרת יותר של החוק השני של ניוטון.
אולם, יש סיטואציות שבהן המסה כן משתנה בזמן. לדוגמה, כאשר משגרים טיל או רקטה ושורפים דלק, מסת הרקטה משתנה בזמן. טילים גדולים כמו אלה של SpaceX שורפים דלק בקצב של מאות קילוגרמים בשנייה, ואז לאיבר $\frac{dm}{dt}\mathbf{v}$ יש משמעות.
משוואת תנועה דיפרנציאלית
הקשר $\mathbf{F} = m\mathbf{a}$ נראה תמים, אבל זוהי משוואת מפתח.
מכיוון ש-$\mathbf{a} = \frac{d^2\mathbf{r}}{dt^2}$, הכוח החיצוני יכול להיות תלוי במקום של הגוף או במהירות הגוף:
\[\mathbf{F}(\mathbf{r}, \dot{\mathbf{r}}) = m\ddot{\mathbf{r}}\]זוהי משוואה דיפרנציאלית עבור $\mathbf{r}(t)$ - וקטור המקום כפונקציה של הזמן - שמכילה את הנגזרות של $\mathbf{r}(t)$: את $\dot{\mathbf{r}}$ (המהירות) ואת $\ddot{\mathbf{r}}$ (התאוצה).
למשוואה שמכילה את הפונקציה ונגזרותיה קוראים משוואה דיפרנציאלית, והפתרון של המשוואה הדיפרנציאלית נותן לנו את הנעלם שהוא הפונקציה הווקטורית $\mathbf{r}(t)$.
לפעמים קורה שהכוח תלוי רק במהירות:
\[\mathbf{F}(\dot{\mathbf{r}}) = m\ddot{\mathbf{r}}\]ואז זו תהיה משוואה דיפרנציאלית ביחס לווקטור המהירות.
החוק השני של ניוטון - משמעות עמוקה
זוהי משוואה שמכילה לא את $\mathbf{r}$ עם $\dot{\mathbf{r}}$ ו-$\ddot{\mathbf{r}}$, אלא רק את $\dot{\mathbf{v}}$ ו-$\mathbf{v}$.
החוק השני של ניוטון הוא משוואת המפתח. הפתרון שלו, ברגע שמתארים את המציאות באמצעותו, שקול הכוחות שווה למסה כפול תאוצה, הוא חוק טבע. זה לא רשום בעולם המתמטיקה - זו תוצאה של הבנת המציאות, הבנת החוקיות במציאות.
לקיחת ההבנה של החוקיות במציאות, יישומה על מערכת פיזיקלית מסוימת, מניבה משוואה דיפרנציאלית עבור וקטור המקום של הגוף, ופתרון המשוואה נותן את וקטור המקום של הגוף כפונקציה של הזמן בכל זמן $t$, ובפרט בזמן $t$ עתידי.
הנגזרות תמיד הן לפי הזמן. בהמשך נדבר על מושגים שגם דורשים אינטגרציה לפי מקום, אך נניח לזה לעת עתה.
מקור החוק השני
מאין מגיע חוק זה? ניוטון הגיע לחוק זה בצורה אמפירית. הוא בחן מערכות של גופים, בדק את קצב שינוי התנע שלהם, וגילה שהוא פרופורציונלי לשקול הכוחות.
אפשר לומר במידה רבה שהשינוי בתנע מגדיר את שקול הכוחות שפועל על הגוף, אבל זו התחכמות פילוסופית. ניוטון הגיע לכך באופן אמפירי - המשוואות האלו הגיעו מתוך תובנות אמפיריות.
כיום, ההבנה היא לא רק “איך” אלא גם “למה”. המשוואה הזאת היא משוואה שממזערת פונקציה מסוימת (הנקראת “פעולה”) המתארת את המציאות, ושצריכה לקבל מינימום כדי שהמציאות תתפתח כפי שהיא מתפתחת. זהו פורמליזם מורכב, עמוק ומעניין, אך לא ניכנס אליו כעת.
בכל מקרה, זהו פורמליזם קלאסי. תורת היחסות, שמחליפה את המכניקה הניוטונית, נותנת פרספקטיבה אחרת לגמרי על המציאות.
החוק השלישי של ניוטון
החוק השלישי של ניוטון קובע שאם שני גופים באים במגע, כל אחד מפעיל על הגוף השני כוח ששווה בגודלו והפוך בכיוונו לכוח שהגוף השני מפעיל עליו.
במילים אחרות, באינטראקציה:
\[\mathbf{F}_{1\rightarrow2} = -\mathbf{F}_{2\rightarrow1}\]
אם גוף 1 מפעיל על גוף 2 כוח $\mathbf{F}$ בכיוון מסוים, הרי שגוף 2 יפעיל על גוף 1 את אותו כוח רק בכיוון ההפוך. כוחות אלה נקראים “כוחות פעולה ותגובה”.
אלו הם שלושת החוקים של ניוטון, ואיתם אפשר לעשות נפלאות. להלן כמה דוגמאות.
יישום חוקי ניוטון
אם חל תנאי ההתמדה (החוק הראשון) בציר מסוים, אז בציר הזה יש משוואה אלגברית שמסכמת את הכוחות לאפס.
אם חל החוק השני, אז יכולה להיות אחת משתי אפשרויות: מתקבלת או משוואה אלגברית עבור התאוצה, או משוואה דיפרנציאלית עבור המהירות או המקום.
הקשר בין כיוון הכוח וכיוון התנועה
נקודה חשובה לפני שניגש לדוגמאות ספציפיות: כפי שדובר בשיעור שעבר, המהירות קובעת את כיוון תנועת הגוף. וקטור המהירות תמיד משיק למסלול תנועתו של הגוף.
מהחוק השני של ניוטון, $\mathbf{F} = m\mathbf{a}$, רואים מיד שהכוח הוא בכיוון התאוצה והתאוצה היא בכיוון הכוח. כלומר, וקטור התאוצה הוא בכיוון וקטור שקול הכוחות.
זה מעניין ולא אינטואיטיבי. בהחלט ייתכן שהתאוצה תהיה ניצבת למהירות.
לדוגמה, אם נזרוק חפץ בכיוון אופקי, כוח המשיכה של כדור הארץ מושך אותו למטה, אבל המהירות ההתחלתית שניתנה לו גורמת לו להמשיך בכיוון אופקי. בכיוון הניצב לרדיוס כדור הארץ לא פועלים כוחות, אז אם הוענקה לו מהירות $v_0$ בכיוון אופקי, הוא ימשיך לנוע באותה מהירות כל הזמן בכיוון האופקי. אבל פועל עליו כוח בכיוון אנכי שמאיץ אותו כלפי מטה.
כלומר, הוא יואץ כלפי מטה, התאוצה תהיה בכיוון מטה, מהירות קבועה תהיה בכיוון אופקי (כי החוק הראשון חל בכיוון זה), ותתקבל כתוצאה מכך תנועה פרבולית כלפי מטה.
התאוצה אינה בכיוון המהירות; התאוצה היא כלפי מטה. למרות שהמהירות משיקה לפרבולה, התאוצה תהיה כלפי מטה.
זו נקודה חשובה: התאוצה תמיד בכיוון שקול הכוחות, ושקול הכוחות תמיד בכיוון התאוצה. המהירות תמיד משיקה למסלול התנועה. לא חייב להיות קשר בין המהירות לבין שקול הכוחות, למעט בתנועה בממד אחד. בממד אחד, המהירות, התאוצה ושקול הכוחות עשויים להיות באותו כיוון או בכיוון מנוגד.
דוגמה 1: מסה תלויה משני חוטים
הנה דוגמה טריוויאלית: תקרה, חוט, זווית $\alpha$ וזווית $\beta$, ומסה התלויה מהתקרה באמצעות שני חוטים. בסיטואציה הזאת, המערכת נמצאת במנוחה. המסה נמצאת במנוחה.
אם היא נמצאת במנוחה, החוק הראשון של ניוטון רלוונטי לגביה. כלומר, חל על המסה תנאי ההתמדה.
ראשית, נאתר את כל הכוחות שפועלים על המסה. בבדיקה פיזיקלית על מסה מסוימת, מה שמסביב אינו מעניין; מה שמעניין הוא המסה הספציפית הזאת.
יש כאן שני חוטים. יש להגדיר את הכוח שהחוט מפעיל על המסה. כוח זה נקרא המתיחות בחוט. מקור המתיחות בחוט הוא אינטראקציה אלקטרומגנטית - כוח המשיכה בין האטומים שבונים את החוט.
במעבדה, מסתכלים על זה באופן אפקטיבי כמתיחות בחוט. המתיחויות אינן ידועות והבעיה אינה סימטרית, ולכן נסמן אותן ב-$T_1$ ו-$T_2$. האות $T$ היא מהמילה tension (מתיחות).
בקירוב לבעיה הספציפית הזאת, החוטים חסרי מסה. אם הייתה להם מסה, היה צורך לקחת אותה בחשבון.
המסה לא הייתה חשה שום מתיחות בחוט אם כדור הארץ לא היה מושך אותה כלפי מטה. לכוח המשיכה שבו כדור הארץ מושך כלפי מטה נקרא $W$, מהמילה Weight (משקל). משקל אינו מסה. משקל מבטא את כוח המשיכה.
ניתוח הכוחות במערכת
כעת נפעיל את החוק הראשון על הגוף הזה. החוק הראשון נותן משוואה וקטורית:
\[\mathbf{T}_1 + \mathbf{T}_2 + \mathbf{W} = 0\]זאת המשוואה הווקטורית שמתארת את הבעיה. החוק הראשון אומר ששקול הכוחות שווה לאפס.
כעת נפרק את המשוואה לרכיביה. כלומר, נחפש שני צירים נוחים, עדיף שאחד הצירים לפחות יתלכד עם אחד הכוחות, ונבנה את שיווי המשקל בכל אחד מהצירים.
אם נבחר את ציר $x$ בכיוון אופקי וציר $y$ בכיוון אנכי, בציר $x$ מתקיים:
\[T_2 \cos\beta - T_1 \cos\alpha = 0\]ובציר $y$:
\[T_2 \sin\beta + T_1 \sin\alpha - W = 0\]ניתן לרשום זאת כך:
\[T_1 \cos\alpha = T_2 \cos\beta\]כלומר שני הכוחות בציר $x$ מאזנים זה את זה, ומתקיים:
\[T_1 \sin\alpha + T_2 \sin\beta = W\]הזוויות $\alpha$ ו-$\beta$ נתונות, $T_1$ ו-$T_2$ אינם ידועים (המתיחות לא ידועה), ו-$W$ (המשקל) בדרך כלל נתון. קיבלנו שתי משוואות בשני נעלמים: הגודל של $T_1$ והגודל של $T_2$, ומתוכן ניתן לחלץ את $T_1$ ו-$T_2$ במונחים של $\alpha$, $\beta$ ו-$W$.
מקרה מיוחד: זוויות זהות
נבחן את המקרה המעניין שבו הזוויות זהות, כלומר המסה תלויה כך שבשני הצדדים יש את אותה זווית $\alpha$.
מתנאי שיווי המשקל בציר $x$ מתקיים:
\[T_1 \cos\alpha = T_2 \cos\alpha\]או $T_1 = T_2 = T$. מהמשוואה השנייה בציר $y$ מקבלים:
\[T \sin\alpha + T \sin\alpha = W\]כלומר, $2T \sin\alpha = W$. מכאן:
\[T = \frac{W}{2\sin\alpha}\]המתיחות בחוט הולכת כמו אחד חלקי סינוס הזווית.
שימו לב, כאשר $\alpha = \frac{\pi}{2}$ (זווית ישרה), $\sin\alpha = 1$, ואז $T = \frac{W}{2}$. כלומר, כל חוט נושא מחצית מהמשקל, וזה הגיוני.
אבל מה קורה כאשר $\alpha \to 0$ (החוטים אופקיים)? אז $\sin\alpha \to 0$ ו-$T \to \infty$. לא יכול להתקיים מצב שבו המסה נמצאת במרכז ושני חוטים אופקיים תומכים בה. הסיבה היא שבציר ה-$y$ אין מה שיאזן את המשקל $W$. אין רכיב אנכי בציר $y$ מהמתיחות בחוטים, ולכן נדרש כוח אינסופי כדי להחזיק את החוטים במצב מאוזן.
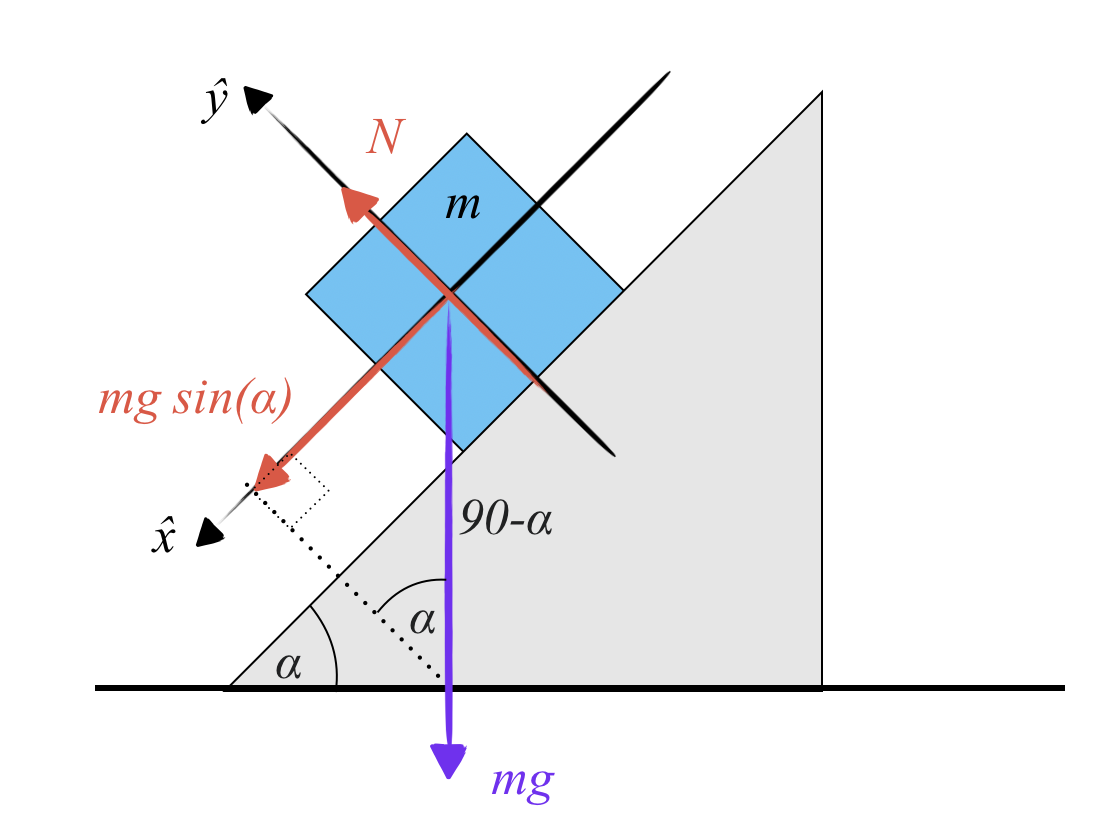
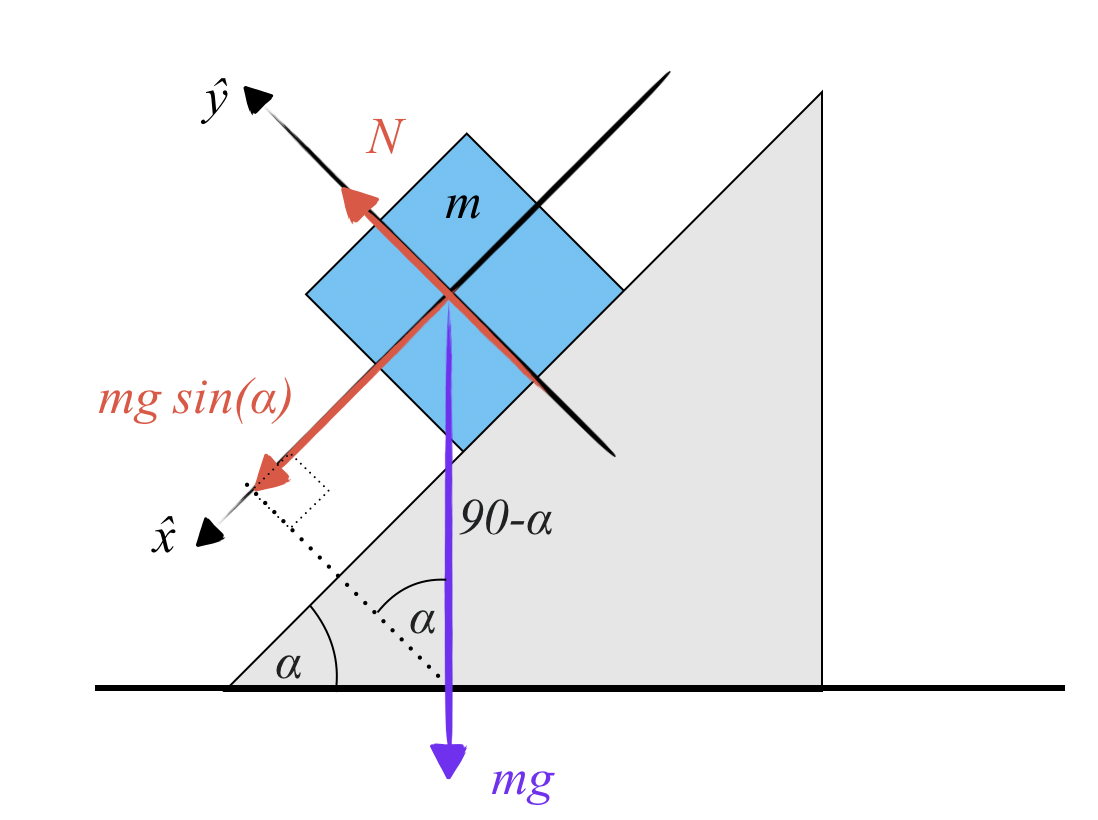
דוגמה 2: גוף על מישור משופע
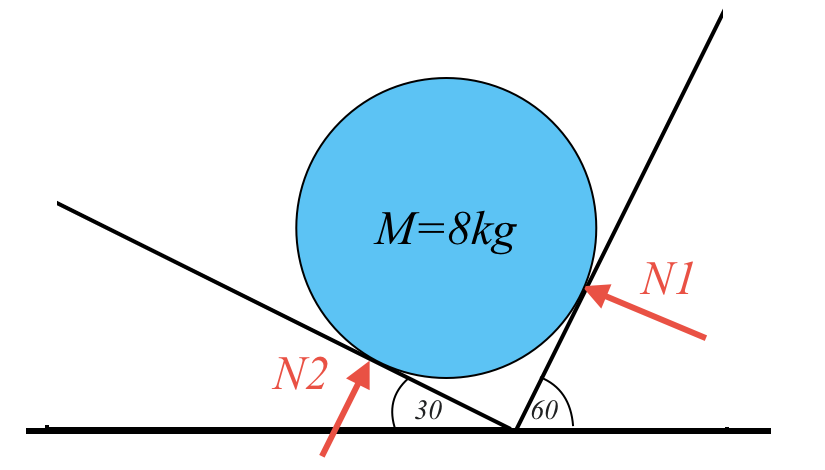
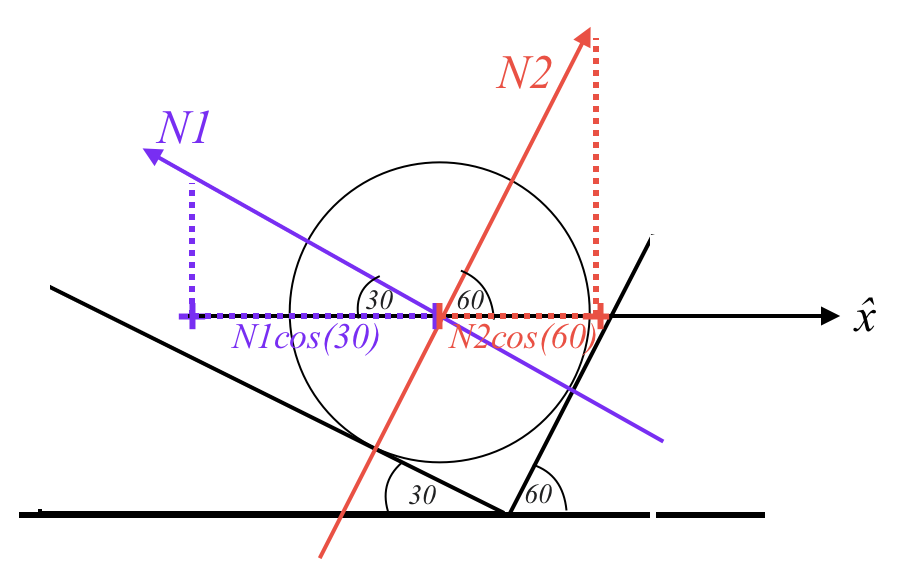
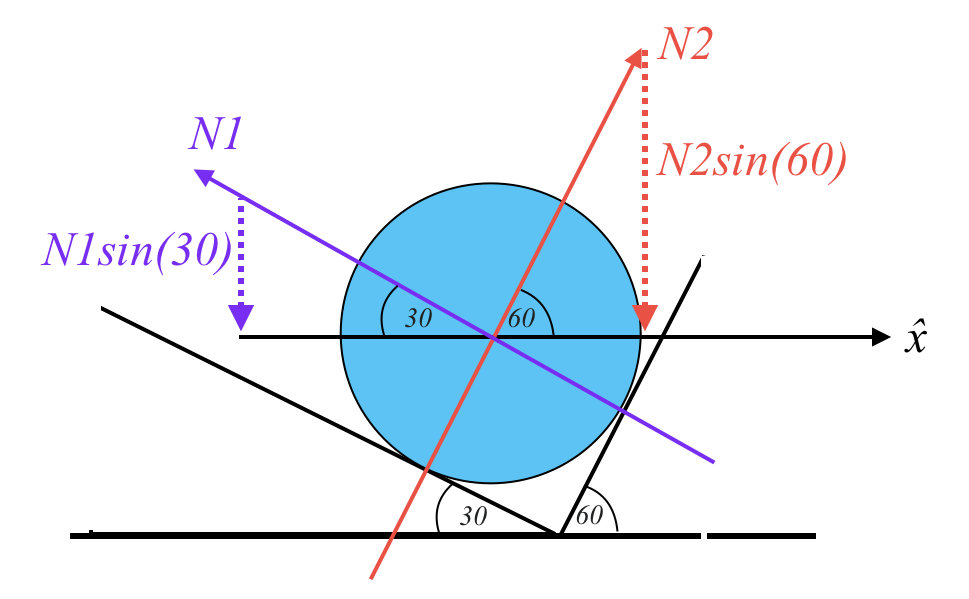
כעת נתבונן בגוף על מישור משופע בזווית $\alpha$. פועל עליו כוח משיכה $W$ כלפי מטה, וגם כוח נורמלי $N$ שהמשטח מפעיל על הגוף.
כפי שדובר, שני גופים במגע מפעילים זה על זה כוחות נורמליים הניצבים למשטח המגע ביניהם.
אלו הם הכוחות שפועלים על הגוף. אם זו זווית $\alpha$, ניתן לפרק את כוח המשיכה $W$ לשני רכיבים: רכיב מקביל למישור שגודלו $W \sin\alpha$, ורכיב ניצב למישור שגודלו $W \cos\alpha$.
על הציר הניצב למישור, המסה אינה נעה - היא לא קופצת מהמישור ולא חודרת אותו. כלומר בציר זה מתקיים חוק ההתמדה, ולכן:
\[N = W \cos\alpha\]תנאי ההתמדה בכיוון הניצב למישור מתקבל מהפעלת החוק הראשון של ניוטון.
בעוד שבציר המקביל למישור, פועל רק כוח אחד - רכיב המשקל $W \sin\alpha$ - ואין מה שיאזן אותו. ולכן מתקיים החוק השני של ניוטון:
\[ma = W \sin\alpha\]אז יש שתי משוואות שמתארות שתי תנועות. בכיוון מקביל למישור יש תאוצה:
\[ma = W \sin\alpha\]ובכיוון ניצב למישור יש תנאי התמדה (אין תנועה):
\[N = W \cos\alpha\]בשיעור הבא יוצגו דוגמאות מורכבות ועמוקות יותר, עם יותר פיזיקה ומתמטיקה.
שיעור 5 - מערכות התמד
תאריך: 27/04/2025טרנספורמציות גליליי
נושא חשוב הוא טרנספורמציות גליליי. נדון בנושא זה בצורה אנליטית.
מהן טרנספורמציות גליליי? הוגדר כי מערכת התמד היא מערכת שמאופיינת על ידי מהירות קצובה. יש לדייק בהגדרה - מהירות קצובה ביחס למה? מהירות קצובה ביחס לצופה אחד אינה בהכרח מהירות קצובה ביחס לצופה אחר הנע ביחס אליו.
ניתן להניח קיומה של מערכת ייחוס אבסולוטית, שביחס אליה ניתן להגדיר תנועה במהירות קצובה.
לדוגמה, כדור הארץ מסתובב סביב צירו ומשלים סיבוב ב-24 שעות. מערכת שמסתובבת אינה מערכת במהירות קצובה, כי סיבוב הוא תנועה מואצת. תנועה על פני מעגל היא תנועה המואצת לעבר המרכז.
עם זאת, הסיבוב של כדור הארץ הוא איטי מאוד. ניתן לחשב את המהירות הזוויתית, הקשורה לזמן המחזור דרך הקשר:
\[\omega = \frac{2\pi}{T}\]כאשר $T$ הוא זמן המחזור.
בתנועה מעגלית, וקטור המקום מתואר על ידי:
\[\vec{r}(t) = R \cos(\omega t) \hat{x} + R \sin(\omega t) \hat{y}\]הקוסינוס והסינוס הן פונקציות מחזוריות, כאשר המחזור הוא $2\pi$. כלומר, אחרי $\omega t = 2\pi$, הגוף חוזר לאותה פוזיציה. אם $t$ מתאר את הזמן ו-$T$ מתאר את זמן המחזור, אז:
\[\omega T = 2\pi \Rightarrow \omega = \frac{2\pi}{T}\]זמן המחזור $T$ של כדור הארץ הוא 24 שעות. לכן, המהירות הזוויתית $\omega$ של כדור הארץ היא:
\[\omega = \frac{2\pi}{24 \cdot 3600} \approx \frac{2 \cdot 3.14}{86400} \approx 7.27 \times 10^{-5} \text{ rad/s}\]המהירות הזוויתית של כדור הארץ נמוכה מאוד, ובקירוב מצוין כל מה שעל פני כדור הארץ יכול להיחשב כמערכת התמד. כלומר, התאוצה זניחה והמהירות כמעט קבועה.
הדבר דומה לטענה שכדור הארץ שטוח. בקירוב של סביבה מקומית (כיתה, עיר), כדור הארץ נראה שטוח. רק מגובה רב ניתן להבחין בעקמומיות שלו. כדור הארץ גדול והסביבה המיידית שלנו קטנה.
לכן, ניתן להתייחס למרחב הכיתה כאל מרחב קרטזי ולתאוצת הכיתה כאל אפסית ביחס למערכת הייחוס של כדור הארץ.
יש לציין כי המהירות הזוויתית של כדור הארץ בתנועתו סביב השמש נמוכה אף יותר (זמן מחזור של 365 ימים), ומהירות הסיבוב של מערכת השמש סביב מרכז הגלקסיה נמוכה עוד יותר (זמן מחזור של כ-220 מיליון שנה).
בקירוב מצוין, עבור הבעיות הנדונות כאן, ניתן להתייחס לכדור הארץ כמערכת התמד.
הגדרת טרנספורמציות גליליי
נתונות שתי מערכות התמד, $S$ ו-$S’$, הנעות זו ביחס לזו במהירות קצובה.
המהירות הקצובה של $S’$ ביחס ל-$S$ היא $\vec{u}$. אם בזמן $t=0$ הראשיות של המערכות התלכדו, אז בזמן $t > 0$ וקטור המרחק בין הראשיות הוא $\vec{u} t$.
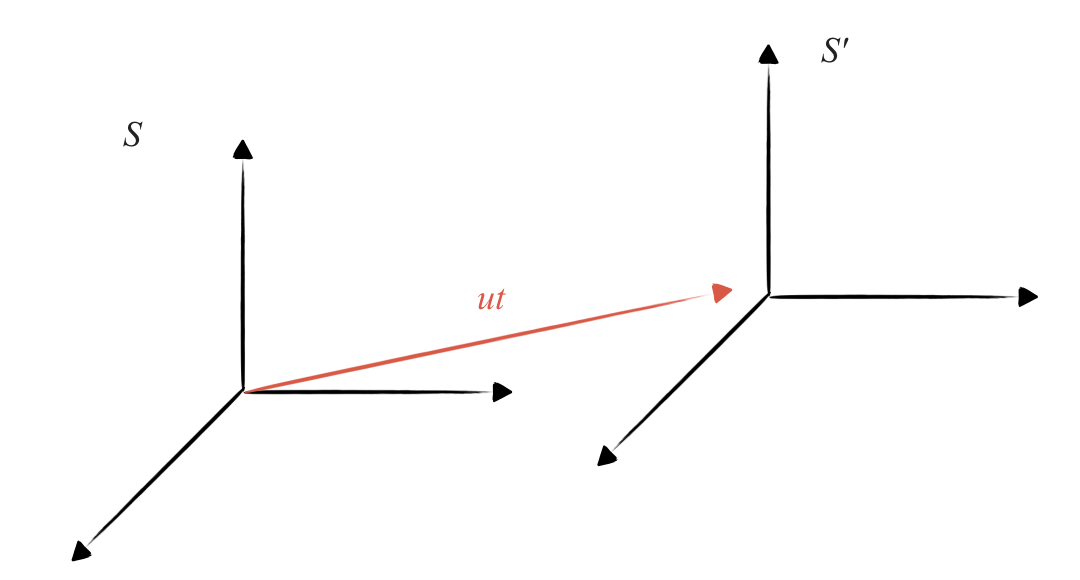
וקטור המקום של ראשית $S’$ ביחס לראשית $S$ בזמן $t$ הוא $\vec{u} t$.
נתבונן בחלקיק הנע במערכת $S$. וקטור המקום שלו הוא $\vec{r}$. וקטור המקום שלו במערכת $S’$ הוא $\vec{r}’$. הקשר בין וקטורי המקום הוא:
\[\vec{r} = \vec{r}' + \vec{u} t\]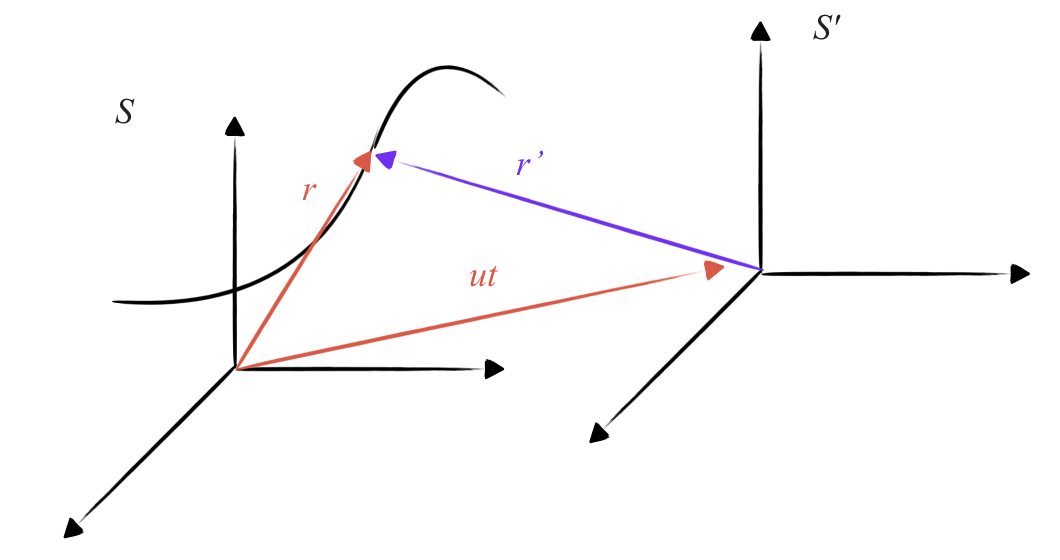
וקטור המקום במערכת $S$ הוא סכום וקטור המקום במערכת $S’$ והווקטור $\vec{u} t$.
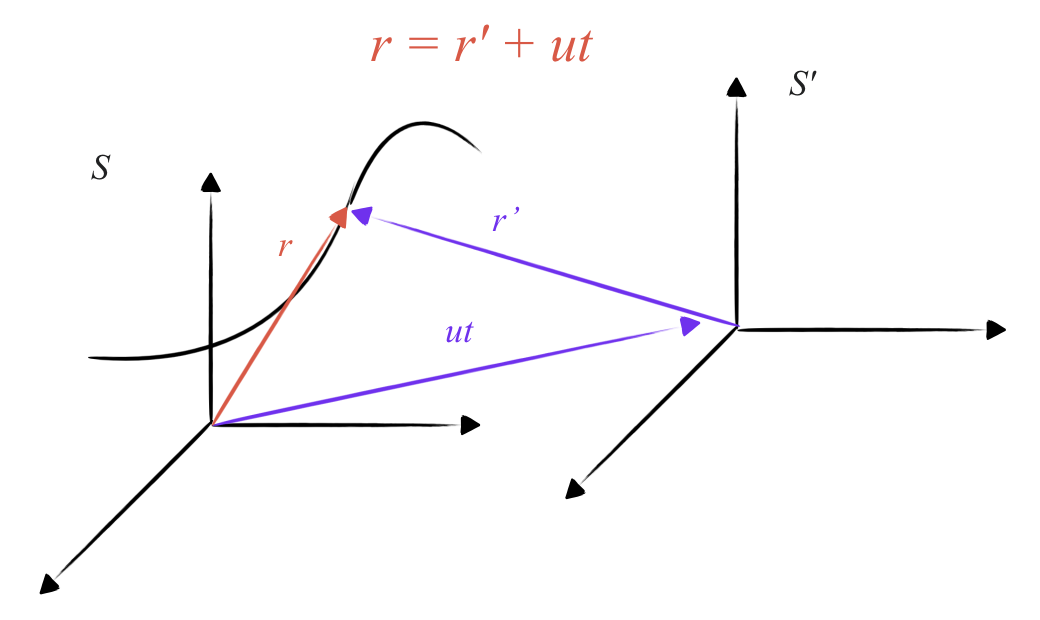
מכאן, חוק הטרנספורמציה של וקטורי המקום הוא:
\[\vec{r}' = \vec{r} - \vec{u} t\]מהירויות הן נגזרות של וקטורי המקום לפי הזמן. מהירות החלקיק $\vec{v}’$ במערכת $S’$ היא:
\[\vec{v}' = \frac{d\vec{r}'}{dt} = \frac{d\vec{r}}{dt} - \frac{d(\vec{u} t)}{dt} = \vec{v} - \vec{u}\]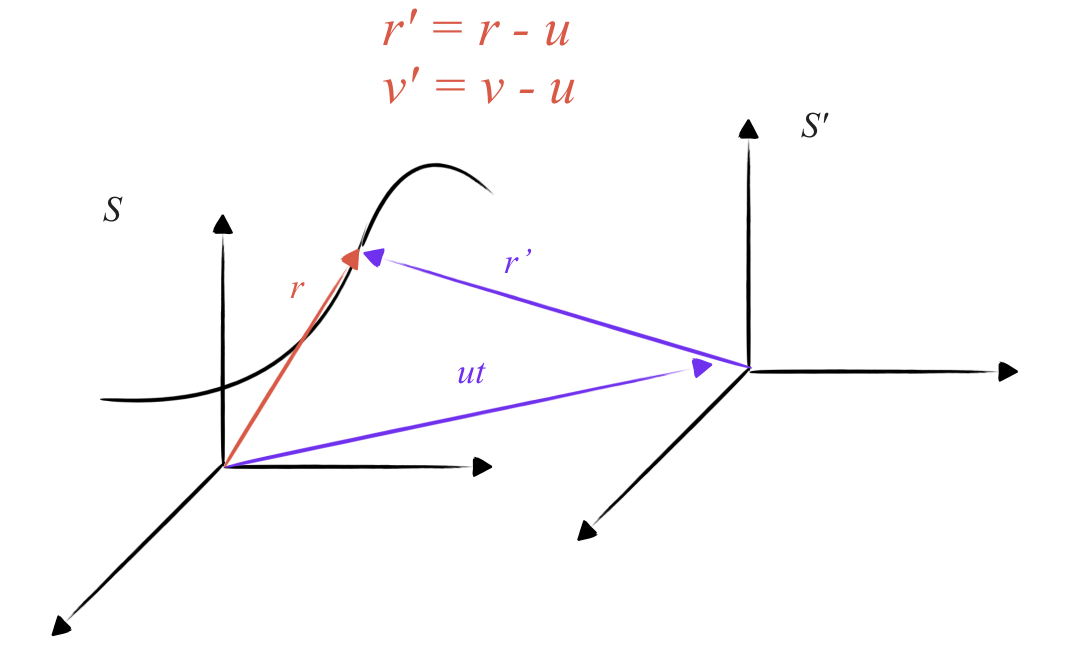
בנוסחה זו נעשה שימוש אינטואיטיבי בחישוב מהירויות יחסיות, עוד לפני ההגדרה הפורמלית של טרנספורמציות גליליי.
אם נגזור פעם נוספת לפי הזמן, ומכיוון שהווקטור $\vec{u}$ קבוע, נקבל:
\[\vec{a}' = \frac{d\vec{v}'}{dt} = \frac{d\vec{v}}{dt} - \frac{d\vec{u}}{dt} = \vec{a} - 0 = \vec{a}\]כלומר, התאוצות בשתי מערכות ההתמד שוות זו לזו. יש הבדל בין וקטורי המקום והמהירות, אך אין הבדל בין וקטורי התאוצה.
מכאן, מתוך החוק השני של ניוטון $\vec{F} = m\vec{a}$, ניתן להסיק שגם אין הבדל בכוחות:
\[\vec{F} = \vec{F}'\]לכן, ניתן להחיל את חוקי ניוטון באופן זהה בכל מערכות ההתמד.
מערכות התמד ומערכות מואצות
הפיתוח המתואר לעיל, שנעשה על ידי מדענים במאות ה-17 וה-18, התבסס על הנחה סמויה: הזמן הוא פרמטר אוניברסלי, זהה בכל המערכות. הנחה זו, שנראית סבירה מנקודת מבט אינטואיטיבית, הופרכה על ידי איינשטיין. תיקון הנחה זו הוביל לפיתוח תורת היחסות, שהיוותה קפיצת מדרגה בהבנת הפיזיקה.
מערכת התמד היא מערכת הנעה במהירות קצובה ביחס למערכת ייחוס אבסולוטית (למשל, היקום הסטטי). בתורה הניוטונית, החוק השני של ניוטון, $\vec{F} = m\vec{a}$ או $\vec{F} = \frac{d\vec{p}}{dt}$, תקף בכל מערכות ההתמד, ללא תלות במהירותן היחסית.
דוגמאות ליישום חוקי ניוטון במערכות שונות
הדיון החל מהקביעה שהכיתה היא מערכת התמד, מכיוון שמהירותה ביחס לכדור הארץ היא אפס (גודל קבוע).
אולם, ניתן לטעון שכדור הארץ עצמו אינו מערכת התמד, שכן הוא מסתובב סביב צירו, ותנועה מעגלית היא תנועה מואצת.
התשובה לכך היא שתאוצת כדור הארץ קטנה מאוד. המהירות הזוויתית $\omega$ זניחה, ולכן התאוצה הצנטריפטלית קטנה מאוד. לכל צורך מעשי בניסויים הנערכים בכיתה (כמו מטוטלת), ניתן להתייחס לכיתה כאל מערכת התמד.
גם אם הכיתה הייתה נעה במהירות של 1000 קמ”ש ביחס לכדור הארץ, כל עוד מהירות זו קבועה, עדיין ניתן היה להחיל את החוק השני של ניוטון.
לעומת זאת, מעלית הנמצאת בתאוצה אינה מערכת התמד. יש להבחין בין תנועה במהירות קבועה (מערכת התמד) לבין תנועה בתאוצה (מערכת לא-אינרציאלית).
גם גוף הנע במהירות של 200,000 ק”מ/שנייה נמצא במערכת התמד, כל עוד מהירותו קבועה. אין הבדל מהותי בין מנוחה לתנועה במהירות קצובה, שכן תמיד ניתן לבצע טרנספורמציית גליליי למערכת שבה הגוף נמצא במנוחה. בתורה הניוטונית, אין הגבלה על גודל המהירות. בתורת היחסות, המצב משתנה ככל שמתקרבים למהירות האור.
תאוצת הנפילה החופשית ודוגמאות נוספות
נחדד את הרעיונות באמצעות דוגמה. נתבונן במערכת של שתי מסות התלויות על חוט הכרוך סביב גלגלת חסרת חיכוך.
ראשית, יש לזכור כי בניסויי מעבדה, תאוצת הנפילה החופשית של גופים בקרבת פני כדור הארץ היא גודל קבוע, המסומן ב-$g$, וערכו כ-9.8 מטר לשנייה בריבוע (ובקירוב 10 לצורך חישובים). המשמעות היא שמהירותו של גוף נופל גדלה בכל שנייה בערך זה.
עבור תאוצה קבועה, מתקיימות משוואות התנועה:
\[v(t) = v_0 + gt\]ו-
\[x(t) = x_0 + v_0t + \frac{1}{2}gt^2\](כאשר ציר $x$ חיובי כלפי מטה).
החוק השני של ניוטון, $\vec{F} = m\vec{a}$, תקף. הכוח הגורם לתאוצת הנפילה החופשית הוא כוח הכובד, $W$. לכן:
\[W = mg\]מעתה ואילך, כוח המשיכה בקרבת פני כדור הארץ יסומן כ-$mg$. קביעה זו נובעת מהידיעה האמפירית שתאוצת הנפילה החופשית קבועה בקרבת פני כדור הארץ.
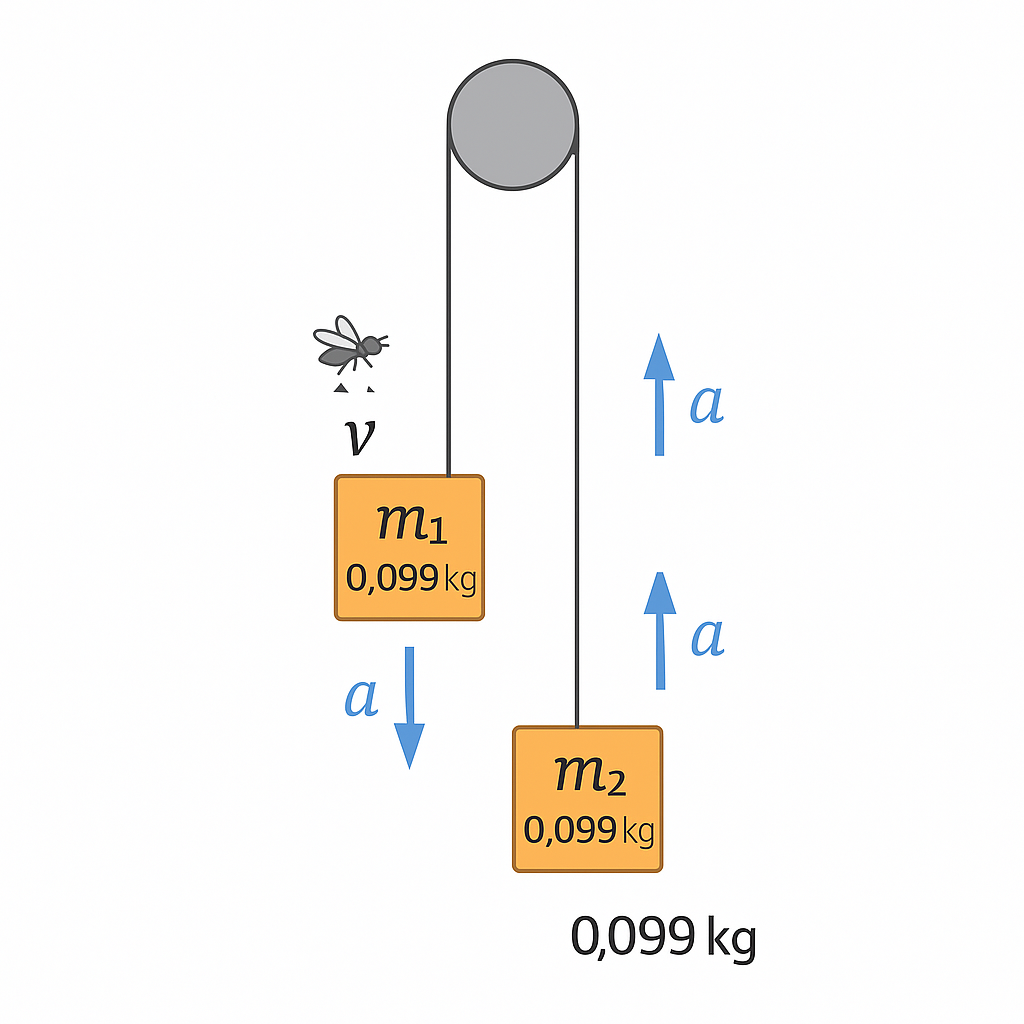
נחזור למערכת הגלגלת. אם שתי המסות שוות ($m_1=m_2=m$) והמערכת משוחררת ממנוחה, היא תישאר במנוחה. שקול הכוחות הוא אפס, ולכן, לפי החוק הראשון של ניוטון, המערכת תתמיד במצבה. הכוחות הפועלים על כל מסה הם המתיחות בחוט $T$ (כלפי מעלה) וכוח הכובד $mg$ (כלפי מטה). במצב שיווי משקל, $T=mg$.
אם נשים את המערכת הזאת בחללית הנעה במהירות קבועה של 200,000 ק”מ/שנייה ביחס לכדור הארץ, התוצאה תהיה זהה. היות שהחללית היא מערכת התמד, חוקי ניוטון תקפים בה באותו אופן.
כעת, נניח שבכיתה, אנו מעניקים למסה אחת מהירות התחלתית $v$ כלפי מטה. המסה השנייה תעלה במהירות $v$ כלפי מעלה. מכיוון ששקול הכוחות הוא אפס, הגופים יתמידו במהירותם הקבועה.
גם אם נבצע ניסוי זה בחללית הנעה במהירות קבועה, התוצאה תהיה זהה. ההבדל היחיד יהיה במהירות הנמדדת של המסות ביחס לכיתה, שתדרוש חיבור וקטורי של מהירות החללית.
בשלב הבא, נבחן את המקרה שבו המסות שונות ושקול הכוחות אינו אפס.
הערה על הדוגמה הקודמת
לפני שנמשיך, יש להבהיר נקודה לגבי הדוגמה של הגלגלת בחללית. הכוונה הייתה שהחללית, על אף מהירותה הגבוהה, עדיין נמצאת תחת השפעת כוח המשיכה של כדור הארץ. ללא כוח משיכה, הבעיה הייתה שונה. הנקודה החשובה היא שאותם כוחות פועלים הן במערכת הכיתה והן במערכת החללית, מכיוון ששתיהן מערכות התמד.
מערכות לא מאוזנות - מכונת אטווד
כעת נבחן מצב שבו המערכת אינה מאוזנת. יש לנו גלגלת עם מסה $M_1$ מצד אחד ומסה $M_2$ מצד שני, כאשר $M_1 \neq M_2$.
הכוחות הפועלים על $M_2$ הם כוח הכבידה $M_2g$ כלפי מטה והמתיחות $T$ כלפי מעלה. הכוחות הפועלים על $M_1$ הם כוח הכבידה $M_1g$ כלפי מטה והמתיחות $T$ כלפי מעלה. המתיחות בחוט אחידה.
הדרך הנכונה לפתור את הבעיה היא להחיל את החוק השני של ניוטון על כל מסה בנפרד. נניח ש-$M_2 > M_1$, ולכן המערכת מואצת כך ש-$M_2$ יורדת ו-$M_1$ עולה בתאוצה $a$.
עבור המסה $M_2$, החוק השני של ניוטון (בכיוון מטה) הוא:
\[M_2g - T = M_2a\]עבור המסה $M_1$, החוק השני של ניוטון (בכיוון מעלה) הוא:
\[T - M_1g = M_1a\]קיבלנו מערכת של שתי משוואות עם שני נעלמים, $T$ ו-$a$. אם נחבר את שתי המשוואות, המתיחות $T$ תתבטל:
\[M_2g - T + T - M_1g = M_2a + M_1a\] \[(M_2 - M_1)g = (M_2 + M_1)a\]מכאן ניתן לבודד את התאוצה $a$:
\[a = \frac{M_2 - M_1}{M_2 + M_1} \cdot g\]אם $M_2 > M_1$, התאוצה $a$ חיובית, כפי שהנחנו. אם $M_2 = M_1$, אז $a = 0$. אם $M_2 < M_1$, אז $a < 0$, כלומר התאוצה היא בכיוון ההפוך.
טרנספורמציית גליליי מבטיחה שזו תהיה התוצאה גם במערכת התמד אחרת, כמו חללית הנעה במהירות קבועה.
ניתן לפתור את הבעיה גם על ידי החלת החוק השני על המערכת כולה. שקול הכוחות החיצוניים המניעים את המערכת הוא $(M_2 - M_1)g$. המסה הכוללת של המערכת היא $(M_1 + M_2)$. לכן:
\[(M_2 - M_1)g = (M_1 + M_2)a\]ומקבלים את אותה התוצאה עבור $a$.
תנועה במעלית וכוחות מדומים
נבחן כעת מה קורה לאדם במעלית. נניח שבמעלית עומד אדם. כאשר המעלית עולה במהירות קצובה, היא מערכת התמד. שקול הכוחות הפועל על האדם הוא אפס.
הכוחות הפועלים על האדם הם:
- כוח הכבידה $mg$ כלפי מטה.
- הכוח הנורמלי $N$ מהרצפה כלפי מעלה.
מהחוק הראשון של ניוטון:
\[N = mg\]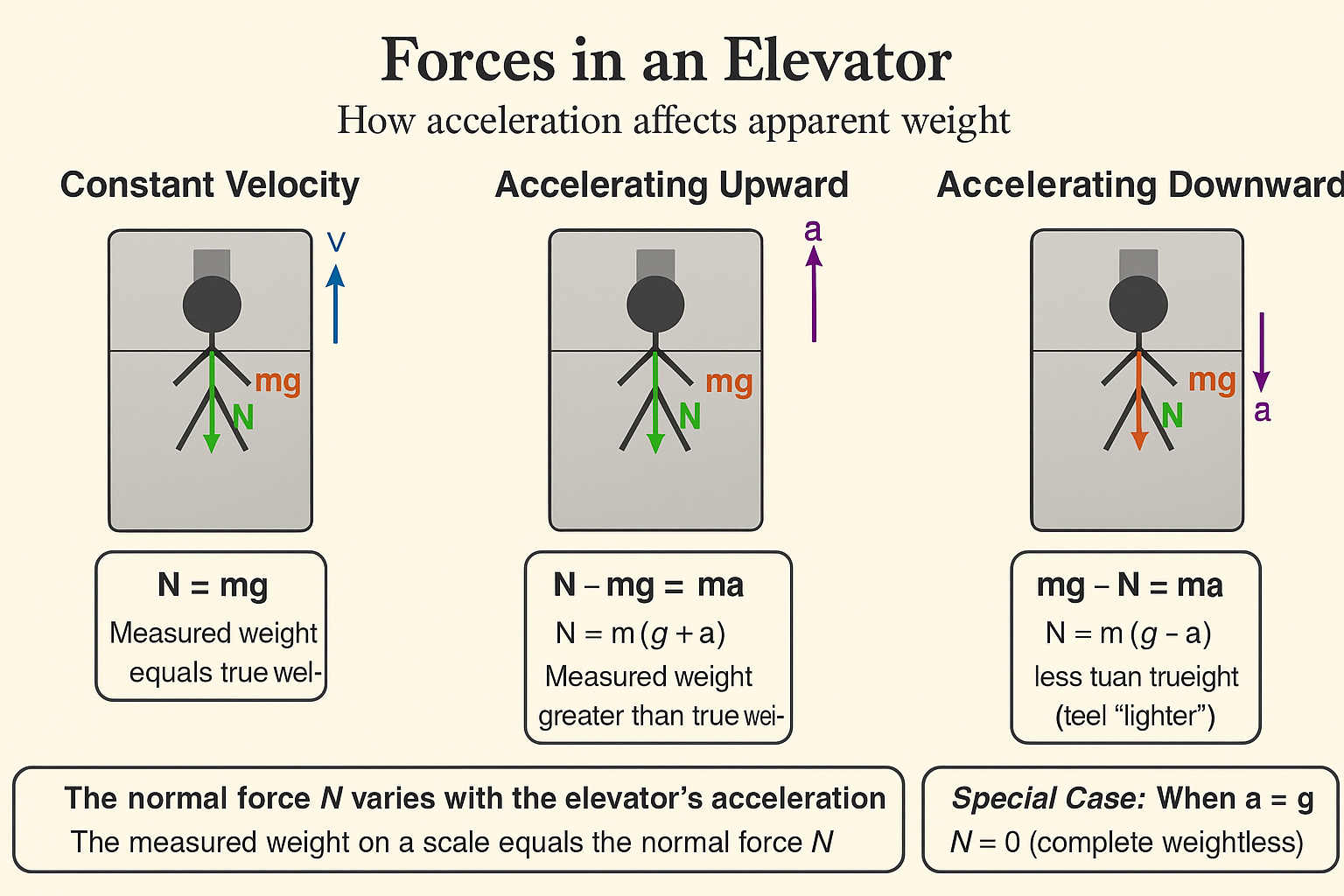
אם מסת האדם היא 80 ק”ג, אז $N = 80 \mathrm{[kg]} \cdot 10 \mathrm{[m/s^2]} = 800 \mathrm{[N]}$.
כעת, נניח שהמעלית מואצת כלפי מעלה בתאוצה $a$. המעלית אינה מערכת התמד. גם האדם שבתוכה מואץ באותה תאוצה. מהחוק השני של ניוטון:
\[N - mg = ma\]מכאן:
\[N = m(g + a)\]אם במעלית הייתה מונחת מאזני משקל, הן היו מודדות את הכוח הנורמלי $N$. לכן, כאשר המעלית מואצת כלפי מעלה, המשקל הנמדד של האדם גדול יותר. למשל, אם $a = 2 \mathrm{ m/s^2}$:
\[\text{observed weight} = 80 \mathrm{ kg} \cdot (10 + 2) \mathrm{ m/s^2} = 960 \mathrm{ N}\]במקרה ההפוך, כאשר המעלית מואצת כלפי מטה בתאוצה $a$, מתקיים:
\[mg - N = ma\]מכאן:
\[N = m(g - a)\]במקרה זה, המשקל הנמדד קטן יותר. אם המעלית נופלת נפילה חופשית ($a=g$), אז $N=0$ והאדם מרחף במצב של חוסר משקל.
כוחות מדומים במערכות מואצות
כיצד ניתן לפתור בעיה במערכת מואצת, למרות שחוקי ניוטון תקפים רק במערכות התמד? בדיון הקודם, פתרנו את הבעיה ממערכת התמד חיצונית (הבניין), וקבענו שהאדם מואץ יחד עם המעלית.
אך ניתן לפתור את הבעיה גם מתוך המערכת המואצת עצמה (המעלית). לשם כך, יש להשתמש במושג של “כוחות מדומים” (fictitious forces).
כדי להמחיש זאת, נתבונן באדם העומד על רצפה חלקה באוטובוס שחלונותיו אטומים. כאשר הנהג מאיץ קדימה, האדם מרגיש שהוא “נדחף” לאחור, למרות שאין כוח ממשי שדוחף אותו.
מנקודת מבט חיצונית, האוטובוס האיץ קדימה, אך האדם, בשל התמדתו, נטה להישאר במקומו. הרצפה החלקה גרמה לאוטובוס “לברוח” מתחת לרגליו.
מנקודת מבטו של האדם בתוך האוטובוס, פעל עליו כוח “מסתורי” אחורה. כוחות אלו, הנובעים מהתבוננות ממערכת מואצת, נקראים “כוחות מדומים”. הם אינם כוחות אמיתיים אלא תוצאה של תאוצת מערכת הייחוס.
גודלו של הכוח המדומה הוא:
\[\vec{F}_{\text{imaginary}} = -m\vec{a}_{\text{system}}\]כאשר $m$ היא מסת הגוף ו-$\vec{a}_{\text{system}}$ היא תאוצת מערכת הייחוס. הסימן השלילי מציין שהכוח המדומה פועל בכיוון ההפוך לתאוצת המערכת.
אם נחזור למעלית המואצת כלפי מעלה בתאוצה $a$, נוכל לנתח את המצב מתוך המעלית. נוסיף למערכת הכוחות כוח מדומה $ma$ הפועל כלפי מטה. כעת, מנקודת המבט של צופה במעלית, האדם נמצא בשיווי משקל, ולכן:
\[N - mg - ma = 0\]מכאן:
\[N = m(g + a)\]זו אותה תוצאה שקיבלנו קודם, אך הפעם היא הושגה על ידי ניתוח בתוך המערכת הלא-אינרציאלית.
דוגמה: גוף על מישור משופע
נתבונן בגוף המונח על מישור משופע חלק. ישנו טריז בזווית $\alpha$ ביחס לאופק, ועליו מונחת מסה $m$ המחליקה מטה ללא חיכוך.
הכוחות הפועלים על המסה הם:
- כוח הכבידה $mg$ כלפי מטה.
- כוח נורמלי $N$ מהמישור, בניצב למישור.
נגדיר מערכת צירים שבה ציר $x$ מקביל למישור (במורד) וציר $y$ ניצב לו. נפרק את וקטור הכבידה $mg$ לרכיביו:
- רכיב $x$: $mg \sin{\alpha}$
- רכיב $y$: $mg \cos{\alpha}$
מהחוק השני של ניוטון בציר $x$:
\[mg \sin{\alpha} = ma\]מכאן, תאוצת הגוף במורד המישור היא:
\[a = g \sin{\alpha}\]בציר $y$ אין תנועה, ולכן שקול הכוחות הוא אפס:
\[N - mg \cos{\alpha} = 0 \implies N = mg \cos{\alpha}\]דוגמה מורכבת: טריז נייד
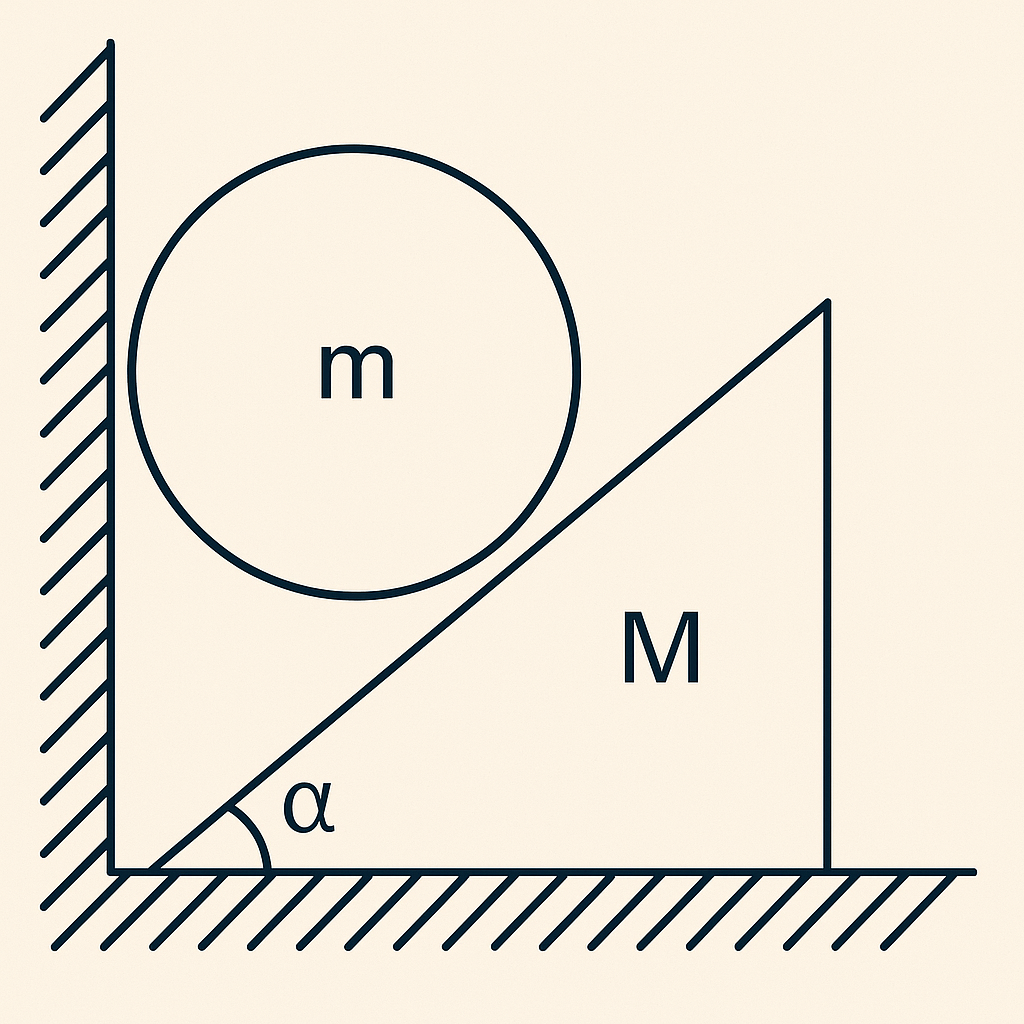
לבסוף, נבחן בעיה מורכבת יותר: טריז שמסתו $M$ נמצא על מישור אופקי חלק, כך שהוא חופשי לנוע. על הטריז מונחת מסה קטנה $m$.
כאשר המסה $m$ מונחת על הטריז, היא מחליקה מטה ודוחפת את הטריז ימינה. הטריז מאיץ ימינה, ולכן המסה $m$ נמצאת במערכת מואצת. כדי לפתור את הבעיה מנקודת מבטה של המסה $m$, יש להתחשב בכוח המדומה.
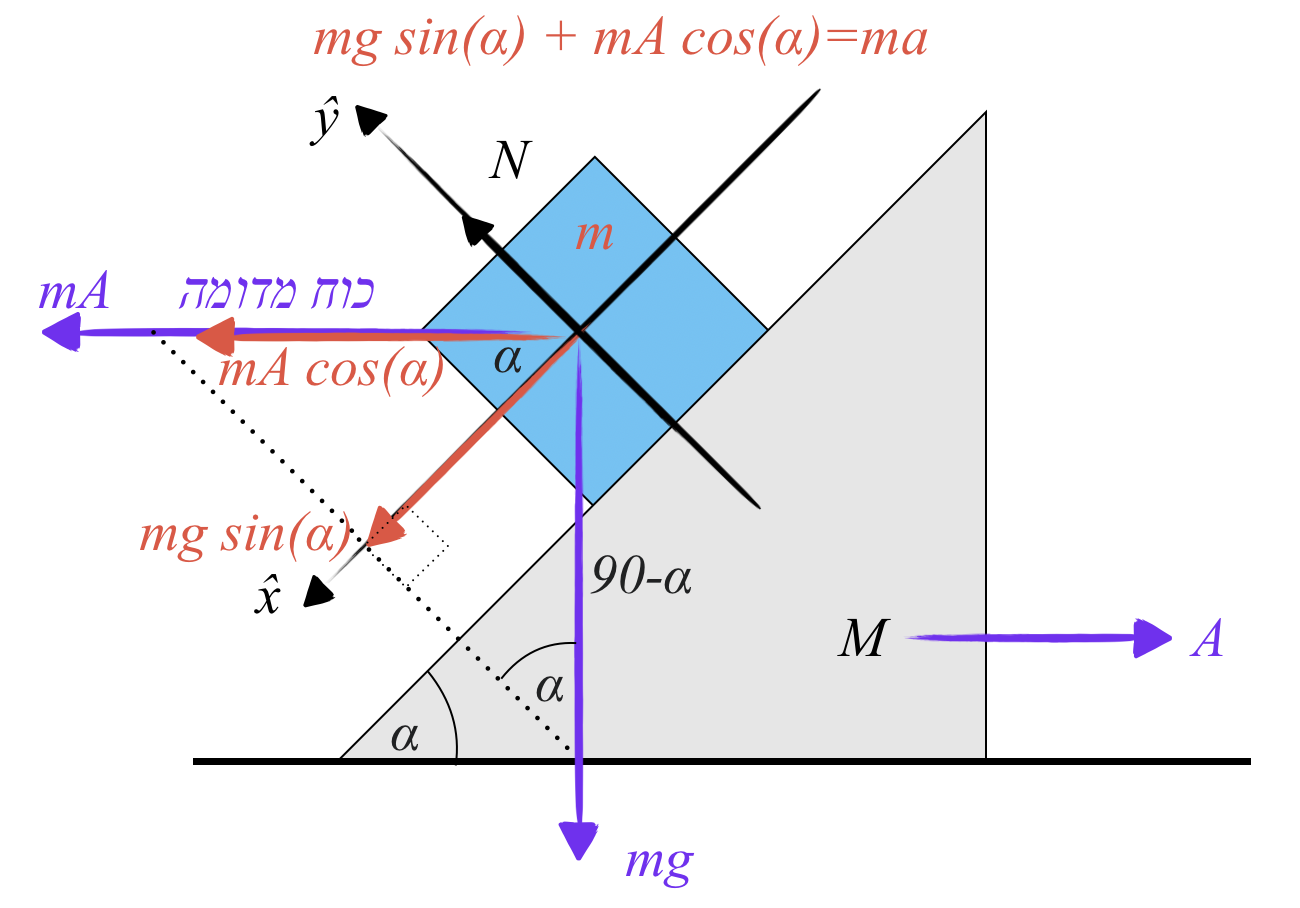
הכוחות הפועלים על המסה $m$ (במערכת הייחוס של הטריז) הם:
- כוח הכבידה $mg$ כלפי מטה.
- כוח נורמלי $N$ מהטריז, בניצב למישור המשופע.
- כוח מדומה $ma_M$ בכיוון אופקי שמאלה, כאשר $a_M$ היא תאוצת הטריז ימינה.
נגדיר מערכת צירים שבה ציר $x$ מקביל למישור המשופע (במורד) וציר $y$ ניצב לו. נפרק את הכוחות לרכיביהם:
משוואת התנועה בציר $x$ (תנועת $m$ ביחס לטריז בתאוצה $a$):
\[mg \sin{\alpha} - ma_M \cos{\alpha} = ma\]משוואת הכוחות בציר $y$ (אין תנועה בניצב למישור):
\[N + ma_M \sin{\alpha} - mg \cos{\alpha} = 0\]בנוסף, נכתוב את משוואת התנועה עבור הטריז עצמו (במערכת המעבדה). הכוח המניע את הטריז ימינה הוא הרכיב האופקי של הכוח הנורמלי שהמסה $m$ מפעילה עליו (מהחוק השלישי של ניוטון):
\[N \sin{\alpha} = Ma_M\]קיבלנו מערכת של שלוש משוואות עם שלושה נעלמים: $a$, $a_M$ ו-$N$, אשר פתרונה יספק את תיאור התנועה המלא.
סיכום
בשיעור זה נלמדו שתי גישות לטיפול במערכות לא-אינרציאליות (מואצות):
- פתרון מחוץ למערכת המואצת, תוך שימוש בחוקי ניוטון ממערכת התמד חיצונית.
- פתרון מתוך המערכת המואצת, תוך הוספת כוחות מדומים למערך הכוחות.
בשיעור הבא נרחיב את הדיון לבעיות עם חיכוך, ונעבור למצבים שבהם החוק השני של ניוטון מוביל למשוואות דיפרנציאליות.
שיעור 6 - מערכות התמד, חיכוך וכוחות מדומים
תאריך: 28/04/2025סקירה על כוחות מדומים
בשיעור שעבר נדונו כוחות מדומים - אלו אותם כוחות שמופיעים במערכת שאיננה מערכת התמד (מערכת לא אינרציאלית). כוחות אלה נובעים למעשה מהעובדה שלכל גוף בעל מסה יש התמדה, כלומר כל גוף, בגלל המסה שלו, מתנגד לשינוי מצבו הנוכחי.
למעשה, כל מסה היא מעין “מחסן” של התמדה - היא מבטאת את התמדתו של הגוף. כשהגוף נמצא בתוך מערכת מואצת, ההתמדה הזאת מייצרת כוחות מדומים בתוך המערכת המואצת. כדי להפעיל את חוקי ניוטון על מערכת מואצת, יש לקחת בחשבון את הכוחות המדומים הללו.
מהם הכוחות המדומים? הכוחות המדומים הם:
\[\mathbf{F}_{imaginary} = -m\mathbf{a}_{system}\]כלומר, מסת הגוף כפול תאוצת המערכת, והם פועלים בכיוון המנוגד לתאוצת המערכת.
לדוגמה, באוטובוס שבו אדם עומד על רצפה חלקה לגמרי והאוטובוס פתאום מאיץ, מנקודת מבטו של צופה הנמצא בתוך המערכת המואצת, פועל עליו פתאום כוח הדוחף אותו לעבר החלק האחורי של האוטובוס.
הכוח הזה הוא “כוח רפאים” - כוח שכביכול הגיע משום מקום. מנקודת ראותו של האדם במערכת המואצת, זהו כוח שלכאורה אין לו שום מקור. ומהו המקור האמיתי? מנקודת מבט של מערכת התמד (מערכת אינרציאלית), המקור הוא התמדת המסה - התמדת הגוף. המערכת שבה הוא נמצא מואצת ו”בורחת” מתחת לרגליו, ולכן נראה כאילו פועל עליו כוח שדוחף אותו לעבר הקיר האחורי.
הבחנה בין מערכות התמד ומערכות לא-התמד
חשוב לחזור לנקודה מרכזית שהושארה פתוחה: כיצד ניתן להבדיל בין מערכת התמד אמיתית לבין מערכת שאיננה מערכת התמד?
בתחילה הוגדרה מערכת התמד כמערכת הנמצאת במהירות קבועה ביחס למציאות אבסולוטית כלשהי. אך האמת היא שבטבע אין מציאות אבסולוטית כזו.
הראשון שהבין זאת היטב היה גלילאו גליליי, אך הוא ניסח זאת באופן מתמטי לא נכון. כל מי שבא אחריו, עד איינשטיין, הלך בעקבות הטעות של גליליי וניסח באופן לא נכון את העובדה שאין מערכת התמד אבסולוטית. בגלל ניסוח שגוי זה, כולם אימצו את טרנספורמציות גליליי, והדבר הוביל לשגיאה בסיסית מאוד בהבנת המציאות.
איינשטיין היה הראשון שהבין שיש כאן בעיה, וניסח נכון את העובדה שאין מערכת אבסולוטית שביחס אליה אפשר לומר שמערכת נמצאת במהירות קצובה, פשוט מפני שאיננו יכולים להבחין במערכת אבסולוטית כזו.
אם כך, איך בכל זאת נדע מהי מערכת התמד ומהי מערכת שאיננה מערכת התמד?
התשובה פשוטה: יש להניח במערכת מכשיר המודד כוחות מדומים. אם במערכת נמדדים כוחות מדומים - המערכת איננה מערכת התמד. אם במערכת לא נמדדים כוחות מדומים - המערכת היא מערכת התמד.
כלומר, הקריטריון להבחנה בין מערכת התמד למערכת שאיננה מערכת התמד הוא קיומם של כוחות מדומים.
מטוטלת כמד תאוצה (אקסלרומטר)
כיצד ניתן להבחין בכוחות מדומים? לדוגמה, אדם היושב באוטובוס ופתאום מרגיש שכוח לא מוסבר מצמיד אותו למשענת המושב האחורי - אותו נוסע למעשה “מודד” כוחות מדומים, והופך באותו רגע למעין מד כוחות מדומים.
דוגמה נוספת: נניח שאנו נמצאים בקרון של רכבת הנעה במהירות קצובה. אם נתלה מטוטלת מתקרת הרכבת, וכל עוד הרכבת נעה במהירות קצובה (כלומר, היא מערכת התמד), החוט יישאר אנכי והמשקולת תהיה תלויה בדיוק מתחתיו.
אולם אם הרכבת פתאום מאיצה (למשל לכיוון ימין), המשקולת תתפוס זווית מסוימת - החוט המחזיק את המשקולת ייטה בזווית ביחס לאנך. מדוע זה קורה? כי למשקולת יש התמדה. הרכבת מאיצה לכיוון ימין, אך ההתמדה של המשקולת, מנקודת מבט של מערכת התמד, שואפת להשאיר אותה במקום.
כתוצאה מכך, המשקולת כאילו “נשארת מאחור” כשהרכבת מאיצה קדימה, וזה יוצר זווית בין האנך לבין החוט המחזיק את המשקולת.
כלומר, יש לנו פתאום קריטריון או מכשיר שמודד תאוצה - מד תאוצה. המשקולת התלויה על חוט היא סוג של מד תאוצה (אקסלרומטר). כל עוד החוט אנכי, התאוצה היא אפס. ברגע שהחוט נוטה בזווית, התאוצה שונה מאפס.
באמצעות מדידת הזווית נוכל לדעת במדויק מהי תאוצת הרכבת. כאשר החוט יוצר זווית, אנו יודעים שהמערכת איננה מערכת התמד.
ניתוח מתמטי של דוגמת המטוטלת
בואו ננתח את דוגמת המטוטלת ברכבת באופן מתמטי. נניח שהמטוטלת (המשקולת) תלויה בזווית $\theta$ ביחס לאנך.
ניתן להסתכל על המערכת בשתי דרכים:
מנקודת מבט של מערכת התמד (מחוץ לרכבת)
מחוץ לרכבת, נראה שעל המשקולת פועלים שני כוחות:
- כוח הכובד $mg$ כלפי מטה
- מתיחות החוט $T$
נפרק את הבעיה לשני צירים:
- ציר $Y$ (אנכי)
- ציר $X$ (אופקי)
בציר $Y$, המשקולת נמצאת במנוחה, לכן:
\[T \cos \theta = mg\]זה מחוק ראשון של ניוטון (תנאי התמדה).
בציר $X$, המשקולת מאיצה יחד עם הרכבת, לכן:
\[T \sin \theta = ma\]זה מחוק שני של ניוטון.
אם נחלק את המשוואה השנייה במשוואה הראשונה, נקבל:
\[\frac{T \sin \theta}{T \cos \theta} = \frac{ma}{mg}\]ומכאן:
\[\tan \theta = \frac{a}{g}\]כלומר:
\[a = g \tan \theta\]זוהי נוסחה המבטאת את תאוצת המערכת כפונקציה של זווית הנטייה של החוט.
מנקודת מבט של מערכת מואצת (בתוך הרכבת)
כאשר יושבים בתוך הרכבת, רואים את המשקולת במצב סטטי - היא תלויה בזווית קבועה. מנקודת מבט זו, המשקולת לא זזה, ולכן מבינים שיש כאן “כוח רפאים” שמחזיק אותה בזווית.
אם מצבה הרגיל של המשקולת היה אמור להיות אנכי, והיא נמצאת כעת בזווית, מבינים שיש תאוצה במערכת. הכוח הרלוונטי הוא כוח מדומה:
\[F_{imaginary} = -ma_{system}\]שהוא מסת המשקולת כפול תאוצת המערכת (בכיוון ההפוך).
בתנאי שיווי משקל (מצב סטטי בתוך הרכבת):
\[T \sin \theta - ma = 0\]זהו החוק הראשון של ניוטון המתוקן בתוך מערכת מואצת.
שתי נקודות המבט הללו אקוויוולנטיות: האחת מוחלטת יותר (מערכת התמד, שבה חל החוק השני), והשנייה יחסית (מערכת מואצת, שבה מיישמים את החוק הראשון אך חייבים להוסיף את הכוחות המדומים).
כוחות על מישור משופע
נזכיר שכאשר בחנו גוף על מישור משופע בזווית $\alpha$, הראינו שאפשר לפרק את הבעיה לשני צירים קרטזיים:
- ציר אחד בכיוון התנועה (במורד המישור)
- ציר שני ניצב לתנועה
תמיד רצוי לפרק את הבעיה לצירים המכבדים את הסימטריה של הבעיה, כי זה מקל על הפתרון.
במקרה זה, הכוחות הפועלים על המסה הם:
- כוח הכובד $mg$ (כלפי מטה)
- הכוח הנורמלי $N$ מהמישור המשופע
כאשר מפרקים את כוח הכובד לרכיביו, מקבלים:
- במורד המישור: $mg \sin \alpha$
- ניצב למישור: $mg \cos \alpha$
המשוואות הן:
- בציר במורד המישור: $mg \sin \alpha = ma$ (חוק שני של ניוטון)
- בציר הניצב למישור: $N = mg \cos \alpha$ (מצב סטטי)
מכאן מקבלים שהתאוצה היא:
\[a = g \sin \alpha\]ניתן לראות שכאשר $\alpha = 0$ (מישור אופקי), $\sin 0 = 0$ ולכן $a = 0$. כאשר $\alpha = 90°$ (נפילה חופשית), $\sin 90° = 1$ ולכן $a = g$.
חיכוך ותכונותיו
במקרים רבים, במערכת יש חיכוך. מה שמאפיין את כוח החיכוך, וזוהי עובדה אמפירית, הוא שכוח החיכוך תמיד פרופורציונלי (מתכונתי) לכוח הנורמלי:
\[F = \mu N\]כאשר $\mu$ הוא מקדם החיכוך.
כמובן שכוח החיכוך הוא כוח אפקטיבי, לא כוח יסודי. הכוחות האמיתיים הם הכוחות האלקטרומגנטיים הפועלים בין המולקולות של שני המשטחים, אבל ממרחק זה נראה כמו כוח חיכוך.
חשוב לציין שהמשוואה $F = \mu N$ אינה משוואה וקטורית. כוח החיכוך אמנם פרופורציונלי בגודלו לכוח הנורמלי, אבל בכיוונו הוא תמיד מנוגד לכיוון התנועה או לכיוון שבו הגוף נוטה לנוע. לכן, אם גוף נוטה לנוע במורד מישור משופע, כוח החיכוך יפעל במעלה המישור - בכיוון הפוך לכוח $mg \sin \alpha$ ולא בכיוון הכוח הנורמלי.
יש להבחין בין שני סוגי חיכוך:
- חיכוך קינטי ($F_k$) - כאשר הגוף בתנועה
- חיכוך סטטי ($F_s$) - כאשר הגוף במנוחה
לכל אחד מהם מקדם חיכוך משלו:
- $\mu_k$ - מקדם חיכוך קינטי
- $\mu_s$ - מקדם חיכוך סטטי
ותמיד מתקיים:
\[F_k \leq F_s\] \[\mu_k \leq \mu_s\]כלומר, כוח החיכוך הקינטי תמיד קטן יותר או לכל היותר שווה לכוח החיכוך הסטטי.
נניח שגוף מחליק במורד מישור משופע עם חיכוך. המשוואות הרלוונטיות הן:
בציר במורד המישור: \(mg \sin \alpha - F_k = ma\)
בציר הניצב למישור: \(N = mg \cos \alpha\)
מכיוון ש-$F_k = \mu_k N = \mu_k mg \cos \alpha$, נקבל:
\[mg \sin \alpha - \mu_k mg \cos \alpha = ma\]ולכן:
\[a = g(\sin \alpha - \mu_k \cos \alpha)\]כאשר $\mu_k = 0$ (אין חיכוך), חוזרים לנוסחה $a = g \sin \alpha$.
מקדם החיכוך $\mu$ בדרך כלל נע בין 0 ל-1. כאשר $\mu = 0$, אין חיכוך.
אגב, המשוואה $F = \mu N$ אינה נכונה וקטורית אבל היא כן נכונה טנזורית. אם נתייחס ל-$\mu$ כטנזור (מעין הכללה של מטריצה), אפשר לכתוב:
\[\mathbf{F} = \overleftrightarrow{\mu} \cdot \mathbf{N}\]כאשר טנזור כפול וקטור אכן נותן וקטור.
כוחות מדומים וחיכוך יחד
בשיעור שעבר נפתרה בעיה במערכת מואצת ללא חיכוך. באותה צורה אפשר לפתור בעיה שיש בה גם תאוצה וגם חיכוך. במקרה כזה, נוסיף לכוחות הפועלים על הגוף את כוח החיכוך $F_k$.
בבעיה כזו יופיעו גם כוחות מדומים וגם כוח חיכוך. יש להכניס את כוח החיכוך בצורה נכונה ולפתור את הבעיה של המערכת המואצת.
יחסי כוחות במערכת הטריז המואץ
כמובן שהמסה הקטנה יושבת על המסה הגדולה, ולכן מפעילה על המסה הגדולה כוח נורמלי בכיוון ניצב למשטח המגע. כוח נורמלי זה מאיץ את המסה הגדולה ימינה, ומכאן שהמסה הקטנה יושבת למעשה בתוך “קרון רכבת” שמאיץ ימינה. כתוצאה מכך, פועלים על המסה הקטנה כוחות מדומים.
חשוב להבהיר - המסה הגדולה אינה יושבת על המסה הקטנה. המסה הגדולה מונחת על המשטח האופקי. לפי החוק השלישי של ניוטון, אם המסה הקטנה דוחפת את המסה הגדולה בכוח $N$ בכיוון מסוים, אז המסה הגדולה דוחפת את המסה הקטנה בכוח $N$ בכיוון ההפוך.
ניתן לשאול שאלה מעניינת: מה צריכה להיות התאוצה $a_M$ של המסה הגדולה כדי שהמסה הקטנה תתנתק ממנה? כדי לענות על שאלה זו, יש למצוא באיזו תאוצה הכוח הנורמלי מתאפס. ברגע שהכוח הנורמלי מתאפס, המסה הקטנה ניתקת מהמסה הגדולה.
החוק השלישי של ניוטון
יש להדגיש נקודה חשובה לגבי החוק השלישי של ניוטון. כאשר המסה הגדולה $M$ מפעילה על המסה הקטנה $m$ כוח נורמלי בכיוון מסוים, החוק השלישי קובע שהמסה הקטנה מפעילה על המסה הגדולה כוח נורמלי שווה בגודלו ומנוגד בכיוונו:
\[\mathbf{N}_{M \to m} = -\mathbf{N}_{m \to M}\]חשוב להבחין בין החוק השלישי לחוק הראשון של ניוטון:
- בחוק הראשון מדובר על אוסף כוחות הפועלים על אותו גוף, כאשר שקול הכוחות מתאפס
- בחוק השלישי מדובר על שני כוחות שונים הפועלים על שני גופים שונים, כאשר הכוחות שווים בגודלם ומנוגדים בכיוונם
להמחשה, כאשר אדם עומד על הרצפה, פועלים עליו שני כוחות: כוח הכבידה $mg$ כלפי מטה והכוח הנורמלי $N$ שהרצפה מפעילה עליו כלפי מעלה. לפי החוק הראשון, הכוחות הללו שווים בגודלם: $N = mg$.
לפי החוק השלישי, אם הרצפה מפעילה על האדם כוח נורמלי כלפי מעלה, הרי שהוא מפעיל על הרצפה כוח נורמלי כלפי מטה באותו גודל.
דוגמה נוספת: כאשר גוף נופל בנפילה חופשית, כדור הארץ מושך אותו בכוח $mg$ כלפי מטה. באותה עת, לפי החוק השלישי, הגוף מושך את כדור הארץ בכוח $mg$ כלפי מעלה. הסיבה שכדור הארץ כמעט לא מואץ כלפי מעלה היא שמסתו אדירה בהשוואה למסת הגוף:
\[a_{\text{earth}} = \frac{mg}{M_{\text{earth}}} \approx 10^{-21} \text{m/s}^2\]כלומר, התאוצה של כדור הארץ כלפי הגוף היא מזערית ביותר - כ-$10^{-21}$ מטר לשנייה בריבוע, שזה פחות ממיליונית של מיליונית של מיליונית של מטר לשנייה בריבוע.
מעבר ממשוואות אלגבריות למשוואות דיפרנציאליות
עד כה, עסקנו בבעיות פיזיקליות פשוטות יחסית, שבהן נבנה תרשים כוחות, זוהו הצירים השונים, הופעל החוק הראשון או השני של ניוטון (בהתאם לצורך), והגענו למשוואות אלגבריות פשוטות.
אולם בחיים האמיתיים, הבעיות מורכבות יותר. במערכות פיזיקליות רבות יש משוב (איזונים חוזרים), ובמקרים כאלה החוק השני של ניוטון מתרגם למשוואה דיפרנציאלית ולא למשוואה אלגברית.
משוואות דיפרנציאליות מופיעות בכל תחומי המדע, ובפרט בביולוגיה, משום שכמעט כל התהליכים הביולוגיים כוללים משוב, ולכן ניתן למדל אותם באמצעות משוואות דיפרנציאליות.
דוגמה: בעיית הצנחן וכוחות גרר
הבעיה הראשונה שנבחן, שחורגת מעבר לבעיות אלגבריות פשוטות, היא בעיית הצנחן.
כאשר גוף נופל בנפילה חופשית, הכוח היחיד שפועל עליו הוא כוח הכבידה, והתאוצה היא קבועה ושווה ל-$g$ (בקירוב 10 מטר לשנייה בריבוע). אולם בחיים האמיתיים, יש גם את התנגדות האוויר. כוח הגרר $F$ (התנגדות האוויר) גדל ככל שהמהירות ($v$) גדלה.
את כוח הגרר ניתן לייצג בצורות שונות:
-
כוח גרר פרופורציונלי למהירות:
\[\mathbf{F}_{\text{drag}} = -\beta \mathbf{v}\] -
כוח גרר פרופורציונלי לריבוע המהירות:
\[\mathbf{F}_{\text{drag}} = -\beta v^2 \frac{\mathbf{v}}{|\mathbf{v}\vert}\] -
בחלק מהמקרים, כוח הגרר עשוי להיות פרופורציונלי לחזקות גבוהות יותר של המהירות
מהו כוח הגרר? זהו הכוח שבו האוויר (או כל תווך אחר, כגון מים) מתנגד לתנועת הגוף. בשונה מכוח חיכוך, כוח הגרר:
- פועל על כל שטח הפנים של הגוף ולא רק על משטח המגע
- מדובר באינטראקציה בין גוף מוצק לבין גז או נוזל (בשונה מחיכוך בין שני מוצקים)
- התווך (האוויר או המים) יכול להתעוות כתוצאה מהתנועה, בשונה ממשטחים קשיחים
ניתוח בעיית הצנחן
נניח שצנחן נופל ופועלים עליו שני כוחות:
- כוח הכבידה $mg$ כלפי מטה
- כוח הגרר $\beta v$ כלפי מעלה (מנוגד לכיוון התנועה)
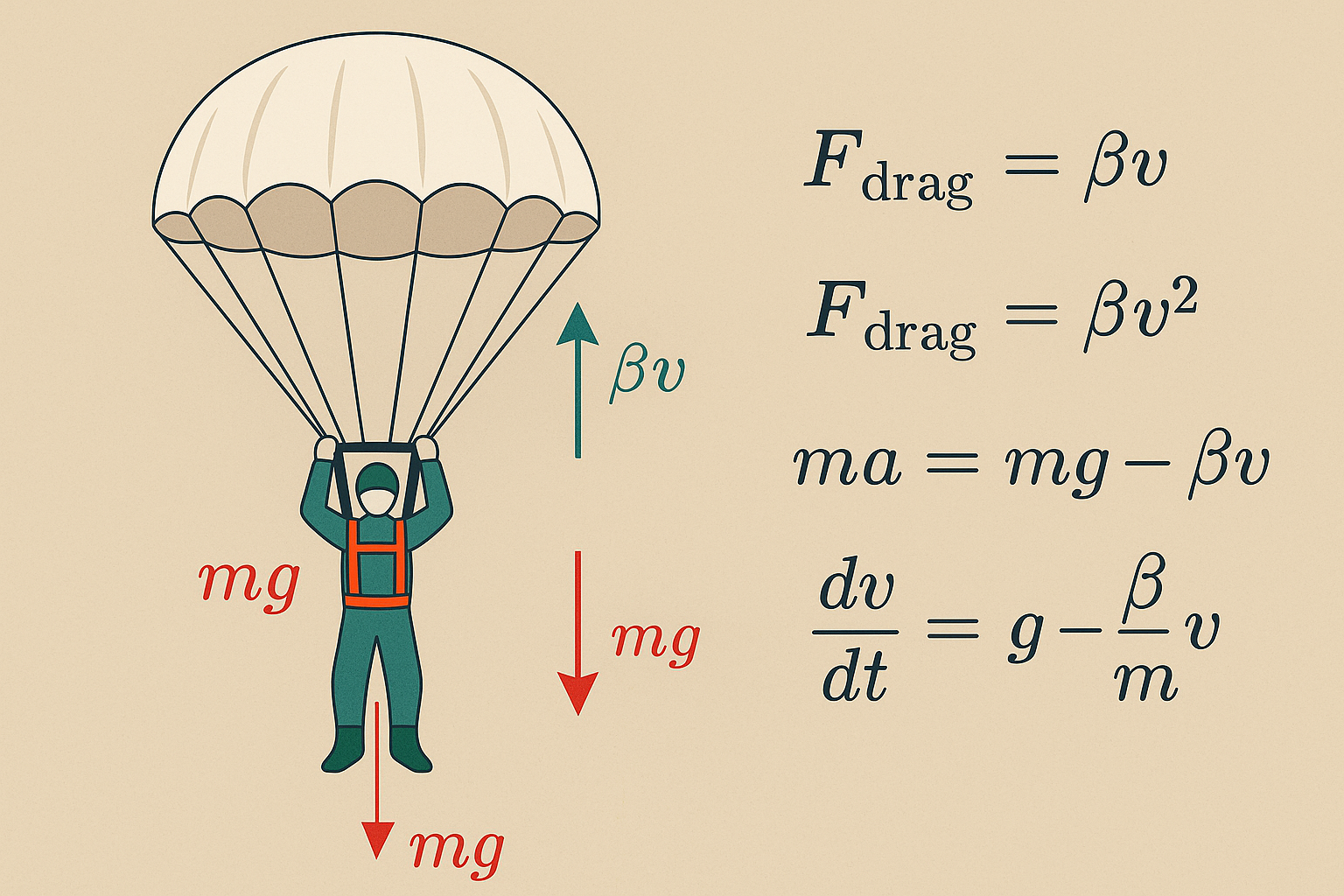
מהחוק השני של ניוטון:
\[ma = mg - \beta v\]כאשר התאוצה היא למעשה הנגזרת של המהירות לפי הזמן:
\[m\frac{dv}{dt} = mg - \beta v\]הערה (דור): שימו לב שאנחנו בדרך כלל בוחרים את מערכת הצירים כך שכיוון התנועה הוא חיובי (כלפי מטה במקרה של צניחה), ולכן כוח הגרר פועל בכיוון שלילי (כלפי מעלה).
בתרגולים בחרנו לפעמים לסמן בעזרת ציר $z$ במקום $x$.
נחלק את שני האגפים ב-$m$:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v\]זוהי משוואה דיפרנציאלית מסדר ראשון במהירות (ומסדר שני במיקום). נפתור אותה באמצעות הפרדת משתנים.
מהירות טרמינלית
כאשר גוף נופל באוויר, מהירותו גדלה בהדרגה, ובהתאם גדל גם כוח הגרר. בסופו של דבר, כוח הגרר משתווה לכוח הכובד, ובנקודה זו מתאפסת התאוצה והגוף ממשיך ליפול במהירות קבועה. מהירות זו נקראת המהירות הטרמינלית.
המהירות הטרמינלית מקיימת את התנאי:
\[\beta v_{\text{terminal}} = mg\]ומכאן:
\[v_{\text{terminal}} = \frac{mg}{\beta}\]זוהי המהירות המקסימלית שהגוף יכול להגיע אליה. ברגע שמגיעים למהירות זו, שקול הכוחות מתאפס, התאוצה מתאפסת, והגוף ממשיך לנוע במהירות קבועה.
היחידות של $\beta$ הן יחידות של כוח חלקי מהירות, כלומר:
\[[\beta] = \frac{[\mathrm{N}]}{[\text{m/s}]} = \frac{\mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2}{\mathrm{m}/\mathrm{s}} = \frac{\mathrm{kg}}{\mathrm{s}}\]פתרון המשוואה הדיפרנציאלית
כדי לפתור את המשוואה הדיפרנציאלית:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v\]נשתמש בשיטת הפרדת משתנים. ראשית, נארגן מחדש את המשוואה כך שכל האיברים המכילים $v$ יהיו בצד אחד וכל האיברים המכילים $t$ יהיו בצד השני:
\[\frac{dv}{g - \frac{\beta}{m}v} = dt\]כעת נוכל לעשות אינטגרציה לשני צדי המשוואה. באגף ימין, האינטגרל של $dt$ הוא פשוט $t + C$, כאשר $C$ הוא קבוע האינטגרציה.
באגף שמאל, עלינו לחשב:
\[\int \frac{dv}{g - \frac{\beta}{m}v}\]זהו אינטגרל מהצורה $\int \frac{du}{a - bu}$, שהפתרון שלו הוא:
\[-\frac{1}{b} \ln|a - bu| + C\]במקרה שלנו, $a = g$, $b = \frac{\beta}{m}$, ולכן:
\[\int \frac{dv}{g - \frac{\beta}{m}v} = -\frac{m}{\beta} \ln \left|g - \frac{\beta}{m}v \right| + C_1\]נוכל גם להגיע לתוצאה הזו באמצעות החלפת משתנים. נגדיר $Y = g - \frac{\beta}{m}v$. כדי לקשר בין $dv$ ל-$dY$, נגזור את $Y$ לפי $v$:
\[\frac{dY}{dv} = -\frac{\beta}{m}\]ולכן:
\[dY = -\frac{\beta}{m}dv\]או:
\[dv = -\frac{m}{\beta}dY\]כעת האינטגרל שלנו הופך ל:
\[\int \frac{dv}{g - \frac{\beta}{m}v} = \int \frac{-\frac{m}{\beta}dY}{Y} = -\frac{m}{\beta}\int \frac{dY}{Y} = -\frac{m}{\beta}\ln|Y| + C_1\]כלומר:
\[-\frac{m}{\beta}\ln \left|g - \frac{\beta}{m}v \right| = t + C\]כאשר $C = C_2 - C_1$ הוא קבוע האינטגרציה המשולב.
פתרון עבור המהירות כפונקציה של הזמן
נארגן את המשוואה כדי לבודד את $v$:
\[\ln \left|g - \frac{\beta}{m}v \right| = -\frac{\beta}{m}t - \frac{\beta C}{m}\]נגדיר $C’ = -\frac{\beta C}{m}$ ונקבל:
\[\ln \left|g - \frac{\beta}{m}v \right| = -\frac{\beta}{m}t + C'\]כעת נעביר לצורה אקספוננציאלית:
\[g - \frac{\beta}{m}v = e^{-\frac{\beta}{m}t + C'} = e^{C'} \cdot e^{-\frac{\beta}{m}t}\]נגדיר $A = e^{C’}$ ונקבל:
\[g - \frac{\beta}{m}v = A \cdot e^{-\frac{\beta}{m}t}\]כעת נבודד את $v$:
\[-\frac{\beta}{m}v = A \cdot e^{-\frac{\beta}{m}t} - g\] \[v = \frac{m}{\beta} \left( g - A \cdot e^{-\frac{\beta}{m}t} \right) = \frac{mg}{\beta} - \frac{m}{\beta} A \cdot e^{-\frac{\beta}{m}t}\]נגדיר $B = \frac{m}{\beta}A$ ונקבל:
\[v(t) = \frac{mg}{\beta} - B \cdot e^{-\frac{\beta}{m}t}\]קביעת קבוע האינטגרציה באמצעות תנאי התחלה
עד כה, $B$ הוא קבוע אינטגרציה שטרם נקבע. כדי לקבוע אותו, נשתמש בתנאי ההתחלה. אם בזמן $t = 0$ המהירות היא $v_0$, אז:
\[v_0 = \frac{mg}{\beta} - B \cdot e^{-\frac{\beta}{m} \cdot 0} = \frac{mg}{\beta} - B\]מכאן נקבל:
\[B = \frac{mg}{\beta} - v_0\]ולכן הפתרון המלא הוא:
\[v(t) = \frac{mg}{\beta} - \left(\frac{mg}{\beta} - v_0 \right) e^{-\frac{\beta}{m}t}\]ניתן לרשום זאת בצורה קומפקטית יותר, במיוחד עבור המקרה שבו $v_0 = 0$ (התחלה ממנוחה):
\[\boxed{v(t) = \frac{mg}{\beta} \left(1 - e^{-\frac{\beta}{m}t} \right)}\]המשמעות הפיזיקלית של הפתרון
הפתרון שקיבלנו מראה כי:
-
המהירות הטרמינלית: כאשר $t \to \infty$, הביטוי $e^{-\frac{\beta}{m}t} \to 0$, ולכן המהירות מתקרבת לערך $\frac{mg}{\beta}$. זוהי המהירות הטרמינלית - המהירות שבה כוח הגרר משתווה לכוח הכובד.
-
התנהגות התחלתית: בזמן $t = 0$, המהירות היא $v_0$ כפי שנדרש מתנאי ההתחלה.
-
קצב ההתקרבות למהירות הטרמינלית: הביטוי $e^{-\frac{\beta}{m}t}$ דועך במהירות, במיוחד כאשר היחס $\frac{\beta}{m}$ גדול. כלומר, גופים קלים עם מקדם גרר גדול יגיעו למהירות הטרמינלית שלהם מהר יותר.
חשוב לציין כי פתרון זה תקף רק עבור מודל שבו כוח הגרר פרופורציונלי למהירות. במציאות, במהירויות גבוהות, כוח הגרר עשוי להיות פרופורציונלי לריבוע המהירות או אף לחזקות גבוהות יותר.
בשיעור הבא, נמשיך לחשב את המיקום $x(t)$ על ידי אינטגרציה של $v(t)$ לפי הזמן:
\[x(t) = \int v(t) dt\]זהו פתרון מלא של בעיית הצנחן, המראה כיצד החוק השני של ניוטון מוביל למשוואה דיפרנציאלית שפתרונה מתאר את התנועה האמיתית בנוכחות התנגדות אוויר.
שיעור תגבור - חוקי ניוטון ומערכות ייחוס (בעיית הטריז וצנחנית)
תאריך: 04/05/2025חוקי ניוטון ומערכות ייחוס
עסקנו בכתה בחוק הראשון, השני והשלישי של ניוטון, ולמדנו שבסיטואציות שבהן המערכת נמצאת בשיווי משקל, או שהיא נמצאת במצב של התמדה (כלומר, לא מורגשים בה כוחות מדומים), ושקול הכוחות שווה לאפס - בסיטואציה כזו אנחנו משתמשים בחוק הראשון של ניוטון.
לחלופין, כאשר המערכת שלנו נמצאת בתאוצה, אנחנו יכולים להשתמש בחוק השני של ניוטון.
כאשר מדובר במערכת שהיא לא מערכת התמדה (לא אינרציאלית), אנחנו יכולים להשתמש בחוק הראשון והשני, ובלבד שנכניס את העובדה שיש כוחות מדומים במערכת.
כוחות מדומים (כוחות דלמברט)
הכוחות המדומים במערכת הם מסת הגוף שאנחנו בודקים את התנועה שלו כפול תאוצת המערכת, כאשר כיוון הכוח הוא מנוגד לכיוון התאוצה.
כלומר, ביחס לכוח מדומה (נקרא לו $F_{imaginary}$ או כל שם אחר), מתקיים:
\[F_{imaginary} = -m\vec{a}\]כאשר $\vec{a}$ היא תאוצת המערכת. אנחנו צריכים להכניס את הכוח $F_{imaginary}$ לתוך מאזן הכוחות כדי שנוכל לטפל נכון בבעיה.
אגב, לכוח מדומה מהצורה הזאת יש גם שם מיוחד משלו - קוראים לו כוח דלמברט (D’Alembert).
כזכור, כוחות דלמברט הם כוחות “רפאים”, כלומר, שום דבר לא יוצר אותם מנקודת המבט של הגוף שנמצא במערכת המאיצה. הם פשוט מופיעים “משום מקום”, ומקורם בהתמדה של הגוף. המערכת של הגוף נמצאת בתאוצה ולכן היא “בורחת” ממנו, והבריחה הזאת מבטאת את העובדה שהוא מרגיש כאילו פועל עליו איזשהו כוח שדוחף אותו לאחת הפינות.
דוגמה: בעיית גליל על טריז
קיבלנו בשיעורי הבית כל מיני דוגמאות, למשל מקרה של גוף שמונח על מסה שמחליקה או דבר דומה. ראינו שאנחנו צריכים להוסיף את כוחות דלמברט כדי לפתור את הבעיה מתוך המערכת המאיצה. אם אנחנו לא בתוך המערכת המאיצה, אז אנחנו לא צריכים להוסיף את כוחות דלמברט, אלא התאוצה פשוט באה לידי ביטוי בתאוצת הגוף.
ניתוח המערכת
נסתכל על בעיה שבה יש לנו גליל (מסה קטנה $m$) על טריז (מסה גדולה $M$). נבחר מערכת צירים כך שציר $x$ פונה ימינה, וציר $y$ פונה כלפי מעלה.
הטריז נמצא בזווית $\alpha$ ביחס למישור האופקי, כאשר הגליל נמצא עליו.
הכוחות על המסה הגדולה ($M$)
נסתכל תחילה על המסה הגדולה (הטריז). הכוחות הפועלים עליה:
- כוח נורמלי $N_1$ מהגליל (המסה הקטנה) על הטריז
- כוח המשיכה $Mg$ הפועל כלפי מטה
- כוח נורמלי $\tilde{N}$ מהרצפה על הטריז
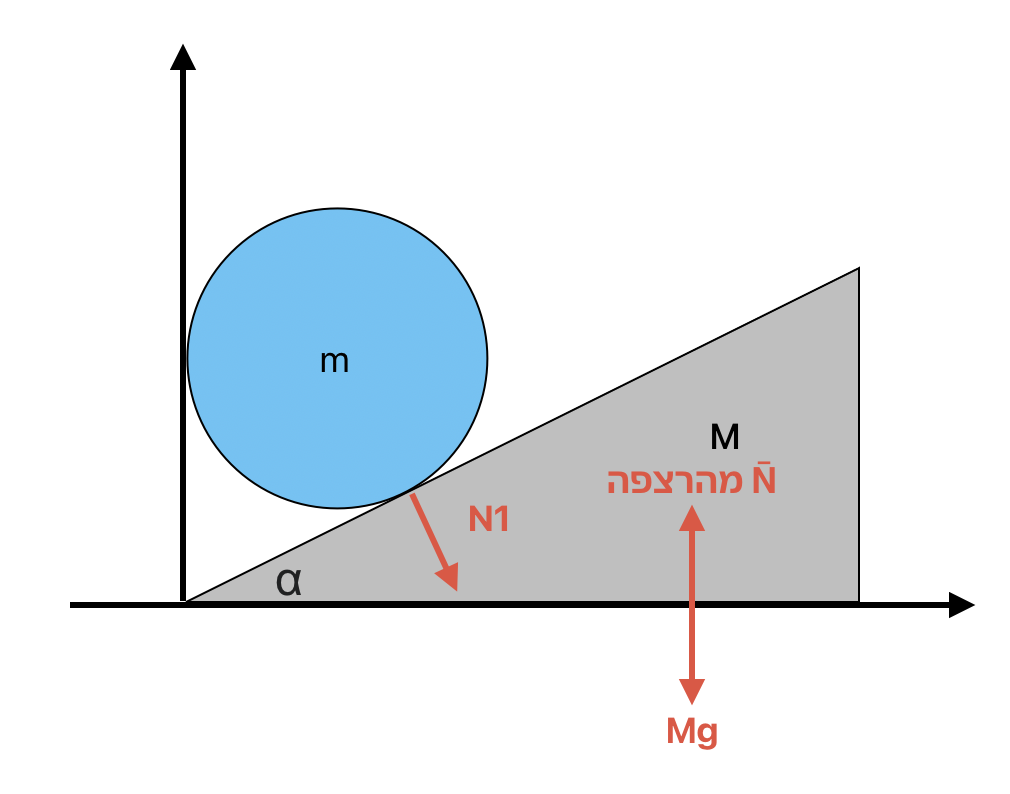
לפי החוק השני של ניוטון, בכיוון ציר $x$:
\[N_1 \sin \alpha = MA\]כאשר $A$ היא התאוצה של הטריז בכיוון ציר $x$ החיובי.
בכיוון ציר $y$, אין תאוצה (הטריז לא מתרומם), ולכן לפי החוק הראשון של ניוטון:
\[N_1 \cos \alpha + Mg = \tilde{N}\]
הכוחות על המסה הקטנה ($m$)
עכשיו נסתכל על המסה הקטנה (הגליל). הכוחות הפועלים עליה:
- כוח נורמלי $N_1$ מהטריז על הגליל (בכיוון הפוך לכוח שהגליל מפעיל על הטריז)
- כוח המשיכה $mg$ כלפי מטה
- כוח נורמלי $N_2$ מהקיר על הגליל
שימו לב שהגליל נלחץ בין הטריז לבין הקיר, ולכן מרגיש את הכוח הנורמלי $N_2$ מהקיר.
מכיוון שהגליל צמוד לקיר ולא מבצע תנועה בכיוון ציר $x$, מתקיים לפי החוק הראשון של ניוטון:
\[N_1 \sin \alpha = N_2\]בכיוון ציר $y$, לפי החוק השני של ניוטון (אם נגדיר את הכיוון החיובי כלפי מטה):
\[mg - N_1 \cos \alpha = ma\]כאשר $a$ היא התאוצה של הגליל כלפי מטה.
אילוץ גיאומטרי
מהגיאומטריה של הבעיה, ניתן להסיק שהיחס בין התאוצה בציר $y$ לבין התאוצה בציר $x$ חייב להיות קבוע ושווה לטנגנס של הזווית $\alpha$:
\[\frac{a}{A} = \tan \alpha\]כלומר, $a = A \tan \alpha$.
פתרון הבעיה
יש לנו שלוש משוואות בשלושה נעלמים ($N_1$, $A$, $a$):
- $N_1 \sin \alpha = MA$ (מהניתוח של הטריז)
- $mg - N_1 \cos \alpha = ma$ (מהניתוח של הגליל)
- $a = A \tan \alpha$ (מהאילוץ הגיאומטרי)
מהמשוואה הראשונה, נקבל:
\[A = \frac{N_1 \sin \alpha}{M}\]מהמשוואה השנייה, נקבל:
\[a = \frac{mg - N_1 \cos \alpha}{m}\]כעת נשתמש במשוואה השלישית ונציב:
\[\frac{mg - N_1 \cos \alpha}{m} = \frac{N_1 \sin \alpha}{M} \tan \alpha\]נפשט את המשוואה:
\[\frac{mg - N_1 \cos \alpha}{N_1 \sin \alpha} \cdot \frac{M}{m} = \tan \alpha\] \[\frac{mg}{N_1 \sin \alpha} \cdot \frac{M}{m} - \frac{N_1 \cos \alpha}{N_1 \sin \alpha} \cdot \frac{M}{m} = \tan \alpha\] \[\frac{Mg}{N_1 \sin \alpha} - \frac{M \cos \alpha}{m \sin \alpha} = \tan \alpha\] \[\frac{Mg}{N_1 \sin \alpha} - \frac{M}{m} \cdot \frac{1}{\tan \alpha} = \tan \alpha\]מכאן ניתן לחלץ את $N_1$:
\[\frac{Mg}{N_1 \sin \alpha} = \tan \alpha + \frac{M}{m} \cdot \frac{1}{\tan \alpha}\] \[\frac{Mg}{N_1 \sin \alpha} = \tan \alpha + \frac{M}{m \tan \alpha}\] \[N_1 = \frac{Mg}{\sin \alpha \left(\tan \alpha + \frac{M}{m \tan \alpha}\right)}\]לאחר שמצאנו את $N_1$, ניתן להציב חזרה במשוואות ולמצוא את $A$ ואת $a$.
הערות נוספות
- החישוב הזה הוא אלגברי בלבד, ואינו דורש שימוש במספרים.
- אם היינו רוצים למצוא את $N_2$, היינו משתמשים במשוואה $N_1 \sin \alpha = N_2$.
- הביטויים שקיבלנו מכילים פרמטרים פיזיקליים ($m$, $M$, $\alpha$, $g$) שמאפיינים את המערכת ואינם משתנים עם הזמן.
- בקורס זה, בדרך כלל נפתור בעיות באופן פרמטרי, ללא הצבת מספרים.
צניחה חופשית עם התנגדות אוויר
הבעיה הפיזיקלית
הבעיה שנתתי בתרגיל הבית עסקה בצנחנית (או צונחת) הנמצאת בצניחה חופשית. על פי נתוני הבעיה, פועל עליה כוח גרר שמתכונתי לריבוע המהירות שלה. נבחן את הכוחות הפועלים על הצנחנית ואת התנועה שלה כפונקציה של הזמן.
הכוחות הפועלים
אם אנחנו מדמים את הצנחנית כנקודה חומרית, הכוחות הפועלים עליה הם:
- כוח הכבידה כלפי מטה: $mg$
- כוח הגרר (התנגדות האוויר) כלפי מעלה: $\beta v^2$
כאשר הצנחנית מתחילה את הצניחה ממהירות אפס, ברור ש-$mg > \beta v^2$ בהתחלה, ולכן היא מאיצה כלפי מטה. אולם, ככל שהמהירות גדלה, כוח הגרר ($\beta v^2$) גדל גם הוא.
מהירות טרמינלית
התהליך של הגדלת המהירות נמשך עד שמגיעים למצב שבו $\beta v^2 = mg$. ברגע זה, שקול הכוחות שווה לאפס, חל תנאי ההתמדה (החוק הראשון של ניוטון), והצנחנית תתמיד במהירות קבועה - זוהי המהירות הטרמינלית.
המהירות הטרמינלית ($v_T$) ניתנת על ידי:
\[\beta v_T^2 = mg\]ומכאן:
\[v_T = \sqrt{\frac{mg}{\beta}}\]במקרה של צונחת רגילה, $\beta$ הוא בסדר גודל של 6, והמהירות הטרמינלית היא בסביבות 200 קמ”ש (בגבהים נמוכים). בגבהים גבוהים יותר (כמו 10 ק”מ), צפיפות האוויר נמוכה יותר, כוח הגרר קטן יותר, ולכן המהירות הטרמינלית גבוהה יותר.
המשוואה הדיפרנציאלית
כעת נבנה את המשוואה הדיפרנציאלית המתארת את התנועה. לפי החוק השני של ניוטון:
\[m \frac{dv}{dt} = mg - \beta v^2\]נחלק את שני האגפים ב-$m$:
\[\frac{dv}{dt} = g - \frac{\beta}{m} v^2\]לשם נוחות, נגדיר פרמטר חדש:
\[\alpha^2 = \frac{\beta}{m}\]כך שהמשוואה הופכת ל:
\[\frac{dv}{dt} = g - \alpha^2 v^2\]פתרון המשוואה הדיפרנציאלית
שלב 1: הפרדת משתנים
נפריד את המשתנים במשוואה:
\[\frac{dv}{g - \alpha^2 v^2} = dt\]שלב 2: ביצוע האינטגרציה
נבצע אינטגרציה משני צדי המשוואה:
\[\int \frac{dv}{g - \alpha^2 v^2} = \int dt = t + C\]לפתרון האינטגרל בצד שמאל, נעשה טריק אלגברי. נכפול ונחלק את האינטגרל ב-$\alpha$:
\[\int \frac{dv}{g - \alpha^2 v^2} = \frac{1}{\alpha} \int \frac{\alpha \, dv}{g - \alpha^2 v^2}\]נגדיר $y = \alpha v$, כך ש-$dy = \alpha \, dv$, ונקבל:
\[\frac{1}{\alpha} \int \frac{dy}{g - y^2}\]שלב 3: פתרון בעזרת פונקציות היפרבוליות
נעשה החלפת משתנים נוספת: $y = \sqrt{g} \tanh \phi$, כאשר $\phi$ משתנה חדש.
נבדוק מה המכנה במונחים של $\phi$:
\[g - y^2 = g - g \tanh^2 \phi = g(1 - \tanh^2 \phi) = \frac{g}{\cosh^2 \phi}\]כעת נחשב את $dy$:
\[dy = \sqrt{g} \cdot \frac{d(\tanh \phi)}{d\phi} \cdot d\phi = \frac{\sqrt{g}}{\cosh^2 \phi} \, d\phi\]נציב במשוואה:
\[\frac{1}{\alpha} \int \frac{dy}{g - y^2} = \frac{1}{\alpha} \int \frac{\frac{\sqrt{g}}{\cosh^2 \phi} \, d\phi}{\frac{g}{\cosh^2 \phi}} = \frac{1}{\alpha \sqrt{g}} \int d\phi = \frac{\phi}{\alpha \sqrt{g}} + C\]שלב 4: חזרה למשתנה המקורי
מהגדרת $\phi$ אנחנו יודעים ש:
\[\frac{\alpha v}{\sqrt{g}} = \tanh \phi\]לכן:
\[\phi = \tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right)\]נציב בפתרון:
\[\frac{1}{\alpha \sqrt{g}} \tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right) = t + C\]נכפול את שני הצדדים ב-$\alpha \sqrt{g}$:
\[\tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right) = \alpha \sqrt{g} \, t + C'\]שלב 5: קביעת קבוע האינטגרציה
נשתמש בתנאי ההתחלה: בזמן $t = 0$, המהירות $v = 0$.
\[\tanh^{-1}\left(\frac{\alpha \cdot 0}{\sqrt{g}}\right) = \alpha \sqrt{g} \cdot 0 + C'\]מכיוון ש-$\tanh^{-1}(0) = 0$, נקבל $C’ = 0$.
שלב 6: המהירות כפונקציה של הזמן
כעת נוציא את $v$ מהמשוואה על ידי הפעלת פונקציית $\tanh$ על שני צדי המשוואה:
\[\frac{\alpha v}{\sqrt{g}} = \tanh(\alpha \sqrt{g} \, t)\]ומכאן:
\[v(t) = \frac{\sqrt{g}}{\alpha} \tanh(\alpha \sqrt{g} \, t)\]בדיקת יחידות
נבדוק אם היחידות במשוואה הסופית הגיוניות:
מהמשוואה $\frac{dv}{dt} = g - \alpha^2 v^2$, נובע ש-$\alpha^2 v^2$ חייב להיות בעל יחידות של תאוצה (מטר לשנייה בריבוע). כלומר:
\[[\alpha^2 v^2] = [\alpha^2] \cdot [v^2] = [\alpha^2] \cdot \frac{m^2}{s^2} = \frac{m}{s^2}\]מכאן:
\[[\alpha^2] = \frac{1}{m}\] \[[\alpha] = \frac{1}{\sqrt{m}}\]בפתרון הסופי:
\[v(t) = \frac{\sqrt{g}}{\alpha} \tanh(\alpha \sqrt{g} \, t)\]היחידות של $\sqrt{g}$ הן $\sqrt{\frac{m}{s^2}} = \frac{\sqrt{m}}{s}$. כשמחלקים ב-$\alpha$ שיחידותיו $\frac{1}{\sqrt{m}}$, מקבלים $\frac{m}{s}$, שהן אכן יחידות של מהירות, כנדרש.
התנהגות המהירות לאורך זמן
-
בזמן $t = 0$:
\[v(0) = \frac{\sqrt{g}}{\alpha} \tanh(0) = 0\]כמצופה, המהירות ההתחלתית היא אפס.
-
כאשר $t \to \infty$:
\[v(t) \to \frac{\sqrt{g}}{\alpha} \tanh(\infty) = \frac{\sqrt{g}}{\alpha} \cdot 1 = \frac{\sqrt{g}}{\alpha}\]מכיוון ש-$\alpha^2 = \frac{\beta}{m}$, נקבל:
\[v(t) \to \frac{\sqrt{g}}{\sqrt{\frac{\beta}{m}}} = \sqrt{\frac{mg}{\beta}}\]וזוהי בדיוק המהירות הטרמינלית שחישבנו קודם.
הערה חשובה על כיוון המהירות
חשוב לציין שהפתרון שמצאנו מניח שהצנחנית נעה כלפי מטה (בכיוון החיובי של ציר ה-$y$). אם היא הייתה קופצת כלפי מעלה בתחילת התנועה, אז כוח הגרר היה פועל בכיוון מנוגד, וצריך היה לשנות את סימנו במשוואה עד לנקודה שבה המהירות משנה כיוון.
סיכום
פתרנו את המשוואה הדיפרנציאלית המתארת את תנועת הצנחנית בנוכחות כוח גרר הפרופורציונלי לריבוע המהירות. הפתרון מראה כיצד המהירות גדלה עם הזמן ומתקרבת בהדרגה למהירות הטרמינלית.
הגרפים של המהירות כפונקציה של הזמן יראו עקומה העולה במהירות בתחילה, ואז מתמתנת בהדרגה ומתקרבת אסימפטוטית למהירות הטרמינלית.
שיעור 7 - בעיית החבל המשתלשל ואוסצילטור הרמוני
תאריך: 05/05/2025בעיית החבל המשתלשל
נניח שחבל משתלשל מקצה של שולחן. הפרמטרים והיחידות שלהם:
- $L\ \mathrm{m}$ - אורך החבל הכולל
- $g\ \mathrm{m/s}^2$ - תאוצת הכבידה
- $x(t)$ - אורך החבל המשתלשל (מחוץ לשולחן) בזמן $t$
- $\rho\ \mathrm{[kg/m]}$ - צפיפות החבל
- $t\ \, \mathrm{s}$ - זמן
- $v(t)\ \mathrm{m/s}$ - מהירות החבל
הערה מקדימה: צורת ביטוי אחרת, שהמרגל השתמש בה, אינה משתמשת בצפיפות החבל אלא מציגה את המאסה מהאורכים היחסיים של החלקים:
- $\frac{L-x(t)}{L}m$ - החלק של החבל שעל השולחן
- $\frac{x(t)}{L}m$ - החלק של החבל המשתלשל
אישית מצאתי את צורת הביטוי הזו אינטואיטיבית יותר. בכל מקרה הפרמטר של המשקל הצטמצם.
תנאי התחלה ($t=0$)
\[\begin{cases} x(0) = x_0\ \mathrm{m} \\[10pt] \dot{x}(0) = v(0) = 0\ \mathrm{m/s} \end{cases}\]אנחנו מניחים שהחבל מתחיל ממנוחה, כלומר המהירות ההתחלתית היא אפס, וצריכים למצוא:
- $v(t)\ \mathrm{m/s}$ - מהירות החבל בזמן $t$
- $x(t)\ \mathrm{m}$ - אורך החבל המשתלשל בזמן $t$
- $T\ \, \mathrm{s}$ - זמן ההחלקה המלאה של החבל מהשולחן (כאשר $x(T) = L$)
תחילה נניח שאין חיכוך. נסמן:
- $m = \rho L$ - המסה הכוללת של החבל [ק״ג]
- $\overset{*}{m} = \rho x$ - המסה של החלק המשתלשל [ק״ג]
נתבונן בכוחות הפועלים על המערכת:
- כוח הכבידה על החלק המשתלשל: $F_g = \overset{*}{m} g = \rho x g \left[\mathrm{N}\right]$
- אין חיכוך בין החבל לשולחן
לפי החוק השני של ניוטון, הכוח השקול מייצר תאוצה בכל המסה של החבל. בצורה הכללית של החוק השני של ניוטון:
\[\underbrace{F}_{\text{force}} = \underbrace{m}_{\text{mass}} \cdot \underbrace{a}_{\text{velocity}} \tag{1}\]נציב את הערכים המתאימים במשאוואה $(1)$:
\[\underbrace{\rho x(t) g}_{\text{forces on the rope}} = \underbrace{\rho L}_{\text{rope mass}} \cdot \underbrace{\ddot{x}(t)}_{\text{rope velociry}} \tag{2}\]נסביר את משוואה $(2)$:
-
הכוח הפועל: $\underbrace{\rho x g}_{\text{weight of the falling part}}$
- $\rho$ = צפיפות החבל [ק״ג/מטר]
- $x(t)$ = אורך החלק המשתלשל בזמן $t$ [מטר]
- $g$ = תאוצת הכבידה [מטר/שנייה²]
-
המסה המואצת: $\underbrace{\rho L}_{\text{rope velocity}}$
- $\rho$ = צפיפות החבל [ק״ג/מטר]
- $L$ = האורך הכולל של החבל [מטר]
-
התאוצה: $\underbrace{\ddot{x}}_{\text{2nd derivient of }x\text{ in time t}}$
נפשט את משוואה $(2)$:
\[\begin{aligned} \rho x g &= \rho L \ddot{x} \\[10pt] \ddot{x} &= \underbrace{\frac{g}{L}}_{\text{constant}} \cdot \underbrace{x}_{\text{falling part length}} \end{aligned}\]זוהי המשוואה הדיפרנציאלית המתארת את תנועת החבל. אם נסמן $\omega^2 = \frac{g}{L}$, נקבל:
\[\ddot{x} = \underbrace{\omega^2}_{\text{constant}} \cdot x \tag{3}\]היחידות של $\omega^2$ הן [1/שנייה²], מכיוון ש-$g$ הוא תאוצת הכבידה [מטר/שנייה²] ו-$L$ הוא אורך החבל [מטר].
פתרון המשוואה הדיפרנציאלית
משוואה $(3)$ היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני. הפתרון הכללי הוא:
\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) \,\mathrm{m} \tag{4}\]כאשר:
- $\cosh(y) = \frac{e^y + e^{-y}}{2}$ (פונקציית הקוסינוס ההיפרבולי)
- $\sinh(y) = \frac{e^y - e^{-y}}{2}$ (פונקציית הסינוס ההיפרבולי)
- $A$ ו-$B$ הם קבועים שנקבעים לפי תנאי ההתחלה [M]
מציאת הקבועים A ו-B
נשתמש בתנאי ההתחלה כדי למצוא את הקבועים $A$ ו-$B$:
-
תנאי ראשון: $x(0) = x_0$
נציב $t = 0$ בפתרון הכללי (משוואה $(4)$):
\[x(0) = A\cosh(0) + B\sinh(0)\]מכיוון ש-$\cosh(0) = 1$ ו-$\sinh(0) = 0$, מתקבל:
\[x_0 = A \cdot 1 + B \cdot 0 = A\]לכן $\boxed{A = x_0 \ \mathrm{m}}$.
-
תנאי שני: $\dot{x}(0) = 0$
נחשב את הנגזרת של $x(t)$:
\[\dot{x}(t) = A\omega\sinh(\omega t) + B\omega\cosh(\omega t) \,\mathrm{m/s}\]נציב $t = 0$:
\[\dot{x}(0) = A\omega\sinh(0) + B\omega\cosh(0)\]מכיוון ש-$\sinh(0) = 0$ ו-$\cosh(0) = 1$, מתקבל:
\[\begin{aligned} 0 &= 0 + B\omega \cdot 1 \\[10pt] B \omega &= 0 \end{aligned}\]לכן $\boxed{B = 0 \ \mathrm{m}}$.
הפתרון המלא
כעת, כאשר $A = x_0$ ו-$B = 0$, הפתרון המלא הוא:
\[\begin{aligned} x(t) &= \underbrace{A}_{x_0}\cosh(\omega t) + \underbrace{B}_{0}\sinh(\omega t) \\[10pt] &= x_0 \cosh(\omega t) + 0 \\[10pt] &= x_0 \cosh(\omega t) \,\mathrm{m} \end{aligned}\]סך הכל:
\[\boxed{x(t) = x_0 \cosh(\omega t) \,\mathrm{m}}\]והמהירות:
\[\boxed{v(t) = \dot{x}(t) = x_0 \omega \sinh(\omega t) \,\mathrm{m/s}}\]חישוב זמן ההחלקה המלאה
זמן ההחלקה המלאה $T$ הוא הזמן שבו $x(T) = L$, כלומר, כל החבל נמצא מחוץ לשולחן:
\[x_0 \cosh(\omega T) = L\] \[\cosh(\omega T) = \frac{L}{x_0}\] \[\omega T = \cosh^{-1}\left(\frac{L}{x_0}\right)\] \[T = \frac{1}{\omega}\cosh^{-1}\left(\frac{L}{x_0}\right) = \sqrt{\frac{L}{g}}\cosh^{-1}\left(\frac{L}{x_0}\right) \,\mathrm{s}\]הסבר פיזיקלי
תנועת החבל לא בתאוצה קבועה אלא בתאוצה שגדלה עם הזמן. ככל שיותר חבל משתלשל, כך גדל הכוח המושך, וכתוצאה מכך גדלה התאוצה. זהו מקרה של ״משוב חיובי״ - תהליך שמגביר את עצמו.
ככל שהחלק המשתלשל ההתחלתי ($x_0$) גדול יותר, כך זמן ההחלקה ($T$) קטן יותר. זה הגיוני פיזיקלית כי חלק משתלשל גדול יותר מייצר כוח משיכה חזק יותר מההתחלה.
גרסה עם חיכוך
הסבר על חיכוך
החיכוך הוא כוח המתנגד לתנועה היחסית בין שני משטחים במגע. יש שני סוגים של חיכוך:
- חיכוך סטטי ($f_s$) - פועל כאשר הגוף במנוחה ומונע ממנו להתחיל לנוע
- חיכוך קינטי ($f_k$) - פועל כאשר הגוף בתנועה ומאט אותו
עוצמת כוח החיכוך הקינטי $f_k$ מתוארת על ידי:
\[f_k = \mu_k N \left[\mathrm{N}\right]\]כאשר $\mu_k$ הוא מקדם החיכוך הקינטי (חסר יחידות) ו-$N$ הוא הכוח הנורמלי.
ניתוח הכוחות עם חיכוך
הכוח הנורמלי שווה למשקל החלק של החבל שעל השולחן כפול תאוצת הכבידה (החוק השני של ניוטון):
\[\begin{aligned} N &= (m-\overset{*}{m})g \\[10pt] &= (\rho L - \rho x)g \\[10pt] &= \rho(L-x)g \left[\mathrm{N}\right] \end{aligned}\]הערה: כוחות הם וקטורים, אבל לנוחות אנחנו מתייחסים להבנתי לדברים כגדלים.
לכן, כוח החיכוך הקינטי יהיה:
\[f_k = \mu_k N = \mu_k \underbrace{\rho (L - x) g }_{N}\left[\mathrm{N}\right]\]ניעזר בחוק השני של ניוטון(הכוח השקול הפועל על גוף שווה למכפלת מסת הגוף בתאוצתו: $F = m \cdot a$), כדי לקבל משוואות תנועה עם חיכוך:
שלב 1: זיהוי הכוחות הפועלים על המערכת
הכוחות העיקריים הפועלים על החבל:
-
כוח הכובד על החלק המשתלשל ($\overset{*}{m} g$):
- פועל כלפי מטה
- $\overset{*}{m} = \rho x$ היא מסת החלק המשתלשל
- $\overset{*}{m} g = \rho x g \ \mathrm{N}$
-
כוח החיכוך הקינטי ($f_k$):
- פועל בכיוון המתנגד לתנועה (מושך את החבל חזרה)
- $f_k = \mu_k N$ כאשר $N$ הוא הכוח הנורמלי
- $N = \rho (L-x) g$ היא משקל החלק הנמצא על השולחן
- $f_k = \mu_k \rho (L-x) g \ \mathrm{N}$
שלב 2: חישוב הכוח השקול (סכום הכוחות)
הכוח השקול הוא ההפרש בין כוח הכובד המושך את החבל מטה לבין כוח החיכוך המעכב את התנועה:
\[\sum F = \overset{*}{m} g - f_k\]נציב את הביטויים המפורשים:
\[\sum F = \rho x g - \mu_k \rho (L-x) g\]שלב 3: יישום החוק השני של ניוטון
לפי החוק השני של ניוטון, הכוח השקול שווה למכפלת המסה בתאוצה. המסה של כל החבל היא $m = \rho L$, והתאוצה היא $\ddot{x}$:
\[\sum F = m \cdot a\] \[\rho x g - \mu_k \rho (L-x) g = \rho L \cdot \ddot{x}\]שלב 4: פיתוח מתמטי לקבלת המשוואה הדיפרנציאלית
נפתח את המשוואה שלב אחר שלב:
\[\rho L \cdot \ddot{x} = \rho x g - \mu_k \rho (L-x) g\]נחלק את שני האגפים ב-$\rho L$ כדי לבודד את התאוצה $\ddot{x}$:
\[\ddot{x} = \frac{\rho x g - \mu_k \rho (L-x) g}{\rho L}\]נצמצם את $\rho$ באגף ימין:
\[\ddot{x} = \frac{x g - \mu_k (L-x) g}{L}\]נוציא גורם משותף $g$:
\[\ddot{x} = \frac{g}{L} [x - \mu_k (L-x)]\]נפתח את הסוגריים הפנימיים:
\[\ddot{x} = \frac{g}{L} [x - \mu_k L + \mu_k x]\]נכנס איברים:
\[\ddot{x} = \frac{g}{L} [(1 + \mu_k)x - \mu_k L]\]נפתח את הסוגריים שוב:
\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \frac{g}{L} \mu_k L\]נפשט:
\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \mu_k g \left[\frac{\mathrm{m}}{\mathrm{s}^2}\right]\]סיכום והסבר פיזיקלי
המשוואה הסופית שקיבלנו:
\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \mu_k g\]או בניסוח שקול ואולי יפה יותר (שהופיעה במבחן מועד א׳ 2024):
\[\begin{aligned} \ddot{x} &= \frac{g}{L} (1 + \mu_k) x - g \mu_k \\[10pt] &= \frac{g\left(1 + \mu_k\right)}{L} \left(x - \frac{\mu_k L}{1 + \mu_k}\right) \end{aligned}\]משמעות פיזיקלית:
- האיבר הראשון $\frac{g}{L} (1 + \mu_k) x$ מייצג את ההאצה בגלל כוח הכובד וההשפעה של החיכוך על החלק המשתלשל. ככל שהחלק המשתלשל גדל, כך גדלה ההאצה.
- האיבר השני $\mu_k g$ הוא קבוע שלילי המייצג את ההשפעה המעכבת של החיכוך.
כשמגדירים $\omega^2 = \frac{g}{L} (1 + \mu_k)$, מקבלים משוואה דיפרנציאלית בצורה קומפקטית:
\[\ddot{x} = \omega^2 x - \mu_k g\]זוהי משוואה דיפרנציאלית לינארית לא הומוגנית מסדר שני, שהפתרון שלה יהיה סכום של פתרון המשוואה ההומוגנית ופתרון פרטי.
נגדיר $\omega^2 = \frac{g}{L} (1 + \mu_k) \ \text{[1/s²]}$, כך שהמשוואה הסופית היא:
\[\ddot{x} = \omega^2 x - \mu_k g\]זוהי משוואה דיפרנציאלית לא הומוגנית מסדר שני.
פתרון המשוואה הדיפרנציאלית עם חיכוך
הפתרון הכללי למשוואה מסוג זה מורכב מהפתרון של המשוואה ההומוגנית (ללא האיבר הקבוע) ומפתרון פרטי:
\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) + C \,\mathrm{m}\]נציב את הפתרון הפרטי $C$ במשוואה המקורית:
\[\ddot{C} = \omega^2 C - \mu_k g\]מכיוון ש-$C$ הוא קבוע, אז $\ddot{C} = 0$:
\[0 = \omega^2 C - \mu_k g\] \[C = \frac{\mu_k g}{\omega^2} = \frac{\mu_k g}{\frac{g}{L} (1 + \mu_k)} = \frac{\mu_k L}{1 + \mu_k} \,\mathrm{m}\]לכן, הפתרון הכללי:
\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) + \frac{\mu_k L}{1 + \mu_k}\]נשתמש בתנאי ההתחלה כדי למצוא את הקבועים $A$ ו-$B$:
-
תנאי ראשון: $x(0) = x_0$
\[x(0) = A\cosh(0) + B\sinh(0) + \frac{\mu_k L}{1 + \mu_k}\] \[x_0 = A \cdot 1 + 0 + \frac{\mu_k L}{1 + \mu_k}\] \[A = x_0 - \frac{\mu_k L}{1 + \mu_k} \,\mathrm{m}\] -
תנאי שני: $\dot{x}(0) = 0$
\[\dot{x}(t) = A\omega\sinh(\omega t) + B\omega\cosh(\omega t) + 0\] \[\dot{x}(0) = A\omega\sinh(0) + B\omega\cosh(0)\] \[0 = 0 + B\omega \cdot 1\] \[B = 0 \,\mathrm{m}\]
לכן, הפתרון המלא:
\[x(t) = \left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega t) + \frac{\mu_k L}{1 + \mu_k} \,\mathrm{m}\]והמהירות:
\[v(t) = \left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\omega\sinh(\omega t) \,\mathrm{m/s}\]תנאי הסף להחלקה
טרם תחילת התנועה, חיכוך סטטי מונע את תנועת החבל. החבל יתחיל להחליק רק כאשר כוח המשיכה של החלק המשתלשל יהיה גדול מכוח החיכוך הסטטי המקסימלי:
\[F_{\text{drag}} > F_{\text{max static friction}}\] \[\rho g x_0 > \mu_s \rho g (L - x_0)\]פישוט:
\[x_0 > \frac{\mu_s L}{1 + \mu_s} \,\mathrm{m}\]זהו תנאי הסף להחלקה: אם החלק המשתלשל ההתחלתי קטן מדי, החבל לא יתחיל בכלל להחליק!
זמן ההחלקה המלאה עם חיכוך
לחישוב זמן ההחלקה המלאה, נציב $x(T) = L$:
\[\left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega T) + \frac{\mu_k L}{1 + \mu_k} = L\]פישוט:
\[\left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega T) = L - \frac{\mu_k L}{1 + \mu_k} = \frac{L}{1 + \mu_k}\] \[\cosh(\omega T) = \frac{\frac{L}{1 + \mu_k}}{x_0 - \frac{\mu_k L}{1 + \mu_k}} = \frac{L}{(1 + \mu_k)(x_0 - \frac{\mu_k L}{1 + \mu_k})}\]ומכאן:
\[T = \frac{1}{\omega}\cosh^{-1}\left(\frac{L}{(1 + \mu_k)(x_0 - \frac{\mu_k L}{1 + \mu_k})}\right) \,\mathrm{s}\] \[T = \sqrt{\frac{L}{g(1+\mu_k)}}\cosh^{-1}\left(\frac{L(1+\mu_k)}{(1+\mu_k)x_0 - \mu_k L}\right) \,\mathrm{s}\]הסבר פיזיקלי להשפעת החיכוך
החיכוך מתנגד לתנועת החבל ומאט את קצב ההחלקה. כתוצאה מכך:
- נדרש ערך מינימלי של $x_0$ כדי שהחבל יתחיל בכלל להחליק. אם $x_0 \leq \frac{\mu_s L}{1 + \mu_s}$, החבל יישאר במנוחה.
- זמן ההחלקה המלאה $T$ גדול יותר בהשוואה למקרה ללא חיכוך, שכן החיכוך מאט את תנועת החבל.
- הפתרון כולל איבר קבוע $\frac{\mu_k L}{1 + \mu_k}$ שמייצג את ההשפעה של החיכוך על דינמיקת המערכת.
- החיכוך גם משנה את ערך $\omega$ (מ-$\sqrt{\frac{g}{L}}$ ל-$\sqrt{\frac{g}{L}(1+\mu_k)}$), מה שמשפיע על קצב הגידול של המהירות וההאצה.
במקרה הגבולי שבו $\mu_k = 0$ (אין חיכוך), נקבל $\omega^2 = \frac{g}{L}$ ו-$C = 0$, והפתרון יהיה זהה לפתרון שמצאנו במקרה הראשון:
\[x(t) = x_0 \cosh(\omega t)\]זה מאשר את נכונות הפתרון הכללי שלנו.
אוסצילטור הרמוני
הגדרת האוסצילטור ההרמוני
נתונה מערכת המורכבת מקיר ורצפה נטולת חיכוך, שעליה מונחת מסה $M$ המחוברת בקפיץ לקיר.
חוק הוק והכוח המחזיר
מבחינה פיזיקלית, קפיץ אידיאלי מפעיל כוח מחזיר ($\mathbf{F}$) כאשר הוא נמתח או נדחס. לפי חוק הוק, כוח זה פרופורציונלי (יחסי) להעתק ($\Delta x$) של הקפיץ ממצב שיווי המשקל שלו.
באופן וקטורי (בתלת-ממד), הכוח מתואר על ידי:
\[\mathbf{F} = -k \cdot \mathbf{r}\]כאשר:
- $\mathbf{F}$ הוא הכוח המחזיר.
- $k$ הוא קבוע הקפיץ, המבטא את קשיחותו. יחידותיו הן ניוטון למטר ($\mathrm{N/m}$). ככל ש-$k$ גדול יותר, הקפיץ קשיח יותר.
- $\mathbf{r}$ הוא וקטור ההעתק מנקודת שיווי המשקל.
הסימן השלילי מציין שהכוח פועל תמיד בכיוון המנוגד להעתק, כלומר, הוא שואף להחזיר את המערכת למצב שיווי משקל.
במקרה של תנועה בממד אחד, ניתן לכתוב את חוק הוק בצורה סקלרית:
\[F_x = -k \cdot x\]במודל זה, מניחים כי נקודת שיווי המשקל היא ב-$x=0$, שם הכוח מתאפס. במערכות פיזיקליות רבות, כמו תנודות של אטומים בסריג גבישי, נקודת שיווי המשקל היא נקודה יציבה שסביבה מתרחשות התנודות, והכוח המחזיר פרופורציונלי להסטה מנקודה זו.
במקרים של קפיץ בעל אורך רפוי $x_0$ שונה מאפס, הנוסחה תהיה:
\[F_x = -k \cdot (x - x_0)\]כאשר $x_0$ הוא האורך הרפוי. הכוח מתאפס כאשר $x = x_0$.
המשוואה הדיפרנציאלית של האוסצילטור ההרמוני
לצורך פיתוח המשוואה, נניח אורך רפוי אפס ($x_0 = 0$). לפי החוק השני של ניוטון:
\[\mathbf{F} = m\mathbf{a} = m \ddot{\mathbf{x}}\]הכוח הפועל על המסה הוא כוח הקפיץ:
\[\mathbf{F} = -k \mathbf{x}\]מהשוואת שני הביטויים לכוח, מתקבל:
\[-k x = m \ddot{x}\]לאחר סידור מחדש, מקבלים את המשוואה הדיפרנציאלית של התנועה:
\[\ddot{x} = -\frac{k}{m} x\]נהוג להגדיר את התדירות הזוויתית $\omega$ של המערכת:
\[\omega^2 = \frac{k}{m}\]כך שהמשוואה מקבלת את הצורה הקנונית:
\[\ddot{x} = -\omega^2 x\]זוהי משוואת האוסצילטור ההרמוני הפשוט. מערכת המתוארת על ידי משוואה זו נקראת “מתנד (אוסצילטור) הרמוני”. תנודות הרמוניות הן תנודות מחזוריות המתוארות על ידי פונקציות סינוס וקוסינוס. למודל זה חשיבות יסודית בפיזיקה, והוא משמש לתיאור מגוון רחב של תופעות, מתנודות אטומים במולקולות ועד למעגלים חשמליים.
פתרון המשוואה הדיפרנציאלית של האוסצילטור ההרמוני
המשוואה הדיפרנציאלית $\ddot{x} = -\omega^2 x$ היא משוואה לינארית, הומוגנית, מסדר שני, עם מקדמים קבועים. הפתרון הכללי שלה הוא צירוף לינארי של פונקציות שנגזרתן השנייה היא מינוס הפונקציה עצמה (כפול קבוע). פונקציות אלו הן סינוס וקוסינוס.
הפתרון הכללי הוא:
\[x(t) = A \cos(\omega t) + B \sin(\omega t) \quad [\mathrm{m}]\]כאשר $A$ ו-$B$ הם קבועים הנקבעים על פי תנאי ההתחלה של המערכת (מיקום ומהירות בזמן $t=0$).
קביעת הקבועים באמצעות תנאי התחלה
נניח שבזמן $t=0$, מיקום המסה הוא $x(0) = x_0$ ומהירותה היא $v(0) = v_0$.
-
קביעת A (מצב התחלתי): נציב $t=0$ בפתרון הכללי:
\(x(0) = x_0 = A\underbrace{\cos(0)}_{=1} + B\underbrace{\sin(0)}_{=0} = A\) מכאן נובע:
\[\boxed{A = x_0}\] -
קביעת B (מהירות התחלתית):
נגזור את $x(t)$ כדי לקבל את המהירות $v(t)$:
\[v(t) = \frac{dx}{dt} = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\]נציב $t=0$:
\[v(0) = v_0 = -A\omega\underbrace{\sin(0)}_{=0} + B\omega\underbrace{\cos(0)}_{=1} = B\omega\]מכאן נובע:
\[\boxed{B = \frac{v_0}{\omega}}\]
הפתרון המלא עבור תנאי ההתחלה הנתונים הוא:
\[\boxed{x(t) = x_0\cos(\omega t) + \frac{v_0}{\omega}\sin(\omega t)}\]צורה אלטרנטיבית של הפתרון: אמפליטודה ופאזה
ניתן לבטא את הפתרון גם בצורה של פונקציית קוסינוס (או סינוס) בודדת עם הזזת פאזה:
\[x(t) = C\cos(\omega t + \phi)\]כאשר $C$ היא האמפליטודה (משרעת) של התנודה, ו-$\phi$ היא זווית המופע (פאזה).
באמצעות הזהות הטריגונומטרית:
\[\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)\]ניתן לקשר בין שתי הצורות של הפתרון:
\[x(t) = C\cos(\phi)\cos(\omega t) - C\sin(\phi)\sin(\omega t)\]מהשוואת מקדמים עם הפתרון $x(t) = A \cos(\omega t) + B \sin(\omega t)$, מקבלים:
\[A = C\cos(\phi) \quad \text{and} \quad B = -C\sin(\phi)\]מכאן ניתן לחלץ את $C$ ו-$\phi$:
-
אמפליטודה (C):
\[A^2 + B^2 = C^2\cos^2(\phi) + C^2\sin^2(\phi) = C^2(\cos^2\phi + \sin^2\phi) = C^2\] \[C = \sqrt{A^2 + B^2} = \sqrt{x_0^2 + \left(\frac{v_0}{\omega}\right)^2}\]האמפליטודה מייצגת את ההעתק המרבי של הגוף מנקודת שיווי המשקל. התנועה חסומה בתחום $[-C, +C]$.
-
זווית פאזה ($\phi$):
\[\frac{B}{A} = \frac{-C\sin(\phi)}{C\cos(\phi)} = -\tan(\phi)\] \[\phi = \arctan\left(-\frac{B}{A}\right) = \arctan\left(-\frac{v_0}{\omega x_0}\right)\]
זמן המחזור של התנודה
התנודה ההרמונית היא מחזורית. זמן המחזור ($T$) הוא הזמן הדרוש להשלמת תנודה מלאה אחת. הוא מתקיים כאשר הארגומנט של הפונקציה הטריגונומטרית גדל ב-$2\pi$:
\[\omega T = 2\pi\]לכן, זמן המחזור הוא:
\[T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{m}{k}}\]זמן המחזור תלוי רק במסת הגוף ובקבוע הקפיץ, ואינו תלוי באמפליטודה של התנודה (עבור תנודות קטנות).
סיכום
המתנד ההרמוני הוא מודל פיזיקלי בסיסי המתאר תנודה סביב נקודת שיווי משקל יציבה. התנועה היא הרמונית, כלומר מתוארת על ידי פונקציות סינוס וקוסינוס. המאפיינים העיקריים של התנועה הם:
- תדירות זוויתית ($\omega$): קובעת את מהירות התנודה.
- אמפליטודה ($C$): ההעתק המרבי מנקודת שיווי המשקל.
- זמן מחזור ($T$): הזמן להשלמת תנודה אחת.
האלגנטיות והפשטות של המודל הופכות אותו לכלי חיוני בניתוח מערכות פיזיקליות מורכבות רבות.
שאלות ותשובות נפוצות
שאלה: מדוע $\omega^2 = \frac{k}{m}$?
תשובה: הגדרה זו נובעת מצורת המשוואה הדיפרנציאלית $\ddot{x} = -(\frac{k}{m})x$. סימון $\frac{k}{m}$ כ-$\omega^2$ מפשט את צורת המשוואה ומדגיש את הקשר לתדירות התנודה. בכל גזירה של פונקציית הפתרון ($\sin(\omega t)$ או $\cos(\omega t)$), הגורם $\omega$ “יוצא החוצה” לפי כלל השרשרת, כך שבגזירה שנייה מתקבל גורם של $\omega^2$.
שאלה: מדוע הפתרון הכללי דורש גם סינוס וגם קוסינוס?
תשובה: משוואה דיפרנציאלית מסדר שני דורשת שני פתרונות בלתי תלויים לינארית כדי לבנות פתרון כללי. סינוס וקוסינוס הם שני פתרונות כאלה. הצירוף הלינארי של שניהם מאפשר לפתרון לעמוד בכל זוג תנאי התחלה אפשריים (מיקום ומהירות). במקרים פרטיים, אחד המקדמים ($A$ או $B$) עשוי להתאפס, אך הפתרון הכללי חייב לכלול את שתי האפשרויות.
שאלה: מהן היחידות של $\omega$?
תשובה: היחידות של $\omega$ הן רדיאנים לשנייה ($\mathrm{rad/s}$). מכיוון ש-$\omega^2 = k/m$, יחידותיו הן $(\mathrm{N/m})/\mathrm{kg} = (\mathrm{kg \cdot m/s^2}/m)/\mathrm{kg} = 1/\mathrm{s}^2$. לכן, היחידות של $\omega$ הן $1/\mathrm{s}$. התדירות הרגילה ($f$), הנמדדת בהרץ (Hz), קשורה לתדירות הזוויתית על ידי $f = \omega / (2\pi)$.
שאלה: האם המסה $m$ היא של הקפיץ או של הגוף?
תשובה: במודל האוסצילטור ההרמוני הפשוט, $m$ היא מסת הגוף המתנדנד. מניחים שהקפיץ הוא “חסר מסה” (מסת הקפיץ זניחה ביחס למסת הגוף).
שיעור תגבור - מטוטלת מואצת, תנודות הרמוניות וחיכוך
תאריך: 11/05/2025הקדמה לבעיית המטוטלת בקרון מואץ
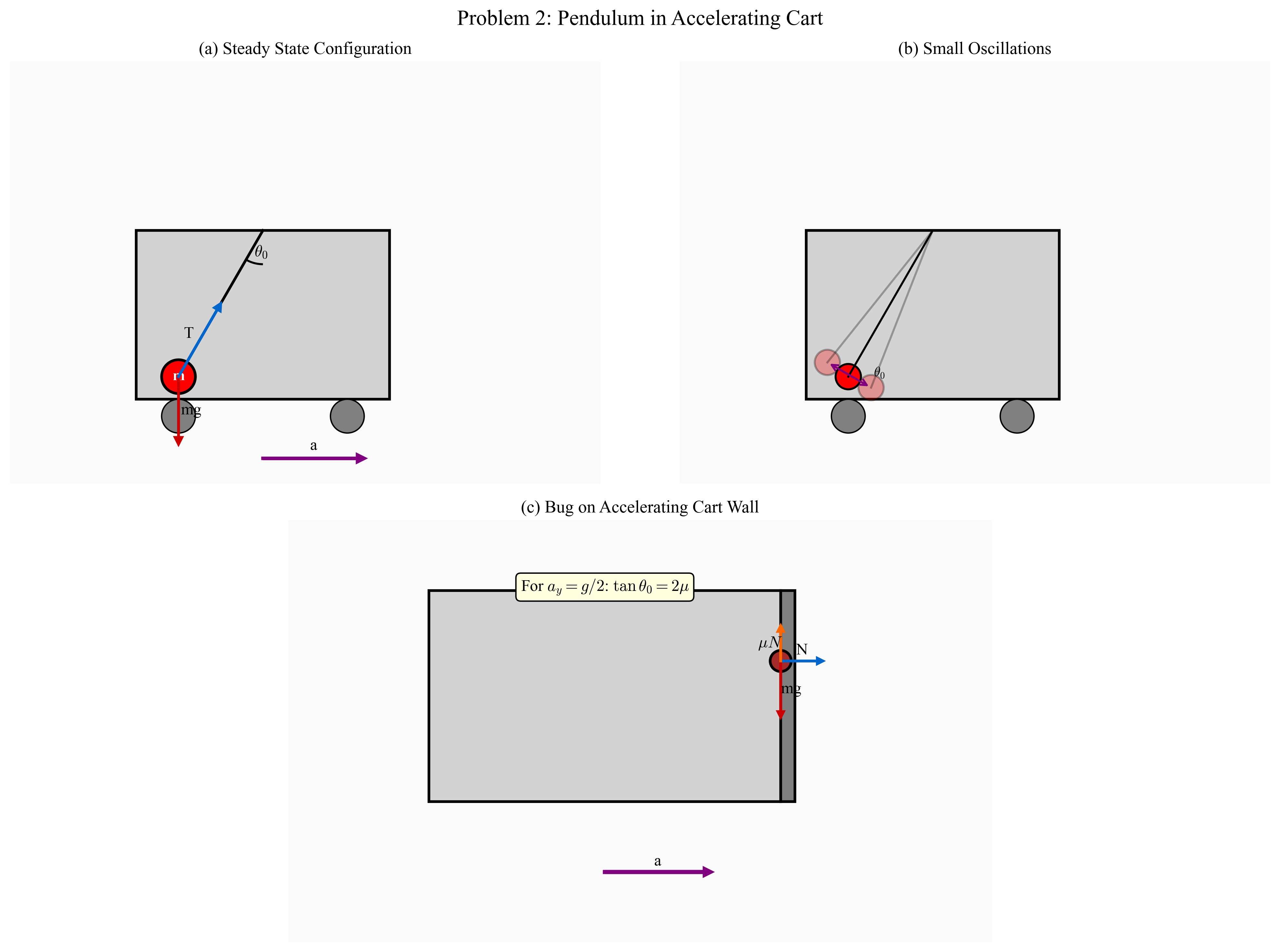
מסה $m$ מחוברת לתקרה של קרון עם חוט באורך $\ell$. הקרון מאיץ ימינה בתאוצה $A$. אנחנו צריכים לחקור את המערכת הזאת.
משחררים את המטוטלת כך שהחוט נפרש בזווית פרישה מסוימת $\theta_0$ הנשמרת כל העת במהלך התנועה. מהי התאוצה במונחים של הפרמטרים בבעיה?
שימו לב שהביטוי שקיבלתם משמש מעין “מד תאוצה”.
מסיטים את המסה $m$ למצב אנכי ומשחררים ממנוחה. מיד לאחר מכן היא מבצעת תנודות הרמוניות סביב הזווית $\theta_0$ (נקודת שיווי המשקל של המערכת).
מהי תדירות התנודות ומהי המשרעת שלהן בהנחה של זוויות קטנות (כלומר כאשר $sin \theta \approx \theta$)?
תוך כדי תנועת הקרון ימינה נצמד חרק לדופן הימנית (חזית הקרון המאיץ) והוא מחליק מטה בתאוצה בהיותו צמוד לדופן.
מקדם החיכוך בין החרק לדופן הוא $\mu$.
מה צריכה להיות זווית הפרישה $\theta_0$ כדי שתאוצתו של החרק מטה תהיה בדיוק $A = g/2$?
במהלך התנודה נקרע לפתע החוט כשהוא מתוח בזווית $\theta = 0^\circ$ ביחס לאנך. ציירו סקיצה כיצד ייראה מסלול הנפילה של המסה מנקודת המבט של צופה הנמצא בתוך העגלה.
אפיינו את הציר באמצעות צירים וזוויות והסבירו אותו.
שלב ראשון: מציאת זווית שיווי המשקל
ניתוח מתוך הקרון (מערכת ייחוס מואצת)
השלב הראשון הוא לקבוע את זווית שיווי המשקל. אנחנו נמצאים בתוך הקרון, מחזיקים את המסה, ובעדינות רבה מביאים אותה למקום שבו היא נשארת יציבה במצבה הנוכחי. זה בזווית $\theta_0$ (זווית שיווי המשקל).
השאלה: מה הקשר בין $\theta_0$ ל-$A$? והאם אפשר להשתמש ב-$\theta_0$ כדי למצוא את תאוצת הקרון?
התשובה: בוודאי שכן!
כוחות במערכת המואצת
כשאנחנו נמצאים בתוך הקרון, מבחינתנו הכל במנוחה, למרות שאנחנו מואצים. אנחנו נמצאים במערכת ייחוס לא אינרציאלית ומרגישים כוחות מדומים.
הכוחות הפועלים על המסה:
- $\downarrow mg$ כלפי מטה (כוח הכבידה)
- $\leftarrow mA$ שמאלה (כוח מדומה, הפוך לכיוון התאוצה)
משוואות שיווי המשקל
בשיווי משקל, שקול הכוחות שווה לאפס (החוק הראשון של ניוטון במערכת מואצת):
הערה: לכאורה אפשר להגיע לאותן משוואות משני החוקים - זה רלוונטי לשאלות נוספות שבהן גוף שנמצא בתוך מערכת מואצת מרגיש כוחות מדומים, כמו בעיית מד המשקל וסיבוב כדור הארץ. השאלה איך מסתכלים על הבעיה ככל הנראה תלויה בשיטת הלימוד.
המרצה ככל הנראה מבחין ביין המצבים הבאים:
כשמסתכלים על הרכבת מבחוץ (מערכת אינרציאלית, כלומר מערכת התמד או מערכת לא מואצת) - חוק שני של ניוטון (כוחות):
\[T\sin(\theta_0) = mA\]כשמסתכלים על הרכבת מבפנים (מערכת לא אינרציאלית, כלומר מערכת מואצת) - חוק ראשון של ניוטון (שיווי משקל), עם תיקון לכוחות מדומים.
\[T\sin(\theta_0) - mA = 0\]
בכיוון האנכי: (רדיאלי - באיור ↗)
\[T \cos(\theta_0) -mg = 0\] \[\boxed{T \cos(\theta_0) = mg} \tag{1}\]בכיוון האופקי: (משיקי - באיור ↘)
\[T \sin(\theta_0) - mA = 0\] \[\boxed{T \sin(\theta_0) = mA} \tag{2}\]הערה: בשיעור נעשה תיקון בגרף שקצת בלבל אותי ביחס לזוויות ההתחלה. מאיור מעלה מציג את התיקון.
מציאת הקשר בין התאוצה לזווית
חילוק שתי המשוואות $(1)$ ו$(2)$:
\[\frac{T \sin(\theta_0)}{T \cos(\theta_0)} = \frac{mA}{mg}\] \[\tan(\theta_0) = \frac{A}{g}\]לכן:
\[\boxed{A = g \tan\left(\theta_0\right) \, \mathrm{[m/s^2]}}\]זהו מד תאוצה (אקסלרומטר)! אם אני נמצא בתוך המערכת המואצת ואני מודד את הזווית $\theta_0$, אני יודע בדיוק באיזה תאוצה המערכת שלי מתנועת.
שלב שני: דינמיקה של התנודות
הבעיה הדינמית
עכשיו אני לוקח את המסה, מוריד אותה למטה ומשחרר. היא תרצה לחזור למצב שיווי המשקל ותתחיל להתנדד סביב הזווית $\theta_0$.
ניתוח הכוחות במהלך התנועה
הכוח השקול הפועל על המסה:
\[\vec{F} = mA \hat{x} - mg \hat{y}\]גודל הכוח השקול:
\[\vert \vec{F}\vert = \sqrt{(m\underbrace{A}_{g\tan^2(\theta_0)})^2 + (-mg)^2} = mg\sqrt{1 + \tan^2(\theta_0)}\]מהזהות הטריגונומטריות:
\[1 + \tan^2(\theta_0) = \frac{1}{\cos^2(\theta_0)}\]נקבל:
\[\vert \vec{F}\vert = \frac{mg}{\cos(\theta_0)}\]פירוק לקואורדינטות פולאריות
בקואורדינטות פולאריות (רדיאלי ומשיקי):
בכיוון הרדיאלי: (רדיאלי - באיור ↗)
\[T - F\cos(\theta) = m\frac{v^2_{\theta}}{\ell}\]כאשר $F\cos(\theta)$ הוא ההיטל של הכוח השקול על הכיוון הרדיאלי.
בכיוון המשיקי: (משיקי - באיור ↘)
\[mL\ddot{\theta} = -F\sin(\theta)\]קירוב לזוויות קטנות
עבור זוויות קטנות, $\sin(\theta) \approx \theta$:
\[mL\ddot{\theta} = -F\theta\] \[\ddot{\theta} = -\frac{F}{mL}\theta\]מאחר ש-$F = \frac{mg}{\cos(\theta_0)}$:
\[\boxed{\ddot{\theta} = -\frac{g}{\ell\cos(\theta_0)}\theta} \tag{3}\]זוהי משוואת תנודה הרמונית פשוטה מהצורה:
\[\ddot{\theta} = -\omega^2 \theta\]כאשר המהירות הזווית $\omega=\dot{\theta}$ היא:
\[\boxed{\omega = \sqrt{\frac{g}{\ell\cos(\theta_0)}} \,\mathrm{[rad/s]}}\]תדירות התנודות והמשרעת
ניזכר בהגדרה של תדירות התנודות $f$:
\[\boxed{f = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{g}{\ell\cos(\theta_0)}} \,\mathrm{[Hz]}}\]משרעת התנודות
המשרעת של התנודות היא הזווית ההתחלתית ביחס לזווית שיווי המשקל $\theta_0$. אם המסה משוחררת ממצב אנכי, המשרעת תהיה:
\[\boxed{\theta_{0} \,\mathrm{[rad]}}\]פתרון משוואת התנודות
הפתרון הכללי של משוואת התנודות הרמונית הוא, ובפרט למשוואה (3):
\[\theta(t) = \theta_{0} \cos(\omega t)\]כאשר $\theta_{0}$ הוא הזווית ההתחלתית ביחס לזווית שיווי המשקל $\theta_0$.
המהירות המשיקית
נגזור את הפתרון כדי למצוא את המהירות המשיקית:
\[v_{\theta} = \ell\dot{\theta} = -\ell\omega \theta_{0} \sin(\omega t)\]המתיחות כפונקציה של הזמן
\[T(t) = F\cos(\theta) + m\frac{v^2_{\theta}}{\ell}\]זוהי פונקציה מתנדנדת של הזמן.
שלב שלישי: בעיית החיכוך
תיאור הבעיה
עכשיו אני (בעל מסה $M$) נמצא על דופן הקרון. הרכבת נעה בתאוצה $A$, ויש מקדם חיכוך $\mu$ ביני לבין הדופן.
השאלה: מה צריכה להיות זווית הנטייה $\theta_0$ כדי שאני אחליק כלפי מטה בתאוצה של $\frac{g}{2}$?
ניתוח הכוחות
הכוחות הפועלים עליי:
- $Mg$ כלפי מטה (כבידה)
- $N$ כלפי חוץ מהדופן (כוח נורמלי)
- $\mu N$ כלפי מעלה (חיכוך, נגד כיוון התנועה)
משוואות תנועה
בכיוון האופקי:
\[N = MA \tag{1}\]בכיוון האנכי:
\[M \cdot \frac{g}{2} = Mg - \mu N \tag{2}\]פתרון
מהמשוואה הראשונה והביטוי שקיבלנו ל-$A$:
\[N = MA = Mg\tan(\theta_0)\]נציב את $N$ במשוואה השנייה:
\[M \cdot \frac{g}{2} = Mg - \mu \cdot Mg\tan(\theta_0)\]נחלק ב-$Mg$:
\[\frac{1}{2} = 1 - \mu\tan(\theta_0)\] \[\mu\tan(\theta_0) = \frac{1}{2}\] \[\tan(\theta_0) = \frac{1}{2\mu}\] \[\boxed{\theta_0 = \arctan\left(\frac{1}{2\mu}\right) \,\mathrm{[rad]}}\]שלב רביעי: נפילה חופשית לאחר קריעת החוט
לאחר שהחוט נקרע, המסה נופלת חופשית בתוך הקרון המואץ.
ניתוח התנועה
בתוך הקרון, המסה מרגישה:
- תאוצה $g$ כלפי מטה
- תאוצה $A$ בכיוון האופקי
מסלול התנועה
מאחר ששתי התאוצות קבועות:
\[\begin{align} \Delta x &= \frac{1}{2}At^2 \\ \Delta y &= \frac{1}{2}gt^2 \end{align}\]המסלול הוא קו ישר בזווית $\phi$ מתחת לאופק:
\[\tan(\phi) = \frac{\Delta y}{\Delta x} = \frac{g}{A}\]סיכום
המטוטלת בקרון מואץ מדגימה עקרונות חשובים בפיזיקה:
- כוחות מדומים במערכות ייחוס מואצות - הכוח $mA$ שמאלה
- מד תאוצה - $A = g\tan(\theta_0)$
- תנודות הרמוניות במערכת מואצת - $\omega = \sqrt{\frac{g}{\ell\cos(\theta_0)}}$
- חיכוך במערכות מואצות
- תנועה פרבולית במערכת ייחוס מואצת
הערה חשובה: כל הניתוחים נעשו מתוך מערכת הייחוס המואצת (הקרון), תוך התחשבות בכוחות המדומים המתאימים.
שיעור 8 - תנועה הרמונית וקואורדינטות פולאריות
תאריך: 12/05/2025מבוא ותזכורת
בשיעורים הקודמים, כולל בשיעור התגבור, ראינו שבסיטואציות מסוימות החוק השני של ניוטון מוביל למשוואה דיפרנציאלית המתארת תנועה הרמונית.
המשוואה הדיפרנציאלית של תנועה הרמונית
החוק השני של ניוטון הוא:
\[m \cdot a = F \tag{1}\]כאשר $F$ זה שקול הכוחות.
החוק הזה, במקרים מסוימים, מוביל אותנו אל המשוואה הדיפרנציאלית של תנועה הרמונית פשוטה:
\[\ddot{x} = -\omega^2 \cdot x\]הסיטואציה הזאת מתרחשת כאשר מדובר במימד אחד והכוח הוא כוח מחזיר שמתכונתי להעתק. הסיטואציה הטריוויאלית והמובהקת ביותר היא כאשר:
\[F = -k \cdot x \tag{2}\]משוואה $(2)$ מתארת את הכוח של קפיץ, כאשר $k$ הוא הקבוע של הקפיץ. הכוח הזה הוא כוח מחזיר, כלומר הוא פועל בכיוון ההפוך להעתק $x$.
ממשוואות $(1)$ ו-$(2)$ נוכל לפתח את משוואת התנועה ההרמונית הפשוטה:
\[\begin{align} m \cdot a &= \underbrace{-k \cdot x}_{F} \\[10pt] m \cdot \ddot{x} &= -k \cdot x \tag{$a=\ddot{x}$} \\[10pt] \ddot{x} &= -\frac{k}{m} \cdot x \tag{$\div m$} \\[10pt] \ddot{x} &= -\omega^2 \cdot x \tag{$\omega^2 = \frac{k}{m}$} \end{align}\]סך הכל:
\[\boxed{\ddot{x} = -\omega^2 \cdot x} \tag{Simple Harmonic Motion}\]כוח מחזיר ונקודת שיווי משקל
בסיטואציות רבות נגיע אל המשוואה הזאת לא באמצעות הכוח הפשוט שמתואר במשוואה $(1)$. המשוואה הזאת יכולה להתקבל בסיטואציות רבות נוספות. זה מקרה מאוד אלמנטרי שבו יש לנו קפיץ, ואנחנו יודעים שקפיצים מתנדנדים. קל לדמיין שהכוח המחזיר של הקפיץ מתכונתי למתיחה שלו מהאורך הרפוי.
שימו לב, פה רשמנו $F = -kx$, כלומר הכוח מתאפס כש-$x = 0$, אבל בחיים האמיתיים הוא יותר דומה ל:
\[F = -k \cdot \Delta x\]כאשר $\Delta x = x - x_0$, ו-$x_0$ הוא האורך הרפוי. כאשר $x = x_0$, $F = 0$.
שימו לב שהתנאי $F = 0$ מייצר את נקודת שיווי המשקל: זאת אותה נקודה שבה הכוח הוא אפס. אם הכוח הוא אפס, התאוצה היא אפס. ברגע שנרחיק את המסה מנקודת שיווי המשקל, נוצר כוח מחזיר, ואז שקול הכוחות שונה מאפס, ואז יש לנו תאוצה.
דוגמה: מסה תלויה על קפיץ
לדוגמה, נניח שתולים מסה על קפיץ שהאורך הרפוי שלו הוא 0 ($x_0 = 0$), כלומר, שהאורך הרפוי של הקפיץ נמצא למעלה. אפשר לראות שבמצב של שיווי משקל מתקיים:
\[mg = k\overset{*}{x}\]כאשר \(k\overset{*}{x}\) הוא הכוח שקשור בעובדה שהקפיץ נמתח ומושך כלפי מעלה. \(\overset{*}{x}\) הוא ה-$x$ של שיווי המשקל. במצב הזה $F_{total} = 0$ (שקול הכוחות שווה לאפס).
מכאן נקבל:
\[\overset{*}{x} = \frac{mg}{k}\]זו נקודת שיווי המשקל, ואנחנו נצפה שהמסה תתנדנד סביבה ברגע שנשחרר אותה. מה שמכתיב את נקודת שיווי המשקל זה ששקול הכוחות שווה לאפס. זאת אותה נקודה בודדת בתוך התנועה שעבורה שקול הכוחות שווה לאפס.
פתרון המשוואה הדיפרנציאלית
אם נמתח את הקפיץ ואז נשחרר, המסה תתנדנד. במקרה הזה, לפי החוק השני של ניוטון ($F = ma$), משוואת התנועה תהיה:
\[\begin{aligned} ma &= \underbrace{mg -kx}_{F} \\[10pt] m\ddot{x} &= mg - kx \end{aligned}\]זה החוק השני של ניוטון, כאשר $(-kx)$ הוא הכוח המחזיר ו-$mg$ הוא כוח הכבידה. אם נבודד את התאוצה $\ddot{x}$, נקבל:
\[\begin{align} m\ddot{x} &= mg - kx \tag{/m} \\[10pt] \ddot{x} &= g - \frac{k}{m}x \\[10pt] \ddot{x} &= -\frac{k}{m}\left(\underbrace{x - \frac{mg}{k}}_{y}\right) \tag{3} \end{align}\]נסמן:
\[y = x - \frac{mg}{k}\]ואז אם נציב את $y$ במשוואה $(3)$, נקבל את המשוואה הדיפרנציאלית של התנועה ההרמונית:
\[\ddot{y} = -\omega^2 y\]כאשר $\omega^2 = \frac{k}{m}$
הפתרון למשוואה הזאת הוא:
\[y(t) = A\cos(\omega t) + B\sin(\omega t)\]לכן, אם נציב $y=x - \frac{mg}{k}$, כדי להחזיר את $x$ למשוואה, נקבל:
\[\begin{align} x(t) - \frac{mg}{k} &= A\cos(\omega t) + B\sin(\omega t) \\[10pt] x(t) &= A\cos(\omega t) + B\sin(\omega t) + \frac{mg}{k} \tag{4} \end{align}\]תנאי התחלה
עכשיו צריך להכניס את תנאי ההתחלה. אם:
\[\begin{aligned} x(t=0) &= x_0 \\[10pt] v(t=0) &= v_0 \end{aligned}\]ניקח לדוגמה את המקרה של $x_0 = 0$ ו-$v_0 \neq 0$.
נציב את התנאי $x(0) = 0$ במשוואה $(4)$:
\[\begin{aligned} x(t=0) &= A\cos(0) + B\sin(0) + \frac{mg}{k} \\[10pt] 0 &= A \cdot 1 + B \cdot 0 + \frac{mg}{k} \end{aligned}\]מכאן:
\[\boxed{A = -\frac{mg}{k}}\]ביחס לתנאי על התאוצה ההתחלתית, אנחנו למעשה צריכים לגזור את משוואה $(4)$, כי התאוצה ($\ddot{x}$) היא נגזרת שנייה של $x$:
\[\begin{aligned} v(t)=\dot{x}(t) &= -A\omega\sin(\omega t) + B\omega\cos(\omega t) \\[10pt] &= -\frac{mg}{k}\omega\sin(\omega t) + B\omega\cos(\omega t) \end{aligned}\]עכשיו נציב את התנאי $v(0) = v_0$ במשוואה $(4)$:
\[\begin{aligned} v(t=0) = v_0 &= -\frac{mg}{k}\omega\sin(0) + B\omega\cos(0) \\[10pt] &= B\omega \end{aligned}\]מכאן:
\[\boxed{B = \frac{v_0}{\omega}}\]ולכן הפתרון לפי תנאי ההתחלה שנתנו הוא:
\[\boxed{x(t) = \frac{mg}{k}\left(1 - \cos(\omega t)\right) + \frac{v_0}{\omega}\sin(\omega t)}\]דוגמה מורכבת: תנועה הרמונית של שתי מסות מחוברות בקפיץ
תיאור המערכת
יש לנו מערכת הכוללת:
- רצפה חלקה (ללא חיכוך)
- מסה גדולה $M$ הנמצאת על הרצפה החלקה
- מסה קטנה $m$ הנמצאת על גבי המסה הגדולה
- קפיץ המחבר בין שתי המסות
- אין חיכוך בין המסות: $\mu = 0$
הגדרת קואורדינטות
נגדיר כי האורך הטבעי של הקפיץ הוא $x = 0$.
בזמן $t = 0$:
- אנו מותחים את הקפיץ (מסה קטנה נמצאת במיקום שלילי)
- משחררים את שתי המסות בו-זמנית
ניתוח הכוחות והתנועה
מה קורה לאחר השחרור?
כאשר אנו משחררים את המערכת:
- הקפיץ רוצה להתכווץ (כי הוא מתוח)
- הקפיץ מושך את המסה הקטנה ימינה (לכיוון $x = 0$)
- אותו קפיץ דוחף את המסה הגדולה שמאלה (כוח תגובה)
מערכות ייחוס
חשוב להבין: המסה הקטנה נמצאת במערכת ייחוס מואצת (של המסה הגדולה), ולכן פועלים עליה כוחות מדומים.
בניית משוואות התנועה
הגדרת משתנים
- $A$ = תאוצת המסה הגדולה (שמאלה, חיובית)
- $a$ = תאוצת המסה הקטנה יחסית למסה הגדולה (ימינה, חיובית)
- $x$ = מיקום המסה הקטנה במערכת ייחוס של המסה הגדולה
משוואה עבור המסה הקטנה
המסה הקטנה מרגישה:
- כוח הקפיץ: $-kx$ (מחזיר לעמדת שיווי משקל)
- כוח מדומה: $mA$ (בכיוון הפוך לתאוצת המערכת)
מהחוק השני של ניוטון ($\sum F = ma$):
\[m \cdot a = -kx + m \cdot A \tag{1}\]משוואה עבור המסה הגדולה
על המסה הגדולה פועל רק כוח הקפיץ. שוב לפי החוק השני של ניוטון:
\[M \cdot A = -kx\]מכאן:
\[\boxed{A = -\frac{k}{M}x}\]חיבור המשוואות
נציב את הביטוי עבור $A$ במשוואה $(1)$:
\[\begin{align} m \cdot a &= -kx + m \cdot \left(-\frac{k}{M}x\right) \\[10pt] m \cdot a &= -kx - \frac{mk}{M}x \\[10pt] m \cdot a &= -k\left(1 + \frac{m}{M}\right)x \\[10pt] a &= -\frac{k}{m}\left(1 + \frac{m}{M}\right)x \end{align}\]עיבוד לצורה סטנדרטית
\[\begin{align} a &= -\frac{k}{m} \cdot \frac{M + m}{M} \cdot x \\[10pt] a &= -\frac{k(M + m)}{mM} \cdot x \tag{2} \end{align}\]המסה המצומצמת
נגדיר את המסה המצומצמת:
\[\mu = \frac{mM}{m + M}\]אז המשוואה $(2)$ הופכת ל:
\[a = -\frac{k}{\mu}x\]או במונחים של נגזרות:
\[\frac{d^2x}{dt^2} = -\frac{k}{\mu}x\]הערה: ההצבה של $\mu$ מאפשרת לראות את התנועה ההרמונית של שתי המסות כבעיה של מסה יחידה $\mu$ המחוברת לקפיץ עם קבוע $k$. לדעתי היא לא טריוויאלית, ואני בספק אם הייתי מגיע אליה לבד.
פתרון המשוואה - תנועה הרמונית
המשוואה שקיבלנו היא משוואת תנועה הרמונית פשוטה:
\[\ddot{x} = -\omega^2 x\]כאשר:
\[\begin{align} \omega^2 &= \frac{k}{\mu} \\[10pt] &= \frac{k(m + M)}{mM} \\[10pt] \omega &= \sqrt{\frac{k(m + M)}{mM}} \end{align}\]הפתרון הכללי
\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]כאשר $A$ ו-$B$ נקבעים מתנאי ההתחלה.

תכונות התנועה
תדירות ומחזור
המהירות הזוויתית: $\omega = \sqrt{\frac{k(m + M)}{mM}}$
זמן מחזור: $T = \frac{2\pi}{\omega}$
תדירות: $f = \frac{1}{T} = \frac{\omega}{2\pi}$
זמן התנגשות
הזמן עד להתנגשות בין המסות (כאשר $x = 0$) הוא רבע מחזור:
\[t_{collision} = \frac{T}{4} = \frac{\pi}{2\omega}\]סיכום
60% מהבעיה - הבנת הסיטואציה הפיזיקלית:
- זיהוי הכוחות הפועלים
- הבנת מערכות הייחוס המואצות
- זיהוי הכוחות המדומים
30% מהבעיה - בניית משוואות התנועה:
- יישום חוק ניוטון השני
- חיבור המשוואות
10% מהבעיה - הפתרון המתמטי:
- פתרון משוואה דיפרנציאלית רגילה
- יישום תנאי התחלה
תובנה פיזיקלית
המערכת מתנהגת כמו מסה יחידה $\mu$ (המסה המצומצמת) המחוברת לקפיץ בעל קבוע $k$. זוהי תובנה חשובה שמאפשרת לנו לפתור בעיות מורכבות של שתי מסות כבעיה פשוטה יותר של מסה יחידה.
הערה: כדי לפתור באופן מלא את מיקומי שתי המסות בזמן, יש צורך לפתור גם את המשוואה עבור המסה הגדולה, מה שמצריך אינטגרציה כפולה של הפתרון שמצאנו.
מעבר לנושא חדש: קואורדינטות פולאריות
התעסקנו בבעיות וקטוריות שנוח לטפל בהן באמצעות קואורדינטות קרטזיות. היה נוח לחלק את הכוחות לציר $x$, ציר $y$, ולפרק את הבעיה התלת-ממדית לשתיים או שלוש בעיות חד-ממדיות.
אבל לא מעט פעמים נתקלים במצב שבו לבעיה יש סימטריה גלילית או כדורית. בעיה פיזיקלית עם סימטריה רדיאלית היא בעיה שבה הכל תלוי אך ורק במרחק מהראשית. כלומר, תלוי בגודל של וקטור המקום $\vec{r}$.
סימטריה רדיאלית
אם יש לנו בעיה שתלויה אך ורק במרחק מהראשית, משמעות הדבר שהכוח במקומות שבמרחק זהה מהראשית הוא זהה, כי זה אותו מרחק מהראשית. אם אני בונה מעגל, כל נקודה על פני המעגל אינה מיוחדת ביחס לאף נקודה אחרת, כי בכל נקודה הכוח תלוי רק בווקטור שמוביל מהראשית אליה.
בסיטואציות כאלה נוח מאוד לעבוד בקואורדינטות שמכבדות סימטריה רדיאלית, ולא בקואורדינטות קרטזיות שאינן מכבדות סימטריה רדיאלית.
מערכת צירים פולרית
במערכת צירים פולרית, יש לנו:
- רדיוסים בכיוונים שונים (קרניים)
- מעגלים ברדיוסים שונים
הקואורדינטות שמתארות את המערכת הזאת הן $r$ ו-$\theta$, כאשר:
- $r$ - המרחק מהראשית
- $\theta$ - הזווית שהרדיוס יוצר ביחס לציר $x$
וקטורי יחידה במערכת פולרית
נגדיר במערכת הפולארית שני וקטורי יחידה:
-
וקטור יחידה רדיאלי ($\hat{r}$):
\[\hat{r} = \cos\theta \cdot \hat{x} + \sin\theta \cdot \hat{y}\] -
וקטור יחידה אזימוטלי ($\hat{\theta}$):
\[\hat{\theta} = -\sin\theta \cdot \hat{x} + \cos\theta \cdot \hat{y}\]
שימו לב ש-$\hat{r}$ ו-$\hat{\theta}$ ניצבים זה לזה (המכפלה הסקלרית שלהם היא אפס) ושניהם וקטורי יחידה (אורכם 1).
וקטור המקום יינתן תמיד על ידי:
\[\vec{r} = r \cdot \hat{r}\]כאשר $r$ ו-$\hat{r}$ תלויים בזמן אם הגוף נע.
מהירות במערכת פולרית
מהירות היא הנגזרת של וקטור המקום לפי הזמן:
\[\vec{v} = \frac{d\vec{r}}{dt} = \dot{r}\hat{r} + r\dot{\hat{r}} \tag{1}\]מכיוון ש-$\hat{r}$ תלוי בזמן דרך $\theta(t)$, נמצא תחילה את $\dot{\hat{r}}$, כלומר, את הנגזרת של $\hat{r}$ לפי הזמן:
\[\begin{aligned} \dot{\hat{r}} &= \frac{d}{dt}(\cos\theta \cdot \hat{x} + \sin\theta \cdot \hat{y}) \\[10pt] &= (-\sin\theta \cdot \dot{\theta}) \cdot \hat{x} + (\cos\theta \cdot \dot{\theta}) \cdot \hat{y} \\[10pt] &= \dot{\theta} \cdot \hat{\theta} \end{aligned}\]נציב את $\dot{\hat{r}}$ במשוואה $(1)$ ונקבל שהמהירות היא:
\[\boxed{\vec{v} = \dot{r}\hat{r} + r\underbrace{\dot{\theta}\hat{\theta}}_{\dot{\hat{r}}}} \tag{2}\]יש לנו כאן שני רכיבים של המהירות:
- מהירות רדיאלית - $\dot{r}\hat{r}$ - המהירות בכיוון הרדיאלי
- מהירות משיקית - $r\dot{\theta}\hat{\theta}$ - המהירות בכיוון המשיק למעגל
זה מזכיר את מה שחלק אולי למדו בשיעורי פיזיקה בתיכון: $v = r\omega$ (כאשר $\omega = \dot{\theta}$ היא המהירות הזוויתית).
תאוצה במערכת פולרית
התאוצה היא הנגזרת של המהירות לפי הזמן:
\[\vec{a} = \frac{d\vec{v}}{dt} = \frac{d}{dt}(\dot{r}\hat{r} + r\dot{\theta}\hat{\theta})\]פתיחת הנגזרת לפי כלל המכפלה:
\[\vec{a} = \ddot{r}\hat{r} + \dot{r}\dot{\hat{r}} + \dot{r}\dot{\theta}\hat{\theta} + r\ddot{\theta}\hat{\theta} + r\dot{\theta}\dot{\hat{\theta}}\]מצאנו כבר ש-$\dot{\hat{r}} = \dot{\theta}\hat{\theta}$. נחשב גם את $\dot{\hat{\theta}}$:
\[\begin{aligned} \dot{\hat{\theta}} &= \frac{d}{dt}(-\sin\theta \cdot \hat{x} + \cos\theta \cdot \hat{y}) \\[10pt] &= (-\cos\theta \cdot \dot{\theta}) \cdot \hat{x} + (-\sin\theta \cdot \dot{\theta}) \cdot \hat{y} \\[10pt] &= -\dot{\theta} \cdot \hat{r} \end{aligned}\]לכן, התאוצה היא:
\[\boxed{\vec{a} = \underbrace{(\ddot{r} - r\dot{\theta}^2)\hat{r}}_{a_r} + \underbrace{(r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}}_{a_{\theta}}} \tag{3}\]משוואה $(3)$ היא ביטוי כללי לתאוצה במערכת קואורדינטות פולאריות. היא מורכבת משני רכיבים:
- תאוצה רדיאלית - התאוצה בכיוון הרדיאלי: $a_r = (\ddot{r} - r\dot{\theta}^2)\hat{r}$
- תאוצה משיקית - התאוצה בכיוון המשיקי (האזימוטלי): $a_\theta = (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}$
התאוצה בכיוון הרדיאלי משלבת בתוכה גם את הנגזרת של $\theta$ לפי הזמן וגם את הנגזרת של $r$ לפי הזמן.
נסכם את הביטויים שפיתחנו:
- וקטור המקום: $\vec{r} = r\hat{r}$
- וקטור המהירות: $\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta} = v_r\hat{r} + v_{\theta}\hat{\theta}$
- וקטור התאוצה: $\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta} = a_r\hat{r} + a_{\theta}\hat{\theta}$
יישום למקרה של תנועה מעגלית
רציתי לפתור את הבעיה של המטוטלת עם הקואורדינטות האלו, כי הן קואורדינטות מאוד נוחות. המטוטלת מבצעת תנודה שקל לתאר בקואורדינטות פולאריות. אבל היות ולא אספיק בשש או שבע הדקות שנשארו, אני רק אומר לכם שזה מחזיר אותנו פחות או יותר לשיעור הראשון או השני כשלמדנו על תנועה מעגלית.
כזכור, שכשלמדנו תנועה מעגלית (שיעור 3), ראינו שווקטור המקום היה שווה ל:
\[\vec{r} = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}\]אבל $\cos(\omega t)\hat{x} + \sin(\omega t)\hat{y}$ זה פשוט $\hat{r}$. כלומר, בתנועה מעגלית וקטור המקום תמיד מצביע לעבר נקודה על המעגל. גודלו $R$ לא משתנה עם הזמן, וכיוונו $\hat{r}$.
כזכור, וקטור המהירות בתנועה מעגלית קצובה היה שווה ל:
\[\vec{v} = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}\]וזה שווה, כפי שאתם מבינים, ל:
\[\vec{v} = \omega R\hat{\theta}\]משום ש-$-\sin(\omega t)\hat{x} + \cos(\omega t)\hat{y}$ זה $\hat{\theta}$. זהו וקטור המהירות בתנועה מעגלית.
וקטור התאוצה בתנועה מעגלית היה שווה ל:
\[\vec{a} = -\omega^2 R\hat{r}\]שימו לב, כשהרדיוס $R$ קבוע, $\dot{r}$ מתאפס, $\ddot{r}$ מתאפס, ואם גם $\dot{\theta}$ קבוע (כלומר $\ddot{\theta}=0$), מקבלים:
\[\vec{a} = -R\omega^2\hat{r}\]סיכום: תיאור אלגנטי של תנועה מעגלית בקואורדינטות פולאריות
בתיאור הכי יפה, אלגנטי וכללי שמכבד את העובדה שאנחנו נעים על פני מעגל:
- וקטור המקום שלי הוא $\vec{r} = R\hat{r}$ (פונקציה של $t$)
- וקטור המהירות שלי הוא $\vec{v} = R\omega\hat{\theta}$ - זאת המהירות המשיקית
- וקטור התאוצה שווה ל-$\vec{a} = -\omega^2 R\hat{r}$ - זאת התאוצה הצנטריפטלית
והכוח שווה למסה כפול התאוצה, כלומר הכוח הוא רדיאלי (מופנה לכיוון מרכז המעגל).

נראה שתיארנו את הבעיה מכל היבט שאפשר להעלות על הדעת:
- מיהו וקטור המקום כפונקציה של הזמן
- מיהו וקטור המהירות כפונקציה של הזמן, כגודל וככיוון
- מיהו וקטור התאוצה כפונקציה של הזמן, בייחס לוקטור המקום
- התאוצה בכיוון מינוס וקטור המקום - תאוצה צנטריפטלית
- שקול הכוחות שווה למסה כפול תאוצה
הכל נמצא בתיאור הזה. תיאור בפיזיקה סובב סביב תיאור המציאות כפי שהיא מתפתחת בזמן. כל הגדלים תלויים ב-$t$ - זהו תיאור מושלם (לשימושים שלנו).
שיעור 9 - המטוטלת המתמטית
תאריך: 19/05/2025חלק א: וקטורים בקואורדינטות גליליות
בשיעור הקודם סיימנו עם וקטורי המקום, המהירות והתאוצה בקואורדינטות גליליות.
נזכיר את הביטויים שפיתחנו:
וקטור המקום:
\[\vec{r} = r \hat{r}\]וקטור המהירות:
\[\vec{v} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta}\]וקטור התאוצה:
\[\vec{a} = (\ddot{r} - r \dot{\theta}^2) \hat{r} + (r \ddot{\theta} + 2\dot{r}\dot{\theta}) \hat{\theta}\]הביטויים האלו מבטאים את וקטור המקום, המהירות והתאוצה של גוף שנע במישור, כאשר מבטאים אותם בקואורדינטות גליליות (פולאריות).
מה הן קואורדינטות גליליות?
קואורדינטות גליליות (פולאריות) מורכבות מ:
- מעגלים קונצנטריים
- קרניים היוצאות מהמרכז
הקרניים הן הקואורדינטות הרדיאליות, והפריסה של הקרן מציר ה-x היא הקואורדינטה הזוויתית.
אם אני נמצא בנקודה מסוימת במישור, אני יכול לפרוש שני וקטורי יחידה:
- $\hat{r}$ - וקטור יחידה בכיוון הרדיאלי
- $\hat{\theta}$ - וקטור יחידה בכיוון המשיק למעגל (ניצב לכיוון הרדיאלי)
וקטורי היחידה האלו תלויים בזמן, מכיוון שהגוף מבצע תנועה כלשהי במישור. כלומר, בכל נקודה במסלול, המישור נפרס על ידי שני וקטורי יחידה שתלויים במקום (וכתוצאה מכך בזמן).
מקרה פרטי: תנועה מעגלית קצובה
במקרה של תנועה מעגלית קצובה:
- $r = \text{constant}$ (כלומר $\dot{r} = 0$)
- $\dot{\theta} = \omega = \text{constant}$ (כלומר $\ddot{\theta} = 0$)
מכאן נקבל:
\[\vec{v} = r\omega \hat{\theta}\] \[\vec{a} = -r\omega^2 \hat{r} = -\omega^2 r \hat{r}\]כלומר, התאוצה בתנועה מעגלית קצובה היא תמיד לכיוון מרכז המעגל.
חלק ב: המטוטלת המתמטית
עכשיו ניקח דוגמה מהחיים האמיתיים ונתאר את תנועת המטוטלת באמצעות קואורדינטות פולאריות.
מה היא מטוטלת מתמטית?
מטוטלת מתמטית היא מודל פשוט שבו:
- יש חוט מתוח שתלוי מתקרה
- בקצה החוט יש מסה נקודתית $m$
- אורך החוט הוא $L$
- החוט תמיד נשאר מתוח
כאשר מושכים את המטוטלת לזווית מסוימת $\theta$ ומשחררים, היא מתחילה להתנדנד בצורה שבה החוט נשאר מתוח.
מדוע להשתמש בקואורדינטות פולאריות?
המטוטלת היא דוגמה קלאסית למערכת עם סימטריה פולרית:
- הרדיוס של התנועה קבוע (אורך החוט $L$)
- מספיק לדעת את הזווית $\theta$ כדי לתאר את מיקום המסה במלואו
אם היינו משתמשים בקואורדינטות קרטזיות, היינו צריכים לטפל בשני משתנים ($x$ ו-$y$), והביטויים היו מסובכים יותר. בנוסף, המערכת הייתה מאיצה גם בכיוון $x$ וגם בכיוון $y$.
מטוטלת פיזיקלית לעומת מטוטלת מתמטית
בחיים האמיתיים אין מטוטלות מתמטיות, אלא מטוטלות פיזיקליות:
- המסה אינה נקודתית
- לחוט יש מסה
- יכולות להיות דרגות חופש נוספות (כמו סיבוב הגוף סביב מרכז הכובד שלו)
- יכול להיות איבוד אנרגיה
מטוטלת פיזיקלית היא מערכת מורכבת יותר עם מספר דרגות חופש.
דרגות חופש
דרגת חופש היא משתנה בלתי תלוי שחוקי הפיזיקה מכתיבים את התפתחותו בזמן.
- מטוטלת מתמטית פשוטה: דרגת חופש אחת (הזווית $\theta$)
- מטוטלת כפולה: שתי דרגות חופש (שתי זוויות, $\theta$ ו-$\phi$)
- בעיה בתלת-מימד: שלוש דרגות חופש ($x(t)$, $y(t)$, $z(t)$)
חלק ג: ניתוח המטוטלת המתמטית
אפיון המערכת
ראשית, נזהה את הפרמטרים של הבעיה:
- מסת המטוטלת $m$
- אורך החוט $L$
- תאוצת הכבידה $g$
נשתמש בקואורדינטות פולאריות עם הזווית $\theta(t)$ כמשתנה שמתאר את מצב המערכת.
הכוחות במערכת
יש שני כוחות שפועלים על המסה:
- כוח המשיכה $mg$ שפועל כלפי מטה (בכיוון שלילי של ציר $y$)
- מתיחות החוט $T$ שפועלת לאורך החוט (בכיוון $-\hat{r}$)
כדי לבנות את משוואות התנועה בקואורדינטות פולאריות, נפרק את כוח הכבידה למרכיבים בכיוונים הרדיאלי והמשיקי:
- המרכיב הרדיאלי: $mg\cos\theta$ בכיוון $\hat{r}$
- המרכיב המשיקי: $mg\sin\theta$ בכיוון $\hat{\theta}$
משוואות התנועה
נשתמש בחוק השני של ניוטון: $\vec{F} = m\vec{a}$
בכיוון הרדיאלי:
\[\begin{aligned} T &= m(r\dot{\theta}^2 + g\cos\theta) \\[10pt] -mr\dot{\theta}^2 &= mg\cos\theta - T \end{aligned}\]מכיוון שבמטוטלת מתמטית הרדיוס קבוע ($r = L$), נוכל לכתוב:
\[-mL\dot{\theta}^2 = mg\cos\theta - T\]בכיוון המשיקי (הזוויתי):
\[mL\ddot{\theta} = -mg\sin\theta\]או:
\[\ddot{\theta} = -\frac{g}{L}\sin\theta\]זאת משוואת התנועה של המטוטלת המתמטית. מדובר במשוואה דיפרנציאלית לא לינארית מסדר שני, שאין לה פתרון אנליטי מדויק במקרה הכללי.
תזכורת מפיזיקה בתיכון
בתיכון למדנו:
\[mr\omega^2 = T - mg\cos\theta\]כאשר $r$ במקרה שלנו הוא $L$ (אורך המטוטלת). קראנו לביטוי $mr\omega^2$ התאוצה הצנטריפטלית $a_c$.
נזכור ש:
\[ma_c = \sum F_{\text{radial}}\]התאוצה הצנטריפטלית שקשורה בתנועה המעגלית שווה לשקול הכוחות בכיוון הרדיאלי. זה מה שלמדנו בתיכון.
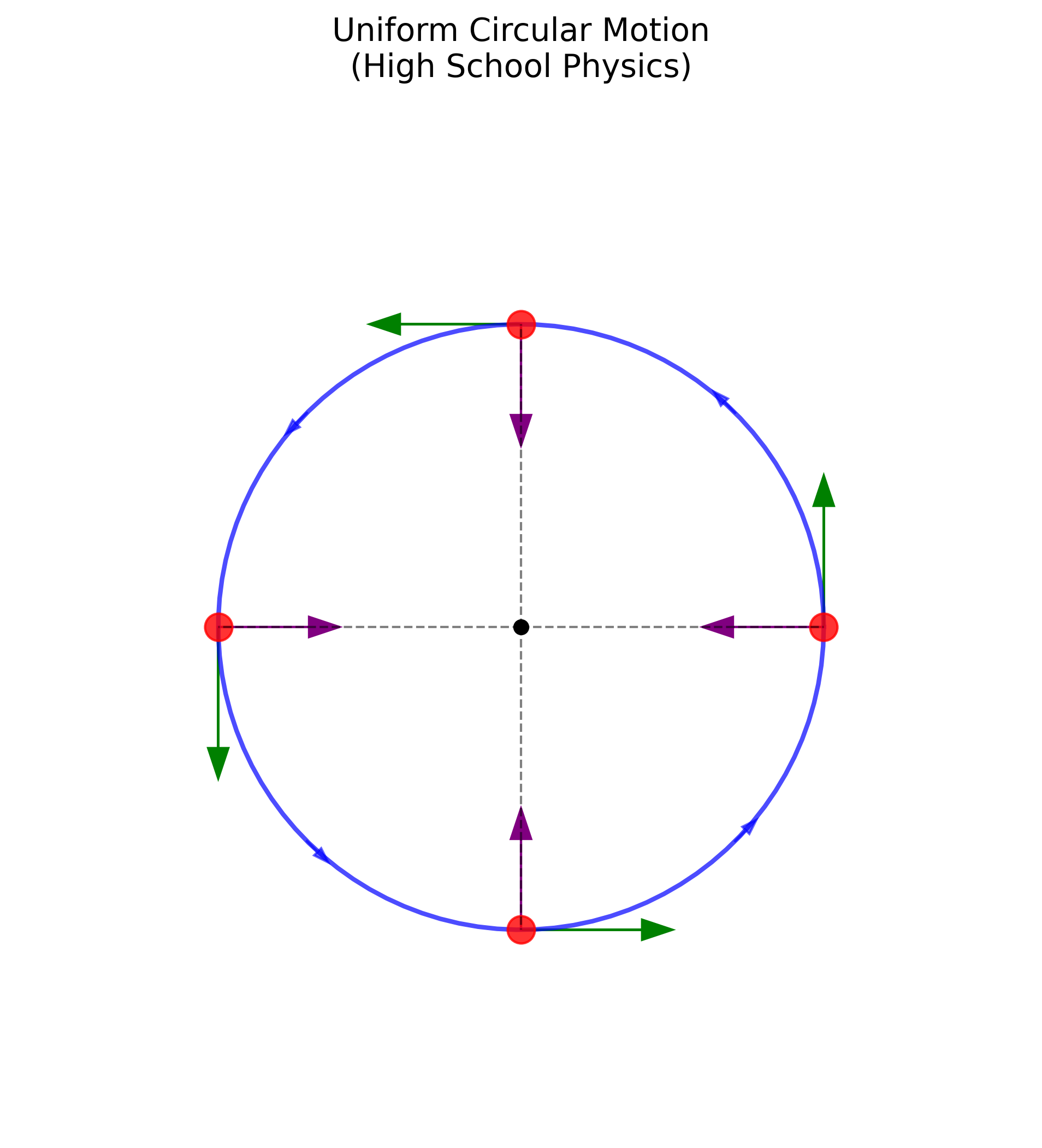
הבנה מעמיקה של התנועה המעגלית
הביטוי שלנו יותר אלגנטי ונותן ראייה רחבה יותר של המציאות. חשוב לשים לב:
- בתיכון קראנו למהירות הזוויתית $\omega$ והתייחסנו אליה כקבועה (בתנועה מעגלית קצובה).
- אך במטוטלת, $\omega$ (או $\dot{\theta}$) תלויה בזמן - עובדה שבתיכון התעלמו ממנה.
- התאוצה הרדיאלית היא למעשה פונקציה של הזמן כי המהירות הזוויתית משתנה.
לכן, יותר הגיוני להסתכל על התאוצה הרדיאלית (או צנטריפטלית) כך:
\[a_r = r\dot{\theta}^2\]ומשוואת התנועה בכיוון הרדיאלי:
\[ma_r = T - mg\cos\theta\]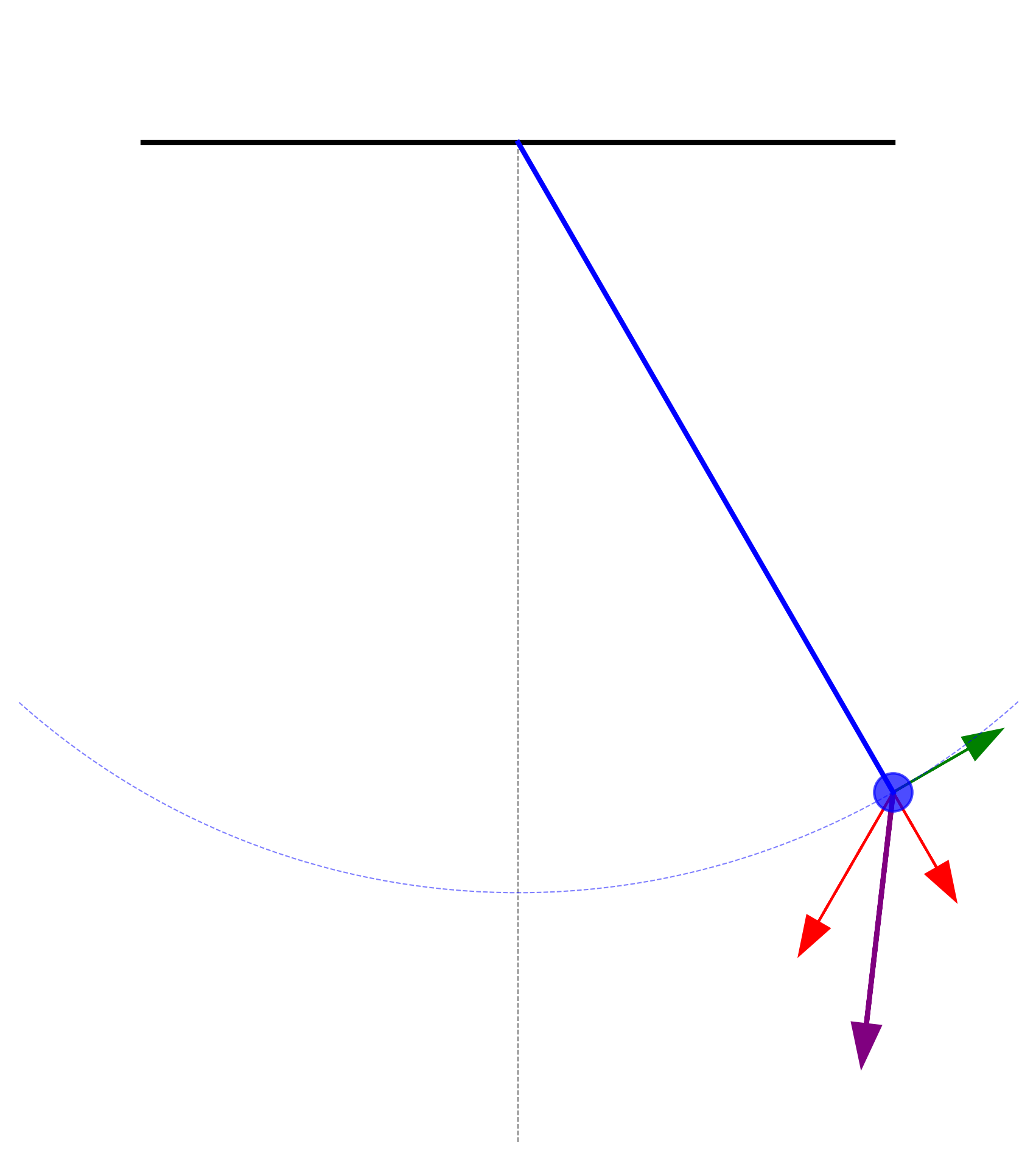
המתיחות בחוט
חשוב להבין שהמתיחות בחוט היא לא קבועה! טעות שעושים תלמידי תיכון היא לחשוב ש:
\[T = mg\cos\theta\]זו טעות! החוק הראשון של ניוטון ($\sum F = 0, \text{when no a}$) אינו תקף כאן כי יש תנועה מעגלית. החוק השני תקף ($\sum F = ma$), ולכן המתיחות תלויה גם במהירות הזוויתית של המטוטלת ($\dot{\theta}$).
\[\begin{aligned} T &= ma_r + mg\cos\theta \\[10pt] &= mr\dot{\theta}^2 + mg\cos\theta \end{aligned}\]כלומר, המתיחות בחוט מורכבת משני מרכיבים:
- $mr\dot{\theta}^2$ - הכוח הצנטריפטלי הנדרש לשמירה על התנועה המעגלית
- $mg\cos\theta$ - איזון מרכיב הכבידה בכיוון הרדיאלי (שפועל החוצה)
תלמידי תיכון מפספסים את המרכיב הראשון ולא מבינים שגם בתנועה מעגלית במהירות קבועה יש תאוצה צנטריפטלית ($a_r = r\dot{\theta}^2$) שדורשת כוח צנטריפטלי.
נקודות מיוחדות במסלול המטוטלת
- בנקודה התחתונה ($\theta = 0$): המתיחות היא מקסימלית כי:
- $\cos(0) = 1$ - מרכיב הכבידה מקסימלי
- $\dot{\theta}$ מקסימלי - התאוצה הצנטריפטלית מקסימלית
- בנקודות הקיצוניות של התנועה: המהירות הזוויתית $\dot{\theta} = 0$, ולכן התאוצה הצנטריפטלית מתאפסת, והמתיחות קטנה יותר.
משוואות התנועה של המטוטלת
לסיכום, שתי המשוואות שמתארות את תנועת המטוטלת הן:
-
בכיוון הרדיאלי:
\[ma_r = T - mg\cos\theta\] -
בכיוון הזוויתי (טנגנציאלי):
\[mL\ddot{\theta} = -mg\sin\theta\]
המשוואה השנייה היא המשוואה החשובה לתיאור התנועה. נוכל לכתוב אותה בצורה:
\[\ddot{\theta} = -\frac{g}{L}\sin\theta\]נסמן $\omega_0^2 = \frac{g}{L}$ ונקבל:
\[\boxed{\ddot{\theta} = -\omega_0^2\sin\theta} \tag{1}\]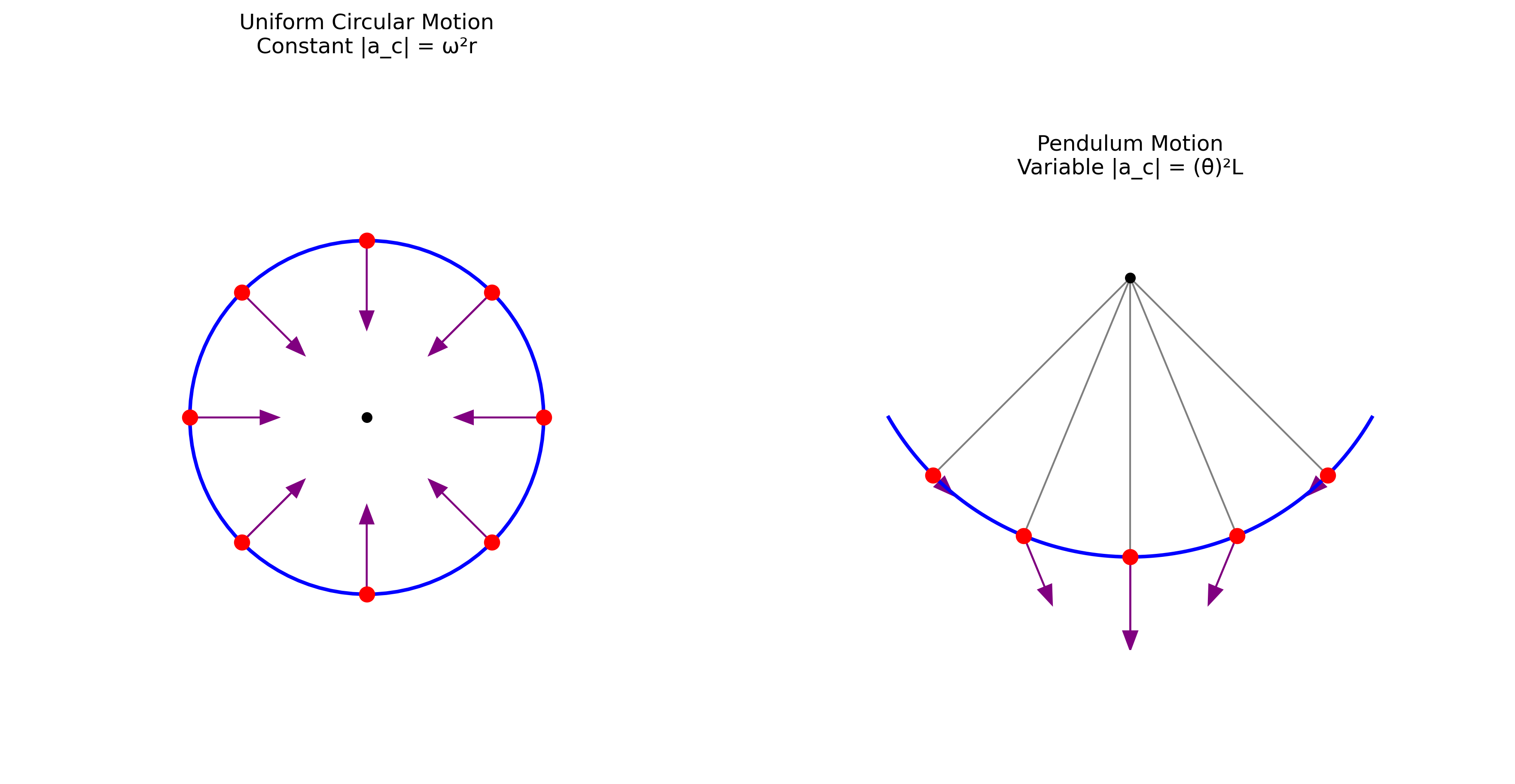
פתרון משוואת המטוטלת
משוואה $(1)$ היא משוואה דיפרנציאלית אליפטית שאין לה פתרון אנליטי מדויק. אפשר לפתור אותה:
- בשיטות נומריות
- בקירוב לזוויות קטנות
קירוב לזוויות קטנות
לזוויות קטנות, נוכל לפתח את $\sin\theta$ בטור טיילור:
\[\sin\theta \approx \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \ldots\]אם נתעלם מכל האיברים מלבד הראשון, נקבל פתרון מקורב למשוואה $(1)$:
\[\ddot{\theta} \approx -\omega_0^2\theta\]זוהי משוואת התנודד ההרמוני הפשוט, שהפתרון שלה הוא:
\[\theta(t) = C\cos(\omega_0 t + \phi) \tag{2}\]כאשר $C$ ו-$\phi$ הם קבועים שנקבעים על ידי תנאי ההתחלה.
פתרון עם תנאי התחלה
נניח שיש לנו:
- $\theta(t=0) = \theta_0$ (זווית התחלתית)
- $\dot{\theta}(t=0) = \alpha$ (מהירות זוויתית התחלתית)
אז נוכל לפתח את משוואה $(2)$. תחילה נגזור אותה (כדי להיעזר במהירות הזוויתית ההתחלתית שנתונה לנו).
\[\theta(t) = C\cos(\omega_0 t + \phi)\] \[\implies \dot{\theta}(t) = -\omega_0 C\sin(\omega_0 t + \phi)\]נציב את תנאי ההתחלה:
\[\theta_0 = C\cos\phi\] \[\alpha = -\omega_0 C\sin\phi\]מחלוקת המשוואה השנייה בראשונה:
\[\frac{\alpha}{\theta_0} = -\omega_0\tan\phi\]ומכאן:
\[\phi = \arctan\left(-\frac{\alpha}{\omega_0\theta_0}\right)\]במקרה המיוחד שבו $\alpha = 0$ (מהירות התחלתית אפס), מקבלים $\phi = 0$, ולכן:
\[\boxed{\theta(t) = \theta_0\cos(\omega_0 t)}\]זו תנועה הרמונית פשוטה עם אמפליטודה $\theta_0$: המטוטלת מתנודדת בין $\theta_0$ ל-$-\theta_0$ סביב מצב שיווי המשקל $\theta = 0$.
הפתרון הכללי עם תנאי התחלה שונים
הפתרון שקיבלנו קודם ($\theta(t) = \theta_0\cos(\omega_0 t)$) תקף רק למקרה שבו המהירות הזוויתית ההתחלתית היא אפס ($\alpha = 0$).
במבחן כמובן, לא אשאל תמיד על המקרה הפרטי הזה. אוכל למשל לשאול על מצב שבו מושכים את המטוטלת למטה ($\theta_0 = 0$) ונותנים לה “קיק” (דחיפה) התחלתי, כלומר $\alpha \neq 0$.
הפתרון הכללי של משוואת המטוטלת (בקירוב לזוויות קטנות) הוא:
\[\theta(t) = C\cos(\omega_0 t + \phi)\]כאשר:
- $C = \sqrt{\theta_0^2 + \frac{\alpha^2}{\omega_0^2}}$ (האמפליטודה)
- $\phi = \arctan\left(-\frac{\alpha}{\omega_0\theta_0}\right)$ (הפאזה)
- $\omega_0 = \sqrt{\frac{g}{L}}$ (התדירות הזוויתית הטבעית)
מקרה מיוחד: $\theta_0 = 0$ ו-$\alpha \neq 0$
במקרה שבו מתחילים בתחתית ($\theta_0 = 0$) עם מהירות זוויתית התחלתית $\alpha$:
- $\phi = \arctan\left(-\frac{\alpha}{0}\right) = -\frac{\pi}{2}$ (כי טנגנס של $\frac{\pi}{2}$ הוא אינסוף)
- $C = \frac{\alpha}{\omega_0}$
ולכן הפתרון הוא:
\[\theta(t) = -\frac{\alpha}{\omega_0}\sin(\omega_0 t)\]שכן $\cos(\omega_0 t - \frac{\pi}{2}) = \sin(\omega_0 t)$
תקופת התנודות של המטוטלת
זמן המחזור של המטוטלת הוא הזמן שלוקח לה להשלים תנודה שלמה ולחזור לאותו מצב. כאשר:
\[\omega_0 T = 2\pi\]ולכן:
\[T = \frac{2\pi}{\omega_0} = 2\pi\sqrt{\frac{L}{g}}\]ככל שהחוט ארוך יותר, זמן המחזור ארוך יותר.
המהירות בנקודות מיוחדות במסלול
המהירות בתחתית המסלול (רבע זמן מחזור)
ברבע זמן מחזור ($t = \frac{T}{4} = \frac{\pi}{2\omega_0}$), המהירות הזוויתית היא:
\[\begin{aligned} \dot{\theta} &= -\omega_0\theta_0\sin(\omega_0 t) \\[10pt] &= -\omega_0\theta_0\sin\left(\frac{\pi}{2}\right) \\[10pt] &= -\omega_0\theta_0 \end{aligned}\]זו המהירות הזוויתית המקסימלית (בערך מוחלט), כי $\sin(\frac{\pi}{2}) = 1$.
המהירות בנקודות אחרות
- בשמינית זמן מחזור ($t = \frac{T}{8}$): המהירות היא פחות מהמקסימום
- בשלושת רבעי זמן מחזור ($t = \frac{3T}{4}$): המהירות זהה בגודלה למהירות ברבע זמן מחזור, אך בכיוון ההפוך
הקשר בין המהירות הזוויתית והמהירות המשיקית
בתנועה מעגלית, אנו יודעים ש:
- אורך הקשת: $s = L\theta$
- המהירות המשיקית: $v_\theta = L\dot{\theta}$
- התאוצה המשיקית: $a_\theta = L\ddot{\theta}$
נתייחס לתכונה משיקית (tangential) בעזרת הסימונים הבאים:
\[a_T = a_\parallel = a_{\theta}\]
במקרה של המטוטלת המתמטית כאשר $\theta(t) = \theta_0\cos(\omega_0 t)$:
- $v_\theta = -L\omega_0\theta_0\sin(\omega_0 t)$
- $a_\theta = -L\omega_0^2\theta_0\cos(\omega_0 t)$
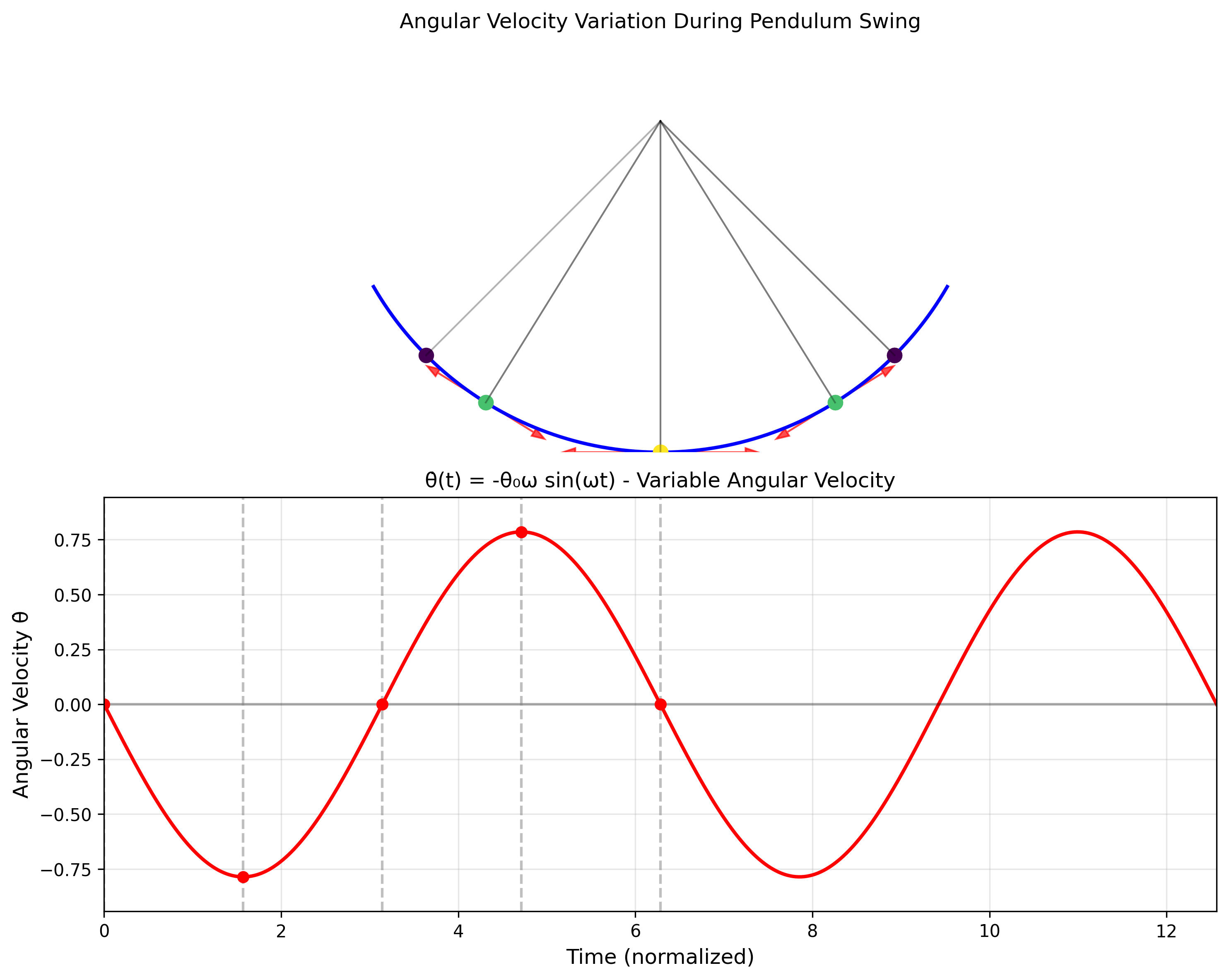
התאוצה הצנטריפטלית והמתיחות בחוט
משוואת התנועה בכיוון הרדיאלי:
\[T - mg\cos\theta = m\frac{v_\theta^2}{L}\]או:
\[T = mg\cos\theta + m\frac{v_\theta^2}{L}\]בנקודות קיצוניות של התנועה
- בנקודות הקיצוניות (כאשר $\theta = \theta_0$ או $\theta = -\theta_0$):
- $v_\theta = 0$ (המהירות המשיקית מתאפסת)
- $a_{\text{צנטריפטלית}} = \frac{v_\theta^2}{L} = 0$ (התאוצה הצנטריפטלית מתאפסת)
- $T = mg\cos\theta_0$ (המתיחות בחוט היא הקטנה ביותר)
- בתחתית המסלול (כאשר $\theta = 0$):
- $v_\theta = L\omega_0\theta_0$ (המהירות המשיקית מקסימלית)
- $a_{\text{צנטריפטלית}} = \frac{v_\theta^2}{L} = L\omega_0^2\theta_0^2$ (התאוצה הצנטריפטלית מקסימלית)
- $T = mg + mL\omega_0^2\theta_0^2$ (המתיחות בחוט היא הגדולה ביותר)
בנקודות ביניים במסלול, וקטור התאוצה הכולל אינו מכוון אל מרכז המעגל ואינו בכיוון המשיק בלבד, אלא יש לו מרכיב בשני הכיוונים.
שיעור תגבור - קוארדינטות פולריות, מסות תלויות וגליל מסתובב
תאריך: 25/05/2025פתרון שאלה 3 משיעורי הבית
שתי מסות זהות:
\[m_1 = m_2 = 99_{grams} = 0.099_{kg}\]קשורות בחוט הכרוך על גלגלת שצירה מקובע בגובה רב מעל הרצפה.
בתחילה המסות נמצאות במנוחה בגובה זהה מעל הרצפה.
זבוב שמסתו \(m = 2_{grams} = 0.002_{kg}\) נוחת בעדינות על מסה \(m_1\) (נניח, זו הימנית).
לאחר שתי שניות מתעופף לו הזבוב, ולאחר שתי שניות נוספות הוא נוחת בעדינות על מסה $m_2$ השמאלית.
הנחות: מסת החוט, מסת הגלגלת, והחיכוך ביניהם ניתנים להזנחה.
דיאגרמה בזמן נחיתת הזבוב
ציירו את המערכת בזמן $t = 0$, זמן נחיתת הזבוב על $m_1$, הוסיפו על הציור סקיצה של וקטורי המהירות והתאוצה של שתי המסות (אין צורך בחישוב).
תיאור תנועת $m_2$
תארו מילולית את תנועת המסה $m_2$ (תנועה קצובה, תאוצה קבועה, תאוצה משתנה, כיווני תנועה ותאוצה) בכל אחד משלושת פרקי הזמן:
- א) $0 \leq t < 2s$
- ב) $2s \leq t < 4s$
- ג) $t \geq 4s$
חישוב התאוצה
חשבו את התאוצה של $m_2$ בכל אחד מפרקי הזמן:
- א) $0 \leq t < 2s$
- ב) $2s \leq t < 4s$
- ג) $t \geq 4s$
כתבו את המהירות כפונקציה של הזמן של המסה $m_2$ עבור עשר השניות הראשונות של התנועה. השתמשו באותו פרמטר זמן $t$ לכל שלבי התנועה.
גרף מהירות
ציירו גרף כמותי של מהירות $m_2$ עבור עשר השניות הראשונות של התנועה.
קבלו את ההעתק הכולל של המסה $m_2$ בעשר השניות הראשונות לתנועה מבלי להיעזר במשוואות מקום-זמן.
1. דיאגרמה בזמן נחיתת הזבוב
| לפני הזבוב | הזבוב מגיע |
2. תיאור תנועת $m_2$
(א) $0 \leq t < 2s$
$m_2$ מאיצה מעלה בתאוצה קבועה ממהירות התחלתית 0.
(ב) $2s \leq t < 4s$
המערכת נמצאת בהתמדה, כלומר שקול הכוחות הפועלים עליה שווה לאפס. $m_2$ מתמידה במהירותה כלפי מעלה (החוק הראשון של ניוטון).
(ג) $t \geq 4s$
התאוצה מחליפה כיוון $-a$, כלומר שהיא בכיוון מנוגד למהירות. מצב כזה (תאוצה בכיוון מנוגד למהירות) נקרא תאוטה. בשלב מסוים יתהפך כיוון המהירות.
3. חישוב התאוצה של $m_2$
(א) $0 \leq t < 2s$
ניעזר בכל השני של ניוטון ($F = ma$). תחילה נרשום את המשוואות שפועלים על כל אחת מהמסות.
על המסה הימנית (שהזבוב נוחת עליה) - היא נעה כלפי מטה:
\[(M+m)g - T = (M+m)a \tag{1}\]על המסה השמאלית (שלא נוחת עליה הזבוב) - היא נעה כלפי מעלה:
\[T - Mg = Ma \tag{2}\]שימו לב שהכוח $T$ הוא מתיחה בחוט, והוא פועל על המסה השמאלית כלפי מעלה, ועל המסה הימנית כלפי מטה, בדומה לכוח המשיכה. מכאן ההבדל בסימנים.
נחבר את משוואות $(1)$ ו$(2)$:
\[\begin{aligned} (M+m)g - T + T - Mg &= (M+m)a + Ma \\ \cancel{Mg} + mg - \cancel{Mg} &= 2Ma + ma \\ mg &= (2M + m)a \\ a &= \frac{mg}{2M + m} \end{aligned}\]סכך הכך:
\[a = \frac{mg}{2M + m} \tag{3}\]נציב את הערכים הנתונים במשוואת התאוצה $(3)$:
\[a = \frac{0.002 \cdot 10}{0.2} = \frac{0.02}{0.2} = 0.1 \, \mathrm{m/s^2}\]סך הכל התאוצה בזמן $0 \leq t < 2s$ היא:
\[\boxed{a_{0 \leq t < 2s} = 0.1 \, \mathrm{m/s^2}}\](ב) $2s \leq t < 4s$
כאמור, בשלב הזה המערכת מתמידה. התאוצה של המסה $m_2$ היא אפס, כלומר:
\[\boxed{a_{2s \leq t < 4s} = 0 \, \mathrm{m/s^2}}\](ג) $t \geq 4s$
זה מצב סימטרי אבל עם כיוון הפוך:
\[\boxed{a_{t \geq 4s} = -0.1 \, \mathrm{m/s^2}}\]4. כתיבת המהירות כפונקציה של הזמן
אפשר להשתמש בנוסחה:
\[\boxed{v(t) = v_0 + at}\]במקרה שלנו, $v_0 = 0$ (מהירות התחלתית) ו-$a$ הוא התאוצה של המסה $m_2$ בכל אחד מהשלבים.
\[v(t) = \begin{cases} 0.1t & 0 \leq t < 2s \\ 0.2 & 2s \leq t < 4s \\ 0.2 - 0.1(t-4) & t \geq 4s \end{cases}\]אפשר גם לחשב את המהירות על ידי אינטגרציה של התאוצה $a$ לפי הזמן, כלומר:
לשלמות התמונה נכתוב את וקטור המקום כפונקציה של הזמן עבור כל אחד מהשלבים.
כאשר גוף נע בתאוצה קבועה:
\[x(t) = \cancel{x_0} + \cancel{v_0} t + \frac{1}{2}at^2 \tag{6}\]האיברים הראשונים מתבטלים מתנאי ההתחלה $x_0 = 0$ ו-$v_0 = 0$, כלומר:
\[\begin{cases} a &= 0.1 \\ v_0 &= 0 \\ \end{cases}\]נציב את הביטוי המלא של התאוצה $a$:
\[\begin{align} x(0 \leq t < 2s) &= \frac{mg}{2(2M+m) }t^2 \\ &= \frac{0.002 \cdot 10}{0.4} t^2 \\ &= \frac{0.02}{0.4} t^2 \\ &= 0.05 t^2 \tag{6} \end{align}\]ובקצרה:
\[\frac{1}{2}at^2 = \frac{1}{2} \cdot 0.1 \cdot t^2 = 0.05t^2\]הנוסחה $(6)$ נובעת מאינטגרציה של התאוצה $a$ לפי הזמן, כלומר, ולאחר מכן אינטגרציה של המהירות $v$ לפי הזמן. הצבה של תנאי ההתחלה מבטלת את האיברים הקבועים.
\[v(t) = \int a(t) dt = \int 0.1 dt = 0.1t + C\]כאשר $C$ הוא קבוע האינטגרציה, שמתקבל מתנאי ההתחלה $v(0) = 0$.
5. גרף מהירות
גרף ליניארי למקוטעין:
- עולה מ-0 ל-0.2 m/s בין $t=0$ ל-$t=2s$
- קבוע ב-0.2 m/s בין $t=2s$ ל-$t=4s$
- יורד מ-0.2 ל-(-0.4) m/s בין $t=4s$ ל-$t=10s$

6. קבלת ההעתק הכולל של המסה $m_2$
ההעתק הוא השטח מתחת לגרף מהירות-זמן:
- משולש: $\frac{1}{2} \times 2 \times 0.2 = 0.2$ m
- מלבן: $2 \times 0.2 = 0.4$ m
- טרפז: $\frac{1}{2} \times 6 \times (0.2 - 0.4) = -0.6$ m
סה”כ: $0.2 + 0.4 - 0.6 = 0 \, \mathrm{m}$
המערכת חוזרת למצבה ההתחלתי!
גליל מסתובב עם מסה (גולה) נופלת
הערה מקדימה: השאלה הצוגה במקור בשיעור התגבור עבורו מוקדש העמוד, אבל בהמשך הופיעה בבחינת הגמר של מועד א׳ 2025.
נוסח השאלה, כמו גם הפתרונות, היו שונים. להלן הגרסה האחרונה של השאלה כפי שהופיעה במבחן. ההבדל המהותי היה שבשיעור התגבור המרצה התייחס לתאוצה הכבידה, וקבע את מערכת הצירים באופן שונה.
גליל מסתובב עם כוח צנטריפוגלי בלבד
ניסוח הבעיה
גליל אופקי באורך $L$ מסתובב נגד כיוון השעון במהירות זוויתית קבועה $\omega$. מסה $m$ מתחילה במרכז הגליל (במיקום $r = L/2$) ממצב מנוחה, ונעה תחת השפעת הכוח הצנטריפוגלי בלבד.
נתונים:
תנאי התחלה:
- $r(t=0) = \frac{L}{2}$ (מיקום התחלתי במרכז הגליל)
- $\dot{r}(t=0) = 0$ (מהירות רדיאלי התחלתי אפס - ממנוחה)
הפרמטרים של המערכת:
- $\omega$ = מהירות זוויתית קבועה של הגליל
- $L$ = אורך הגליל
- $m$ = מסת הגוף
מטרה: למצוא את התנועה $r(t)$ של המסה והזמן ($t$) שבו היא מגיעה לקצה הגליל ($r = L$).
שלב 1: יישום חוק ניוטון השני במערכת ייחוס מסתובבת
במערכת ייחוס מסתובבת עם מהירות זוויתית קבועה $\omega$, הכוח הצנטריפוגלי פועל על מסה הנמצאת במרחק $r$ מהמרכז:
\[\mathbf{F}_{\text{centrifugal}} = m\omega^2 r\]הכוח מכוון החוצה ברכיב הרדיאלי $\hat{r}$.
שלב 2: משוואת התנועה
יישום החוק השני של ניוטון בכיוון הרדיאלי:
\[m\ddot{r} = m\omega^2 r\]המסה מצטמצמת:
\[\ddot{r} = \omega^2 r \tag{1}\]שלב 3: פתרון המשוואה הדיפרנציאלית
משוואה (1) היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני עם מקדמים קבועים.
המשוואה האופיינית:
\[\lambda^2 = \omega^2\]הפתרונות: $\lambda = \pm\omega$
הפתרון הכללי:
\[r(t) = A e^{\omega t} + B e^{-\omega t}\]או בצורה היפרבולית שקולה:
\[r(t) = C \cosh(\omega t) + D \sinh(\omega t) \tag{2}\]שלב 4: יישום תנאי התחלה
תנאי התחלה:
- $r(0) = \frac{L}{2}$
- $\dot{r}(0) = 0$
מהתנאי הראשון:
\[r(0) = C = \frac{L}{2}\]לכן:
\[r(t) = \frac{L}{2} \cosh(\omega t) + D \sinh(\omega t)\]מהתנאי השני:
\[\dot{r}(t) = \frac{L}{2} \omega \sinh(\omega t) + D \omega \cosh(\omega t)\] \[\dot{r}(0) = D \omega = 0\]לכן: $D = 0$
שלב 5: הפתרון הסופי
\[r(t) = \frac{L}{2} \cosh(\omega t) \tag{3}\] \[\dot{r}(t) = \frac{L \omega}{2} \sinh(\omega t) \tag{4}\] \[\ddot{r}(t) = \frac{L \omega^2}{2} \cosh(\omega t) \tag{5}\]שלב 6: חישוב זמן ההגעה לקצה הגליל
המסה מגיעה לקצה הגליל כאשר $r(t) = L$:
\[L = \frac{L}{2} \cosh(\omega t)\] \[2 = \cosh(\omega t)\] \[\omega t = \cosh^{-1}(2)\] \[\boxed{t = \frac{\cosh^{-1}(2)}{\omega}}\]הגרסה שהופיעה בתגבור
גליל מסתובב נגד כיוון השעון במהירות זוויתית קבועה. מסה $m$ מתחילה במרכז הגליל ונופלת תחת השפעת הכבידה.
נתונים
תנאי התחלה:
- $r(t=0) = 0$ (מיקום רדיאלי התחלתי)
- $v(t=0) = 0$ (מהירות התחלתית)
פרמטרי המערכת:
- $\theta(t) = \omega t$ (מיקום זוויתי של הגליל)
- $\omega$ = מהירות זוויתית קבועה של הגליל
- $m$ = מסת הגוף הנופל
מטרה: למצוא את התנועה $r(t)$ של המסה.
| מסה בגליל | מסה נופלת |
פתרון
שלב 1: יישום חוק ניוטון השני בקואורדינטות קוטביות
במערכת ייחוס מסתובבת, חוק ניוטון השני הוא:
\[m\vec{a} = \vec{F}\]התאוצה בקואורדינטות קוטביות:
\[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta} \tag{1}\]שלב 2: זיהוי הכוחות
כוח הכבידה במערכת קואורדינטות מסתובבת:
\[\vec{F} = mg\cos(\theta - 90°)\hat{r} - mg\sin(\theta - 90°)\hat{\theta}\]באמצעות זהויות טריגונומטריות:
- $\cos(\theta - 90°) = \sin(\theta)$
- $\sin(\theta - 90°) = -\cos(\theta)$
לכן:
\[\vec{F} = mg\sin(\theta)\hat{r} + mg\cos(\theta)\hat{\theta}\]שלב 3: הצבת ערכים ידועים
כיוון ש-$\theta(t) = \omega t$ כאשר $\omega$ קבועה:
- $\dot{\theta} = \omega$
- $\ddot{\theta} = 0$
שלב 4: משוואות לפי רכיבים
הצבה בחוק ניוטון השני ($F = ma$), כאשר $a=(1)$:
\[m[(\ddot{r} - r\omega^2)\hat{r} + (2\dot{r}\omega)\hat{\theta}] = mg\sin(\theta)\hat{r} + mg\cos(\theta)\hat{\theta}\]המסה מצטמצמת.
שלב 5: הפרדת רכיבים
רכיב רדיאלי ($\hat{r}$):
\[\begin{align} \ddot{r} - r\omega^2 &= g\sin(\theta) \\ \ddot{r} &= r\omega^2 + g\sin(\theta) \end{align}\]רכיב משיקי ($\hat{\theta}$):
\[\begin{align} 2\dot{r}\omega &= g\cos(\theta) \\ \dot{r} &= \frac{g\cos(\theta)}{2\omega} \end{align}\]שלב 6: משוואות דיפרנציאליות
הצבת $\theta = \omega t$:
\[\begin{cases} \ddot{r} = r\omega^2 + g\sin(\omega t) \\[0.5em] \dot{r} = \frac{g\cos(\omega t)}{2\omega} \end{cases}\]שתי המשוואות המצומדות האלה מתארות את התנועה של המסה הנופלת בגליל המסתובב.
הערות
- הפתרון של המשוואה הראשונה מהצורה ($\ddot{r} = r\omega^2$), הוא ב-$\cosh$ ו-$\sinh$.
- המשוואה השנייה נותנת קשר בין $\dot{r}$ לזמן
- ניתן לאמת עקביות על ידי גזירת המשוואה השנייה ובדיקה מול הראשונה
- הפתרון המלא דורש פתרון של משוואת הדיפרנציאל הלא-הומוגנית
שיעור תגבור - משוואות דיפרנציאליות מצומדות לשתי מסות וקפיץ
תאריך: 08/06/2025פתרון משוואות דיפרנציאליות בבעיות דינמיות
כאשר אנו פותרים בעיות דינמיות מורכבות, עלינו להיות מסוגלים לטפל במשוואות דיפרנציאליות מהצורות הבסיסיות הבאות. אם נתבקש לפתור משוואות דיפרנציאליות, הפתרונות יגיעו מתוך ארבע האפשרויות העיקריות שנלמדו, כולל האפשרות של הזזה בקבוע.
לדוגמה, עבור משוואת האוסילטור ההרמוני:
\[\ddot{x} = -\omega^2 x\]יתכן שנקבל משוואה מהצורה:
\[\ddot{x} = -\omega^2 x + \lambda\]כאשר $\lambda$ הוא גודל קבוע. במקרה זה, עלינו להעביר את המשוואה לצורה:
\[\ddot{x} = -\omega^2 \left(x - \frac{\lambda}{\omega^2}\right)\]נגדיר משתנה חדש $y = x - \frac{\lambda}{\omega^2}$, ונקבל משוואה מהצורה:
\[\ddot{y} = -\omega^2 y\]שהפתרונות שלה הם:
\[y(t) = C\cos(\omega t + \phi)\]מכיוון ש-$y = x - \frac{\lambda}{\omega^2}$, נוכל לכתוב:
\[x(t) = C\cos(\omega t + \phi) + \frac{\lambda}{\omega^2}\]המשוואות הדיפרנציאליות הרלוונטיות
המשוואות הבסיסיות שעלינו להכיר הן:
- אוסילטור הרמוני: $\ddot{x} = -\omega^2 x$ עם פתרונות סינוסיים וקוסינוסיים
- אוסילטור הפוך: $\ddot{x} = \omega^2 x$ עם פתרונות אקספוננציאליים (בשיעור ובכתה התייחסנו לפתרונות בצורות $x(t) = A\cosh(\omega t) + B\sinh(\omega t)$, אבל ניתן גם לכתוב את הפתרונות בצורות אקספוננציאליות פשוטות כמו $x(t) = C e^{\omega t} + D e^{-\omega t}$)
- דעיכה אקספוננציאלית: $\dot{x} = -\gamma x$ עם פתרון $x(t) = x_0 e^{-\gamma t}$ - למשל בשאלות של קליע, להבנתי.
- צורה נוספת: $\dot{v} = -\beta^2 v$ או משוואות דומות
ניתוח מערכת של שתי מסות מצומדות
תיאור המערכת
נבחן מערכת המורכבת משתי מסות: מסה קטנה $m$ ומסה גדולה $M$, המחוברות באמצעות קפיץ. המסה הקטנה נמצאת על משטח משופע בזווית $\alpha$, והמסה הגדולה יכולה לנוע אופקית. קבוע הקפיץ הוא $k$, ואורך הקפיץ במצב מנוחה הוא $L$ (ייתכן שהיה נוח לבחור $L=0$).
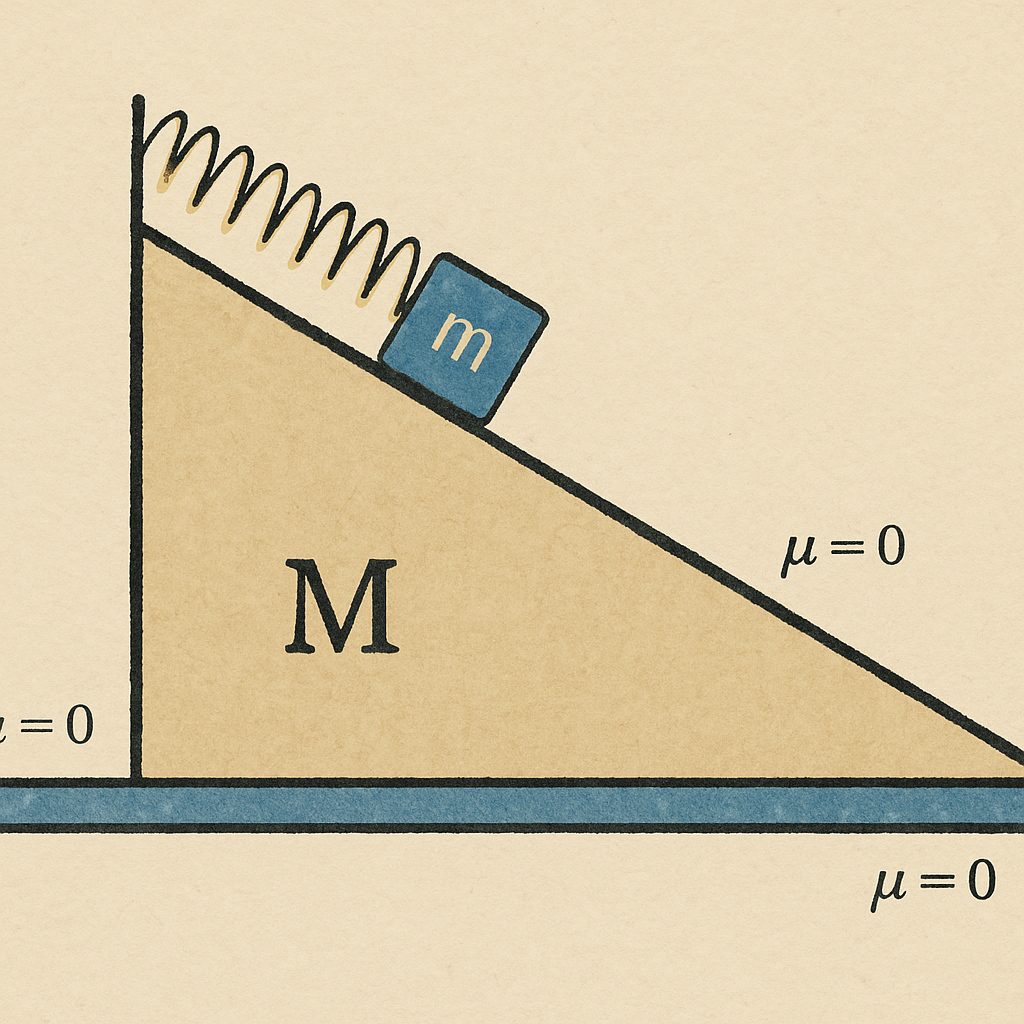
כוחות במערכת
במערכת פועלים מספר סוגי כוחות:
כוח מחזיר של קפיץ: מבחינה וקטורית, כוח מחזיר תמיד מתואר על ידי:
\[\vec{F} = -k\vec{r}\]כאשר $\vec{r}$ הוא וקטור המקום מנקודת השיווי. הכוח תמיד מנוגד לוקטור המקום ומתכונתי לו בגודלו.
נסמן ב-$A$ את התאוצה של המסה הגדולה שמאלה, וב-$x$ את המקום של המסה הקטנה על המשטח המשופע. מכאן שתאוצת המסה הקטנה היא $\ddot{x}$.
מערכת לא אינרציאלית
חשוב להבין שהמסה הקטנה נמצאת במערכת ייחוס לא אינרציאלית, מכיוון שהיא מחוברת למסה הגדולה הנעה בתאוצה. לכן עלינו להתחשב בכוחות מדומים. זה דומה למצב של נוסע באוטובוס המאיץ - הנוסע מרגיש כוח “מדומה” בכיוון הפוך לתאוצה.
המסה הגדולה, לעומת זאת, נמצאת במערכת אינרציאלית ולא מרגישה כוחות מדומים.
ניתוח הכוחות על המסה הקטנה
ניתוח הכוחות בכיוון המקביל למשטח המשופע (↘)
עבור המסה הקטנה $m$ הנמצאת על המשטח המשופע, נבחר ציר חיובי לכיוון מטה לאורך המשטח. הכוחות הפועלים בכיוון זה הם:
- רכיב כוח הכבידה: $mg\sin\alpha$ כלפי מטה.
- כוח מדומה: $mA\cos\alpha$ (בשל תאוצת המסה הגדולה). לפי הפתרון בבלוג, המסה הגדולה מאיצה שמאלה, ולכן הכוח המדומה פועל בכיוון ההפוך לתאוצה של המסה הגדולה (כלומר ימינה).
- כוח הקפיץ: $-k(x - L)$ (כוח מחזיר), במעלה המישור המשופע (ומכאן שלילי).
המשוואה הדינמית למסה הקטנה, מהחוק השני של ניוטון ביחס לציר המקביל למשטח המשופע, היא:
\[mg\sin\alpha + mA\cos\alpha - k(x - L) = m\ddot{x} \tag{1}\]ניתוח הכוחות בכיוון הניצב למשטח (↗)
במערכת הלא אינרציאלית של המסה הקטנה, בכיוון הניצב למשטח המשופע (ציר $y$), המסה תמיד צמודה לפני המשטח. המשמעות היא ש-$y = 0$ בכל זמן, ולכן אין תאוצה בכיוון זה. במצב הזה ניתן להפעיל את החוק הראשון של ניוטון (שיווי משקל של כוחות $\sum F_y = 0$), שכן בתוך המערכת המאיצה אין דינמיקה בציר $y$.
הכוחות הפועלים על המסה הקטנה בכיוון הניצב למשטח הם:
- הכוח הנורמלי: $N$ פועל בכיוון הניצב למשטח, אך יש לו רכיב בכיוון התנועה של המסה הקטנה. למעלה וימינה.
- רכיב כוח הכבידה: $mg\cos\alpha$
- רכיב הכוח המדומה: $mA\sin\alpha$ (כי $\cos(90° - \alpha) = \sin\alpha$)
משוואת שיווי המשקל בכיוון הניצב למשט, לפי החוק הראשון של ניוטון, היא:
\[N + mA\sin\alpha = mg\cos\alpha \tag{2}\]מכאן נקבל:
\[\boxed{N = mg\cos\alpha - mA\sin\alpha}\]ניתוח הכוחות על המסה הגדולה
המסה הגדולה $M$ נעה אופקית תחת השפעת:
- כוח המשיכה $Mg$ (כלפי מטה, אך אין לו רכיב אופקי).
- רכיב הכוח הנורמלי: $N\sin\alpha$ (בכיוון התנועה של המסה הגדולה, כלומר שמאלה ומטה). מדובר בכוח שהמסה הקטנה מפעילה על המסה הגדולה.
- כוח הקפיץ: $-k(x - L)\cos\alpha$ בשמו הפורמאלי - הכוח המחזיר של הקפיץ.
- הכוח הנורמאלי $N’$ של המסה הגדולה, הפועל בכיוון הניצב למשטח המשופע (כלפי מעלה).
המשוואה הדינמית למסה הגדולה:
\[N\sin\alpha - k(x - L)\cos\alpha = MA \tag{3}\]פתרון המערכת המצומדת
אסטרטגיית הפתרון
יש לנו מערכת של שלוש נעלמים: $x$, $A$, ו-$N$. כעת נוכל לפתור את מערכת המשוואות המצומדות בשיטה הבאה:
- נציב את הביטוי עבור $N$ במשוואה של המסה הגדולה (משוואה 3).
- נקבל משוואה דיפרנציאלית יחידה במשתנה $x$
- נפתור אותה כאוסילטור הרמוני עם איבר קבוע
האסטרטגיה היא להתנער מהנעלמים $N$ ו-$A$, ולהשאיר רק את $x$ ונגזרותיו.
הצבה ופיתוח המשוואה
מהמשוואה של המסה הגדולה:
\[N\sin\alpha - k(x-L)\cos\alpha = MA\]נציב את הביטוי עבור $N$:
\[\left(mg\cos\alpha - mA\sin\alpha\right)\sin\alpha - k(x-L)\cos\alpha = MA\]פיתוח הביטוי:
\[mg\cos\alpha\sin\alpha - mA\sin^2\alpha - k(x-L)\cos\alpha = MA\]העברת האיברים ואיסוף:
\[mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha = MA + mA\sin^2\alpha\]מכאן נוכל להוציא את $A$:
\[A = \frac{mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha}{M + m\sin^2\alpha}\]הצבה במשוואה של המסה הקטנה
נציב את הביטוי עבור $A$ במשוואה של המסה הקטנה (משוואה 1):
\[mg\sin\alpha + m\left(\frac{mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha}{M + m\sin^2\alpha}\right)\cos\alpha - k(x-L) = m\ddot{x}\]נפתח את הביטוי:
\[mg\sin\alpha + \frac{m^2g\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \frac{mk(x-L)\cos^2\alpha}{M + m\sin^2\alpha} - k(x-L) = m\ddot{x}\] \[mg\sin\alpha + \frac{m^2g\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right)k(x-L) = m\ddot{x}\]נחלק את המשוואה ב-$m$:
\[\ddot{x} = g\sin\alpha + \frac{mg\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)(x-L)\] \[\ddot{x} = g\sin\alpha \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right) - \left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)(x-L)\]נגדיר משתנה מוזז $\tilde{x} = x - L$, ונקבל כך ש-$ֿ\ddot{\tilde{x}} = \ddot{x}$:
\[\ddot{\tilde{x}} = - \underbrace{\left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)}_{\omega^2} \tilde{x} + \underbrace{g\sin\alpha \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right)}_{\tilde{x_0}}\]הפתרון הכללי
הפתרון הכללי למשוואה זו הוא:
\[x(t) = A\cos(\omega t) + B\sin(\omega t) + \frac{\tilde{x_0}}{\omega^2}\]התאמה לתנאי התחלה
בהנחה שהמערכת מתחילה ממנוחה בזמן $t=0$ עם $x(0) = L$ ו-$\dot{x}(0) = 0$:
מתנאי המקום ההתחלתי:
\[L = A\cos(0) + B\sin(0) + \frac{\tilde{x_0}}{\omega^2} = A + \frac{\tilde{x_0}}{\omega^2}\]לכן:
\[A = L - \frac{\tilde{x_0}}{\omega^2}\]מתנאי המהירות ההתחלתית:
\[\dot{x}(t) = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\] \[\dot{x}(0) = B\omega = 0\]לכן:
\[B = 0\]הסיבה ש-$B = 0$ היא שהתחלנו ממהירות אפס - שחררנו את המסה ממנוחה.
הפתרון הסופי
הפתרון הסופי עם תנאי ההתחלה הוא:
\[x(t) = \left(L - \frac{\tilde{x_0}}{\omega^2}\right)\cos(\omega t) + \frac{\tilde{x_0}}{\omega^2}\]ניתוח התנועה
זמן הגעה לנקודת שיווי המשקל
המסה הקטנה תגיע לנקודת שיווי המשקל החדשה לראשונה בזמן $t^*$ המקיים:
\[t^* = \frac{T}{4} = \frac{\pi}{2\omega}\]כאשר $T = \frac{2\pi}{\omega}$ הוא זמן המחזור של התנודה.
הסיבה לכך היא שבתנועה קוסינוסואידית, אנו מתחילים מנקודת השיווי, יורדים למטה (זה רבע זמן מחזור), מגיעים לנקודה מקסימלית, חוזרים לנקודת השיווי (חצי זמן מחזור), עולים למעלה (שלושת רבעי זמן מחזור), וחוזרים שוב לנקודת השיווי (זמן מחזור שלם).
התדירות המותאמת
חשוב לציין שהתדירות $\omega$ במערכת זו אינה התדירות הפשוטה $\sqrt{k/m}$ של קפיץ בודד, אלא תדירות מותאמת התלויה במסות שתי הגופים ובזווית המשטח:
\[\omega = \sqrt{\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}}\]בגבול שבו $M \to \infty$, התדירות מתקרבה ל-$\sqrt{k/m}$ (עד כדי איבר זווית), מכיוון שאז חוזרים למצב של משטח משופע קבוע שעליו מתנדנדת מסה.
בהמשך עלתה דוגמה מורכבת עם חיכוך.
שיעור 10 - מעבר מחוקי ניוטון לתורת האנרגיה - תנע, מתקף ועבודה
תאריך: 09/06/2025מבוא: מחוקי ניוטון לכלים אלגנטיים יותר
עד כה התמקדנו בשלושת חוקי ניוטון כבסיס להבנת הדינמיקה של מערכות פיזיקליות. למרות העוצמה הרבה של חוקים אלה, קיימים כלים נוספים ואלגנטיים יותר לטיפול בבעיות מכניות. אחד הכלים החשובים ביותר הוא מושג האנרגיה, אותו נפתח בהדרגה.
כהכנה למושג האנרגיה, נעמיק תחילה בשני מושגים יסודיים: התנע (momentum) והמתקף (impulse). מושגים אלה, יחד עם מושג האנרגיה, יספקו לנו ארגז כלים מלא להתמודדות עם בעיות מכניות מורכבות.
התנע ושימורו
הגדרת התנע
התנע של גוף בודד מוגדר כמכפלת המסה במהירות:
\[\vec{p} = m\vec{v}\]זהו גודל וקטורי המבטא את “כמות התנועה” של הגוף. התנע מורכב משני רכיבים:
- המסה - המבטאת את תכונת ההתמדה (אינרציה) של הגוף
- המהירות - המבטאת את מצב התנועה הרגעי
הערה: לפי האקדמיה ללשון ״תנע״ הוא זכר.
תנע: (בפיזיקה) המכפלה של מסת העצם במהירותו (בלועזית: מוֹמֶנְטוּם) האקדמיה ללשון העברית
דוגמה: זבוב מול נושאת מטוסים
נשווה בין זבוב במסה של 1 גרם לנושאת מטוסים במסה של 500,000 טון, כאשר שניהם נעים במהירות של 1 מ’/שנייה:
-
זבוב:
\[p = 10^{-3} \, \mathrm{kg} \times 1\, \mathrm{ m/s} = \boxed{10^{-3} \, \, \mathrm{ kg⋅m/s}}\] -
נושאת מטוסים:
\[p = 5 \times 10^8 \, \, \mathrm{ kg} \times 1 \, \,\mathrm{ m/s} = \boxed{5 \times 10^8 \, \,\mathrm{ kg⋅m/s}}\]
התנע של נוסעת המטוסים גדול פי $10^{11}$ מזה של הזבוב! זה ממחיש כיצד התנע מבטא את התנועתיות האמיתית, הכוללת גם את האינרציה של הגוף.
תנע של מערכת גופים
עבור מערכת של $n$ גופים, התנע הכולל הוא סכום וקטורי של תנעי הגופים:
\[\vec{p}_{total} = \sum_{i=1}^{n} \vec{p}_i = \sum_{i=1}^{n} m_i\vec{v}_i\]חוק שימור התנע
מהחוק השני של ניוטון נובע שכאשר שקול הכוחות החיצוניים על מערכת הוא אפס, התנע הכולל נשמר:
\[\sum \vec{F}_{ext} = \frac{d\vec{p}_{total}}{dt} = 0 \Rightarrow \vec{p}_{total} = \text{const}\]הערות חשובות:
- כוחות פנימיים בין גופי המערכת אינם משפיעים על התנע הכולל
- שימור תנע יכול להתקיים ברכיב אחד בלבד אם רק בכיוון זה אין כוחות חיצוניים
דוגמה: התנגשות על שולחן ביליארד
על שולחן ביליארד חלק (ללא חיכוך), כדורים מבצעים התנגשויות. למרות שהכדורים מפעילים כוחות זה על זה, התנע הכולל של כל הכדורים נשמר כי אין כוחות חיצוניים בכיוון התנועה (כוח הכבידה פועל בניצב למישור השולחן).
דוגמה: התנגשות חד-ממדית
שני גופים במסות $M_1$ ו-$M_2$ נעים על ציר ישר במהירויות $V_1$ ו-$V_2$ ומתנגשים. מחוק שימור התנע:
\[M_1V_1 + M_2V_2 = M_1V_1' + M_2V_2'\]כאשר $V_1’$ ו-$V_2’$ הן המהירויות לאחר ההתנגשות.
המתקף
הגדרת המתקף
המתקף (Impulse) מוגדר כאינטגרל הכוח על פני הזמן:
\[\vec{J} = \int_{t_1}^{t_2} \vec{F}(t) dt\]המתקף מבטא את ההצטברות של פעולת הכוח לאורך זמן (בשונה למשל מהעבודה, שהיא הצטברות לאורך מסלול - מקום ולא זמן).
משפט מתקף-תנע
באמצעות החוק השני של ניוטון נוכל להראות:
\[\vec{J} = \int_{t_1}^{t_2} \vec{F} dt = \int_{t_1}^{t_2} \frac{d\vec{p}}{dt} dt = \vec{p}(t_2) - \vec{p}(t_1) = \Delta\vec{p}\]משפט מתקף-תנע: המתקף הפועל על גוף שווה לשינוי בתנע הגוף.
דוגמה דרמטית: נפילה ממגדל
נניח שאדם נופל ממגדל גבוה ופוגע בקרקע. המתקף שהקרקע מפעילה עליו הוא:
\[\vec{J} = \vec{p}_{final} - \vec{p}_{initial} = 0 - m\vec{v}_{impact}\]מכיוון שזמן האינטראקציה עם הקרקע קצר מאוד ($\Delta t$ קטן), והמתקף $J$ נתון, הכוח הממוצע חייב להיות גדול מאוד:
\[F_{avg} \approx \frac{J}{\Delta t}\]הפתרון: מזרן עבה מאריך את זמן האינטראקציה. אם $\Delta t$ גדל פי 100 (מ-0.01 שנייה לשנייה אחת), הכוח הממוצע קטן פי 100, מה שעשוי להציל חיים.
המתקף והחוק השלישי
מהחוק השלישי של ניוטון נובע שכאשר שני גופים מפעילים כוחות זה על זה, המתקפים שווים בגודלם והפוכים בכיוונם:
\[\vec{J}_{1 \rightarrow 2} = -\vec{J}_{2 \rightarrow 1}\]עבודה (Work)
הגדרת העבודה
אלמנט אינפיניטסימלי של עבודה מוגדר כמכפלה סקלרית של הכוח באלמנט ההעתק:
\[dW = \vec{F} \cdot d\vec{r} = \vert \vec{F}|\vert d\vec{r}\vert \cos(\theta)\]כאשר $\theta$ היא הזווית בין הכוח לכיוון התנועה.
העבודה הכוללת לאורך מסלול מ- $\vec{r}_i$ ל- $\vec{r}_f$ היא:
\[W = \int_{\vec{r}_{initial}}^{\vec{r}_{final}} \vec{F} \cdot d\vec{r}\]משמעות פיזיקלית
העבודה מבטאת את הצטברות פעולת הכוח בכיוון התנועה לאורך המסלול. רק הרכיב של הכוח בכיוון התנועה תורם לעבודה.
משפט העבודה-אנרגיה קינטית
נוכל להראות שהעבודה שמבצע כוח על גוף שווה לשינוי באנרגיה הקינטית שלו:
\[W = \int_{\vec{r}_i}^{\vec{r}_f} \vec{F} \cdot d\vec{r} = \int_{t_i}^{t_f} \frac{d\vec{p}}{dt} \cdot \vec{v} dt = \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 = \Delta E_k\]כאשר האנרגיה הקינטית מוגדרת:
\[\boxed{E_k = \frac{1}{2}mv^2 = \frac{\vert \vec{p}|^2}{2m}}\]יחידות
- תנע: $\mathrm{kg⋅m/s}$ (אין יחידה מיוחדת)
- עבודה ואנרגיה: ג’אול $\mathrm{(Joule) = N⋅m = kg⋅m²/s²}$
תלות במערכת ייחוס
נקודה קריטית: התנע והאנרגיה הקינטית תלויים במערכת הייחוס. הם אינם גדלים אבסולוטיים.
דוגמה: מטאוריט בחלל
מטאוריט במסה של קילומטר מעוקב של קרח ($10^{12}$ ק”ג) נע במהירות 60 קמ”ש ביחס לכדור הארץ:
- במערכת המנוחה של המטאוריט: $E_k = 0$
- במערכת הייחוס של כדור הארץ:
זוהי אנרגיה השקולה לכ-100,000 פצצות מימן! אך אנרגיה זו קיימת רק במערכת הייחוס של כדור הארץ.
חישובים מעשיים
חישוב מתקף וקטורי
נתון כוח המשתנה בזמן:
\[\vec{F}(t) = 4\mathbf{\hat{x}} + t\mathbf{\hat{y}} - \frac{1}{2}gt^2\mathbf{\hat{z}}\]המתקף במשך 4 שניות:
אינטגרל על רכיב $x$:
\[\int_0^4 4 dt = 16\]אינטגרל על רכיב $y$:
\[\int_0^4 t dt = \left[\frac{t^2}{2}\right]_0^4 = 8\]אינטגרל על רכיב $z$:
\[\int_0^4 -\frac{1}{2}gt^2 dt = -\frac{1}{2}g\left[\frac{t^3}{3}\right]_0^4 = -\frac{1}{2}g\cdot\frac{64}{3} = -\frac{32g}{3}\]סך הכל:
\[\vec{J} = \int_0^4 \vec{F}(t) dt = 16\mathbf{\hat{x}} + 8\mathbf{\hat{y}} - 107\mathbf{\hat{z}} \, \, \, \mathrm{ N⋅s}\]חישוב עבודה
עבור כוח קבוע $\vec{F} = 2\mathbf{\hat{x}}$ לאורך מסלול מ-(0,0) ל-(1,1) דרך (1,0):
(1,1)
↑
|
(0,0) → (1,0)
-
קטע ראשון (0,0)←(1,0):
\[W_1 = \int_0^1 2dx = 2\,\,\, \mathrm{J}\] -
קטע שני (1,0)←(1,1):
\[W_2 = 0\](כי $dx=0$)
-
עבודה כוללת: $\boxed{W = 2 \, \, \mathrm{J}}$
סיכום
בשיעור זה הכרנו שלושה מושגים יסודיים:
- התנע - מדד וקטורי לתנועתיות, הנשמר במערכות מבודדות
- המתקף - הצטברות פעולת הכוח בזמן, השווה לשינוי בתנע
- העבודה - הצטברות פעולת הכוח לאורך מסלול, השווה לשינוי באנרגיה קינטית
מושגים אלה מהווים בסיס להבנת האנרגיה ושימורה, נושא שנעמיק בו בשיעורים הבאים.
שיעור 11 - גרדיאנט, עבודה, כוחות משמרים ושימור אנרגיה
תאריך: 16/06/2025עבודה ואנרגיה במכניקה - כוחות משמרים וחוקי שימור: סיכום שיעור ותרגול 10
תוכן עניינים:
- הקדמה: חזרה על מושג הגרדיאנט מהשיעור הקודם
- נגזרות חלקיות
- אופרטור הגרדיאנט
- הדיפרנציאל של פונקציה תלת-ממדית
- עבודה ומשפט עבודה-אנרגיה
- כוחות משמרים
- אנרגיה פוטנציאלית
- גזירת חוק שימור האנרגיה
- תכונות ייחודיות של כוחות משמרים
- כוחות יסודיים וכוחות משמרים
- סיכום עקרונות מקדימים
- התנגשות אלסטית
- התנגשות פלסטית
- דוגמה 1: כוח הכבידה בקרבת פני כדור הארץ
- דוגמה 2: כוח מחזיר (קפיץ)
- סיכום ומבט קדימה
- תרגול
הקדמה: חזרה על מושג הגרדיאנט מהשיעור הקודם
בשיעור הקודם התחלנו ללמוד על מושג הגרדיאנט, מושג חשוב שישמש אותנו בלימודי אנרגיה. נחזור על עיקרי הדברים.
נגזרות חלקיות
כהקדמה להגדרת הגרדיאנט, יש להגדיר תחילה את מושג הנגזרת החלקית. עבור פונקציה של מספר משתנים - במקרה זה, פונקציה של שלושה משתנים המייצגת נקודה במרחב - ניתן לסמן אותה כפונקציה של וקטור המקום $\mathbf{r}$.
בפונקציה מרובת משתנים, הנגזרת החלקית של $F$ מוגדרת לפי כל אחד מהמשתנים - כלומר, הנגזרת של $F$ ביחס למשתנה מסוים כאשר שאר המשתנים נשארים קבועים.
לדוגמה, $\frac{\partial F}{\partial x}$ היא הנגזרת של $F$ לפי המשתנה $x$, והיא מוגדרת באופן הבא:
\[\frac{\partial F}{\partial x} = \lim_{\Delta x \to 0} \frac{F(x + \Delta x, y, z) - F(x, y, z)}{\Delta x}\]כאשר $y$ ו-$z$ נשארים קבועים.
באופן אנלוגי מוגדרות הנגזרות החלקיות לפי $y$ ולפי $z$, כאשר בכל מקרה שני המשתנים האחרים נשארים קבועים.
לפיכך, לפונקציה של שלושה משתנים קיימות שלוש נגזרות חלקיות: $\frac{\partial F}{\partial x}$, $\frac{\partial F}{\partial y}$ ו-$\frac{\partial F}{\partial z}$. כל נגזרת מתארת את השינוי האינפיניטסימלי של $F$ בעת תזוזה אינפיניטסימלית לאורך הציר המתאים.
אופרטור הגרדיאנט
הגרדיאנט הוא אופרטור וקטורי המוגדר כך:
\[\nabla = \hat{\mathbf{x}} \frac{\partial}{\partial x} + \hat{\mathbf{y}} \frac{\partial}{\partial y} + \hat{\mathbf{z}} \frac{\partial}{\partial z}\]כאשר האופרטור פועל על פונקציה $F$, מתקבל:
\[\nabla F = \hat{\mathbf{x}} \frac{\partial F}{\partial x} + \hat{\mathbf{y}} \frac{\partial F}{\partial y} + \hat{\mathbf{z}} \frac{\partial F}{\partial z}\]חשוב להבחין: בעוד ש-$\nabla$ הוא אופרטור, $\nabla F$ (הגרדיאנט של הפונקציה $F$) הוא וקטור שרכיביו הם הנגזרות החלקיות של $F$:
- רכיב ה-$x$: $\frac{\partial F}{\partial x}$
- רכיב ה-$y$: $\frac{\partial F}{\partial y}$
- רכיב ה-$z$: $\frac{\partial F}{\partial z}$
דוגמה 1: $\nabla \left(\sin\left(xyz\right)\right)$
נתונה הפונקציה:
\[F(x,y,z) = \sin(xyz)\]הגרדיאנט של $F$ מחושב כך:
\[\nabla F = \hat{\mathbf{x}} \frac{\partial F}{\partial x} + \hat{\mathbf{y}} \frac{\partial F}{\partial y} + \hat{\mathbf{z}} \frac{\partial F}{\partial z}\]חישוב כל רכיב:
- רכיב $\hat{\mathbf{x}}$: גזירה לפי $x$ (כאשר $y,z$ קבועים) נותנת $yz \cos(xyz)$
- רכיב $\hat{\mathbf{y}}$: גזירה לפי $y$ (כאשר $x,z$ קבועים) נותנת $xz \cos(xyz)$
- רכיב $\hat{\mathbf{z}}$: גזירה לפי $z$ (כאשר $x,y$ קבועים) נותנת $xy \cos(xyz)$
לכן:
\[\nabla F = yz \cos(xyz) \hat{\mathbf{x}} + xz \cos(xyz) \hat{\mathbf{y}} + xy \cos(xyz) \hat{\mathbf{z}}\]דוגמה 2: $\nabla \left(x e^{yz}\right)$
נתונה הפונקציה:
\[F(x,y,z) = x e^{yz}\]חישוב הגרדיאנט:
- רכיב $\hat{\mathbf{x}}$: $\frac{\partial F}{\partial x} = e^{yz}$
- רכיב $\hat{\mathbf{y}}$: $\frac{\partial F}{\partial y} = xz e^{yz}$
- רכיב $\hat{\mathbf{z}}$: $\frac{\partial F}{\partial z} = xy e^{yz}$
לכן:
\[\nabla F = e^{yz} \hat{\mathbf{x}} + xz e^{yz} \hat{\mathbf{y}} + xy e^{yz} \hat{\mathbf{z}}\]המשמעות הפיזיקלית של הגרדיאנט
הגרדיאנט של פונקציה מצביע בכל נקודה לכיוון השיפוע המקסימלי של הפונקציה באותה נקודה. זהו וקטור התלוי במיקום $(x,y,z)$, כאשר בכל נקודה הוא מצביע לכיוון העלייה התלולה ביותר של הפונקציה.
אינטואיטיבית, אם הפונקציה מתארת משטח גבהים ונניח טיפת מים על המשטח, הטיפה תזרום בכיוון ההפוך לגרדיאנט (כיוון הירידה התלולה ביותר), בעוד הגרדיאנט עצמו מצביע לכיוון העלייה התלולה ביותר.
הדיפרנציאל של פונקציה תלת-ממדית
הגדרה ומוטיבציה
נתבונן בפונקציה סקלרית $\phi(x,y,z)$ - פונקציה המקבלת ערך סקלרי בכל נקודה במרחב התלת-ממדי. דוגמה פיזיקלית לפונקציה כזו היא התפלגות הטמפרטורה בחדר, כאשר לכל נקודה $(x,y,z)$ מותאם ערך טמפרטורה $\phi(x,y,z)$. באופן דומה ניתן לתאר התפלגות לחץ במרחב באמצעות פונקציה סקלרית.
נוסחת הדיפרנציאל
בהכללה לדיפרנציאל של פונקציה חד-ממדית $dF = F’(x)dx$, הדיפרנציאל של פונקציה תלת-ממדית מוגדר כך:
\[d\phi = \frac{\partial \phi}{\partial x} dx + \frac{\partial \phi}{\partial y} dy + \frac{\partial \phi}{\partial z} dz\]ביטוי זה מתאר את השינוי האינפיניטסימלי ב-$\phi$ כתוצאה משינוי אינפיניטסימלי סימולטני בקואורדינטות $x$, $y$ ו-$z$. הוכחה ריגורוזית של נוסחה זו נלמדת בקורסי חשבון דיפרנציאלי ואינטגרלי מתקדמים.
ייצוג וקטורי של הדיפרנציאל
הדיפרנציאל ניתן לביטוי כמכפלה סקלרית של שני וקטורים:
\[d\phi = \begin{pmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{pmatrix} \cdot \begin{pmatrix} dx \\ dy \\ dz \end{pmatrix}\]ניתן לפרק ביטוי זה לצורה:
\[d\phi = \left(\frac{\partial \phi}{\partial x} \hat{\mathbf{x}} + \frac{\partial \phi}{\partial y} \hat{\mathbf{y}} + \frac{\partial \phi}{\partial z} \hat{\mathbf{z}}\right) \cdot \left(dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}\right)\]הווקטור הראשון במכפלה הוא הגרדיאנט של $\phi$:
\[\nabla \phi = \frac{\partial \phi}{\partial x} \hat{\mathbf{x}} + \frac{\partial \phi}{\partial y} \hat{\mathbf{y}} + \frac{\partial \phi}{\partial z} \hat{\mathbf{z}}\]הווקטור השני הוא הדיפרנציאל של וקטור המקום $d\mathbf{r}$.
הוכחה ש-$d\mathbf{r} = dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}$
וקטור המקום מוגדר כ:
\[\mathbf{r} = x\hat{\mathbf{x}} + y\hat{\mathbf{y}} + z\hat{\mathbf{z}}\]לפי הגדרת הדיפרנציאל:
\[d\mathbf{r} = \frac{\partial \mathbf{r}}{\partial x} dx + \frac{\partial \mathbf{r}}{\partial y} dy + \frac{\partial \mathbf{r}}{\partial z} dz\]חישוב הנגזרות החלקיות:
- $\frac{\partial \mathbf{r}}{\partial x} = \hat{\mathbf{x}}$ (כאשר $y,z$ קבועים)
- $\frac{\partial \mathbf{r}}{\partial y} = \hat{\mathbf{y}}$ (כאשר $x,z$ קבועים)
- $\frac{\partial \mathbf{r}}{\partial z} = \hat{\mathbf{z}}$ (כאשר $x,y$ קבועים)
לכן:
\[d\mathbf{r} = dx \hat{\mathbf{x}} + dy \hat{\mathbf{y}} + dz \hat{\mathbf{z}}\]הקשר המרכזי בין גרדיאנט לדיפרנציאל
מהניתוח לעיל מתקבל הקשר החשוב:
\[\boxed{d\phi = \nabla \phi \cdot d\mathbf{r}}\]כלומר, הדיפרנציאל של פונקציה סקלרית $\phi$ הוא מכפלה סקלרית של הגרדיאנט שלה עם הדיפרנציאל של וקטור המקום.
הקשר הזה מהווה כלי יסודי בפיזיקה מתמטית ויישומיו רבים.
עבודה ומשפט עבודה-אנרגיה
הגדרת עבודה
העבודה מוגדרת כמכפלה סקלרית של כוח ותזוזה. עבור תזוזה אינפיניטסימלית:
\[dW = \mathbf{F} \cdot d\mathbf{r}\]ביטוי זה מבטא שרק רכיב הכוח בכיוון התנועה תורם לעבודה (כלומר, כוח שניצב לכיוון התנועה לא מבצע עבודה).
העבודה הכוללת לאורך מסלול מנקודה $\mathbf{r}_1$ לנקודה $\mathbf{r}_2$ היא:
\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F}(\mathbf{r}) \cdot d\mathbf{r}\]כאשר הכוח $\mathbf{F}$ עשוי להיות תלוי במיקום לאורך המסלול.
משפט עבודה-אנרגיה
החוק השני של ניוטון קובע ש-$\mathbf{F} = \frac{d\mathbf{p}}{dt}$. בשילוב עם הקשרים:
- $d\mathbf{r} = \mathbf{v} dt$
- $\mathbf{p} = m\mathbf{v}$
ניתן להראות כי:
\[W = E_{k,\text{final}} - E_{k,\text{initial}}\]כאשר האנרגיה הקינטית מוגדרת:
\[E_k = \frac{1}{2}mv^2 = \frac{p^2}{2m}\]ניסוח מתמטי של המשפט
משפט עבודה-אנרגיה קובע:
\[\begin{aligned} W_{1 \to 2} &= E_k(\mathbf{r}_2) - E_k(\mathbf{r}_1) \\[5pt] &= \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 \\[5pt] &= \frac{p_2^2}{2m} - \frac{p_1^2}{2m} \end{aligned}\]המשפט מבטא את העיקרון הפיזיקלי שהעבודה שמבצע כוח על גוף שווה לשינוי באנרגיה הקינטית שלו.
כוחות משמרים
כוחות משמרים מהווים משפחת כוחות מרכזית ויסודית בפיזיקה. למרות שההגדרה עשויה להיראות אבסטרקטית בתחילה, חשיבותה תתבהר מהתובנות הפיזיקליות הנובעות ממנה.
כוח משמר - הגדרה מתמטית
כוח משמר הוא כוח הניתן לביטוי בצורה:
\[\mathbf{F} = -\nabla \phi\]כאשר $\phi$ היא פונקציה סקלרית של המיקום. הסימן השלילי הוא קונבנציה שנוחה לטיפול המתמטי בהמשך.
בניסוח מקוצר: כוח נקרא משמר אם הוא “נגזר” מפונקציה סקלרית. יש להדגיש שמדובר בגזירה באמצעות אופרטור הגרדיאנט, שכן לא ניתן להפיק וקטור (הכוח) מפונקציה סקלרית באמצעות גזירה רגילה.
חישוב העבודה שמבצע כוח משמר
נחשב את העבודה שמבצע כוח משמר על גוף הנע במסלול כלשהו מנקודה $\mathbf{r}_1$ לנקודה $\mathbf{r}_2$.
מהגדרת העבודה:
\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F} \cdot d\mathbf{r}\]הצבת הביטוי לכוח משמר:
\[W = -\int_{\mathbf{r}_1}^{\mathbf{r}_2} (\nabla \phi) \cdot d\mathbf{r}\]מהקשר שהוכח קודם, $(\nabla \phi) \cdot d\mathbf{r} = d\phi$, לכן:
\[W = -\int_{\mathbf{r}_1}^{\mathbf{r}_2} d\phi\]ביצוע האינטגרל:
\[W = -[\phi]_{\mathbf{r}_1}^{\mathbf{r}_2} = -\phi(\mathbf{r}_2) + \phi(\mathbf{r}_1)\]או בצורה סופית:
\[\boxed{W = \phi(\mathbf{r}_1) - \phi(\mathbf{r}_2)}\]תוצאה מרכזית: העבודה שמבצע כוח משמר תלויה אך ורק בנקודות ההתחלה והסיום, ולא במסלול שעובר ביניהן. זוהי תכונה ייחודית וחשובה של כוחות משמרים.
אנרגיה פוטנציאלית
הגדרה ויחידות
הפונקציה הסקלרית $\phi$ המופיעה בהגדרת הכוח המשמר נקראת אנרגיה פוטנציאלית (לעיתים מסומנת גם ב-$U$). היא מתארת את האנרגיה האצורה במערכת כתוצאה מהכוח המשמר.
מניתוח היחידות:
- עבודה = כוח × מרחק = ניוטון × מטר = ג’אול
- ממשפט עבודה-אנרגיה: לעבודה יש יחידות של אנרגיה
- לכן ל-$\phi$ יש יחידות של אנרגיה (ג’אול)
הקשר בין עבודה לאנרגיה פוטנציאלית
מהחישוב לעיל נובע:
\[W_{1 \to 2} = U(\mathbf{r}_1) - U(\mathbf{r}_2) = U_{\text{initial}} - U_{\text{final}}\]כאשר $U \equiv \phi$ מסמנת את האנרגיה הפוטנציאלית.
כלומר, העבודה שמבצע כוח משמר שווה להפרש האנרגיה הפוטנציאלית בין נקודת ההתחלה לנקודת הסיום.
גזירת חוק שימור האנרגיה
מהניתוח הקודם התקבלו שתי משוואות לעבודה:
- ממשפט עבודה-אנרגיה: $W = E_{k,\text{final}} - E_{k,\text{initial}}$
- מהגדרת כוחות משמרים: $W = \phi_{\text{initial}} - \phi_{\text{final}}$
השוואת שתי המשוואות נותנת:
\[E_{k,\text{final}} - E_{k,\text{initial}} = \phi_{\text{initial}} - \phi_{\text{final}}\]סידור מחדש של האיברים:
\[E_{k,\text{initial}} + \phi_{\text{initial}} = E_{k,\text{final}} + \phi_{\text{final}}\]הגדרת האנרגיה המכנית
הגודל $E = E_k + \phi$ מוגדר כאנרגיה מכנית של המערכת.
מהמשוואה לעיל נובע:
\[\boxed{E_{\text{initial}} = E_{\text{final}}}\]זהו חוק שימור האנרגיה המכנית: האנרגיה המכנית הכוללת נשמרת במהלך התנועה תחת כוחות משמרים בלבד.
האנרגיה המכנית מורכבת משני רכיבים:
- אנרגיה קינטית: $E_k = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi(\mathbf{r})$
גודל הנשמר במהלך התנועה נקרא קבוע תנועה או שמורה (invariant). לכן האנרגיה המכנית היא שמורה של מערכת הפועלים בה כוחות משמרים בלבד.
תכונות ייחודיות של כוחות משמרים
אי-תלות במסלול
מהחישוב הקודם עולה תוצאה מרכזית: העבודה של כוח משמר בין שתי נקודות $\mathbf{r}_1$ ו-$\mathbf{r}_2$ היא:
\[W = \phi(\mathbf{r}_1) - \phi(\mathbf{r}_2)\]התוצאה תלויה אך ורק בנקודות הקצה, ללא תלות במסלול המחבר ביניהן. בין אם המסלול ישר, עקום, או מקיף את כל כדור הארץ - העבודה זהה.
זוהי תכונה ייחודית ומגדירה של כוחות משמרים: העבודה אינה תלויה במסלול, אלא רק בנקודות הקצה.
עבודה במסלול סגור
עבור מסלול סגור (המתחיל ומסתיים באותה נקודה $\mathbf{r}$):
\[W = \phi(\mathbf{r}) - \phi(\mathbf{r}) = 0\]לכן, עבור כל כוח משמר:
\[\boxed{\oint \mathbf{F}_{\text{conservative}} \cdot d\mathbf{r} = 0}\]כאשר $\oint$ מסמן אינטגרל על מסלול סגור.
כוחות יסודיים וכוחות משמרים
כל הכוחות היסודיים בטבע הם כוחות משמרים. זוהי תכונה עמוקה של חוקי הטבע. כוחות לא-משמרים (כגון חיכוך) הם תמיד כוחות מקרוסקופיים הנובעים מאינטראקציות מורכבות.
דוגמה: מערכת כדור הארץ-שמש
כוח הכבידה בין השמש לכדור הארץ הוא כוח משמר. כדור הארץ נע במסלול סגור (בקירוב) סביב השמש, ולכן:
- העבודה שמבצע כוח הכבידה במחזור שלם היא אפס
- אין “התעייפות” או הפסד אנרגיה בתנועה זו
- התנועה יכולה להימשך ללא הגבלת זמן
תופעה זו מסבירה כיצד כדור הארץ מקיף את השמש כחמישה מיליארד שנה ללא צורך ב”מקור אנרגיה” חיצוני. העבודה הכוללת במחזור שלם היא אפס, ולכן אין צורך בהשקעת אנרגיה נוספת לשמירת התנועה.
זהו ביטוי ישיר לעקרון שימור האנרגיה ולתכונות המיוחדות של כוחות משמרים.
סיכום עקרונות מקדימים
בחלק הקודם נידונו המושגים הבאים:
- כוח משמר: כוח שהעבודה שהוא מבצע אינה תלויה במסלול התנועה
- עבודה במסלול סגור: עבור כוח משמר, העבודה במסלול סגור היא אפס
- חוק שימור האנרגיה המכנית: סכום האנרגיה הקינטית והאנרגיה הפוטנציאלית נשמר תחת כוחות משמרים
בחלק זה נבחן יישום של עקרונות אלו להתנגשויות בין גופים.
התנגשות אלסטית
התנגשות אלסטית היא התנגשות בה נשמרת האנרגיה המכנית הכוללת של המערכת. במקרה של גופים חופשיים (ללא אנרגיה פוטנציאלית), משמעות הדבר היא שימור האנרגיה הקינטית הכוללת.
תיאור המערכת
נתבונן בשני גופים בעלי מסות $m_1$ ו-$m_2$:
- לפני ההתנגשות: מהירויות $\mathbf{v}_1$ ו-$\mathbf{v}_2$
- אחרי ההתנגשות: מהירויות $\mathbf{u}_1$ ו-$\mathbf{u}_2$
חוקי השימור בהתנגשות אלסטית
בהיעדר כוחות חיצוניים, שני חוקי שימור חלים על המערכת:
1. חוק שימור התנע
\[m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 = m_1 \mathbf{u}_1 + m_2 \mathbf{u}_2\]או בסימון תנע:
\[\mathbf{p}_{1,\text{initial}} + \mathbf{p}_{2,\text{initial}} = \mathbf{p}_{1,\text{final}} + \mathbf{p}_{2,\text{final}}\]2. חוק שימור האנרגיה הקינטית
\[\frac{1}{2}m_1 v_1^2 + \frac{1}{2}m_2 v_2^2 = \frac{1}{2}m_1 u_1^2 + \frac{1}{2}m_2 u_2^2\]פיתוח הקשר בין המהירויות
שלב 1: ארגון מחדש של משוואות השימור
מחוק שימור התנע:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2)\]מחוק שימור האנרגיה (לאחר ביטול הגורם $\frac{1}{2}$):
\[m_1(v_1^2 - u_1^2) = m_2(u_2^2 - v_2^2)\]שלב 2: שימוש בזהות אלגברית
נזכור כי $a^2 - b^2 = (a-b)(a+b)$. בהכללה למכפלות סקלריות:
\[\mathbf{a} \cdot \mathbf{a} - \mathbf{b} \cdot \mathbf{b} = (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b})\]ניתן לוודא זאת על ידי פיתוח הביטוי:
\[(\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} + \mathbf{a} \cdot \mathbf{b} - \mathbf{b} \cdot \mathbf{a} - \mathbf{b} \cdot \mathbf{b}\]כאשר $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$ (תכונת החילופיות של מכפלה סקלרית), האיברים האמצעיים מתבטלים.
לכן משוואת האנרגיה הופכת ל:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) \cdot (\mathbf{v}_1 + \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{u}_2 + \mathbf{v}_2)\]שלב 3: הצבה ופישוט
מחוק שימור התנע:
\[m_1(\mathbf{v}_1 - \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2)\]הצבה במשוואת האנרגיה:
\[m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{v}_1 + \mathbf{u}_1) = m_2(\mathbf{u}_2 - \mathbf{v}_2) \cdot (\mathbf{u}_2 + \mathbf{v}_2)\]לאחר צמצום $m_2$ והוצאת גורם משותף:
\[(\mathbf{u}_2 - \mathbf{v}_2) \cdot [(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2)] = 0\]שלב 4: ניתוח התוצאה
חשוב לציין כי אמנם לא ניתן לבצע פעולת חילוק בווקטור (פעולה כזו אינה מוגדרת מתמטית), אך ניתן לנתח מתי מכפלה סקלרית שווה לאפס.
המשוואה
\[(\mathbf{u}_2 - \mathbf{v}_2) \cdot [(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2)] = 0\]מתקיימת באחד משלושה מקרים:
- $\mathbf{u}_2 - \mathbf{v}_2 = \mathbf{0}$ (כלומר $\mathbf{u}_2 = \mathbf{v}_2$)
- $(\mathbf{v}_1 + \mathbf{u}_1) - (\mathbf{u}_2 + \mathbf{v}_2) = \mathbf{0}$
- שני הווקטורים ניצבים זה לזה
המקרה הראשון מתאר מצב בו הגוף השני אינו משנה את מהירותו כלל. זה פתרון בלתי סביר עבור התנגשות כללית, שכן בהתנגשות בין גופים עם מהירויות התחלתיות בלתי תלויות, אין סיבה פיזיקלית מקדימה שהגוף השני ישמור על המהירות המקורית שלו.
המקרה השלישי (ניצבות) דורש תנאי מיוחד על המהירויות שאינו מתקיים באופן כללי.
לכן, עבור התנגשות אמיתית, מתקיים המקרה השני.
התוצאה הסופית
מהמקרה השני נובע:
\[\mathbf{v}_1 + \mathbf{u}_1 = \mathbf{u}_2 + \mathbf{v}_2\]סידור מחדש נותן:
\[\boxed{\mathbf{v}_1 - \mathbf{v}_2 = -(\mathbf{u}_1 - \mathbf{u}_2)}\]פירוש פיזיקלי
משוואה זו מבטאת עיקרון חשוב: בהתנגשות אלסטית, המהירות היחסית בין הגופים משנה כיוון אך שומרת על גודלה.
אם נגדיר:
- $\Delta \mathbf{v} = \mathbf{v}_2 - \mathbf{v}_1$ - המהירות היחסית לפני ההתנגשות
- $\Delta \mathbf{u} = \mathbf{u}_2 - \mathbf{u}_1$ - המהירות היחסית אחרי ההתנגשות
אז:
\[\Delta \mathbf{u} = -(\mathbf{v}_2 - \mathbf{v}_1) = \mathbf{v}_1 - \mathbf{v}_2\]משוואות ההתנגשות האלסטית - סיכום
התנגשות אלסטית בין שני גופים מאופיינת במלואה על ידי שתי משוואות:
-
חוק שימור התנע
\[m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 = m_1 \mathbf{u}_1 + m_2 \mathbf{u}_2\] -
חוק היפוך המהירות היחסית
\[\mathbf{v}_1 - \mathbf{v}_2 = \mathbf{u}_2 - \mathbf{u}_1\]
המשוואה השנייה, שנגזרה משילוב חוקי שימור התנע והאנרגיה, מחליפה למעשה את משוואת שימור האנרגיה. השימוש בה מפשט משמעותית את החישובים בבעיות התנגשות אלסטית, שכן היא מאפשרת עבודה עם משוואות וקטוריות ליניאריות במקום משוואות סקלריות ריבועיות.
שתי המשוואות יחד מספקות מערכת מלאה לפתרון בעיות התנגשות אלסטית, כאשר נתונים הפרמטרים ההתחלתיים של המערכת.
התנגשות פלסטית
התנגשות פלסטית היא התנגשות בה שני הגופים המתנגשים נדבקים זה לזה ונעים לאחר מכן במהירות משותפת. השם נגזר מהאנלוגיה לחומרים פלסטיים כמו פלסטלינה, הנדבקים זה לזה בעת התנגשות.
ניתוח התנגשות פלסטית בין שתי מסות
נתבונן בשתי מסות $m$ ו-$M$:
- לפני ההתנגשות:
- מסה $m$ נעה במהירות $\mathbf{v}$
- מסה $M$ נעה במהירות $\mathbf{V}$
- אחרי ההתנגשות: שתי המסות נעות יחד במהירות משותפת $\mathbf{u}$
יישום חוק שימור התנע:
בהיעדר כוחות חיצוניים, חוק שימור התנע נותן:
\[m \mathbf{v} + M \mathbf{V} = (m + M) \mathbf{u}\]מכאן נובעת המהירות המשותפת:
\[\boxed{\mathbf{u} = \frac{m \mathbf{v} + M \mathbf{V}}{m + M}}\]אי-שימור האנרגיה: בניגוד להתנגשות אלסטית, בהתנגשות פלסטית האנרגיה הקינטית אינה נשמרת.
הסיבה: לאחר ההתנגשות, הפרש המהירויות בין הגופים הוא אפס ($\Delta \mathbf{u} = 0$), בעוד שלפני ההתנגשות $\Delta \mathbf{v} = \mathbf{v} - \mathbf{V} \neq 0$ (בדרך כלל). זה מנוגד לתנאי השימור שנגזר עבור התנגשויות אלסטיות.
חישוב אובדן האנרגיה בהתנגשות פלסטית
האנרגיה הקינטית ה”אובדת” הופכת ל:
- עיוותים פלסטיים: שינויי צורה בלתי הפיכים בגופים
- אנרגיה תרמית: חום הנוצר בעת ההתנגשות
נפתח את הביטוי לאובדן האנרגיה הקינטית. שינוי האנרגיה הקינטית מוגדר כ:
\[\Delta E_k = E_{k,\text{final}} - E_{k,\text{initial}}\]כאשר:
\[E_{k,\text{initial}} = \frac{1}{2}mv^2 + \frac{1}{2}MV^2\] \[E_{k,\text{final}} = \frac{1}{2}(m + M)u^2\]הצבת הביטוי עבור $\mathbf{u}$ וביצוע החישוב האלגברי מובילים לתוצאה:
\[\boxed{\Delta E_k = -\frac{1}{2}\mu(\Delta \mathbf{v})^2}\]כאשר:
- $\Delta \mathbf{v} = \mathbf{v} - \mathbf{V}$ - הפרש המהירויות ההתחלתיות
- $\mu = \frac{mM}{m + M}$ - המסה המצומצמת של המערכת
תכונות התוצאה:
-
סימן שלילי: $\Delta E_k \le 0$, המאשר כי אנרגיה אובדת (או נשמרת במקרה הקיצון) בתהליך
-
תלות בהפרש המהירויות: האנרגיה האובדת פרופורציונית לריבוע הפרש המהירויות ההתחלתיות
-
בדיקת תקינות: כאשר $\mathbf{v} = \mathbf{V}$ (אין מהירות יחסית), $\Delta E_k = 0$ - אין אובדן אנרגיה כיוון שאין התנגשות ממשית
סיכום
התנגשות פלסטית מאופיינת בהידבקות הגופים ותנועה במהירות משותפת. בעוד שהתנע נשמר, האנרגיה הקינטית אינה נשמרת, כאשר האובדן תלוי בהפרש המהירויות ההתחלתיות ובמסה המצומצמת של המערכת.
בחלק הבא נעסוק בשאלה מעשית: בהינתן כוח $\mathbf{F}$, כיצד מוצאים את האנרגיה הפוטנציאלית $\phi$ המקיימת $\mathbf{F} = -\nabla \phi$ (בהנחה שהכוח משמר)?
תהליך זה אינו תמיד טריוויאלי, אך ניתן לביצוע עבור כוחות רבים בעלי חשיבות פיזיקלית.
דוגמה 1: כוח הכבידה בקרבת פני כדור הארץ
בחלק זה נעסוק בשיטה למציאת האנרגיה הפוטנציאלית $\phi$ מתוך הכוח $\mathbf{F}$, בהנחה שמדובר בכוח משמר המקיים $\mathbf{F} = -\nabla \phi$.
הקדמה והבחנה חשובה
נתחיל בניתוח כוח הכבידה בקרבת פני כדור הארץ. יש להדגיש כי הטיפול בכוח הכבידה בקרבת פני כדור הארץ שונה מהותית מהטיפול בכוח הכבידה במרחקים גדולים מכדור הארץ, נושא שיידון בנפרד.
הגדרת הכוח
בקרבת פני כדור הארץ, כאשר ציר ה-$y$ מוגדר כלפי מעלה:
\[\mathbf{F} = -mg\hat{\mathbf{y}}\]כוח הכבידה פועל כלפי מטה, גודלו $mg$, וכיוונו במינוס $\hat{\mathbf{y}}$.
תזכורת: $\hat{\mathbf{y}}$ הוא וקטור יחידה בכיוון ציר ה-$y$ (כלפי מעלה). $g$ הוא סקאלר שמתאים לתאוצת הכבידה (בערך $10 \, \text{m/s}^2$).
מציאת האנרגיה הפוטנציאלית של כוח הכבידה
מהתנאי לכוח משמר:
\[\mathbf{F} = -\nabla \phi = -\frac{\partial \phi}{\partial x}\hat{\mathbf{x}} - \frac{\partial \phi}{\partial y}\hat{\mathbf{y}} - \frac{\partial \phi}{\partial z}\hat{\mathbf{z}}\]השוואה עם הביטוי לכוח הכבידה:
\[-mg\hat{\mathbf{y}} = -\frac{\partial \phi}{\partial x}\hat{\mathbf{x}} - \frac{\partial \phi}{\partial y}\hat{\mathbf{y}} - \frac{\partial \phi}{\partial z}\hat{\mathbf{z}}\]נקודה חשובה: זאת משוואה וקטורית. הזהות חייבת להתקיים לא רק מבחינה אריתמטית אלא גם מבחינה מבנית - אם באגף שמאל יש וקטור בכיוון מסוים, באגף ימין חייב להיות וקטור באותו כיוון.
מכיוון שהכוח הוא בכיוון $\hat{\mathbf{y}}$ בלבד, הרכיבים בכיווני $\hat{\mathbf{x}}$ ו-$\hat{\mathbf{z}}$ חייבים להתאפס:
- $\frac{\partial \phi}{\partial x} = 0$
- $\frac{\partial \phi}{\partial z} = 0$
ולכן נותרת המשוואה:
\[-mg\hat{\mathbf{y}} = -\frac{\partial \phi}{\partial y}\hat{\mathbf{y}}\]ביטול הכיוון הווקטורי משני האגפים:
\[mg = \frac{\partial \phi}{\partial y}\]אינטגרציה נותנת:
\[\phi(y) = mgy + C\]כאשר $C$ הוא קבוע אינטגרציה. מקובל לבחור $C = 0$, ולכן:
\[\boxed{\phi(y) = mgy}\]המשמעות: האנרגיה הפוטנציאלית של גוף בעל מסה $m$ בגובה $y$ מעל מישור הייחוס (למשל, פני הים) היא $mgy$.
יישום: נפילה חופשית ממגדל
נתבונן בגוף הנופל מגובה $h$ (למשל, ממגדל אייפל). נבחר את מישור הקרקע כנקודת הייחוס ($y = 0$).
ניתוח אנרגטי
מצב התחלתי (בגובה $h$):
- אנרגיה קינטית: $E_{k,\text{initial}} = 0$ (התחלה ממנוחה)
- אנרגיה פוטנציאלית: $\phi_{\text{initial}} = mgh$
מצב סופי (רגע לפני הפגיעה בקרקע):
- אנרגיה קינטית: $E_{k,\text{final}} = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi_{\text{final}} = 0$
מחוק שימור האנרגיה:
\[E_{k,\text{initial}} + \phi_{\text{initial}} = E_{k,\text{final}} + \phi_{\text{final}}\]הצבת הערכים:
\[0 + mgh = \frac{1}{2}mv^2 + 0\]פתרון למהירות:
\[v = \sqrt{2gh}\]הערה חשובה: בחירת מישור הייחוס (איפה $y = 0$) היא שרירותית לחלוטין. הגודל הפיזיקלי המשמעותי הוא הפרש האנרגיות הפוטנציאליות, שאינו תלוי בבחירת נקודת הייחוס.
הכללה: התחלה ממהירות שונה מאפס
במקרה כללי יותר, כאשר הגוף מתחיל את תנועתו במהירות $v_{\text{initial}}$:
\[\frac{1}{2}mv_{\text{initial}}^2 + mgh = \frac{1}{2}mv_{\text{final}}^2\]לאחר צמצום המסה:
\[v_{\text{final}}^2 = v_{\text{initial}}^2 + 2gh\]תובנה חשובה: התוצאה אינה תלויה בכיוון המהירות ההתחלתית (כלפי מעלה או מטה), שכן במשוואת האנרגיה מופיע $v^2$ - ריבוע המהירות אינו רגיש לכיוון.
הקשר לקינמטיקה
המשוואה שהתקבלה:
\[v_{\text{final}}^2 = v_{\text{initial}}^2 + 2gh\]זהה למשוואה הקינמטית המוכרת לתנועה בתאוצה קבועה:
\[v^2 = v_0^2 + 2a\Delta x\]כאשר במקרה של נפילה חופשית $a = g$ ו-$\Delta x = h$.
יתרון שיטת האנרגיה: ניתן להגיע לתוצאה ללא צורך בידע מפורט בקינמטיקה. חישובי אנרגיה מפשטים משמעותית בעיות רבות במכניקה.
דוגמה 2: כוח מחזיר (קפיץ)
נתון כוח מחזיר:
\[\mathbf{F} = -k\mathbf{r}\]כאשר $k$ הוא קבוע הקפיץ ו-$\mathbf{r}$ הוא וקטור המיקום.
המטרה: למצוא את האנרגיה הפוטנציאלית $\phi$ המקיימת את התנאי לכוח משמר:
\[\mathbf{F} = -\nabla \phi\]גרדיאנט בקואורדינטות רדיאליות
הערה מקדימה: עבור פונקציה התלויה רק בגודל המרחק $r = \vert \mathbf{r} \vert$, הגרדיאנט בקואורדינטות רדיאליות הוא:
\[\nabla \phi(r) = \frac{d\phi}{dr} \hat{\mathbf{𝒓}}\]כאשר $\hat{\mathbf{𝒓}}$ הוא וקטור היחידה הרדיאלי. נושא זה יידון בהרחבה בשיעור הבא.
מציאת האנרגיה הפוטנציאלית של קפיץ
ננחש את הצורה של האנרגיה הפוטנציאלית:
\[\phi = \frac{1}{2}k\mathbf{r} \cdot \mathbf{r} = \frac{1}{2}kr^2\]אימות התוצאה
נבדוק שאכן $\mathbf{F} = -\nabla \phi$:
שלב 1: חישוב הגרדיאנט
\[-\nabla \phi = -\frac{d\phi}{dr} \hat{\mathbf{𝒓}}\]שלב 2: הצבת הפונקציה
\[-\nabla \phi = -\frac{d}{dr}\left(\frac{1}{2}kr^2\right) \hat{\mathbf{𝒓}}\]שלב 3: ביצוע הגזירה
יש לשים לב כי:
\[\mathbf{r} \cdot \mathbf{r} = |\mathbf{r}|^2 = r^2\]לכן:
\[-\nabla \phi = -\frac{k}{2} \frac{d}{dr}(r^2) \hat{\mathbf{𝒓}}\]על פי כלל הגזירה: $\frac{d}{dr}(r^2) = 2r$
שלב 4: התוצאה הסופית
\[-\nabla \phi = -\frac{k}{2} \cdot 2r \cdot \hat{\mathbf{𝒓}} = -kr\hat{\mathbf{𝒓}} = -k\mathbf{r}\]קיבלנו בדיוק את הכוח הנתון, מה שמאמת את הביטוי לאנרגיה הפוטנציאלית.
המקרה החד-ממדי: קפיץ ליניארי
עבור קפיץ בממד אחד (לאורך ציר $x$), האנרגיה הפוטנציאלית היא:
\[\boxed{\phi(x) = \frac{1}{2}kx^2}\]זהו מקרה פרטי של הנוסחה הכללית $\phi = \frac{1}{2}kr^2$ עבור תנועה חד-ממדית.
הפירוש הפיזיקלי
כאשר מותחים קפיץ, מכניסים לתוכו אנרגיה פוטנציאלית. אנרגיה זו קשורה לכוח המשמר שהקפיץ מפעיל בניסיון לחזור למצב שיווי המשקל.
יישום: תנועת מסה על קפיץ
נתבונן במערכת הבאה:
- קפיץ בעל קבוע $k$
- מסה $m$ מחוברת לקפיץ
- המסה נמתחת למרחק $x$ ומשוחררת ממנוחה
השאלה: מהי מהירות המסה כאשר היא עוברת דרך נקודת שיווי המשקל?
הנחה מפשטת: אורך הקפיץ הרפוי הוא אפס (ניתן להכליל למקרה כללי)
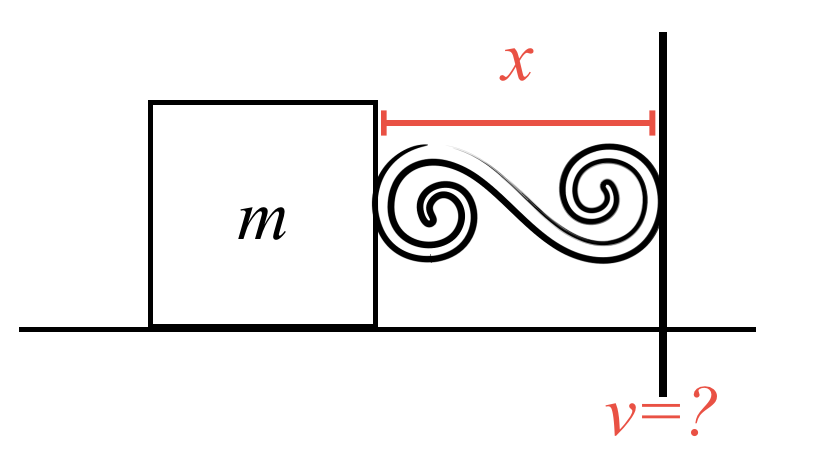
פתרון באמצעות שימור אנרגיה
מצב התחלתי (במרחק $x$ מהמקור):
- אנרגיה קינטית: $E_{k,\text{initial}} = 0$ (התחלה ממנוחה)
- אנרגיה פוטנציאלית: $\phi_{\text{initial}} = \frac{1}{2}kx^2$
מצב סופי (בנקודת שיווי המשקל):
- אנרגיה קינטית: $E_{k,\text{final}} = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi_{\text{final}} = 0$
מחוק שימור האנרגיה המכנית:
\[\underbrace{\frac{1}{2}m \cdot 0^2 + \frac{1}{2}kx^2}_{E_i} = \underbrace{\frac{1}{2}mv^2 + \frac{1}{2}k \cdot 0^2}_{E_f}\]פישוט:
\[\frac{1}{2}kx^2 = \frac{1}{2}mv^2\] \[kx^2 = mv^2\]פתרון למהירות:
\[v^2 = \frac{k}{m}x^2\]קשר לתדירות הזוויתית
נזכור כי $\omega^2 = \frac{k}{m}$ היא התדירות הזוויתית של התנודה, לכן:
\[v = \omega x\]התוצאה הזאת מתאימה לידוע מתורת התנודות ההרמוניות.
סיכום ומבט קדימה
-
כוח האנרגיה: שימוש בשימור אנרגיה מאפשר חישוב מהירויות ללא צורך בפתרון משוואות התנועה המלאות
- תנאי היישום: השיטה יעילה כאשר:
- הכוחות הם משמרים
- ידועה האנרגיה הפוטנציאלית
- האנרגיה המכנית נשמרת
- מגבלות: במקרים של כוחות לא-משמרים (כגון חיכוך) או תהליכים לא-אלסטיים (כגון התנגשויות פלסטיות), חלק מהאנרגיה הופך לחום או לעיוותים, והשיטה דורשת התאמה.
בשיעור הבא נחדד את הנקודה הזאת, נדבר על תהליכים שלא משמרים אנרגיה, ונדבר גם על עוד אנרגיות פוטנציאליות של כוחות, כולל דוגמאות ספציפיות.
אבל זה יהיה כנראה אחרי הבחינה, בתקווה שתהיה בחינה ביום שני. ואם לא תתקיים בחינה ביום שני מפאת המצב, נמשיך את הדיון הזה ביום שני הבא.
תרגול
חזרה - עקרונות יסוד
משפט עבודה-אנרגיה (חזרה)
העבודה הכוללת המבוצעת על גוף שווה לשינוי באנרגיה הקינטית שלו:
\[W_{\text{net}} = \Delta E_k = E_{k,\text{final}} - E_{k,\text{initial}}\]הגדרת עבודה (חזרה)
עבודה מוגדרת כתוצר הכוח בתזוזה:
\[W = \mathbf{F} \cdot \mathbf{d} = Fd\cos\theta\]עבור כוח משתנה:
\[W = \int \mathbf{F} \cdot d\mathbf{r}\]שאלה 1: משפט עבודה-אנרגיה במישור משופע
גוף מחליק במורד מדרון מחוספס עם מקדם חיכוך קינטי $\mu_k$. הגוף משוחרר ממנוחה מגובה $h$ מעל תחתית המדרון.
בהנחה שהגוף התחיל במנוחה, מה השינוי באנרגיה הקינטית שלו במהלך תנועתו?
|\ | \ ↖ fₖ h | \ N↗ 🔹 | \ ↓mg | \ | θ \ ---------הכוחות הפועלים על הגוף:
- כוח הכבידה: $mg$ (אנכי כלפי מטה)
- כוח נורמלי: $N = mg\cos\theta$
- כוח חיכוך: $f_k = \mu_k N = \mu_k mg\cos\theta$
דרך 1: שימור אנרגיה עם כוחות לא משמרים
\[\begin{aligned} \Delta E_k &= W_{\text{conservative}} + W_{\text{non-conservative}} \\ \Delta E_k &= \Delta E_p -W_{f_k} \\ &= mgh - f_k \cdot \ell \\ &= mgh - (\mu_k mg \cos \theta) \cdot \left(\frac{h}{\sin\theta}\right) \\ &= mgh - \mu_k mg h \frac{\cos\theta}{\sin\theta} \\ \Delta E_k &= \boxed{mgh \left(1 - \mu_k \cot\theta\right)} \end{aligned}\]הבהרה לגבי $h/\sin\theta$:
|\ h | \ ℓ (distance along incline) | \ | \ | θ \ -------השוויון נובע מכך ש:
\[\ell = \frac{h}{\sin\theta}\]הבהרה נוספת:
לגבי $f_k = \mu_k N = \mu_k mg\cos\theta$:
mg (total gravitational force, pointing straight down) | | ↓ |\ h | \ | \ ← mg cos θ (perpendicular to incline) | \ | θ \ ------- → mg sin θ (parallel to incline, down the slope)השוויון נובע מכך ש:
\[N = mg\cos\theta\]דרך 2: לפי משפט עבודה-אנרגיה
\[\begin{aligned} \Delta E_k = W_{\text{net}} &= \int_0^{\ell} F_{\text{net}} \, dx \\ &= \int_0^{h/\sin\theta} (mg\sin\theta - \mu_k mg\cos\theta) \, dx \\ &= \left(mg\sin\theta - \mu_k mg\cos\theta \right) \cdot \frac{h}{\sin\theta} \\ &= mgh - \mu_k mgh \cot\theta \\ &= \boxed{mgh(1 - \mu_k \cot\theta)} \end{aligned}\]מסקנה פיזיקלית
- כאשר $\mu_k = 0$ (ללא חיכוך): $\Delta E_k = mgh$ - כל האנרגיה הפוטנציאלית הופכת לקינטית
- כאשר $1 - \mu_k \cot\theta \le 0$:
- $\Delta E_k \le 0$ - הגוף לא יאיץ (או לא יזוז כלל אם החיכוך הסטטי מספיק גדול)
- בכל מקרה אחר: חלק מהאנרגיה הפוטנציאלית “אובד” לחיכוך (הופך לחום)
שאלה 2: כוחות משמרים
כוח הוא משמר אם העבודה שהוא מבצע לאורך כל מסלול סגור שווה לאפס:
\[\oint \mathbf{F} \cdot d\mathbf{r} = 0\]משמעות פיזיקלית: עבודה שמבוצעת על ידי כוח משמר תלויה רק בנקודות ההתחלה והסיום, לא במסלול עצמו.
איזה מהכוחות הבאים אינו משמר?
- $\mathbf{F} = (x,y,0)$
- $\mathbf{F} = (\cos x, 0, 0)$
- $\mathbf{F} = (y,x,0)$
- $\mathbf{F} = (xy,xy,0)$
- $\mathbf{F} = (xy^2,yx^2,0)$
הבהרה: המטרה היא למצוא כוח אחד ומסלול סגור אחד שעבורם:
\[\oint \mathbf{F} \cdot d\mathbf{r} \neq 0\]לשלמות התמונה (ניתן להוכיח באמצעות תנאי הרוטור $\nabla \times \mathbf{F} = \mathbf{0}$):
- $\mathbf{F} = (x,y,0)$ - משמר
- $\mathbf{F} = (\cos x, 0, 0)$ - משמר
- $\mathbf{F} = (y,x,0)$ - משמר
- $\mathbf{F} = (xy,xy,0)$ - לא משמר
- $\mathbf{F} = (xy^2,x^2y,0)$ - משמר (הייתה טעות בניסוח המקורי)
בדיקת שמרנות: $\mathbf{F} = (xy,xy,0)$
נבחר מסלול מלבני במישור $xy$ מ-$(0,0)$ דרך $(1,0)$, $(1,2)$, $(0,2)$ וחזרה ל-$(0,0)$.
(0,2) ←──I₃── (1,2) ↑ ↑ I₄ I₂ ↓ ↓ (0,0) ──I₁──→ (1,0)המסלול כולל ארבע צלעות:
\[\oint \mathbf{F} \cdot d\mathbf{r} = \int_{I_1} + \int_{I_2} + \int_{I_3} + \int_{I_4}\]חישוב אינטגרלים
צלע $I_1$: $(0,0) \to (1,0)$ ($y=0, dy=0, d\mathbf{r}=dx\hat{\mathbf{x}}$)
\[\int_0^1 (x \cdot 0, x \cdot 0, 0) \cdot (dx, 0, 0) = \int_0^1 0 \, dx = 0\]צלע $I_2$: $(1,0) \to (1,2)$ ($x=1, dx=0, d\mathbf{r}=dy\hat{\mathbf{y}}$)
\[\int_0^2 (1 \cdot y, 1 \cdot y, 0) \cdot (0, dy, 0) = \int_0^2 y \, dy = \left[ \frac{y^2}{2} \right]_0^2 = 2\]צלע $I_3$: $(1,2) \to (0,2)$ ($y=2, dy=0, d\mathbf{r}=-dx\hat{\mathbf{x}}$)
\[\int_1^0 (x \cdot 2, x \cdot 2, 0) \cdot (dx, 0, 0) = \int_1^0 2x \, dx = \left[ x^2 \right]_1^0 = 0 - 1 = -1\]צלע $I_4$: $(0,2) \to (0,0)$ ($x=0, dx=0, d\mathbf{r}=-dy\hat{\mathbf{y}}$)
\[\int_2^0 (0 \cdot y, 0 \cdot y, 0) \cdot (0, dy, 0) = \int_2^0 0 \, dy = 0\]סך הכל:
\[\oint \mathbf{F} \cdot d\mathbf{r} = 0 + 2 - 1 + 0 = 1 \neq 0\]ולכן הכוח אינו משמר.
שאלה 3: התפוצצות
עגלה במסה $M$ ובתוכה כדור במסה $m$ נעות ימינה במהירות משותפת $v$ על מסילה ללא חיכוך. ברגע מסוים נפער בור בתחתית העגלה והכדור נפל דרכו למטה.
מהי מהירות העגלה לאחר שהכדור נפל?
before: [m+M]→v after: [M]→U , [m]→uאם נזניח את האינטראקציה האנכית, על ציר ה-$x$ לא פועלים כוחות חיצוניים על המערכת (עגלה+כדור). לכן התנע האופקי נשמר. כאשר הכדור נופל, אין כוח אופקי שפועל עליו או על העגלה. לכן, המהירות האופקית של כל גוף נשמרת.
מהירות אופקית התחלתית של הכדור: $v_x = v$. מהירות אופקית התחלתית של העגלה: $V_x = v$.
לאחר הנפילה, המהירות האופקית של הכדור היא $u_x = v$. המהירות האופקית של העגלה היא $U_x = v$.
\[\boxed{U = v}\]כלומר, גם העגלה וגם הכדור שומרים על מהירותם האופקית.
שאלה 4: התנגשות אלסטית
כדור שמסתו $m$ נע ימינה בתוך מסגרת מלבנית, במקביל לצלע שאורכה $\ell$, במהירות קבועה $v$.
מסת המסגרת היא $M = \alpha m$ (כאשר $\alpha > 0$).
לאחר זמן מסוים הכדור מתנגש חזיתית ואלסטית במסגרת. התנועה היא במישור אופקי ללא חיכוך.
- חשבו את מהירות הכדור והמסגרת מיד לאחר ההתנגשות.
- מה קורה כאשר $\alpha \to 0, \alpha = 1, \alpha \gg 1$? הסבירו את התוצאות.
- עבור $\alpha > 0$, כמה זמן יעבור בין ההתנגשות הראשונה לשנייה?
M=αm ┌───────────────┐ │ [m]→v │ └───────────────┘ ───ℓ───→ [M=αm]הקדמה:
- נסמן מהירויות לפני התנגשות: $v_m = v$, $v_M = 0$.
- נסמן מהירויות אחרי התנגשות: $u_m$, $u_M$.
- הבעיה חד-ממדית.
1. חישוב מהירויות לאחר ההתנגשות
מערכת המשוואות להתנגשות אלסטית חד-ממדית:
שימור תנע:
\[mv_m + \cancel{Mv_M} = mu_m + Mu_M\] \[\implies \boxed{mv = mu_m + (\alpha m)u_M}\]שימור אנרגיה (או היפוך מהירות יחסית):
\[v_m - \cancel{v_M} = u_M - u_m\] \[\implies v = u_M - u_m\]נפשט את משוואת התנע:
\[v = u_m + \alpha u_M \quad (*)\]ממשוואת המהירות היחסית:
\[u_m = u_M - v \quad (**)\]נציב את \((**)\) ב-\((*)\):
\[v = (u_M - v) + \alpha u_M\] \[2v = u_M(1 + \alpha)\] \[\boxed{u_M = \frac{2v}{1 + \alpha}}\]נציב חזרה ב-$(**)$:
\[\begin{aligned} u_m &= \frac{2v}{1 + \alpha} - v \\[10pt] &= \frac{2v - v(1+\alpha)}{1+\alpha} \\[10pt] &= \frac{v(1-\alpha)}{1+\alpha} \end{aligned}\] \[\boxed{ u_M = \frac{2v}{1 + \alpha}, \quad u_m = v\frac{1 - \alpha}{1 + \alpha}}\]2. מקרים מיוחדים
כאשר $\alpha \to 0$ (מסגרת חסרת מסה):
\[u_M \to 2v, \qquad u_m \to v\]לא פיזיקלי, המסגרת לא יכולה לנוע מהר יותר מהכדור שפגע בה.
כאשר $\alpha = 1$ (מסות שוות):
\[u_M = v, \qquad u_m = 0\]הכדור נעצר ומעביר את כל התנע שלו למסגרת, כמו במטוטלת של ניוטון.
כאשר $\alpha \gg 1$ (מסגרת כבדה מאוד):
\[u_M \to 0, \qquad u_m \to -v\]המסגרת בקושי זזה, והכדור חוזר אחורה באותה מהירות (כמו כדור שקופץ מקיר).
3. זמן בין ההתנגשויות
הכדור צריך לעבור מרחק $\ell$ יחסית לקצה השני של המסגרת. המהירות היחסית לאחר ההתנגשות היא:
\[\begin{aligned} \Delta u &= u_m - u_M \\[10pt] &= v\frac{1 - \alpha}{1 + \alpha} - \frac{2v}{1 + \alpha} \\[10pt] &= \frac{v(1 - \alpha - 2)}{1 + \alpha} \\[10pt] &= \frac{v(-1 - \alpha)}{1 + \alpha} = -v \end{aligned}\]המהירות היחסית היא בגודל $v$ - הכדור מתרחק מהקיר הראשון ומתקרב לקיר השני במהירות יחסית $v$.
\[\boxed{t = \frac{\ell}{|\Delta u|} = \frac{\ell}{v}}\]
שאלה 5: התנגשות דו-מימדית
כדור בעל מסה $2m$ מחליק על משטח אופקי חלק במהירות $v_0$ לאורך ציר $x$.
הכדור מתנגש בכדור אחר בעל מסה $m$ שנמצא במנוחה.
לאחר ההתנגשות נע החלקיק שמסתו $m$ במהירות $v_0/2$ בכיוון היוצר זווית בת $\theta = 30^\circ$ עם ציר ה-$x$.
- מה המהירות (גודל וכיוון) של החלקיק שמסתו $2m$ לאחר ההתנגשות?
- האם ההתנגשות אלסטית לחלוטין?
↗ v₀ v₀/2 / → / θ=30^\circ -●------------○-----→ 2m m x1. מהירות החלקיק בעל המסה $2m$ לאחר ההתנגשות
נשתמש בשימור תנע (לא נתון מידע על סוג ההתנגשות). נסמן את מהירות הגוף $2m$ לאחר ההתנגשות ב-$\mathbf{u}$.
התנע ההתחלתי: לפני ההתנגשות רק הכדור בעל המסה $2m$ נע, ורק על ציר $x$:
\[\mathbf{p}_i = (2m v_0) \hat{\mathbf{x}}\]התנע הסופי: לאחר ההתנגשות שני הכדורים נעים, אחד במהירות $v_0/2$ בזווית של $30^\circ$, והשני במהירות $\mathbf{u}$:
\[\mathbf{p}_f = (2m) \mathbf{u} + m \left(\frac{v_0}{2}\cos\theta \hat{\mathbf{x}} + \frac{v_0}{2}\sin\theta \hat{\mathbf{y}}\right)\]נשווה רכיבים:
ציר $x$: →
\[\begin{aligned} p_{x,i} &= p_{x,f} \\ 2mv_0 &= 2mu_{x} + m\frac{v_{0}}{2} \cos(30^\circ) \\ 2v_0 &= 2u_x + \frac{v_0}{2} \frac{\sqrt{3}}{2} \\ 2u_x &= 2v_0 - \frac{v_0\sqrt{3}}{4} \\ u_{x} &= v_0 \left(1 - \frac{\sqrt{3}}{8}\right) \end{aligned}\]ציר $y$: ↑
\[\begin{aligned} p_{y,i} &= p_{y,f} \\ 0 &= 2mu_{y} + m\frac{v_{0}}{2} \sin(30^\circ) \\ 0 &= 2u_y + \frac{v_0}{2} \frac{1}{2} \\ u_{y} &= -\frac{v_0}{8} \end{aligned}\]גודל $u$:
\[\begin{aligned} u = |\mathbf{u}| &= \sqrt{u_x^2 + u_y^2} \\[10pt] &= v_0 \sqrt{\left(1 - \tfrac{\sqrt{3}}{8}\right)^2 + \left(-\tfrac{1}{8}\right)^2} \\[10pt] &\approx \boxed{0.793 v_0} \end{aligned}\]כיוון $u$:
\[\phi = \arctan\left(\frac{u_y}{u_x}\right) = \arctan\left(\tfrac{-1/8}{1 - \sqrt{3}/8}\right) \approx \boxed{-9.1^\circ}\]2. האם ההתנגשות אלסטית לחלוטין
נבדוק שימור אנרגיה קינטית:
לפני ההתנגשות:
\[E_{k,i} = \frac{1}{2} (2m) v_0^2 = \boxed{mv_0^2}\]אחרי ההתנגשות:
\[\begin{aligned} E_{k,f} &= \frac{1}{2} (2m) u^2 + \frac{1}{2} m \left(\frac{v_0}{2}\right)^2 \\[10pt] &= m (0.793v_0)^2 + \frac{m v_0^2}{8} \\[10pt] &= m v_0^2 (0.793^2 + 1/8) \\[10pt] &= m v_0^2 (0.629 + 0.125) = \boxed{0.754mv_0^2} \end{aligned}\]מכיוון ש-$E_{k,f} < E_{k,i}$, ההתנגשות אינה אלסטית.
הערה: האנרגיה הקינטית של המערכת לאחר ההתנגשות קטנה מהאנרגיה הקינטית לפני ההתנגשות, כפי שצריך להיות בהתנגשות לא-אלסטית.
עקרונות מרכזיים - סיכום
עקרון נוסחה הסבר ותכונות משפט עבודה-אנרגיה \(W_{\text{net}} = \Delta E_k\) • כולל את כל הכוחות (משמרים ולא משמרים)
• חיכוך תמיד מפחית אנרגיה קינטיתכוחות משמרים \(\oint \mathbf{F} \cdot d\mathbf{r} = 0\) • עבודה תלויה רק בנקודות קצה
• מאפשרים הגדרת אנרגיה פוטנציאליתשימור תנע \(\mathbf{p}_{\text{total}} = \text{constant}\) • תקף תמיד כשאין כוחות חיצוניים
• עובד בכל ממד בנפרדהתנגשויות תלוי בסוג ההתנגשות • אלסטית: נשמרים תנע ואנרגיה קינטית
• אי-אלסטית: נשמר רק תנע
• פלסטית (אי-אלסטית מושלמת): הגופים נדבקים יחדשיטות פתרון - • חד-מימדי: משוואות אלגבריות פשוטות
• דו-מימדי: שימור תנע בכל ציר בנפרד
• בדיקת עקביות: תמיד לבדוק שימור אנרגיהטיפים לפתרון בעיות - • זהה את כל הכוחות הפועלים
• בחר מערכת צירים מתאימה
• השתמש בשימורים הרלוונטיים
• בדוק עקביות התוצאות
• פרש פיזית את התוצאותשיעור 12 - שימור אנרגיה מכנית ויישומיה
תאריך: 23/06/2025חזרה: חוק שימור האנרגיה המכנית
בשיעור הקודם למדנו על אחד העקרונות החשובים בפיזיקה - חוק שימור האנרגיה המכנית. כדי להבין אותו נתחיל מהמושג הבסיסי של עבודה.
הגדרת העבודה
העבודה $W$ שמבצע כוח $\vec{F}$ על גוף הנע לאורך מסלול מנקודה $\vec{r}_1$ לנקודה $\vec{r}_2$ מוגדרת כאינטגרל המסלולי:
\[W = \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d\vec{r}\]שימו לב שהעבודה היא גודל סקלרי (מספר) - היא מחושבת ממכפלה סקלרית של וקטורים. היחידות שלה הן יחידות של אנרגיה - ג’אול (Joule).
הקשר בין עבודה לאנרגיה
התגלית המרכזית היא שניתן לבטא את גודל העבודה בשתי דרכים שונות:
1. מצד האנרגיה הקינטית:
\[W = E_{kf} - E_{ki} = \Delta E_K\]כאשר האנרגיה הקינטית מוגדרת תמיד כ:
\[E_K = \frac{1}{2}mv^2 = \frac{p^2}{2m}\]2. מצד האנרגיה הפוטנציאלית (עבור כוחות משמרים בלבד):
\[W = \phi_{i} - \phi_{f} = -\Delta \phi\]שימו לב לסימן המינוס: כאשר האנרגיה הפוטנציאלית יורדת, העבודה חיובית.
כוחות משמרים
מהו כוח משמר?
כוח משמר הוא כוח בעל תכונה מיוחדת: העבודה שהוא מבצע תלויה רק בנקודות ההתחלה והסיום, ולא במסלול ביניהן. מתמטית, כוח משמר $\vec{F}$ ניתן לכתיבה כ:
\[\vec{F}_{\text{conservative}} = -\nabla \phi\]כלומר, הכוח הוא מינוס הגרדיאנט של פונקציית הפוטנציאל $\phi$.
התכונה המגדירה של כוח משמר
עבור כוח משמר, העבודה על מסלול סגור (כאשר נקודת ההתחלה והסיום זהות) היא תמיד אפס:
\[\oint \vec{F} \cdot d\vec{r} = 0\]דוגמה מעניינת: כאשר הירח מקיף את כדור הארץ במסלול סגור, כוח הכבידה (שהוא כוח משמר) מבצע עבודה כוללת של אפס - למרות שהכוח פועל כל הזמן!
חוק שימור האנרגיה המכנית
כעת, אם נשווה את שני הביטויים לעבודה:
- $W = E_{kf} - E_{ki}$
- $W = \phi_{i} - \phi_{f}$
נקבל:
\[E_{kf} - E_{ki} = \phi_{i} - \phi_{f}\]או לאחר סידור מחדש:
\[\boxed{E_{ki} + \phi_{i} = E_{kf} + \phi_{f}}\]זהו חוק שימור האנרגיה המכנית: סכום האנרגיה הקינטית והפוטנציאלית נשאר קבוע לאורך התנועה (כאשר פועלים רק כוחות משמרים).
כאשר פועלים גם כוחות שאינם משמרים (כמו חיכוך), נוסיף את העבודה של כוחות אלה:
\[\boxed{W_{\text{NC}} = E_{f} - E_{i}}\]כאשר $W_{\text{NC}}$ היא העבודה של כוחות לא משמרים (None Conservative), $E_f$ ו-$E_i$ הן האנרגיה המכנית הכוללת בסוף ובתחילת התנועה (כוללת גם אנרגיה קינטית וגם פוטנציאלית).
דוגמאות לאנרגיה פוטנציאלית
1. כוח כובד קבוע (ליד פני כדור הארץ)
עבור גוף בגובה $h$ מעל נקודת ייחוס:
\[\phi_{\text{gravity}} = mgh\]2. כוח אלסטי (קפיץ אידיאלי)
עבור קפיץ עם קבוע קפיץ $k$ והעתקה $x$ ממצב שיווי משקל:
\[\phi_{\text{elastic}} = \frac{1}{2}kx^2\]סוגי התנגשויות
כששני גופים מתנגשים, אנו מבחינים בין שני סוגים עיקריים:
1. התנגשות אלסטית
- נשמר התנע: \(\vec{p}_{i} = \vec{p}_{f}\)
- נשמרת האנרגיה המכנית: $E_{i} = E_{f}$
- הגופים “קופצים” זה מזה לאחר ההתנגשות
2. התנגשות פלסטית (לא-אלסטית לחלוטין)
- נשמר התנע: \(\vec{p}_{i} = \vec{p}_{f}\)
- האנרגיה המכנית אינה נשמרת (חלק ממנה הופך לחום, עיוות, וכו’)
- במקרה הקיצוני, הגופים נצמדים זה לזה לאחר ההתנגשות
דוגמה טריוויאלית: נפילה חופשית
נניח שגוף נופל מגובה $h_1$ לגובה $h_2$ (כאשר $h_1 > h_2$). נוכל להשתמש בחוק שימור האנרגיה:
\[\underbrace{mgh_1}_{\phi_1} + \underbrace{\frac{1}{2}mv_1^2}_{E_{K,1}} = \underbrace{mgh_2}_{\phi_2} + \underbrace{\frac{1}{2}mv_2^2}_{E_{K,2}}\]היופי בשיטה זו הוא שאיננו צריכים לדעת כלום על המסלול או על הזמן - רק את המצב ההתחלתי והסופי! זה הופך בעיות מורכבות לפשוטות הרבה יותר.
לדוגמה, אם הגוף מתחיל ממנוחה ($v_1 = 0$) בגובה $h_1$, נוכל למצוא את מהירותו בגובה $h_2$:
\[mgh_1 = mgh_2 + \frac{1}{2}mv_2^2\]ולאחר פישוט:
\[v_2 = \sqrt{2g(h_1 - h_2)}\]שימו לב כיצד המסה $m$ מצטמצמת - כל הגופים נופלים באותו קצב בשדה כבידה אחיד!
2 יישום: תנועת מטוטלת
נסתכל על מטוטלת פשוטה: מסה נקודתית $m$ התלויה על חוט חסר מסה באורך $L$. מסיטים את המטוטלת בזווית $\theta_0$ ביחס לאנך ומשחררים ממנוחה.
שאלה: מהי מהירות המטוטלת בנקודה הנמוכה ביותר של מסלולה?
נבחר את מישור הייחוס לאנרגיה פוטנציאלית ($\phi_g=0$) בנקודה הנמוכה ביותר ($h=0$).
הגובה ההתחלתי של המטוטלת, כאשר היא בזווית $\theta_0$, הוא:
\[h_0 = L - L\cos\theta_0 = L(1 - \cos\theta_0)\]
כעת נשתמש בחוק שימור האנרגיה המכנית:
\[E_{i} = E_{f}\]בנקודה ההתחלתית (בזווית $\theta_0$):
- אנרגיה קינטית: $E_{ki} = 0$ (שוחרר ממנוחה)
- אנרגיה פוטנציאלית: $\phi_i = mgh_0 = mgL(1 - \cos\theta_0)$
בנקודה הנמוכה ביותר:
- אנרגיה קינטית: $E_{kf} = \frac{1}{2}mv^2$
- אנרגיה פוטנציאלית: $\phi_f = 0$ (לפי בחירתנו)
משימור אנרגיה:
\[0 + mgL(1 - \cos\theta_0) = \frac{1}{2}mv^2 + 0\]נצמצם את $m$ ונפתור עבור $v$:
\[\boxed{v = \sqrt{2gL(1 - \cos\theta_0)}}\]שימו לב: אם $\theta_0 = 90^\circ = \frac{\pi}{2}$ (שחרור ממצב אופקי), אז $\cos(\pi/2) = 0$ ונקבל:
\[v = \sqrt{2gL}\]זו בדיוק המהירות של גוף בנפילה חופשית מגובה $L$!
הקואורדינטה המוכללת של המטוטלת
בתנועת המטוטלת, הקואורדינטה הנוחה לתיאור המערכת היא הזווית $\theta$. אורך הקשת שהמטוטלת עוברת הוא:
\[s = L\theta\]לכן המהירות המשיקית היא:
\[v = \frac{ds}{dt} = L\frac{d\theta}{dt} = L\dot{\theta}\]כאשר $\dot{\theta}$ היא המהירות הזוויתית.
האנרגיה הכוללת של המטוטלת כפונקציה של $\theta$ ו-$\dot{\theta}$:
\[\begin{aligned} E &= E_K + \phi_g = \frac{1}{2}mv^2 + mgh \\ &= \frac{1}{2}m(L\dot{\theta})^2 + mgL(1 - \cos\theta) \end{aligned}\]$\theta$ היא הקואורדינטה המוכללת - דרגת החופש הדינמית היחידה בבעיה. האנרגיה המכנית הכוללת $E$ היא קבוע של התנועה.
מציאת משוואת התנועה משימור אנרגיה
אם האנרגיה קבועה בזמן, הנגזרת שלה לפי הזמן היא אפס: $\frac{dE}{dt} = 0$. נגזור את הביטוי לאנרגיה:
\[\frac{dE}{dt} = \frac{d}{dt} \left( \frac{1}{2}mL^2\dot{\theta}^2 + mgL(1 - \cos\theta) \right) = 0\] \[\frac{1}{2}mL^2 \cdot (2\dot{\theta} \cdot \ddot{\theta}) + mgL(0 - (-\sin\theta \cdot \dot{\theta})) = 0\] \[mL^2\dot{\theta}\ddot{\theta} + mgL\dot{\theta}\sin\theta = 0\]נוציא גורם משותף $mL\dot{\theta}$:
\[mL\dot{\theta}(L\ddot{\theta} + g\sin\theta) = 0\]בהנחה שהמטוטלת בתנועה ($\dot{\theta} \neq 0$, למעט בנקודות הקצה), נוכל לחלק ולקבל:
\[\boxed{\ddot{\theta} + \frac{g}{L}\sin\theta = 0}\]זוהי בדיוק משוואת התנועה של המטוטלת, אותה ניתן לקבל גם מהחוק השני של ניוטון!
הערה חשובה: כוח המתיחות בחוט $\vec{T}$ הוא כוח אילוץ. הוא תמיד ניצב לכיוון התנועה (במסלול מעגלי), ולכן העבודה שהוא מבצע היא אפס ($\vec{T} \cdot d\vec{r} = 0$). לכן, הוא אינו משפיע על האנרגיה המכנית של המערכת.
3 המטוטלת הבליסטית
המטוטלת הבליסטית היא מכשיר למדידת מהירות של קליעים. היא מורכבת מגוף מסיבי (למשל, בול עץ) במסה $M$, התלוי על חוטים באורך $L$. יורים לתוכו קליע במסה $m$ ובמהירות אופקית $v$.
התהליך מורכב משני שלבים נפרדים:
- ההתנגשות: התנגשות פלסטית מהירה מאוד.
- התנודה: תנועת המטוטלת (עם הקליע בתוכה) כלפי מעלה.
מקרה א’: הקליע נתקע בתוך הגוש
זוהי התנגשות פלסטית מושלמת.
שלב 1 - ההתנגשות (שימור תנע): במהלך ההתנגשות הקצרה, התנע האופקי של המערכת (קליע + גוש) נשמר. האנרגיה המכנית אינה נשמרת.
\[p_{\text{before}} = p_{\text{after}}\] \[mv = (m + M)V\]כאשר $V$ היא המהירות המשותפת של הגוש והקליע מיד לאחר ההתנגשות:
\[V = \frac{m}{m + M}v\]שלב 2 - העלייה (שימור אנרגיה): מרגע שהקליע נתקע, המערכת המשולבת (מסה $m+M$) מתחילה לנוע כמטוטלת. בשלב זה, האנרגיה המכנית כן נשמרת.
\[E_{i} = E_{f}\] \[\frac{1}{2}(m + M)V^2 = (m + M)gh\]מכאן ניתן למצוא את הגובה המקסימלי $h$ שאליו המערכת מגיעה:
\[h = \frac{V^2}{2g} = \frac{1}{2g} \left( \frac{m}{m+M}v \right)^2 = \frac{m^2v^2}{2g(m + M)^2}\]
מקרה ב’: הקליע עובר דרך הגוש
נניח שהקליע נכנס במהירות $v$ ויוצא מהצד השני במהירות $v_2$. זוהי התנגשות אי-אלסטית (לא פלסטית מושלמת).
שלב 1 - ההתנגשות (שימור תנע): התנע עדיין נשמר:
\[mv = MV' + mv_2\]כאשר $V’$ היא מהירות הגוש מיד לאחר שהקליע יצא ממנו.
\[V' = \frac{m(v - v_2)}{M}\]חשוב: איננו יכולים להניח שימור אנרגיה מכנית במהלך ההתנגשות עצמה.
שלב 2 - העלייה (שימור אנרגיה): לאחר ההתנגשות, הגוש (מסה $M$) עולה לגובה $h$ תוך שימור אנרגיה:
\[\frac{1}{2}M(V')^2 = Mgh \implies h = \frac{(V')^2}{2g}\]4 חוק הכבידה האוניברסלי
ניוטון גילה שכל שתי מסות ביקום מושכות זו את זו. גודל כוח המשיכה ההדדי הוא:
\[\boxed{F_g = G\frac{m_1m_2}{r^2}}\]כאשר $G \approx 6.674 \times 10^{-11} \, \text{N}\cdot\text{m}^2/\text{kg}^2$ הוא קבוע הכבידה האוניברסלי, ו-$r$ הוא המרחק בין מרכזי המסות.
בצורה וקטורית, הכוח שמפעילה מסה $m_1$ על מסה $m_2$ הוא:
\[\vec{F}_{1 \to 2} = -G\frac{m_1m_2}{r^2}\hat{r}_{12}\]כאשר $\hat{r}_{12}$ הוא וקטור יחידה המצביע מ-$m_1$ אל $m_2$. הסימן השלילי מציין שזהו כוח משיכה.
דוגמה: כוח המשיכה בין השמש לכדור הארץ
הכוח שהשמש ($M_{\odot}$) מפעילה על כדור הארץ ($M_{\oplus}$):
\[\vec{F}_{\text{sun}\to\text{earth}} = -G\frac{M_{\odot}M_{\oplus}}{r^2}\hat{r}\]מהחוק השלישי של ניוטון, הכוח שכדור הארץ מפעיל על השמש שווה בגודלו והפוך בכיוונו:
\[\vec{F}_{\text{earth}\to\text{sun}} = -\vec{F}_{\text{sun}\to\text{earth}} = +G\frac{M_{\odot}M_{\oplus}}{r^2}\hat{r}\]כן, כדור הארץ מושך את השמש באותו כוח! ההבדל הדרמטי הוא בתאוצה: $a = F/m$. מכיוון שמסת השמש גדולה פי כ-333,000 ממסת כדור הארץ, תאוצתה זניחה בהשוואה לתאוצת כדור הארץ.
תאוצת הכבידה על פני כדור הארץ
הכוח על גוף במסה $m$ על פני כדור הארץ (ברדיוס $R_{\oplus}$) הוא מה שאנו מכנים “משקל”:
\[F_g = G\frac{M_{\oplus}m}{R_{\oplus}^2}\]לפי החוק השני של ניוטון, $F_g = mg$. נשווה ונקבל:
\[mg = G\frac{M_{\oplus}m}{R_{\oplus}^2} \implies g = \frac{GM_{\oplus}}{R_{\oplus}^2}\]עם הערכים: $M_{\oplus} \approx 5.97 \times 10^{24}$ ק”ג, $R_{\oplus} \approx 6.37 \times 10^6$ מ’, נקבל:
\[g = \frac{(6.674 \times 10^{-11}) \cdot (5.97 \times 10^{24})}{(6.37 \times 10^6)^2} \approx 9.8 \, \text{m/s}^2\]\[F_g = G\frac{m_1m_2}{r^2} = (6.674 \times 10^{-11}) \cdot \frac{80 \cdot 60}{1^2}\] \[F_g \approx 3.2 \times 10^{-7} \, \text{N}\]כוח המשיכה בין תלמידים
שאלה: באיזה כוח מושכים זה את זה שני תלמידים, שמסתם 80 ק”ג ו-60 ק”ג, היושבים במרחק מטר זה מזה?
זהו כוח זעיר ביותר, שקול למשקל של כ-30 מיקרוגרם! לשם השוואה, משקלו של כל תלמיד הוא מאות ניוטונים.
השתנות g עם הגובה
$g$ אינו קבוע, אלא תלוי במרחק $r$ ממרכז כדור הארץ:
\[g(r) = \frac{GM_{\oplus}}{r^2}\]בגובה של 400 ק”מ (מסלול תחנת החלל הבינלאומית):
\[r = R_{\oplus} + h = 6370 \, \text{km} + 400 \, \text{km} = 6770 \, \text{km}\] \[g_{400} = \frac{GM_{\oplus}}{(6.77 \times 10^6)^2} \approx 8.7 \, \text{m/s}^2\]כלומר, בתחנת החלל, תאוצת הכבידה היא כ-89% מערכה על פני הים. “חוסר המשקל” שאסטרונאוטים חווים נובע מהנפילה החופשית המתמדת שלהם סביב כדור הארץ, לא מהיעדר כבידה.
דור פסקלשיעור 13 - פתרון בחינת אמצע לדוגמה
תאריך: 30/06/2025מבנה הבחינה והנחיות כלליות
מועדי הבחינה
- מועד א’: 14 ביולי.
- מועד ב’: 14 באוגוסט.
- מועד ג’: יתקיים במועד נפרד ומיועד בעיקר למשרתי מילואים.
- כללי: ניתן לגשת לשני המועדים (א’ ו-ב’), והציון הגבוה מביניהם הוא הקובע.
פורמט הבחינה
- הבחינה מנוהלת על ידי מדור הבחינות של אוניברסיטת בר-אילן.
- מבנה: 8 שאלות אמריקאיות, יש לענות על 7 שאלות בלבד.
- ניקוד: כל שאלה שווה 15 נקודות.
- 4 שאלות נכונות = 60 נקודות.
- 5 שאלות נכונות = 75 נקודות.
- 6 שאלות נכונות = 90 נקודות.
- 7 שאלות נכונות = 100 נקודות.
- אופן הבדיקה: התוכנה בודקת את 7 התשובות הראשונות. אם עניתם על 8 שאלות, יש למחוק את השאלה שאינכם רוצים שתיבדק.
- ערבול: סדר השאלות והתשובות (המסיחים) מעורבל, כך שכל סטודנט מקבל טופס ייחודי.
- משך הבחינה: 3 שעות.
- חומר עזר: ניתן להכניס כל חומר עזר כתוב (דפי נוסחאות, סיכומים). לא מומלץ להביא ספרים.
- מחשבון: מותר להשתמש במחשבון מדעי פשוט (לחישוב סינוס, קוסינוס וכו’). אסור להשתמש במחשבונים המסוגלים לפתור משוואות, אינטגרלים או בעיות פיזיקליות מורכבות.
- איסורים: אסור להכניס אמצעי תקשורת מכל סוג.
חומר הלימוד לבחינה
הבחינה כוללת את כל הנושאים שנלמדו במהלך הסמסטר:
- קינמטיקה: וקטורי מקום, מהירות ותאוצה.
- דינמיקה: שלושת חוקי ניוטון.
- מתקף ותנע.
- עבודה ואנרגיה.
נושאים שלא נכללים בבחינה:
- חישוב אינטגרלים מסלוליים.
- מכניקת זורמים.
- מומנטים ותנע זוויתי.
שיעורי תגבור
- יתקיימו שיעורי תגבור נוספים לפני הבחינה, בתיאום עם הסטודנטים.
- שיעור תגבור יתקיים אם יהיו לפחות שני סטודנטים המעוניינים בכך.
- בשיעורי התגבור המרצה יענה על שאלות ספציפיות של הסטודנטים.
פתרון שאלות לדוגמה
שאלה 1: תנועת מסטיק על גלגל אופניים (ציקלואידה)
הבעיה: מסטיק נדבק לצמיג של גלגל אופניים ברדיוס $a$. הקואורדינטות של המסטיק נתונות על ידי:
\[x(t) = a(\theta(t) - \sin(\theta(t)))\] \[y(t) = a(1 - \cos(\theta(t)))\]כאשר $\theta(t)$ היא זווית הסיבוב של הגלגל התלויה בזמן.
השאלה: מהו וקטור היחידה המצביע על כיוון המהירות של המסטיק?
פתרון:
וקטור המקום: נרשום את וקטור המקום $\vec{r}(t)$ של המסטיק:
\[\vec{r}(\theta) = a(\theta - \sin\theta)\hat{x} + a(1 - \cos\theta)\hat{y}\]וקטור המהירות: נגזור את וקטור המקום לפי הזמן $t$ כדי למצוא את וקטור המהירות $\vec{v}(t)$, תוך שימוש בכלל השרשרת ($\frac{d}{dt} = \frac{d\theta}{dt} \frac{d}{d\theta} = \dot{\theta} \frac{d}{d\theta}$):
\[\vec{v}(\theta) = \frac{d\vec{r}}{dt} = \dot{\theta} \frac{d\vec{r}}{d\theta}\] \[\vec{v}(\theta) = a\dot{\theta}(1 - \cos\theta)\hat{x} + a\dot{\theta}(\sin\theta)\hat{y}\]נוציא את הגורם המשותף $a\dot{\theta}$:
\[\vec{v}(\theta) = a\dot{\theta} \left[ (1 - \cos\theta)\hat{x} + \sin\theta\hat{y} \right]\]גודל המהירות: נחשב את הגודל (נורמה) של וקטור המהירות, $\vert \vec{v} \vert$:
\[\vert \vec{v} \vert = \sqrt{(v_x)^2 + (v_y)^2} = \sqrt{(a\dot{\theta}(1-\cos\theta))^2 + (a\dot{\theta}\sin\theta)^2}\] \[\vert \vec{v} \vert = a\dot{\theta} \sqrt{(1-\cos\theta)^2 + \sin^2\theta}\]נפתח את הסוגריים:
\[\vert \vec{v} \vert = a\dot{\theta} \sqrt{1 - 2\cos\theta + \cos^2\theta + \sin^2\theta}\]נשתמש בזהות $\sin^2\theta + \cos^2\theta = 1$:
\[\vert \vec{v} \vert = a\dot{\theta} \sqrt{1 - 2\cos\theta + 1} = a\dot{\theta} \sqrt{2(1 - \cos\theta)}\]וקטור יחידה: נחשב את וקטור היחידה של המהירות, $\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert}$:
\[\hat{v} = \frac{a\dot{\theta} \left[ (1 - \cos\theta)\hat{x} + \sin\theta\hat{y} \right]}{a\dot{\theta} \sqrt{2(1 - \cos\theta)}}\]הגורם $a\dot{\theta}$ מצטמצם:
\[\hat{v} = \frac{(1 - \cos\theta)}{\sqrt{2(1 - \cos\theta)}}\hat{x} + \frac{\sin\theta}{\sqrt{2(1 - \cos\theta)}}\hat{y}\]פישוט הביטוי:
\[\frac{\sin\theta}{\sqrt{1 - \cos\theta}} = \frac{\sqrt{(1-\cos\theta)(1+\cos\theta)}}{\sqrt{1 - \cos\theta}} = \sqrt{1+\cos\theta}\]
- רכיב x: $\frac{1 - \cos\theta}{\sqrt{1 - \cos\theta}} = \sqrt{1 - \cos\theta}$. לכן הרכיב הוא $\sqrt{\frac{1 - \cos\theta}{2}}\hat{x}$.
- רכיב y: נשתמש בזהות $\sin\theta = \sqrt{1-\cos^2\theta} = \sqrt{(1-\cos\theta)(1+\cos\theta)}$.
לכן הרכיב הוא $\sqrt{\frac{1 + \cos\theta}{2}}\hat{y}$.
התשובה הסופית:
\[\boxed{\hat{v} = \sqrt{\frac{1 - \cos\theta}{2}}\hat{x} + \sqrt{\frac{1 + \cos\theta}{2}}\hat{y}}\]
שאלה 2: כוחות נורמליים על כדור בפינה
הבעיה: כדור במסה $m$ מונח בתוך פינה ישרה ($90^\circ$). הדופן הימנית נטויה בזווית $60^\circ$ ביחס לאופק, והשמאלית בזווית $30^\circ$. הכדור במנוחה.
- $N_1$: הכוח הנורמלי שהדופן הימנית (זווית $60^\circ$) מפעילה על הכדור.
- $N_2$: הכוח הנורמלי שהדופן השמאלית (זווית $30^\circ$) מפעילה על הכדור.
השאלה: מהו היחס בין $N_1$ ל-$N_2$?
פתרון:
המערכת נמצאת במנוחה, ולכן על פי החוק הראשון של ניוטון, שקול הכוחות הפועלים על הכדור הוא אפס בכל ציר.
\[\sum \mathbf{F} = 0\]ננתח את הכוחות בציר $x$ (אופקי).
- הכוח $N_1$ פועל בזווית $60^\circ$ ביחס לאנך, כלומר $30^\circ$ ביחס לאופק. הרכיב שלו בציר $x$ הוא $N_1 \cos(30^\circ)$ בכיוון ימין.
- הכוח $N_2$ פועל בזווית $30^\circ$ ביחס לאנך, כלומר $60^\circ$ ביחס לאופק. הרכיב שלו בציר $x$ הוא $N_2 \cos(60^\circ)$ בכיוון שמאל.
הערה: בשיעור המרצה סימן סינוס, אבל להבנתי ההיטל על ציר $x$ הוא קוסינוס.
שקול הכוחות בציר $x$ הוא אפס:
\[\sum F_x = N_1 \cos(30^\circ) - N_2 \cos(60^\circ) = 0\] \[N_1 \cos(30^\circ) = N_2 \cos(60^\circ)\]נציב את ערכי הקוסינוס:
\[N_1 \cdot \frac{\sqrt{3}}{2} = N_2 \cdot \frac{1}{2}\]נכפיל ב-2 ונקבל את היחס:
\[\boxed{N_2 = \sqrt{3} N_1}\]היה אפשר גם לפתור עם סינוסים, אבל אז היה מצטרף למשוואה $mg$ (כוח הכבידה) שצריך היה לבטל.
כלומר, היינו מקבלים:
\[N_1 \sin(30^\circ) + N_2 \sin(60^\circ) = mg\] \[\frac{N_1}{2} + N_2 \cdot \frac{\sqrt{3}}{2} \approx 80\]והיינו נתקעים עם:
\[N_1 + \sqrt{3} N_2 = 160\]
שאלה 3: התנתקות מסה ממסה אחרת המחוברת לקפיץ
הבעיה: מסה $M$ מונחת על משטח אופקי חלק ומחוברת לקפיץ בעל קבוע $k$. על גבי מסה $M$ מונחת מסה קטנה $m$. מקדם החיכוך הסטטי בין שתי המסות הוא $\mu$. מותחים את הקפיץ במרחק $d$ ממצב שיווי המשקל ומשחררים ממנוחה.
השאלה: מהו הערך המינימלי של $d$ שיגרום למסה $m$ להתנתק (להחליק) מהמסה $M$?
פתרון:
- התנאי להתנתקות: המסה $m$ תתנתק מהמסה $M$ כאשר התאוצה של המערכת תהיה גדולה מספיק כדי שהכוח המדומה הפועל על $m$ (במערכת הייחוס של $M$) יתגבר על כוח החיכוך הסטטי המקסימלי.
\[mA > \mu mg \implies A > \mu g\]
- כוח החיכוך הסטטי המקסימלי: $f_{s,max} = \mu N \overset{\star}{=} \mu mg$.
הבהרה לגבי $\star$: $N=mg$ משקול הכוחות ששווה לאפס בציר $y$.
- הכוח המדומה הפועל על $m$: $F_{inertial} = mA$, כאשר $A$ היא תאוצת המסה $M$.
עקרונית הכוח המדומה הוא $-mA$, המרצה הציג את זה בעזרת כיוון החץ שצייר.
- תנאי ההתנתקות:
כלומר, אנחנו צריכים למצוא את $A$ כדי למצוא את $d$.
- תנועת המערכת: כל עוד המסות נעות יחד, הן מתנהגות כמסה אחת $(M+m)$ המבצעת תנועה הרמונית פשוטה.
מיקום המערכת כפונקציה של הזמן (שחרור ממנוחה במרחק $d$):
\[x(t) = d\cos(\omega t) \tag{1}\]התדירות הזוויתית של התנועה:
\[\omega = \sqrt{\frac{k}{M+m}} \tag{2}\]תאוצת המערכת: נגזור פעמיים את המיקום $(1)$ לקבלת התאוצה:
\[v(t) = \frac{dx}{dt} = -d\omega\sin(\omega t)\] \[A(t) = \frac{dv}{dt} = -d\omega^2\cos(\omega t)\]התאוצה המקסימלית בגודלה מתרחשת ב-$t=0$ (רגע השחרור), כאשר $\cos(\omega t)=1$:
\[x_{max} = A= -\omega^2 d\]היינו יכולים להגיע לביטוי הזה גם מכיוון שבתנועה מעגלית (שהיא מקרה פרטי של תנועה הרמונית פשוטה) התאוצה המקסימלית היא $a_{max} = r\omega^2$, כאשר $r$ הוא הרדיוס של התנועה. כאן $r=d$.
מציאת d: נציב את התאוצה המקסימלית בתנאי ההתנתקות:
\[A_{max} > \mu g\] \[d\omega^2 > \mu g\]נציב את הביטוי עבור $\omega^2$ מתוך (2):
\[d \left( \frac{k}{M+m} \right) > \mu g\]נבודד את $d$:
\[\boxed{d > \frac{\mu g (M+m)}{k}}\]התשובה הסופית: הערך המינימלי של $d$ הוא $\frac{\mu g (M+m)}{k}$.
שאלה 4: כוחות על פשפש בתקליט מסתובב
הבעיה: פשפש נמצא בתוך חריץ ישר על תקליט המסתובב במהירות זוויתית קבועה $\omega$. הפשפש נמצא במרחק קבוע $R$ מהמרכז. הכוחות הפועלים על הפשפש במישור הסיבוב הם:
- כוח נורמלי ($N$): מהדופן הפנימית של החריץ, מכוון כלפי מרכז הסיבוב.
- כוח גרר: מתכונתי למהירות, $F_{drag} = -\beta v$, כאשר $\beta$ הוא קבוע.
- כוח חיכוך ($f_k$): המשטח מפעיל על הפשפש, בכיוון הסיבוב.
השאלה: מהי משוואת התנועה של הפשפש בקואורדינטות פולריות?
פתרון:
- וקטור שקול הכוחות: נרשום את כל הכוחות הפועלים על הפשפש כווקטורים:
- כוח נורמלי: $\mathbf{F}_N = -N\mathbf{\hat{r}}$ (מכוון כלפי המרכז, בכיוון רדיאלי שלילי).
זה הכוח הצנטריפיטלי. הוא הכוח שמשאיר את הפשפש בתנועה מעגלית, כלומר הוא מאזן את התאוצה הרדיאלית.
כוח גרר: פועל בניגוד לכיוון המהירות. במקרה הזה המהירות היא משיקית עם רדיוס קבוע, $\vec{v} = R\dot{\theta} \mathbf{\hat{\theta}}=R\omega\mathbf{\hat{\theta}}$. לכן כוח הגרר הוא
\[\mathbf{F}_{drag} = -\beta (R\omega\mathbf{\hat{\theta}}) = -\beta R\omega \mathbf{\hat{\theta}}\]כוח חיכוך: פועל בכיוון התנועה:
\[\mathbf{F}_f = f_k \mathbf{\hat{\theta}}= \mu mg \mathbf{\hat{\theta}}\]שקול הכוחות:
\[\sum \mathbf{F} = -N\mathbf{\hat{r}} + (\mu mg - \beta R\omega)\mathbf{\hat{\theta}}\]וקטור התאוצה בקואורדינטות פולריות:
\[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\mathbf{\hat{r}} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}}\]מכיוון שהפשפש במרחק קבוע $R$ ובמהירות זוויתית קבועה $\omega$:
\[r=R \implies \boxed{\dot{r}=0, \ddot{r}=0}\] \[\dot{\theta}=\omega \implies \boxed{\ddot{\theta}=0}\]נציב ונקבל:
\[\vec{a} = (\cancel{\ddot{r}} - r\dot{\theta}^2)\mathbf{\hat{r}} + \cancel{(2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}}}\] \[\boxed{\vec{a} = -R\omega^2 \mathbf{\hat{r}}}\]משוואת התנועה (בקואורדינטות פולריות):
החוק השני של ניוטון: $\sum \mathbf{F} = m\vec{a}$
\[-N\mathbf{\hat{r}} + (\mu mg - \beta R\dot{\theta})\mathbf{\hat{\theta}} = m(-R\omega^2 \mathbf{\hat{r}})\]- השוואת רכיבים:
בכיוון הרדיאלי ($\mathbf{\hat{r}}$):
\[-N = -mR\omega^2 \implies N = mR\omega^2\]בכיוון המשיקי ($\mathbf{\hat{\theta}}$):
\[\underbrace{mR\ddot{\theta}}_{\overset{\star}{=0}} = \mu mg - \beta R\omega\]התשובה הסופית: משוואות התנועה המתארות את הכוחות הן:
- בכיוון הרדיאלי: $N = mR\omega^2$
- בכיוון המשיקי: $ \mu mg = \beta R\omega$
סך הכל:
\[\boxed{-mR\omega^2 \mathbf{\hat{r}}= -N\mathbf{\hat{r}} + \mu mg \mathbf{\hat{\theta}} - \beta R \omega \mathbf{\hat{\theta}}}\]הערה: המרצה לא הרחיב על זה בשיעור אבל להבנתי $\ddot{\theta}$ מתאפס כי נתון שהמהירות הזוויתית קבועה, כלומר $\ddot{\theta} = 0$.