פיזיקה לרפואנים - כל התרגולים

כל התרגולים בעמוד אחד

כל סיכומי התרגולים בקורס פיזיקה לרפואנים זמינים כאן להדפסה מרוכזת או ייצוא כ-PDF. התוכן מוצג בסדר כרונולוגי - מהסיכומים המוקדמים ביותר למאוחרים ביותר. העמודים כוללים נוסחאות מתמטיות, ייתכן שייקח להן מספר שניות להיטען. למידה מהנה!

תרגול 1 - מבוא לחשבון וקטורי

תאריך: 20/03/2025

מבוא לחשבון וקטורי

חשבון וקטורים משמש לניתוח סיטואציות במכניקה:

בגדול, כשאנחנו מסתכלים אחד על השני פה, אין לנו שום וקטור בינינו… זה אנחנו לא רואים, זה תוספת שלנו, אנושית, של המנתחים למה שקורה, וזה עוזר לנו להבין וגם לנבא מה הולך לקרות.

דרגות חופש והצירים הניצבים

בעולם שלנו יש 3 דרגות חופש
“כשאני נע, או כוחות שגורמים לי להאיץ בכיוון ציר מסוים, אם אני לוקח ציר ניצב, הציר הניצב לא יודע מה קורה בציר השני”
מספר דרגות החופש של מרחב קובע את כמות הצירים שמתארת אותו
כל דרגת חופש מייצגת מידע חדש שלא ניתן להביא מדרגות החופש האחרות
אם אחד הצירים משפיע על מה שקורה בציר אחר, הם אינם ניצבים
צירים ניצבים = עצמאיים, כל אחד לא משפיע על האחר

הגדרת וקטור והתכונות שלו

וקטור מאופיין על ידי שני גדלים:
1. גודל (אורך הוקטור)
2. כיוון (אוריינטציה במרחב)
וקטור במרחב תלת-ממדי מתואר על ידי שלושה מספרים (קומפוננטות)
אורך וקטור נקבע לפי משפט פיתגורס:
\[\vert \vec{A}\vert = \sqrt{A_x^2 + A_y^2 + A_z^2}\]
וקטורי יחידה מוגדרים כוקטורים שאורכם 1:
- $\hat{x} = (1,0,0)$
- $\hat{y} = (0,1,0)$
- $\hat{z} = (0,0,1)$
וקטור יחידה בכיוון כלשהו:
\[\hat{v} = \frac{\vec{v}}{\vert \vec{v}\vert}\]

פעולות עם וקטורים

מכפלה של סקלר בוקטור: $\alpha\vec{A} = (\alpha A_x, \alpha A_y, \alpha A_z)$
- אם $\alpha > 1$: מתיחה של הוקטור
- אם $0 < \alpha < 1$: כיווץ של הוקטור
- אם $\alpha < 0$: הפיכת כיוון (פליפ) ושינוי אורך
חיבור וקטורים: $\vec{A} + \vec{B} = (A_x + B_x, A_y + B_y, A_z + B_z)$
חיסור וקטורים: $\vec{A} - \vec{B} = (A_x - B_x, A_y - B_y, A_z - B_z)$

בעיה 1: שחיין חוצה נהר

שחיין חוצה נהר מדרום לצפון במהירות $1\left[ \frac{m}{s} \right]$ והנהר זורם ממערב למזרח במהירות $5\left[ \frac{m}{s} \right]$.

איזו מערכת צירים מתאימה לבעיה

כמה דרגות חופש נדרשות לתיאור? מדוע הזנחנו דרגת חופש

האם מהירות הזרם מושפעת ממהירות השחיין

האם מהירות החציה מושפעת ממהירות הזרם?

האם שני הצירים שבחרנו לתאר את הבעיה ניצבים זה לזה?

איזו מהירות יזהה צופה חיצוני שיש לשחיין? האם תדעו לחשב את כיוונה?

פתרון:

מערכת צירים קרטזית:
- ציר $x$ במזרח (כיוון הזרם)
- ציר $y$ בצפון (כיוון השחיין)
דרגות חופש:
- שתי דרגות חופש בלבד $(x,y)$
- הזנחנו את הציר האנכי $(z)$ כי הבעיה מתרחשת במישור
- מציאותית, יש אולי שינויי גובה במים, אבל הם פחות מעניינים לבעיה הנוכחית
מהירות הזרם אינה מושפעת מהשחיין (בהנחה שהנהר גדול מספיק)
מהירות החצייה אינה מושפעת מהזרם:

בכל צעד שהוא עושה, למרות שהוא נסחף, שום דבר לא יזיז אותו אחורה או קדימה. אין את ההתערבות של המים בקצב ההתקדמות שלו בציר $y$. הוא הלך קדימה מטר, נסחף חמישה, הלך קדימה מטר, נסחף חמישה… זה אותו דבר מבחינת הזמן שלקח לו לעבור את הגדה.
הצירים ניצבים זה לזה - השפעת הזרם לא משנה את המהירות של השחיין לכיוון צפון-דרום
המהירות הכוללת של השחיין:
\[\boxed{V^2 = V_x^2 + V_y^2 = 5^2 + 1^2 = 26 \, \mathrm{[m/s]}^2}\] \[\vert \vec{v} \vert = \sqrt{26} \text{ [m/s]} \approx 5.1 \text{ [m/s]}\]
הערה: שימו לב להבדל בין $v = \text{speed}$ (מהירות) לבין $\mathbf{v} = \text{velocity}$ (וקטור מהירות):
- $v=\vert\mathbf{v}\vert$ היא גודל בלבד (ללא כיוון)
- $\mathbf{v}=\vec{v}$ היא וקטור עם גודל וכיוון
- במקרה זה, $\vec{V} = (5, 1)$
- וקטור יחידה בכיוון התנועה:
\[\hat{V} = \frac{\vec{V}}{\vert \vec{V}\vert} = \left(\frac{5}{\sqrt{26}}, \frac{1}{\sqrt{26}}\right) \approx (0.98, 0.20)\]
הכיוון:
\[\tan(\theta) = \frac{V_y}{V_x} = \frac{1}{5} = 0.2\] \[\theta = \arctan(0.2) \approx 11.3° \mathrm{[degrees]}\]

המרצה מוסיף

כאשר $x$ קרוב ל-0, אפשר לקרב: $\sin(x) \approx x$ ו-$\cos(x) \approx 1$

בעיה 2: כריש רודף טרף

טרף של כריש שוחה אחריו בהתלהבות במורד האוקיאנוס בכדי להזכיר לו שהוא צריך לרדוף אחריו ולא להיפך. מהירות הכירוש היא $5 \left[ \frac{m}{s} \right]$ שמאלה, $2 \left[ \frac{m}{s} \right]$ למטה ו $3 \left[ \frac{m}{s} \right]$ החוצה. מהירות הטרף היא ב-$10\% $ גבוהה יותר בכל כיוון.

מהם רכיבי המהירות של הטרף? כיצד נרשום זאת בצורה וקטורית?

מהו גודל המהירות שלו? מהו וקטור היחידה בכיוון תנועתו?

רשום בכתיב וקטורי את המהירות היחסית בין הגיבורים של העלילה. מהו גודל המהירות היחסית הכולל?

האם הטרף משיג את הכריש? אז מה יקרה?

פתרון:

רכיבי מהירות הטרף:
\[\vec{v}_{\text{shark}} = (-5, -2, 3) = -5\hat{x} - 2\hat{y} + 3\hat{z}\] \[\vec{v}_{\text{food}} = (-5.5, -2.2, 3.3) = -5.5\hat{x} - 2.2\hat{y} + 3.3\hat{z}\]
גודל המהירות של הטרף:
\[\vert \vec{v}_{\text{food}}\vert = \sqrt{(-5.5)^2 + (-2.2)^2 + (3.3)^2} = \sqrt{30.25 + 4.84 + 10.89} = \sqrt{45.98} \approx \sqrt{46} \text{ [m/s]} \approx 6.8 \text{ [m/s]}\]
וקטור היחידה (וקטור מנורמל):
\[\hat{v}_{\text{food}} = \frac{\vec{v}_{\text{food}}}{\vert \vec{v}_{\text{food}}\vert} = \left(\frac{-5.5}{\sqrt{46}}, \frac{-2.2}{\sqrt{46}}, \frac{3.3}{\sqrt{46}}\right) \approx (-0.81, -0.32, 0.49)\]
(ניתן לבדוק שאכן האורך הוא 1)
המהירות היחסית:
\[\Delta\vec{v} = \vec{v}_{\text{shark}} - \vec{v}_{\text{food}} = (-5, -2, 3) - (-5.5, -2.2, 3.3) = (0.5, 0.2, -0.3)\] \[|\Delta\vec{v} \vert = \sqrt{0.5^2 + 0.2^2 + 0.3^2} = \sqrt{0.25 + 0.04 + 0.09} = \sqrt{0.38} \approx 0.616 \text{ [m/s]}\]
כאשר הכריש מהפך את כיוונו:
\[\vec{v}_{\text{shark\_new}} = (5, 2, -3)\] \[\Delta\vec{v}_{\text{חדש}} = \vec{v}_{\text{shark\_new}} - \vec{v}_{\text{food}} = (5, 2, -3) - (-5.5, -2.2, 3.3) = (10.5, 4.4, -6.6)\] \[|\Delta\vec{v}_{\text{new}}\vert = \sqrt{10.5^2 + 4.4^2 + 6.6^2} \approx 13 \text{ [m/s]}\]

מסקנה:

כריש פחות מסוכן למגלן (הצופה) והטרף מסוכן יותר לכריש מאשר להיפך
הטרף לא ישיג את הכריש כיוון שבכל הצירים הוא מצמצם מרחק (המהירות היחסית היא 0.616 מ’/ש’)
אם הכריש משנה את כיוונו, הוא ממשיך באותו כיוון והמהירות היחסית החדשה בין הגיבורים היא גדולה הרבה יותר (13 מ’/ש’)

מערכות קואורדינטות שונות

קואורדינטות גליליות.

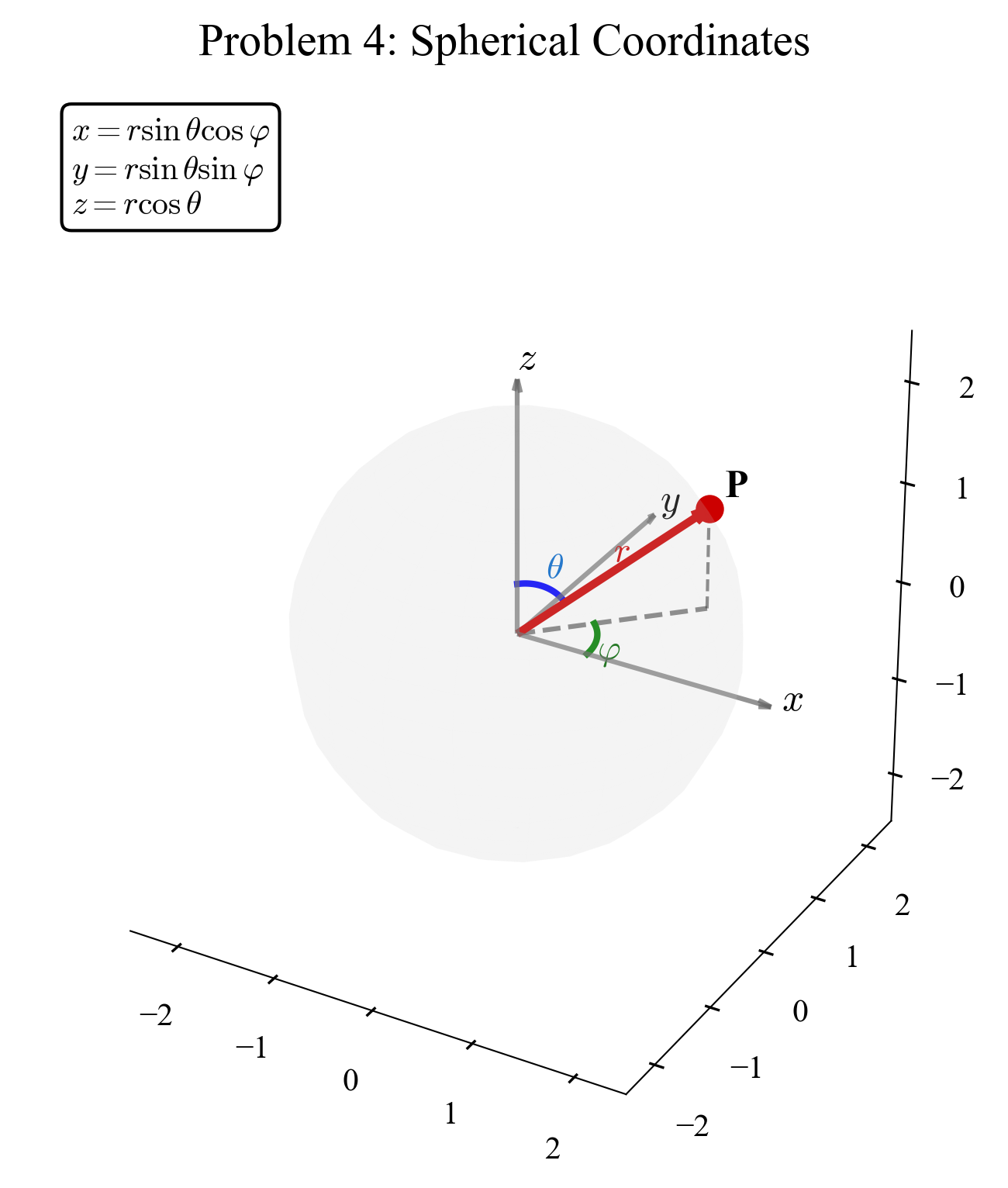
הביטוי באיור מעלה בנקודה $P$ אשר מרחקה מהראשית הוא $r$. הוקטור היוצא מהראשית ומצעי אל הנקודה הזו נתון בביטוי
\[\vec{r} = x \hat{x} + y \hat{y} + z \hat{z}\]
כאשר $\left(x,y,z\right)$ הן קואורדינטות קרטזיות של הנקודה $P$. תהיינה $\left(\rho,\theta,\phi\right)$ קואורדינטות חדשות כמתואר באיור. הצמד $\left(\rho,\theta\right)$ מכונה קואורדינטות קוטביות (ולעיתים קרובות גם קואורדינטות פולריות). והשלשה $\left(\rho,\theta,\phi\right)$ מכונה קואורדינטות גליליות (ולעיתים קרובות גם קואורדינטות צילינדריות).

הראו את נוסחאות המעבר:
\[\begin{aligned} x &= \rho \cos\phi \\[10pt] y &= \rho \sin\theta \\[10pt] \rho &= \sqrt{x^2 + y^2} \\[10pt] \theta &= \arctan\left(\frac{y}{x}\right) \end{aligned}\]

קבלו את הקשר הפיתגוראי
\[r^2 = \rho^2 + z^2 = x^2 + y^2 + z^2\]


קואורדינטות גליליות

תיאור קרטזי וקואורדינטות פולריות/גליליות

המרצה מסביר:

XYZ זה קרטזי, $r$ (radius), $\theta$ (theta), ו-$\phi$ (phi) וכל מיני כאלה זה פולרי… כשאת זזה במעגלים, המיקום $X$ שלך וה-$Y$ משתנים כל הזמן. אבל אם אתה מנסה להביע את זה בעזרת $r$ ו-$\theta$, הדבר היחידי שישתנה זה $\theta$. ואם יש מהירות קבועה, אז ה-$\theta$ תשתנה באופן קבוע.

קואורדינטות גליליות:

נקודה $P = (\rho, \theta, z) = (x, y, z)$
הקשרים בין הקואורדינטות:
\[x = \rho \cos \theta\] \[y = \rho \sin \theta\] \[\rho = \sqrt{x^2 + y^2}\] \[\theta = \tan^{-1}\left(\frac{y}{x}\right)\] \[r^2 = \rho^2 + z^2 = x^2 + y^2 + z^2\]
$(\rho,\theta)$ מכונה קואורדינטות קוטביות (פולריות)
השלשה $(\rho,\theta,z)$ נקראת קואורדינטות גליליות
קואורדינטות כדוריות מוגדרות כ-$(r, \theta, \phi)$ כאשר $\phi$ היא הזווית ביחס לציר $z$

יתרונות קואורדינטות פולריות:

נוחות לתיאור תנועה מעגלית
כאשר גוף נע במעגל, רק $\theta$ משתנה ו-$\rho$ נשאר קבוע
בתנועה מעגלית במהירות קבועה, $\theta$ גדל באופן קבוע (מהירות זוויתית קבועה)

בעיה 3: מסלול ראלי

Road Rally Problem

The figure below gives an incomplete map of a road rally. From the starting point (at the origin), you must use available roads to go through the following displacements:

$\vec{a}$ to checkpoint Able, magnitude $36$ km, due east.

$\vec{b}$ to checkpoint Baker, due north.

$\vec{c}$ to checkpoint Charlie, magnitude $25$ km, at the angle shown.

The magnitude of your net displacement $\vec{d}$ from the starting point is $62.0$ km. What is the magnitude $b$ of $\vec{b}$?

נתון: מפה לא מלאה של מסלול ראלי. מנקודת התחלה (בראשית הצירים), עליך לנסוע דרך ההעתקים הבאים:

וקטור $\vec{a}$ לנקודת ציון Able, גודל 36 ק”מ, מזרחה
וקטור $\vec{b}$ לנקודת ציון Baker, צפונה
וקטור $\vec{c}$ לנקודת ציון Charlie, גודל 25 ק”מ, בזווית 135°

ההעתק הכולל $\vec{d}$ מנקודת ההתחלה הוא 62.0 ק”מ. מהו הגודל $b$ של וקטור $\vec{b}$?

פתרון:

הרעיון המרכזי: ההעתק הנטו $\vec{d}$ הוא סכום וקטורי של שלושת ההעתקים הבודדים:

\[\vec{d} = \vec{a} + \vec{b} + \vec{c}\]

ניתן לפרש זאת במונחי קואורדינטות:

\[\vec{a} = (36, 0)\] \[\vec{b} = (0, y_B)\] \[\vec{c} = (25\cos(135), 25\sin(135)) = \left(-\frac{25}{\sqrt{2}}, \frac{25}{\sqrt{2}}\right)\]

לכן:

\[(x_C, y_C) = (36, 0) + (0, y_B) + \left(-\frac{25}{\sqrt{2}}, \frac{25}{\sqrt{2}}\right)\] \[x_C = 36 - \frac{25}{\sqrt{2}}\] \[y_C = y_B + \frac{25}{\sqrt{2}}\]

לפי הנתון:

\[x_C^2 + y_C^2 = 62^2\]

מציבים:

\[\left(36 - \frac{25}{\sqrt{2}}\right)^2 + \left(y_B + \frac{25}{\sqrt{2}}\right)^2 = 62^2\]

פיתוח:

\[62^2 = \left(36 - \frac{25}{\sqrt{2}}\right)^2 + \left(y_B + \frac{25}{\sqrt{2}}\right)^2\] \[\Rightarrow \sqrt{2}y_B + 25 = \sqrt{2 \cdot 62^2 - (\sqrt{2} \cdot 36 - 25)^2} = 83.75\] \[\Rightarrow y_B = \frac{83.75 - 25}{\sqrt{2}} = 41.55\] \[\Rightarrow |b| = |y_B| = 41.55 \text{ [km]}\]

בדיקה:

\[b^2 = (x_B - x_A)^2 + (y_B - y_A)^2 = (0 - 36)^2 + (41.55 - 0)^2 = 36^2 + 41.55^2\]

אך נכון יותר: $\vert b \vert = y_B = 41.55 \, \mathrm{[km]}$

חשוב: מערכת צירים היא בחירתנו ועדיף לבחור בזו שתקל עלינו.

תרגול 2

תאריך: 27/03/2025

שאלה 1

נתונים שני וקטורים:
\[\begin{aligned} \vec{a} &= \hat{x} + \sqrt{2}\,\hat{y} - \sqrt{3}\,\hat{z} \\[10pt] \vec{b} &= \sqrt{3}\,\hat{x} - \sqrt{2}\,\hat{y} + \hat{z} \end{aligned}\]

מצאו את הזווית בין $\vec{a}$ ל־$\vec{b}$.

מצאו את וקטור היחידה המצביע בכיוון שהשקול הווקטורי של שני הווקטורים.

מציאת הזווית

הזווית בין הווקטורים נתונה על ידי:

\[\theta = \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}| \vert \vec{b}\vert}\]

המכפלה הסקלרית יצאה $-2$. אורך כל אחד מהווקטורים הוא $\sqrt{6}$. לכן:

\[\cos \theta = \frac{-2}{6} = -\frac{1}{3} \rightarrow \theta = 109.47^\circ\]

(או $2\pi/3$ רדיאן).

דברים שאפשר ליפול בהם:

לא לשכוח לעשות שורש כשמחשבים את אורך הוקטור בעזרת מכפלה סקלרית שלו עם עצמו.

מציאת וקטור היחידה בכיוון הווקטור השקול

השקול הווקטורי של שני הווקטורים הוא:

\[\vec{c} = \vec{a} + \vec{b} = (1+\sqrt{3})\hat{x} + (\sqrt{2}-\sqrt{2})\hat{y} + (-\sqrt{3}+1)\hat{z}\]

כלומר:

\[\vec{c} = (1+\sqrt{3})\hat{x} + 0\hat{y} + (1-\sqrt{3})\hat{z}\]

וקטור היחידה בכיוון השקול הוא:

\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{(1+\sqrt{3})\hat{x} + (1-\sqrt{3})\hat{z}}{\sqrt{(1+\sqrt{3})^2 + (1-\sqrt{3})^2}}\]

שאלה 2

נתונים שני וקטורים:
\[\begin{aligned} \vec{a} &= (3, -3) \\[10pt] \vec{b} &= (-2, 1) \end{aligned}\]

קבלו את הסינוס והקוסינוס הזווית של הווקטור $2a - 3b$ ביחס לציר $x$ (אין צורך לחשב את הזווית עצמה).

נתון הווקטור $\vec{c} = (\pi, e)$. קבלו את כל הווקטורים שבעולם הניצבים לו.

רשמו את הווקטור $\vec{c}$ בבסיס שנפרס ע״י הווקטורים $\vec{a}$ ו־$\vec{b}$.

מציאת הסינוס והקוסינוס

חישוב הווקטור:
\[\begin{aligned} \vec{c} &= 2\vec{a}-3\vec{b} \\[10pt] &= 2(3, -3) - 3(-2, 1) \\[10pt] &= (6, -6) - (-6, 3) = (12, -9) \end{aligned}\]
לחישוב ה־$\cos$ וה־$\sin$ של הזווית עם ציר ה־$x$:
\[\cos \theta = \frac{x}{c} = \frac{12}{\sqrt{12^2 + (-9)^2}} = \frac{12}{\sqrt{225}} = \frac{12}{15} = \frac{4}{5}\] \[\sin \theta = \frac{y}{c} = \frac{-9}{15} = -\frac{3}{5}\]

המתרגל הסביר:

“אז $\cos$ הזווית שווה ל… נרכיב ה־$x$, זה $\cos$ הזווית, אז נשתמש בזה בהשוואה לאורך. אז זה $x$, בואו נרשום את זה פה, $x$ שווה… תראה לכם, $x$ שווה ל־4, $\cos$ הזווית, אז למה שווה $\cos$ הזווית? $x$ חלקי $r$. $x$ חלקי $r$, $r$ זה האורך.”

חלק שני - מציאת וקטורים ניצבים

וקטור $\vec{d}=(d_x, d_y)$ ניצב ל־$\vec{c}=(\pi, e)$ אם:

\[\vec{c} \cdot \vec{d} = 0\]

לכן נדרוש:

\[\pi d_x + e d_y = 0 \rightarrow d_x = -\frac{e}{\pi} d_y\]

ולכן כל וקטור מהצורה:

\[\vec{d} = \left( -\frac{e}{\pi} d_y, \, d_y \right)\]

יהיה ניצב ל־$\vec{c}$.

חלק שלישי: בסיסים וקטוריים ופריסת וקטורים

נמצא $\alpha$ ו־$\beta$ כך ש:

\[\vec{c} = \alpha \vec{a} + \beta \vec{b}\]

נרשום את הווקטורים:

\[\vec{a} = (3, -3) \quad \vec{b} = (-2, 1) \quad \vec{c} = (\pi, e)\]

נרשום את המשוואה:

\[\begin{pmatrix} 3 & -2 \\[10pt] -3 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\[10pt] \beta \end{pmatrix} = \begin{pmatrix} \pi \\[10pt] e \end{pmatrix}\]

שאלה 3

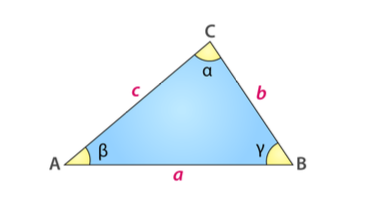
נתון המשולש למעלה. הוכיחו את משפט הקוסנוסים:
\[c^2 = a^2 + b^2 - 2ab \cos \theta\]
באמצעות שימוש טריוואלי במכפלה הסקלרית.

הוכחה באמצעות מכפלה סקלרית היא יחסית קצרה: במשולש עם צלעות $a, b, c$ והזווית $\gamma$ ביניהן, ניתן לייצג צלעות $\vec{a}, \vec{b}$ כווקטורים באותו ראש, כך:

\[\vert \vec{a}|=a,\quad \vert \vec{b}|=b,\quad \text{תיווזה } \gamma \text{ ןהיניב}.\]

אז הצלע השלישית (אורכה $c$) מתקבלת למשל כ־$\vec{a}-\vec{b}$. לכן

\[\begin{aligned} c^2 &= \vert \vec{a}-\vec{b}|^2 \\[10pt] &= (\vec{a}-\vec{b})\cdot(\vec{a}-\vec{b}) \\[10pt] &= \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b} - 2\,(\vec{a}\cdot\vec{b}) \\[10pt] &= a^2 + b^2 - 2\,ab\,\cos(\gamma) \end{aligned}\]

וזהו משפט הקוסינוסים.

שאלה 4 - קואורדינטות כדוריות

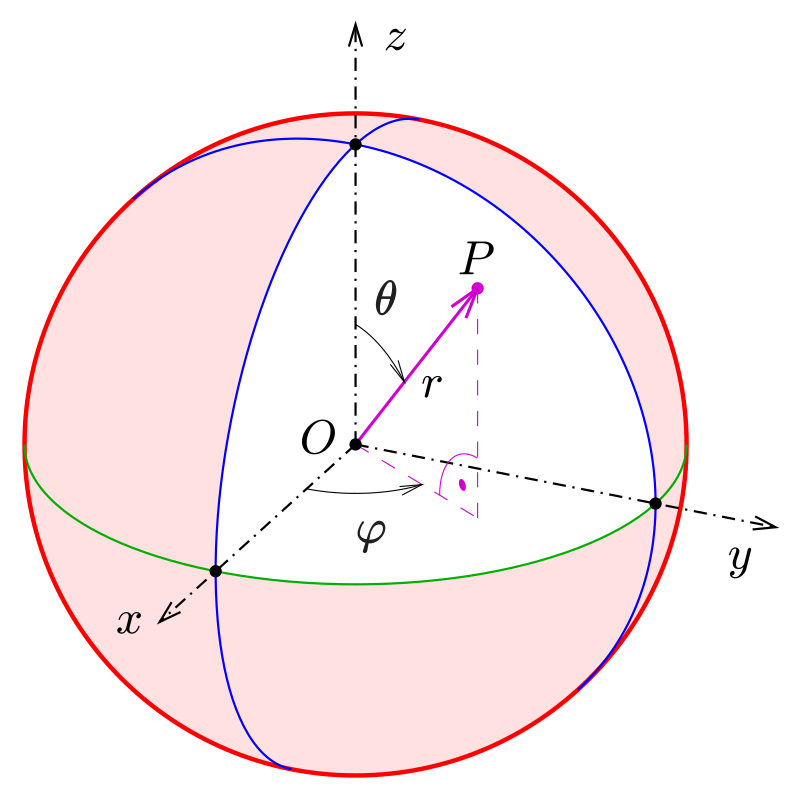
alt text

אנו רוצים להראות כי עבור $(r,\theta,\varphi)$ מתקיים:

\[\begin{aligned} x &= r\,\sin(\theta)\cos(\varphi),\\[10pt] y &= r\,\sin(\theta)\sin(\varphi),\\[10pt] z &= r\,\cos(\theta). \end{aligned}\]

(א) זוהי ההגדרה הסטנדרטית של קואורדינטות כדוריות:
- תחילה מקרינים את הנקודה על מישור $xy$ בעזרת $\sin(\theta)$.
- אחר כך מפרקים לרכיבי $\cos(\varphi)$ ו־$\sin(\varphi)$ במישור.
- הרכיב האנכי (ציר $z$) הוא $r\,\cos(\theta)$.
(ב) הראו ש־$x^2 + y^2 + z^2 = r^2$:
\[\begin{aligned} x^2 + y^2 + z^2 &= (r\sin\theta\cos\varphi)^2 + (r\sin\theta\sin\varphi)^2 + (r\cos\theta)^2 \\[10pt] &= r^2\sin^2(\theta)\bigl[\cos^2(\varphi) + \sin^2(\varphi)\bigr] + r^2\cos^2(\theta) \\[10pt] &= r^2\bigl[\sin^2(\theta) + \cos^2(\theta)\bigr] \\[10pt] &= r^2. \end{aligned}\]

שאלה 5 - מרחק כתלות בזמן

5. וקטור המקום של גוף מסוים המבצע תנועה קלשתי מתואר באמצעות
\[\vec{r}(t) = \vec{a} \sin(\omega t) + \vec{b} \cos(\omega t)\]
באשר $\vec{a}, \vec{b}$ הם וקטורים קבועים (כלומר הם אינם תלויים בזמן).

קבלו את המרחק של הגוף מהראשית כפונקציה של הזמן.

קבלו ביטוי עבור וקטור המהירות של הגוף.

קבלו ביטוי עבור וקטור היחידה תלוי-הזמן המתאר את כיוון תנועתו של הגוף בכל רגע ורגע.

קבלו את המכפלה $\vec{r}(t) \cdot \vec{v}(t)$.

חלק שלישי: תנועה במישור

6. וקטור המקום של חלקיק כלשהו הנע במישור נתון ע”י
\[\vec{r}(t) = \left( e^{-\alpha t} \cos \omega t \right) \hat{x} + \left( e^{-\alpha t} \sin \omega t \right) \hat{y}\]
באשר $\alpha, \omega$ הם פרמטרים כלשהם.

מהן היחידות של הפרמטרים $\omega, \alpha$?

הראו שהחלקיק נע בספירלה מעגלית שמתכנסת לעבר המרכז.

קבלו את וקטור המהירות של החלקיק כתלות בזמן.

מהו גודל וקטור המהירות של החלקיק כתלות בזמן?

חלק רביעי: המרחק בין שתי נקודות

נדון נושא המרחק בין שתי נקודות:

“מדדו את המרחק בין הצירים. בי, המרחק. אה, עוד דיברנו על המרחק, נכון? איך מוצאים מרחק בין שתי נקודות? נשארי, ספר לדוגמה, נשארי.”

הוסבר שהמרחק בין שני וקטורים $\vec{a}$ ו־$\vec{b}$ הוא:

\[d = \vert \vec{b} - \vec{a}\vert = \sqrt{(b_x - a_x)^2 + (b_y - a_y)^2 + (b_z - a_z)^2}\]

חלק חמישי: תנועה במרחב ופונקציות וקטוריות של הזמן

המתרגל הסביר את התיאור של תנועה במרחב באמצעות פונקציות וקטוריות של הזמן:

“אני מצייר שתי נקודות ואז אני מושך קו ישר. פה יש לי סירה אדומה, ופה יש לי סירה צהובה. עם הזמן הסירות זזות, כי הווקטור משתנה.”

דוגמה עם שתי סירות

סירה ראשונה התחילה בנקודה $(1, 1)$ ונעה בכיוון $(1, 0)$
סירה שנייה התחילה בנקודה $(2, 2)$ ונעה בכיוון $(1, 1)$

אחרי שנייה אחת:

“רגע לפני זה, אחרי שנייה אחת, איפה הסירה הזאת נמצאת? $(2,1)$ — היא פה. ואיפה זאת? $(3,3)$ — היא פה.”

חישוב המהירות:

“אהלן, מהירות. בואו נמצא את המהירות שלה, ונמצא את המהירות של השנייה. מה המהירות של הראשונה? איך עושים את זה? גוזרים כל רכיב בנפרד. מה קורה כשאני גוזר? מקבלים: $(1,0)$. איזה כיוון זה? $x$. וזה מה שציירתי פה — היא נעה בכיוון $x$. מה הנגזרת של השנייה? $(1,1)$. כלומר, היא זזה אחד ימינה ואחד למעלה כל הזמן.”

חלק שישי: תנועה מעגלית וספירלית

בהמשך התרגול, נדונה תנועה מעגלית ותנועה ספירלית:

“אוקיי, נעבור על תנועה מעגלית וספירלית שמתכנסת. מה זה הגודל הזה? מה זה?”

הוסבר שבתנועה מעגלית אחידה, הזווית משתנה לינארית עם הזמן:

\[\theta(t) = \omega t\]

כאשר $\omega$ היא המהירות הזוויתית (ברדיאנים לשנייה):

”$\omega$ זה קצב שינוי הזווית. איך מגדירים את $\omega$?”

וקטור המקום בתנועה מעגלית:

\[\vec{r}(t) = r \cos(\omega t) \hat{x} + r \sin(\omega t) \hat{y}\]

לגבי תנועה ספירלית:

“אז זו בעצם תנועה מעגלית עם רדיוס שקטן כל הזמן. הוא יכול להתחיל גדול ואז יקטן, או ההפך, תלוי בזמן.”

תנועה ספירלית אקספוננציאלית:

\[r(t) = r_0 e^{\alpha t}\]

אם $\alpha > 0$ — הרדיוס גדל, תנועה ספירלית החוצה
אם $\alpha < 0$ — הרדיוס קטן, תנועה ספירלית פנימה

חלק שביעי: מימדים ויחידות פיזיקליות

בסוף התרגול נדונו מימדים ויחידות פיזיקליות:

“יש לנו כמה… יש שלושה ושניים מימדים במכניקה. יש עוד מימד אחד ב… פיזיקה אחת — במכניקה. פיזיקה שתיים — שני מימדים, אז יתווסף עוד מימד.”

בפיזיקה קלאסית קיימים שלושה מימדים בסיסיים:

זמן
מסה
מרחק (אורך)

לגבי יחידות של זווית והקשר למימדים:

“זה גודל זוויתי, מה היחידות שלו? רדיאנים. או… מה לא? רדיאנים. אז מה היחידות של זווית? אין מימדים. אני ארשום את זה כ־1 — חסר מימד.”

מהירות זוויתית $\omega$:

“אז היחידות של $\omega$ הן רדיאנים לשנייה, כלומר: $\left[\omega\right] = \frac{\text{rad}}{\text{sec}}$. זה נכתב עם סוגריים מרובעים סביב הגודל הפיזיקלי.”

חלק שמיני: חישוב וקטור המהירות בתנועה מורכבת

בסיום התרגול, המתרגל הראה כיצד לחשב את וקטור המהירות עבור תנועה מורכבת:

“קיבלת וקטור מיקום של החלקיק כתלות בזמן. מה עושים כדי לקבל את המהירות?”

וקטור מיקום כללי:

\[\vec{r}(t) = r_0 e^{\alpha t} \left( \cos(\omega t) \hat{x} + \sin(\omega t) \hat{y} \right)\]

נגזרת של כל רכיב בנפרד:

“נגזור את רכיב ה־$x$ בנפרד, ואז את רכיב ה־$y$. זה קצת ארוך, אבל ככה עושים את זה.”

לגזירת רכיב ה־$x$:

\[\frac{d}{dt} \left( r_0 e^{\alpha t} \cos(\omega t) \right) = r_0 e^{\alpha t} \left( \alpha \cos(\omega t) - \omega \sin(\omega t) \right)\]

(אותו רעיון לגבי רכיב ה־$y$)

המתרגל הסביר את כלל הנגזרת של מכפלה:

“כשגוזרים $\cos$, מקבלים מינוס סינוס כפול $\omega$.”

לבסוף חושב גודל המהירות:

\[\vert \vec{v}(t)| = \sqrt{v_x^2 + v_y^2}\]

“זה מה שנעשה בסוף — מה גודל וקטור המהירות בזמן נתון. כלומר שורש סכום הריבועים של $v_x$ ו־$v_y$.”

תרגול 3 - מיקום, מהירות ותאוצה

תאריך: 03/04/2025

3.1 מבוא לקינמטיקה

קינמטיקה זה כיף! אמנם יש בה אתגרים, אבל היא מעניינת. זה תחום שיש בו לפעמים דברים גאוניים. כשמרצים על קינמטיקה, אפשר לספר כל מיני אגדות מעניינות.

קינמטיקה עוסקת בתיאור התנועה של גופים במרחב, ללא התייחסות לכוחות הגורמים לתנועה זו. אפשר להבחין בין שני סוגי קינמטיקה:

קינמטיקה פשוטה: העקרונות הבסיסיים של תנועה
קינמטיקה למהנדסים: כוללת תנועות מורכבות, מדידות, תצפיות ותנועות בהן המשקל משתנה

לדוגמה, תנועת טיל היא דוגמה של קינמטיקה למהנדסים, והיא עבודה מורכבת הדורשת התחשבות במשתנים רבים.

3.2 יחידות מדידה והסטנדרט הבינלאומי

3.2.1 הפיתוח של הסטנדרט הבינלאומי

היה תיאום בין האירופאים לאמריקאים לגבי יחידות מידה. האמריקאים השתמשו ביחידות שונות (אינצ’ים, פאונדים), אך במדע הם משתדלים לעבוד בצורה מסודרת. לכן נוצר הסטנדרט הבינלאומי (International Standard) שמבוסס על מטר, קילוגרם ושנייה - המערכת המכונה MKS.

ככל שמתקדמים בפיזיקה, הדברים מסתבכים. למשל, איינשטיין בתורת היחסות הפרטית מערער על המסה, המטר והשנייה, אבל באופן כללי אלו אותן מדידות רק בסקאלות אחרות.

3.2.2 ממדים ויחידות

לפעמים אנחנו רוצים לדבר על ממדים, כלומר אנחנו מעוניינים ביחידות המדידה. אנחנו מסמנים זאת בסוגריים מרובעים [ ].

הממדים הבסיסיים:

[M] - מסה (קילוגרם)
[L] - אורך (מטר)
[T] - זמן (שנייה)

כאשר שואלים מה הממדים, נותנים את זה באותיות האלה. כאשר שואלים מה היחידות, עונים על כך בהתאם למערכת המדידה (למשל, מטר לשנייה).

חשוב מאוד להכיר יחידות ומעברים ביניהן. זה ההבדל בין איש מקצוע (פיזיקאי) לבין מי שלא לומד את זה. פיזיקאי מסתכל על היחידות ומקבל אינטואיציה מהירה על משמעותן, כי יש לו הערכות טובות על המציאות.

3.2.3 ניתוח ממדים (Dimensional Analysis)

כשאנחנו מנתחים משוואות פיזיקליות, חשוב לוודא שהיחידות של כל צד במשוואה מתאימות. הנה ניתוח של יחידות התאוצה:

הממדים של $x$ הם $[L]$ (אורך), והממדים של זמן בריבוע הם $[T^2]$ (זמן בריבוע). לכן, ממדי התאוצה $a$ הם $[L]/[T^2] = [L/T^2]$ (אורך חלקי זמן בריבוע).

כיצד מחשבים תאוצה?

\[a = \frac{\Delta v}{\Delta t}\]

אם נבצע ניתוח ממדים:

\[[a] = \frac{[v]}{[t]} = \frac{[L/T]}{[T]} = [L/T^2]\]

וזה מתאים למה שציפינו.

3.3 הגדרות בסיסיות בקינמטיקה

נתחיל עם קינמטיקה חד-ממדית, קרטזית. זוכרים שלמדנו שיש כמה מערכות קואורדינטות:

קרטזית
פולארית
גלילית
כדורית

אבל נתחיל עם קינמטיקה חד-ממדית.

3.3.1 מיקום

אנחנו מסמנים מיקום בעזרת $x(t)$ באופן אופייני. אפשר לרשום את זה גם כ-$r(t)$, אפשר לרשום את זה באלף דרכים אחרות. אנחנו סומכים פה על האינטליגנציה של מי שקורא את זה ועובד עם אותה בעיה, שיבין למה הייתה הכוונה.

3.3.2 מהירות

מהירות היא קצב שינוי המיקום, כלומר, כמה מהר משתנה המיקום. היחידות הן מטרים לשנייה.

אנחנו כבר מכירים נגזרות, אז בעצם קצב שינוי = נגזרת, וזה קצב שינוי מקומי. אנחנו מסמנים את זה ב-$\frac{dx}{dt}$ או $\dot{x}$.

אפשר גם לבדוק שיפוע בין שתי נקודות - להעביר קו בין נקודה 1 ונקודה 2. נניח שיש לנו גרף של מיקום כפונקציה של הזמן, אז לדבר הזה אנחנו יכולים בין שתי נקודות A ו-B להצמיד שיפוע ממוצע.

מהירות רגעית לעומת מהירות ממוצעת

מהירות ממוצעת: $\Delta x$ חלקי $\Delta t$ ייתן לנו את המהירות הממוצעת, אבל בכל רגע נתון תהיה מהירות אחרת - זו המהירות הרגעית שמחושבת כנגזרת.

דוגמה: את נוסעת מפרדס חנה לתל אביב, לקח לך 3 שעות (10,800 שניות), והמרחק הוא 120 קילומטר (120,000 מטר). המהירות הממוצעת היא 120,000 מטר חלקי 10,800 שניות. אבל במהלך הדרך, בכל רגע נתון הייתה לך מהירות אחרת - לפעמים 100 קמ״ש, לפעמים 0 כי עמדת ברמזור.

מהירות רגעית: זו המהירות באותו רגע בדיוק. הדרך לחשב אותה פיזית היא כמעט נגזרת, או למשל לבדוק כמה זמן לוקח לגלגל הרכב לעשות סיבוב אחד.

3.3.3 תאוצה

תאוצה היא קצב שינוי המהירות. אם אומרים שהתאוצה של כדור הארץ היא 10 מטרים לשנייה בכל שנייה (10 מטר/שנייה²), זה אומר שהמהירות משתנה ב-10 מטרים לשנייה בכל שנייה.

אם עוזבים חפץ ממגדל פיזה, זו בערך התאוצה שלו. הוא יתחיל מאפס, אחרי שנייה תהיה לו מהירות של 10 מטרים לשנייה, אחרי עוד שנייה - 20 מטרים לשנייה וכן הלאה.

תאוצה ממוצעת

תאוצה ממוצעת קיימת אך פחות שימושית. למשל, אם נסעת באוטופילוט בסוף הנסיעה, התאוצה הממוצעת תהיה שינוי המהירות לאורך זמן הנסיעה.

הערה חשובה: עד מהירות הכל די אינטואיטיבי. ברגע שמגיעים לתאוצה, האינטואיציה פחות טובה. כשמגיעים לנגזרות גבוהות יותר (נגזרת שלישית וכו’), זה כבר מעבר ליכולת האינטואיטיבית שלנו, וצריך להסתמך על המתמטיקה.

3.3.4 דוגמה - התנהגות ברמזור

נדמיין מצב שאנחנו ניגשים לרמזור אדום. מה קורה? אתה מתחיל לאט, כי אתה לא רוצה לדפוק את הרכב שלפניך. לפעמים אין ברירה ואתה מגביר את התאוצה.

אפשר לצייר גרף של מהירות כפונקציה של הזמן. נניח שהמהירות יורדת (אתה בולם) ואז השיפוע של הגרף הוא שלילי - זוהי תאוצה שלילית או האטה.

אם נסתכל על מהירות שיורדת מ-10 ל-5, אז התאוצה הממוצעת תהיה:

\[a_{average} = \frac{\Delta v}{\Delta t} = \frac{v_2 - v_1}{t_2 - t_1} = \frac{5 - 10}{5 - 0} = \frac{-5}{5} = -1\]

כלומר תאוצה שלילית של 1 מטר לשנייה בריבוע.

3.4 קינמטיקה בתלת-ממד

כשעוברים לתלת-ממד, המשוואות נראות יותר מורכבות, אבל הן למעשה אותן משוואות.

כשרואים משוואה בתלת-ממד וקטורית, למשל $\vec{v}(t) = \frac{d\vec{r}}{dt}$, זו למעשה קבוצה של שלוש משוואות (אחת לכל ציר).

כפי שדיברנו, ציר X לא “יודע” מי זה ציר Y, וציר Y לא “יודע” מי זה ציר X, וכך גם ציר Z. הם לא “מתקשרים” זה עם זה.

אז המשמעות היא:

\[v_x = \frac{dx}{dt}, \quad v_y = \frac{dy}{dt}, \quad v_z = \frac{dz}{dt}\]

באופן דומה, התאוצה היא נגזרת של המהירות (או נגזרת שנייה של המיקום):

\[a_x = \frac{dv_x}{dt}, \quad a_y = \frac{dv_y}{dt}, \quad a_z = \frac{dv_z}{dt}\]

אנחנו מסמנים זאת גם ב-$\vec{a} = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} = \ddot{\vec{r}}$

3.5 אינטגרציה: ממהירות למיקום

לפעמים אני יודע את התאוצה אבל לא יודע את המיקום. לדוגמה, בטלפון יש חיישן תאוצה (חיישן אינרציאלי) שיכול למדוד תאוצות וסיבובים, אבל קשה להבין ממנו את המיקום.

כדי לעבור מתאוצה למיקום, אני צריך לבצע אינטגרציה כפולה.

המיקום בזמן t פחות המיקום בזמן 0 שווה לאינטגרל מ-0 עד t של המהירות:

\[\vec{r}(t) - \vec{r}(0) = \int_0^t \vec{v}(s) ds\]

שימו לב שאני משתמש כאן ב-s כמשתנה אינטגרציה כדי שלא יהיה בלבול עם t שכבר מופיע בגבולות האינטגרל.

זו נוסחה לחישוב המיקום שתלויה במיקום ההתחלתי ובאינטגרל של המהירות.

3.5.1 אינטגרציה של תנועה הרמונית

כאשר יש לנו תאוצה משתנה בזמן, למשל בתנועה הרמונית, אנחנו צריכים לבצע אינטגרציה כדי למצוא את המהירות והמיקום.

נניח שהתאוצה היא:

\[a(t) = A \sin(\omega t)\]

כדי לחשב את המהירות, נבצע אינטגרציה:

\[v(t) = v_0 + \int_0^t a(s)ds = v_0 + \int_0^t A\sin(\omega s)ds\] \[v(t) = v_0 + A \cdot \frac{-\cos(\omega t) + \cos(0)}{\omega} = v_0 + \frac{A}{\omega}(1-\cos(\omega t))\]

כדי לחשב את המיקום, נבצע אינטגרציה נוספת:

\[x(t) = x_0 + \int_0^t v(s)ds = x_0 + \int_0^t \left[v_0 + \frac{A}{\omega}(1-\cos(\omega s))\right]ds\] \[x(t) = x_0 + v_0t + \frac{A}{\omega}\left[t - \frac{\sin(\omega t)}{\omega}\right]\]

3.6 הפרשי מיקום ומהירות - יחסיות בתנועה

3.6.1 הפרשי מיקום

כשאני מסמן $\Delta x$, אני מתכוון ל-$x_2 - x_1$.

משמעותו: המיקום של נקודה 2 מנקודת המבט של מערכת שיושבת ב-1.

בואו נחשוב על זה: נניח שיש לנו שתי נקודות על ציר x, $x_2$ ו-$x_1$.

כשאני מחסר $x_2 - x_1$, אני מקבל מספר חיובי (בהנחה ש-$x_2 > x_1$).

זה לא יכול להיות שאני עומד במערכת 2 ואומר שההפרש בינינו הוא חיובי, כי מבחינתי במערכת 2, הנקודה 1 נמצאת בכיוון השלילי של ציר x.

ולכן, $x_2 - x_1$ מייצג את המיקום של נקודה 2 כפי שרואים אותה מנקודה 1. זה המרחק של 2 מ-1 בכיוון החיובי של ציר x.

3.6.2 הפרשי מהירויות

באופן דומה, הפרש מהירויות $v_2 - v_1$ משמעותו המהירות של נקודה 2 מנקודת המבט של מערכת 1.

נחשוב על שני גופים שנעים ימינה (בכיוון החיובי של ציר x) במהירויות $v_1$ ו-$v_2$, כאשר $v_2 > v_1$. במקרה כזה, $v_1$ מנסה לרדוף אחרי $v_2$, אבל $v_2$ מהיר יותר.

מנקודת המבט של $v_1$, הגוף השני מתרחק ממנו במהירות של $v_2 - v_1$.

3.7 תנועה יחסית - דוגמה ימית

3.7.1 יחידות מדידה ימיות

במהלך השיעור דנו בבעיה הקשורה לספינות הנעות במהירויות וכיוונים שונים. הגענו לשאלה חשובה: מהי יחידת ה”קשר”?

קשר (Knot) היא יחידת מהירות ימית:

קשר אחד = 1.852 קילומטר לשעה (או כ-1.8 קילומטר לשעה בקירוב)
מקור השם בשיטה עתיקה שבה ימאים היו פורסים חבל עם קשרים במרחקים קבועים כדי למדוד את מהירות הספינה

3.7.2 מערכות צירים ומדידת כיוונים

כאשר עובדים עם כיוונים ימיים, משתמשים במערכת קואורדינטות מיוחדת:

צפון = 0° (או 360°)
מזרח = 90°
דרום = 180°
מערב = 270°

הזוויות נמדדות בכיוון השעון, בניגוד למערכת הקואורדינטות המתמטית הרגילה שבה הזוויות נמדדות נגד כיוון השעון.

3.7.3 פתרון בעיית תנועה יחסית

נתונים:

ספינת נופשים מפליגה דרום-מערב (225°) במהירות 10 קשרים

ספינת מטען נוסעת צפונה (0°) במהירות 20 קשרים

השאלה: באיזו מהירות ובאיזה כיוון רואה צופה בספינת המטען את ספינת הנופשים מתרחקת ממנו?

ניתוח וקטורי של הבעיה

כדי לפתור את הבעיה, עלינו למצוא את וקטור המהירות היחסית. כשאנו רוצים לדעת איך צופה במערכת אחת רואה מערכת שנייה, נשתמש בנוסחה:

\[\vec{v}_{1\rightarrow2} = -(\vec{v}_2 - \vec{v}_1)\]

כאשר:

$\vec{v}_{1\rightarrow2}$ היא המהירות של גוף 1 כפי שנראית ממערכת 2
$\vec{v}_1$ היא מהירות גוף 1 (ספינת הנופשים)
$\vec{v}_2$ היא מהירות גוף 2 (ספינת המטען)

הגדרת מערכת הצירים

עבור פתרון זה, הגדרנו:

ציר x: מערב-מזרח (חיובי לכיוון מזרח)
ציר y: דרום-צפון (חיובי לכיוון צפון)

מציאת רכיבי הווקטורים

ספינת הנופשים (וקטור $\vec{v}_1$):

כיוון: 225° (דרום-מערב)
רכיבים:
- $v_{1x} = 10 \cdot \cos(225°) = 10 \cdot (-\frac{\sqrt{2}}{2}) = -5\sqrt{2}$
- $v_{1y} = 10 \cdot \sin(225°) = 10 \cdot (-\frac{\sqrt{2}}{2}) = -5\sqrt{2}$

ספינת המטען (וקטור $\vec{v}_2$):

מהירות: 20 קשרים
כיוון: 0° (צפונה)
רכיבים:
- $v_{2x} = 20 \cdot \cos(0°) = 0$
- $v_{2y} = 20 \cdot \sin(0°) = 20$

חישוב וקטור המהירות היחסית

מכאן, המהירות היחסית:

\[\vec{v}_{1\rightarrow2} = -((0, 20) - (-5\sqrt{2}, -5\sqrt{2})) = -(5\sqrt{2}, 20+5\sqrt{2}) = (-5\sqrt{2}, -(20+5\sqrt{2}))\]

חישוב גודל וכיוון המהירות היחסית

גודל המהירות היחסית:

\[\vert \vec{v}_{1\rightarrow2}\vert = \sqrt{(-5\sqrt{2})^2 + (-(20+5\sqrt{2}))^2} = \sqrt{50 + (20+5\sqrt{2})^2} \approx 28 \text{ קשרים}\]

כיוון המהירות היחסית:

\[\theta = \tan^{-1}\left(\frac{-(20+5\sqrt{2})}{-5\sqrt{2}}\right) + 180° \approx 255°\]

או בשפה ימית: 15° מערבה מהדרום, או 195° לפי הספירה של הימאים.

3.7.4 מסקנות פיזיקליות

תנועה יחסית - מה שספינה אחת רואה תלוי במהירות וכיוון שלה עצמה
שינוי מערכת ייחוס - כאשר עוברים ממערכת ייחוס אחת לאחרת, מהירויות וכיוונים משתנים
חישוב וקטורי - בבעיות תנועה יחסית, ניתוח וקטורי מאפשר לפתור בעיות מורכבות

3.8 תנועה מעגלית והרמונית

תנועה מעגלית קשורה באופן הדוק לתנועה הרמונית. בואו נבחן כמה מושגים בסיסיים:

3.8.1 פרמטרים בסיסיים

זמן מחזור ($T$)

זמן מחזור הוא הזמן הדרוש להשלמת סיבוב שלם. למשל, אם זמן המחזור הוא 3 שניות, פירוש הדבר שנדרשות 3 שניות להשלים סיבוב שלם.

תדירות ($f$)

תדירות היא מספר הסיבובים ליחידת זמן, בדרך כלל לשנייה. התדירות מתקשרת לזמן המחזור באופן הבא:

\[f = \frac{1}{T}\]

אם זמן המחזור הוא 3 שניות, אז התדירות היא $\frac{1}{3}$ סיבובים לשנייה.

מהירות זוויתית ($\omega$)

המהירות הזוויתית היא קצב שינוי הזווית ביחס לזמן:

\[\omega = \frac{d\theta}{dt}\]

במערכת הרדיאנים, סיבוב שלם הוא $2\pi$ רדיאנים. לכן, הקשר בין המהירות הזוויתית לתדירות הוא:

\[\omega = 2\pi f = \frac{2\pi}{T}\]

3.8.2 תנועה הרמונית פשוטה

בתנועה הרמונית פשוטה, המיקום ניתן על ידי:

\[x(t) = A\cos(\omega t + \phi)\]

כאשר:

$A$ הוא המשרעת (האמפליטודה)
$\omega$ היא המהירות הזוויתית
$\phi$ היא פאזת ההתחלה

התנועה מחזורית עם זמן מחזור $T = \frac{2\pi}{\omega}$. כאשר $t = T$, הפונקציה חוזרת לערכה ההתחלתי:

\[\cos(\omega \cdot T) = \cos(2\pi) = 1\]

המהירות בתנועה הרמונית היא:

\[v(t) = -A\omega\sin(\omega t + \phi)\]

והתאוצה היא:

\[a(t) = -A\omega^2\cos(\omega t + \phi) = -\omega^2 x(t)\]

3.8.3 הפרמטרים $A$ ו-$B$ בתנועה מעגלית

בדיון על תנועה מעגלית, עלתה שאלה לגבי הפרמטרים $A$ ו-$B$ במשוואה הכללית של תנועה מעגלית:

\[r(t) = A\cos(\omega t) + B\sin(\omega t)\]

בתנועה מעגלית אמיתית, הפרמטרים $A$ ו-$B$ חייבים לקיים תנאים מסוימים:

אם מדובר במעגל מושלם, אז $\vert A\vert = \vert B\vert = R$ (כאשר $R$ הוא רדיוס המעגל)
אם $A$ ו-$B$ אינם שווים בגודלם, נקבל תנועה אליפטית במקום מעגלית

בתנועה מעגלית, הנתיב במישור $xy$ ניתן על ידי:

\[x(t) = R\cos(\omega t), \quad y(t) = R\sin(\omega t)\]

וניתן לבטא זאת בצורה וקטורית:

\[\vec{r}(t) = (R\cos(\omega t), R\sin(\omega t))\]

הערה על סימני הפרמטרים: הפרמטרים $A$ ו-$B$ אינם חייבים להיות חיוביים. הם יכולים להיות גם שליליים, ומשמעות הדבר היא היפוך הפאזה של התנועה. אם שני הפרמטרים חיוביים, כיוון התנועה הוא נגד כיוון השעון. אם שניהם שליליים, כיוון התנועה הוא עם כיוון השעון.

3.9 תנועה בליסטית עם השפעות חיצוניות

תנועה ב־3 מימדים

כדורגלנית בועטת כדור מראשית הצירים במהירות התחלתית $v_0$ בזווית $\theta_0$ במישור $X\text{-}Y$ , כמתואר בתרשים (בתרשים ציר ה־$X$ במישור הקרקע וציר ה־$Y$ מאונך לקרקע).

רוח נושבת על הכדור במהירות $U$ לכיוון $Z$ (ציר $Z$ יוצא החוצה מהדף במאונך לדף, בתרשים במישור הקרקע) ומעניקה לו מהירות קבועה $U$ בכיוון $Z$. התאוצה היא תאוצת הכובד, כלומר יש תאוצה קבועה כלפי מטה (לכיוון השלילי של ציר ה־$Y$) וגודלה $-g$.
   y
   ↑
   |     ↗ v₀
   |   /
   | / θ
   +•——————→ x
שאלות

רשמו את וקטור התוצאה.

מצאו את וקטור המהירות והמיקום כתלות בזמן.

מה המרחק של הכדור בין נקודת המוצא ונקודת הפגיעה בקרקע?

3.9.1 תנועה בליסטית עם רוח

בבעיית תנועה בליסטית עם רוח, אנו מנתחים את תנועת הכדור בהשפעת כוח הכבידה והרוח.

נניח שהמהירות ההתחלתית היא $\vec{v}_0$ בזווית $\theta_0$ במישור $xy$, ורוח נושבת במהירות $u$ בכיוון ציר $z$.

וקטור המהירות ההתחלתי:

\[\vec{v}_0 = (v_0\cos\theta_0, v_0\sin\theta_0, u)\]

וקטור התאוצה:

\[\vec{a} = (0, -g, 0)\]

כאשר $g$ היא תאוצת הכובד.

לחישוב וקטור המהירות בזמן $t$, אנו מבצעים אינטגרציה:

\[\vec{v}(t) = \vec{v}_0 + \int_0^t \vec{a}ds = \vec{v}_0 + \vec{a}t = (v_0\cos\theta_0, v_0\sin\theta_0 - gt, u)\]

המשמעות הפיזיקלית: המהירות בכיוון $x$ קבועה, המהירות בכיוון $y$ קטנה באופן לינארי בגלל הכבידה, והמהירות בכיוון $z$ נשארת קבועה (בגלל הרוח).

לחישוב המיקום, נבצע אינטגרציה נוספת:

\[\vec{r}(t) = \vec{r}_0 + \int_0^t \vec{v}(s)ds = \vec{r}_0 + \vec{v}_0 t + \frac{1}{2}\vec{a}t^2\]

מה שנותן:

\[\vec{r}(t) = \vec{r}_0 + (v_0\cos\theta_0 \cdot t, v_0\sin\theta_0 \cdot t - \frac{1}{2}gt^2, u \cdot t)\]

3.9.2 דיון על השפעת הרוח

בבעיית התנועה הבליסטית שנידונה, היה חשוב להבהיר את השפעת הרוח:

הרוח משפיעה על הכדור במהירות $u$ קבועה בכיוון ציר $z$
בניגוד לטעות נפוצה, לא מדובר בכוח חיכוך אלא בהשפעה קבועה
מכיוון שהמהירות בכיוון $z$ היא קבועה, התאוצה בכיוון זה היא אפס

בשאלה נאמר ש”רוח נושבת על הכדור במהירות $u$ לכיוון $z$”, כלומר הכדור נע במהירות $u$ באופן קבוע בכיוון זה. כלומר, המהירות ההתחלתית של הכדור בכיוון $z$ היא $u$, והיא נשארת קבועה לאורך כל התנועה.

תרגול 4 - חוקי ניוטון

תאריך: 24/04/2025

תרגיל 1: מספר כוחות פועלים על תיבה

מצא את הכח השקול, בהצגה קרטזית ופולארית.

מה התאוצה הפועלת על התיבה אם משקלה 2 קילוגרם?

מהו הכח המינימלי שיש להפעיל (גודל וכיוון) על מנת שהתיבה תעמוד במקום?

פתרון

חלק 1: מציאת הכח השקול

נתונים בשרטוט כוחות של 6N בזווית 60° מעל הציר האופקי, כוח של 6N בזווית 60° מתחת לציר האופקי, וכוח אנכי כלפי מטה של 4N.

תזכורת לזוויות טריגונומטריות חשובות:
\[\boxed{ \begin{aligned} \sin(60°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\ \cos(60°) &= \frac{1}{2} = 0.5 \\ \tan(60°) &= \sqrt{3} \approx 1.732 \\ \sin(30°) &= \frac{1}{2} = 0.5 \\ \cos(30°) &= \frac{\sqrt{3}}{2} \approx 0.866 \end{aligned}}\]

נחשב את רכיבי הכוחות. בציר $x$ נשתמש ב-$\cos(60°)$ ובציר $y$ נשתמש ב-$\sin(60°)$.

ציר $x$:

\[\begin{aligned} F_{xT} &= \sum F_x = 6 \cdot \cos(60°) + 6 \cdot \cos(60°) \\[5pt] &= 6 \cdot \frac{1}{2} + 6 \cdot \frac{1}{2} \\[5pt] &= 6 \, \mathrm{[N]} \end{aligned}\]

ציר $y$:

\[\begin{aligned} F_{yT} &= \sum F_y = 6 \cdot \sin(60°) - 6 \cdot \sin(60°) - 4 \\[5pt] &= 6 \cdot \frac{\sqrt{3}}{2} - 6 \cdot \frac{\sqrt{3}}{2} - 4 \\[5pt] &= 0 - 4 \\[5pt] &= -4 \, \mathrm{[N]} \end{aligned}\]

לכן הכח השקול בצורה קרטזית הוא:

\[\boxed{\vec{F_T} = \left(6, -4\right)}\]

הגודל של הכח השקול:

\[\vert \vec{F_T}\vert = \sqrt{6^2 + 4^2} = \sqrt{36 + 16} = \sqrt{52} \approx 7.21 \, \mathrm{[N]}\]

מכאן האורך שלו, או הרדיוס, הוא:

\[\boxed{r = 7.21}\]

הזווית של הכח השקול ביחס לציר ה-x החיובי:

\[\theta = \arctan\left(\frac{F_y}{F_x}\right) = \arctan\left(\frac{-4}{6}\right) \approx -33.7\]

לכן הכח השקול בצורה פולרית הוא:

\[\boxed{\vec{F_T}(r, \theta) = (7.21, -33.7)}\]

חלק 2: חישוב התאוצה

מהחוק השני של ניוטון:

\[\vec{a} = \frac{\vec{F_T}}{m} = \frac{[6, -4](N)}{2[kg]} = [3, -2] \mathrm{[\frac{m}{s^2}]}\]

או בצורה פולרית:

\[\vec{a} = \frac{\vert \vec{F_T}\vert}{m} \angle \theta = \frac{7.21[N]}{2[kg]} \angle -33.7° = 3.61[\frac{m}{s^2}] \angle -33.7°\]

חלק 3: הכח המינימלי להחזקת התיבה במקום

כדי שהתיבה תעמוד במקום, יש להפעיל כח שהוא שווה בגודלו והפוך בכיוונו לכח השקול:

\[\vec{F} = -\vec{F_T} = [-6, 4]\]

או בצורה פולרית:

\[\vec{F} = 7.21\mathrm{[N]} \angle 146.3°\]

alt text

תרגיל 2: אדם מושך ארגז

אדם גורר ארגז שמשקלו 50 ק”ג. הוא מפעיל כוח של 196 ניוטון בזוויות שונות:

בהנחה שהארגז נגרר על גבי משטח חסר חיכוך והחבל אופקי, מה תהיה תאוצת הארגז? מה יהיה כוח הנורמל?

בהנחה שהארגז נגרר על גבי משטח חסר חיכוך והחבל בזווית של 32 מעלות לכיוון האופקי, מה תהיה תאוצת הארגז? מה יהיה כוח הנורמל?

עבור אותו הכוח מסעיף ב’, בהנחה שהארגז נע במהירות קבועה, מה גודלו של כוח החיכוך הפועל באופן מנוגד לכיוון התנועה?

פתרון

חלק א: החבל אופקי

במקרה זה, הכוח פועל רק בכיוון האופקי:

\[F_{Tx} = F = 196 \, \mathrm{[N]}\]

הכוחות בכיוון האנכי מאוזנים (הארגז לא מתרומם או שוקע) $N=mg$.

התאוצה בכיוון האופקי:

\[a_x = \frac{F_{Tx}}{m} = \frac{196\mathrm{[N]}}{50\mathrm{[kg]}} = 3.92 \mathrm{[\frac{m}{s^2}]}\]

חלק ב: החבל בזווית 32°

alt text

במקרה הזה הכוח מתפצל לרכיבים:

\[F_x = F \cdot \cos(32°) = 196 \cdot 0.848 = 166.2 \mathrm{[N]}\] \[F_y = F \cdot \sin(32°) = 196 \cdot 0.53 = 103.9 \mathrm{[N]}\]

הכוחות בכיוון האנכי:

\[\begin{aligned} F_y + N - mg &= 0 \\ N &= mg - F_y \end{aligned}\]

כאשר $m = 50 \, \mathrm{[kg]}$ ו-$g = 9.8 \, \mathrm{[\frac{m}{s^2}]}$, נקבל את הנורמאל:

\[\begin{aligned} F_y + N - mg &= 0 \\ N &= mg - F_y \\ N &= 50 \cdot 9.8 - 103.9 \\ N &= 490 - 103.9 \\ N &= 386.1 \, \mathrm{[N]} \end{aligned}\]

התאוצה בכיוון האופקי:

\[a_x = \frac{F_x}{m} = \frac{166.2\mathrm{[N]}}{50\mathrm{[kg]}} = 3.32 \mathrm{[\frac{m}{s^2}]}\]

חלק ג: תנועה במהירות קבועה

אם הארגז נע במהירות קבועה, אז התאוצה היא אפס, ולכן סך הכוחות האופקיים הוא אפס:

\[F_x - F_{friction} = 0 \Rightarrow F_{friction} = F_x = 166.2 \mathrm{[N]}\]

תרגיל 3: יחסי תאוצות

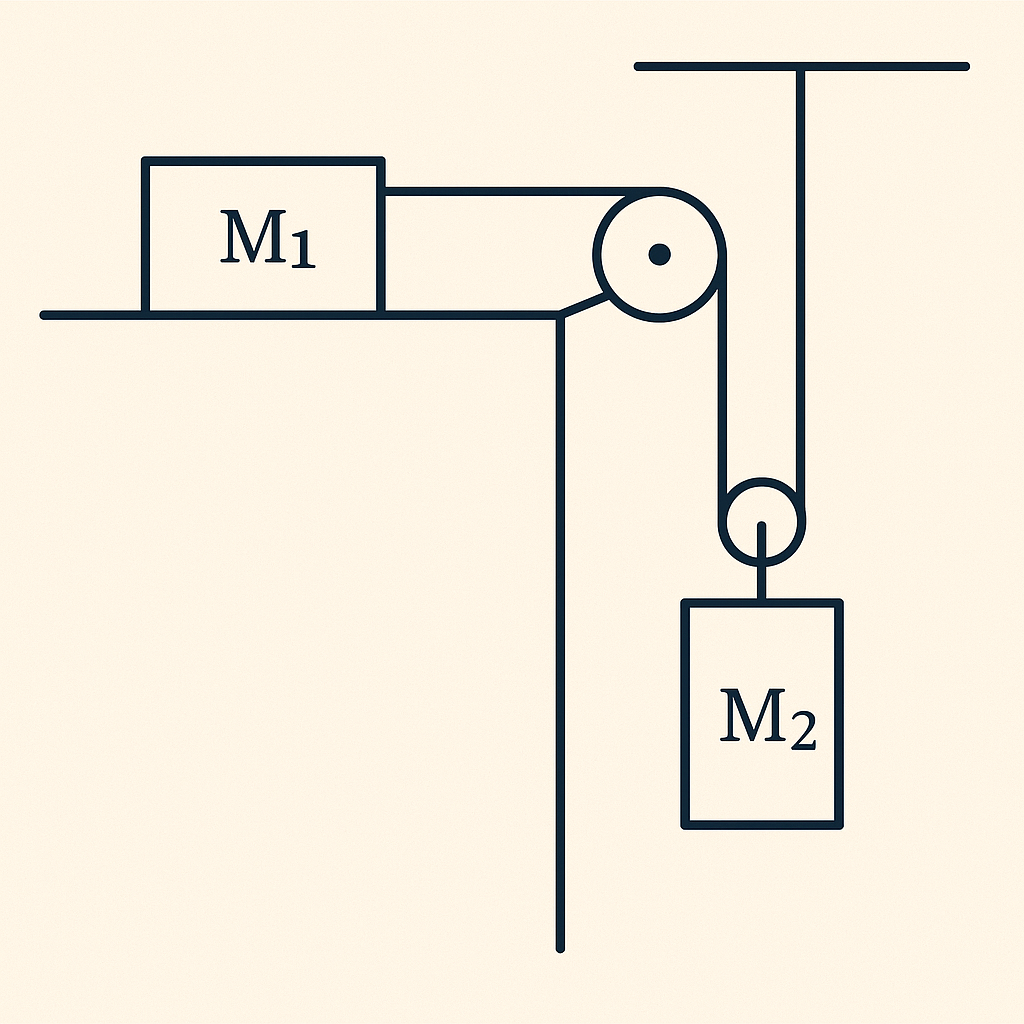
בתרגיל זה מוצגת מערכת גלגלות עם שני גופים בעלי מסות M1 ו-M2. מה יחס התאוצות של שני הגופים?

נבחן את היחס בין תזוזות ומהירויות במערכת:

\[v_{2y} = \frac{\Delta x}{\Delta t} = \frac{v_{1x}}{2}\]

וכן את היחס בין התאוצות:

\[a_{2y} = \frac{\Delta v_{2y}}{\Delta t} = \frac{1}{2}a_{1x}\]

כלומר:

\[\frac{a_{1x}}{a_{2y}} = 2\]

alt text

תרגיל 4: חישוב כוח קבוע

מצאו את הכוח הקבוע הדרוש להאיץ מסה של עשרה טון לאורך קו ישר ממהירות של 54 קמ״ש למהירות של 108 קמ״ש במשך חמש דקות.

פתרון

נשתמש בנוסחה $F = ma = m\frac{\Delta v}{\Delta t}$:

\[F = m \cdot \frac{v_2 - v_1}{\Delta t} = 10 \cdot 1000[kg] \cdot \frac{\frac{108 \cdot 1000[m]}{3600[s]} - \frac{54 \cdot 1000[m]}{3600[s]}}{5 \cdot 60[s]}\] \[= 10000[kg] \cdot \frac{30 - 15[\frac{m}{s}]}{300[s]} = 10000[kg] \cdot \frac{15[\frac{m}{s}]}{300[s]} = 500 \mathrm{[N]}\]

תרגול 5 - בעיית הטריז, בעיית הצנחנית וחבל על מסמר

תאריך: 02/05/2025

סקירת כוחות ועקרונות יסודיים

הכוחות הנפוצים שאנחנו עובדים איתם פועלים בניגוד לכיוון התנועה. נתחיל בכוח החיכוך בין משטחים - זוהי התנגדות לתנועה בין שני משטחים. כוח זה מוגדר באמצעות מקדם:

אם שני המשטחים נמצאים במנוחה, זה מקדם סטטי ($\mu_s$) כפול הכוח הנורמלי ביניהם.
אם שני המשטחים נעים ביחס אחד לשני, אז כוח החיכוך הוא מקדם קינטי ($\mu_k$) כפול הכוח הנורמלי שפועל בין שני המשטחים.

באופן כללי, המקדם הסטטי ($\mu_s$) גדול מהמקדם הקינטי ($\mu_k$).

כוח נוסף שלמדנו ותרגלנו הוא כוח המשיכה של כדור הארץ. קרוב לפני הקרקע, המשקל שלנו (כוח המשיכה של כדור הארץ) הוא המסה שלנו כפול תאוצת המשיכה של כדור הארץ:

\[F_g = m \cdot g\]

כיוון הכוח הזה הוא למרכז כדור הארץ, והגודל של תאוצת הכבידה על פני כדור הארץ הוא בקירוב $g = 10 \mathrm{\frac{m}{s^2}}$.

חשוב לציין שאם לוקחים גוף קל וגוף כבד ומפילים אותם (למשל מהמגדל של פיזה), אז בהיעדר חיכוך משמעותי עם האוויר, שניהם יגיעו לקרקע באותו זמן מכיוון שלשניהם אותה תאוצה. לכולנו יש אותה תאוצה תחת כוח הכבידה.

שלבי עבודה בפתרון בעיות דינמיקה

כשפותרים בעיות דינמיקה, עלינו לעקוב אחר השלבים הבאים:

הכנת תרשים כוחות לכל גוף
בחירת מערכת צירים
רישום משוואות התנועה בהתאם לחוקי ניוטון
פתרון משוואות קינמטיקה לביצוע המשימה

סקירת שאלות תרגיל

לפני שנעבור לשאלה המרכזית, הפרופסור מזכיר מספר תרגילים חשובים:

תרגיל 8 מהדף הקודם, שהוא יחסית מורכב
התרגיל הבא אחריו שעוסק בכוח משתנה ומשוואות דיפרנציאליות
מהדף החדש (דף חמש), שאלה שלוש שהיא ארוכה ושאלה ארבע שהיא “טריקית”

כמו כן, הפרופסור מציין שהמצגת והתשובות זמינות למעקב.

בעיית הטריז והגליל

הבעיה שאנו פותרים היא כדלקמן:

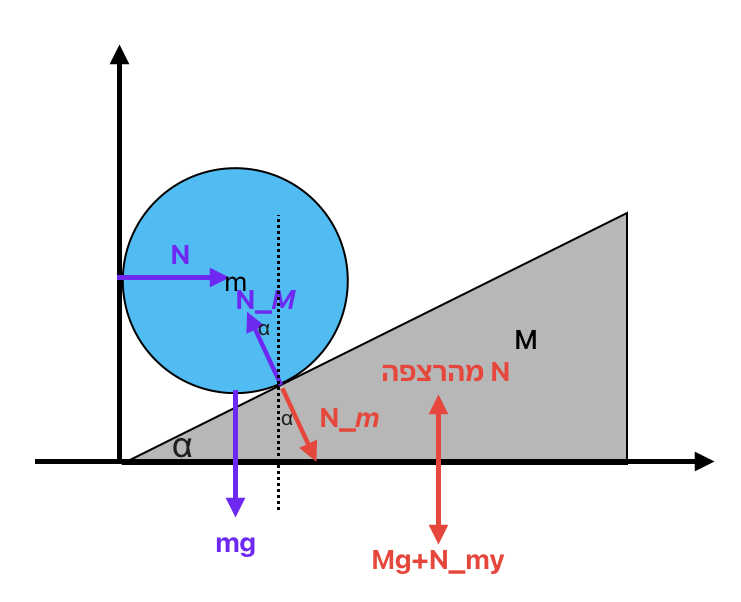
טריז משולש שמסתו $M$ מונח על רצפה אופקית וצמוד לקיר אנכי. על הטריז מונח גליל שמסתו $m$, המפעיל כוח על הטריז הן כלפי מטה והן כלפי צד. זווית השיפוע של הטריז היא $\alpha = 30^{\circ}$. אין חיכוך בין הטריז לרצפה. כוחות המשיכה שמפעיל כדור הארץ על הטריז והגליל הם $M \cdot g$ ו-$m \cdot g$ בהתאמה.

שאלה א׳: מהם הכוחות הנורמליים הפועלים על המערכת?

נתחיל עם ניתוח הכוחות הפועלים על הטריז ($M$):

כוח המשיכה: $M \cdot g$ (כלפי מטה)
הכוח הנורמלי מהרצפה: $N_{\text{floor}}$ (כלפי מעלה)
הכוח הנורמלי מהגליל: $N_m$ (בניצב למישור המשופע)
הכוח הנורמלי מהקיר: $N_{\text{wall}}$ (בכיוון אופקי שמאלה)

כעת נבחן את הכוחות הפועלים על הגליל ($m$):

כוח המשיכה: $m \cdot g$ (כלפי מטה)
הכוח הנורמלי מהטריז: $N_M$ (בניצב למישור המשופע בכיוון הפוך)
הכוח הנורמלי מהקיר: $N_{\text{wall}}$ (בכיוון אופקי ימינה)

alt text

ניתוח הזוויות במערכת

הזוויות במערכת הן כדלקמן:

זווית הטריז עם הרצפה היא $\alpha = 30^{\circ}$
הכוח הנורמלי מהרצפה פועל בזווית של $90^{\circ}$ ביחס לרצפה
הכוח הנורמלי מהקיר פועל בזווית של $90^{\circ}$ ביחס לקיר
הכוח הנורמלי בין הטריז לגליל פועל בזווית של $90^{\circ} - \alpha = 60^{\circ}$ ביחס לאנך

שאלה ב׳: משוואות התנועה כאשר המערכת לא מקובעת

נבחר מערכת צירים כך ש-$x$ הוא בכיוון אופקי (ימינה חיובי) ו-$y$ הוא בכיוון אנכי (מטה חיובי).

משוואות התנועה עבור הגליל

בכיוון ציר $x$:

\[\sum F_x = m \cdot a_x\] \[N_{\text{wall}} - N_m \cdot \sin(30^{\circ}) = m \cdot a_x\]

מכיוון שהגליל לא יכול לזוז בכיוון $x$ (הוא צמוד לקיר), $a_x = 0$, ולכן:

\[N_{\text{wall}} = N_m \cdot \sin(30^{\circ}) = N_m \cdot \frac{1}{2}\]

בכיוון ציר $y$:

\[\sum F_y = m \cdot a_y\] \[M \cdot g - N_m \cdot \cos(30^{\circ}) = m \cdot a_y\] \[\boxed{\text{Galil } a_y = g - \frac{N_m \cdot \cos(30^{\circ})}{m} = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m}}\]

משוואות התנועה עבור הטריז

בכיוון ציר $x$:

\[\sum F_x = M \cdot a_x\] \[N_m \cdot \sin(30^{\circ}) = M \cdot a_x\] \[\boxed{\text{Triz } a_x = \frac{N_m \cdot \sin(30^{\circ})}{M} = \frac{N_m \cdot \frac{1}{2}}{M}}\]

בכיוון ציר $y$:

\[\sum F_y = M \cdot a_y\] \[M \cdot g + N_m \cdot \sin(30^{\circ}) - N_{\text{floor}} = M \cdot a_y\]

מכיוון שהטריז לא יכול לזוז בכיוון $y$ (הוא מונח על הרצפה), $a_y = 0$, ולכן:

\[N_{\text{floor}} = M \cdot g + N_m \cdot \sin(30^{\circ}) = M \cdot g + N_m \cdot \frac{1}{2}\]

בשלב זה, אנו זקוקים לקשר נוסף בין התאוצות כדי למצוא את $N_m$. כשהמערכת אינה מקובעת, הטריז והגליל יתחילו לנוע. הטריז ינוע אופקית (בכיוון ציר $x$) והגליל ינוע אנכית (בכיוון ציר $y$). התנועה המשולבת הזו דורשת ניתוח נוסף כדי למצוא את הקשר בין תאוצות הטריז והגליל ולפתור את המערכת במלואה.

כדי להשלים את הפתרון, אנו צריכים למצוא את היחס בין תאוצת הגליל לתאוצת הטריז. בהתאם לגיאומטריה של המערכת:

\[a_y = a_x \cdot \tan(30°)\]

כאשר:

$a_y$ היא תאוצת הגליל בכיוון אנכי (מטה)
$a_x$ היא תאוצת הטריז בכיוון אופקי (ימינה)

הסבר הקשר: כאשר הטריז נע מרחק $\Delta x$ ימינה, הגליל נע מרחק $\Delta y$ מטה. היחס בין המרחקים האלה הוא $\frac{\Delta y}{\Delta x} = \tan(30°)$. מכאן נובע שגם היחס בין התאוצות הוא אותו יחס.

ידוע ש-$\tan(30°) = \frac{1}{\sqrt{3}}$, ולכן:

\[a_y = a_x \cdot \frac{1}{\sqrt{3}}\]

פתרון המערכת

נזכור את המשוואות שפיתחנו קודם:

\[a_x = \frac{N_m \cdot \sin(30°)}{M} = \frac{N_m}{2M}\] \[a_y = g - \frac{N_m \cdot \cos(30°)}{m} = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m}\]

כעת נציב את היחס שמצאנו:

\[g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = \frac{N_m}{2M} \cdot \frac{1}{\sqrt{3}}\]

נבצע פישוט אלגברי:

\[g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = \frac{N_m}{2M \cdot \sqrt{3}}\] \[g = \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} + \frac{N_m}{2M \cdot \sqrt{3}}\] \[g = N_m \cdot \left( \frac{\sqrt{3}}{2m} + \frac{1}{2M \cdot \sqrt{3}} \right)\] \[N_m = \frac{g}{\frac{\sqrt{3}}{2m} + \frac{1}{2M \cdot \sqrt{3}}}\]

לאחר פישוט נוסף:

\[\boxed{N_m = \frac{2gMm\sqrt{3}}{M\sqrt{3}^2 + m} = \frac{20Mm\sqrt{3}}{3M + m}}\]

כאשר הצבנו $g = 10 \mathrm{m/s^2}$.

עם ערך זה של $N_m$, אנו יכולים לחשב את התאוצות:

\[a_x = \frac{N_m}{2M} = \frac{10m\sqrt{3}}{3M + m}\] \[a_y = g - \frac{N_m \cdot \frac{\sqrt{3}}{2}}{m} = 10 - \frac{10M\sqrt{3}^2}{3M + m} = 10 - \frac{30M}{3M + m} = \frac{10(3M+m) - 30M}{3M+m} = \frac{10m}{3M+m}\]

סיכום בעיית הטריז והגליל

בתהליך הפתרון ביצענו את השלבים הבאים:

פירוק כוחות בזהירות - תהליך עדין שבו קל לטעות
ניתוח הכוחות על כל גוף - לכל אחד מהגופים פעלו שלושה כוחות
בחירת מערכת צירים מתאימה - בדרך כלל בכיוון התאוצות הצפויות
משוואות תנועה - ארבע משוואות עם ארבעה נעלמים, אך שתיים מהן מתבטלות מכיוון שאין תאוצה אנכית לטריז ואין תאוצה אופקית לגליל
מציאת קשר נוסף - היחס הגיאומטרי בין התאוצות התבסס על הגיאומטריה של המערכת

חשוב לציין כי הפתרון תלוי במסות של הגופים - הנורמל בין המשטחים קשור ביחס המסות. ללא ערכים מספריים של המסות, לא ניתן לקבל תשובה מספרית סופית.

בעיה חדשה: כוח התלוי בזמן

נעבור כעת לשאלה האחרונה בדף מספר ארבע:

גוף בעל מסה $M$ ומהירות התחלתית $v_0$ כלשהי בכיוון ציר $x$ מושפע מכוח. מצאו את משוואת המהירות כאשר הכוח תלוי בזמן:
\[F(t) = F_0 \cos(\omega t) \cdot \hat{x}\]
כאשר $\omega$ ו-$F_0$ הם קבועים.

פתרון המהירות כתלות בזמן

נזכור שקשר בין מהירות לתאוצה הוא:

\[v(t) = v_0 + \int_0^t a(s) ds\]

לפי החוק השני של ניוטון:

\[F(t) = M \cdot a(t)\]

מכאן:

\[a(t) = \frac{F(t)}{M} = \frac{F_0 \cos(\omega t)}{M} \cdot \hat{x}\]

נציב בביטוי למהירות:

\[v(t) = v_0 + \int_0^t \frac{F_0 \cos(\omega s)}{M} ds\] \[v(t) = v_0 + \frac{F_0}{M} \int_0^t \cos(\omega s) ds\]

האינטגרל של $\cos(\omega s)$ הוא $\frac{\sin(\omega s)}{\omega}$, ולכן:

\[v(t) = v_0 + \frac{F_0}{M\omega} \sin(\omega t)\]

זהו הפתרון לסעיף א’.

בעיה חדשה: כוח התלוי במהירות (כוח גרר)

בסעיף ב’ נתון שהכוח תלוי במהירות הגוף:

\[F = -\beta v\]

זהו כוח גרר (או חיכוך סטוקס) האופייני לתנועה בנוזלים צמיגים. קיים גם כוח גרר מסוג אחר (ברנולי) הפרופורציוני למהירות בריבוע, האופייני למטוסים ולתנועה במהירויות גבוהות.

פתרון כאשר הכוח פרופורציוני למהירות

לפי החוק השני של ניוטון:

\[F = M \cdot a = -\beta v\]

נרשום את התאוצה כנגזרת של המהירות:

\[M \cdot \frac{dv}{dt} = -\beta v\]

נקבל משוואה דיפרנציאלית:

\[\frac{dv}{dt} = -\frac{\beta}{M} v\]

זוהי משוואה דיפרנציאלית מסדר ראשון שניתן לפתור בשיטת הפרדת משתנים:

\[\frac{dv}{v} = -\frac{\beta}{M} dt\]

נבצע אינטגרציה:

\[\int \frac{dv}{v} = -\frac{\beta}{M} \int dt\] \[\ln|v| = -\frac{\beta}{M} t + C\]

כאשר $C$ הוא קבוע האינטגרציה.

נבצע העלאה ב-$e$:

\[v(t) = e^{-\frac{\beta}{M} t + C} = e^C \cdot e^{-\frac{\beta}{M} t} = A \cdot e^{-\frac{\beta}{M} t}\]

כאשר $A = e^C$ הוא דרגת החופש של האינטגרציה.

כדי לקבוע את ערך $A$, נשתמש בתנאי ההתחלה $v(0) = v_0$:

\[v_0 = A \cdot e^0 = A\]

ולכן:

\[v(t) = v_0 \cdot e^{-\frac{\beta}{M} t}\]

זוהי התוצאה לסעיף ב’.

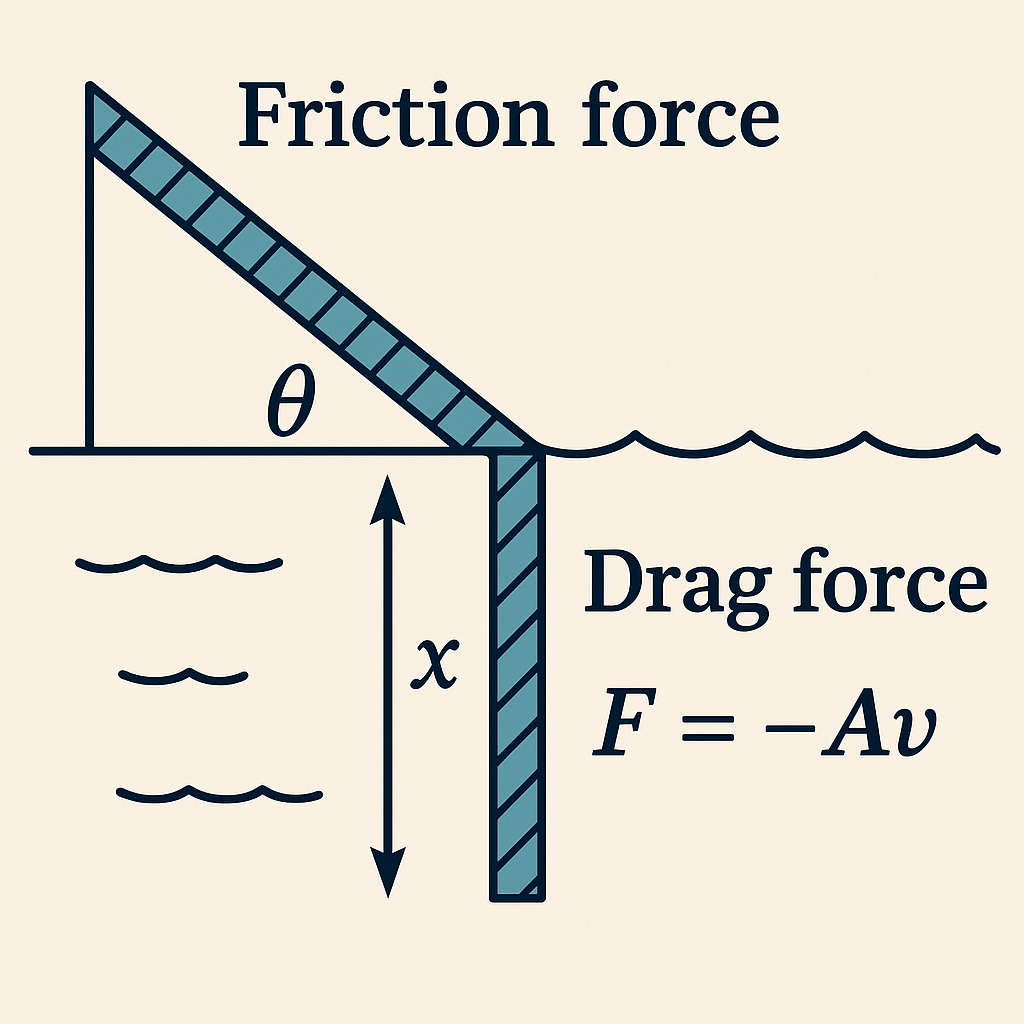
בעיה חדשה: צניחה חופשית עם התנגדות אוויר

נעבור כעת לבעיה חדשה העוסקת בצניחה חופשית:

צנחנית צונחת ללא פתיחת מצנח בשדה הכבידה של כדור הארץ. אנו מניחים:

תאוצת הנפילה החופשית היא $g = 10 \mathrm{m/s^2}$

כוח ההתנגדות של האוויר לתנועתה במהלך צניחתה הוא $F_{resisting force} = \beta v^2$

חלק א’: מציאת ביטוי למהירות הטרמינלית

המהירות הטרמינלית היא המהירות שבה כוח ההתנגדות של האוויר מאזן את כוח הכבידה, כך שהצנחנית צונחת במהירות קבועה.

נבצע ניתוח כוחות: בכיוון אנכי (חיובי כלפי מטה):

כוח הכבידה: $F_g = mg$ (כלפי מטה, חיובי)
כוח התנגדות האוויר: $F_{resisting force} = -\beta v^2$ (כלפי מעלה, שלילי)

במצב של מהירות טרמינלית ($v_T$), התאוצה מתאפסת:

\[\sum F = ma = 0\] \[Mg - \beta v_T^2 = 0\] \[\beta v_T^2 = mg\] \[v_T = \sqrt{\frac{mg}{\beta}}\]

זהו הביטוי למהירות הטרמינלית של הצנחנית.

ניתוח הכוחות והמהירות הטרמינלית

נתחיל עם ניתוח הכוחות הפועלים על הצנחנית. נבחר ציר $z$ חיובי כלפי מטה (בכיוון התנועה):

כוח הכבידה: $F_g = mg$ (כלפי מטה, חיובי)
כוח התנגדות האוויר: $F_{\text{התנגדות}} = -\beta v^2$ (כלפי מעלה, שלילי)

לפי החוק השני של ניוטון:

\[\sum F = ma\] \[Mg - \beta v^2 = ma\]

במצב של מהירות טרמינלית ($v_T$), התאוצה מתאפסת ($a = 0$):

\[Mg - \beta v_T^2 = 0\] \[\beta v_T^2 = mg\] \[v_T = \sqrt{\frac{mg}{\beta}}\]

חישוב מקדם ההתנגדות $\beta$

נתון כי משקל הצנחנית הוא 600 ניוטון (כ-60 ק”ג), והמהירות הטרמינלית שלה היא 216 קמ״ש.

נמיר את המהירות למטרים לשנייה:

\[v_T = \frac{216 \text{ km/h}}{3.6} = 60 \text{ m/s}\]

כעת נחשב את $\beta$:

\[\beta = \frac{mg}{v_T^2}\] \[\beta = \frac{600 \text{ N}}{(60 \text{ m/s})^2} = \frac{600}{3600} = \frac{1}{6} \text{ kg/m}\]

יחידות המידה של $\beta$ הן:

\[[\beta] = \frac{[F]}{[v]^2} = \frac{\mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2}{(\mathrm{m}/\mathrm{s})^2} = \frac{\mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2}{\mathrm{m}^2/\mathrm{s}^2} = \frac{\mathrm{kg}}{\mathrm{m}}\]

משוואה דיפרנציאלית לתנועת הצנחנית

נרשום את החוק השני של ניוטון עבור הצנחנית:

\[Mg - \beta v^2 = ma\]

נחלק ב-$m$:

\[g - \frac{\beta}{m}v^2 = a = \frac{dv}{dt}\] \[\frac{dv}{dt} = g \left(1 - \frac{\beta v^2}{mg}\right)\]

נגדיר פרמטר $\alpha$ כך ש-$\alpha^2 = \frac{\beta}{mg}$:

\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]

יחידות המידה של $\alpha$ הן $\frac{1}{\text{מ’/שנייה}}$ (הופכי של יחידות מהירות).

פתרון המשוואה הדיפרנציאלית

נתון כי הפתרון למשוואה זו, בהנחה שהצנחנית מתחילה ממהירות אפס ($v(0) = 0$), הוא:

\[v(t) = \sqrt{\frac{mg}{\beta}} \tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]

נדרשים להוכיח שפתרון זה מקיים:

את תנאי ההתחלה: $v(0) = 0$
את המשוואה הדיפרנציאלית: $\frac{dv}{dt} = g(1 - \alpha^2 v^2)$

בדיקת תנאי ההתחלה

נציב $t = 0$:

\[v(0) = \sqrt{\frac{mg}{\beta}} \tanh(0) = 0\]

כיוון ש-$\tanh(0) = 0$, התנאי מתקיים.

בדיקת המשוואה הדיפרנציאלית

נחשב את הנגזרת של $v(t)$:

\[\frac{dv}{dt} = \sqrt{\frac{mg}{\beta}} \cdot \frac{d}{dt}\tanh\left(\sqrt{\frac{\beta g}{m}}t\right)\]

נזכור כי הנגזרת של $\tanh(x)$ היא $\frac{1}{\cosh^2(x)}$, ונשתמש בכלל שרשרת הנגזרות:

\[\frac{dv}{dt} = \sqrt{\frac{mg}{\beta}} \cdot \frac{1}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)} \cdot \sqrt{\frac{\beta g}{m}}\]

נפשט:

\[\frac{dv}{dt} = \frac{mg}{\beta} \cdot \frac{\sqrt{\frac{\beta g}{m}}}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)} = \frac{g}{\cosh^2\left(\sqrt{\frac{\beta g}{m}}t\right)}\]

נשתמש בזהות טריגונומטרית היפרבולית: $\frac{1}{\cosh^2(x)} = 1 - \tanh^2(x)$:

\[\frac{dv}{dt} = g \left(1 - \tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right)\right)\]

נציב את $v(t)$ בחזרה:

\[v^2(t) = \frac{mg}{\beta} \tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right)\]

לכן:

\[\tanh^2\left(\sqrt{\frac{\beta g}{m}}t\right) = \frac{\beta}{mg} v^2 = \alpha^2 v^2\]

ולבסוף:

\[\frac{dv}{dt} = g(1 - \alpha^2 v^2)\]

מה שמוכיח שהפתרון אכן מקיים את המשוואה הדיפרנציאלית.

התכנסות למהירות הטרמינלית

ניתן להראות כי כאשר $t \to \infty$, המהירות $v(t)$ מתכנסת למהירות הטרמינלית:

\[\lim_{t \to \infty} v(t) = \sqrt{\frac{mg}{\beta}} \lim_{t \to \infty} \tanh\left(\sqrt{\frac{\beta g}{m}}t\right) = \sqrt{\frac{mg}{\beta}}\]

זאת כיוון ש-$\lim_{t \to \infty} \tanh(t) = 1$.

מיקום הצנחנית כפונקציה של הזמן

כדי למצוא את מיקום הצנחנית $z(t)$, נבצע אינטגרציה על המהירות:

\[z(t) = \int_0^t v(s) ds = \sqrt{\frac{mg}{\beta}} \int_0^t \tanh\left(\sqrt{\frac{\beta g}{m}}s\right) ds\]

האינטגרל של $\tanh(x)$ הוא $\ln(\cosh(x))$, ולכן:

\[z(t) = \sqrt{\frac{mg}{\beta}} \cdot \frac{1}{\sqrt{\frac{\beta g}{m}}} \ln\left(\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right) = \frac{m}{\beta} \ln\left(\cosh\left(\sqrt{\frac{\beta g}{m}}t\right)\right)\]

מכיוון ש-$\ln(\cosh(0)) = 0$, נקבל $z(0) = 0$, כמצופה.

בעיה חדשה: חבל על מסמר

הפתרון המלא זמין בפתרון מטלה 5.

תרגול 6 - בעיות במכניקה

תאריך: 08/05/2025

סיכום אלגוריתם לפתרון בעיות מכניקה

סיימנו חזרה פה, והיה כאן גם אלגוריתם על איך אנחנו ניגשים לבעיה במכניקה:

שלב אפס: לקבל פרפרים בבטן
שלב ראשון: לרשום תרשים כוחות לכל גוף - זה שלב קשה שדורש להזיע
שלב שני: בחירת מערך צירים ופירוק הכוחות לרכיבים - חשוב לבחור אותם בצורה חכמה כדי לא להסתבך
שלב שלישי: רישום משוואות התנועה בהתאם למה שנדרש בשאלה

החשוב ביותר הוא השלב הראשון - הפירוט של הכוחות. אם עשיתם אותו כמו שצריך, אז “יש לכם את השאלה ביד”.

בעיה: מסה על עגלה עם חיכוך סטטי

יש לנו מסה קטנה $m$ שצמודה לעגלה (קרונית). בין המסה לבין העגלה פועל כוח חיכוך, עם מקדם חיכוך סטטי $\mu_s$.

נשאל:

מה צריכה להיות התאוצה של העגלה על מנת שהמסה לא תחליק למטה?

מה הערכים האפשריים של המהירות?

ניתוח הכוחות

כוחות על המסה הקטנה $m$

↓ כוח הכבידה ($mg$) - פועל כלפי מטה
→ כוח נורמלי ($N$) - פועל מהעגלה על המסה בכיוון אופקי
↑ כוח חיכוך סטטי ($F_s$) - פועל כלפי מעלה

הערה לגבי כיוון החיכוך:

החיכוך תמיד פועל בכיוון הפוך למה שהכוח השני “רוצה”. במקרה הזה, המסה “רוצה” ליפול למטה בגלל כוח הכבידה, ולכן החיכוך פועל כלפי מעלה.

בחירת מערכת צירים

נבחר מערכת צירים סטנדרטית:

ציר $y$ כלפי מעלה
ציר $x$ לימין

משוואות התנועה

נסתכל על הגוף הקטן (המסה) וננתח את הכוחות הפועלים עליו:

בכיוון ציר $\uparrow y$ (אנכי)

סכום הכוחות בכיוון $y$:

\[F_s - mg = 0\]

שווה לאפס בהנחה שהמסה לא מחליקה למטה (שיווי משקל אנכי). מכאן נקבל:

\[F_s = mg\]

בכיוון ציר $\rightarrow x$ (אופקי)

סכום הכוחות בכיוון $x$:

\[N = ma\]

כאשר $a$ היא התאוצה האופקית (תאוצת העגלה ששווה לתאוצת המסה הקטנה). זה נובע מהחוק השני של ניוטון.

תנאי על כוח החיכוך הסטטי

אנחנו יודעים שכוח החיכוך הסטטי מוגבל:

\[\underbrace{F_s}_{mg} \leq \mu_s \cdot \underbrace{N}_{=ma}\]

מכיוון ש-$F_s = mg$ ו-$N = ma$, נקבל:

\[mg \leq \mu_s \cdot ma\]

נחלק ב-$m$ משני הצדדים:

\[g \leq \mu_s \cdot a\]

לכן:

\[a \geq \frac{g}{\mu_s}\]

התשובה

התאוצה המינימלית הנדרשת כדי שהמסה לא תחליק למטה היא:
\[\boxed{a \geq \frac{g}{\mu_s} \, \mathrm{m/s^2}}\]
הערכים האפשריים של המהירות:

כאשר תנאי התאוצה מתקיים, אין מגבלה על המהירות. המהירות יכולה לקבל כל ערך אפשרי.

הערות מהדיון בכיתה

לגבי מקדם החיכוך $\mu_s$

מקדם החיכוך $\mu_s$ הוא חסר יחידות.
זה מספר טהור (סקאלר) שמתאר את היחס בין כוח החיכוך המקסימלי לכוח הנורמלי.

לגבי הקשר בין כוח החיכוך למשטח

החיכוך אינו תלוי בשטח המגע, רק בכוח הנורמלי.
אפילו אם יש לנו שני גופים מאותו חומר, אחד עם שטח קטן ואחד עם שטח גדול, שניהם יתחילו להחליק באותה זווית של שיפוע - זה מפתיע ולא אינטואיטיבי.

לגבי ההגיון הפיזיקלי

אם העגלה לא מאיצה מספיק, המסה תיפול כלפי מטה.
ככל שהעגלה מאיצה יותר, כוח הנורמל גדל וכך גם כוח החיכוך המקסימלי, מה שמאפשר למסה להישאר צמודה לעגלה.
כאשר התאוצה מספיק גדולה, החיכוך הסטטי מצליח להתנגד לכוח הכבידה ולמנוע החלקה של המסה.

לגבי התאוצה והמהירות

אין הגבלה על המהירות - כל עוד התאוצה גדולה או שווה ל-$\frac{g}{\mu_s}$.
המהירות יכולה לגדול ולגדול “עד 300 מיליון ק”מ לשעה” (קירוב לא יחסותי).

בעיה: מטפסת הדוחפת קיר

תיאור הבעיה

ברוח התקופה, אנו בוחנים מקרה של מטפסת (ולא מטפס) הדוחפת קיר בכוח $F$.

נתון:

מקדם החיכוך בין הגב לקיר הוא $\mu_s$

מקדם החיכוך בין הרגליים לקיר הוא גם $\mu_s$ (אותו מקדם חיכוך סטטי)

השאלה: מה הכוח $F$ שהיא צריכה להפעיל בשביל לשמור על שיווי משקל?

ניתוח הכוחות בבעיית המטפסת

אנחנו צריכים לסרטט את הסיטואציה ולנתח את הכוחות שפועלים על המטפסת.

הערה: אנחנו מעוניינים רק בכוחות שפועלים על המטפסת.

כוחות שפועלים על המטפסת

באזור הגב

$F_1$: הכוח שהמטפסת מפעילה על הקיר (כלפי חוץ)
$N_1$: כוח נורמלי שהקיר מפעיל על המטפסת בתגובה (מכיוון שאין תנועה, בגלל החוק השלישי של ניוטון)
$f_{friction_1}$: כוח חיכוך שפועל כלפי מעלה

באזור הרגליים

$F_2$: כוח נוסף שהמטפסת מפעילה על הקיר (אינטואיטיבית היינו רוצים להגיד שזהו אותו $F_1$, אך תכף נראה מתוך המשוואות)
$N_2$: כוח נורמלי שהקיר מפעיל על המטפסת באזור הרגליים
$f_{friction_2}$: כוח חיכוך שפועל כלפי מעלה באזור הרגליים

כוח נוסף

$mg$: כוח הכבידה שפועל על המטפסת כלפי מטה

דיון על היחס בין הכוחות

תלמיד/ה: האם אנחנו נצטרך לחבר את שני ה-$F$ (כלומר את $F_1$ ואת $F_2$) או שמספיק אחד?

מרצה: אני חושב שהם יוצאים זהים, אבל באופן כללי לא. כי נניח שהנעליים שלה יש להן כוח חיכוך אחר מאשר המכנסיים, ובמיוחד אם היא דרכה על שמן לפני זה. זה לא בהכרח אותו כוח חיכוך, אבל פה עשו הפשטה. עדיין, אותו כוח שתפעיל החוצה.

תלמיד/ה: כן, נכון.

מרצה: זאת אומרת, תכל’ס, ה-$F_1$ שווה ל-$N_1$ בגלל החוק השלישי של ניוטון, ואותו דבר $N_2$ שווה ל-$F_2$.

משוואות שיווי משקל

בחירת צירים

נעשה בחירה של צירים, ונגדיר את ציר ה-$x$ בכיוון אופקי.

סכום הכוחות בציר $x$

\[\sum F_x = 0\]

תלמיד/ה: שווה ל-$N_1$ ועוד $N_2$?

מרצה: $N_1$ ועוד $N_2$ פחות…

תלמיד/ה: גם אני הייתי רוצה להגיד פה… [מתבלבל/ת קצת] זה מה שפועל על הקיר, לא עליה?

מרצה: בסדר, הקיר מפעיל עליה בחזרה, זה ה-$N$.

אז בעצם $N_1$ שווה ל-$N_2$, אז זה נחמד. ומכיוון שיש לנו חוק שלישי, אז זה גם כן:

\[F_1 = N_1 = N_2 = F_2\]

שאלה על נוטציה

תלמיד/ה: סתם שאלה, למה אתה קורא לזה $N$?

מרצה: $N$ מ”נורמל”, לא בגלל משהו מיוחד.

תלמיד/ה: כי זה כאילו אמור להיות שווה ל-$\mu \cdot N$?

מרצה: נכון.

תלמיד/ה: כאילו אני פתאום מבינה כי בהגדרה נורמל זה $F$ שווה $\mu \cdot N$.

מרצה: נכון.

תלמיד/ה: איך $F$ שווה…? [נראה כי התלמיד/ה מתבלבל/ת בין החוק השני של ניוטון לבין הקשר בין כוח החיכוך לכוח הנורמלי]

מרצה: אני מבין מה את שואלת. שאלה ממש טכנית. לא, סופר ל-$N$… [נראה שהוא מנסה להסביר את הקשר בין הנוטציות]

בעייה: בעיית האוסצילטור - תנועת מסה בין שני קפיצים

תיאור הבעיה - אוסצילטור עם שני קפיצים

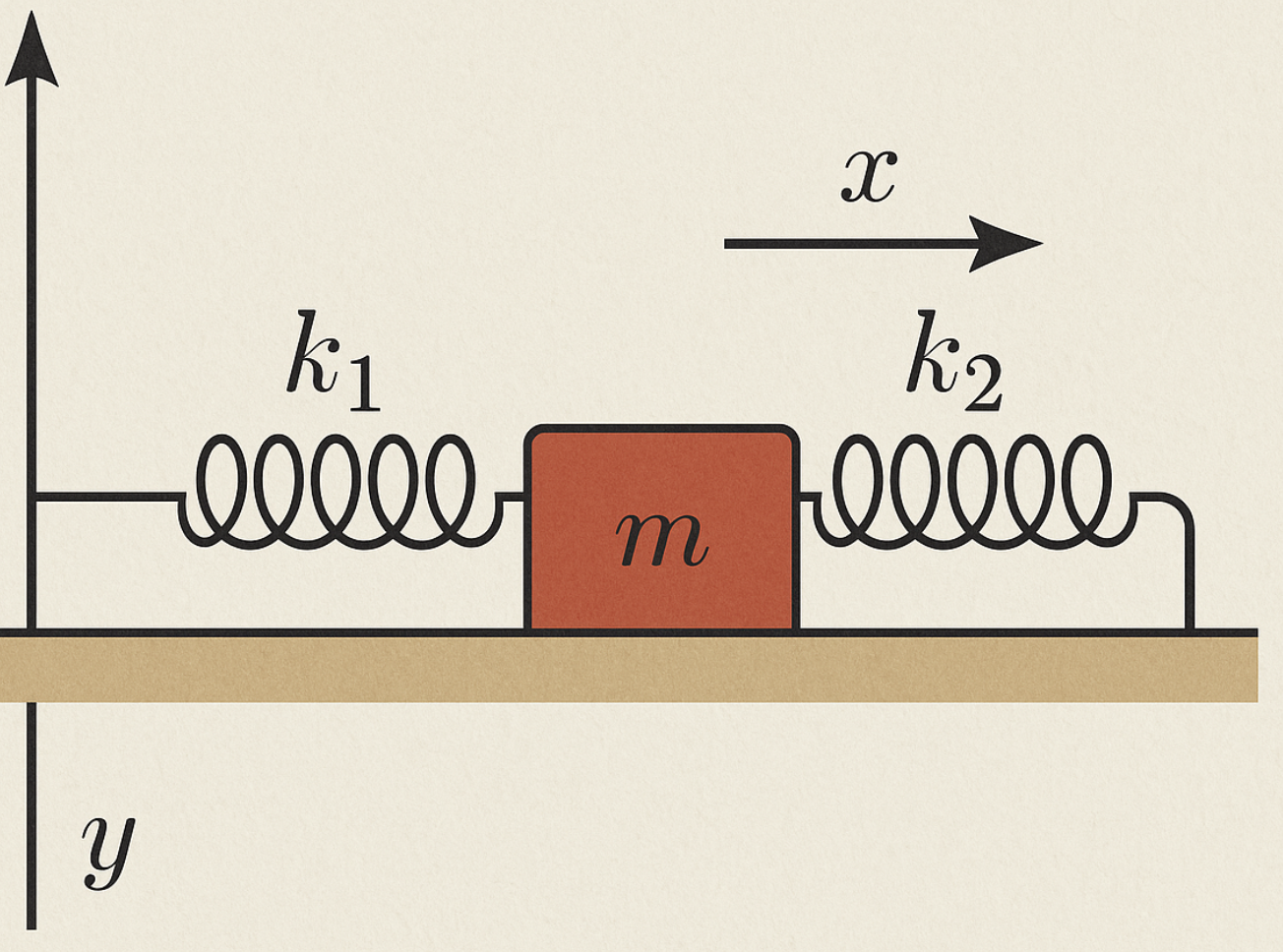
מסה על משטח אופקי מחוברת לשני קפיצים, אחד מצד שמאל ואחד מצד ימין.

אנחנו בוחרים את מערכת הצירים כך שציר ה-$x$ מכוון ימינה, וציר ה-$y$ מכוון כלפי מעלה. נקודת שיווי המשקל של המערכת (כאשר שני הקפיצים במצב לא מתוח) נקבעת כמקור הצירים: $x_0 = 0$.

הבעיה: מושכים את המסה למרחק $A$ (חיובי) מנקודת שיווי המשקל ומשחררים אותה ממנוחה. מבקשים למצוא:

את מיקום המסה כפונקציה של הזמן

את הזמן הדרוש למסה לחזור לראשונה לנקודת שיווי המשקל

ניתוח הכוחות בבעיית האוסצילטור

נסמן:

$m$ - מסת הגוף
$k_1$ - קבוע הקפיץ השמאלי
$k_2$ - קבוע הקפיץ הימני
$x(t)$ - מיקום המסה בזמן $t$
$A$ - המיקום ההתחלתי (מרחק מנקודת שיווי המשקל)

כאשר המסה נמצאת במיקום $x$, הכוחות הפועלים עליה הם:

כוח הקפיץ השמאלי: $F_1 = -k_1 \cdot x$
- אם $x > 0$ (המסה נמצאת מימין לנקודת שיווי המשקל), הכוח מושך שמאלה
- אם $x < 0$ (המסה נמצאת משמאל לנקודת שיווי המשקל), הכוח דוחף ימינה
כוח הקפיץ הימני: $F_2 = -k_2 \cdot x$
- אם $x > 0$, הקפיץ הימני נדחס ודוחף את המסה שמאלה
- אם $x < 0$, הקפיץ הימני נמתח ומושך את המסה ימינה

המשוואה הדיפרנציאלית

לפי החוק השני של ניוטון:

\[\sum F = m \cdot a\]

סכום הכוחות בכיוון $x$ הוא:

\[F_1 + F_2 = -k_1 \cdot x - k_2 \cdot x = -(k_1 + k_2) \cdot x\]

המשוואה הדיפרנציאלית המתקבלת:

\[m \cdot \ddot{x} = -(k_1 + k_2) \cdot x\]

או:

\[\ddot{x} = -\frac{k_1 + k_2}{m} \cdot x\]

נסמן $\omega^2 = \frac{k_1 + k_2}{m}$, ונקבל:

\[\ddot{x} = -\omega^2 \cdot x\]

זוהי משוואה דיפרנציאלית מסדר שני. הפתרון הכללי של משוואה זו הוא:

\[x(t) = c_1 \cdot \sin(\omega t) + c_2 \cdot \cos(\omega t)\]

כאשר $c_1$ ו-$c_2$ הם קבועים שנקבעים לפי תנאי ההתחלה.

פתרון המשוואה הדיפרנציאלית

נשתמש בתנאי ההתחלה כדי למצוא את $c_1$ ו-$c_2$:

המיקום ההתחלתי: $x(0) = A$
\[A = c_1 \cdot \sin(0) + c_2 \cdot \cos(0) = c_2\]
מכאן $c_2 = A$
המהירות ההתחלתית: $\dot{x}(0) = 0$
\[\dot{x}(t) = c_1 \cdot \omega \cdot \cos(\omega t) - c_2 \cdot \omega \cdot \sin(\omega t)\] \[0 = c_1 \cdot \omega \cdot \cos(0) - c_2 \cdot \omega \cdot \sin(0) = c_1 \cdot \omega\]
מכאן $c_1 = 0$

לכן הפתרון הוא:

\[x(t) = A \cdot \cos(\omega t)\]

כאשר $\omega = \sqrt{\frac{k_1 + k_2}{m}}$

חישוב הזמן לחזרה לנקודת שיווי המשקל

נקודת שיווי המשקל היא בנקודה $x = 0$. אנחנו מחפשים את הזמן $t^\star$ הראשון (שגדול מאפס) כך ש-$x(t^\star) = 0$.

\[A \cdot \cos(\omega t^\star) = 0\]

פתרון המשוואה הזו הוא:

\[\omega t^\star = \frac{\pi}{2} + k\pi \quad (k \in \mathbb{Z})\]

מכאן:

\[t^\star = \frac{\pi}{2\omega} = \frac{\pi}{2\sqrt{\frac{k_1 + k_2}{m}}} = \frac{\pi}{2} \cdot \sqrt{\frac{m}{k_1 + k_2}}\]

זהו הזמן הדרוש למסה לחזור לראשונה לנקודת שיווי המשקל.

התנהגות המערכת לאורך זמן

התנועה של המסה היא תנועה הרמונית פשוטה, שבה המסה נעה בין $+A$ ל-$-A$ ובחזרה. כשהמסה נמצאת במיקום $x = 0$ (נקודת שיווי המשקל), המהירות שלה מקסימלית. כשהמסה נמצאת בנקודות הקיצון ($x = \pm A$), המהירות שלה אפס.

מכיוון שאין חיכוך במערכת, התנועה תמשיך לנצח בלי לדעוך. בעולם האמיתי, כמובן, יש תמיד חיכוך וכוחות אחרים שגורמים לדעיכה של התנודות עם הזמן.

הערות נוספות מהדיון בכיתה

המערכת נעה בצורה סינוסואידלית עם הזמן
זמן המחזור המלא של התנועה הוא $T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k_1 + k_2}}$
אם היינו מתחילים עם מהירות התחלתית שונה מאפס, היינו מקבלים גם את האיבר עם הסינוס בפתרון
ניתן גם לכתוב את הפתרון בצורה $x(t) = C \cos(\omega t + \phi)$ כאשר $C$ ו-$\phi$ הם קבועים שתלויים בתנאי ההתחלה
בתוך גרעינים אטומיים וברמה המיקרוסקופית של החומר, תנודות מסוג זה מתרחשות כמעט ללא דעיכה (בטמפרטורה נמוכה מאוד)

תרגול 7 - תנועה הרמונית ותנועה מעגלית

תאריך: 15/05/2025

1. מבוא לתנועה הרמונית

תנועה הרמונית היא תנועה שחוזרת על עצמה - הגוף מבצע תנודה, חוזר לנקודת ההתחלה, ומבצע שוב את אותה תנודה וכן הלאה.

דוגמאות לתנועה הרמונית:

מטוטלת שמבצעת תנודות
קפיץ שמבצע תנודות

2. מושגי יסוד בתנועה הרמונית

נקודת שיווי משקל

בתנועה הרמונית, התנודות מתבצעות סביב נקודת שיווי משקל. נקודת שיווי משקל היא הנקודה היציבה - הנקודה שאם הגוף נמצא בה ואינו בתנועה, הוא יישאר במנוחה.

דוגמאות:

במטוטלת: נקודת שיווי המשקל היא כאשר המטוטלת אנכית לחלוטין (הנקודה הנמוכה ביותר)
בקפיץ: נקודת שיווי המשקל היא כאשר הקפיץ אינו מתוח ואינו מכווץ

כאשר מזיזים את הגוף מעט מנקודת שיווי המשקל, הוא “ירצה” לחזור לנקודה זו. אולם, בגלל האינרציה, הגוף יעבור את נקודת שיווי המשקל וימשיך לצד השני, ואז שוב ירצה לחזור לנקודת שיווי המשקל. כך נוצרות התנודות ההרמוניות.

מדדים לתנועה הרמונית

כאשר חוקרים תנועה הרמונית, ישנם מספר מדדים חשובים:

זמן מחזור $(T)$: הזמן שלוקח לגוף להשלים תנודה שלמה ולחזור לנקודת ההתחלה.
אמפליטודה $(A)$: המרחק המקסימלי שהגוף מתרחק מנקודת שיווי המשקל. האמפליטודה תלויה בתנאי ההתחלה (למשל, כמה מתחנו את הקפיץ או כמה הרמנו את המטוטלת).
תדירות $(f)$: מספר התנודות שהגוף מבצע בשנייה אחת. זהו הערך ההופכי של זמן המחזור:

\[f = \frac{1}{T}\]

3. תיאור מתמטי של תנועה הרמונית

גרף התנועה

התנועה ההרמונית מתוארת על-ידי פונקציות סינוס או קוסינוס. אם מציירים גרף של המיקום $(x)$ כפונקציה של הזמן $(t)$, נקבל עקומת סינוס או קוסינוס.

כוח מחזיר

בתנועה הרמונית פועל כוח מחזיר - כוח שמנסה להחזיר את הגוף לנקודת שיווי המשקל. כוח מחזיר זה פרופורציונלי למרחק מנקודת שיווי המשקל, אך פועל בכיוון הנגדי:

\[F = -kx\]

כאשר:

$F$ הוא הכוח
$k$ הוא קבוע הפרופורציונליות (קבוע הקפיץ במקרה של קפיץ)
$x$ הוא המרחק מנקודת שיווי המשקל
הסימן המינוס מציין שהכוח פועל בכיוון הנגדי למרחק

המשמעות של המינוס:

אם $x$ חיובי (הגוף נמצא מימין לנקודת שיווי המשקל), הכוח יהיה שלילי (כלומר, כלפי שמאל)
אם $x$ שלילי (הגוף נמצא משמאל לנקודת שיווי המשקל), הכוח יהיה חיובי (כלומר, כלפי ימין)

משוואת התנועה

לפי החוק השני של ניוטון:

\[F = ma\]

כאשר $a$ היא התאוצה, שהיא הנגזרת השנייה של המיקום:

\[a = \frac{d^2x}{dt^2}\]

לכן:

\[F = m \frac{d^2x}{dt^2}\]

ואם נשלב עם משוואת הכוח המחזיר:

\[-kx = m \frac{d^2x}{dt^2}\]

ממנה נקבל:

\[\frac{d^2x}{dt^2} = -\frac{k}{m}x\]

זוהי משוואה דיפרנציאלית לינארית הומוגנית מסדר שני. אם נסמן $\omega^2 = \frac{k}{m}$, נקבל:

\[\frac{d^2x}{dt^2} = -\omega^2 x\]

פתרון המשוואה הדיפרנציאלית

הפתרון של המשוואה הדיפרנציאלית הזו הוא:

\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]

או לחלופין:

\[x(t) = A\cos(\omega t + \phi)\]

כאשר:

$A$ היא האמפליטודה (הערך המקסימלי של $x$)
$\omega = \sqrt{\frac{k}{m}}$ הוא התדירות הזוויתית
$\phi$ היא הפאזה ההתחלתית

משמעות הפאזה

הפאזה $\phi$ קובעת את נקודת ההתחלה של התנועה. כלומר, היא מגדירה באיזה מצב של התנודה הגוף נמצא בזמן $t=0$.

אם $\phi = 0$, אז בזמן $t=0$ המיקום הוא $x = A\cos(0) = A$, כלומר הגוף נמצא באמפליטודה המקסימלית החיובית.
אם $\phi = \pi$, אז בזמן $t=0$ המיקום הוא $x = A\cos(\pi) = -A$, כלומר הגוף נמצא באמפליטודה המקסימלית השלילית.
אם $\phi = \frac{\pi}{2}$, אז בזמן $t=0$ המיקום הוא $x = A\cos(\frac{\pi}{2}) = 0$, כלומר הגוף עובר דרך נקודת שיווי המשקל.

4. מקרים מיוחדים

לעתים המשוואה הדיפרנציאלית כוללת איבר נוסף:

\[\frac{d^2x}{dt^2} = -\omega^2 x + C\]

במקרה כזה, הפתרון יהיה דומה אך יכלול מרכיב נוסף. זוהי עדיין תנועה הרמונית, אבל סביב נקודת שיווי משקל שונה מהמקור.

משמעות ותפקיד של $\omega$ (אומגה)

ה-$\omega$ (אומגה), שמופיעה במשוואה כ-$\omega^2$, היא התדירות הזוויתית של התנועה ההרמונית. יחידות המידה של $\omega$ הן:

\[[\omega] = \frac{1}{s} \text{ (per second)}\]

כאשר $\omega$ גדולה, התנודות מהירות יותר. כאשר $\omega$ קטנה, התנודות איטיות יותר. התדירות הזוויתית $\omega$ קובעת את קצב התנודות.

הקשר בין $\omega$ וזמן המחזור $T$

מכיוון שפונקציית הסינוס והקוסינוס חוזרות על עצמן כל $2\pi$ רדיאנים, זמן המחזור $T$ של התנועה ההרמונית ניתן על ידי:

\[\omega T = 2\pi\]

ומכאן:

\[\boxed{T = \frac{2\pi}{\omega}}\]

כזכור, $\omega = \sqrt{\frac{k}{m}}$, ולכן:

\[T = 2\pi \sqrt{\frac{m}{k}}\]

זמן המחזור תלוי במסה ובקבוע הקפיץ - ככל שהמסה גדולה יותר, זמן המחזור ארוך יותר (תנודות איטיות יותר), וככל שקבוע הקפיץ גדול יותר, זמן המחזור קצר יותר (תנודות מהירות יותר).

מציאת קבועי האינטגרציה $A$ ו-$B$

הקבועים $A$ ו-$B$ במשוואה $x(t) = A\cos(\omega t) + B\sin(\omega t)$ נקבעים על-ידי תנאי ההתחלה של המערכת.

אם בזמן $t=0$ הגוף נמצא בנקודת המוצא ($x=0$) ואין לו מהירות התחלתית, אז $A=0$ ו-$B=0$ (אין תנועה).
אם בזמן $t=0$ הגוף נמצא במרחק מקסימלי מנקודת שיווי המשקל ($x=A$) ואין לו מהירות התחלתית, אז $A$ יהיה האמפליטודה ו-$B=0$ (הפתרון יהיה רק קוסינוס).
אם בזמן $t=0$ הגוף נמצא בנקודת שיווי המשקל ($x=0$) ויש לו מהירות התחלתית, אז $A=0$ והפתרון יכלול רק סינוס.
במקרים אחרים, כאשר בזמן $t=0$ הגוף נמצא במיקום כלשהו ויש לו מהירות כלשהי, הפתרון יכלול גם קוסינוס וגם סינוס.

5. דוגמה: מערכת של שתי מסות וקפיץ

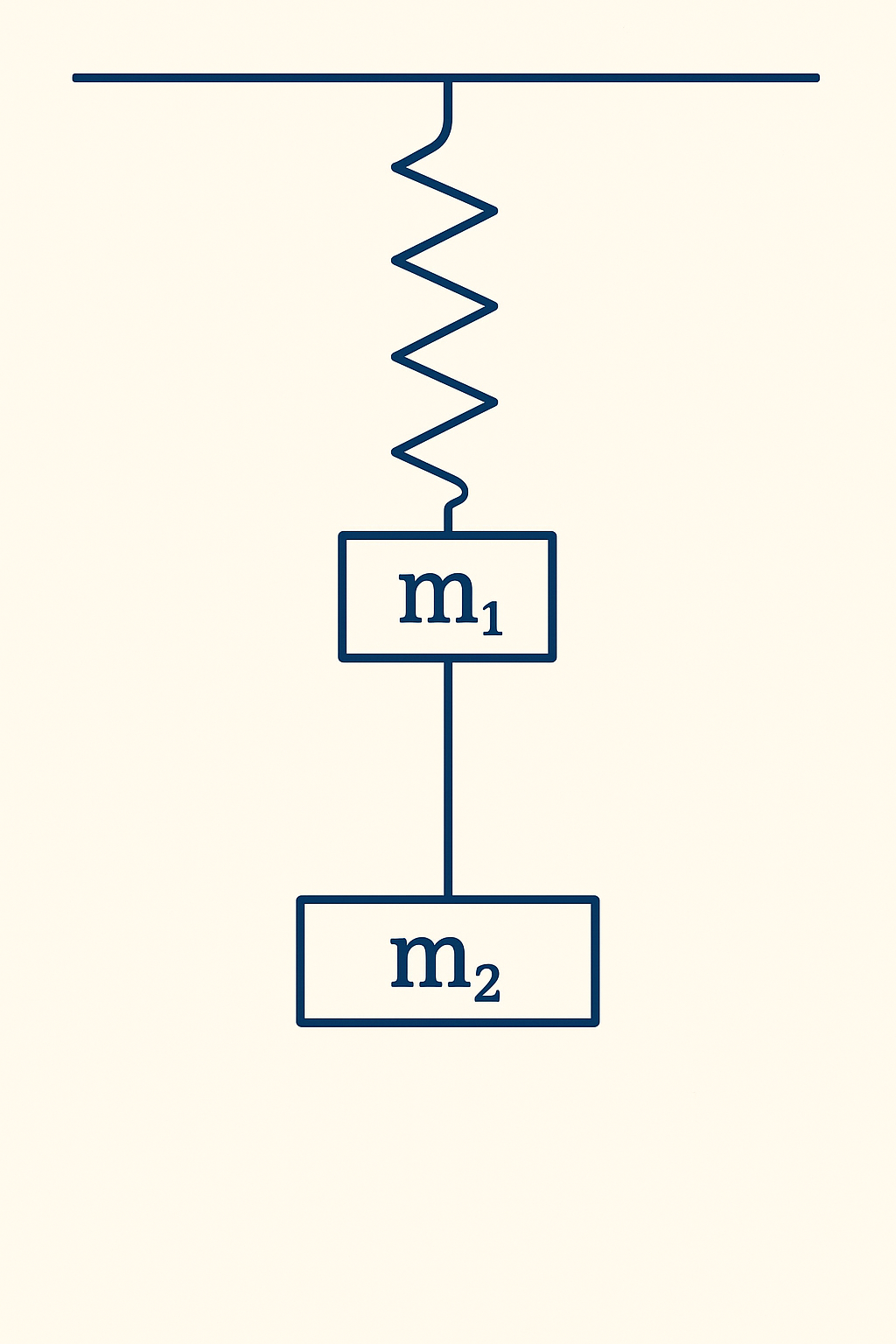
נתונה מערכת שבה מסה $m_2$ קשורה למסה $m_1$ באמצעות חוט דק. המסה $m_1$ קשורה לקפיץ אנכי שקבוע הקפיץ שלו הוא $K$. המערכת נמצאת במנוחה.

אם חותכים את החוט, המסה $m_1$ תתחיל לבצע תנודות הרמוניות.

מהי האמפליטודה של התנודה ההרמונית?

מהי התדירות של התנועה?

איך התשובה הייתה משתנה אם המערכת נמצאת במעלית המאיצה בתאוצה של $A$ כלפי מעלה?

סעיף 1: מציאת האמפליטודה של התנודה ההרמונית

הרעיון: נמצא את נקודת שיווי המשקל של המערכת לפני חיתוך החוט, ואת נקודת שיווי המשקל החדשה אחרי חיתוך החוט. ההפרש בין שתי נקודות שיווי המשקל הוא האמפליטודה של התנודה ההרמונית.

שלב 1: המצב היציב לפני חיתוך החוט

הגדרת מערכת הצירים

ראשית בחרנו את מערכת הצירים כך ש:

ראשית הצירים היא בנקודה שבה הקפיץ רפוי (אורכו הטבעי)
הכיוון החיובי של ציר ה-$y$ מוגדר כלפי מטה
המשתנה $y$ מציין את המרחק של המסה $m_1$ מראשית הצירים

הערה: בתרגילים אחרים, וגם כאן, אולי יהיה נוח יותר לכתוב $x_0$ במקום $y$.

ניתוח הכוחות

נרשום את הכוחות הפועלים על כל מסה:

על המסה $m_1$:

כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)
מתיחות החוט כלפי מטה: $T$ (חיובי)

על המסה $m_2$:

כוח הכבידה כלפי מטה: $m_2g$ (חיובי)
מתיחות החוט כלפי מעלה: $-T$ (שלילי)

alt text

משוואות שיווי המשקל

כאשר המערכת נמצאת בשיווי משקל, סכום הכוחות על כל מסה הוא אפס:

עבור $m_1$:

\[m_1g - Ky + T = 0 \tag{1}\]

עבור $m_2$:

\[m_2g - T = 0 \tag{2}\]

ממשוואה $(2)$ אנחנו מקבלים:

\[T = m_2g\]

נציב את הביטוי של $T$ במשוואה $(1)$ כדי לקבל את ערך $y$ בנקודת שיווי המשקל:

\[\begin{aligned} m_1g - Ky + m_2g &= 0 \\[10pt] Ky &= m_1g + m_2g \\[10pt] &= (m_1 + m_2)g \\[10pt] y &= \frac{(m_1 + m_2)g}{K} \end{aligned}\]

כלומר, התארכות הקפיץ במצב של שיווי המשקל, או במילים אחרות - נקודת שיווי המשקל לפני שהחוט נקרע, היא במרחק של $y$ מהראשית של מערכת הצירים, כאשר $y$ הוא:

\[\boxed{y = \frac{(m_1 + m_2)g}{K}}\]

שלב 2: מה קורה אחרי שהחוט נקרע

אחרי שהחוט נקרע:

המסה $m_2$ נופלת ויוצאת מהמערכת
מתיחות החוט $T$ לא פועלת יותר על $m_1$
נקודת שיווי המשקל של המערכת משתנה

הכוחות החדשים על $m_1$

כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)

נקודת שיווי המשקל החדשה

במצב שיווי המשקל החדש, סכום הכוחות יהיה אפס:

\[\begin{aligned} m_1g - Ky_{new} &= 0 \\[10pt] Ky_{new} &= m_1g \\[10pt] y_{new} &= \frac{m_1g}{K} \end{aligned}\]

המעבר בין שתי נקודות שיווי המשקל

המעבר בין שתי נקודות שיווי המשקל גורם לתנועה הרמונית של המסה $m_1$.

לפני חיתוך החוט, המסה נמצאת במיקום $y_{old} = \frac{(m_1 + m_2)g}{K}$. אחרי חיתוך החוט, נקודת שיווי המשקל החדשה היא $y_{new} = \frac{m_1g}{K}$.

ההפרש בין שתי נקודות שיווי המשקל נותן את האמפליטודה $A$ של התנודה ההרמונית:

\[\begin{aligned} \Delta y &= y_{old} - y_{new} \\[10pt] &= \frac{(m_1 + m_2)g}{K} - \frac{m_1g}{K} \\[10pt] &= \frac{m_2g}{K} \end{aligned}\]

זה ה”צעד” הראשוני שיגרום לתנועה ההרמונית, כאשר המסה $m_1$ תתחיל לנוע מעלה לכיוון נקודת שיווי המשקל החדשה.

האמפליטודה של התנודה ההרמונית היא:

\[\boxed{A = \frac{m_2g}{K}}\]

alt text

סעיף 2: מציאת התדירות של התנועה

המשוואה הדיפרנציאלית של התנועה

נסמן ב-$\eta$ את הסטייה של המסה $m_1$ מנקודת שיווי המשקל החדשה:

\[\eta = y - y_{new}\]

לפי החוק השני של ניוטון, הכוח הפועל על המסה $m_1$ שווה לשינוי התנועה שלה כפול המסה:

\[m_1 \frac{d^2\eta}{dt^2} = m_1g - K(y_{new} + \eta) \tag{3}\]

נציב במשוואה $(3)$ את $y_{new} = \frac{m_1g}{K}$ ונקבל:

\[\begin{aligned} m_1 \frac{d^2\eta}{dt^2} &= m_1g - K\left(\frac{m_1g}{K} + \eta\right) \\[10pt] &= m_1g - m_1g - K\eta \\[10pt] &= -K\eta \end{aligned}\]

נבודד את $\frac{d^2\eta}{dt^2}$ על ידי חילוק ב-$m_1$:

\[\frac{d^2\eta}{dt^2} = -\frac{K}{m_1}\eta \tag{4}\]

נגדיר $\omega^2 = \frac{K}{m_1}$, ונציב במשוואה $(4)$. נקבל את המשוואה הדיפרנציאלית של התנועה ההרמונית:

\[\boxed{\frac{d^2\eta}{dt^2} = -\omega^2\eta}\]

הפתרון של התנועה ההרמונית

הפתרון של המשוואה הדיפרנציאלית הזו הוא:

\[\eta(t) = A\cos(\omega t + \phi)\]

כאשר:

$A$ היא האמפליטודה, שבמקרה זה $A = \frac{m_2g}{K}$ (הסטייה ההתחלתית)
$\omega = \sqrt{\frac{K}{m_1}}$ היא התדירות הזוויתית
$\phi$ היא הפאזה ההתחלתית (במקרה זה $\phi = \pi$ כי התנועה מתחילה מהסטייה המקסימלית בכיוון השלילי)

המיקום המלא של המסה $m_1$ כפונקציה של הזמן יהיה:

\[\begin{aligned} y(t) &= y_{new} + \eta(t) \\[10pt] &= \frac{m_1g}{K} + \frac{m_2g}{K}\cos(\omega t + \pi) \end{aligned}\]

או בפשטות:

\[y(t) = \frac{m_1g}{K} - \frac{m_2g}{K}\cos(\omega t)\]

זמן המחזור של התנודות יהיה:

\[T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{m_1}{K}}\]

התדירות היא הערך ההופכי של זמן המחזור, מכאן:

\[\boxed{f = \frac{1}{T} = \frac{1}{2\pi}\sqrt{\frac{K}{m_1}}}\]

הניתוח המתמטי אחרי חיתוך החוט - הסבר נוסף

כאשר החוט נחתך, המערכת עוברת לנקודת שיווי משקל חדשה. בשלב זה, הכוחות על המסה $m_1$ הם:

כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)

המשוואה הדיפרנציאלית המתארת את התנועה:

\[\frac{d^2y}{dt^2} = \frac{K}{m_1}y + g\]

זוהי משוואה דיפרנציאלית מהצורה:

\[\frac{d^2y}{dt^2} = -\omega^2y + C\]

כאשר $\omega^2 = \frac{K}{m_1}$ וכאשר יש פה מינוס נוסף (כי הגדרנו את הכיוון החיובי כלפי מטה).

הפתרון של משוואה כזו הוא תנועה הרמונית סביב נקודת שיווי משקל חדשה. האומגה ($\omega$) קובעת את קצב התנודות:

\[\omega = \sqrt{\frac{K}{m_1}}\]

אומגה זו קובעת כמה מהר התנודות מתרחשות. ככל שאומגה גדולה יותר, התנודות מהירות יותר, וככל שהיא קטנה יותר, התנודות איטיות יותר.

סעיף 3: השפעת מעלית מואצת על המערכת

השפעת מעלית מואצת על המערכת

כעת נבחן מה קורה כאשר כל המערכת נמצאת בתוך מעלית המאיצה כלפי מעלה בתאוצה $A$.

יש שתי דרכים להסתכל על הבעיה:

1. מנקודת מבט חיצונית

אם מסתכלים מבחוץ, התאוצה של המסה $m_1$ מורכבת משני חלקים:

התאוצה של התנודות $\frac{d^2y}{dt^2}$
התאוצה של המעלית $A$

2. מנקודת מבט בתוך המעלית

אם נמצאים בתוך המעלית ולא יודעים שהיא מאיצה, נרגיש “כוח מדומה” הפועל בכיוון ההפוך לתאוצת המעלית. הכוח המדומה שווה ל-$-m_1A$ (כלפי מטה).

המשוואה הדיפרנציאלית תהיה:

\[m_1\frac{d^2y}{dt^2} = m_1g - Ky - m_1A\]

שאפשר לכתוב כ:

\[\frac{d^2y}{dt^2} = g - \frac{K}{m_1}y - A\]

או:

\[\frac{d^2y}{dt^2} = -\frac{K}{m_1}y + (g-A)\]

כאשר משווים למשוואה הסטנדרטית, מקבלים:

$\omega^2 = \frac{K}{m_1}$ (זהה למקרה ללא מעלית)
$C = g-A$ (שונה מהמקרה ללא מעלית, שבו $C = g$)

מה משתנה במעלית מואצת?

התדירות: לא משתנה! האומגה נשארת זהה: $\omega = \sqrt{\frac{K}{m_1}}$
נקודת שיווי המשקל: משתנה. במעלית מואצת, נקודת שיווי המשקל החדשה תהיה במיקום שבו:
\[Ky = m_1(g-A)\] \[y = \frac{m_1(g-A)}{K}\]
האמפליטודה: תלויה בתנאי ההתחלה ובהפרש בין נקודות שיווי המשקל הישנה והחדשה.

מה שחשוב לזכור זה שתדירות התנודות לא משתנה כאשר המערכת נמצאת במעלית מואצת. זו תכונה חשובה של תנועה הרמונית - התדירות תלויה רק בקבוע הקפיץ ובמסה, ולא בתנאי הסביבה כמו תאוצת המעלית.

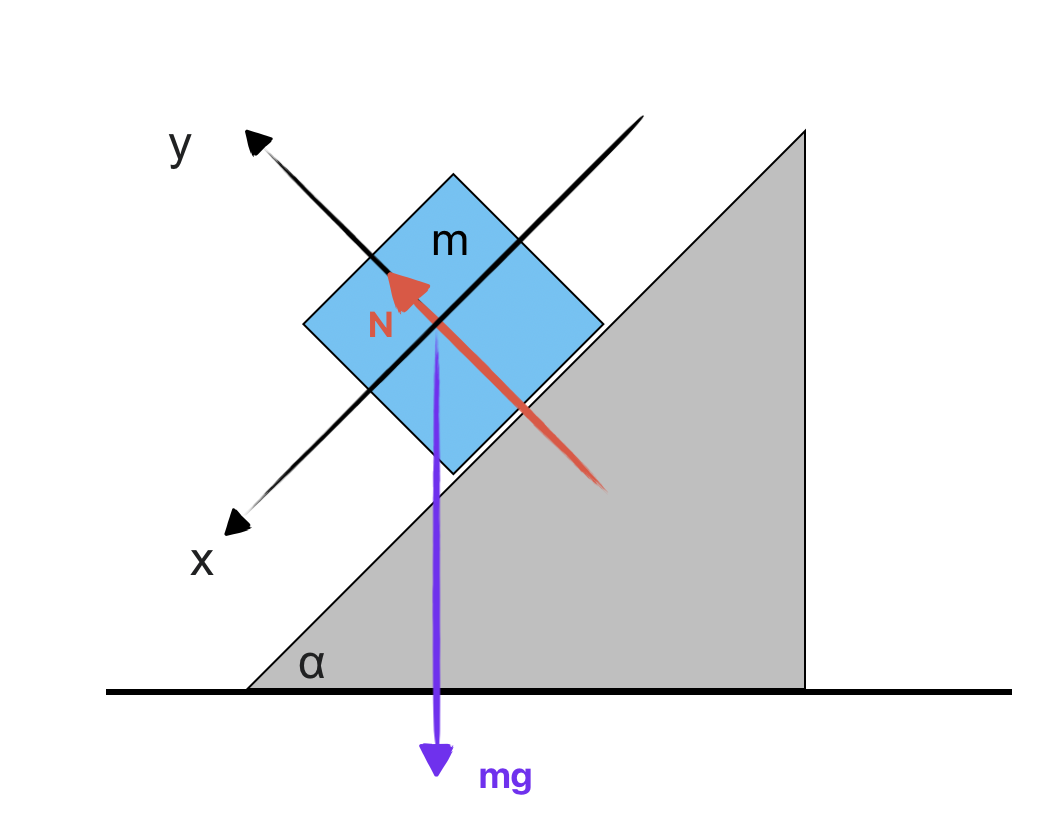
דוגמה נוספת: גוף על מישור משופע עם קפיץ

נעבור לשאלה הבאה משיעורי הבית. בסופו של דבר, נרצה להגיע למשוואה מהצורה:

\[\frac{d^2x}{dt^2} + \omega^2 x = 0\]

או מהצורה:

\[\frac{d^2y}{dt^2} + \omega^2 y = 0\]

ואז נקבל תנודות של קפיץ.

תיאור המערכת הפיזיקלית

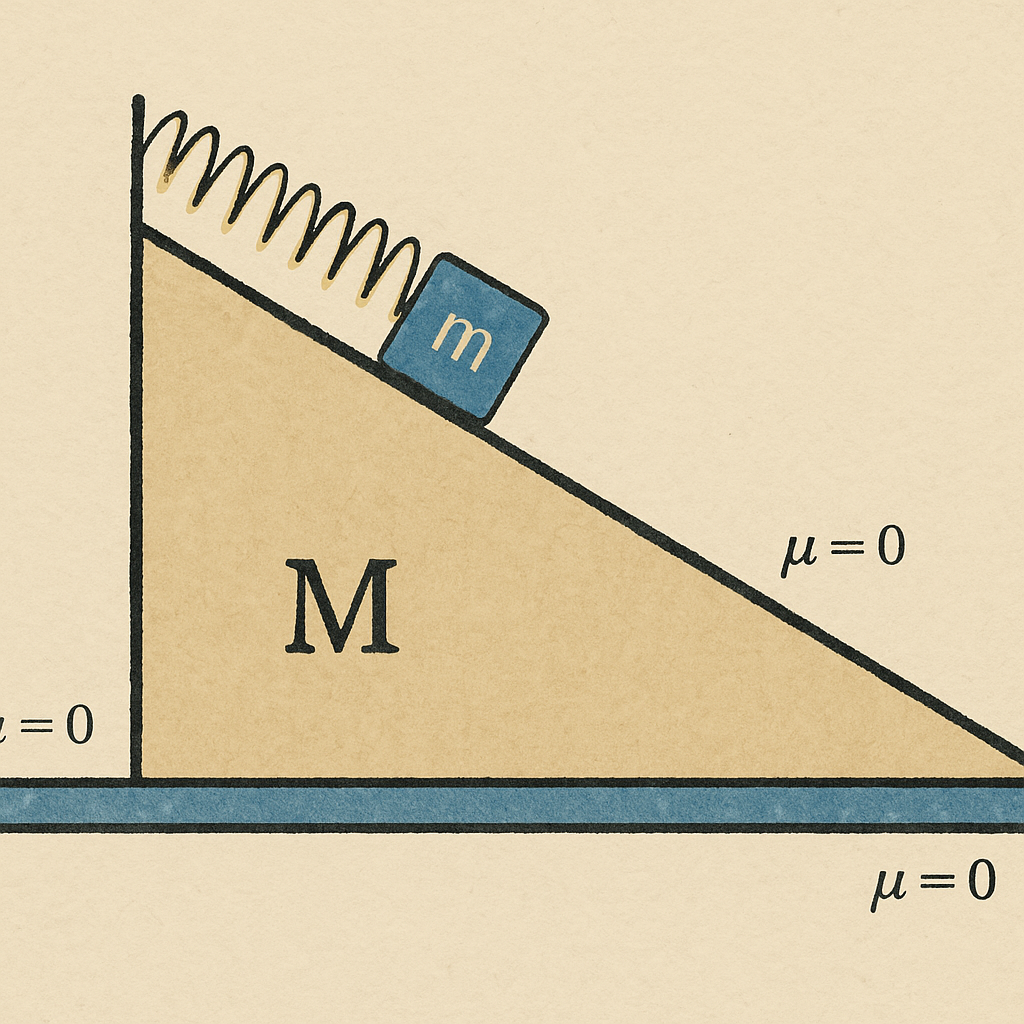
נסתכל על התרגיל הזה: קוביה שמונחת על מישור משופע, מחוברת בקפיץ למסה שמחוברת למשולש.

השאלה המקורית:

על גבי מישור משופע חסר חיכוך מונחת מסה המחוברת אל ראשו בקפיץ. המישור המשופע יכול להחליק ללא חיכוך על רצפה אופקית.

שיפוע המישור המשופע הוא $\alpha$. קבוע הכוח של הקפיץ הוא $k$ ואורכו הרפוי הוא $\ell$.

נכנה ב-$x(t)$ את המרחק של $m$ מראש המישור המשופע (מהמקום בו הקפיץ מחובר אל המישור המשופע).

מניחים בעדינות את המסה $m$ במקום בו הקפיץ רפוי
\[x(t=0) = \ell\]
ומשחררים ממנה.

נציין את תאוצת המישור המשופע $M$ על הרצפה האופקית ב-$A$, ואת תאוצה המסה $m$ על גבי המישור המשופע באות $a$, כך ש:
\[a = \ddot{x}\]
במערכת הצמודה ל-$M$, כמה זמן ייקח עד ש-$m$ תיעצר על המישור המשופע לראשונה?

רמז: המסה $m$ מתנדנדת הרמונית.

הגדרת הבעיה

יש לי גוף עם מסה $M$ שמחוברת לקפיץ, והיא מחוברת למשולש. היא מחליקה על המשולש ואין ביניהם חיכוך.

נתונים:

שיפוע המישור המשופע: $\alpha$
קבוע הקפיץ: $k$
אורכו הרפוי של הקפיץ: $\ell$

alt text

התנהגות המערכת

כשהקפיץ רפוי, אורכו הוא $\ell$. כשמניחים אותו בשיפוע, הוא ימתח קצת בגלל כוח הכבידה - חלק הרכיב האחד של כוח הכבידה ימתח אותו טיפה.

בעקבות המתיחה הזאת, הקפיץ יתחיל לעשות תנודות סביב נקודת שיווי המשקל החדשה שלו.

מנגנון התנודה:

כשהמסה עוברת לצד אחד, המשולש (שמתחת) מנסה לזוז לצד השני
כשהמסה חוזרת, המשולש מנסה לזוז לצד ההפוך
גם המסה וגם המשולש יבצעו תנודות במקביל

זה כמו שאתם עומדים על קורקינט - אם תלכו לצד אחד, הקורקינט יעוף לצד השני.


תיאור לא מדויק - ניסיתי להמחיש את הרעיון של התנודות. שימו לב שמה שה״קיר״ מחובר כולו למאסה הגדולה (בניגוד למה שרואים ב-GIF).

ניתוח כוחות

שלב 1: זיהוי הכוחות

הדבר הראשון שאני עושה הוא לרשום כוחות על כל אחד מהגופים.

כוחות הפועלים על המסה הקטנה ($m$):

מתיחות של הקפיץ: $F_{\text{spring}}$
כוח כבידה: $mg$ כלפי מטה
כוח נורמלי: $N$ בניצב למשטח

כוחות הפועלים על המשולש ($M$):

כוח נורמלי מהרצפה
כוח כבידה: $Mg$ כלפי מטה
כוח נורמלי מהמסה הקטנה (לפי החוק השלישי של ניוטון)
כוח הקפיץ

alt text

שלב 2: קביעת מערכת הצירים

אני קובע מערכת צירים משופעת עבור הגוף הקטן - זה יותר נוח. עבור המשולש אני קובע מערכת צירים רגילה.

עבור המסה הקטנה:

כיוון $x$ חיובי: כלפי מטה לאורך השיפוע
כיוון $y$ חיובי: בניצב למעלה מהמשטח

עבור המשולש:

כיוון $X$ חיובי: ימינה
כיוון $Y$ חיובי: כלפי מעלה

שלב 3: פירוק הכוחות לרכיבים

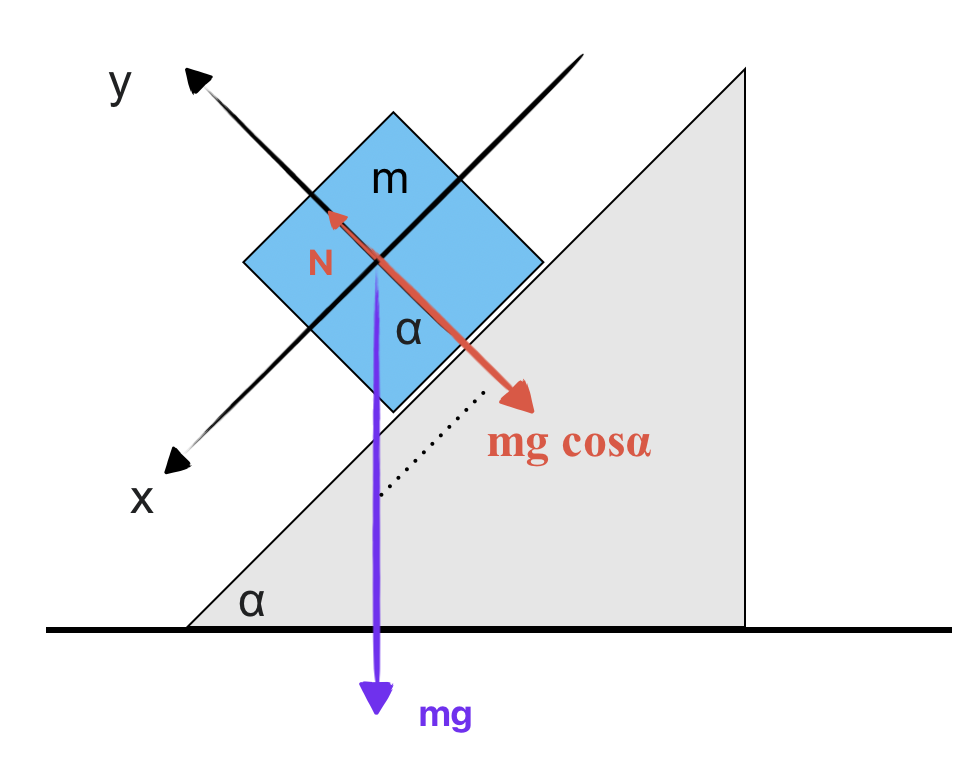
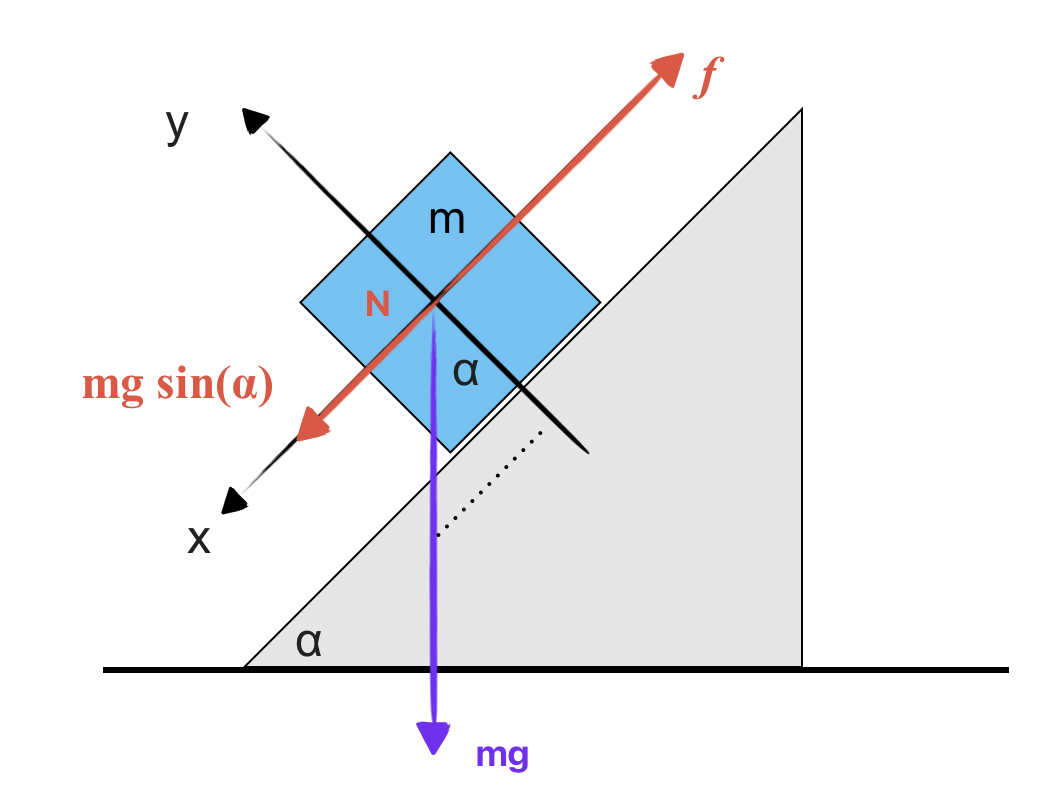
חלק מהכוחות לא יושבים על הצירים, אז צריך לפרק אותם לרכיבים.

עבור המסה הקטנה, צריך לפרק:

$mg$ ← $mg\cos\alpha$ ו-$mg\sin\alpha$
$mA$ ← $mA\cos\alpha$ ו-$mA\sin\alpha$
כוח הקפיץ: $k(x-\ell)$ ← $k(x-\ell)\cos\alpha$ ו-$k(x-\ell)\sin\alpha$
$N_{21}$ ← $N_{21}\cos\alpha$ ו-$N_{21}\sin\alpha$

הכוחות המדומים

כשהמסה הקטנה יושבת על המשולש, והמשולש נע בתאוצה $A$, המסה הקטנה מרגישה כוח מדומה.

הכוח המדומה:

כיוון: נגד כיוון התאוצה של המשולש
גודל: $mA$ (כאשר $A$ היא תאוצת המשולש)

זה כמו במעלית - כשהמעלית עולה למעלה בתאוצה, אתם מרגישים כוח מדומה למטה.

משוואות התנועה

שלב 4: כתיבת משוואות התנועה

לכל ציר ולכל גוף נכתוב משוואת תנועה:

עבור המשולש (כיוון X):

\[MA = k(x-\ell)\cos\alpha - N_{21}\sin\alpha\]

עבור המשולש (כיוון Y):

\[0 = N - N_{21}\cos\alpha - Mg - k(x-\ell)\sin\alpha\]

עבור המסה הקטנה (כיוון x):

\[m a_x = \sum F_x\]

עבור המסה הקטנה (כיוון y):

\[0 = \sum F_y\]

ספירת נעלמים ומשוואות

נעלמים:

$A$ (תאוצת המשולש)
$a_x$ (תאוצת המסה הקטנה)
$N_{21}$ (כוח נורמלי)
$N$ (כוח נורמלי מהרצפה)

מספר משוואות: 4

מספר נעלמים: 4

לכן, המערכת ניתנת לפתרון!

פתרון והגעה לתדירות

אחרי פתרון המערכת (שזה חישוב מורכב), נקבל משוואה מהצורה:

\[\frac{d^2x}{dt^2} + \omega^2 x = C\]

המקדם $\omega^2$ הוא התדירות הזוויתית בריבוע של התנודות.

סיכום: תנודות הרמוניות

התנודה ההרמונית מאופיינת על ידי שני פרמטרים עיקריים:

1. התדירות ($\omega$)

התדירות קובעת את קצב התנודות. אני מוצא אותה ברגע שאני מקבל משוואה מהצורה:

\[\frac{d^2x}{dt^2} + \omega^2 x = 0\]

אני מסתכל על המקדם של $x$ (עד כדי מינוס), וזה התדירות בריבוע.

2. האמפליטודה

האמפליטודה היא כמה מתחתי את הגוף מעבר לנקודת שיווי המשקל. את האמפליטודה אני מוצא לפי תנאי ההתחלה.

אנלוגיה פיזיקלית

כשאני מסתכל על תנודה הרמונית, אני חושב על קערה עם כדור:

הכדור נמצא למטה בנקודת שיווי המשקל
אני מסיט אותו מעבר לנקודת שיווי המשקל
הכדור מתחיל להתנדד סביב נקודת שיווי המשקל של הקערה

הערות נוספות על כוחות מדומים

בבעיה זו השתמשנו בכוחות מדומים במקום להתעסק עם תאוצות מורכבות. זה עדיף כי:

יותר קל לזהות כיוונים בכוחות מאשר בתאוצות
אנחנו רגילים לפרק כוחות לרכיבים ולא תאוצות
זה מפשט את החישובים

עיקרון כללי: אם גוף נמצא במערכת שנעה בתאוצה, הוא ירגיש כוח מדומה בכיוון הפוך לתאוצה.

תרגול 8 - קואורדינטות פולאריות

תאריך: 22/05/2025

מטרת השיעור

בשיעור זה נלמד כיצד לתאר תנועה במערכת קואורדינטות פולאריות, נגזור את הביטויים למהירות ותאוצה, ונחיל זאת על דוגמה קונקרטית של תנועה מעגלית.

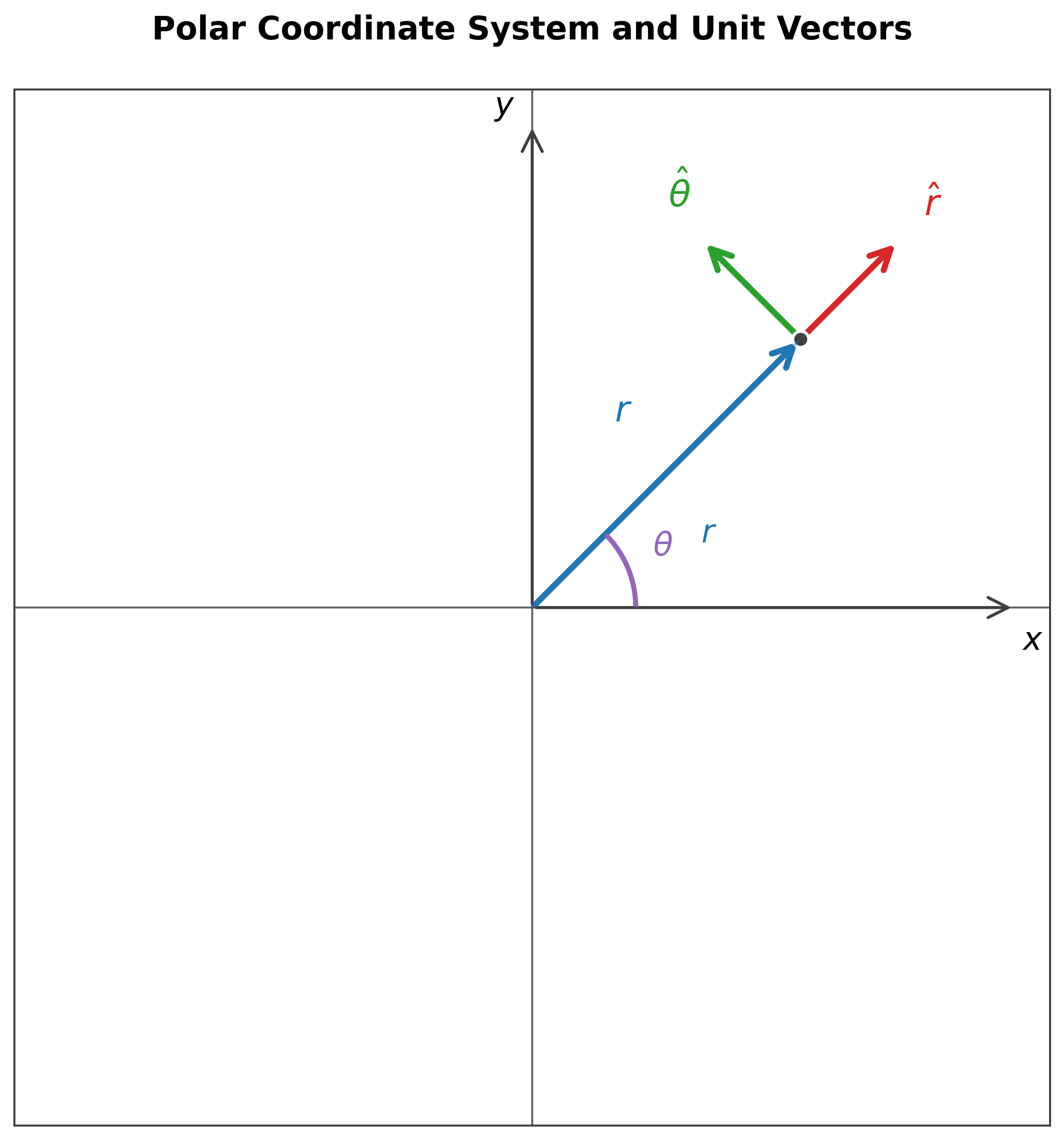
וקטורי יחידה בקואורדינטות פולאריות

הגדרת וקטורי היחידה

בקואורדינטות פולאריות יש לנו שני וקטורי יחידה:

\[\begin{align} \hat{r} &= \cos\theta \, \hat{x} + \sin\theta \, \hat{y} \tag{1} \\[10pt] \hat{\theta} &= -\sin\theta \, \hat{x} + \cos\theta \, \hat{y} \tag{2} \end{align}\]

$\hat{r}$ הוא וקטור היחידה בכיוון הרדיאלי (מהמרכז החוצה)
$\hat{\theta}$ הוא וקטור היחידה בכיוון המשיקי - טנגנציאלי (ניצב ל-$\hat{r}$) (בכיוון התנועה סביב המעגל)

alt text

נגזרות וקטורי היחידה

נקודת מפתח חשובה: וקטורי היחידה $\hat{r}$ ו-$\hat{\theta}$ תלויים בזמן כאשר הזווית $\theta$ משתנה עם הזמן.

נגזור את וקטור היחידה של הציר הרדיאלי ($\hat{r}$) שבהגדרה $(1)$ לפי הזמן $t$:

\[\begin{align} \frac{d\hat{r}}{dt} &= \frac{d}{dt}(\cos\theta \, \hat{x} + \sin\theta \, \hat{y}) \\[10pt] &= -\sin\theta \cdot \frac{d\theta}{dt} \, \hat{x} + \cos\theta \cdot \frac{d\theta}{dt} \, \hat{y} \\[10pt] &= \dot{\theta}(-\sin\theta \, \hat{x} + \cos\theta \, \hat{y}) \\[10pt] &= \dot{\theta} \, \hat{\theta} \end{align}\]

באופן דומה נגזור את וקטור היחידה המשיקי $\hat{\theta}$ שבהגדרה $(2)$:

\[\begin{align} \frac{d\hat{\theta}}{dt} &= \frac{d}{dt}(-\sin\theta \, \hat{x} + \cos\theta \, \hat{y}) \\[10pt] &= -\cos\theta \cdot \dot{\theta} \, \hat{x} - \sin\theta \cdot \dot{\theta} \, \hat{y} \\[10pt] &= -\dot{\theta}(\cos\theta \, \hat{x} + \sin\theta \, \hat{y}) \\[10pt] &= -\dot{\theta} \, \hat{r} \end{align}\]

תוצאות מרכזיות - הנגזרות של וקטורי היחידה בקואורדינטות פולאריות:

\[\begin{align} \dot{\hat{r}} &= \dot{\theta} \, \hat{\theta} \tag{3} \\[10pt] \dot{\hat{\theta}} &= -\dot{\theta} \, \hat{r} \tag{4} \end{align}\]

התוצאות האלה יסייעו לנו להגיע לנוסחת התאוצה והמהירות בקואורדינטות פולאריות. החשיבות היא שבניגוד למערכות אחרות, וקטורי היחידה כאן הם פונקציה - הם משתנים עם הזמן.

alt text

וקטור המהירות בקואורדינטות פולאריות

גזירת וקטור המקום

וקטור המקום הוא המרחק מהמרכז לכיוון הנקודה במערכת קואורדינטות פולאריות. הוא מוגדר כ:

\[\vec{r} = r \, \hat{r} \tag{5}\]

הערה: נראה שבחלק מהמקומות מסמנים $R$ במקום $r$.

המהירות היא הנגזרת של וקטור המקום ($5$) לפי הזמן. וקטור המקום עצמו כאמור תלוי בזמן, ולכן נשתמש בכלל השרשרת:

\[\begin{align} \vec{v} &= \frac{d\vec{r}}{dt} \\[10pt] &\overset{(5)}{=} \frac{d}{dt}(r \, \hat{r}) \\[10pt] &= \frac{dr}{dt} \, \hat{r} + r \, \frac{d\hat{r}}{dt} \tag{$\text{chain rule}$} \\[10pt] &= \dot{r} \, \hat{r} + r \, \dot{\theta} \, \hat{\theta} \tag{6} \end{align}\]

הביטוי האחרון במשוואה $(6)$ התקבל מהצבת הנגזרת של וקטור היחידה $\hat{r}$ מהתוצאה $(3)$. סך הכל מצאנו שוקטור המהירות בקואורדינטות פולאריות הוא:

\[\boxed{\vec{v} = \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}} \tag{7}\]

alt text

פרשנות פיזיקלית

$v_r = \dot{r}$: רכיב המהירות הרדיאלי (שינוי המרחק מהמרכז)
$v_{\theta} = r\dot{\theta}$: רכיב המהירות המשיקי (תנועה לאורך העיגול)

וקטור התאוצה בקואורדינטות פולאריות

גזירת וקטור המהירות

התאוצה היא נגזרת וקטור המהירות לפי הזמן ($7$):

\[\begin{aligned} \vec{a} &= \frac{d\vec{v}}{dt} \\[10pt] &\overset{(7)}{=} \frac{d}{dt}(\dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}) \\[10pt] &= \ddot{r} \, \hat{r} + \dot{r} \, \frac{d\hat{r}}{dt} + \dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} + r\dot{\theta} \, \frac{d\hat{\theta}}{dt} \end{aligned}\]

החלפת הנגזרות של וקטורי היחידה:

\[\begin{aligned} \vec{a} &= \ddot{r} \, \hat{r} + \dot{r} \cdot \overbrace{\dot{\theta} \, \hat{\theta}}^{(3)} + \dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} + r\dot{\theta} \cdot (-\dot{\theta} \, \hat{r}) \\[10pt] &= \ddot{r} \, \hat{r} - r\dot{\theta}^2 \, \hat{r} + 2\dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} \end{aligned}\]

ביטוי התאוצה בקואורדינטות פולאריות:

\[\boxed{\vec{a} = (\ddot{r} - r\dot{\theta}^2) \, \hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \, \hat{\theta}} \tag{8}\]

רכיבי התאוצה

$a_r = \ddot{r} - r\dot{\theta}^2$: תאוצה רדיאלית
$a_{\theta} = 2\dot{r}\dot{\theta} + r\ddot{\theta}$: תאוצה משיקית

alt text

דוגמה 1: נמלה על תקליט מסתובב

נמלה יושבת על התקליט במרחק קבוע $R$ מהמרכז. תקליט מסתובב כך שהזווית משתנה לפי: $\theta(t) = \pi t^2$. כלומר, כך שהמהירות הזוויתית הולכת וגדלה.

מה מיקום הנמלה בקוארדינטות קרטזיות?

וקטור המהירות והתאוצה

הזווית בין מיקום הנמלה לבין כיוון תנועת הנמלה

מהי התאוצה הרדיאלית והמשיקית והזוויתית?

ניתוח התנועה

נתחיל בניתוח התנועה של הנמלה על התקליט המסתובב. נשתמש בקואורדינטות פולאריות כדי לתאר את התנועה.

וקטור המקום:

\[\vec{r}(t) = R \, \hat{r}\]

נמצא את הביטוי לנגזרות של וקטור המקום לפי הזמן. מאחר ש-$R$ קבוע:

\[\begin{aligned} \dot{r} &= 0 \\[10pt] \ddot{r} &= 0 \end{aligned}\]

המהירות הזוויתית:

ניעזר בנתון $\theta(t) = \pi t^2$ כדי לחשב את המהירות הזוויתית - נגזרת הזווית לפי הזמן:

\[\begin{aligned} \omega = \dot{\theta} &= \frac{d}{dt}(\pi t^2) = 2\pi t \end{aligned}\]

התאוצה הזוויתית:

זו הנגזרת השנייה של הזווית לפי הזמן:

\[\begin{aligned} \alpha = \ddot{\theta} &= \frac{d\omega}{dt} = 2\pi \end{aligned}\]

סעיף 1: מיקום הנמלה בקואורדינטות קרטזיות

בכתה פתרנו את התרגיל בלי להיעזר בקואורדינטות קרטזיות, עם התמקדות בסעיפים 2 ו-4. ככל הנראה לא מומלץ להתבסס על קואורדינטות קרטזיות במקרה זה, מאחר שהבעיה מתאימה יותר לקואורדינטות פולאריות. לשלמות התמונה התשובה לסעיף 1 היא:

\[\begin{aligned} x(t) &= R \cos(\pi t^2) \\[10pt] y(t) &= R \sin(\pi t^2) \end{aligned}\]

סעיף 2: וקטור המהירות והתאוצה

חישוב המהירות

מאחר שזו תנועה מעגלית ($r = R$ קבוע), אין רכיב רדיאלי של המהירות ($\dot{r} = 0$). נשתמש בנוסחה הכללית לתנועה מעגלית:

\[\vec{v} = r\omega \, \hat{\theta}\]

כאשר $\omega = \dot{\theta}$. נציב את הערכים $r= R$ ו-$\omega = 2\pi t$ ונקבל:

\[\vec{v} = R \cdot 2\pi t \, \hat{\theta} = 2\pi Rt \, \hat{\theta}\]

זו התשובה - וקטור המהירות הוא:

\[\boxed{\vec{v} = 2\pi Rt \, \hat{\theta}} \tag{9}\]

תוצאה: המהירות המשיקית גדלה ליניארית עם הזמן.

הערה: אם $R$ היה משתנה, היינו צריכים לחשב גם את רכיב המהירות הרדיאלי $\dot{r} \, \hat{r}$, אך מאחר ש-$R$ קבוע, רכיב זה הוא אפס. הנוסחה הכללית הייתה:

\[\vec{v} = \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}\]

alt text

חישוב התאוצה

נשתמש בנוסחה הכללית לתאוצה בקואורדינטות פולאריות $(8)$:

\[\begin{aligned} \vec{a} &= (0 - R(2\pi t)^2) \, \hat{r} + (0 + R \cdot 2\pi) \, \hat{\theta} \\[10pt] &= -4\pi^2 Rt^2 \, \hat{r} + 2\pi R \, \hat{\theta} \end{aligned}\]

וקטור התאוצה הוא:

\[\boxed{\vec{a} = -4\pi^2 Rt^2 \, \hat{r} + 2\pi R \, \hat{\theta}}\]

סעיף 3: הזווית בין מיקום הנמלה לכיוון תנועתה

המרצה לא התמקד בסעיף הזה בכתה. בכל מקרה, להלן הצעת פתרון:

הזווית בין וקטור המקום $\vec{r}$ לכיוון התנועה $\vec{v}$ ניתנת על ידי:

\[\begin{aligned} \cos\phi &= \frac{\vec{r} \cdot \vec{v}}{\vert \vec{r}| \vert \vec{v}\vert} \\[10pt] &= \frac{R \hat{r} \cdot (2\pi Rt \, \hat{\theta})}{R \cdot 2\pi Rt} \\[10pt] &= \frac{R \cdot 2\pi Rt \cdot 0}{R \cdot 2\pi Rt} = 0 \end{aligned}\]

הזווית $\phi$ היא:

\[\phi = \frac{\pi}{2} \text{ radian} = 90^\circ\]

סעיף 4: תאוצה רדיאלית ומשיקית

פרשנות פיזיקלית לתרגיל הנמלה

רכיב רדיאלי

\[a_r = -4\pi^2 Rt^2\]

הסימן השלילי מציין שהתאוצה פונה לעבר המרכז
זוהי תאוצה צנטריפטלית (centripetal acceleration)
גודלה גדל כ-$t^2$ - ככל שהמהירות הזוויתית עולה, התאוצה הצנטריפטלית גדלה

alt text

רכיב משיקי

\[a_{\theta} = 2\pi R\]

זוהי תאוצה קבועה בכיוון המשיקי
גורמת להאצת התנועה המעגלית

alt text

דוגמה 2: מטוטלת במעלית מואצת

יש לנו מעלית עם מטוטלת באורך $L$. המעלית מואצת כלפי מעלה בתאוצה $A$.

השאלה המרכזית: איך משפיעה תאוצת המעלית על תנועת המטוטלת?

הערה: השאלה המלאה מתרגול אחר הייתה למצוא את שיווי המשקל ביחס לצופה מהמערכת, תדירות התנודות ואת זמן המחזור ($T$) במצבים הבאים:

המערכת נמצאת בתוך מעלית הנעה בתאוצה קבועה $A$ כלפי מעלה.

המערכת נמצאת ברכבת הנעה בתאוצה קבועה $A$ ימינה.

המערכת נמצאת ברכבת הנעה במהירות קבועה ימינה.

סעיף 1

כוחות מדומים

כאשר המעלית מואצת כלפי מעלה, מתבוננים במטוטלת ממערכת הייחוס של המעלית ורואים כוח פיקטיבי נוסף.

על הכדור פועלים שני כוחות:

כוח הכבידה: $mg$ כלפי מטה
כוח מדומה: $mA$ כלפי מטה

alt text

הכלל: הכוח המדומה הוא תמיד מסה כפול תאוצת המערכת בכיוון הפוך.

כוח הכבידה האפקטיבי

במעלית מואצת, כוח הכבידה האפקטיבי הוא:

\[F_{\text{effective}} = m(g + a)\]

זה בדיוק כמו מטוטלת רגילה, רק שכוח הכבידה חזק יותר.

\[F_{\text{imaginary}} = ma \quad \downarrow\]

המהירות הזוויתית החדשה

במטוטלת רגילה, המהירות הזוויתית של תנודות קטנות היא:

\[\omega = \sqrt{\frac{g}{L}}\]

במעלית מואצת, מחליפים את $g$ ב-$(g+a)$:

\[\boxed{\omega = \sqrt{\frac{g+a}{L}}}\]

alt text

משוואת התנועה

נשתמש בקואורדינטות פולאריות ובחוק השני של ניוטון ($F = ma$) כדי למצוא את משוואת התנועה של המטוטלת.

בכיוון המשיקי

התאוצה המשיקית היא:

\[a_{\theta} = L\ddot{\theta}\]

הכוח המשיקי הוא הרכיב המשיקי של כוח הכבידה האפקטיבי:

\[F_{\theta} = -m(g+a)\sin\theta \tag{1}\]

בתנודות קטנות: $\sin\theta \approx \theta$. נציב את השקילות הזאת ב-($1$) ונקבל:

\[F_{\theta} \approx -m(g+a)\theta \tag{2}\]

נשתמש בחוק השני של ניוטון בכיוון המשיקי:

\[-m(g+a)\theta = mL\ddot{\theta}\]

נחליף בין הצדדים לנוחות ונבודד את $\ddot{\theta}$:

\[\begin{align} mL\ddot{\theta} &= -m(g+a)\theta \tag{$\div mL$} \\[10pt] \ddot{\theta} &= -\frac{(g+a)}{L}\theta \end{align}\]

סך הכל, משוואת התנועה של המטוטלת במעלית מואצת היא:

\[\boxed{\ddot{\theta} = -\frac{g+a}{L}\theta}\]

זו משוואת תנועה הרמונית פשוטה עם תדירות זוויתית $\omega = \sqrt{\frac{g+a}{L}}$.

בכיוון הרדיאלי

גם בכיוון הרדיאלי יש תאוצה צנטריפטלית: $a_r = -L\dot{\theta}^2$

החוק השני בכיוון הרדיאלי:

\[T - m(g+a)\cos\theta = mL\dot{\theta}^2\]

לכן מתיחות החוט היא:

\[\boxed{T = mL\dot{\theta}^2 + m(g+a)\cos\theta}\]

alt text

ההבחנה בין קואורדינטות

מדוע קואורדינטות פולאריות?

במטוטלת, התנועה היא מעגלית. בקואורדינטות פולאריות:

כיוון רדיאלי: אין תנועה (המרחק $L$ קבוע)
כיוון משיקי: יש תנועה (הזווית $\theta$ משתנה)

זה יותר פשוט מקואורדינטות קרטזיות שבהן שני הצירים משתנים.

הקשר לתורת היחסות

רעיון מעניין: תופעה זו הובילה את איינשטיין לפתח את תורת היחסות(?).

עקרון השקילות: אדם במעלית סגורה לא יכול להבחין בין:

מעלית נייחת בכוח כבידה $g$
מעלית מואצת בתאוצה $A$ במרחב ללא כבידה

בשני המקרים הוא חש “כוח כבידה” של $g+A$.

במעלית נופלת חופשית ($A = -g$): הכוח האפקטיבי הוא אפס - כולם “צפים” כמו אסטרונאוטים.

תשובה פורמאלית לסעיף 1

נקודת שיווי המשקל נמצאת כשהכדור והחוט מאונחים לקרקע.

\[\sum F_r = ma_r\]

נציב את הכוחות בכיוון הרדיאלי:

\[(mg + mA)\cos\theta - T = mL\dot{\theta}^2\]

נציב את הכוחות בכיוון המשיקי:

\[\sum F_{\theta} = ma_{\theta}\] \[-(mg + mA)\sin\theta = mL\ddot{\theta}\]

בקירוב של זוויות קטנות ($\sin\theta \approx \theta$):

\[-(mg + mA)\theta = mL\ddot{\theta}\]

מכאן נובע ש:

\[\ddot{\theta} = -\frac{(g + A)}{L}\theta\] \[\omega = \sqrt{\frac{g + A}{L}}\]

זמן המחזור של המטוטלת הוא:

\[T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{L}{g + A}}\]

סעיף 2 - מטוטלת ברכבת מואצת ימינה

הפתרון לתרגיל הופיע בשיעור תגבור.

סיכום מושגים עיקריים

נגזרות וקטורי יחידה

\[\begin{align} \dot{\hat{r}} &= \dot{\theta} \, \hat{\theta} \\[10pt] \dot{\hat{\theta}} &= -\dot{\theta} \, \hat{r} \end{align}\]

מהירות ותאוצה כלליות

\[\begin{align} \vec{v} &= \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta} \\[10pt] \vec{a} &= (\ddot{r} - r\dot{\theta}^2) \, \hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \, \hat{\theta} \end{align}\]

מקרה מיוחד: תנועה מעגלית ($r =$ קבוע)

\[\begin{align} \vec{v} &= r\omega \, \hat{\theta} \\[10pt] \vec{a} &= -r\omega^2 \, \hat{r} + r\alpha \, \hat{\theta} \end{align}\]

כאשר:

$\omega = \dot{\theta}$ - מהירות זוויתית
$\alpha = \ddot{\theta}$ - תאוצה זוויתית
$-r\omega^2 \, \hat{r}$ - תאוצה צנטריפטלית
$r\alpha \, \hat{\theta}$ - תאוצה משיקית

מינוח

תאוצה צנטריפטלית: תאוצה הפונה לעבר מרכז העיגול
תאוצה צנטריפוגלית: תאוצה הפונה החוצה ממרכז העיגול
תאוצה רדיאלית: תאוצה בכיוון הרדיאלי (יכולה להיות לכיוון המרכז או ממנו)

תרגול 9 - מכניקה של מערכות מסתובבות וניתוח כוחות

תאריך: 29/05/2025

שאלות:

שאלה מקדימה: פיתוח וקטורי המקום, המהירות והתאוצה בקואורדינטות פולריות
שאלה 1: השפעת סיבוב כדור הארץ על המשקל
שאלה 2: חוט מחליק (חבל משתלשל) עם כוחות מעקבים
שאלה 3: מכונת ארטווד

שאלה מקדימה: פיתוח וקטורי המקום, המהירות והתאוצה בקואורדינטות פולריות

וקטור המקום בקואורדינטות קרטזיות הוא:

\[\vec{r} = x \hat{x} + y \hat{y}\]

אם נשתמש בקואורדינטות פולריות $(r,\theta)$, נוכל לכתוב את וקטור המקום כך:

\[\vec{r} = r \cdot \cos \left(\theta\right) \hat{x} + r \cdot \sin \left(\theta\right) \hat{y}\]

בכתיבה שמדגישה את התלות בזמן $\theta(t)$:

\[\vec{r}(t) = r(t) \cdot \cos \left(\theta(t)\right) \hat{x} + r(t) \cdot \sin \left(\theta(t)\right) \hat{y}\]

מכאן שוקטור היחידה הוא:

\[\boxed{\hat{r}(t) = \cos \left(\theta(t)\right) \hat{x} + \sin \left(\theta(t)\right) \hat{y}}\]

הווקטור הזה הוא בכיוון וקטור הרדיוס שמתחיל בראשית ומציע לעבר המיקום המדובר.

וקטור היחידה הפולארי השני הוא $\hat{\theta}$, המכוון בניצב לוקטור $\hat{r}$:

\[\boxed{\hat{\theta}(t) = -\sin \left(\theta(t)\right) \hat{x} + \cos \left(\theta(t)\right) \hat{y}}\]

אפשר לוודא על ידי מכפלה סקלרית.

בכתיב מקוצר:

\[\boxed{\hat{r} = \cos \theta \hat{x} + \sin \theta \hat{y}, \quad \hat{\theta} = -\sin \theta \hat{x} + \cos \theta \hat{y}}\]

לפי כלל השרשרת:

\[\frac{d\hat{r}}{dt} = \dot{\theta} \hat{\theta} \implies \boxed{\frac{d\hat{r}}{dt} = \dot{\theta} \hat{\theta}}\] \[\frac{d\hat{\theta}}{dt} = -\dot{\theta} \hat{r} \implies \boxed{\frac{d\hat{\theta}}{dt} = -\dot{\theta} \hat{r}}\]

חישוב המהירות ורכיביה הפולאריים:

\[\begin{aligned} \vec{r} &= r \cos \theta \hat{x} + r \sin \theta \hat{y} = r \hat{r} \\[10pt] \vec{v} &= \frac{d\vec{r}}{dt} = \dot{r} \hat{r} + r \frac{d\hat{r}}{dt} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta} \end{aligned}\] \[\implies \boxed{\vec{v} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta}}\]

חישוב התאוצה ורכיביה הפולאריים:

\[\begin{aligned} \vec{a} &= \frac{d\vec{v}}{dt} = \ddot{r} \hat{r} + \dot{r} \frac{d\hat{r}}{dt} + r \frac{d}{dt}(\dot{\theta} \hat{\theta}) \\[10pt] &= \ddot{r} \hat{r} + \dot{r} \dot{\theta} \hat{\theta} + r \left(\ddot{\theta} \hat{\theta} + \dot{\theta} \frac{d\hat{\theta}}{dt}\right) \\[10pt] &= \ddot{r} \hat{r} + \dot{r} \dot{\theta} \hat{\theta} + r \left(\ddot{\theta} \hat{\theta} - \dot{\theta}^2 \hat{r}\right) \\[10pt] &= \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) \hat{\theta} \end{aligned}\] \[\boxed{\vec{a} = \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) \hat{\theta}}\] \[\boxed{a_r = \ddot{r} - r \dot{\theta}^2, \quad a_\theta = r \ddot{\theta} + 2 \dot{r} \dot{\theta}}\]

שאלה 1: השפעת סיבוב כדור הארץ על המשקל

העריכו כיצד משפיעה התנועה הסיבובית של כדור הארץ על הערך שיראה מד המשקל? האם זה קשור למיקום על פני כדור הארץ?

הערה: רדיוס כדור הארץ הוא כ-6300 קילומטר וזמן מחזור סיבובו סביב ציר הסיבוב שלו הוא כ-24 שעות (קצת פחות, למה?)

במערכת הייחוס הסובבת עם כדור הארץ, הכוחות הפועלים על אדם העומד על פני כדור הארץ הם:

כוח הכבידה: $mg$ הפועל לכיוון מרכז כדור הארץ
כוח הנורמלי מהקרקע: $N$ הפועל מאונך למשטח
כוח צנטריפוגלי: $m\omega^2 r$ הפועל בכיוון רדיאלי החוצה מציר הסיבוב

עבור אדם הנמצא בקו רוחב $\theta$, רדיוס הסיבוב סביב ציר כדור הארץ הוא:

\[\boxed{r = R_E \cos\theta}\]

הכוח הצנטריפוגלי החוצה מציר הסיבוב הוא:

\[F_{cf,\;vertical} = m\omega^{2}R_E\cos^{2}\theta\]

alt text

כאשר מפרקים את הכוח הצנטריפוגלי לרכיבים:

רכיב רדיאלי (ממרכז כדור הארץ לכיוון האדם והחוצה ↗): $m\omega^2 R_E \cos\theta \cdot \cos\theta = m\omega^2 R_E \cos^2\theta$
רכיב טנגנציאלי (משיק לציר הריאלי ↖): $m\omega^2 R_E \cos\theta \cdot \sin\theta$

מכיוון שהכוח הצנטריפוגלי קטן מאוד ביחס לכוח הכבידה (~0.3%), ניתן לבצע קירוב ולהתייחס רק להשפעה על הרכיב האנכי של התאוצה האפקטיבית. כלומר, להתמקד בציר הרדיאלי ממרכז כדור הארץ (↖). בפתרון שהיה בדפי התרגול התייחסו גם לכוח החיכוך בציר הזה, למרות שלהבנתי מיותר.

הכוחות שפועלים בציר הזה הם $mg$ כלפי מטה ו-$N$ כלפי מעלה - ביחד עם ההיטל של הכוח הצנטריפוגלי, שהוא:

\[\begin{aligned} F_{cf, vertical} &= \cos \left( \theta\right) m\omega^2r \\[10pt] &= m\omega^2 R_E \cos^2\theta \end{aligned}\]

alt text

לפי החוק השני של ניוטון במערכת לא אינרציאלית:

\[N + m\omega^2 R_E \cos^2\theta = mg\]

מכאן, הירידה במשקל הנמדד ביחס למשקל “האמיתי” היא:

\[\boxed{\Delta W = mg - N = m\omega^2 R_E \cos^2\theta}\]

עבור כדור הארץ:

\[\omega = \frac{2\pi}{T} = \frac{2\pi}{24 \mathrm{h} \cdot 3600 \mathrm{s/h}} = \frac{2\pi}{86,400 \mathrm{s}} \approx 7.27 \times 10^{-5} \, \mathrm{rad/s}\] \[R_E \approx 6300 \mathrm{km} = 6.3 \times 10^6 \, \mathrm{m}\]

בקו המשווה ($\theta = 0°$):

\[\frac{\Delta W}{W} = \frac{m\omega^2 R_E \cos^2(0°)}{mg} = \frac{\omega^2 R_E}{g} \approx \frac{(7.27 \times 10^{-5})^2 \cdot 6.3 \times 10^6}{10 \mathrm{m/s}^2} \approx 0.0033\]

בקוטב ($\theta = 90°$):

\[\frac{\Delta W}{W} = \frac{m\omega^2 R_E \cos^2(90°)}{mg} = 0\]

מסקנות:

ההשפעה מקסימלית בקו המשווה (ירידה של בערך 0.33% במד המשקל)
ההשפעה מתאפסת בקטבים ($\theta = 90°$)
בקו רוחב 45° הירידה בכ-0.17%

שאלה 2: חוט מחליק (חבל משתלשל) עם כוחות מעקבים

המערכת הבאה משוחררת ממנוחה כמתואר באיור. צפיפות החבל אחידה ומסתו $M$ ואורך החבל $\ell$. הזווית של המישור המשופע היא $\theta$.

בתוך המים יש כוח גרר כמתואר באיור ($A$ נתון). על המישור המשופע יש כוח חיכוך. כתבו משוואה דיפרנציאלית המתארת את התנועה. בדקו את מקרה הקצה $\theta=\frac{\pi}{2}$ ואין כוח גרר.

alt text

נערוך פירוק כוחות לכל חלק בנפרד, כי כל חלק של החבל חווה כוחות שונים. היחס בין 2 החלקים משתנה.

משקל החוט שבתוך המים:

\[\frac{x}{\ell} \cdot M\]

משקל החוט שמעל המים:

\[\left(\frac{\ell - x}{\ell}\right) \cdot M\]

משוואת הכוחות על החלק שבתוך המים בכיוון הנפילה היא (↓):

\[\begin{aligned} \underbrace{\frac{x}{\ell} \cdot M}_{\text{mass of fallig part}} a_{\text{falling}} &= \sum F_{\text{falling}} \\[10pt] &= \frac{x}{\ell} \cdot M g - \underbrace{Av}_{\text{drag}} - T \\[10pt] \frac{x}{\ell} M \ddot{x} &= \frac{x}{\ell} M g - A\dot{x} - T \end{aligned}\]

נסמן:

\[\boxed{\frac{x}{\ell} M \ddot{x} = \frac{x}{\ell} M g - A\dot{x} - T}\tag{1}\]

משוואת הכוחות על החלק שעל ״המגלשה״ בכיוון הנפילה (↘):

\[\underbrace{\left(\frac{\ell - x}{\ell}\right) \cdot M}_{\text{mass of sliding part}} a_{\text{sliding}} = \sum F_{\text{sliding}}\] \[= T - f_k + \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \sin \theta\]

נסמן:

\[\boxed{\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - f_k + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta} \tag{2}\]

מתוך סכום הכוחות הניצבים לכיוון הגלישה נוכל לקבל משוואה נוספת (↗):

\[0 = \sum F_{\text{normal}} = N - \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta\]

מסיקים:

\[\boxed{N = \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta}\]

כוח החיכוך הדינמי הוא $f_k = \mu_k N$, כאשר $\mu_k$ הוא מקדם החיכוך הדינמי. נחבר את $N$ שקיבלנו למשוואה זו:

\[\boxed{f_k = \mu_k N = \mu_k \left(\frac{\ell - x}{\ell}\right) \cdot M g \cdot \cos \theta}\]

נציב את $f_k$ במשוואת הכוחות בכיוון הגלישה (2):

\[\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta \tag{2}\]

סך הכל קיבלנו שתי משוואות:

\[\boxed{\frac{x}{\ell} M \ddot{x} = \frac{x}{\ell} M g - A\dot{x} - T}\tag{1}\] \[\boxed{\left(\frac{\ell - x}{\ell}\right) M \ddot{x} = T - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta} \tag{2}\]

נחבר את שתי המשוואות (1) ו-(2) כדי להיפטר מהכוח $T$:

\[\begin{aligned} \frac{x}{\ell} M \ddot{x} +& \left(\frac{\ell - x}{\ell}\right) M \ddot{x} =\\[10pt] \frac{x}{\ell} M g &- A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta \\[10pt] &+ \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta \end{aligned}\]

נפתח את המשוואה:

\[M\ddot{x} \left(\frac{x + \ell - x}{\ell}\right) = \frac{x}{\ell} M g - A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta\]

נפשט את המשוואה:

\[M\ddot{x} = \frac{x}{\ell} M g - A\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) M g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) M g \cdot \sin \theta\]

נחלק ב-$M$:

\[\ddot{x} = \frac{x}{\ell} g - \frac{A}{M}\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) g \cdot \sin \theta\] \[\boxed{\ddot{x} = \frac{x}{\ell} g - \frac{A}{M}\dot{x} - \mu_k \left(\frac{\ell - x}{\ell}\right) g \cdot \cos \theta + \left(\frac{\ell - x}{\ell}\right) g \cdot \sin \theta}\]

נבדוק מה קורה כאשר $\theta = \frac{\pi}{2}$ וללא כוח גרר עם המים - כלומר, כאשר החוט נופל בנפילה חופשית. נקווה שבמצב כזה יתקיים $M\ddot{x} = Mg$.

במצב זה, נציב $\theta = \frac{\pi}{2}$, כלומר $\cos \theta = 0$ ו-$\sin \theta = 1$. כמו כן, נניח שאין כוח גרר, כלומר $A = 0$. אז המשוואה תהפוך ל:

\[\ddot{x} = \frac{x}{\ell} g - 0 - 0 + \left(\frac{\ell - x}{\ell}\right) g\] \[\ddot{x} = \frac{x}{\ell} g + \left(\frac{\ell - x}{\ell}\right) g\] \[\ddot{x} = \frac{g}{\ell} (x + \ell - x) = \frac{g}{\ell} \ell = g\] \[\boxed{\ddot{x} = g}\]

כך שהאצה של החוט היא $g$, כלומר הוא נופל בנפילה חופשית, כפי שציפינו.

שאלה 3: מכונת ארטווד

נתונה המערכת באיור. המסה $M$ יכולה לנוע אנכית. המסה $m$ יכולה לנוע לכל כיוון.

נתון $m = M$.

כתבו מערכת משוואות המתארות את התנועה של מרחק המסה $m$ מציר הסיבוב (הרדיוס) והזווית.

השתמשו בקירוב של זוויות קטנות.

האם יכולות להיות תנודות כאשר הרדיוס קבוע?

חלק א׳: משוואות התנועה

alt text

על המסה השמאלית (שמקובעת רק לציר ה-$y$) פועלים כוחות:

כוח הכבידה $Mg$ כלפי מטה (בחרנו את כיוון $y$ כלפי מטה ומכאן $g$ חיובי)
מתיחות החוט $T$ כלפי מעלה נגד ציר $y$

לכן, לפי החוק השני של ניוטון:

\[ma_y = \sum F_y = mg - T\]

על המסה הימנית (שיכולה לנוע לכל כיוון) נחיל מערכת צירים פולארית.

בציר הרדיאלי (מהחיבור לתקרה - חיובי כלפי המסה מטה):

\[ma_r = \sum F_r = mg \cos \theta - T = m\left(\ddot{r} - r \dot{\theta}^2\right)\]

בציר הטנגנציאלי (בניצב לציר הרדיאלי, חיובי בכיוון התנועה):

\[ma_\theta = \sum F_\theta = mg \sin \theta = m\left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right)\]

נבחין שמתחקיים :

\[\Delta y = \Delta r\]

כי המתיחות בחוט נשמרת. נזכיר ש$r$ הוא המרחק מהמסה הימנית לציר הסיבוב, כלומר אורך החוט. מכאן ש:

\[\boxed{a_y=\ddot{r}}\]

קיבלנו שלוש משוואות בקואורדינטות פולריות בשלושה נעלמים: $T$, $r$ ו-$\theta$.

\[\begin{align} m\ddot{r} & = mg-T \tag{1} \\[10pt] m\left(\ddot{r} - r \dot{\theta}^2\right) &= mg \cos \left(\theta\right) = T \tag{2} \\[10pt] m\left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) &= mg \sin \theta \tag{3} \end{align}\]

נחלץ את $T$ מהמשוואה (1) ונציב אותו במשוואה (2):

\[T = m\left(g - \ddot{r}\right)\]

נציב את $T$ במשוואה (2):

\[\cancel{m}\left(\cancel{\ddot{r}} - r \dot{\theta}^2\right) = mg \cos \theta - \cancel{m}\left(g - \cancel{\ddot{r}}\right)\]

נחבר את משוואות (1) ו-(2):

\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= g(\cos \theta - 1) \\[10pt] r\ddot{\theta}^2 + 2\dot{r}\dot{\theta} &= g \sin \theta \end{aligned}}\]

זו התשובה הסופית שמתארת את התנועה במשתנים הקינמטיים $r$ ו-$\theta$.

חלק ב׳: קירוב של זוויות קטנות

מטורי טיילור:

\[\begin{cases} \cos \theta -1 \approx - \frac{\theta^2}{2} \\[10pt] \sin \theta \approx \theta \end{cases}\]

נציב את הקירובים במשוואות:

\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= -\frac{g\theta^2}{2} \\[10pt] r\ddot{\theta} + 2\dot{r}\dot{\theta} &= g \theta \end{aligned} }\]

חלק ג׳: האם יכולות להיות תנודות כאשר הרדיוס קבוע?

השאלה האם תתכן תנועה זוויתית כאשר $r$ קבוע שואלת האם ייתכן כי $\dot{r} = \dot{r} = 0$ וכן $\dot{theta} \neq 0, \, \ddot{\theta} \neq 0$.

המתרגל פיתח את המשוואות הקודמות לביטוי של $\theta$:

\[\boxed{ \begin{aligned} -r\dot{\theta}^2 &= -\frac{g\theta^2}{2} \\[10pt] \theta = \pm \sqrt{\frac{2r}{g}} \dot{\theta}^2 \\[10pt] \end{aligned}}\]

הוא הציב את הביטוי הזה במשוואה השנייה וקיבל שכאשר $\dot{r} = 0$ ו-$\ddot{\theta} \neq 0$, מתקיים:

\[\boxed{ \begin{aligned} r\ddot{\theta} + 2\underbrace{\dot{r}}_{=0}\dot{\theta} &= g \theta \\[10pt] r\ddot{\theta} &= \pm g \cdot \sqrt{\frac{2r}{g}} \dot{\theta}^2 \end{aligned}}\]

למשוואה הזאת יש פתרון, מכאן שייתכנו תנודדות מטוטלת גם כאשר 2 המסות לא עולות ויורדות.

תרגול 10 - כוחות, תנועה הרמונית ותנועה מעגלית

תאריך: 05/06/2025

שאלה 1: גוף במישור משופע

גוף בעל מסה $m$ נמצא על משטח משופע בזווית $\theta$ ביחס לאופק. מקדם החיכוך הסטטי בין הגוף למשטח הוא $\mu_s$.

באילו זוויות הגוף ישאר במקומו ולא יחליק?

במידה שהזווית גדולה יותר, מהו המרחק שהגוף יעבור ב-$t$ שניות?

מהי הזווית עבורה הגוף ינוע במהירות קבועה במורד?

האם הוא יכול לנוע במהירות קבועה במעלה המישור המשופע?

פתרון מפורט

א. תנאי שיווי משקל

נבחר מערכת צירים: ציר $x$ במקביל למשטח (חיובי במורד), ציר $y$ ניצב למשטח.

alt text

משוואות שיווי משקל בכיוון $y$:

\[\sum F_y = N - mg\cos\theta = 0\]

לכן הכוח הנורמלי:

\[\boxed{N = mg\cos\theta}\]

alt text

משוואות שיווי משקל בכיוון $x$:

\[\sum F_x = mg\sin\theta - f_s = 0\]

כאשר $f_s \leq \mu_s N$, סכום הכוחות שווה לאפס מכיוון שבתחילה הגוף במנוחה. כלומר:

\[\begin{aligned} mg\sin\theta - f_s &\leq 0 \\[10pt] mg\sin\theta &\leq f_s \\[10pt] &\leq \mu_s N \end{aligned}\]

alt text

נציב את $N$ שמצאנו, אז לאחר שהעברנו את $f_s$ אגף:

\[\begin{aligned} mg\sin\theta &\leq \mu_s mg\cos\theta \\[10pt] \tan\theta &\leq \mu_s \\[10pt] \implies \theta &\leq \arctan(\mu_s) \end{aligned}\]

$\tan(\theta)$ פוקציה עולה ולכן:

\[\implies 0 \leq \theta \leq \arctan(\mu_s)\]

כלומר, הגוף יישאר במקומו כאשר הזווית $\theta$ קטנה או שווה לזווית הקריטית:

\[\boxed{\theta \leq \arctan(\mu_s)}\]

ב. המרחק כאשר הגוף מתחיל להחליק

כאשר $\theta > \arctan(\mu_s)$, הגוף מתחיל להחליק במורד המישור, ואז יש להשתמש בחיכוך קינטי $f_k = \mu_k N$. מכאן:

\[\begin{aligned} \sum F_x &= mg\sin\theta - \mu_k mg\cos\theta = ma_x \\[10pt] & \cancel{m}g \sin\theta - \mu_k \cancel{m}g\cos\theta = \cancel{m}a_x \\[10pt] \implies a_x &= g(\sin\theta - \mu_k\cos\theta) \end{aligned}\]

כלומר, התאוצה של הגוף במורד המישור היא:

\[\boxed{a_x = g(\sin\theta - \mu_k\cos\theta)}\]

זוהי תאוצה קבועה, ולכן לפי נוסחת מיקום בתאוצה קבועה נוכל לקבל את המרחק שהגוף עובר לאחר זמן $t$:

\[\begin{aligned} x(t) - x(0) &= \Delta x = v_0 t + \frac{1}{2}a_x t^2 = \frac{g(\sin\theta - \mu_k\cos\theta)}{2} t^2 \\[10pt] \implies \Delta x &= \frac{g}{2}(\sin\theta - \mu_k\cos\theta)t^2 \end{aligned}\]

כלומר, המרחק שהגוף עובר לאחר זמן $t$ הוא:

\[\boxed{\Delta x = \frac{g}{2}(\sin\theta - \mu_k\cos\theta)t^2}\]

ג. מה הזווית עבורה הגוף ינוע במהירות קבועה במורד המישור?

השאלה השקולה היא באיזו זווית התאוצה $a_x = 0$

\[\begin{aligned} \sin(\theta_0) &= \mu_k\cos(\theta_0) \\[10pt] \implies \tan(\theta_0) &= \mu_k \\[10pt] \implies \theta_0 &= \arctan(\mu_k) \end{aligned}\]

כלומר, הגוף ינוע במהירות קבועה במורד המישור כאשר הזווית היא:

\[\boxed{\theta_0 = \arctan(\mu_k)}\]

ד. האם הגוף יכול לנוע במהירות קבועה במעלה המישור?

לא. בתנועה במעלה המישור כוח החיכוך הקינטי פועל כלפי מטה, ויצטרף לכוח הכובד. $\sum F_x$ חיובי ממש, שגורם לתאוצה חיובית בכיוון המורד ולא תתקיים מהירות קבועה.

שאלה 2: תנועה הרמונית פשוטה

גוף בעל מסה $m = 0.1 \mathrm{kg}$ נע בתנועה הרמונית לאורך ציר $x$ עם:

משרעת התנודה: $C = 0.25 \mathrm{[m]}$

זמן המחזור: $T = 2 \mathrm{[s]}$

מיקום התחלתי: $x_0 = x(t=0) = 0.12 \mathrm{[m]}$

נדרש למצוא:

את הכוח הפועל על הגוף בזמן $t = \frac{1}{3}$ שנייה

את המהירות בזמן $t = 0$

את המהירות כשהגוף עובר בנקודת שיווי המשקל

פתרון מפורט

הגדרת משוואת התנועה

התנועה ההרמונית מתוארת על ידי:

\[x(t) = A\cos(\omega t + \phi)\]

כאשר $A$ היא האמפליטודה, $\omega$ התדירות הזוויתית, ו-$\phi$ הפאזה ההתחלתית.

מהנתונים נוכל לקבל את ערכי $A$, $\omega$ ו-$\phi$:

\[A = C = 0.25 \mathrm{[m]}\]

מהנתון על זמן המחזור $T$:

\[\begin{aligned} T &= 2 \mathrm{[s]} \\[10pt] &\implies f = \frac{1}{T} = \frac{1}{2} \mathrm{[Hz]} \\[10pt] &\implies \omega = 2\pi f = 2\pi \cdot \frac{1}{2} = \pi \mathrm{ [rad/s]} \end{aligned}\]

כלומר:

$\omega = \frac{2\pi}{T} = \frac{2\pi}{2} = \pi$ רד/שנייה

מציאת הפאזה ההתחלתית $\phi$

מתנאי ההתחלה $x(0) = 0.12 \mathrm{[m]}$:

\[\begin{aligned} x(0) &= A\cos(\omega \cdot 0 + \phi) = 0.12 \\[10pt] &= A\cos(\phi) \\[10pt] &= 0.25\cos(\phi) \end{aligned}\] \[0.25\cos(\phi) = 0.12\] \[\begin{aligned} \cos(\phi) &= \frac{0.12}{0.25} \\[10pt] \implies \phi &= \arccos\left(0.48\right) = 1.07 \mathrm{[rad]} \end{aligned}\]

משוואת המיקום המלאה:

\[\boxed{x(t) = 0.25\cos(\pi t + 1.07)}\]

חלק א: הכוח בזמן $t = \frac{1}{3}$ שנייה

המהירות:

\[\dot{x}(t) = -0.25\pi\sin(\pi t + 1.07)\]

התאוצה:

\[\ddot{x}(t) = -0.25\pi^2\cos(\pi t + 1.07)\]

בזמן $t = \frac{1}{3}$:

\[x\left(\frac{1}{3}\right) = 0.25\cos\left(\frac{\pi}{3} + 1.07\right) = 0.25\cos(2.12) \approx -0.125 \mathrm{[m]}\]

הכוח:

\[F = m\ddot{x} = 0.1 \times (-\pi^2) \times (-0.125) = 0.1 \times 9.87 \times 0.125\] \[\boxed{F\left(\frac{1}{3}\right) = 0.123 \mathrm{[N]}}\]

חלק ב: המהירות ההתחלתית

\[v(0) = \dot{x}(0) = -0.25\pi\sin(1.07)\] \[\boxed{v(0) = -0.69 \mathrm{[m/s]}}\]

חלק ג: המהירות בנקודות שיווי המשקל

הגוף עובר בנקודת שיווי המשקל כאשר $x = 0$:

\[\cos(\pi t + 1.07) = 0\] \[\pi t + 1.07 = \frac{\pi}{2} + n\pi\]

לכן:

\[t_n = \frac{1}{\pi}\left(\frac{\pi}{2} + n\pi - 1.07\right)\]

המהירות בזמנים אלו:

\[v(t_n) = -0.25\pi\sin\left(\frac{\pi}{2} + n\pi\right) = (-1)^{n+1} \times 0.25\pi\]

עבור $n = 0$:

\[t_0 = 0.16 \mathrm{[s]}\] \[\boxed{v(t_0) = -\frac{\pi}{4} = -0.785 \mathrm{[m/s]}}\]

שאלה 3: תנועה מעגלית עם תאוצה זוויתית משתנה

ילד עומד במרחק $R$ ממרכז קרוסלה. הקרוסלה מתחילה ממנוחה עם תאוצה זוויתית:
\[a_t = (1 - e^{-t})\]
תנאי התחלה: $v(0) = 0$, $\theta(0) = 0$

נדרש למצוא:

את התאוצה הזוויתית ($\ddot{\theta}$)

את המהירות הזוויתית ($\omega(t)$) כפונקציה של הזמן

פתרון מפורט

הערה: הסימונים הבאים שקולים:
\[a_t = \vec{a_\theta} = a_{\text{tangential}}\]

ניזכר בנוסחאות שפיתחנו בשיעור:

\[\begin{aligned} \vec{a} &= \vec{a_r} \mathbf{\hat{r}} + \vec{a_\theta} \mathbf{\hat{\Theta}} \\[10pt] &= \underbrace{\left(\ddot{r} - r\dot{\theta}^2\right)}_{\vec{a_r}}\mathbf{\hat{r}} + \underbrace{\left(2\dot{r}\dot{\theta} + r\ddot{\theta}\right)}_{\vec{a_\theta}}\mathbf{\hat{\Theta}} \end{aligned}\]

במקרה הזה אין לנו תאוצה רדיאלית - כי מדובר בקרוסלה, כלומר:

\[\vec{a} = \vec{a_\theta} \mathbf{\hat{\Theta}}\]

ניעזר בפיתוח של וקטור התאוצה בקואורדינטות פולריות:

\[\vec{a_\theta} = \left(\cancel{2\underbrace{\dot{r}}_{=0}\dot{\theta}} + r\ddot{\theta}\right) = R\ddot{\theta}\]

הביטוי שמתקבל הוא $R\ddot{\theta}$, בגלל שבקרוסלה הילד לא משנה את הרדיוס, כלומר $\dot{r} = 0$.

מציאת התאוצה הזוויתית ($\ddot{\theta}$)

\[\boxed{\ddot{\theta}(t) = \frac{\vec{a_\theta}}{R} = \frac{\left(1-e^{-t}\right)}{R}}\]

מציאת המהירות הזוויתית ($\omega = \dot{\theta}$)

המהירות הזוויתית קשורה לתאוצה הזוויתית על ידי:

\[\ddot{\theta} = \frac{d\dot{\theta}}{dt} = \frac{d\omega}{dt}\]

נוכל להוציא את $\omega$ על ידי אינטגרציה של $\ddot{\theta}$:

\[\implies \omega(t)-\underbrace{\omega(0)}_{=0} = \int_0^t \ddot{\theta}(s) ds\]

נציב את התאוצה שמצאנו ונפתור את האינטגרל לקבלת המהירות הזוויתית:

\[\begin{aligned} \implies \omega(t) &= \int_0^t \frac{1-e^{-s}}{R} ds = \frac{1}{R}\left[s + e^{-s}\right]_0^t \\[10pt] &= \frac{t+ e^{-t} - 1}{R} \end{aligned}\]

המהירות הזוויתית:

\[\boxed{\omega(t) = \frac{t + e^{-t} - 1}{R} \mathrm{[rad/s]}}\]

מציאת הזווית הכוללת ($\theta(t)$)

\[\begin{aligned} \theta(t) &= \int_0^t \omega(s) ds \\[10pt] &= \frac{1}{R}\int_0^t (s + e^{-s} - 1) ds \\[10pt] &= \frac{1}{R}\left[\frac{s^2}{2} - e^{-s} - s\right]_0^t \end{aligned}\] \[\boxed{\theta(t) = \frac{1}{R}\left(\frac{t^2}{2} + 1 - e^{-t} - t\right) \mathrm{[rad]}}\]

וקטור התאוצה בקואורדינטות פולריות

בקואורדינטות פולריות, התאוצה הכוללת:

\[\vec{a} = (\vec{a_r})\mathbf{\hat{r}} + (\vec{a_\theta})\mathbf{\hat{\Theta}}\]

כאשר:

התאוצה הרדיאלית (צנטריפטלית), ממה שמצאנו קודם על המהירות הזוויתית:
\[\vec{a_r} = -R\omega^2 = -R\left(\frac{t + e^{-t} - 1}{R}\right)^2\]
התאוצה המשיקית, מהנתון:
\[\vec{a_\theta} = R\alpha = 1 - e^{-t}\]

לכן:

\[\boxed{\vec{a}(t) = -\frac{(t + e^{-t} - 1)^2}{R}\mathbf{\hat{r}} + (1 - e^{-t})\mathbf{\hat{\Theta}}}\]

וקטור המהירות

הנוסחה לחישוב וקטור המהירות בקואורדינטות פולריות:

\[\vec{v} = \dot{r}\mathbf{\hat{r}} + r\dot{\theta}\mathbf{\hat{\Theta}}\]

כאמור הנגזרת של הרדיוס היא אפס, כלומר $\dot{r} = 0$. לכן:

\[\vec{v} = R\dot{\theta}\mathbf{\hat{\Theta}} = R\left(\frac{t + e^{-t} - 1}{R}\right)\mathbf{\hat{\Theta}}\] \[\boxed{\vec{v}(t) = (t + e^{-t} - 1)\mathbf{\hat{\Theta}}}\]

וקטור המיקום בקואורדינטות קרטזיות

בהנחה שבזמן $t = 0$ הילד נמצא על ציר $x$ החיובי:

\[\begin{aligned} \vec{r}(t) &= R\cos\left[\theta(t)\right]\hat{x} + R\sin\left[\theta(t)\right]\hat{y} \\[10pt] &= R\cos\left[\frac{t^2/2 + 1 - e^{-t} - t}{R}\right]\hat{x} + R\sin\left[\frac{t^2/2 + 1 - e^{-t} - t}{R}\right]\hat{y} \end{aligned}\]

סיכום עקרונות מרכזיים

1. ניתוח כוחות במישור משופע

תמיד יש לפרק את כוח הכובד לרכיבים מקבילים וניצבים למשטח
הזווית הקריטית תלויה רק במקדם החיכוך ולא במסה
$\tan\theta_c = \mu_s$ היא נוסחה אוניברסלית

2. תנועה הרמונית פשוטה

הכוח פרופורציונלי להעתק: $F = -kx$
התדירות אינה תלויה באמפליטודה
המהירות המקסימלית: $v_{max} = A\omega$

3. תנועה מעגלית

בתנועה מעגלית תמיד קיימת תאוצה צנטריפטלית: $\vec{a_r} = -R\omega^2$
כאשר המהירות הזוויתית משתנה, קיימת גם תאוצה משיקית: $\vec{a_\theta} = R\alpha$
וקטור התאוצה הכולל הוא סכום וקטורי של שני הרכיבים

תרגול 11 - תנועה דו-ממדית ועבודה-אנרגיה

תאריך: 24/06/2025

להלן שאלות התרגול:

1. תנועה בשני ממדים עם כוח תלוי זמן

נתון גוף בעל מסה $m = 1.5 \, \mathrm{kg}$ הנע במישור $(x,y)$ מתחיל בתנועתו מהנקודה $(0,0)$. המישור חסר חיכוך.

וקטור מהירות הגוף נתון ביחידות של מטר לשנייה:
\[\mathbf{v}(t) = (1 - 2t)\hat{\mathbf{x}} + (2t - 3t^2)\hat{\mathbf{y}}\]

חשבו את מהירות הגוף כאשר הוא מגיע בחזרה לנקודת המוצא $(0,0)$.

חשבו את הזמן $t_m$ שבו גודל הכוח הפועל על הגוף הוא מינימלי.

כמה עבודה עשה הכוח הפועל על הגוף מתחילת התנועה עד לזמן $t = 2 \, \mathrm{s}$?

האם הכוח הפועל על הגוף הוא כוח משמר? נמקו בצורה ברורה ותמציתית.

alt text

1.1 מציאת המהירות כאשר הגוף חוזר לנקודת המוצא

נמצא את הזמן שבו הגוף חוזר לראשית, ואז נוכל לחשב את מהירותו באותו זמן.

לא תמיד מובטח שיש זמן $t \ne 0$ שבו $\mathbf{r}(t) = \left(x(t), y(t)\right) = (0, 0)$, אבל במקרה הזה זה עולה מהשאלה.

נחשב את וקטור המיקום $\mathbf{r}(t)$ על ידי אינטגרציה של $\mathbf{v}(t)$.

עבור רכיב $x$:

\[x(t) = x(0) + \int_0^t v_x(s)\,ds = 0 + \int_0^t (1 - 2s)\,ds = t - t^2\]

עבור רכיב $y$:

\[y(t) = y(0) + \int_0^t v_y(s)\,ds = 0 + \int_0^t (2s-3s^2)\,ds = t^2 - t^3\]

מציאת זמן החזרה לראשית:

הגוף חוזר לראשית כאשר $x(t) = 0$ וגם $y(t) = 0$ (עבור $t > 0$).

מהתנאי $x(t) = 0$:

\[t - t^2 = 0 \implies t(1 - t) = 0\]

הפתרונות הם $t = 0$ או $t = 1$.

מהתנאי $y(t) = 0$:

\[t^2 - t^3 = 0 \implies t^2(1 - t) = 0\]

הפתרונות הם $t = 0$ או $t = 1$.

לכן, הגוף חוזר לראשית בזמן $t = 1 \, \mathrm{s}$.

המהירות בזמן החזרה:

נחשב את וקטור המהירות בזמן $t = 1$:

\[\begin{aligned} \mathbf{v}(1) &= \left(1 - 2(1)\right)\hat{\mathbf{x}} + \left(2(1) - 3(1)^2\right)\hat{\mathbf{y}} \\[5pt] &= (-1)\hat{\mathbf{x}} + (-1)\hat{\mathbf{y}} \\[5pt] &= -\hat{\mathbf{x}} - \hat{\mathbf{y}} \end{aligned}\]

גודל המהירות:

\[|\mathbf{v}(1)| = \sqrt{(-1)^2 + (-1)^2} = \sqrt{2} \, \mathrm{m/s}\]

השאלה ביקשה את “מהירות הגוף”, שלרוב מתכוונת לווקטור המהירות.

\[\boxed{\mathbf{v}(t=1) = (-1, -1) \, \mathrm{m/s}}\]

1.2 הזמן שבו גודל הכוח מינימלי

לפי החוק השני של ניוטון, $\mathbf{F} = m\mathbf{a}$. כיוון שהמסה קבועה, הכוח פרופורציונלי לתאוצה, שהיא נגזרת המהירות לפי הזמן.

\[\begin{aligned} \mathbf{a}(t) &= \frac{d\mathbf{v}}{dt} = \frac{d}{dt}\left[(1 - 2t)\hat{\mathbf{x}} + (2t - 3t^2)\hat{\mathbf{y}}\right] \\[5pt] &= -2\hat{\mathbf{x}} + (2 - 6t)\hat{\mathbf{y}} \end{aligned}\]

גודל הכוח:

\[|\mathbf{F}(t)| = m|\mathbf{a}(t)| = m\sqrt{(-2)^2 + (2 - 6t)^2} = m\sqrt{4 + (2 - 6t)^2}\]

גודל הכוח $\vert \mathbf{F}(t)\vert $ הוא מינימלי כאשר הביטוי שבתוך השורש, $4 + (2 - 6t)^2$, הוא מינימלי. זה קורה כאשר $(2 - 6t)^2 = 0$, כלומר:

\[2 - 6t = 0 \implies \boxed{t_m = \frac{1}{3} \, \mathrm{s}}\]

1.3 העבודה שביצע הכוח

העבודה שביצע הכוח מ-$t = 0$ עד $t = 2 \, \mathrm{s}$ ניתנת על ידי משפט עבודה-אנרגיה:

\[W = \Delta E_k = \frac{1}{2}m|\mathbf{v}(2)|^2 - \frac{1}{2}m|\mathbf{v}(0)|^2\]

נחשב את המהירויות:

\[\mathbf{v}(0) = (1 - 0)\hat{\mathbf{x}} + (0 - 0)\hat{\mathbf{y}} = \hat{\mathbf{x}}\]

לכן

\[|\mathbf{v}(0)|^2 = 1^2 = 1\]

נחשב את $\mathbf{v}(2)$:

\[\mathbf{v}(2) = (1 - 4)\hat{\mathbf{x}} + (4 - 12)\hat{\mathbf{y}} = -3\hat{\mathbf{x}} - 8\hat{\mathbf{y}}\]

לכן

\[|\mathbf{v}(2)|^2 = (-3)^2 + (-8)^2 = 9 + 64 = 73\]

נציב את הערכים:

\[W = \frac{1}{2}m(73 - 1) = \frac{1}{2}(1.5)(72) = \boxed{54 \, \mathrm{J}}\]

דרך חלופית (מסובכת יותר) היא לחשב את העבודה בעזרת אינטגרל מסלולי:
\[W = \int_{t=0}^{t=2} \mathbf{F}(t) \cdot \mathbf{v}(t) \, dt\]
כאשר $\mathbf{F}(t) = m\mathbf{a}(t) = m(-2, 2 - 6t)$ ו-$\mathbf{v}(t) = (1 - 2t, 2t - 3t^2)$.
\[W = m \int_{0}^{2} \left[ -2(1 - 2t) + (2 - 6t)(2t - 3t^2) \right] dt\]
לאחר פתיחת סוגריים ואינטגרציה, מתקבלת אותה תוצאה: $W = 54 \, \mathrm{J}$.

1.4 האם הכוח משמר?

כוח משמר מוגדר ככוח שעבודתו על מסלול סגור כלשהו שווה לאפס. במקרה שלנו, הגוף יוצא מנקודת המוצא $(0,0)$ בזמן $t=0$ וחוזר אליה בזמן $t=1$. זהו מסלול סגור. נחשב את העבודה על מסלול זה:

\[W_{0\to1} = \Delta E_k = \frac{1}{2}m\left(|\mathbf{v}(1)|^2 - |\mathbf{v}(0)|^2\right)\]

כבר חישבנו:

\[\begin{aligned} |\mathbf{v}(1)|^2 &= (-\hat{\mathbf{x}} - \hat{\mathbf{y}}) \cdot (-\hat{\mathbf{x}} - \hat{\mathbf{y}}) = 2 \\[5pt] |\mathbf{v}(0)|^2 &= (\hat{\mathbf{x}}) \cdot (\hat{\mathbf{x}}) = 1 \end{aligned}\]

לכן:

\[W_{0\to1} = \frac{1}{2}(1.5)(2 - 1) = 0.75 \, \mathrm{J}\]

מסקנה: מכיוון שהעבודה על מסלול סגור ($W_{0\to1} = 0.75 \, \mathrm{J}$) אינה שווה לאפס, הכוח אינו משמר.

דרך נוספת להראות זאת היא לבדוק אם הכוח תלוי רק במיקום. הכוח $\mathbf{F}(t) = m\mathbf{a}(t)$ תלוי מפורשות בזמן, ולכן אינו יכול להיות משמר (כוח משמר תלוי במיקום בלבד).

alt text

2. התנגשויות במערכת מטוטלת

משקולת בעלת מסה $m$ מחוברת למטוטלת בעלת חוט באורך $\ell$. המשקולת משוחררת ממנוחה מגובה $\ell$ (כלומר, כשהחוט אופקי) ופוגעת בקוביה במנוחה בעלת מסה $2m$ הנמצאת בנקודה הנמוכה ביותר של המסלול. לאחר הפגיעה, המטוטלת והקוביה נעות.

לאיזה גובה תעלה המטוטלת ($m$) לאחר הפגיעה בכל אחד מהמקרים הבאים?

ההתנגשות אלסטית לחלוטין.

ההתנגשות אינה אלסטית, והקוביה נעה לאחר ההתנגשות במהירות השווה למהירות המטוטלת לפני ההתנגשות.

ההתנגשות פלסטית לחלוטין (הכדור והקוביה נדבקים זה לזה).

alt text

2.1 התנגשות אלסטית

שלב א’: מציאת מהירות המטוטלת לפני ההתנגשות

משימור אנרגיה מכנית במהלך נפילת המטוטלת מגובה $h=\ell$ לנקודה הנמוכה ביותר: האנרגיה הפוטנציאלית ההתחלתית הופכת לאנרגיה קינטית.

\[mg\ell = \frac{1}{2}mv_1^2\]

מכאן, מהירות המטוטלת רגע לפני הפגיעה היא:

\[\boxed{v_1 = \sqrt{2g\ell}}\]

שלב ב’: ניתוח ההתנגשות האלסטית

בהתנגשות אלסטית חד-ממדית בין מסה $m_1=m$ למסה $m_2=2m$ (שנמצאת במנוחה), נשמרים גם התנע וגם האנרגיה הקינטית. נסמן את מהירות המטוטלת לאחר ההתנגשות ב-$u_1$ ואת מהירות הקוביה ב-$u_2$.

שימור תנע:
\[\begin{aligned} mv_1 + (2m) \cdot 0 &= mu_1 + (2m)u_2 \\[5pt] \implies v_1 &= u_1 + 2u_2 \quad (1) \end{aligned}\]
שימור אנרגיה קינטית:
\[\begin{aligned} \frac{1}{2}mv_1^2 + 0 &= \frac{1}{2}mu_1^2 + \frac{1}{2}(2m)u_2^2 \\[5pt] \implies v_1^2 &= u_1^2 + 2u_2^2 \quad (2) \end{aligned}\]

מפתרון מערכת המשוואות (1) ו-(2) עבור $u_1$ (מהירות המטוטלת לאחר ההתנגשות), מקבלים:

\[u_1 = \frac{m_1 - m_2}{m_1 + m_2} v_1 = \frac{m - 2m}{m + 2m} v_1 = -\frac{1}{3}v_1\]

הסימן השלילי מציין שהמטוטלת נעה בכיוון ההפוך (אחורה).

שלב ג’: מציאת הגובה המקסימלי לאחר ההתנגשות

משימור אנרגיה עבור המטוטלת לאחר ההתנגשות, האנרגיה הקינטית שלה הופכת לאנרגיה פוטנציאלית:

\[\begin{aligned} \frac{1}{2}mu_1^2 &= mgh_{\text{max}} \\[5pt] \implies h_{\text{max}} &= \frac{u_1^2}{2g} \end{aligned}\]

נציב את $u_1 = -\frac{1}{3}v_1$ ואת $v_1 = \sqrt{2g\ell}$:

\[h_{\text{max}} = \frac{\left(-\frac{1}{3}\sqrt{2g\ell}\right)^2}{2g} = \frac{\frac{1}{9}(2g\ell)}{2g} = \frac{\ell}{9}\] \[\boxed{h_{\text{max}} = \frac{\ell}{9}}\]

2.2 התנגשות לא-אלסטית עם תנאי מיוחד

נתון שלאחר ההתנגשות, מהירות הקוביה ($u_2$) שווה למהירות המטוטלת לפני ההתנגשות ($v_1$).

\[u_2 = v_1 = \sqrt{2g\ell}\]

נשתמש בשימור תנע כדי למצוא את מהירות המטוטלת לאחר ההתנגשות, $u_1$:

\[mv_1 = mu_1 + (2m)u_2\]

נציב $u_2 = v_1$:

\[\begin{aligned} mv_1 &= mu_1 + 2mv_1 \\[5pt] \implies u_1 &= v_1 - 2v_1 \\[5pt] &= -v_1 \end{aligned}\]

המטוטלת נעה אחורה במהירות שגודלה שווה למהירות הפגיעה. משימור אנרגיה, היא תגיע בחזרה בדיוק לגובה ההתחלתי.

\[h_{\text{max}} = \frac{u_1^2}{2g} = \frac{(-v_1)^2}{2g} = \frac{v_1^2}{2g} = \frac{2g\ell}{2g} = \ell\] \[\boxed{h_{\text{max}} = \ell}\]

הערה: מצב זה אינו פיזיקלי, מכיוון שהאנרגיה הקינטית לאחר ההתנגשות גדולה מהאנרגיה הקינטית לפניה, מה שסותר את חוק שימור האנרגיה.

2.3 התנגשות פלסטית

בהתנגשות פלסטית, שני הגופים נדבקים ונעים יחד לאחר ההתנגשות במהירות משותפת $\mathbf{u}$.

שלב א’: שימור תנע

\[mv_1 = (m + 2m)u = 3mu\]

מכאן, המהירות המשותפת לאחר ההתנגשות היא:

\[u = \frac{mv_1}{3m} = \frac{v_1}{3} = \frac{\sqrt{2g\ell}}{3}\]

שלב ב’: מציאת הגובה המקסימלי

משימור אנרגיה עבור המערכת המאוחדת (מסה $3m$) לאחר ההתנגשות:

\[\frac{1}{2}(3m)u^2 = (3m)gh_{\text{max}} \implies h_{\text{max}} = \frac{u^2}{2g}\]

נציב את $u$:

\[h_{\text{max}} = \frac{\left(\frac{\sqrt{2g\ell}}{3}\right)^2}{2g} = \frac{\frac{2g\ell}{9}}{2g} = \frac{\ell}{9}\] \[\boxed{h_{\text{max}} = \frac{\ell}{9}}\]

שאלה 3 מתרגול 11:

מערכת של שני קיפצים

מערכת של שני קיפצים, כל אחד בעל אורך $a$, בשיווי משקל וקבוע קפיץ $k$. הקיפצים מחוברים זה לזה ומקובעים בקצה האחר בנקודות $(-a, 0)$, $(a, 0)$. נניח שהקיפצים יכולים להתכווץ או להתרחב, אך לא להתכופף.

הראה שהפוטנציאל של המערכת, עבור העברת נקודת החיבור מ$(0,0)$ ל-$(x, y)$ כלשהי, הוא:
\[\phi = \frac{k}{2} \left[ \sqrt{(x + a)^2 + y^2} - a \right]^2 + \frac{k}{2} \left[ \sqrt{(x - a)^2 + y^2} - a \right]^2\]

כיוון שהפוטנציאל תלוי ב-$x$ וב-$y$, נצטרך להשתמש בנגזרות חלקיות על מנת למצוא את הכוחות. זכור שנגזרת חלקית של פונקציה $f(x,y)$ מוגדרת בעזרת הנגזרת המלאה כך:
\[\frac{\partial f (x,y)}{\partial x}= \frac{df(x,y=\text{const})}{dx}\] \[\frac{\partial f (x,y)}{\partial y}= \frac{df(x=\text{const},y)}{dy}\]
מצא את הכוח $\vec{F}_x$ והראה שעבור $\mathbf{r}=0$ מתקיים $\vec{F}_x = 0$.

מצא את הכוח $\vec{F}_y$ עבור $x=0$. בדוק שסימן התוצאה (חיובית או שלילית) הגיוני.

alt text

סעיף 1 - פוטנציאל המערכת בעת הזזה

הרעיון הוא להבין כיצד כל הזזה משפיעה על אורך הקפיצים. נעביר מערכת צירים במצב המאוזן ונבדוק בכמה מתארך או מתכווץ כל קפיץ $\Delta \ell_1$ ו-$\Delta \ell_2$. מכאן $\phi = \frac{k}{2}(\Delta \ell_1^2 + \Delta \ell_2^2)$.

\[\ell_1 = \sqrt{(a+x)^2 + y^2}\] \[\ell_2 = \sqrt{(a-x)^2 + y^2}\] \[\Delta \ell_1^2 = \left(\ell_{1 f} - \ell_{1 i}\right)^2 = \left(\sqrt{(a+x)^2 + y^2} - a\right)^2\] \[\Delta \ell_2^2 = \left(\ell_{2 f} - \ell_{2 i}\right)^2 = \left(\sqrt{(a-x)^2 + y^2} - a\right)^2\] \[\boxed{\phi = \frac{k}{2} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2}\]

סעיף 2 - כוח $\vec{F}_x$ בנקודה $(0,0)$

כוח הוא נגזרת של פוטנציאל:

\[\vec{F}_x = -\frac{\partial \Phi}{\partial x}\]

נחשב את הנגזרת החלקית של $\Phi$ לפי $x$:

\[\begin{aligned} \frac{\partial \Phi}{\partial x} &= \frac{k}{2} \frac{\partial}{\partial x} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \frac{\partial}{\partial x} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2 \\[5pt] &= k \left[ \frac{(a+x)}{\sqrt{(a+x)^2 + y^2}} \right] \left[ \sqrt{(a+x)^2 + y^2} - a \right] - k \left[ \frac{(a-x)}{\sqrt{(a-x)^2 + y^2}} \right] \left[ \sqrt{(a-x)^2 + y^2} - a \right] \end{aligned}\]

כעת נציב $x=0$:

\[\begin{aligned} \frac{\partial \Phi}{\partial x} &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] - \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a - \sqrt{a^2 + y^2} + a \right] \right] \\[5pt] &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \cdot 0 \right] = 0 \end{aligned}\]

לכן, הכוח $\vec{F}_x$ בנקודה $(0,0)$ הוא:

\[\boxed{\vec{F}_x = 0}\]

סעיף 3 - כוח $\vec{F}_y$ עבור $x=0$

כעת נחשב את הכוח $\vec{F}_y$ עבור $x=0$:

\[\vec{F}_y = -\frac{\partial \Phi}{\partial y}\]

נחשב את הנגזרת החלקית של $\Phi$ לפי $y$:

\[\begin{aligned} \frac{\partial \Phi}{\partial y} &= \frac{k}{2} \frac{\partial}{\partial y} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \frac{\partial}{\partial y} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2 \\[5pt] &= k \left[ \frac{y}{\sqrt{(a+x)^2 + y^2}} \right]\left[ \sqrt{(a+x)^2 + y^2} - a \right] + k \left[ \frac{y}{\sqrt{(a-x)^2 + y^2}} \right]\left[ \sqrt{(a-x)^2 + y^2} - a \right] \end{aligned}\]

נציב $x=0$:

\[\begin{aligned} \frac{\partial \Phi}{\partial y} &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] + \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a + \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \cdot 2\left(\sqrt{a^2 + y^2} - a\right) \right] \end{aligned}\]

לכן, הכוח $\vec{F}_y$ עבור $x=0$ הוא:

\[\vec{F}_y = -k \left[ \frac{y}{\sqrt{a^2 + y^2}} \cdot 2\left(\sqrt{a^2 + y^2} - a\right) \right]\] \[\boxed{\vec{F}_y = -2k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left(\sqrt{a^2 + y^2} - a\right) \right]}\]

אפשר לראות שהכיוון של הכוח תלוי בסימן של $y$ ובניגוד לכיוון של הווקטור $\hat{\mathbf{y}}$:

אם $y > 0$, אז $\vec{F}_y < 0$ (כוח כלפי מטה).
אם $y < 0$, אז $\vec{F}_y > 0$ (כוח כלפי מעלה).

כלומר, הקפיץ ״רוצה״ לחזור את המערכת למצב שיווי המשקל, שבו $y=0$.

תודה למתרגל על טיוטת הפתרון הבהירה.

תרגול מיום 26 ביוני 2025.

מהירות בריחה

אנרגיית הכבידה הפועלת בין שני גופים מחוץ לכדור הארץ היא:
\[\phi(r) = -\frac{G M m}{r}\]
כאשר $r$ הוא המרחק בין הגופים, $m$ מסת הגוף הנמשך, $M$ מסת הגוף המושך ו- $G=6.67\tfrac{\mathrm{m}^3}{\mathrm{s}^2 \cdot \mathrm{kg}}$ הוא קבוע הכבידה.

מה הסיבה לסימן השלילי? כיצד הוא מבטא את העובדה שכוח הכבידה הוא כוח משיכה?

הראו שכוח הכבידה הנגזר מאנרגיה זו הוא:
\[\mathbf{F}(r) = -\frac{G M m}{r^2} \hat{\mathbf{r}}\]

הראו שסמוך לפני כדור הארץ, כוח הכבידה הוא בקירוב:
\[\mathbf{F} \approx -mg \hat{\mathbf{r}}\]
כאשר $R_E \approx 6400 \, \mathrm{km}$ הוא רדיוס כדור הארץ, $M_E \approx 6 \times 10^{24} \, \mathrm{kg}$ היא מסת כדור הארץ, ו-$g \approx 10 \, \mathrm{m/s^2}$.

מצאו את השינוי באנרגיה הדרוש להעביר גוף מפני כדור הארץ למרחק אינסופי ממנו. מהי מהירות המילוט מפני כדור הארץ?

ציירו גרף של האנרגיה הפוטנציאלית כתלות במרחק $r$. מה מייצגת בגרף האנרגיה הקינטית המינימלית הדרושה לגוף כדי להימלט מכוח המשיכה של הפלנטה?

סעיף 1 - הסיבה לסימן השלילי

אינטואיטיבית, כדי להרחיק 2 גופים מסיביים נדרשת עבודה חיובית.

הסבר מקלוד:

הסימן השלילי באנרגיה הפוטנציאלית $\phi(r) = -\frac{GMm}{r}$ משקף את העובדה שכוח הכבידה הוא כוח משיכה:

הסבר פיזיקלי:

אנרגיה פוטנציאלית מוגדרת כך ש-$U(\infty) = 0$ (נקודת ייחוס)

כאשר מקרבים שני גופים מאינסוף, כוח הכבידה עושה עבודה חיובית

לפי משפט העבודה-אנרגיה: $W_{gravity} = -\Delta U > 0$

לכן $U(r) - U(\infty) < 0$, כלומר $U(r) < 0$

הסבר מתמטי נוסף (מהתרגול):

דרך נוספת לראות את זה היא מהגדרת העבודה כאינטגרל:

\[W_{r_0 \to \infty} = \int_{r_0}^{\infty} \mathbf{F}_{\text{ext}} \cdot d\mathbf{r} = -\int_{r_0}^{\infty} \mathbf{F}_g \cdot d\mathbf{r} = -\int_{r_0}^{\infty} \left(-\frac{G M m}{r^2}\right) dr\] \[= \Delta U = U(\infty) - U(r_0) = 0 - \left(-\frac{G M m}{r_0}\right) = \frac{G M m}{r_0} > 0\]

סעיף 2 - גזירת כוח הכבידה

נדרש להראות שכוח הכבידה הוא

\[\mathbf{F} = -\frac{G M m}{r^2} \hat{\mathbf{r}}\]

הכוח נגזר מהאנרגיה הפוטנציאלית: $\mathbf{F} = -\nabla U$. במקרה של סימטריה כדורית, כאשר $U$ תלוי רק ב-$r$:

\[\mathbf{F}(r) = -\frac{dU}{dr}\hat{\mathbf{r}} = -\frac{d}{dr}\left(-\frac{G M m}{r}\right)\hat{\mathbf{r}} = - \left(G M m \cdot \left(-\frac{1}{r^2}\right)\right)\hat{\mathbf{r}} = -\frac{G M m}{r^2}\hat{\mathbf{r}}\]

פעולה מ-$\phi$ ל-$\mathbf{F}$ היא הגרדינט של $\phi$:
\[\mathbf{F} = -\nabla U = -\left(\frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z}\right)\]
בשאלה הזאת היה ניתן גם לסמן $\phi = U(r)$, ואז $\mathbf{F} = -\nabla \phi$.

סעיף 3 - כוח הכבידה סמוך לפני כדור הארץ

גודל הכוח הוא:

\[|\mathbf{F}\vert = \frac{G M m}{r^2}\]

סמוך לפני כדור הארץ ($r=R_E$), גודל הכוח הוא:

\[|\mathbf{F}\vert = \frac{G M_E m}{R_E^2}\]

אנו מגדירים את תאוצת הכובד $g$ כ-$g = \frac{G M_E}{R_E^2}$. לכן, $\vert \mathbf{F}\vert = mg$.

נציב ערכים:

$g = \frac{(6.674 \times 10^{-11})(6 \times 10^{24})}{(6.4 \times 10^6)^2} \approx 9.8 \, \mathrm{m/s^2}$.

לכן, סמוך לפני כדור הארץ:

\[\mathbf{F} = -mg \hat{\mathbf{r}}\]

(כיוון הכוח לכיוון מרכז כדור הארץ)

סעיף 4 - השינוי באנרגיה ומהירות המילוט

סעיף 4 - מציאת השינוי באנרגיה ומהירות המילוט.

השינוי באנרגיה הפוטנציאלית להעברת גוף מפני כדור הארץ ($r=R_E$) לאינסוף ($r \to \infty$):

\[\Delta U = U(\infty) - U(R_E) = 0 - \left(-\frac{G M_E m}{R_E}\right) = \frac{G M_E m}{R_E}\]

כדי שהגוף יגיע לאינסוף עם מהירות אפס (התנאי המינימלי למילוט), האנרגיה הקינטית ההתחלתית שלו צריכה להיות שווה בדיוק לשינוי באנרגיה הפוטנציאלית.

לפי שימור אנרגיה: $E_k + U = 0$.

\[\frac{1}{2}mv_{\text{esc}}^2 - \frac{G M_E m}{R_E} = 0 \implies \frac{1}{2}mv_{\text{esc}}^2 = \frac{G M_E m}{R_E}\] \[v_{\text{esc}} = \sqrt{\frac{2G M_E}{R_E}}\]

מאחר ש-$g = \frac{G M_E}{R_E^2}$, נוכל לכתוב $G M_E = g R_E^2$. נציב זאת:

\[v_{\text{esc}} = \sqrt{\frac{2(gR_E^2)}{R_E}} = \sqrt{2gR_E} \approx \sqrt{2 \cdot 9.8 \cdot 6.4 \times 10^6} \approx 11.2 \times 10^3 \, \mathrm{m/s} \approx 11.2 \, \mathrm{km/s}\]

סעיף 5 - גרף האנרגיה הפוטנציאלית

alt text

העקומה הכחולה מייצגת את האנרגיה הפוטנציאלית $U(r) = -\frac{GMm}{r}$
- היא שלילית לכל $r$ סופי
- שואפת ל-0 כאשר $r \to \infty$
- הערך המינימלי הוא ב-$r = R_E$
הקו האדום ($E = 0$) מייצג את האנרגיה הכוללת המינימלית למילוט
- תנאי המילוט: $E_{total} = K + U \geq 0$
- במקרה הגבולי: $E_{total} = 0$
החץ הירוק מייצג את האנרגיה הקינטית המינימלית הדרושה למילוט:
\[K_{min} = -U(R_E) = \frac{GMm}{R_E} = \frac{1}{2}mv_{esc}^2\]

משמעות פיזיקלית:

אם $E_{total} < 0$: הגוף חסום במסלול סגור (אליפסה)
אם $E_{total} = 0$: הגוף בדיוק מסוגל להימלט (מסלול פרבולי)
אם $E_{total} > 0$: הגוף נמלט עם מהירות עודפת (מסלול היפרבולי)

סיכום התוצאות

גודל	ערך
תאוצת הכובד	$g = 9.8 \, \mathrm{m/s^2}$
מהירות המילוט	$v_{esc} = 11.2 \, \mathrm{km/s}$
אנרגיה נדרשת למילוט	$\Delta U = \frac{GMm}{R_E}$

שאלה 2 - חישוב עבודה

נתון גרף של כוח (בניוטון) הפועל בכיוון $x$ על גוף, כתלות במיקום הגוף $x$ (במטרים). הגוף נע מ-$x=1 \, \mathrm{m}$ ל-$x=2 \, \mathrm{m}$.

העריכו את העבודה שנעשתה על הגוף.

alt text

העבודה שנעשית על ידי כוח משתנה לאורך מסלול ישר היא השטח שמתחת לגרף הכוח כפונקציה של המיקום.

\[W = \int_{x_0}^{x_1} F(x) \, dx\]

כדי להעריך את העבודה, יש לחשב את השטח מתחת לעקומת הגרף בין $x=1$ ל-$x=2$.

שאלה 3 - שימוש במשפט עבודה אנרגיה

כדור בעל מסה $m$ מחליק על מסילה חלקה המתוארת באיור, למעט קטע באורך $L$ עם מקדם חיכוך קינטי $\mu_k$. בסוף המסילה ישנו קפיץ בעל קבוע $k$. הכדור מתחיל ממנוחה בנקודה השמאלית ביותר, בגובה $H$.

מהי המהירות ההתחלתית המינימלית שיש להקנות לכדור כדי שיגיע למישור המחוספס?

עבור הנתונים הקודמים, בכמה הקפיץ מתכווץ? אם ההתנגשות היא אלסטית (משמרת אנרגיה), הנח שהכדור פוגע נע ביחד עם הקפיץ עד קצה הכיווץ.

האם האנרגיה נשמרת במקרה בו הכדור מתגלגל ולא מחליק על המשטח על החיכוך? נמק.
  Ball            Peak
  starts here     (3H/2)
                   ∧
    ●            /   \
   ┌─┐         /      \    Friction
 H |  \______/          \  μ_k, L   Spring
  _|_____________________[========] ╲╱╲╱╲╱│

סעיף 1: המהירות ההתחלתית המינימלית

כדי למצוא את המהירות המינימלית, נשתמש בשימור אנרגיה מכנית. הכדור צריך להגיע לפחות לנקודה הגבוהה ביותר במסילה כדי להמשיך הלאה.

נסמן את המהירות ההתחלתית ב-$v_0$. האנרגיה הכוללת בהתחלה היא:

\[E_{i} = \frac{1}{2}mv_0^2 + mgH\]

בנקודה הגבוהה ביותר, המהירות המינימלית היא אפס (תנאי קריטי), לכן:

\[E_{\text{peak}} = mg \cdot \frac{3H}{2}\]

משימור אנרגיה:

\[\frac{1}{2}mv_0^2 + mgH = mg \cdot \frac{3H}{2}\]

נפתור עבור $v_0$:

\[\begin{aligned} \frac{1}{2}mv_0^2 &= mg \cdot \frac{3H}{2} - mgH \\[10pt] &= \frac{mgH}{2} \\[10pt] v_0^2 &= gH \\[10pt] &\implies \boxed{v_0 = \sqrt{gH}} \end{aligned}\]

סעיף 2: כיווץ הקפיץ

נחשב את כיווץ הקפיץ. הכדור מתחיל עם המהירות שמצאנו ועובר את כל המסלול.

שלב א’: מהירות הכדור לפני אזור החיכוך

כשהכדור מגיע לאזור החיכוך (בגובה 0), נשתמש בשימור אנרגיה:

\[\frac{1}{2}mv_0^2 + mgH = \frac{1}{2}mv_1^2\]

כאשר $v_1$ היא המהירות בכניסה לאזור החיכוך.

\[\begin{aligned} \frac{1}{2}m(gH) + mgH &= \frac{1}{2}mv_1^2 \\[10pt] \frac{3}{2}mgH &= \frac{1}{2}mv_1^2 \\[10pt] 3gH &= v_1^2 \\[10pt] v_1 &= \boxed{\sqrt{3gH}} \end{aligned}\]

שלב ב’: אובדן אנרגיה עקב חיכוך

העבודה שעושה כוח החיכוך היא:

\[W_{\text{friction}} = -\mu_k mg L\]

הסימן השלילי מציין שהחיכוך מתנגד לתנועה.

שלב ג’: מהירות הכדור כשהוא פוגע בקפיץ

נשתמש במשפט עבודה-אנרגיה $\text{II}$:

\[W_{\text{NC}} = \Delta E_{\text{tot}}\] \[\begin{aligned} W_{\text{friction}} &= \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 \\[10pt] \frac{1}{2}mv_2^2 &= \frac{1}{2}m(3gH) - \mu_k mg L \\[10pt] v_2^2 &= 3gH - 2\mu_k g L \\[10pt] v_2 &= \boxed{\sqrt{3gH - 2\mu_k g L}} \end{aligned}\]

שלב ד’: כיווץ הקפיץ

כשהכדור פוגע בקפיץ ונע איתו, כל האנרגיה הקינטית הופכת לאנרגיה פוטנציאלית אלסטית:

\[\frac{1}{2}mv_2^2 = \frac{1}{2}kx^2\]

כאשר $x$ הוא כיווץ הקפיץ.

\[x^2 = \frac{m}{k}v_2^2 = \frac{m}{k}(3gH - 2\mu_k g L)\] \[\boxed{x = \sqrt{\frac{m}{k}(3gH - 2\mu_k g L)}}\]

הפתרון תקף רק אם $3gH > 2\mu_k g L$, אחרת הכדור לא יגיע לקפיץ.

סעיף 3: שימור אנרגיה בגלגול ללא החלקה

הערה: השאלה לא ברורה לי, ונראה שלא הייתה ברורה גם לחברים בכתה. מתי למשל כדור מחליק ומתי הוא מתגלגל?

לפי פתרון המתרגל הנוסף, במקרה של גלגל גלגול (גלגל ללא החלקה) - חיכוך סטטי לא תורם עבודה, ולכן יש שימור אנרגיה.

החלקה - חיכוך קינטי (אבל להבנתי המרצה לא הדגיש את ההבדלים בין חיכוך קינטי לחיכוך סטטי).

עגלה ותיבה - מע׳ רב גופית

תיבה שמסתה $m$ מונחת על עגלה שמסתה $M$ היכולה לנוע ללא חיכוך על משטח אופקי (ראו איור). מעניקים לתיבה מהירות התחלתיחת $v=v_0$.

מה הגובה המינימלי $h_{\text{min}}$ של העגלה שימנע את מעבר התיבה לצידה השני?

אם גובה העגלה גדול מ-$h_{\text{min}}$, שחושב בסעיף א, מהן מהירויות העגלה והתיבה כאשר התיבה חוזרת לתחתית העגלה?

נתון: $M = 10 \, \mathrm{kg}$, $m = 1 \, \mathrm{kg}$, $v_0 = 5 \, \mathrm{m/s}$.
             ╭───┐
  v₀ →      ╱    | ↑
   ■      ╱      | h
  ┌──────╯       | ↓
  ╰─●──────────●─╯
──────────────────────

הערה מקדימה: רוב הפיתרון שלהלן נכתב בעזרת LLM, קחו אותו בערבון מוגבל.

נתונים

$m = 1 \, \text{kg}$ (מסת התיבה)
$M = 10 \, \text{kg}$ (מסת העגלה)
$v_0 = 5 \, \text{m/s}$ (מהירות התחלתית של התיבה)
$g \approx 10 \, \text{m/s}^2$ (תאוצת הכבידה)
העגלה נעה ללא חיכוך על משטח אופקי

חלק א’: הגובה המינימלי $h_{\text{min}}$

הרעיון הפיזיקלי

התיבה “מטפסת” על העגלה בזמן שהעגלה מאיצה. הגובה המינימלי הוא הגובה שבו התיבה תעצור בדיוק בראש העגלה ולא תמשיך לצדה השני. ברגע זה, מהירות התיבה והעגלה זהות (אין תנועה יחסית ביניהן).

שלב 1: מציאת המהירות המשותפת באמצעות שימור תנע

מושג - שימור תנע: במערכת סגורה (ללא כוחות חיצוניים), התנע הכולל נשמר.

תנע התחלתי:

התיבה: $p_{m} = mv_0 = 1 \times 5 = 5 \, \text{kg⋅m/s}$
העגלה: $p_{M} = M \times 0 = 0$
תנע כולל: $p_{i} = 5 \, \text{kg⋅m/s}$

תנע סופי (כאשר שתיהן נעות במהירות זהה $v$):

\[p_{f} = (m + M)v = 11v\]

מעקרון שימור התנע:

\[5 = 11v\] \[v = \frac{5}{11} \approx 0.45 \, \text{m/s}\]

זוהי המהירות המשותפת של שני הגופים ברגע שהתיבה מגיעה לגובה המקסימלי.

שלב 2: מציאת הגובה באמצעות שימור אנרגיה

מושג - שימור אנרגיה: האנרגיה הכוללת במערכת נשמרת (קינטית + פוטנציאלית).

אנרגיה התחלתית:

\[E_{i} = \frac{1}{2}mv_0^2 = \frac{1}{2} \times 1 \times 5^2 = 12.5 \, \text{J}\]

אנרגיה סופית:

אנרגיה קינטית של שני הגופים: $\frac{1}{2}(m + M)v^2$
אנרגיה פוטנציאלית של התיבה: $mgh_{\text{min}}$

\[E_{\text{f}} = \frac{1}{2} \times 11 \times \left(\frac{5}{11}\right)^2 + 1 \times 10 \times h_{\text{min}}\] \[E_{\text{f}} = \frac{1}{2} \times 11 \times \frac{25}{121} + 10h_{\text{min}} = \frac{25}{22} + 10h_{\text{min}}\]

מעקרון שימור אנרגיה:

\[12.5 = \frac{25}{22} + 10h_{\text{min}}\] \[10h_{\text{min}} = 12.5 - \frac{25}{22} = \frac{275 - 25}{22} = \frac{250}{22}\] \[h_{\text{min}} = \frac{250}{220} = \frac{25}{22} \approx 1.14 \, \text{m}\]

נוסחה כללית

\[h_{\text{min}} = \frac{v_0^2 M}{2g(m + M)}\]

חלק ב’: מהירויות כאשר התיבה חוזרת לתחתית

הרעיון הפיזיקלי

כאשר גובה העגלה גדול מ-$h_{\text{min}}$, התיבה “מגלשת” חזרה למטה. המצב דומה להתנגשות אלסטית - האנרגיה הפוטנציאלית הרוכשת התיבה בגובה מתמירה חזרה לאנרגיה קינטית.

מערכת המשוואות

שימור תנע אופקי:

\[mv_0 = mv_m + Mv_M\] \[5 = v_m + 10v_M \quad \text{...(1)}\]

שימור אנרגיה (האנרגיה הפוטנציאלית = 0 בתחתית):

\[\frac{1}{2}mv_0^2 = \frac{1}{2}mv_m^2 + \frac{1}{2}Mv_M^2\] \[25 = v_m^2 + 10v_M^2 \quad \text{...(2)}\]

פתרון המערכת

מהמשוואה (1):

\[v_m = 5 - 10v_M\]

נציב במשוואה (2):

\[25 = (5 - 10v_M)^2 + 10v_M^2\] \[25 = 25 - 100v_M + 100v_M^2 + 10v_M^2\] \[0 = 110v_M^2 - 100v_M\] \[0 = v_M(110v_M - 100)\]

הפתרונות:

$v_M = 0$ (מצב התחלתי)
$v_M = \frac{100}{110} = \frac{10}{11} \approx 0.91 \, \text{m/s}$

מהירות העגלה הסופית:

\[v_M = \frac{10}{11} \approx 0.91 \, \text{m/s}\]

מהירות התיבה הסופית:

\[v_m = 5 - 10 \times \frac{10}{11} = 5 - \frac{100}{11} = \frac{55 - 100}{11} = -\frac{45}{11} \approx -4.09 \, \text{m/s}\]

משמעות התוצאות

מהירות התיבה שלילית - התיבה נעה בכיוון הנגדי למהירות ההתחלתית
מהירות העגלה חיובית - העגלה נעה באותו כיוון של המהירות ההתחלתית של התיבה
סכום המהירויות המשוקללות שומר על התנע הכולל: $1 \times (-4.09) + 10 \times 0.91 = 5$

תשובות סופיות

א) הגובה המינימלי

\[\boxed{h_{\text{min}} = 1.14 \, \text{m}}\]

ב) מהירויות כאשר התיבה חוזרת לתחתית

מהירות התיבה: $\boxed{v_m = -4.09 \, \text{m/s}}$ (לאחור)
מהירות העגלה: $\boxed{v_M = 0.91 \, \text{m/s}}$ (קדימה)

בדיקת תוצאות

שימור תנע: $1 \times (-4.09) + 10 \times 0.91 = 5.01 \approx 5$ ✓
שימור אנרגיה: $\frac{1}{2} \times 1 \times 4.09^2 + \frac{1}{2} \times 10 \times 0.91^2 = 12.5$ ✓

הצעת פתרון - בחינת גמר מועד ב׳ 2024

תאריך: 13/07/2025

מבחן פיזיקה א’ - מועד ב תשפ”ד

שאלה 1: קבועי תנועה

בהינתן ההגדרה הבאה:

״קבוע של התנועה הוא גודל כלשהו המאפיין את המערכת הפיזיקלית, אשר אינו משתנה בזמן למרות שמאפיינים אחרים של המערכת – המופיעים בתוך הקבוע - כן עשויים להשתנות בזמן.״

איזה מהטענות הבאות היא מדויקת?

אם האנרגיה המכנית של גוף היא קבוע של התנועה, הרי שגזירתה לפי הזמן מנפקת את משוואות התנועה של הגוף.

אם התנע הזוויתי הוא קבוע של התנועה, הרי ששקול המומנטים במערכת שונה מאפס.

אם האנרגיה הקינטית היא קבוע של התנועה, הרי שבהכרח אין כוחות משמרים במערכת.

אם האנרגיה המכנית היא קבוע של התנועה, הרי שעבודת הכוחות הלא משמרים בהכרח שונה מאפס.

נעבור על כל אחת מהטענות ונבדוק את נכונותה:

טענה א: זו הטענה הנכונה! כאשר האנרגיה המכנית $E$ היא קבוע של התנועה, אז:

\[\frac{dE}{dt} = 0\]

אם נרשום את האנרגיה המכנית:

\[E = \frac{1}{2}m\dot{x}^2 + V(x)\]

ונגזור לפי הזמן:

\[\frac{dE}{dt} = m\dot{x}\ddot{x} + \frac{dV}{dx}\dot{x} = \dot{x}\left(m\ddot{x} + \frac{dV}{dx}\right) = 0\]

מכאן (בהנחה ש-$\dot{x} \neq 0$):

\[m\ddot{x} = -\frac{dV}{dx} = F\]

וזו בדיוק משוואת התנועה של ניוטון!

טענה ב: שגויה. אם התנע הזוויתי $\vec{L}$ הוא קבוע של התנועה, אז:

\[\frac{d\vec{L}}{dt} = \vec{\tau} = 0\]

כלומר, שקול המומנטים חייב להיות אפס, לא שונה מאפס.

טענה ג: שגויה. אנרגיה קינטית קבועה פירושה שגודל המהירות קבוע, אבל זה יכול לקרות גם עם כוחות משמרים (למשל, תנועה מעגלית אחידה תחת כוח מרכזי).

טענה ד: שגויה. אם האנרגיה המכנית נשמרת, אז דווקא עבודת הכוחות הלא משמרים חייבת להיות אפס.

שאלה 2: מתקף

איזה מהטענות הבאות בנוגע למתקף לחלוטין אינה נכונה?

המתקף שמפעיל כוח חיצוני על גוף הוא הצטברות הכוח הפועל על הגוף לאורך הדרך שעשה הגוף במהלך תנועתו.

המתקף הפועל על גוף מבטא את השינוי בתנע של הגוף.

המתקף שמפעיל גוף A על גוף B בזמן אינטראקציה בניהם, שווה בגודלו והפוך בכיוונו למתקף שגוף B מפעיל על גוף A.

המתקף שמפעיל כוח חיצוני כלשהו על מערכת פיזיקלית מכמת את הצטברות הכוח על המערכת במשך כל זמן האינטראקציה בניהם.

המתקף (Impulse) מוגדר כ:

\[\vec{J} = \int_{t_1}^{t_2} \vec{F} dt\]

נבדוק כל טענה:

טענה א: שגויה! זו ההגדרה של עבודה, לא של מתקף. עבודה היא:

\[W = \int \vec{F} \cdot d\vec{r}\]

בעוד שמתקף הוא אינטגרל על זמן, לא על דרך.

טענה ב: נכונה. לפי משפט המתקף-תנע:

\[\vec{J} = \Delta\vec{p} = \vec{p}_f - \vec{p}_i\]

טענה ג: נכונה. לפי החוק השלישי של ניוטון,

\[\vec{F}_{AB} = -\vec{F}_{BA}\]

ולכן:

\[\vec{J}_{AB} = \int \vec{F}_{AB} dt = -\int \vec{F}_{BA} dt = -\vec{J}_{BA}\]

טענה ד: נכונה. זו בדיוק ההגדרה של מתקף - הצטברות הכוח לאורך זמן האינטראקציה.

שאלות 4-3: חבל על גג משופע

חבל מסיבי שאורכו הכולל הוא $L$ מחליק מגג בניין משופע כמוראה באיור.

הזניחו את החיכוך של החבל עם הבניין.
|\ \
| \ \
| θ\ \
|---\ \
    |↑ |
    |x |
    |↓ |
    |
שאלה 3: משוואת התנועה

יהא $x(t)$ החלק המשתלשל מהגג בכל זמן $t$. אזי, המשוואה הדיפרנציאלית המתארת את תנועת החבל היא:

נגדיר את המערכת:

אורך כולל של החבל: $L$
חלק משתלשל: $x$
חלק על הגג המשופע: $L-x$
זווית השיפוע: $\theta$
צפיפות ליניארית של החבל: $\lambda = m/L$

כוחות הפועלים על החבל:

על החלק המשתלשל ($x$): משקל כלפי מטה $\lambda x g$
על החלק שעל הגג ($L-x$): רכיב המשקל במורד השיפוע $\lambda(L-x)g\sin\theta$

משוואת ניוטון עבור כל החבל:

\[ma = \lambda L \ddot{x} = \lambda x g + \lambda(L-x)g\sin\theta\]

נחלק ב-$\lambda L$:

\[\ddot{x} = \frac{g}{L}x(1-\sin\theta) + g\sin\theta\]

שאלה 4: ביטוי המהירות

ידוע כי $\theta = \pi/6$ רדיאנים.

ידועים גם תנאי ההתחלה $x(t=0) = b$, $\dot{x}(t=0) = 0$.

בתנאים אלו גזירת הפתרון של משוואת התנועה מובילה אל המהירות כפונקציה של הזמן:
\[v(t) = (b + L)\omega \sinh(\omega t)\]
באשר $\omega = \sqrt{g/2L}$.

תהא $a(t)$ תאוצת החבל בכל זמן $t$.

הביטוי $a^2 - \omega^2 v^2$ הוא:

נתון ש-$\theta = \pi/6$, לכן $\sin\theta = 1/2$.

המשוואה הדיפרנציאלית הופכת ל:

\[\ddot{x} = \frac{g}{L}x(1-1/2) + g/2 = \frac{g}{2L}x + \frac{g}{2}\]

נבדוק את הביטוי $a^2 - \omega^2 v^2$:

מהמהירות הנתונה:

\[v = (b+L)\omega\sinh(\omega t)\]

התאוצה:

\[a = \frac{dv}{dt} = (b+L)\omega^2\cosh(\omega t)\]

נחשב את $a^2 - \omega^2 v^2$:

\[a^2 = ((b+L)\omega^2\cosh(\omega t))^2 = (b+L)^2\omega^4\cosh^2(\omega t)\] \[v^2 = ((b+L)\omega\sinh(\omega t))^2 = (b+L)^2\omega^2\sinh^2(\omega t)\] \[a^2 - \omega^2 v^2 = (b+L)^2\omega^4\cosh^2(\omega t) - (b+L)^2\omega^2\sinh^2(\omega t)\] \[= (b+L)^2\omega^2(\omega^2\cosh^2(\omega t) - \sinh^2(\omega t))\]

נשתמש בזהות $\cosh^2(x) - \sinh^2(x) = 1$:

\[= (b+L)^2\omega^2\]

מכאן שהביטוי $a^2 - \omega^2 v^2$ הוא קבוע בזמן, תלוי רק בפרמטרים של המערכת.

שאלות 7-5: חרוז על קשת מעגלית

חרוז שמסתו $m$ מחליק ע”ג קשת מעגלית נטולת חיכוך כמוראה בתרשים, כך שהקואורדינטה המתארת את מיקומו כפונקציה של הזמן באופן “הכי טבעי” היא $\theta(t)$.

שאלה 5: האנרגיה המכנית

האנרגיה המכנית של החרוז בהתייחס לתחתית הקשת המעגלית ($y=0$) מקיימת:

במערכת קואורדינטות פולריות עבור תנועה על מעגל ברדיוס $R$:

מיקום: $r = R$ (קבוע), $\theta = \theta(t)$
מהירות: $v = R\dot{\theta}$

אנרגיה קינטית:

\[E_k = \frac{1}{2}mv^2 = \frac{1}{2}mR^2\dot{\theta}^2\]

אנרגיה פוטנציאלית:

הגובה של החרוז מעל נקודת הייחוס (תחתית הקשת):

\[h = R - R\cos\theta = R(1 - \cos\theta)\]

לכן:

\[\phi = mgh = mgR(1 - \cos\theta)\]

אבל בנתוני השאלה בחרו את מישור הייחוס להיות כלפי $y=0$ חיובי כלפי מטה, לכן:

\[\phi = -mgR(1 - \cos\theta)\]

האנרגיה המכנית הכוללת:

\[E = E_k + \phi = \frac{1}{2}mR^2\dot{\theta}^2 - mgR(1 - \cos\theta)\]

שאלה 6: מהירות במערכת צופה

צופה נמצא בתנועה בליסטית כך שמשוואות התנועה שלו הן
\[x = v_0t, \quad y(t) = \frac{1}{2}gt^2\]
הניחו עתה את ראשית הצירים על מרכז הקשת המעגלית.

וקטור המהירות של החרוז במערכת המנוחה של הצופה הוא:

מהירות החרוז במערכת המעבדה:

רכיב x: $v_{x,\text{bead}} = -R\sin\theta \cdot \dot{\theta}$
רכיב y: $v_{y,\text{bead}} = R\cos\theta \cdot \dot{\theta}$

מהירות הצופה:

$v_{x,\text{man}} = v_0$
$v_{y,\text{man}} = gt$

מהירות יחסית:

\[\vec{v}_{\text{bead→man}} = \vec{v}_{\text{bead}} - \vec{v}_{\text{man}}\] \[= (-R\dot{\theta}\sin\theta - v_0)\hat{x} + (R\dot{\theta}\cos\theta - gt)\hat{y}\]

(שאלה 7 כנראה לא בחומר)

שאלות 9-8: כוחות על כדור הארץ המסתובב

שאלה 8: משקל בקו המשווה

משקלו של אדם הנמצא בגובה פני הים בקו המשווה הוא:

בקו המשווה, הכוח הצנטריפוגלי פועל כלפי חוץ (הפוך לכוח הכבידה).

הכוח הצנטריפוגלי:

\[F_{\text{centripetal}} = m\omega^2R_E\]

המשקל האפקטיבי (מה שמודד המשקל):

\[W = mg - m\omega^2R_E\]

שאלה 9: כוח קוריוליס בנפילה חופשית

אדם נמצא בנפילה חופשית בקו המשווה. כוח קוריוליס הפועל עליו ניתן ע”י:

כוח קוריוליס נתון על ידי:

\[\vec{F}_c = -2m(\vec{\omega} \times \vec{v})\]

המהירות של כדור הארץ סביב צירו היא:

\[\vec{\omega} = \omega\hat{z} \quad \text{north pole up}\]

המהירות של אדם בנפילה חופשית היא:

\[\vec{v} = v_x\hat{x} + v_y\hat{y}\]

מכאן:

\[\vec{F}_c = -2m\omega(v_x\hat{y} - v_y\hat{x}) = 2m(\omega v_y\hat{x} - \omega v_x\hat{y})\]

שאלות 11-10: התנגשות כדור ובול עץ

שאלה 10: המתקף על הבול

בול עץ שמסתו היא $M$ מונח על שולחן אופקי חלק. הבול מחובר לקפיץ אשר מקדם הכוח שלו הוא $k$, כמורה באיור.

כדור קטן שמסתו היא $m$ נורה אופקית לעבר הבול, ומהירותו לפני הפגיעה בבול היא $v_0$.

הכדור חוזר את הבול ויוצא מצידו השני במהירות $v_0 / 3$ מבלי לפגוע בקפיץ.

נניח שהשינוי במסה הבול כתוצאה ממעבר הכדור דרכו, זניח.

לאחר מעבר הכדור דרכו, הבול המחובר לקפיץ מבצע תנודות הרמוניות.

וקטור המתקף שפעל על הבול במהלך מעבר הכדור דרכו הוא:

שימור תנע לכדור:

תנע התחלתי: $p_i = mv_0$
תנע סופי: $p_f = m(v_0/3)$
שינוי תנע הכדור: $\Delta p_{\text{bullet}} = -2mv_0/3$

מתקף על הבול:

לפי החוק השלישי של ניוטון:

\[\vec{J}_{\text{tree}} = -\vec{J}_{\text{bullet}} = \frac{2mv_0}{3}\hat{x}\]

המתקף אינו תלוי בהתכווצות הקפיץ כי זמן ההתנגשות קצר מאוד.

שאלה 11: תנועת הבול אחרי ההתנגשות

פונקציית מקום-זמן של הבול לאחר ההתנגשות:

מהמתקף, מהירות הבול מיד אחרי ההתנגשות:

\[Mv_{\text{tree}} = \frac{2mv_0}{3}\] \[v_{\text{tree}} = \frac{2mv_0}{3M}\]

הבול מבצע תנועה הרמונית פשוטה עם:

תדירות זוויתית: $\omega = \sqrt{k/M}$
משרעת: $A = v_{\text{tree}}/\omega = \frac{2mv_0}{3\sqrt{Mk}}$

עם תנאי התחלה $x(0) = 0$, $\dot{x}(0) = v_{\text{tree}}$:

\[x(t) = A\sin(\omega t) = \frac{2mv_0}{3\sqrt{Mk}}\sin\left(\sqrt{\frac{k}{M}}t\right)\]

שאלות 14-12: תנועה בקואורדינטות פולריות

שאלה 12: הכוח מהפוטנציאל

גוף שמסתו $m$ נע בקואורדינטות פולריות תחת פוטנציאל:
\[\phi(r) = -\frac{\alpha}{r}\]
$\alpha$ הוא פרמטר חיובי.

אופרטור הגרדיאנט בקואורדינטות פולריות הוא:
\[\nabla = \hat{r}\frac{\partial}{\partial r} + \hat{\theta}\frac{1}{r}\frac{\partial}{\partial \theta}\]
(אין במערכת כוחות לא משמרים).

הכוח הנגזר מהאנרגיה הפוטנציאלית $\phi(r) = -\alpha/r$ הוא:

באמצעות הגרדיאנט בקואורדינטות פולריות:

\[\vec{F} = -\nabla\phi = -\hat{r}\frac{\partial\phi}{\partial r} - \hat{\theta}\frac{1}{r}\frac{\partial\phi}{\partial\theta}\]

מכיוון ש-$\phi$ תלוי רק ב-$r$:

\[\vec{F} = -\hat{r}\frac{\partial}{\partial r}\left(-\frac{\alpha}{r}\right) = -\hat{r}\frac{\alpha}{r^2}\]

לא בטוח מה התשובה הנכונה.

שאלה 13: האנרגיה המכנית

האנרגיה המכנית של הגוף נתונה בביטוי:

בקואורדינטות פולריות, האנרגיה הקינטית:

\[E_k = \frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2)\]

האנרגיה המכנית הכוללת:

\[E = E_k + \phi = \frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2) - \frac{\alpha}{r}\]

שאלה 14 להבנתי לא בחומר.

שחזור בחינת גמר בפיזיקה - מועד א׳ 2025

תאריך: 14/07/2025

הקדמה

להלן שחזור אפשרי ללא אחריות לבחינת הגמר שנערכה ביום 14 ביולי 2025 (מועד א׳). הבחינה לא הייתה קלה, לעניות דעתי, והתשובות שלהלן מובאות כניחוש בלבד.

אנא אל תפנו אלא לצורך סיוע ותרומה למאמץ. בפרט, שאלות בסגנון של ״מה הייתה השאלה המלאה בשאלה X?״ ״למה התכוונו בשאלה Y?״ ״למה שלא תעשו כך וכך?״ לא יענו.

בכל שאלה אישית או בקשה, נציע לכם לפנות לצוות ההוראה או לפעול בדרכים אחרות, ולעדכן במידע מסייע לאחר מעשה.

בהצלחה!

שאלה 1 - אינטגרציה כפולה

נוסח השאלה המקורי לא זכור לי. ככל הנראה היה חלקיק במסה $m=1$ שפועל עליו כוח וצריך לחשב את המיקום שלו.

הפתרון:

\[\frac{t^3}{6} \mathbf{\hat{x}} - \frac{t^2}{2} \mathbf{\hat{y}}\]

אינטגרציה כפולה. הייתה רק תשובה אחת שקיימה את הנדרש בציר $x$.

שאלה 2 - מסה מחוברת בקפיץ שמונחת עליה מסה קטנה

\[-k X - N \sin{\alpha}\]

שאלה 3 - חישוב מהירות יחסית

לא זוכר את הביטוי המדויק, בערך.

שאלה 4 - זוית תנודות מואצת

מהי $\omega$ של מטוטלת בתוך גוף שמאיץ לצד? השתמשו בקירובים לזוויות קטנות ביחס לזווית שיווי המשקל של המטוטלת.

התשובה הנכונה היא ככל הנראה:

\[\omega^2 = \frac{\sqrt{g^2 + a^2}}{R}\]

הערה חשובה: צוות ההוראה בקורס היה טוב, אבל בשאלה הזו הייתה לדעתי אי-בהירות שלא הובהרה מספיק בהרצאות - ההבחנה בין $g$ כגודל סקלרי לבין $\vec{g}$ כווקטור. כתבתי על חוסר ההבחנה הזה גם בסיכומים שלי לאורך הסמסטר.

במבחן, אחת האפשרויות הייתה:
\[\omega^2 = \frac{g + a}{R}\]
אפשרות זו בעייתית מכמה סיבות:

אם מפרשים אותה כחיבור וקטורי $\frac{\vec{g} + \vec{a}}{R}$, היא שגויה מתמטית (לא ניתן לחלק וקטור בסקלר ולקבל סקלר)

אם מפרשים אותה כחיבור סקלרי של גדלים, היא מתעלמת מכיווני הכוחות

עם זאת, לאורך הקורס לא הוקפד על ההבחנה הזאת:

בהרצאה מיום 22 במאי 2025 (קישור): המרצה פתר תרגיל זהה (מטוטלת במעלית) והתייחס ל-$g$ כגודל סקלרי, כאשר כתב $g_{\text{eff}} = g + a$ למקרה של תאוצה כלפי מעלה

בתרגולים (למשל בקובץ tuttorial7_physics_sol.pdf): לא הופיעה הבחנה ברורה בין $g$ סקלרי ל-$\vec{g}$ וקטורי

הסימון המקובל בקורס: השתמשו ב-$g\hat{z}$ או $g\vec{z}$ כדי לציין את וקטור התאוצה הכבידתית, מה שמרמז ש-$g$ עצמו הוא סקלר (הגודל)

הבעיה המתמטית: גם כאשר הכוחות פועלים באותו כיוון, הביטוי $\sqrt{(g+a)^2} = g+a$ נכון רק אם $g,a > 0$. במקרה הכללי:
\[|\vec{g} + \vec{a}| = \sqrt{|\vec{g}|^2 + |\vec{a}|^2 + 2\vec{g} \cdot \vec{a}}\]
מכיוון שהקונבנציה בקורס הייתה להשתמש ב-$g$ כגודל סקלרי ($\approx 10 \, \mathrm{m/s^2}$) ולא הונהג שימוש עקבי בסימונים $\vec{g}$ או $\mathbf{g}$, סביר להניח שסטודנטים רבים פירשו את התשובה כחיבור של גדלים אפקטיביים. לדעתי, יש מקום לשקול מתן ניקוד חלקי או מלא לסטודנטים שסימנו את התשובה הזאת בהתבסס על הפרשנות הסקלרית שהייתה מקובלת בקורס.

שאלה 6 - התנגשות אלסטית של שתי מסות

מסה $m_1$ במהירות $u$ מתקרבת למסה $m_2$ שנמצאת במנוחה. למסה $m_2$ מחובר קפיץ עם קבוע $k$, בכיוון שממנו מתקרבת המסה $m_1$.

המסה $m_1$ מתנגשת התנשות אלסטית בקפיץ שמחובר למסה $m_2$.

מה התכווצות הקפיץ $d$ המקסימלית? (רמז: מהירות יחסית של המסות).

ככל הנראה:

\[d = \sqrt{\frac{m_1 m_2}{k(m_1 + m_2)}} u\]

לא בטוח כלל וכלל.

שאלה 7 - באנג׳י

אדם עושה באנג’י.

מגדירים ב-z(t) את המרחק המתוח של חבל הבאנג’י (לאחר שקפץ).

כוח הגרר של האוויר מסומן:
\[F_{\text{drag}} = -b \dot{z}\]
משוואת התנועה היא:
\[z(t) = \frac{mg}{k} \left(1 - e^{-\alpha t}\right)\]
השאלה: איזו משוואה מקיים הפרמטר $\alpha$?

פתרון:

היה ניתן לפסול את רוב התשובות על סמך יחידות מידה בלבד.

משוואת הכוחות:

\[m\ddot{z} = mg - kz - b\dot{z}\]

מהפתרון הנתון:

$\dot{z} = \frac{mg\alpha}{k}e^{-\alpha t}$
$\ddot{z} = -\frac{mg\alpha^2}{k}e^{-\alpha t}$

הצבה במשוואת הכוחות:

\[m\left(-\frac{mg\alpha^2}{k}e^{-\alpha t}\right) = mg - k\left(\frac{mg}{k}(1 - e^{-\alpha t})\right) - b\left(\frac{mg\alpha}{k}e^{-\alpha t}\right)\]

פישוט:

\[-\frac{m^2g\alpha^2}{k}e^{-\alpha t} = mge^{-\alpha t} - \frac{bmg\alpha}{k}e^{-\alpha t}\]

חלוקה ב-$e^{-\alpha t}$:

\[-\frac{m^2g\alpha^2}{k} = mg - \frac{bmg\alpha}{k}\]

העברת אגפים:

\[\frac{m^2g\alpha^2}{k} - \frac{bmg\alpha}{k} - mg = 0\]

חלוקה ב-$mg$:

\[\boxed{\frac{m\alpha^2}{k} - \frac{b\alpha}{k} - 1 = 0}\]

בכל מקרה הביטוי המקובל לאלפא הוא בדיעבד:
\[m\alpha^2 - b\alpha - k = 0\]
טעיתי בשאלה הזאת בגלל חוסר תשומת לב. סימנתי אותה ושיניתי כיוון שהצבה של $\alpha \to 0$ גרמה לי לחשוב שמדובר בסתירה: $-1\ne 0$.

שאלה 8 - זמן לנפילה של גולה

\[t=\frac{\cosh^{-1}\left(2\right)}{\omega}\]

הפתרון זמין בסיכום שיעור התגבור.

למי שמתעצלים לחפש:

ניסוח הבעיה

גליל אופקי באורך $L$ מסתובב נגד כיוון השעון במהירות זוויתית קבועה $\omega$. מסה $m$ מתחילה במרכז הגליל (במיקום $r = L/2$) ממצב מנוחה, ונעה תחת השפעת הכוח הצנטריפוגלי בלבד.

נתונים:

תנאי התחלה:

$r(t=0) = \frac{L}{2}$ (מיקום התחלתי במרכז הגליל)

$\dot{r}(t=0) = 0$ (מהירות רדיאלי התחלתי אפס - ממנוחה)

הפרמטרים של המערכת:

$\omega$ = מהירות זוויתית קבועה של הגליל

$L$ = אורך הגליל

$m$ = מסת הגוף

מטרה: למצוא את התנועה $r(t)$ של המסה והזמן ($t$) שבו היא מגיעה לקצה הגליל ($r = L$).

שלב 1: יישום חוק ניוטון השני במערכת ייחוס מסתובבת

במערכת ייחוס מסתובבת עם מהירות זוויתית קבועה $\omega$, הכוח הצנטריפוגלי פועל על מסה הנמצאת במרחק $r$ מהמרכז:

\[\mathbf{F}_{\text{centrifugal}} = m\omega^2 r\]

הכוח מכוון החוצה ברכיב הרדיאלי $\hat{r}$.

שלב 2: משוואת התנועה

יישום החוק השני של ניוטון בכיוון הרדיאלי:

\[m\ddot{r} = m\omega^2 r\]

המסה מצטמצמת:

\[\ddot{r} = \omega^2 r \tag{1}\]

שלב 3: פתרון המשוואה הדיפרנציאלית

משוואה (1) היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני עם מקדמים קבועים.

המשוואה האופיינית:

\[\lambda^2 = \omega^2\]

הפתרונות: $\lambda = \pm\omega$

הפתרון הכללי:

\[r(t) = A e^{\omega t} + B e^{-\omega t}\]

או בצורה היפרבולית שקולה:

\[r(t) = C \cosh(\omega t) + D \sinh(\omega t) \tag{2}\]

שלב 4: יישום תנאי התחלה

תנאי התחלה:

$r(0) = \frac{L}{2}$
$\dot{r}(0) = 0$

מהתנאי הראשון:

\[r(0) = C = \frac{L}{2}\]

לכן:

\[r(t) = \frac{L}{2} \cosh(\omega t) + D \sinh(\omega t)\]

מהתנאי השני:

\[\dot{r}(t) = \frac{L}{2} \omega \sinh(\omega t) + D \omega \cosh(\omega t)\] \[\dot{r}(0) = D \omega = 0\]

לכן: $D = 0$

שלב 5: הפתרון הסופי

\[r(t) = \frac{L}{2} \cosh(\omega t) \tag{3}\] \[\dot{r}(t) = \frac{L \omega}{2} \sinh(\omega t) \tag{4}\] \[\ddot{r}(t) = \frac{L \omega^2}{2} \cosh(\omega t) \tag{5}\]

שלב 6: חישוב זמן ההגעה לקצה הגליל

המסה מגיעה לקצה הגליל כאשר $r(t) = L$:

\[L = \frac{L}{2} \cosh(\omega t)\] \[2 = \cosh(\omega t)\] \[\omega t = \cosh^{-1}(2)\] \[\boxed{t = \frac{\cosh^{-1}(2)}{\omega}}\]

הערה: טעיתי ובחרתי באפשרות של $t = \frac{\sinh^{-1}(2)}{\omega}$ מחוסר תשומת לב.

נתראה במועד הבא, בהצלחה!

דור פסקל

13 ביולי 2025

חזור לעמוד הראשי

סמסטר א

כימיה כללית ופיזיקלית

מתמטיקה

בריאות האוכלוסייה

חשיפה רפואית

מבוא לשפת פייתון

יהדות

סמסטר ב

פיזיקה

כימיה אורגנית

ביולוגיה של התא

סטטיסטיקה לרפואנים

תורת האדם

כלים שימושיים

כלים שימושיים

כל התרגולים בעמוד אחד

תרגול 1 - מבוא לחשבון וקטורי

מבוא לחשבון וקטורי

דרגות חופש והצירים הניצבים

הגדרת וקטור והתכונות שלו

פעולות עם וקטורים

בעיה 1: שחיין חוצה נהר

בעיה 2: כריש רודף טרף

מערכות קואורדינטות שונות

תיאור קרטזי וקואורדינטות פולריות/גליליות

בעיה 3: מסלול ראלי

תרגול 2

שאלה 1

מציאת הזווית

מציאת וקטור היחידה בכיוון הווקטור השקול

שאלה 2

מציאת הסינוס והקוסינוס

חלק שני - מציאת וקטורים ניצבים

חלק שלישי: בסיסים וקטוריים ופריסת וקטורים

שאלה 3

שאלה 4 - קואורדינטות כדוריות

שאלה 5 - מרחק כתלות בזמן

חלק שלישי: תנועה במישור

חלק רביעי: המרחק בין שתי נקודות

חלק חמישי: תנועה במרחב ופונקציות וקטוריות של הזמן

דוגמה עם שתי סירות

חלק שישי: תנועה מעגלית וספירלית

חלק שביעי: מימדים ויחידות פיזיקליות

חלק שמיני: חישוב וקטור המהירות בתנועה מורכבת

תרגול 3 - מיקום, מהירות ותאוצה

3.1 מבוא לקינמטיקה

3.2 יחידות מדידה והסטנדרט הבינלאומי

3.2.1 הפיתוח של הסטנדרט הבינלאומי

3.2.2 ממדים ויחידות

3.2.3 ניתוח ממדים (Dimensional Analysis)

3.3 הגדרות בסיסיות בקינמטיקה

3.3.1 מיקום

3.3.2 מהירות

מהירות רגעית לעומת מהירות ממוצעת

3.3.3 תאוצה

תאוצה ממוצעת

3.3.4 דוגמה - התנהגות ברמזור

3.4 קינמטיקה בתלת-ממד

3.5 אינטגרציה: ממהירות למיקום

3.5.1 אינטגרציה של תנועה הרמונית

3.6 הפרשי מיקום ומהירות - יחסיות בתנועה

3.6.1 הפרשי מיקום

3.6.2 הפרשי מהירויות

3.7 תנועה יחסית - דוגמה ימית

3.7.1 יחידות מדידה ימיות

3.7.2 מערכות צירים ומדידת כיוונים

3.7.3 פתרון בעיית תנועה יחסית

ניתוח וקטורי של הבעיה

הגדרת מערכת הצירים

מציאת רכיבי הווקטורים

חישוב וקטור המהירות היחסית

חישוב גודל וכיוון המהירות היחסית

3.7.4 מסקנות פיזיקליות

3.8 תנועה מעגלית והרמונית

3.8.1 פרמטרים בסיסיים

זמן מחזור ($T$)

תדירות ($f$)

מהירות זוויתית ($\omega$)

3.8.2 תנועה הרמונית פשוטה

3.8.3 הפרמטרים $A$ ו-$B$ בתנועה מעגלית